Modeling transmission dynamics of lyme disease: Multiple vectors, seasonality, and vector mobility

Abstract

Lyme disease is the most prevalent tick-borne disease in the United States, which humans acquire from an infected tick of the genus Ixodes (primarily Ixodes scapularis). While previous studies have provided useful insights into various aspects of Lyme disease, the tick's host preference in the presence of multiple hosts has not been considered in the existing models. In this study, we develop a transmission dynamics model that includes the interactions between the primary vectors involved: blacklegged ticks (I. scapularis), white-footed mice (Peromyscus leucopus), and white-tailed deer (Odocoileus virginianus). Our model shows that the presence of multiple vectors may have a significant impact on the dynamics and spread of Lyme disease. Based on our model, we also calculate the basic reproduction number, ${\mathcal{R}}_0$, a threshold value that predicts whether a disease exists or dies out. Subsequent extensions of the model consider seasonality of the tick's feeding period and mobility of deer between counties. Our results suggest that a longer tick peak feeding period results in a higher infection prevalence. Moreover, while the deer mobility may not be a primary factor for short-term emergence of Lyme disease epidemics, in the long-run it can significantly contribute to local infectiousness in neighboring counties, which eventually reach the endemic steady state.

1. Introduction

Lyme disease is acknowledged as one of the most prevalent tick-borne infections in North America (Levi, Kilpatrick, Mangel, & Wilmers, 2012a, 2012b), for which approximately 30,000 cases are reported annually to the Centers for Disease Control and Prevention (CDC), yet data scientists claim that 300,000 may be a more accurate estimate (Kuehn, 2013). An untreated case of Lyme disease can result in serious joint pain and/or neurological problems, and chronic Lyme disease can become debilitating causing a tremendous decrease in quality of life. With the growing concern of ticks expanding their range due to climate change (Lou, Wu, & Wu, 2014; Magnarelli, Anderson, & Cartter, 1993), it is important to understand the details of the dynamics underlying the spread of Lyme disease. An increase in tick territory may correlate to an increase in Lyme disease incidence rates in the United States (Burtiset al., 2016). Investigating the interactions of the vectors associated with Lyme disease may aid in the efforts toward controlling the spread of the infection, and possible eradication of the disease.

A majority of the previous studies on Lyme disease (Anderson, Johnson, Magnarelli, & Hyde, 1985; Bosler, Ormiston, Coleman, Hanrahan, & Benach, 1984; Burgdorfer, Hayes, & Corwin, 1989; Falco & Fish, 1992; Glass, Amerasinghe, Morgan, & Scott, 1994; Magnarelli et al., 1993; Ostfeld, Miller, & Hazler, 1996; Weisbrod & Johnson, 1989) focused on the vectors involved in the spread of the bacterial agent responsible for the disease, the spirochete Borrelia burgdorferi (Schwan & Piesman, 2000), and related environmental factors. These earlier studies established that the white-footed mouse (Peromyscus leucopus) is one of the main vectors of Lyme disease and a competent reservoir of B. burgdorferi (Ostfeld et al., 1996). However, other studies (Magnarelli, Denicola, Stafford, & Anderson, 1995) have shown that the white-tailed deer (Odocoileus virginianus) can also be a principal vector of Lyme disease and may play a significant role in the ecology of this disease (Jordan, Schulze, & Jahn, 2007). In fact, fully matured female blacklegged ticks feed and mate on the deer (Ogden et al., 2007), and then the adult females detach from the deer and lay a large number of eggs (approximately 2000 eggs on average) shortly before dying (Randolph & Craine, 1995). Therefore, the white-tailed deer, with larger ranges, and the increasingly warm climate might allow for Lyme disease to spread to regions previously uninfected. Thus, modeling the role of white-tailed deer as a host of Lyme disease may be significant for the disease dynamics.

Many mathematical models use a single vector to predict Lyme disease prevalence (Keesing, Holt, & Ostfeld, 2006; Levi et al., 2012). Despite these progresses in the modeling of Lyme disease, the effects of multiple vector interactions and the tick's host preference have not been explored well. The main focus of this study is to get insights into the dynamics of the disease transmission based on the interactions of the tick, the mouse, and the deer; the white-footed mouse plays the role of the main source of the tick's blood meal at the first two life stages, larvae and nymph, while the white-tailed deer acts as the adult tick's final blood meal and site of its reproductive stage. We develop a mathematical model that considers the interactions between the key vectors involved in the spread of Lyme disease: blacklegged ticks (I. scapularis), white-footed mice (Peromyscus leucopus), and white-tailed deer (Odocoileus virginianus). We further extend our basic model to study the effects of seasonality of tick-feeding and spatial movement of deer on the disease epidemics. Using our models, we evaluate how vector-interactions, seasonality, and migration contribute to the exacerbation of the Lyme disease epidemics posing potential devastating impact on human health.

2. Method

2.1. Mathematical models

We first develop a basic mathematical model that incorporates interactions between multiple vectors of Lyme disease. The model is further extended to include the effects of seasonality of tick feeding and deaths as well as deer mating. Moreover, we develop a model to study how deer migration affects the spatial spread of Lyme disease.

2.1.1. Basic multiple-vector model

We consider the three separate life stages of the tick vector: larvae (L), nymphs (N), and adults (A). The nymph and adult tick populations are divided into mutually exclusive susceptible and infected classes, while the larvae have only one class without infection due to the lack of vertical transmission of the disease from adults to their eggs (Bosler et al., 1984). Similarly, the primary mammalian hosts, white-footed mice (M) and white-tailed deer (D), are divided into susceptible and infected classes. Thus, the model consists of five compartments of ticks ($L_s$, $N_s$, $N_i$, $A_s$, $A_i$), two compartments of mice ($M_s$, $M_i$) and two compartments of deer ($D_s$ and $D_i$), where the subscripts s and i stand for susceptible and infected, respectively.

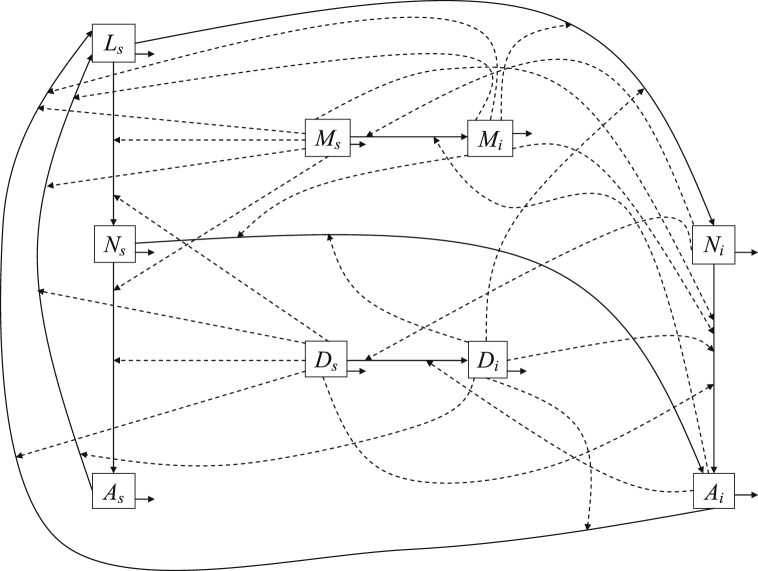
The interaction between the three vectors involved in the transmission dynamics of Lyme disease is complex, which particularly makes the model unique. Fig. 1 provides a schematic diagram for the fundamental design of the model. In this model we assume that the mice and the deer populations follow logistic growth with per capita growth rate $r_M$, and $r_D$, and carrying capacity $K_M$, and $K_D$, respectively. For the growth of the tick population, the adult females first get a blood meal from the hosts, either mice or deer with a scaling factor $b_A$ representing the adult tick's preference to deer compared to mice. $K_L$ represents the carrying capacity of hosts (mice or deer) to provide blood meals to adult ticks, and $r_L$ represents the per capita rate at which eggs are able to hatch from those adults who received a blood meal and become larvae. The larvae interact with the host, mice or deer, at a contact rate ${\beta }_L$ to become nymphs, with a scaling factor $b_L$ representing the ratio of larvae-deer interaction to the larvae-mice interaction. We also account for the intraspecies competition between larvae to become nymphs, which is represented by the ${\epsilon }_L{L}_s^2$ term (Keesing et al., 2006). Similarly, the nymphs interact with the host, mice or deer, at a contact rate ${\beta }_N$ and become adults, with a scaling factor $b_N$ representing the ratio of nymph-deer interaction to the nymph-mice interaction. ${\delta }_N$ and ${\delta }_A$ represent the natural death rates of nymphs and adults, respectively.

Fig. 1.

Schematic diagram, which outlines the vector and host interactions between the five tick compartments ($L_s$, $N_s$, $N_i$, $A_s$, $A_i$) and the four host compartments ($M_s$, $M_i$, $D_s$, $D_i$). The dashed arrows represent tick and host interactions, resulting in tick maturation, and they also represent infectious ticks spreading B. burgdorferi to hosts. The solid arrows represent transitions between compartments and natural loss from a compartment.

In this transmission dynamics, among the total larvae that infest the infected hosts, ${\beta }_L{L}_s\left(M_i+b_L{D}_i\right)$, the proportion ${\psi }_N$ becomes infected nymphs, while among the total nymphs that quest the infected hosts, ${\beta }_N{N}_s\left(M_i+b_N{D}_i\right)$, the proportion ${\psi }_A$ becomes infected adults. Susceptible mice become infected when they interact with infected nymphs and infected adults at a rate ${\beta }_{NM}$ and ${\beta }_{AM}$, respectively. Similarly, susceptible deer become infected when they interact with infected nymphs and infected adults at a rate ${\beta }_{ND}$ and ${\beta }_{AD}$, respectively. With these interactions (Fig. 1), the transmission dynamics of Lyme disease can be described as the following nine-dimensional system of ODEs.

$$\begin{array}{c}\frac{d{L}_s}{dt}=r_L\left(A_s+A_i\right)\left(\left(M_s+M_i\right)+b_A\left(D_s+D_i\right)\right)\left(1-\frac{\left(A_s+A_i\right)}{K_L\left(\left(M_s+M_i\right)+b_A\left(D_s+D_i\right)\right)}\right)\\ -{\beta }_L{L}_s\left(\left(M_s+M_i\right)+b_L\left(D_s+D_i\right)\right)-{\epsilon }_L{L}_s^2,\\ \frac{d{N}_s}{dt}={\beta }_L{L}_s\left(M_s+b_L{D}_s\right)+\left(1-{\psi }_N\right){\beta }_L{L}_s\left(M_i+b_L{D}_i\right)\\ -{\beta }_N{N}_s\left(\left(M_s+M_i\right)+b_N\left(D_s+D_i\right)\right)-{\delta }_N{N}_s,\\ \frac{d{N}_i}{dt}={\psi }_N{\beta }_L{L}_s\left(M_i+b_L{D}_i\right)-{\beta }_N{N}_i\left(\left(M_s+M_i\right)+b_N\left(D_s+D_i\right)\right)-{\delta }_N{N}_i,\\ \frac{d{A}_s}{dt}={\beta }_N{N}_s\left(M_s+b_N{D}_s\right)+\left(1-{\psi }_A\right){\beta }_N{N}_s\left(M_i+b_N{D}_i\right)-{\delta }_A{A}_s,\\ \frac{d{A}_i}{dt}={\psi }_A{\beta }_N{N}_s\left(M_i+b_N{D}_i\right)+{\beta }_N{N}_i\left(\left(M_s+M_i\right)+b_N\left(D_s+D_i\right)\right)-{\delta }_A{A}_i,\\ \frac{d{M}_s}{dt}=r_M\left(M_s+M_i\right)\left(1-\frac{M_s}{K_M}\right)-{\beta }_{NM}{M}_s{N}_i-{\beta }_{AM}{M}_s{A}_i,\\ \frac{d{M}_i}{dt}={\beta }_{NM}{M}_s{N}_i+{\beta }_{AM}{M}_s{A}_i-r_M\left(M_s+M_i\right)\left(\frac{M_i}{K_M}\right),\\ \frac{d{D}_s}{dt}=r_D\left(D_s+D_i\right)\left(1-\frac{D_s}{K_D}\right)-{\beta }_{ND}{D}_s{N}_i-{\beta }_{AD}{D}_s{A}_i,\\ \frac{d{D}_i}{dt}={\beta }_{ND}{D}_s{N}_i+{\beta }_{AD}{D}_s{A}_i-r_D\left(D_s+D_i\right)\left(\frac{D_i}{K_D}\right).\end{array}$$ (1)

2.1.2. Seasonality model

The basic multiple-vector model developed above assumes that each of the parameters is constant. However, some parameters can be time-varying due to seasonal effects, including seasonal tick-feeding behaviors. In particular, the interactions between nymphal ticks and the two vertebrate hosts are largest during the months of June and July (Randolph, Miklisová, Lysy, Rogers, & Labuda, 1999), indicating the time-dependence of ${\beta }_{NM}$ and ${\beta }_{ND}$. Similarly, the peak feeding period for adult ticks (Randolph et al., 1999) is throughout October and November, implying the time-dependency of ${\beta }_{AM}$ and ${\beta }_{AD}$. Also, the white-tailed deer mate during what is often called the rut, which takes place in the fall (Green et al., 2017). After a gestation period of seven months, deer give birth to fawns in the months of May and June (Sparrowe & Springer, 1970). This behavior can be modeled by letting $r_D$ be time-dependent. Moreover, the death rates ${\delta }_N$ and ${\delta }_A$ can be time-varying as a higher death rate for each tick compartment occurs during the winter months (Ghosh & Pugliese, 2004).

To study how the seasonal variation impacts Lyme disease dynamics, we extend our basic multiple-vector model to a seasonality model by taking parameters ${\beta }_{NM}$, ${\beta }_{ND}$, ${\beta }_{AM}$, ${\beta }_{AD}$, $r_D$, ${\delta }_N$, and ${\delta }_A$ as time-dependent periodic functions of a period τ, usually taken as 1 year. Since tick-host interactions, tick feeding and deer birthing take place in a short period of the year, we take ${\beta }_{NM}\left(t\right)$, ${\beta }_{ND}\left(t\right)$, ${\beta }_{AM}\left(t\right)$, ${\beta }_{AD}\left(t\right)$, and $r_D\left(t\right)$ as a step function for each period. However, a higher tick death occurs for a longer period of a year. Therefore, we use cosine functions to represent seasonal death rates of nymphal and tick adults. We use the following formula for the seasonality model.

$${\beta }_j\left(t\right)=\{\begin{array}{l}{\overline{\beta }}_j,n\tau +t_j^a\le t\le n\tau +t_j^b,\hfill \\ 0,\text{otherwise},\hfill \end{array}n=\mathrm{0,1,2},\dots ,$$ (2)

for each $j=NM,ND,AM,AD$.

$$r_D\left(t\right)=\{\begin{array}{l}{\overline{r}}_D,n\tau +t_D^a\le t\le n\tau +t_D^b,\hfill \\ 0,\text{otherwise},\hfill \end{array}n=\mathrm{0,1,2},\dots ,$$ (3)

$${\delta }_j\left(t\right)={\overline{\delta }}_j+{\omega }_j\text{cos}\frac{2\pi }{\tau }\left(t+\varphi \right),$$ (4)

for each $j=N,A$.

2.1.3. Migration model

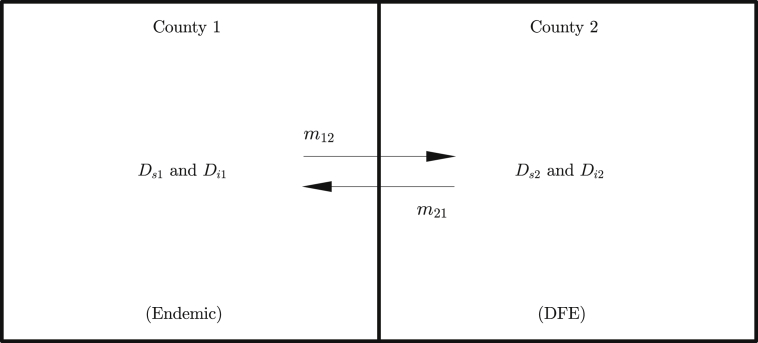
The growing spatial spread of Lyme disease has been a serious concern to public health. It is known that both ticks and mice are not able to travel long distances, while deer travel between two neighboring counties (Glass et al., 1994). To study how the mobility of dear can have an impact on the spatial spread of Lyme disease, we develop a migration model, which incorporates mobility of deer between two neighboring counties. We initialize the dynamics with County-1 in an endemic state and County-2 in a disease free state (Fig. 2), and observe how Lyme disease spreads from the county with the endemic state to the disease free county.

Fig. 2.

Schematic diagram of deer migration between Counties 1 and 2.

Deer move from County-1 to County-2 with a migration rate $m_{12}$ and from County-2 to County-1 with a migration rate $m_{21}$. Since ticks and mice have very limited mobility, we assume these populations do not move between counties. The equations representing their dynamics in each county remain the same as the basic multiple-vector model. The only hosts that are mobile between counties are deer, and their population in County-1 ($D_{s1}$, $D_{i1}$) and in County-2 ($D_{s2}$, $D_{i2}$) are modeled using the following differential equations.

$$\begin{array}{c}\frac{d{D}_{s1}}{dt}=r_D\left(D_{s1}+D_{i1}\right)\left(1-\frac{D_{s1}}{K_D}\right)-{\beta }_{ND}{D}_{s1}{N}_{i1}-{\beta }_{AD}{D}_{s1}{A}_{i1}-m_{12}{D}_{s1}+m_{21}{D}_{s2},\\ \frac{d{D}_{i1}}{dt}={\beta }_{ND}{D}_{s1}{N}_{i1}+{\beta }_{AD}{D}_{s1}{A}_{i1}-r_D\left(D_{s1}+D_{i1}\right)\left(\frac{D_{i1}}{K_D}\right)-m_{12}{D}_{i1}+m_{21}{D}_{i2},\\ \frac{d{D}_{s2}}{dt}=r_D\left(D_{s2}+D_{i2}\right)\left(1-\frac{D_{s2}}{K_D}\right)-{\beta }_{ND}{D}_{s2}{N}_{i2}-{\beta }_{AD}{D}_{s2}{A}_{i2}-m_{21}{D}_{s2}+m_{12}{D}_{s1},\\ \frac{d{D}_{i2}}{dt}={\beta }_{ND}{D}_{s2}{N}_{i2}+{\beta }_{AD}{D}_{s2}{A}_{i2}-r_D\left(D_{s2}+D_{i2}\right)\left(\frac{D_{i2}}{K_D}\right)-m_{21}{D}_{i2}+m_{12}{D}_{i1}.\end{array}$$ (5)

2.2. Parameter estimation

We estimated model parameters using the information from literature sources (Batzli, 1977; Bosler et al., 1984; Daniels, Falco, & Fish, 2000; Goodwin, Ostfeld, & Schauber, 2001; Keesing et al., 2006; Lindsay et al., 1995; LoGiudice, Ostfeld, Schmidt, & Keesing, 2003; Madhav, Brownstein, Tsao, & Fish, 2004; Verme, 1969). The populations presented are in units of per hectare (ha). The basic multiple-vector model contains 18 kinetic parameters. The parameters associated with the population dynamics, such as growth and carrying capacity, are found directly from the literature. However, contact rates are estimated from the known infected populations of deer and mice, where Lyme disease is endemic (Daniels et al., 2000; Madhav et al., 2004).

The growth rates of P. leucopus and O. virginianus are known to be $r_M=0.05$ mice/ha/day (Batzli, 1977) and $r_D=0.00548$ deer/ha/day (Verme, 1969). The estimated growth rate, $r_M=0.05$ mice/ha/day, was calculated using the ratio of the average number of offspring each mouse is able to produce per 100 days, while the growth rate, $r_D=0.0056$ deer/ha/day, was estimated using the ratio of the number of fawns each doe is able to produce per 365 days. The growth rate $r_L$, for the larval tick, was calculated by taking the ratio of the number of eggs that survive to the larval stage to the number of eggs that a female I. scapularis lays (Lindsay et al., 1995), and dividing this value by 730 days (two years based on the tick life-cycle). As a result, we obtained $r_L\approx 0.0012$ larvae/ha/day.

Although mice are considered the primary reservoirs for the disease, it is known that other rodents contribute to the spread of the disease (Salkeld & Lane, 2010). Assuming mice make up roughly 40% of the rodent population, we scaled the average number of mice per hectare by 2.5. On average, there are 20 P. leucopus per hectare (Madhav et al., 2004); thus, we assume a steady-state rodent population to be 50. In addition, Madhav et al. (Madhav et al., 2004) found that there are 0.25 O. virginianus per hectare, which we assumed to be the steady-state deer population. These steady-state values were used as the estimates for carrying capacities, i.e., $K_M=50$ mice/ha and $K_D=0.25$ deer/ha, for our logistic growth dynamics. Madhav et al. (Madhav et al., 2004) found the annual mortality rates of 81% and 98% for nymphs and adults, respectively, which imply the death rates of the nymphs and adult ticks to be ${\delta }_N=0.0022$ number of nymphs/ha/day and ${\delta }_A=0.0027$ number of adults/ha/day, respectively. The parameter ${\epsilon }_L=1.241\times {10}^{-8}$ Larvae/ha/day, which accounts for the intraspecies competition between larvae causing deaths of those who are unable to obtain a blood meal, was taken from Keesing et al. (Keesing et al., 2006).

Note that the parameters $b_L$, $b_N$, and $b_A$ represent ratios of tick-mice interactions to tick-deer interaction, thereby quantifying the I. scapularis host preference. In order to estimate these values, we take the ratio of the number of successful tick blood meals that come from deer versus those that come from mice. Daniels et al. (2000) found that, per hectare, there are approximately 115,000 larval I. scapularis, 13,000 nymphs, and 3300 adults. Also, Madhav et al. (2004) found that approximately 9.45 larval ticks are present on each mouse, whereas 169.32 larvae are found on one deer. We scale 9.45 by 50 in order to find 472.5 larval ticks on rodents per hectare. Since there are 0.25 deer per hectare, we scale the number of larvae found on deer, resulting in 42.33 larvae on deer per hectare. This implies that the total number of larvae found per hectare is 514.83. In order to find the number of successful larval blood meals that come from mice, we take the expected number of nymphal ticks per hectare and multiply this by the percentage of larvae feeding on rodents. We do the same calculation for deer and then compute the ratio of the two values (deer/mice) in order to obtain $b_L=0.089$. With the calculation in a similar fashion, we obtain $b_N=0.003$ and $b_A=3.983$.

While a large number of the parameters are based on literature values, there are some parameters, especially contact rates and infection rates, which are not available. To estimate these rates, we use the steady-states of our model combined with field survey data containing the steady state population and disease endemic states. We discuss the estimates of contact rates and infection rates in Section 3. All the model parameters are provided in Table 1.

Table 1.

Parameter values for basic model, System (1).

Parameter	Value	Units	Source(s)
$b_L$	0.089	Unitless	(Daniels et al., 2000; Madhav et al., 2004)
$b_N$	0.003	Unitless	(Daniels et al., 2000; Madhav et al., 2004)
$b_A$	3.982	Unitless	(Daniels et al., 2000; Madhav et al., 2004)
$r_L$	0.0012	Larvae/ha/Day	Lindsay et al. (1995)
$r_M$	0.05	Mice/ha/Day	Batzli (1977)
$r_D$	0.0055	Deer/ha/Day	Verme (1969)
${\beta }_L$	6.55 $\times {10}^{-6}$	Larvae/ha/(Hosts Day)	Computed
${\beta }_N$	1.36 $\times {10}^{-5}$	Nymphs/ha/(Hosts Day)	Computed
${\epsilon }_L$	$1.24\times {10}^{-8}$	Larvae/ha/Day	Keesing et al. (2006)
${\beta }_{NM}$	2.25 $\times {10}^{-6}$	Nymphs/ha/(Mice Day)	Computed
${\beta }_{AM}$	9.03 $\times {10}^{-6}$	Adults/ha/(Mice Day)	Computed
${\beta }_{ND}$	3.04 $\times {10}^{-7}$	Nymphs/ha/(Deer Day)	Computed
${\beta }_{AD}$	3.38 $\times {10}^{-7}$	Adults/ha/(Deer Day)	Computed
${\delta }_N$	0.0022	Nymphs/ha/Day	Madhav et al. (2004)
${\delta }_A$	0.0027	Adults/ha/Day	Madhav et al. (2004)
$K_L$	115,000	Larvae/ha	Daniels et al. (2000)
$K_M$	50	Mice/ha	LoGiudice et al. (2003)
$K_D$	0.25	Deer/ha	LoGiudice et al. (2003)

3. Results

3.1. Vector-host interaction and Lyme disease infection

In our model, vector-host interactions are represented by parameters ${\beta }_L$ and ${\beta }_N$, while the disease infection is determined by ${\psi }_N$, ${\psi }_A$, ${\beta }_{NM}$, ${\beta }_{AM}$, ${\beta }_{ND}$, and ${\beta }_{AD}$. To understand these important parameters better, we use steady state formulation of our model along with field survey data (Table 2) and compute these rates properly. According to previous studies (Caraco et al., 2002; Wang & Zhao, 2017), the larvae and nymphs, which become nymphs and adults, respectively, after successful interaction with infected mice or infected deer, have an extremely high likelihood of becoming infected (more than 90%). With these levels of probability, our model predicted negligible effects on the biological conclusions when ${\psi }_N<1$ and ${\psi }_A<1$ were used instead of ${\psi }_N=1$ and ${\psi }_A=1$. Therefore, we consider ${\psi }_N=1$ and ${\psi }_A=1$ in the model analyses and simulations presented below.

Table 2.

Equilibria for compartment population values for basic model. Populations for both the disease-free equilibrium and endemic equilibrium are given with references.

Compartment	DFE	Endemic	Reference
$L_{ES}$	115,000	115,000	Daniels et al. (2000)
$N_{ES}$	13,000	8,320	(Daniels et al., 2000; Goodwin et al., 2001)
$N_{EI}$	0	4,680	(Daniels et al., 2000; Goodwin et al., 2001)
$A_{ES}$	3,300	1,155	(Daniels et al., 2000; Goodwin et al., 2001)
$A_{EI}$	0	2,145	(Daniels et al., 2000; Goodwin et al., 2001)
$M_{ES}$	50	31.5	(Bosler et al., 1984; LoGiudice et al., 2003)
$M_{EI}$	0	18.5	(Bosler et al., 1984; LoGiudice et al., 2003)
$D_{ES}$	0.25	0.18	(Bosler et al., 1984; LoGiudice et al., 2003)
$D_{EI}$	0	0.07	(Bosler et al., 1984; LoGiudice et al., 2003)

Using $N_i=A_i=M_i=D_i=0$ in the model, we obtain the disease free equilibrium (DFE) as follows:

$$\begin{array}{c}{L}_{E0}=\frac{-{\beta }_L{K}_L\left(K_M+b_L{K}_D\right)+\sqrt{c_1}}{2{\epsilon }_L{K}_L},\\ N_{E0}=\frac{{\beta }_L{L}_{E0}\left(K_M+b_L{K}_D\right)}{{\beta }_N\left(K_M+b_N{K}_D\right)+{\delta }_N},\\ A_{E0}=\frac{{\beta }_N{N}_{E0}\left(K_M+b_N{K}_D\right)}{{\delta }_A},\\ M_{E0}=K_M,\\ D_{E0}=K_D,\end{array}$$ (6)

where

$$\begin{array}{c}{c}_1={\left(b_L{\beta }_L{K}_L{K}_D\right)}^2+4r_L{b}_A{\epsilon }_L{K}_L^2{K}_D{A}_{E0}+2b_L{\beta }_L^2{K}_L^2{K}_M{K}_D\\ +4r_L{\epsilon }_L{K}_L^2{K}_M{A}_{E0}+{\left({\beta }_L{K}_L{K}_M\right)}^2-4r_L{\epsilon }_L{K}_L{A}_{E0}^2.\end{array}$$ (7)

Now, substituting the parameter values estimated from the literature (Table 1) and the DFE values of larvae, nymph, and adult population obtained from the field survey (Table 2) in Eq. (6), we obtain a value of ${\beta }_N=1.36\times {10}^{-5}$ nymphs/ha/hosts/day and a value of ${\beta }_L=6.56\times {10}^{-6}$ larvae/ha/hosts/day. These estimates show that the interactions between ticks and hosts are higher during the nymphal stage than the larval stage of the tick's life cycle.

Next, we formulate the endemic state equilibrium to calculate the infection rates, ${\beta }_{NM}$, ${\beta }_{ND}$, ${\beta }_{AM}$, and ${\beta }_{AD}$. From our model equations, we find that the mice and deer populations at the disease endemic state, $M_{ES}$, $M_{EI}$, $D_{ES}$, and $D_{EI}$, are obtained by solving the following nonlinear system of four algebraic equations:

$$\begin{array}{c}{M}_{ES}=\frac{-{\beta }_{AM}{K}_M{A}_{EI}-{\beta }_{NM}{K}_M{N}_{EI}+r_M{K}_M-r_M{M}_{EI}+\sqrt{c_2}}{2r_M},\\ M_{EI}=\frac{-r_M{M}_{ES}+\sqrt{r_M{M}_{ES}\left(4K_M\left({\beta }_{NM}{N}_{EI}+{\beta }_{AM}{A}_{EI}\right)+r_M{M}_{ES}\right)}}{2r_M},\\ D_{ES}=\frac{-{\beta }_{AD}{K}_D{A}_{EI}-{\beta }_{ND}{K}_D{N}_{EI}+r_D{K}_D-r_D{D}_{EI}+\sqrt{c_3}}{2r_D},\\ D_{EI}=\frac{-r_D{D}_{ES}+\sqrt{r_D{D}_{ES}\left(4K_D\left({\beta }_{ND}{N}_{EI}+{\beta }_{AD}{A}_{EI}\right)+r_D{D}_{ES}\right)}}{2r_D},\end{array}$$ (8)

where

$$\begin{array}{c}{c}_2={\left({\beta }_{AM}{K}_M{A}_{EI}+{\beta }_{NM}{K}_M{N}_{EI}\right)}^2+2{\beta }_{AM}{r}_M{K}_M{A}_{EI}\left(-2K_M+M_{EI}\right)\\ +2{\beta }_{NM}{r}_M{K}_M{N}_{EI}\left(-2K_M+M_{EI}\right)+{\left(r_M{K}_M+r_M{M}_{EI}\right)}^2,\\ c_3={\left({\beta }_{AD}{K}_D{A}_{EI}+{\beta }_{ND}{K}_D{N}_{EI}\right)}^2+2{\beta }_{AD}{r}_D{K}_D{A}_{EI}\left(-2K_D+D_{EI}\right)\\ +2{\beta }_{ND}{r}_D{K}_D{N}_{EI}\left(-2K_D+D_{EI}\right)+{\left(r_D{K}_D+r_D{D}_{EI}\right)}^2.\end{array}$$

We now use the parameter values estimated from the literature (Table 1) and the disease endemic values of nymph and adult populations obtained from the field survey (Table 2), and solve the System (8) using iterative methods in Maple. Our computations result in the values of host-specific Lyme disease infection rates to be ${\beta }_{NM}=2.25\times {10}^{-6}$ Nymphs/ha/(Mice.Day), ${\beta }_{ND}=3.04\times {10}^{-7}$ Nymphs/ha/(Dear.Day), ${\beta }_{AM}=9.03\times {10}^{-6}$ Adults/ha/(Mice.Day), and ${\beta }_{AD}=3.38\times {10}^{-7}$ Adults/ha/(Mice.Day) (Table 1). From these estimates, we found that the hosts have a higher rate of being infected from adult ticks than nymphs. Also, these rates are higher for mice than deer.

3.2. Basic reproduction number

In epidemiology, the basic reproduction number, ${\mathcal{R}}_0$, is an extremely important threshold value as it can predict whether epidemics can occur. ${\mathcal{R}}_0$ is defined as the average number of secondary cases that is caused by an infected individual, introduced into an entirely susceptible population, during the infectious period (Bacaër, 2007). If ${\mathcal{R}}_0<1$, then the disease stops spreading and eventually dies out, and if ${\mathcal{R}}_0>1$, then there is an outbreak of the disease (Diekmann, Heesterbeek, & Roberts, 2010; van den Driessche & Watmough, 2002). ${\mathcal{R}}_0$ may be affected by several different factors, including the contact rates among the host populations, the probability of infection through contact, and the period of infectiousness.

We compute ${\mathcal{R}}_0$ of our model using the next-generation operator method (NGM) ((Diekmann et al., 2010; van den Driessche & Watmough, 2002)). In order to find the ${\mathcal{R}}_0$ of an epidemiological model, by using the NGM, we need to consider only the equations pertaining to the infectious states, ${\overrightarrow{x}}_i={\left(N_i,A_i,M_i,D_i\right)}^T$. These equations from System (1), linearized about the DFE, results in the following system:

$$\frac{d}{dt}{\overrightarrow{x}}_i={\mathbf{J}}_i{\overrightarrow{x}}_i,$$ (9)

where the Jacobian matrix ${\mathbf{J}}_i$ is given by

$${\mathbf{J}}_i=\left(\begin{array}{cccc}-{\beta }_N\left(K_M+b_N{K}_D\right)-{\delta }_N& 0& {\beta }_L{L}_{S0}& {\beta }_L{b}_L{L}_{S0}\\ {\beta }_N\left(K_M+b_N{K}_D\right)& -{\delta }_A& {\beta }_N{N}_{S0}& {\beta }_N{b}_N{N}_{S0}\\ {\beta }_{NM}{K}_M& {\beta }_{AM}{K}_M& -r_M& 0\\ {\beta }_{ND}{K}_D& {\beta }_{AD}{K}_D& 0& -r_D\end{array}\right).$$ (10)

Now, we define ${\mathbf{J}}_i$  = F - V, where F is the transmission matrix and V is the transition matrix. The transmission matrix describes the births of new infections, while the transition matrix describes the changes of state of the individuals (e.g., death/removal from the system).

$$\text{F}=\left(\begin{array}{cccc}0& 0& {\beta }_L{L}_{S0}& {\beta }_L{b}_L{L}_{S0}\\ {\beta }_N\left(K_M+b_N{K}_D\right)& 0& {\beta }_N{N}_{S0}& {\beta }_N{b}_N{N}_{S0}\\ {\beta }_{NM}{K}_M& {\beta }_{AM}{K}_M& 0& 0\\ {\beta }_{ND}{K}_D& {\beta }_{AD}{K}_D& 0& 0\end{array}\right),$$ (11)

and

$$\text{V}=\left(\begin{array}{cccc}{\beta }_N\left(K_M+b_N{K}_D\right)+{\delta }_N& 0& 0& 0\\ 0& {\delta }_A& 0& 0\\ 0& 0& r_M& 0\\ 0& 0& 0& r_D\end{array}\right).$$ (12)

These matrices give

$$\mathbf{F}{\mathbf{V}}^{-1}=\left(\begin{array}{cccc}0& 0& \frac{{\beta }_L{L}_{S0}}{r_M}& \frac{{\beta }_L{b}_L{L}_{S0}}{r_D}\\ \frac{{\beta }_N\left(K_M+b_N{K}_D\right)}{{\beta }_N\left(K_M+b_N{K}_D\right)+{\delta }_N}& 0& \frac{{\beta }_N{N}_{S0}}{r_M}& \frac{{\beta }_N{b}_N{N}_{S0}}{r_D}\\ \frac{{\beta }_{NM}{K}_M}{{\beta }_N\left(K_M+b_N{K}_D\right)+{\delta }_N}& \frac{{\beta }_{AM}{K}_M}{{\delta }_A}& 0& 0\\ \frac{{\beta }_{ND}{K}_D}{{\beta }_N\left(K_M+b_N{K}_D\right)+{\delta }_N}& \frac{{\beta }_{AD}{K}_D}{{\delta }_A}& 0& 0\end{array}\right).$$ (13)

The basic reproduction number is given by the spectral radius of the matrix in Eq. (13), i.e., ${\mathcal{R}}_0=\rho \left(\mathbf{F}{\mathbf{V}}^{-1}\right)$.

Using the parameter values given in Table 1, we estimate the basic reproduction number of Lyme disease to be ${\mathcal{R}}_0=1.28$. Considering our parameters are based on an endemic steady state, it is expected that ${\mathcal{R}}_0>1$. Our estimate is consistent with the range of ${\mathcal{R}}_0$ values estimated in previous studies (Hartemink, Randolph, Davis, & Heesterbeek, 2008), where $0\le {\mathcal{R}}_0<5$, depending on the fraction of blood meals on competent hosts.

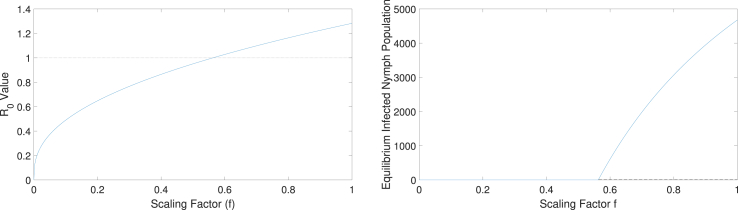
To better understand ${\mathcal{R}}_0$ and related stability of the two equilibria, endemic and disease-free, we now introduce a scaling factor f on the host-specific infection rates ${\beta }_{NM}$, ${\beta }_{ND}$, ${\beta }_{AM}$, and ${\beta }_{AD}$. Note that the scaling factor f can be used to study control measures that alter these infection rates. Applying ${\beta }_{NM}\to f{\beta }_{NM}$, ${\beta }_{ND}\to f{\beta }_{ND}$, ${\beta }_{AM}\to f{\beta }_{AM}$, and ${\beta }_{AD}\to f{\beta }_{AD}$ to our model, we computed the basic reproduction number ${\mathcal{R}}_0$ for the values of f from 0 to 1. We found that ${\mathcal{R}}_0$ is less than 1 when f is less than 0.56; otherwise, ${\mathcal{R}}_0$ is greater than 1 (Fig. 3, left). For these values of f, we performed local stability analysis of equilibria numerically. As presented in a bifurcation diagram for infected nymph populations (Fig. 3, right), we found that for a value of $f<0.56$ (i.e., ${\mathcal{R}}_0<1$), the only equilibrium that exists is the DFE, and it is stable. For $f>0.56$ (i.e., ${\mathcal{R}}_0>1$), two equilibria exist, with the DFE being unstable and the endemic equilibrium being stable. This behavior, which is typical of a transcritical bifurcation, confirms ${\mathcal{R}}_0$ to be a threshold for the disease outbreak. The results suggest that one control measure for Lyme disease may involve limiting the contact of ticks and hosts to less than 56%.

Fig. 3.

(Left) The variation of the ${\mathcal{R}}_0$ value as the host-specific infection rates ${\beta }_{NM}$, ${\beta }_{ND}$, ${\beta }_{AM}$, and ${\beta }_{AD}$ are scaled by a factor f, which ranges from 0 to 1. The dotted line represents the threshold value for the existence of the disease (i.e., ${\mathcal{R}}_0=1$). For $f<0.56$, ${\mathcal{R}}_0$ is less than 1, and when $f>0.56$, ${\mathcal{R}}_0$ is greater than 1. (Right) Bifurcation diagram with the scaling factor f as a bifurcation parameter. For $f<0.56$, $N_i=0$ is the only equilibrium value for infected nymph population and this DFE is stable. For $f>0.56$, two equilibria $N_i=0$ and $N_i=N_i^{\text{*}}>0$ exist with $N_i=0$ being stable and $N_i=N_i^{\text{*}}$ being unstable, showing a shift of stability from the DFE to the endemic equilibrium.

3.3. Long-term disease outcomes: base case

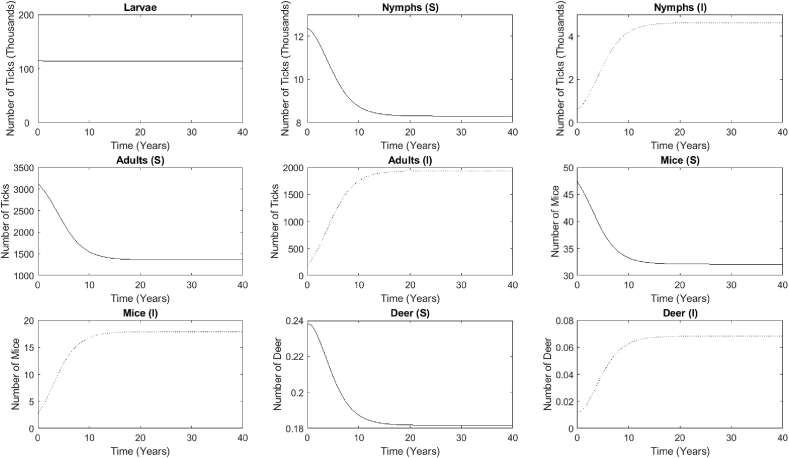
We investigate the long-term disease outcome predicted by the basic multiple-vector model (System (1)) using the parameters given in Table 1. We set the initial conditions to reflect 5% of the infected population for each of the nymphal and adult ticks, mice, and deer compartments, which are all scaled per hectare. The long-term dynamics of each compartment (Fig. 4) indicate that the system eventually reaches an endemic steady state at the values consistent with field studies (Table 2). The model predicts that the number of larvae does not change over time, remaining constant at 115,000 per ha. The nymph population changes over time, with the susceptible population decreasing to 8,322 per ha and the infected population increasing to 4,678 per ha. The nymph compartments eventually reach the endemic equilibrium after approximately 20 years, with the infected individuals higher than the initial number. The adult, mice, and deer compartments exhibit similar patterns, with the gradual increase of the initial infected numbers, which converge to an endemic state in the long run. The susceptible populations decrease to 1352, 32, and 0.18 per ha for the adults, mice, and deer, respectively, while the infected populations increase to 1948, 18, and 0.07 per ha for the adults, mice, and deer, respectively. Similar to the nymph compartments, the adults, mice, and deer compartments approach the endemic steady state after approximately 20 years.

Fig. 4.

The long-term dynamics of the populations in each compartment predicted by the base model, which converges to an endemic steady state after approximately 20 years. The larval tick population of 115,000 does not change over time, but each of the other populations do. The susceptible compartments for the nymphs, adults, mice, and deer decrease to 8322, 1352, 32, and 0.18, respectively. The infected compartments for the nymphs, adults, mice, and deer increase to 4678, 1948, 18, and 0.07, respectively.

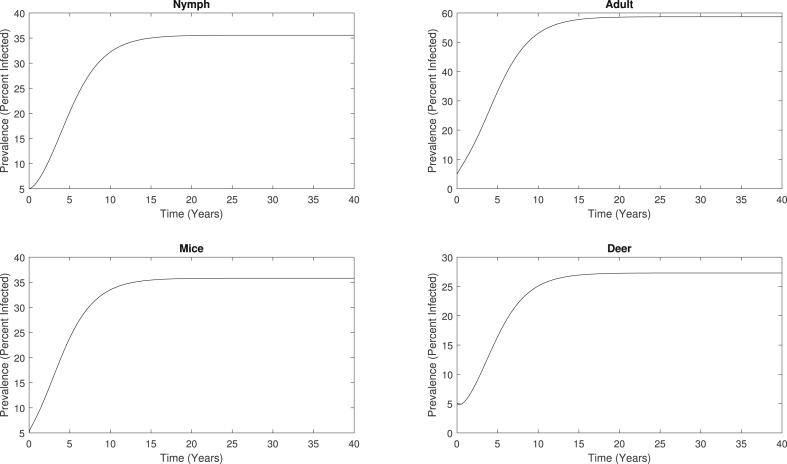
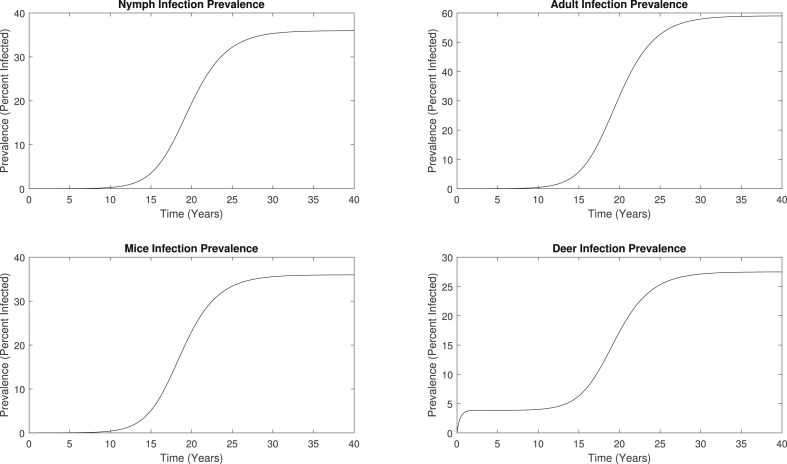
With these dynamics, we calculate the infection prevalences of nymphs, adult ticks, mice, and deer, which is defined as the percentage of the number of infected individuals out of the total number of individuals. The evolution of the infection prevalence for each of the four compartments is shown in Fig. 5, which all exhibit similar patterns to the infected population curves in Fig. 4. The infection prevalences are initially at 5%, and once the system reaches the endemic steady state, the infection prevalence of nymphs, adults, mice, and deer are approximately 35.6%, 58.7%, 35.8%, and 27.3%, respectively. These levels of infection prevalence are consistent with previous studies (Bosler et al., 1984; Goodwin et al., 2001).

Fig. 5.

Infection prevalences of nymphs, adults, mice, and deer predicted by the basic multiple-vector model, which converges to an endemic steady state. The percent of infected individuals increases from 5% to approximately 35.6%, 58.7%, 35.8%, and 27.3% for nymphs, adults, mice, and deer, respectively.

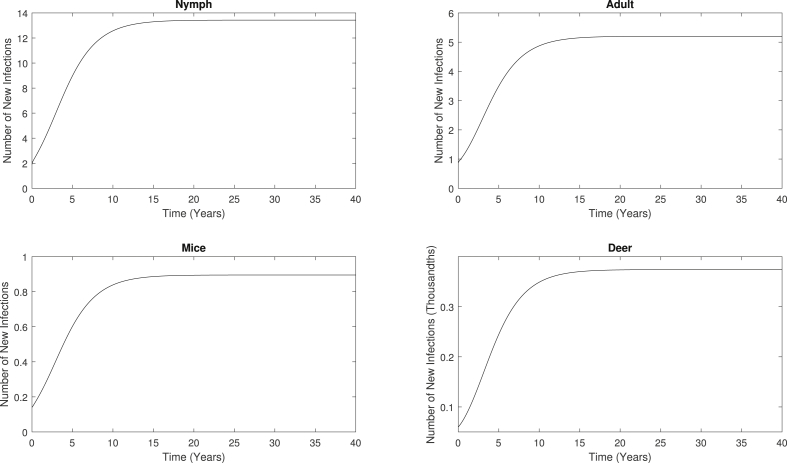
We also compute the rate of new infections generated for each of the four infected types (Fig. 6). We calculate these values by considering only the positive terms in each of the four ODEs in System (1) that correspond to the infected classes ($N_i$, $A_i$, $M_i$, and $D_i$), as the positive terms represent the new infections. After the system reaches the endemic steady state after 20 years, the annual rate of new infections increases from 1.89 to 13.43, 0.87 to 5.2, 0.14 to 0.895, and 0.00006 to 0.00037 per ha for nymphs, adults, mice, and deer, respectively. Furthermore, the total number of new infections starting at time, $t_0$, generated in a year is given by System (14):

$$\begin{array}{c}\text{Total}\text{No}.\text{of}\text{Nymphs}=\underset{t_0}{\overset{t_0+365}{\int }}{\beta }_L{L}_s\left(t\right)\left(M_i\left(t\right)+b_L{D}_i\left(t\right)\right)dt,\\ \text{Total}\text{No}.\text{of}\text{Adults}=\underset{t_0}{\overset{t_0+365}{\int }}\left({\beta }_N{N}_s\right(t\left)\right(M_i\left(t\right)+b_N{D}_i\left(t\right))\\ +{\beta }_N{N}_i\left(t\right)\left(\right(M_s\left(t\right)+M_i\left(t\right))+b_N(D_s\left(t\right)+D_i\left(t\right)\left)\right))dt,\\ \text{Total}\text{No}.\text{of}\text{Mice}=\underset{t_0}{\overset{t_0+365}{\int }}\left({\beta }_{NM}{M}_s\left(t\right)N_i\left(t\right)+{\beta }_{AM}{M}_s\left(t\right)A_i\left(t\right)\right)dt,\\ \text{Total}\text{No}.\text{of}\text{Deer}=\underset{t_0}{\overset{t_0+365}{\int }}\left({\beta }_{ND}{D}_s\left(t\right)N_i\left(t\right)+{\beta }_{AD}{D}_s\left(t\right)A_i\left(t\right)\right)dt.\end{array}$$ (14)

Fig. 6.

Rate of new infections generated of nymphs, adults, mice, and deer as the system converges to an endemic steady state. After the system reaches the endemic equilibrium, approximately 20 years, the rate of new infections for nymphs, adults, mice, and deer increase from 1.89 to 13.43, 0.87 to 5.2, 0.14 to 0.895, and 0.00006 to 0.00037 for nymphs, adults, mice, and deer, respectively.

When System (14) uses the parameter values from Table 1 and the endemic equilibrium compartmental values, we are simply integrating a constant. The calculated annual total number of new infections at the endemic steady state are approximately 4902, 1898, 327, and 0.14 per ha for nymphs, adults, mice, and deer, respectively.

3.4. Effect of seasonality

In this section we examine the effects of seasonality on Lyme disease dynamics using our seasonality model in which some parameters are introduced as time-dependent periodic functions (Eqs. (2)–(4)). Since the peak feeding period for nymphal ticks is during the months of June and July, which comprise days 152 through 212 of each year, we take $t_j^a=152,t_j^b=212,j=NM,ND$. Similarly, corresponding to the peak feeding period of adult ticks, which is between the months of October and November, we take $t_j^a=274,t_j^b=335,j=AM,AD$. The growth rate of deer $r_D\left(t\right)$ is also a step function, which accounts for the high birth rates of deer between the months of May and June, i.e., $t_D^a=121,t_D^b=181$. For a fair comparison, we took the magnitude of the infection rate during feeding period, ${\overline{\beta }}_j$, in such a way that the areas under the ${\beta }_j\left(t\right)$ curve for a period $\tau =365$ days remain the same as that for the basic multiple-vector model. For example, ${\overline{\beta }}_{NM}={\beta }_{NM}\tau /61=1.35\times {10}^{-5}$ Nymphs/ha/(Mice-Day). In the cosine functions representing the time-dependent tick death rates, ${\delta }_N\left(t\right)$ and ${\delta }_A\left(t\right)$, we used the parameters by setting the peak death rate on the first day of January, due to a large percentage of tick deaths in the winter. Since the ticks feed primarily in the summer and fall, the death rates are lowest at these times. The amplitudes of each function were adjusted to match the average levels at the endemic stage with the levels predicted by the basic model.

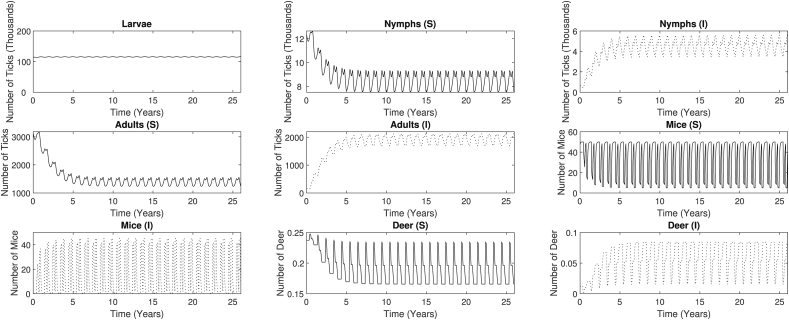
Similar to the base case, we set the initial conditions for the nymphs, adults, mice, and deer each at an infection level of 5%. Due to the periodicity of the time-dependent parameters, we observe oscillations in the overall dynamics of each compartment as expected (Fig. 7), and each compartment eventually reaches a time-varying endemic state with sustained periodic solutions. As expected, the larvae population does not display extreme fluctuations. We observe larger oscillations in the nymph compartments and the adult compartments, while the largest amplitude variation appears in the mice compartments. This great variation in mice population range is likely due to the relatively short lifespan of the P. leucopus, which is about one year (Batzli, 1977). The deer lifespan is longer than that of the mice, which may explain why the oscillations in the deer dynamics are not as extreme as those seen in the mice compartments.

Fig. 7.

The long-term dynamics of each compartment under the seasonality effect. The larvae compartment shows small oscillations, with a constant average population value of 115,360. Despite the periodic behavior of each compartment, the average population values are consistent with those seen in the base model. At the endemic steady state, the average susceptible population values decrease to 8484, 1391, 32, and 0.19 for the nymphs, adults, mice, and deer, respectively. The average infected population values increase to 4582, 1928, 18, and 0.06 for the nymphs, adults, mice, and deer, respectively.

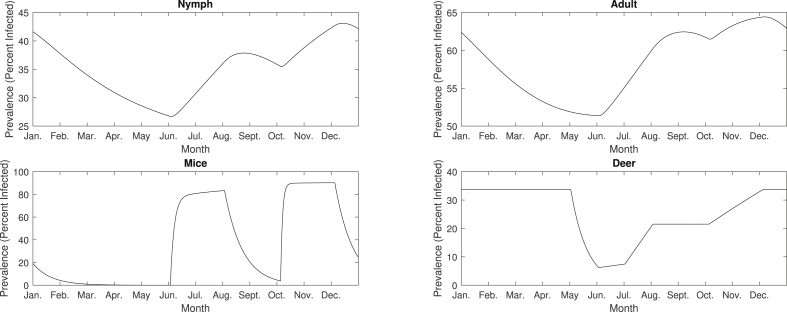
At endemic state, the annual average infection prevalence predicted by the model are 35%, 58%, 36%, and 25% for nymphs, adults, mice, and deer, respectively. Note that these averages are consistent with the infection prevalences observed in the base model, which are 35.6%, 58.7%, 35.8%, and 27.3% for nymphs, adults, mice, and deer, respectively. While the annual average level is not affected by the seasonal variation of the parameters, the disease dynamics during a single period is quite different due to seasonality (Fig. 8). The dynamics during one period exhibits two peaks, where each peak can be associated with the two different questing periods of the nymph and adult stages of the I. scapularis. The solution curves of the nymphs and adults have similar shapes, with large prevalences in January (42% and 62% for nymphs and adults, respectively), but due to high tick death rates, the infection levels decline until the month of June (27% and 51% for nymphs and adults, respectively). Since the peak feeding period of nymphal ticks takes place in June and July, the infection prevalences start increasing at this point (up to 38% and 62% for nymphs and adults, respectively). After this peak period, the prevalences decrease to 35% and 61%, for nymphs and deer, respectively, until the adult ticks start feeding between October and November, after which the second peaks appear toward the end of the year. The infection prevalences of nymphs and adults increase to 43% and 64% and start decreasing in December.

Fig. 8.

The infection prevalences of nymphs, adults, mice, and deer during a period of sustained oscillation of an epidemic. The infection prevalence of each compartment starts increasing in June, due to the beginning of the nymphal tick feeding period. Since the nymphal questing period is not sustained past July, the infection prevalence of each compartment starts to decrease between August and September. The infection prevalences increase again, once the adult tick feeding period begins in October. Since the adult feeding period is not sustained past November, the prevalences will start to decrease in December. This explains the presence of the two peaks observed in each compartment, where one starts in June, and the other one starts in October.

The infection prevalence of mice exhibits the pattern similar to the tick compartments, with an initial infection level of 19%. The prevalence of mice decreases to almost 0% in June, increases to 83% in August due to the nymphal questing period, decreases to 4% in October, increases to 90% in December due to the adult questing period, and then declines at the end of the year. The deer population starts with a high infection prevalence of 34%, which lasts throughout the winter, followed by a rapid decline to 7% between May and June, due to the births of uninfected fawns. Once nymphs start their peak feeding period between June and July, the prevalence increases to approximately 22% and remains constant until the adult ticks peak feeding period starts in October, where the infection level rises to 34%.

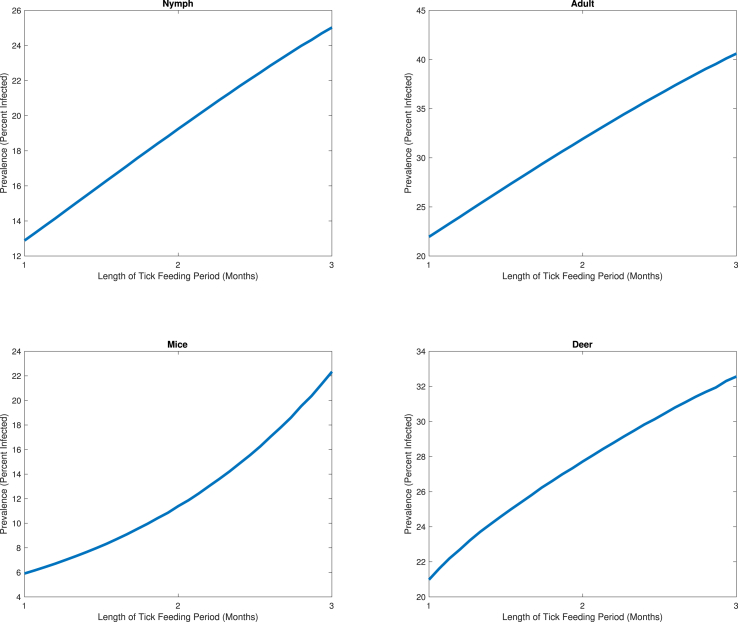
Although the average peak feeding periods of both the nymphal and adult ticks are two months long, these periods may vary depending on the climate. To study how the length of the feeding period affects the dynamics, we performed the model simulations by varying the feeding period, $t_j^b-t_j^a$, from one month to three months, while keeping the infection rates, ${\beta }_j$, the same (Eq. (2)). We see that the infection prevalence of each vector increases as the peak feeding period is elongated (Fig. 9). Starting with a feeding period of one month and progressing to three months, the infection prevalences increase from 13% to 25%, 22%–41%, 6%–22%, and 21%–33% for nymphs, adults, mice, and deer, respectively. This increase in infected populations suggests that if ticks are able to feed for a longer portion of the year, this may result in escalated Lyme disease incidence reports. Therefore, a possible method of Lyme disease control involves processes that aim to shorten the tick's peak feeding periods.

Fig. 9.

The variation of the infection prevalences of nymphs, adults, mice, and deer, with varying tick feeding periods. The nymph infection prevalence is 13% for a feeding period of one month, 19% for a two-month period, and 25% for a three-month period. The adult has infection prevalences of 22%, 32%, and 41% for questing periods of one, two, and three months, respectively. The mice infection prevalence values are 6%, 11%, and 22% for questing periods of one, two, and three months, respectively. The deer infection prevalence values are 21%, 28%, and 33% for feeding periods of one, two, and three months, respectively.

3.5. Effects of deer mobility

As mentioned earlier, we study how the deer migration could influence the spread of Lyme disease between two neighboring counties, where County-1 is at an endemic state and County-2 is at a disease-free state. For our base case computations, we set the rates of dear mobility between counties as $m_{12}=m_{21}={10}^{-3}$.

The long-term disease prevalence in County-2 predicted by the model is shown in Fig. 10. While the deer population show some prevalence, the prevalence among other populations remain almost 0% for about 10 years. The initial small increase in only deer prevalence (0%–3.8%) is because only deer are mobile between counties. After about 10 years, each prevalence begins to increase, and in about 25 years, the disease free county eventually reaches equilibrium values of 36%, 59%, 36% and 27% for nymphs, adults, mice, and deer, respectively. These infection prevalences at the endemic state are consistent with those predicted by the base model. This results show that the deer mobility may not be responsible for the spatial spread of Lyme disease for a short period of time. However, in the long-run, the deer mobility between counties can be an important contributor to the spread of Lyme disease.

Fig. 10.

The infection prevalences of nymphs, adults, mice, and deer as predicted by the migration model. The infection levels of the nymphs, adults, and mice are initially 0%, and remain constant until the ${10}^{th}$ year, after which the prevalences increase to 36%, 59%, and 36%, respectively. The deer infection prevalence rises from 0% to approximately 3.8% within the first two years, remains constant until the ${10}^{th}$ year, then increases to 27%.

Considering a migration rate of $m_{12}=m_{21}={10}^{-3}$ for the base computation, the results imply that it takes approximately 10 years until the local infectiousness is large enough to drive the DFE to the endemic steady state. The migration rates are some of the most difficult parameters to estimate, and we do not have the proper knowledge about their values in reality. Therefore, we assess the sensitivity of the migration rate on the time it takes for the infected nymph population in County-2 to reach 50% of the endemic equilibrium value (Fig. 11). As the migration rate varies between 0 and 0.01, the time it takes for the infected nymph population in County-2 to reach a value of 2,339 (50% of the endemic equilibrium value) decreases from 27.79 years to approximately 17.27 years. Note that the base case migration rate, $m_{12}={10}^{-3}$, allows the system to reach this value in approximately 19.61 years. This result shows that a high migration rate of deer can generate a high rate of infectivity in a shorter time period.

Fig. 11.

The time, in years, it takes for the infected nymph population of Compartment 2 to reach 50% of the infected nymph population predicted by the base model at the endemic equilibrium. As the migration rate increases from 0 to 0.01, the time it takes the infected nymph population to reach a value of 2,339 decreases from 27.79 years to approximately 17.27 years.

4. Discussion

In recent years, Lyme disease has expanded its global range, particularly in the Northeastern and Midwestern regions of the U.S. (Kugeler, Farley, Forrester, & Mead, 2015). This expansion is attributable to several factors, such as the environmental variation and B. burgdorferi reservoir migration (Kugeler et al., 2015). While Lyme disease with the white-footed mouse as the primary host has been well studied, the role of the secondary large-sized host, namely the white-tailed deer, in the disease spread is poorly understood. In this study, we developed Lyme transmission dynamics models, which incorporate the interactions between the blacklegged tick (larval, nymphal, and adult) and two vertebrate hosts (white-footed mouse and white-tailed deer). We further expanded our basic multiple-vector model to study the effects of seasonal variation of tick feeding and migration of deer on the disease epidemics.

The model predicts the Lyme disease dynamics with an increase in the infected populations of all compartments except larvae and a decrease in the susceptible populations, until the system reaches an endemic steady state level comparable to the field studies. Consistent with these dynamics implying convergence to the stable endemic steady state, our model estimates the basic reproduction number of Lyme disease to be ${\mathcal{R}}_0=1.28>1$. The predicted value of ${\mathcal{R}}_0$ indicates that by scaling the infection rates by a factor of $f<0.56$, ${\mathcal{R}}_0$ can be brought down to less than one, resulting in the instability of the endemic steady state and the stability of the disease free equilibrium. Hence, for the control of Lyme disease via strategies that focus on reducing transmission, the infection rate of both hosts needs to be reduced to at most 56%.

Using our models, we have found several interesting results that may be useful for the control of Lyme disease. First, we found that the dynamics did not greatly differ from the base case with different values of $b_L$, $b_N$, and $b_A$. This indicates that a tick's host preference may not be a significant factor in the spread of Lyme disease, even though the presence of two different kinds of host may have significant roles in the disease dynamics due to the difference in their size, birth rate, and death rate.

Second, our model predicts that a tick feeding period is positively correlated with the total number of infected individuals. Note that a study by Brownstein et al. (Brownstein, Holford, & Fish, 2003) revealed that the feeding periods may have grown in length due to an increase in warmer weather during the spring and summer months, which is possibly due to global climate change. Combined with this result, our model indicates that a rise in tick epidemics could be due to an increase of feeding period, as a result of climate change. Implementing control measures focused mainly during the tick's feeding periods may aid in the regulation of the spread of Lyme disease. Another effect of seasonality in our model comes from the sinusoidal tick death rates affected by climate change. Low temperatures during the winter months result in reduced death rates, implying higher tick survival rates during winter, which suggests that more ticks are able to attain successful blood meals, thereby increasing Lyme disease incidence.

Third, we evaluated how deer mobility between two adjoining counties, initially one at an endemic steady state and another at a disease free state, will lead to the emergence of Lyme disease in the second county. The model predicts that there is a long delay for infected vector populations to appear in the second county (Fig. 10). These results from our model indicate that the primary reservoir of the disease is P. leucopus and the minor role of deer in Lyme disease transmission should result in long delays in establishing endemic levels. Perhaps the migration of other vectors or seasonality acts as one of the driving forces behind Lyme disease emergence in a short time. These ideas should be tested in future models and compared to data. After this initial delay however, the local infectiousness becomes large enough, eventually driving this initially disease-free county to an endemic steady state. We also observe that an increase in the deer migration rate can cause the emergence of disease in the neighboring county in a shorter time-period. This result suggests that deer mobility between counties can have a significant impact on the infectiousness of nymphs in the second county over a long period of time. Thus, while deer may not be the sole vector responsible for the spread of Lyme disease in a single county, as previous studies have considered (Bosler et al., 1984; Glass et al., 1994; Magnarelli et al., 1995), their migration can be an important contributor to the spatial spread of the disease in the long run.

There are several limitations and possible future directions of our study. Most of the effort centered on the model parameters estimated from the existing literature with limited data. Future studies of this model should analyze the thorough parameter sensitivity and explore avenues to most effectively reduce the prevalence of the disease. Ideally, this model should be tested against detailed biological data from a single region, such as Martha's Vineyard, where Lyme disease is a very significant health problem (Heller et al., 2010). Our modeling efforts with the nonautonomous model demonstrated that seasonal effects are very significant and could play a major role in attempts to control the disease. However, this nonautonomous periodic model needs further analysis, including computation of thresholds for outbreak, such as infection invasion threshold. Such analysis may require sophisticated mathematical techniques and high performing computations, as in the previous studies with similar nonautonomous models (Liu, Zhao, & Zhou, 2010; Vaidya & Wahl, 2015; Wang & Zhao, 2008). Future studies should also explore more details of the population dynamics of all species and life cycles in this model. Particular attention in an improved model would be linking the time-varying parameters to climate elements, like temperature and precipitation. However, such a study would require a collaboration with field biologists collecting detailed population studies of species. In this study, we have not performed a detailed analysis of the model with vector mobility, and we have not considered migrating birds as another potential vector in our model. In addition to rodents and deer, birds are believed to play an important role in Lyme disease expansion (Reed, Meece, Henkel, & Shukla, 2003; Weisbrod & Johnson, 1989). A future extension of our model may include additional compartments that represent bird populations or combine birds in the small animal compartment with an added contribution to disease migration.

The Lyme disease model in this study provides greater detail and more flexibility than previous models. We have managed to match our model to existing data on this pervasive disease, identifying key parameters and adding time-varying elements lacking in many epidemiological models. We believe this model could be invaluable in studies of the spread or control of Lyme disease if done in conjunction with detailed work of biologists in the field.

Conflict of interest

Authors declare no conflict of interest.

Handling Editor: Dr. J Wu