Figure 3. State estimation with a Kalman filter.

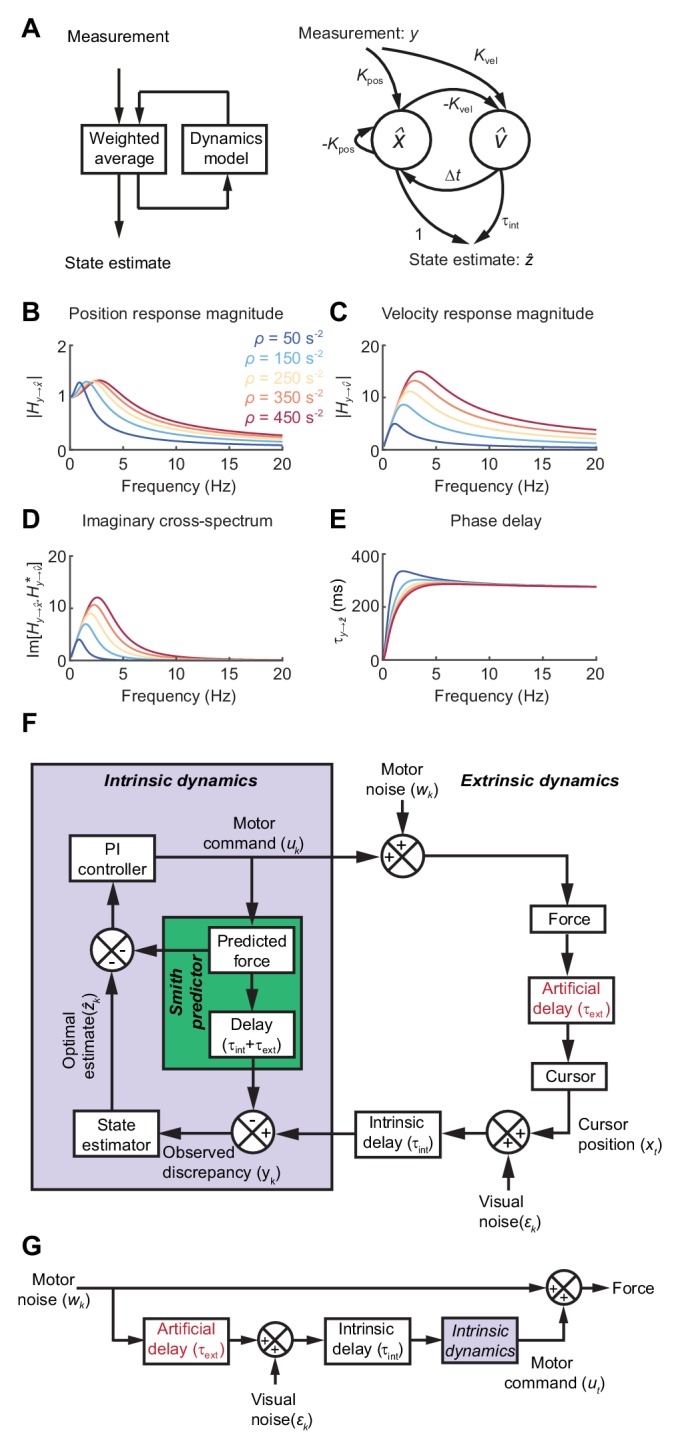
(A) Left: Schematic of a Kalman filter. Noisy measurements are combined with an internal model of the external dynamics to update an optimal estimate of current state. Right: A dynamical system for optimal estimation of position, based on an internal model of position and velocity. (B, C) Magnitude response of transfer function from measurement to position and velocity estimates, respectively, for a Kalman filter with different ratios of process to measurement noise ($\rho$). (D) Imaginary component of cross-spectrum between position and velocity transfer functions. (E) Phase delay of optimal estimate of position based on delayed measurement of position. (F) Schematic of optimal feedback controller model incorporating state estimation and a Smith Predictor architecture to accommodate feedback delays. (G) Simplified rearrangement of (F), showing the feedforward relationship between motor noise and force output. This rearrangement is possible because the Smith Predictor prevents motor corrections reverberating multiple times around the feedback loop.