Computer modeling indicates it may be possible to gradually shape healthy behaviors with real-time sensing technology.
Keywords: Behavior shaping, JITAI, Agent-based model, Reinforcement
Abstract
Adaptive behavioral interventions that automatically adjust in real-time to participants’ changing behavior, environmental contexts, and individual history are becoming more feasible as the use of real-time sensing technology expands. This development is expected to improve shortcomings associated with traditional behavioral interventions, such as the reliance on imprecise intervention procedures and limited/short-lived effects. JITAI adaptation strategies often lack a theoretical foundation. Increasing the theoretical fidelity of a trial has been shown to increase effectiveness. This research explores the use of shaping, a well-known process from behavioral theory for engendering or maintaining a target behavior, as a JITAI adaptation strategy. A computational model of behavior dynamics and operant conditioning was modified to incorporate the construct of behavior shaping by adding the ability to vary, over time, the range of behaviors that were reinforced when emitted. Digital experiments were performed with this updated model for a range of parameters in order to identify the behavior shaping features that optimally generated target behavior. Narrowing the range of reinforced behaviors continuously in time led to better outcomes compared with a discrete narrowing of the reinforcement window. Rapid narrowing followed by more moderate decreases in window size was more effective in generating target behavior than the inverse scenario. The computational shaping model represents an effective tool for investigating JITAI adaptation strategies. Model parameters must now be translated from the digital domain to real-world experiments so that model findings can be validated.
Implications
Practice: A computational model of behavior shaping has been developed in order to aid with the formalization and automation of behavior-shaping procedures within adaptive behavioral interventions that utilize real-time technology.
Policy: Policymakers interested in leveraging real-time sensing technology to automatically personalize behavioral interventions should consider theoretically rooted intervention adaptation strategies.
Research: Further research should be aimed at verifying computational model outcomes with real-world experiments.
INTRODUCTION
Behavior shaping in health interventions
In the USA, the leading causes of death and disease are modifiable behavioral factors such as tobacco use, poor diet, physical inactivity, alcohol consumption, and avoidable injuries [1, 2]. Studies have indicated that preventable, extrinsic factors contribute >70%–90% of lifetime cancer risks [3]. Consequently, enormous gains to public health are achievable through behavior-altering interventions. Most behavioral interventions, though, generate limited, short-lived effects [4], partly due to the reliance on episodic assessments of behavior captured by tools such as counseling sessions, ecological momentary assessments, surveys, and discrete direct observations. In contrast, recent advances in mobile technology have enabled the development of just-in-time, adaptive interventions (JITAIs) that have the potential to improve upon the shortcomings associated with traditional trials [5, 6]. JITAIs typically use assessment technology that is capable of observing and recording behavior in a natural environment on a near-continuous basis over a long period of time. By pairing intensive data collection with analytic systems capable of real-time decision making, JITAIs enable interventions to be provided on an ongoing basis and automatically adapt in response to participants’ varying behaviors, environmental contexts, and past history. This process is hypothesized as an ongoing two-way “conversation” between patients and providers. While still in the preliminary stages, adaptive interventions have been implemented to, for example, encourage physical activity [7], assist with in-home living for older adults [8], and manage HIV medication adherence [9].
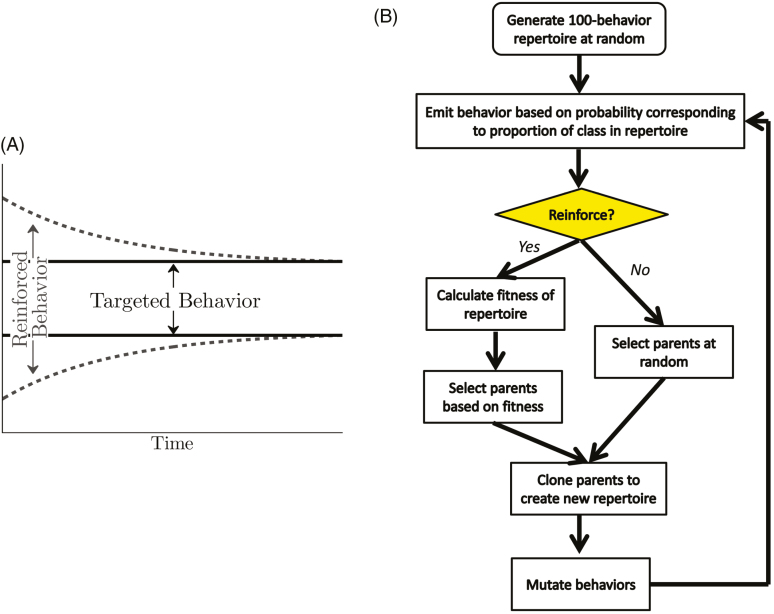
The implementation of JITAIs can be enhanced by consideration of the precise mechanisms by which interventions should adapt in response to participants’ behavior. Often, adaptation strategies are developed in an ad hoc fashion with little consideration of theoretical underpinnings, despite findings indicating that adherence to established theory can increase the efficacy of behavioral interventions [10]. Current behavioral theories provide little insight into this regard because they rarely consider behavior as a dynamic entity [11]. Introducing theoretically sound, responsive adaptation strategies will probably lead to more effective interventions and, furthermore, can generate results that will allow the underlying theories to be refined. One possible adaptation strategy with a theoretical foundation is behavior shaping, defined as the process whereby a targeted behavior is gradually cultivated via the differential reinforcement of successive approximations to the target [12]. When implementing this procedure, the range of behaviors that are reinforced narrows with time (Fig. 1A). The shaping process can lead to complex behaviors that would otherwise not be emitted as quickly, or at all. In a traditional shaping scenario, a practitioner must discriminate which behaviors are sufficiently similar to the target behavior in order to receive reinforcement and determine the optimal time to discontinue the reinforcement associated with crude approximations. The withholding of reinforcement produces a temporary extinction condition that might occasion novel or differential rates of behavior that are appropriate for shaping. This process typically occurs in a controlled environment such as classroom or training center. Proficiency in performing these tasks arbitrates the ultimate effectiveness of shaping routines and specialists such as teachers and coaches do this as an art. JITAIs, though, offer the opportunity to precisely gauge behavior on a nearly constant basis and to continually assess its similarity to a target behavior. This enables shaping procedures to be automatically implemented in a much wider variety of contexts than has typically been possible [13].Many behaviors are reliably shaped throughout society. For instance, the entire educational system can be viewed as a high-level shaping procedure where successively close approximations to proficiency in certain disciplines are reinforced as individuals proceed through each grade. Subsequent to these formal shaping protocols, the environment continues to shape behavior, albeit under less predictable schedules. For example, education is reinforced by the admission to college and subsequent employment. In contrast, behavior-shaping routines that would be deployed in JITAIs, at least during this preliminary stage, are likely to be rudimentary and not have the benefit of a host of strong, supporting contingencies. In some cases, such as when attempting to shape tobacco-smoking cessation, the opposite may even be true and environmental factors could discourage the target behavior. The extent to which simple shaping procedures deployed within a natural environment would be successful in producing elevated levels of healthy human behavior is an open question that this manuscript begins the process of addressing.
Fig. 1.
(A) Behavior shaping schematic. (B) McDowell computational model flowchart.
Outside of the JITAI domain, the effectiveness of behavior shaping in humans has been reliably demonstrated in areas ranging from promoting motor activity in patients recovering from strokes [14] to improving dental treatment acceptance among children [15] to the management of cellular service consumption [16]. For individuals with autism, shaping has been used to promote socioemotional functioning [17], to aid in toilet training [18], to increase the duration of sustained attention [19], and to develop social-cueing skills [20]. The latter of these examples utilized automatic behavior assessment features similar to those that are required for JITAIs.
Behavior shaping and computational models
Using computational models to assess the effectiveness of behavior shaping routines in JITAIs is an attractive preliminary approach since it allows for the components of complex systems to be efficiently isolated and manipulated. Methodologies can be explored, tweaked, and sometimes abandoned without the complications associated with their real-world counterparts. The ultimate aim of the procedure presented herein is to leverage the insight gained within simplified, digital domains to develop increasingly more realistic controlled laboratory experiments and subsequent real-world trials, which will all share a common theoretical underpinning. This will allow behavior shaping programs to be designed with a degree of theoretical fidelity [10] that has been absent in this area thus far.
There is a rich history of implementing digital shaping programs within reinforcing learning models that are popular in the realm of artificial intelligence (AI) research. For example, behavior shaping routines have been implemented in reinforcement learning schemes within computational models of bicycle riding [21] and navigating a rod around obstacles [22]. In addition to experiments occurring in a virtual environment, shaping has also been included within the reinforcement learning protocol for robots learning to simulate foraging and other survival behaviors [23, 24]. The shaping protocols in these reinforcement learning models typically consist of having the agent preliminarily complete a simplified version of the full target task and demonstrating that this priming increases the rate at which the target behavior is acquired. In contrast to the hypothesized implementation of shaping within JITAIs, these shaping routines have only a rudimentary temporal component and do not adapt over time, which limits their generalizability to the JITAI domain.
Due to the shortcomings of the existing computational shaping routines discussed above, this paper aims to develop computational models that are suitable for a JITAI framework. This is accomplished by modifying McDowell’s evolutionary model of behavior dynamics [25] by incorporating behavior shaping. In accordance with Darwinist principles, the McDowell model emits a stream of behaviors chosen from a population via a system of selection, reproduction, and mutation, a process that may be equivalent to reinforcement learning [26]. As will be detailed below, this is an abstract model that considers a digital organism emitting generic behaviors. The absence of specificity regarding behaviors and targets is an attractive feature since, as opposed to the behavior-specific AI reinforcement learning tasks described above, it enables findings to be generalized to many different JITAIs. As described in Table 1, the McDowell computational model has consistently produced results that agree with many material world experimental findings. In the case of temporally adaptive behavior shaping routines, the appropriate real-world experiments required for model comparison have not yet been performed. The results outlined within this paper lay the groundwork for the development of such experiments that will allow the consistency of computational and material-world findings to be assessed in order to inform behavior-shaping JITAIs.
Table 1.
Summary of previous findings from computational model
| Study | Finding |
|---|---|
| Ref. [25] | Consistency with the law of effect |
| Ref. [31] | Consistency with the power-function matching equation |
| Ref. [32] | Consistency with an extension of the power-function matching equation that considers reinforcement magnitude |
| Ref. [33] | Demonstrated the effect of changeover delays when switching between reinforcement schedules |
| Ref. [34] | Changing response preference based on concurrent reinforcement schedules |
| Ref. [35] | Consistency with known inter-response time distributions |
BEHAVIOR SHAPING IN MCDOWELL MODEL
Summary of previous work
McDowell’s model [25] considers a hypothetical digital organism whose behavior evolves over time according to low-level rules informed by principles of behavior. This foundation defines the relationship between the emission of a behavior and its consequence, as specified by the probability of this behavior being emitted in the future. In a process similar to agent-based modeling, the interaction of these rules for various behaviors is simulated via computational experiments that produce emergent, higher-order results that cannot be extrapolated by solely examining the structure of the rules. The system is entirely decentralized without explicit considerations of global outcome and has stochasticity built into it. Drawing on the parallels between operant behavior and natural selection, model components are presented in evolutionary terms.
The behavior of the digital organism evolves over time according to the algorithm illustrated in Fig. 1B and described as follows. Each behavior is associated with a unique integer within the interval [0, 1000], and at each time step, a repertoire of 100 behaviors is active. The integers are stratified into behavior classes, one or more of which represents a targeted class which contains behaviors that are eligible to receive reinforcement when emitted. The experiments detailed herein include three classes: class I: [0, 494], class II: [495, 505], and class III: [506, 1000], the second of which is the target class. The range of integers defining behaviors, the size of the active repertoire, and the specification of the reinforced class can be freely chosen. At each time step, the probability that a particular class of behavior is emitted is given by the proportion of total behaviors within the repertoire that correspond with this class. Based on the probabilities calculated for each class, one class is selected at random for emission. The specific behavior from within the class that is emitted is randomly selected from the behaviors in the repertoire associated with this class. To create the behavioral repertoire at the next time step so this procedure can be iterated, “parent” behaviors are selected from the current behavioral repertoire and “cloned” and “mutated” to generate a new set of 100 behaviors comprising the new repertoire. The full details of this process are detailed in Ref. [25] and in Appendix 1, which describes deviations from the methodology outlined in Ref. [25].
The computational model includes a reinforcement component, which allows behavior shaping to be introduced. Reinforcement is defined as the delivery of a stimulus contingent upon performance of a behavior which results in the increased probability of future occurrences of this behavior and others similar to it [27]. This construct is included in the model as follows. If the emitted behavior is from the target class, a reinforcement schedule is consulted to determine whether this behavior should be reinforced. If reinforcement should occur, the emitted behavior is characterized as “fit” and the fitnesses of the other behaviors in the repertoire are based on their similarity (i.e., distance) to the reinforced behavior. A fitness function, fully detailed in Ref. [25], is then used to select the parent behaviors for the next repertoire that are similar to the emitted, reinforced behavior with preference given to the most similar behaviors. As a result, after cloning and mutation, the behaviors comprising the repertoire at the next time step will be similar to the emitted behavior, satisfying the definition for reinforcement. If the emitted behavior is not reinforced, the parent behaviors are selected at random.
Operationalizing behavior shaping
The primary focus of the research summarized in this manuscript is to operationalize the construct of behavior shaping within the McDowell computational model so that digital experiments concerning its optimal implementation can be performed. To simulate the reinforcing of successive approximations to a target behavior, the McDowell model was modified so that a class of behaviors wider than the target behavior class was reinforced. Because shaping requires, as time progresses, behaviors to be increasingly similar to the desired behavior in order to receive reinforcement, the width of this reinforcement class was gradually tightened according to some nonincreasing function, . The reinforced class at any given time is defined as , where . It follows that defines the reinforcement of only the targeted behavioral class [495, 505]. To ensure that the reinforced class is defined by integers, all the values of are rounded to the nearest odd integer. As the behaviors defining the reinforced class are updated according to , the other classes must be updated as well. class I is thus defined as and class III is defined as . This study aims to identify , the function that optimally narrows the reinforcement class toward the target class.
Discrete shaping procedure
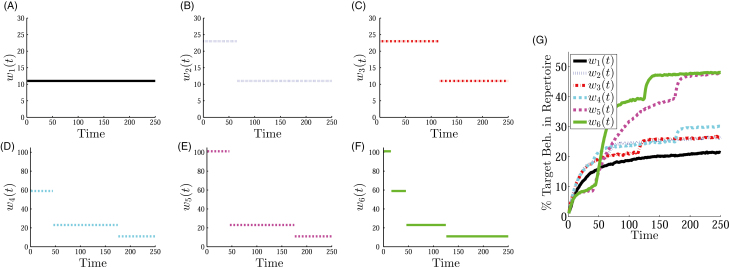
The simplest shaping procedures start with a reinforcement window that is wider than the target window and tighten it at discrete time point(s), which can be summarized by treating as a step function. Several example step functions chosen for exploration and denoted as for are shown in Fig. 2. Figure 2A represents the baseline case where only the target behavior class () is reinforced at all times. Figure 2B and C is denoted as 1-step shaping procedures. In this case, the class [489–511] () was initially reinforced and then the reinforcement window was reduced to the target class at and , respectively. Figure 2D and E illustrates 2-step shaping procedures and Fig. 2F illustrates a 3-step shaping procedure.
Fig. 2.
(A–F) illustrate step functions for discrete shaping and (G) illustrates analytic results for each function.
Figure 2G depicts the results generated by these shaping functions. The metric shown is the percentage of target behaviors in the behavior repertoire at each time step. To account for stochasticity in the system, this value is averaged over 5,000 simulations. After approximately 50 time steps, each of the shaping procedures produces higher levels of the target behavior than does , where only the targeted class was reinforced. This demonstrates that the operationalization of shaping within the computational algorithm is functioning as expected since higher levels of behavior were eventually produced relative to the scenario where only the target behavior class was reinforced. and are both 1-step functions that utilize the same two reinforcement windows, but spend a different amount of time in each window. The different results for these functions demonstrate the effect of this temporal feature on results. The 3-step function produced a higher level of target behavior than the 2-step functions, and , which in turn produced a higher level of behavior than the 1-step functions. Taken together, these results indicate that continuously narrowing the reinforcement with time, as opposed to the discrete contraction used in this section, might lead to more pronounced behavior change.
Continuous shaping procedure
The first step in the continuous shaping procedure is to develop functions that can be used to guide the reinforced class width. These functions are analogous to those illustrated in Fig. 2, but are continuous and nonlinear. The following generic piecewise function is used:
| (1) |
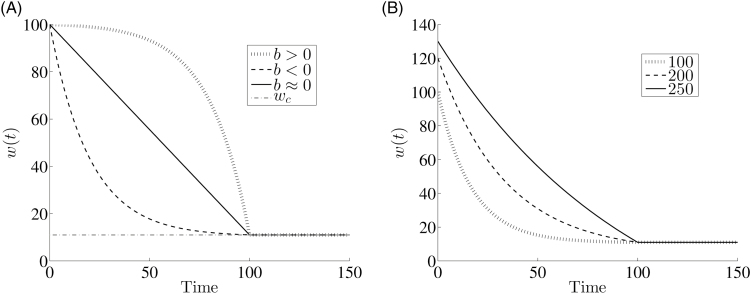
where is the initial width of the reinforcement class, is an exponential loss/gain parameter, is the distance between the horizontal asymptote and , and is the time at which the target reinforcement width is met. For , only behaviors within the target behavior class are reinforced. To ensure that is continuous, the restriction is established, which leads to the condition, .
In equation (1), negative values of correspond to concave-up functions, which represent an initial rapid decrease in the reinforced class. Positive values of correspond to concave-down functions, representative of a gradual initial decrease in the reinforced class along with a rapid narrowing of the reinforced class later in time. For , the nonconstant component of is undefined. However, a linear Taylor expansion about shows that, in the limit, this function can be approximated by a straight line crossing through the two points and , that is, the slope is and the .-intercept is . Therefore, when , the reinforced class is narrowed at a constant rate. Figure 3A illustrates the qualitative shape of equation (1) for different values of .In order to fully define equation (1), values for , , , and are required. The chosen target behavior class of [495,505] corresponds to = 11. was set equal to 100 and the simulations were run until . These three values are free parameters of the system. Exploratory analyses outside the scope of this manuscript indicated that different values for these parameters did not affect the qualitative nature of the findings detailed below. The computational experiments performed in this work explore the effects of varying , the initial value of that can be interpreted as the maximal deviation from the target behavior that will result in reinforcement and , the reinforcement window narrowing rate. The experiments were conducted for values of , where and .
Fig. 3.
(A) Qualitative shapes for the shaping function described by equation (1) for different values of . , depicted as the horizontal line represents the width of the target class. (B) The functions with optimal parameters at time = 100, 200, and 250 for the FR1 simulations outlined in the text. The largest area under the curve of the target behavior trajectories (see next section) was used to determine which parameters were optimal.
Results of the continuous shaping procedure
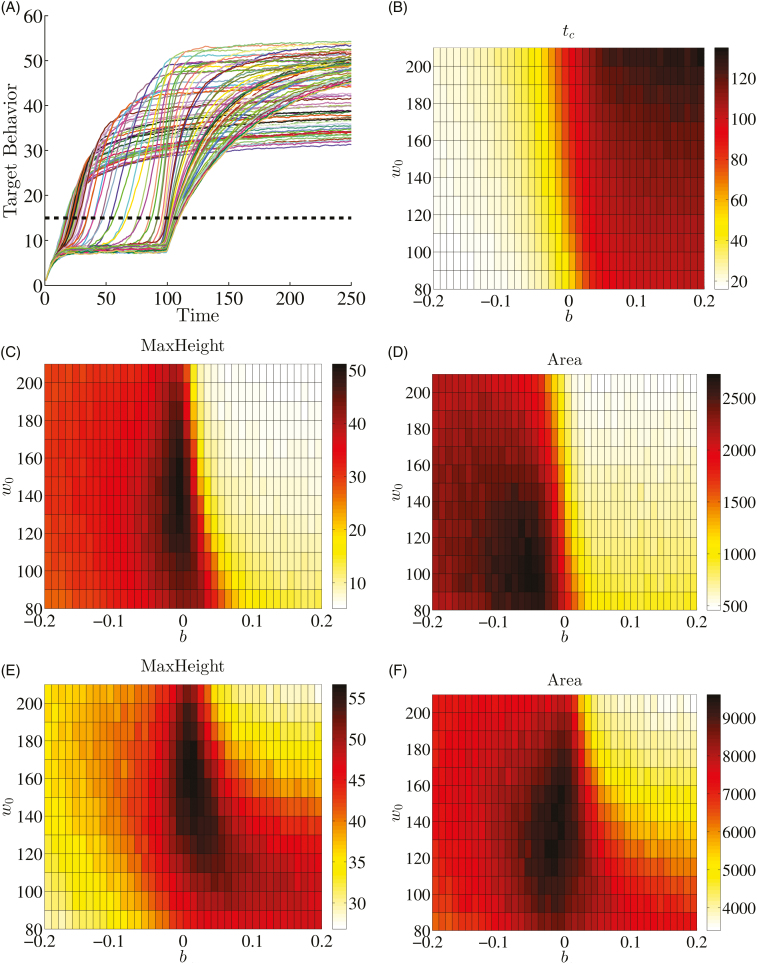
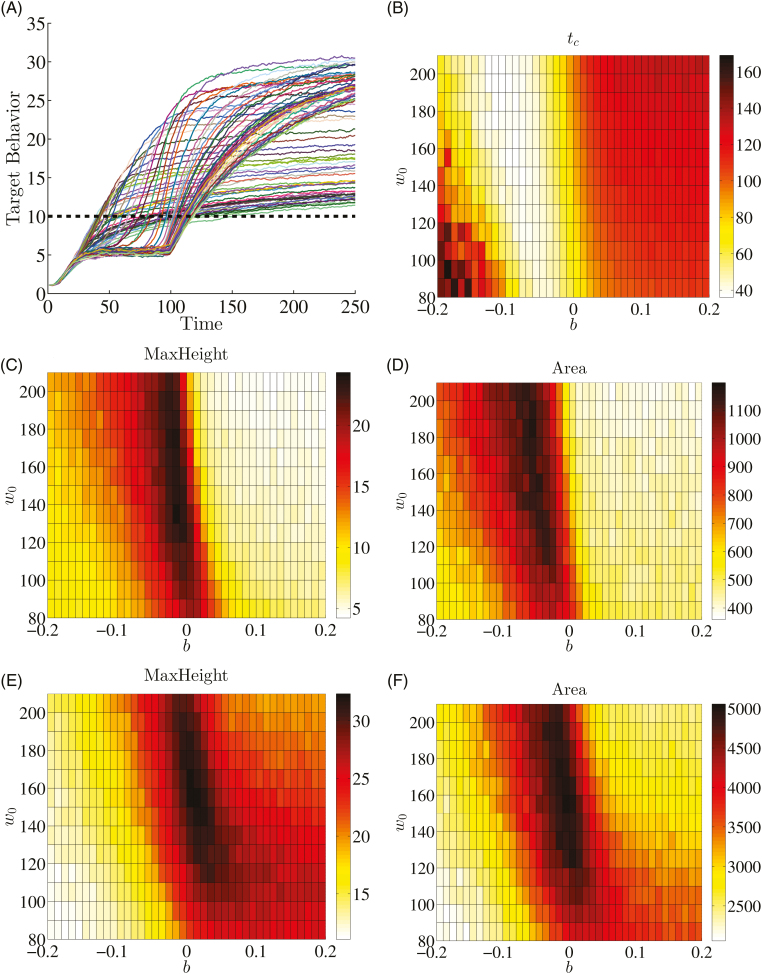
Figure 4A illustrates the target behavior level (measured as in Fig. 2G) as the percentage of target behaviors in the behavioral repertoire at each time step (averaged over 5,000 simulations) versus time for selected values of . For all cases, including those not shown in Fig. 4A, the evolution of target behavior proceeds in, roughly, three different ways. For certain sets of parameters, the percentage of target behavior increases rapidly at the onset of the simulations and then asymptotes. For other sets of parameters, the trajectory is sigmoid-like with a nearly constant low level of behavior followed by a large, rapid jump to a higher level of behavior that approaches an asymptote. The last class of behavior does not begin to increase until , when the target class is reached, and then increases gradually before asymptoting. To characterize the trajectory for the entire set of parameters, the following two metrics were calculated: (a) the time at which the trajectory begins to increase, denoted by and approximated by time at which a target behavior value equal to 15 is first breached (horizontal dashed line in Fig. 4A) and (b) the asymptote as time approaches , denoted by and approximated by the maximum value a given trajectory realizes over the course of a simulation. The highest values summarized in Fig. 4C and E are higher than those produced by the discrete shaping functions in Fig. 2, demonstrating the superiority of continuous shaping procedure.
Fig. 4.
Result of simulations for FR1 reinforcement with the values defined in Table A1. (A) illustrates the level of target behavior with respect to time and (B) illustrates , the time required for the targeted reinforcement to reach a level of 15, for all , where is the concavity and is the initial value of the shaping function . (C) and (D) illustrate the maximum height () and the area under the curve (AUC) for all combinations of parameters calculated at . (E) and (F) are a recalculation of the results in (C) and (D), but with the metrics calculated at rather than . All results are averaged over 5,000 simulations.
Figure 4B and C illustrates and over . The variation in target behavior associated with parameter , the curvature of the function, is much greater than the variation associated with for all metrics. For example, in Fig. 4B, if is fixed at zero and is varied, the range of values is approximately 50 to 90, whereas if is fixed at 150 and is varied, ranges from approximately 20 to 120.
As summarized in Fig. 4B, the smallest value for was 16, generated by six combinations, all located in the bottom-left corner of the figure. These are concave-up shaping functions characterized by a rapid initial decrease in reinforcement class width followed by long time intervals with a width relatively close to . High values for , on the other hand, are produced by parameter combinations in the upper-right corner of Fig. 4B, which represent functions that start relatively far from and decrease very slowly until is near . Both of these results indicate that ’s proximity to is associated with a jump in the level of target behavior.
(the asymptotic height) changes dynamically and only a snapshot at a particular moment can be illustrated. For instance, Fig. 4C presents the results at , where the maximum value is 51.2% of target behaviors in the repertoire, which is associated with the parameter set . In this snapshot, the largest values of are associated with nearly linear functions that have negative values near 0. But , the time at which the trajectory jumps, is larger for these values of than for large negative values of . This represents competing effects where the target behavior trajectories that jump most quickly are not associated with highest levels of target behavior. To account for this competition between and in determining the overall levels of target behavior, the area under the trajectory curve (AUC) was also considered as a metric, as illustrated in Fig. 4D. The maximum AUC is associated with , and in general, larger area values are associated with concave-up functions as opposed to concave-down functions.
The analyses described above were calculated at time . As Fig. 4A illustrates, many trajectories have not reached their maximum height at this time. At , which represents the end of the simulation, the trajectories have developed further, and Fig. 4E and F illustrate and AUC at this time. The concave-down functions associated with positive values now have the highest levels, although the largest values are still associated with essentially linear functions. The highest values are also associated with larger values. This rightward shift in the graph is mirrored when considering the AUC, as shown in Fig. 4F. In this case, the maximum values are for . The functions with negative values, that is, the concave-up shaping functions, jumped to elevated target behavior levels very quickly. Although the concave-down functions take longer time to jump, their values are higher. As longer time frames are considered, this elevated level of behavior outweighs the initial gains made by the concave-up functions and the AUC increases, as shown in Fig. 3B). The maximum values, though, remain centered around , indicating that a linear function will ultimately result in the most target behavior.
To summarize, concave-up shaping functions () produce rapid increases to asymptotic target behavior levels, but this asymptote is lower than that of linear () and concave-down functions (), particularly as the simulation runs for longer periods of time. The linear and concave-down shaping functions result in extended periods of a low rate of target behavior before jumping up to higher levels.
EFFECTS OF MODEL PARAMETER VARIATION
Fixed initial behavioral repertoire
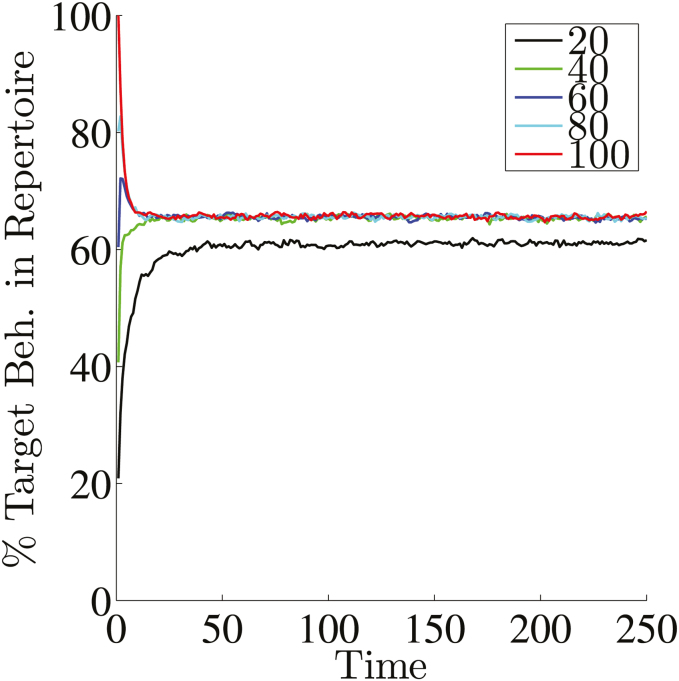
The results summarized in Fig. 4A) point to an upper limit for the horizontal asymptote of the behavior trajectories. The generic functions used in the continuous shaping procedure were selected to capture a range of concavity characteristics. It is possible that more complex shaping functions could ultimately lead to higher levels of targeted behavior. This section explores the level of targeted behavior supported by the computational model with the specific parametrization described in Appendix 1. Simulations were performed where some portion of the initial behavioral repertoire was required from the outset to be from the target behavior class. This stands in contrast to the standard procedure where the initial behavior class is chosen at random. Furthermore, setting a fraction of the initial behavior class to the target behavior simulates a previous learning history for the organism, a scenario which more accurately reflects the real-world conditions to which this model can be applied.
Once a fraction of the initial behavioral repertoire was fixed, only behaviors within the targeted class were reinforced, that is, there was no shaping. The behavior trajectories, averaged over 5,000 simulations, for various proportions are illustrated in Fig. 5. There appears to be an upper limit of approximately 65% for the asymptotic level of targeted behavior, even for the ideal case when all behaviors initially in the repertoire are target behaviors and each of these target behaviors is reinforced when emitted. This feature is due to the shaping and cloning procedures (Ref. [25] and Appendix 1), which result in sufficient variation in the next generation of behaviors to ensure that nontarget behaviors are included in the repertoire. Interestingly, beginning with 60% and 70% of the initial behavioral repertoire in the target class results in an overshoot of this asymptotic level, but eventually the rate of behavior decreases to the asymptote. In the simulations detailed thus far, asymptotes as high as approximately 55% have been observed. Given an upper limit of 65% and the fact that the standard shaping procedure begins with a random initial behavioral repertoire, it is not expected that alternate shaping functions would drastically improve the ultimate levels of behavior generated.
Fig. 5.
Target behavior trajectories for simulations with parameters in Table A1 with no shaping routine. Each line represents fixing a certain proportion of the initial repertoire with behaviors from the target class, rather than choosing the initial repertoire randomly as is the case with other simulations.
Parameter variation within the computational model
In all of the previously detailed findings, a fixed-ratio 1 (FR1) reinforcement schedule was implemented, meaning that every time a behavior from the reinforcement class was emitted, it was reinforced. The effects of utilizing an FR3 schedule, where every third reinforcable behavior that is emitted is reinforced, were also explored. Figure 6 illustrates the effects of this schedule, where differences compared with the previously described results can be seen. As is expected with less reinforcement, the overall target behavior levels are lower. This effect is particularly pronounced for parameter sets pairing large, negative values of with small values of (i.e., the lower left corner of the figure), where values are much larger. It appears that the infrequent reinforcement coupled with a sharp initial reduction in reinforcement window does not result in sufficient reinforcement for shaping to be effective. This reinforcement schedule also resulted in the highest AUC values being more localized around than was the case for previous analyses. As was the case for the FR1 schedule, at , the maximum values are associated with linear functions, but, in general, the values are relatively higher for concave-down shaping functions.
Fig. 6.
Result of simulations with the default values defined in Table A1 but with an FR3 reinforcement schedule. The metrics illustrated in each panel are the same as in Fig. 4 with the exception that (B) illustrates the time required for the targeted reinforcement to reach a level of 10 rather than 15.
The effects of varying the reinforcement strength (how similar the next repertoire is to a reinforced behavior), target class size, and time to target class were also explored. A full accounting of these results is beyond the scope of this article, but the results of these analyses were in accordance with the findings above, namely, they contained a trade-off between trajectories that quickly jump to elevated levels of target behavior versus trajectories that took longer to jump to ultimately higher levels of target behavior. Approximately linear shaping functions produced the highest levels of behavior. This indicates that the results detailed within are not a function of the choice of modeling parameters.
DISCUSSION
This work demonstrated the viability of using computational models to investigate behavior shaping routines, a process that may be valuable in developing an alternative to the ad hoc modifications often incorporated into adaptive, just-in-time, health behavioral interventions. The results indicate that shaping was effective at engendering higher levels of target behavior than when only the target behavior class is reinforced. When shaping target behavior, narrowing the scope of behaviors that are reinforced on a continuous basis rather than at discrete time points is more effective in producing the target behavior. Within this continuous framework, computational experiments were performed to explore the role of both , the initial size of the reinforced behavior class, and , which determines the concavity of reinforced class narrowing, on the effectiveness of shaping routines. The values were more crucial in arbitrating the ultimate effectiveness of shaping. When considering the total amount of target behavior produced, there were two competing effects to consider: concave-up shaping functions that resulted in the percentage of target behavior quickly jumping to a relatively low asymptotic value versus concave-down shaping functions where the percentage of target behavior took a longer period of time to jump to higher asymptotic levels. Approximately linear functions did the best job of managing these two effects and led to the highest levels of target behavior.
There are practical conclusions to be drawn from the results outlined in the previous paragraph. If high levels of target behavior are the chief concern of the shaping system, then either a linear or concave-down shaping function should be used to guide the evolution of reinforcement windows with the latter being appropriate if it is only possible to reinforce behaviors that are relatively similar to the target behavior, that is, small . An example of this scenario is someone training for an athletic competition, where the highest levels of target behavior are desired regardless of the time it takes to reach this goal. As an alternative scenario, consider a target behavior that is defined as the absence of some deleterious behavior, such as cigarette smoking. Shaping routines could be used within a gradual cessation program by informing the scheduling of increasingly longer intervals between prompts designed to support cessation. If a linear or concave-down function is used to guide the shaping, considerable harm could be done during the extended period of low-level target behavior (high levels of smoking). In scenarios like this where it is critical to change the behavior as soon as possible, a concave-up shaping procedure might be preferred. Once the individual has reached a constant level of target behavior that has a sufficiently low risk, the shaping schedule can be transitioned to a linear/concave function that may increase the level (or improve the topography) of targeted behavior even further.
Behavior shaping can be implemented in nearly any domain, but the argument for formalized, automated shaping procedures presented herein requires the use of real-time sensing technology such as accelerometers, particle sensors, and smart outlets. These technologies provide the ability to continually assess an emitted behavior’s similarity to a target behavior in order to determine the ideal moment for reinforcement. As an example, our research team recently completed an intervention that used real-time air monitors in homes to discourage second-hand smoke exposure by providing reinforcement when air particle levels stay below a threshold for some extended period of time [28]. These low-particle time intervals represent approximations to the desired behavior of no particle exposure at any time. Shaping would proceed by requiring increasingly large time intervals in order to receive reinforcement. The computational shaping platform in this manuscript represents a tool to investigate the optimal way to expand the duration of intervals required for reinforcement. The intervention model in this example can be replicated in many fields, including the use of accelerometers to shape shorter bouts of sedentary behavior or the use of screen tracking devices to promote less screen time. Each of these interventions can be informed by the computational shaping model, but as discussed in the next paragraph, the translation to real-world scenarios presents complications to be addressed.
The shaping procedures outlined within this report proceed by reinforcing a class of behaviors that are wider than a target class. In the computational model, the similarity between nontarget and the target behavior is clearly defined as the difference between two integers. This feature is not easily translated into most real-world scenarios. For instance, although a large value in indicates that behaviors that are quite dissimilar from the target will be reinforced at the outset of the shaping procedure, there is no interpretation as to whether this difference is based on function or topography or how the model would handle very rare, distal approximation to the target. It is not likely that it will be possible to associate a one-to-one correspondence between the model constituents and the components of any material-world models. It has been argued in Ref. [29], though, that this lack of accordance is a feature of many successful models. For example, consider quantum theory where underlying model components do not conform to standard descriptions of space and time and, therefore, do not have an analogue in experimental model components. Rather, consistency across model predictions and experimental findings are sufficient to declare the two systems to be computationally equivalent, making the computational model a suitable platform for investigation. Although agreement between McDowell computational model findings and several real-world experiments have been demonstrated, to the best of our knowledge, behavior shaping experiments with continuously adapted reinforcement criteria have not yet been performed (Table 1). Laboratory experiments including this feature are currently under development by the authors of this paper and, when performed, they will allow the computational equivalency of the model and real-world findings to be assessed. This will probably increase the interpretability and generalizability of computational results and refine the ability to automatically programming generalizable-shaping procedures.
In addition to being compared with real-world experiments, the computational modeling can be made more robust by exploring more complex modeling scenarios, such as shaping the extinction rather than the establishment of behavior. More complicated reinforcement schedules can be implemented and the consequences of errors within the shaping routine (e.g., incorrectly reinforcing a behavior that is not eligible for reinforcement) can also be explored. In particular, the use of variable ratio (and interval) reinforcement schedules should be explored since the ultimate goal of public health interventions is to sustain healthy behavior on a long-term basis and variable schedules are known to lead to longer maintenance effects. Whether it is better to implement the shaping routine with a variable schedule or to shape with a continuous schedule and then transition to a variable schedule is an open question to be investigated.
A focus on single simulations rather than aggregate results would be more appropriate for comparison to JITAIs. As these features are added and the computational shaping model becomes more rigorous, it will have an increasing potential to serve as a beneficial tool to be used in the design and refinement of JITAIs.
Acknowledgements:
Research reported in this publication was supported by National Heart, Lung, and Blood Institute of the National Institutes of Health under award number R01HL103684. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
APPENDIX 1. DETAILS OF THE MCDOWELL COMPUTATIONAL MODEL
The computational model begins by randomly selecting a repertoire of 100 behaviors from the 1,001 possibilities and grouping them by their respective classes. The probability that a particular class of behaviors is emitted is defined as the proportion of total behaviors within the repertoire that correspond to this class. Based on these probabilities, a class of behavior is randomly chosen to be emitted and a specific behavior in the repertoire from this class is randomly selected. If the selected behavior is from the target class, a reinforcement schedule is consulted to determine whether this behavior is reinforced. Any behavior that is to be reinforced is characterized as “fit” and the fitness of the other behaviors in the repertoire is based on their similarity (distance) to the reinforced behavior. The fitness metric is used to select 100 “parent” behaviors that will generate the behavior repertoire at the next time step with preferential selection given to behaviors that are most similar to the behavior that is being reinforced. The relationship between a behavior’s fitness and the likelihood of its selection as a parent behavior is governed by a parental fitness function, which can be any function that assigns higher probabilities to smaller distances. The analyses in this report used the exponential parental fitness function developed in Ref. [25] as follows. Let be the probability of reinforcing a fitness value of for . The mean is calculated as . This relationship implies making the cumulative density, . Using this function, inverse transform sampling is used to select a value at random from this distribution. The fitnesses of the current behavioral repertoire are searched for a match and if one does not exist, a new random value is generated. This process continues until 100 parent behaviors have been selected. ∝, the mean, is the only value required to parameterize this procedure. If the reinforcement schedule indicates that reinforcement is not available or if the emitted behavior is not from the target class, then rather than using the procedure described above, 100 parent behaviors are selected at random from the repertoire.
Each of the selected parents is “cloned” to generate the behavior repertoire at the next time step. In the original McDowell model, parent behaviors were “mated” via a bitwise, binary procedure rather than cloned, but diagnostic analyses revealed biases within this procedure that were not present with cloning. Cloning proceeds by considering a collection of Gaussian distributions with a mean set equal to each of the parent behaviors. The standard deviation of these distributions, a free parameter of the system, was set equal to 2 and one new behavior for the next repertoire was then selected from each one of these distributions. A certain percentage of this new generation of behaviors is selected at random for mutation, which is also done by considering a Gaussian distribution, with mean set equal to integer representation of the behavior to be mutated and some standard deviation as a parameter of the system. For the analyses presented herein, a proportion of 0.01 behaviors in the new repertoire were selected, at random, for mutation and the standard deviation was 2.5. For both of the cloning and mutating steps, all calculations are performed using modulo-1,001 arithmetic so that all behaviors are guaranteed to fall within [0, 1000]. Once the mutation has occurred, the behavior repertoire at the next time step has been completely determined and the probability that a particular class will be emitted is updated accordingly as the proportion of total behaviors in this new repertoire that belong to each class. The process then repeats. Table A1 details each of the parameters in the system and default values, if appropriate.
Table A1.
Variable definitions and default values used for all simulations, unless otherwise noted
| Variable | Symbol | Value |
|---|---|---|
| Computational model | ||
| Range of behaviors | – | [0, 1000] |
| Target behavior class | – | [495–505] |
| Number of behaviors in repertoire | – | 100 |
| Fitness function mean (reinforcement strength) | ∝ | 5 |
| Cloning Std. Dev. | – | 2 |
| Proportion mutated | – | 0.01 |
| Mutation Std. Dev. | – | 2.5 |
All model simulations were performed in MATLAB R2012b. The model has a stochastic feature to it so when assessing results it is important to consider outcomes that are averaged over many runs. Due to the dimensionality of the parameter space that was explored, this was a computationally demanding requirement. However, because the runs are not dependent on each other, the computations are “embarrassingly parallel” [30]. To take advantage of this feature, the runs were executed using Matlab’s built-in parallel parfor loops. A batch script was created that allowed multiple, parallelized simulations to be run simultaneously on different nodes within a cluster.
Compliance with Ethical Standards
Conflict of interest: The authors have no potential conflicts of interest.
Primary Data :These findings have not been previously published and this article has not been submitted for review elsewhere. The data within has not been reported before. The authors have full control of all primary data and agree to allow TBM to review upon request.
Authors’ Contribution: Dr. Berardi conceptualized the extension of the previous model to include behavior shaping, created the modeling simulations, and drafted the manuscript. Drs. Carretero-González, Klepeis, Ghanipoor Machiani, and Jahangiri aided with the design of the computational simulations and with the interpretation of results. Drs. Hovell and Bellettiere assisted with incorporating proper behavioral theory into the work and with the interpretation of the results. All authors assisted with the drafting of the manuscript.
Ethical Approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Informed Consent: Helsinki compliance and IRB approval are not applicable.
References
- 1. Danaei G, Ding EL, Mozaffarian D et al. The preventable causes of death in the United States: comparative risk assessment of dietary, lifestyle, and metabolic risk factors. PLoS Med. 2009; 6(4): e1000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Mokdad AH, Marks JS, Stroup DF, Gerberding JL. Actual causes of death in the United States, 2000. JAMA. 2004; 291(10): 1238–1245. [DOI] [PubMed] [Google Scholar]
- 3. Wu S, Powers S, Zhu W, Hannun YA. Substantial contribution of extrinsic risk factors to cancer development. Nature. 2016; 529(7584): 43–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Glanz K, Bishop DB. The role of behavioral science theory in development and implementation of public health interventions. Annu Rev Public Health. 2010; 31: 399–418. [DOI] [PubMed] [Google Scholar]
- 5. Nahum-Shani I, Hekler EB, Spruijt-Metz D. Building health behavior models to guide the development of just-in-time adaptive interventions: A pragmatic framework. Health Psychol. 2015; 34(S): 1209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Spruijt-Metz D, Hekler E, Saranummi N et al. Building new computational models to support health behavior change and maintenance: new opportunities in behavioral research. Transl Behav Med. 2015; 5(3): 335–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Adams MA, Sallis JF, Norman GJ, Hovell MF, Hekler EB, Perata E. An adaptive physical activity intervention for overweight adults: a randomized controlled trial. PloS One. 2013; 8(12): e82901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Reeder B, Meyer E, Lazar A, Chaudhuri S, Thompson HJ, Demiris G. Framing the evidence for health smart homes and home-based consumer health technologies as a public health intervention for independent aging: A systematic review. Int J Med Inform. 2013; 82(7): 565–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Pellowski JA, Kalichman SC, White D, Amaral CM, Hoyt G, Kalichman MO. Real-time medication adherence monitoring intervention: test of concept in people living with HIV infection. J Assoc Nurses AIDS Care 2013; 25(6): 646–651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Rovniak LS, Hovell MF, Wojcik JR, Winett RA, Martinez-Donate AP. Enhancing theoretical fidelity: an e-mail-based walking program demonstration. Am J Health Promot. 2005; 20(2): 85–95. [DOI] [PubMed] [Google Scholar]
- 11. Riley WT, Rivera DE, Atienza AA, Nilsen W, Allison SM, Mermelstein R. Health behavior models in the age of mobile interventions: are our theories up to the task?Transl Behav Med. 2011; 1(1): 53–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Cooper J, Heron T, Heward W.. Applied Behavior Analysis. Always learning. London, UK:Pearson Education, Limited; 2013. [Google Scholar]
- 13. Nakajima T, Lehdonvirta V, Tokunaga E, Kimura H. Reflecting human behavior to motivate desirable lifestyle. In: Ilda Ladeira and Paula Kotzé, eds. Proceedings of the 7th ACM Conference on Designing Interactive Systems NY, NY:ACM; 2008: 405–414. [Google Scholar]
- 14. Taub E, Crago JE, Burgio LD et al. An operant approach to rehabilitation medicine: overcoming learned nonuse by shaping. J Exp Anal Behav. 1994; 61(2): 281–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hoist A, Ek L. Effect of systematized ‘behavior shaping’ on acceptance of dental treatment in children. Community Dent Oral Epidemiol. 1988; 16(6): 349–355. [DOI] [PubMed] [Google Scholar]
- 16. Dawson C, Rick A, Seaman J, Waters T.. Traffic shaping of cellular service consumption through modification of consumer behavior encouraged by cell-based pricing advantages, February, 2008. US Patent 7,328,001. [Google Scholar]
- 17. Corbett BA, Gunther JR, Comins D et al. Brief report: theatre as therapy for children with autism spectrum disorder. J Autism Dev Disord. 2011; 41(4): 505–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kroeger K, Sorensen-Burnworth R. Toilet training individuals with autism and other developmental disabilities: A critical review. Res Autism Spectr Disord. 2009; 3(3): 607–618. [Google Scholar]
- 19. Gutbrod T. Evaluating the Efficacy of Shaping with a Percentile Schedule of Reinforcement to Increase Duration of Sustained interaction in Children Diagnosed with Autism [PhD thesis]. Tampa, FL:University of South Florida; 2014. [Google Scholar]
- 20. Greczek J, Kaszubski E, Atrash A, Mataric M. Graded cueing feedback in robot-mediated imitation practice for children with autism spectrum disorders. In Robot and Human Interactive Communication, 2014 RO-MAN: The 23rd IEEE International Symposium on IEEE; 2014: 561–566. [Google Scholar]
- 21. Randlov J, Alstrom P. Learning to drive a bicycle using reinforcement learning and shaping. In: Shavlik JW, ed. Proceedings of the Fifteenth ACM International Conference on Machine Learning. San Francisco, CA: ACM; 1998: 463–471. [Google Scholar]
- 22. Konidaris G, Barto A. Autonomous shaping: knowledge transfer in reinforcement learning. In: William Cohen and Andrew Moore, eds. Proceedings of the 23rd International Conference on Machine Learning NY, NY:ACM, 2006: 489–496. [Google Scholar]
- 23. Dorigo M, Colombetti M. Robot shaping: developing autonomous agents through learning. Artif Intell. San Francisco, CA: ACM;1994; 71(2): 321–370. [Google Scholar]
- 24. Mataric MJ. Reward functions for accelerated learning. In: William W. Cohen and Haym Hirsh, eds. Proceedings of the Eleventh ACM International Conference on Machine Learning San Francisco, CA:ACM;1994: 181–189. [Google Scholar]
- 25. McDowell JJ. A computational model of selection by consequences. J Exp Anal Behav. 2004; 81(3): 297–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Walsh MM, Anderson JR. Navigating complex decision spaces: Problems and paradigms in sequential choice. Psychol Bull. 2014; 140(2): 466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Skinner BF. The Behavior of Organisms: An Experimental Analysis. NY, NY:Appleton-Century; 1938. [Google Scholar]
- 28. Hughes CC, Bellettiere J, Nguyen B et al. Randomized trial to reduce air particle levels in homes of smokers and children Am J Prev Med. 2018. doi:10.1016/j.amepre.2017.10.017 (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. McDowell JJ. Representations of complexity: how nature appears in our theories. Behav Anal. 2013; 36(2): 345–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Moler C. Matrix computation on distributed memory multiprocessors. In: Michael T. Heath, ed. Proceedings of the First Conference on Hypercube Multiprocessors. Philadelphia, PA: SIAM;1985: 181–195. [Google Scholar]
- 31. McDowell JJ, Caron ML, Kulubekova S, Berg JP. A computational theory of selection by consequences applied to concurrent schedules. J Exp Anal Behav. 2008; 90(3): 387–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. McDowell JJ, Popa A, Calvin NT. Selection dynamics in joint matching to rate and magnitude of reinforcement. J Exp Anal Behav. 2012; 98(2): 199–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Popa A, McDowell JJ. The effect of hamming distances in a computational model of selection by consequences. Behav Processes. 2010; 84(1): 428–434. [DOI] [PubMed] [Google Scholar]
- 34. Kulubekova S, McDowell JJ. Computational model of selection by consequences: patterns of preference change on concurrent schedules. J Exp Anal Behav. 2013; 100(2): 147–164. [DOI] [PubMed] [Google Scholar]
- 35. Kulubekova S, McDowell JJ. A computational model of selection by consequences: Log survivor plots. Behav Processes. 2008; 78(2): 291–296. [DOI] [PubMed] [Google Scholar]