Abstract
We give a non-technical introduction to convergence–divergence models, a new modeling approach for phylogenetic data that allows for the usual divergence of lineages after lineage-splitting but also allows for taxa to converge, i.e. become more similar over time. By examining the  -taxon case in some detail, we illustrate that phylogeneticists have been “spoiled” in the sense of not having to think about the structural parameters in their models by virtue of the strong assumption that evolution is tree-like. We show that there are not always good statistical reasons to prefer the usual class of tree-like models over more general convergence–divergence models. Specifically, we show many
-taxon case in some detail, we illustrate that phylogeneticists have been “spoiled” in the sense of not having to think about the structural parameters in their models by virtue of the strong assumption that evolution is tree-like. We show that there are not always good statistical reasons to prefer the usual class of tree-like models over more general convergence–divergence models. Specifically, we show many 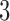 -taxon data sets can be equally well explained by supposing violation of the molecular clock due to change in the rate of evolution along different edges, or by keeping the assumption of a constant rate of evolution but instead assuming that evolution is not a purely divergent process. Given the abundance of evidence that evolution is not strictly tree-like, our discussion is an illustration that as phylogeneticists we need to think clearly about the structural form of the models we use. For cases with four taxa, we show that there will be far greater ability to distinguish models with convergence from non-clock-like tree models. [Akaike information criterion; convergence–divergence models; distinguishability; identifiability; likelihood; molecular clock; phylogeny.]
-taxon data sets can be equally well explained by supposing violation of the molecular clock due to change in the rate of evolution along different edges, or by keeping the assumption of a constant rate of evolution but instead assuming that evolution is not a purely divergent process. Given the abundance of evidence that evolution is not strictly tree-like, our discussion is an illustration that as phylogeneticists we need to think clearly about the structural form of the models we use. For cases with four taxa, we show that there will be far greater ability to distinguish models with convergence from non-clock-like tree models. [Akaike information criterion; convergence–divergence models; distinguishability; identifiability; likelihood; molecular clock; phylogeny.]
It is commonly accepted that although evolution is primarily well described by a tree-like model, there are many important evolutionary processes that are not tree-like. At the genomic level these processes include hybridization, introgression, and horizontal gene transfer (HGT) (Huson and Bryant 2005). At the level of morphological characters convergent selection is a process that can disrupt the tree-like pattern of evolution by acting to make different taxa more similar. In this article, we explore an alternative to strictly tree-like phylogenetic models of character evolution that allows for the possibility of taxa gradually becoming more similar over time.
We will use the term convergent evolution broadly to mean any process by which a set of homologous characters (either morphological or genomic) measured for different taxa become more similar over time. The convergence–divergence models we present here assume that characters are binary, that characters evolve independently, and that evolution is clock-like. We give a deliberately abstract model in terms of how characters behave to allow for the possibility of it being applied to both genotypic or phenotypic characters. Later in the article, we give a range of biological scenarios where the model may be appropriate.
The model that we explore was initially presented in Sumner et al. (2012). There the authors introduced a new model class that generalizes the standard Markov model of character evolution on a phylogenetic tree. The results given in Sumner et al. (2012) are valid for the general Markov model, although so far exploration of the model has focused on the binary symmetric case (Mitchell 2016). The formulation is similar to the idea of an  -taxon process (Bryant 2009), where the Markov process acts on the state space of all possible character patterns for
-taxon process (Bryant 2009), where the Markov process acts on the state space of all possible character patterns for  taxa. Both constructions are capable of capturing standard phylogenetic scenarios where, following lineage-splitting, lineages evolve independently (divergence). More significantly for the discussion we present here the results given in Sumner et al. (2012) can also be used to model convergence.
taxa. Both constructions are capable of capturing standard phylogenetic scenarios where, following lineage-splitting, lineages evolve independently (divergence). More significantly for the discussion we present here the results given in Sumner et al. (2012) can also be used to model convergence.
In his wonderfully entitled article “Should phylogenetic models be ‘trying to fit an elephant’” Steel (2005) suggested two key points to keep in mind when developing new phylogenetic models. His two points were:
Are they capturing a process that is biologically important?
Do they over-fit the data?
With regard to Steel’s first point, we believe that convergence–divergence models have potential to be a useful addition to the phylogeneticists’ toolkit. There are several biological processes that could be better modeled by considering possible convergence of taxa.
For instance, species might become more similar over time as a result of introgression; for example, from Neanderthals (Homo neanderthalensis) into humans (Homo sapiens) (Green et al. 2010) or among domesticated and wild plants (Ellstrand et al. 1999). In the extreme case, despeciation, the loss of unique species, can occur. Rhymer and Simberloff (1996) describe how over time introduced species can lead to despeciation of closely related native species through introgression. Taylor et al. (2006) described a case where environmental changes may be resulting in the convergence of three-spined sticklebacks (Gasterosteus aculeatus) in Enos Lake, Vancouver Island. Sheppard et al. (2008) and Sheppard et al. (2011) identified a case in which two species of bacteria, Campylobacter jejuni and Campylobacter coli, appear to be in the process of undergoing convergence through HGT. Seehausen et al. (2008) argued that a loss of diversity can break down ecological boundaries, allowing more opportunities for the exchange of genetic material among previously independent populations, which can in turn lead to convergence. In some sense, convergence–divergence models can be thought of as a species-level analogue to the population-level isolation/migration model of Hey (2010).
A further scenario where we might consider applying convergence–divergence models is for morphological data where selection acts similarly on different taxa, causing some of the morphological characters to converge. Convergent evolution of morphological characters can lead to organisms possessing analogous traits; traits that perform similar functions despite evolving independently (Holland et al. 2010; Reece et al. 2014). Reece et al. (2014) describe the sugar glider (Petaurus breviceps), an Australian marsupial, and the flying squirrels, North American placental mammals, as an example of species sharing morphological similarities as a result of convergent evolution. There are numerous other examples of convergent evolution, including intelligence in corvids and apes (Emery and Clayton 2004), echolocation in bats and dolphins (Liu et al. 2010), wings in birds and bats (Norberg 1986), and skull shape in marsupials and placental mammals (Werdelin 1986), in particular a similarity between the extinct thylacine (Thylacinus cynocephalus) and the red fox (Vulpes vulpes). Convergent evolution is not necessarily rare. Lengyel et al. (2010) found at least  examples of myrmecochory (seed dispersal by ants) in plants. Sage (2004) found
examples of myrmecochory (seed dispersal by ants) in plants. Sage (2004) found 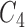 photosynthesis evolved at least
photosynthesis evolved at least 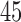 times in
times in  families of angiosperms.
families of angiosperms.
Lewis (2001) was the first to apply Markov models and likelihood methods to morphological character data. He introduced the Mk model, a Markov model for transitions between states of morphological characters. The simplest version of the Mk model assumes all transitions between states occur with the same rate. The model we will discuss can be considered as an extension of the two-state equal-rate Mk model.
While convergence as we have defined it may occur for several reasons, the model that we propose will not always be appropriate. The sorts of scenarios in which we think convergence–divergence models may be appropriate include: 1) modeling the presence or absence of genes in bacterial genomes, which are experiencing ongoing HGT; 2) modeling the presence/absence of homologous fragments of DNA, e.g., double digest restriction-associated DNA (ddRAD) data (Jaccoud et al. 2001), for taxa that are undergoing introgression; and 3) modeling binary morphological characters for taxa undergoing convergent selection, provided the characters are independent (we note that this may not be the case (Felsenstein 2013)). There are also scenarios where the model does not seem appropriate. For instance, the model would not be appropriate for hybrid speciation where a non-gradual event creates a new species; likewise it would not make sense to apply the model to a single HGT event. Our model is also not useful for studying recombination or hybridization events that affect a contiguous DNA sequence alignment; such scenarios would clearly violate the assumption of character independence.
The second point of Steel (2005), regarding models over-fitting the data, is possibly more worrying. As noted in Sumner et al. (2012) convergence–divergence models have a lot of flexibility; in principle there can be arbitrarily many epochs in which arbitrary groups of lineages can either converge or diverge. However, under some reasonable restrictions, convergence–divergence models need not necessarily be more parameter rich than trees. For example, while an 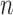 -taxon clock-like tree has
-taxon clock-like tree has  height parameters that define the edge lengths and an
height parameters that define the edge lengths and an  -taxon non-clock-like tree has
-taxon non-clock-like tree has 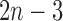 edge parameters, a clock-like convergence–divergence model has at least
edge parameters, a clock-like convergence–divergence model has at least 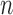 epoch length parameters. For large
epoch length parameters. For large 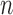 ,
, 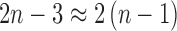 and the number of edge parameters will approximately double if we keep the tree assumption but remove the molecular clock assumption. Alternatively, we have far more flexibility in the number of parameters if we keep the molecular clock assumption but remove the assumption that once lineage-splitting occurs lineages are strictly diverging. We could then increase the number of parameters one at a time until we have optimized the fit.
and the number of edge parameters will approximately double if we keep the tree assumption but remove the molecular clock assumption. Alternatively, we have far more flexibility in the number of parameters if we keep the molecular clock assumption but remove the assumption that once lineage-splitting occurs lineages are strictly diverging. We could then increase the number of parameters one at a time until we have optimized the fit.
Convergence–divergence models are not the only way to achieve an intermediate number of parameters between a strict clock and a non-clock-like tree. When evolutionary timescale is of interest, phylogeneticists commonly adopt a relaxed clock, such as in the models of Drummond et al. (2006) and the models reviewed by Lepage et al. (2007). The relaxed clock models of Drummond et al. (2006) have been popular and effective in terms of giving the flexibility to fit data without requiring too many extra parameters.
In the next section, we give details of how convergence–divergence models are constructed. Following that, we illustrate their use in the 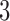 -taxon case and, briefly, the
-taxon case and, briefly, the 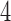 -taxon case.
-taxon case.
Modeling Evolution With Convergence-Divergence Models
The convergence–divergence models of Sumner et al. (2012) can be understood in the context of 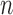 -taxon processes (Bryant 2009), processes on patterns. For the binary symmetric model there are
-taxon processes (Bryant 2009), processes on patterns. For the binary symmetric model there are 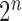 possible patterns. For example, for
possible patterns. For example, for 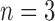 taxa there are
taxa there are 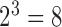 possible combinations of states:
possible combinations of states: 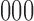 ,
, 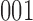 ,
,  ,
,  ,
, 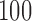 ,
, 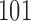 ,
, 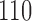 , and
, and 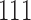 . The first entry is the state of taxon
. The first entry is the state of taxon  , the second entry is the state of taxon
, the second entry is the state of taxon 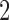 and the third entry is the state of taxon
and the third entry is the state of taxon  . We call theoretical probabilities of combinations of states occurring character pattern probabilities and empirical probabilities character pattern frequencies.
. We call theoretical probabilities of combinations of states occurring character pattern probabilities and empirical probabilities character pattern frequencies.
To determine expressions for each character pattern probability on a tree or convergence–divergence model we start with a probability distribution at the root (e.g., the stationary distribution). We then have an instantaneous splitting event described by the splitting operator of Sumner et al. (2012) that splits the root lineage into two descendant lineages (or more if multifurcations are to be considered), followed by Markov processes acting on the lineages directly below the root lineage over some period of time. A phylogenetic tree or convergence–divergence model can then be constructed from a series of splitting events and Markov processes, with each Markov process occurring in a separate epoch. The epochs are separated by lineage splitting events or the start or end of convergence periods. The interested reader should consult the Supplementary Appendix available on Dryad at https://doi.org/10.5061/dryad.n8m9c, Sumner et al. (2012) or Mitchell (2016) for more mathematical details on the splitting operator and constructing the required rate matrices in general.
In the 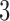 -taxon binary character-state case shown in Figure 1 each epoch has an associated
-taxon binary character-state case shown in Figure 1 each epoch has an associated 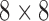 rate matrix, corresponding to the
rate matrix, corresponding to the 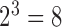 character states possible in this case. In the first epoch lineages 2 and 3 are yet to diverge and therefore it is only possible to be in states where lineages 2 and 3 are identical. Furthermore, transitions such as from state
character states possible in this case. In the first epoch lineages 2 and 3 are yet to diverge and therefore it is only possible to be in states where lineages 2 and 3 are identical. Furthermore, transitions such as from state 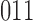 to
to  are possible in a single step. In the second epoch the situation is equivalent to the standard phylogenetic model where all lineages are diverging independently. In this case the
are possible in a single step. In the second epoch the situation is equivalent to the standard phylogenetic model where all lineages are diverging independently. In this case the 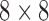 rate matrix can be constructed from three
rate matrix can be constructed from three  rate matrices by assuming that only single-step transitions are possible. In the third epoch taxa
rate matrices by assuming that only single-step transitions are possible. In the third epoch taxa  and
and 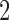 are converging, so states in which
are converging, so states in which 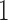 and
and  are mismatched, e.g.,
are mismatched, e.g.,  , can transition back to being in a matched state:
, can transition back to being in a matched state: 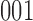 or
or 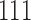 , but the reverse transitions, from
, but the reverse transitions, from 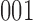 or
or  to
to 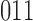 , are not permitted.
, are not permitted.
Figure 1.
Three epochs of a 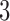 -taxon process. (Top) Divergence of lineages is represented by straight lines emanating from a node, while convergence in the third epoch in Figure 1c is represented by curved lines. (Bottom) State transition diagrams for the last epoch of each subfigure. Dark gray nodes indicate possible states during the epoch, while light gray nodes indicate impossible states. In Figure 1a impossible states are those where lineages
-taxon process. (Top) Divergence of lineages is represented by straight lines emanating from a node, while convergence in the third epoch in Figure 1c is represented by curved lines. (Bottom) State transition diagrams for the last epoch of each subfigure. Dark gray nodes indicate possible states during the epoch, while light gray nodes indicate impossible states. In Figure 1a impossible states are those where lineages  and
and 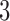 are not identical. Solid lines indicate “regular” transitions, dotted lines in Figure 1a indicate transitions that cannot occur since they involve impossible states and dashed lines indicate “correction” transitions responsible for convergence in Figure 1c.
are not identical. Solid lines indicate “regular” transitions, dotted lines in Figure 1a indicate transitions that cannot occur since they involve impossible states and dashed lines indicate “correction” transitions responsible for convergence in Figure 1c.
Convergence–divergence models are not equivalent to any previous phylogenetic network approaches. Unlike splits-based methods such as Neighbor-Net (Bryant and Moulton 2002), or split decomposition (Bandelt and Dress 1992), convergence–divergence models are directed in time and lead to specific predictions regarding character pattern probabilities. They are also different from the approaches for implementing maximum likelihood on networks (Nakhleh 2010). As described in Nakhleh’s review, a directed network is typically thought of as encoding a set of trees (those displayed by the network). The likelihood is then either a mixture model over these trees (Jin et al. 2006), or each site is allowed to pick the tree that suits it best. Given their stated properties, the convergence–divergence models have different limiting properties to either of these frameworks. For instance, if the convergence process is run for a long enough period of time then the taxa that are converging become arbitrarily close. This is not the case in the mixture-model setting.
Related to the question of whether a model over-fits the data are the fundamental issues of identifiability and distinguishability. In this article, we use the term identifiable in the sense of Allman and Rhodes (2008) to mean that there is an (essentially) one-to-one map between the parameters (e.g., edge lengths or epoch lengths) and the distribution of character pattern probabilities. That is, for every set of parameters there is one possible set of character pattern probabilities and vice versa.
We say that two models with different structural parameters (e.g., a clock-like tree versus a non-clock-like tree) are distinguishable if there is some choice of parameters on one of the models that gives character pattern probabilities which cannot arise on the other model. We say that two models with different structural parameters are distinguishable with respect to a specific set of character pattern probabilities if it is possible for those character pattern probabilities to arise on one model but not the other.
Sumner et al. (2012) raised many questions regarding both identifiability of model parameters and whether or not the induced character pattern probabilities would be distinguishable from character pattern probabilities arising from tree models. These questions were explored in the thesis of Mitchell (2016). To address these questions the sets of constraints on the character pattern probabilities were determined for trees and convergence–divergence models of interest by transforming the character pattern probabilities into the Hadamard basis of Hendy and Penny (1989) and Hendy (1989). For example, one (trivial) constraint that arises on all models is that the sum of all character pattern probabilities must be  . The sets of constraints were compared for different trees and convergence–divergence models to determine whether they were distinguishable. Two models with non-identical sets of constraints are distinguishable, while two models are distinguishable with respect to a specific set of character pattern probabilities if the constraints on one model are met, but not on the other model.
. The sets of constraints were compared for different trees and convergence–divergence models to determine whether they were distinguishable. Two models with non-identical sets of constraints are distinguishable, while two models are distinguishable with respect to a specific set of character pattern probabilities if the constraints on one model are met, but not on the other model.
For the  -taxon case, Mitchell (2016) found some scenarios that were neither identifiable nor distinguishable in general from clock-like trees as well as some scenarios that were both identifiable and distinguishable from trees. In the next sections, we explore a simple
-taxon case, Mitchell (2016) found some scenarios that were neither identifiable nor distinguishable in general from clock-like trees as well as some scenarios that were both identifiable and distinguishable from trees. In the next sections, we explore a simple 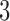 -taxon scenario and show an example of character pattern probabilities where a non-clock-like tree and convergence–divergence model cannot be distinguished on statistical grounds. Following that, 4-taxon convergence-divergence models are presented that can be distinguished from all trees.
-taxon scenario and show an example of character pattern probabilities where a non-clock-like tree and convergence–divergence model cannot be distinguished on statistical grounds. Following that, 4-taxon convergence-divergence models are presented that can be distinguished from all trees.
Choosing Between Models
Many models can be ruled out by an Occam’s razor argument—we do not want to consider models that are not identifiable. Furthermore, if two scenarios produce the same character pattern probabilities then we prefer the scenario with the smaller number of parameters.
An example of a clock-like tree and a convergence–divergence model with the same character pattern probabilities is given in Figure 2; there are two taxa and the Markov model of interest is the binary symmetric model. For a clock-like tree the probabilities of combinations of states depend on the height parameters, while the probabilities for a convergence–divergence model depend on the epoch lengths and whether there is convergence or divergence in the epoch. The 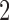 -taxon clock-like tree is identifiable as the specific probabilities can only be achieved by a single edge length. However, since the
-taxon clock-like tree is identifiable as the specific probabilities can only be achieved by a single edge length. However, since the 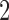 -taxon convergence–divergence model has two parameters, a divergence parameter and a convergence parameter, there are infinitely many pairs of divergence/convergence parameters that give rise to the same probabilities. The 2-taxon convergence–divergence model is neither identifiable nor is it distinguishable from the 2-taxon clock-like tree. As long as the divergence parameter is at least as long in the convergence–divergence model as in the clock-like tree there will always be a convergence parameter that gives equal probabilities under the two models. For a proof see page 77 of Mitchell (2016). The longer the divergence parameter in the convergence–divergence model, the longer the convergence parameter will need to be to “undo” the extra divergence such that the probabilities are equal to those on the clock-like tree.
-taxon convergence–divergence model has two parameters, a divergence parameter and a convergence parameter, there are infinitely many pairs of divergence/convergence parameters that give rise to the same probabilities. The 2-taxon convergence–divergence model is neither identifiable nor is it distinguishable from the 2-taxon clock-like tree. As long as the divergence parameter is at least as long in the convergence–divergence model as in the clock-like tree there will always be a convergence parameter that gives equal probabilities under the two models. For a proof see page 77 of Mitchell (2016). The longer the divergence parameter in the convergence–divergence model, the longer the convergence parameter will need to be to “undo” the extra divergence such that the probabilities are equal to those on the clock-like tree.
Figure 2.
A 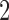 -taxon clock-like tree in Figure 2a and a
-taxon clock-like tree in Figure 2a and a 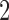 -taxon convergence-divergence model in Figure 2b. The length of the convergence epoch is dependent on the length of the divergence periods on the tree and the convergence–divergence model. The convergence–divergence model is neither identifiable, nor is it distinguishable from the tree.
-taxon convergence-divergence model in Figure 2b. The length of the convergence epoch is dependent on the length of the divergence periods on the tree and the convergence–divergence model. The convergence–divergence model is neither identifiable, nor is it distinguishable from the tree.
Furthermore, for the binary symmetric model Mitchell (2016) argued that if the 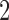 -taxon convergence–divergence model is embedded within a larger model then that model will not be identifiable. It will also not be distinguishable from the model created by removing the convergence period.
-taxon convergence–divergence model is embedded within a larger model then that model will not be identifiable. It will also not be distinguishable from the model created by removing the convergence period.
Referring back to the  -taxon case, from Mitchell (2016) the following scenarios are distinguishable in general: the clock-like tree (which has two height parameters), the non-clock-like tree (which has three edge parameters), and the convergence–divergence model with convergence between non-sister taxa (which has three epoch length parameters) (Fig. 1c). We do not consider the model in which the two sister taxa converge as it is not identifiable (as mentioned above). We also do not consider
-taxon case, from Mitchell (2016) the following scenarios are distinguishable in general: the clock-like tree (which has two height parameters), the non-clock-like tree (which has three edge parameters), and the convergence–divergence model with convergence between non-sister taxa (which has three epoch length parameters) (Fig. 1c). We do not consider the model in which the two sister taxa converge as it is not identifiable (as mentioned above). We also do not consider 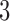 -taxon convergence–divergence models with taxa involved in multiple convergence groups or convergence–divergence models with more than three epochs, i.e. there is at most one period in which previously diverging taxa experience convergence. Considering the taxon labeling choices for three taxa, there are three clock-like trees, a single non-clock-like tree and six convergence–divergence models with convergence between non-sister taxa.
-taxon convergence–divergence models with taxa involved in multiple convergence groups or convergence–divergence models with more than three epochs, i.e. there is at most one period in which previously diverging taxa experience convergence. Considering the taxon labeling choices for three taxa, there are three clock-like trees, a single non-clock-like tree and six convergence–divergence models with convergence between non-sister taxa.
As with trees, counts of character patterns for convergence–divergence models will have multinomial distributions dependent on the specific models. The character pattern probabilities for 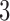 -taxon and
-taxon and 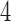 -taxon convergence–divergence models are described in detail in Mitchell (2016). To determine a best-fitting model traditional likelihood methods such as Akaike information criterion (AIC) can be applied for model selection.
-taxon convergence–divergence models are described in detail in Mitchell (2016). To determine a best-fitting model traditional likelihood methods such as Akaike information criterion (AIC) can be applied for model selection.
To choose between the ten models for three taxa given a particular data set (character pattern frequencies) we fit the parameters (node heights, edge lengths or epoch lengths) using a maximum likelihood approach and then calculate 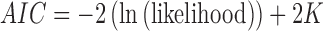 , where
, where 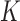 is the number of parameters (Burnham and Anderson 2002). Note that the non-clock-like tree and the non-sister convergence–divergence model have the same number of parameters (three edge or epoch length parameters respectively), whereas the clock-like tree has just two height parameters and so may still be preferred by AIC even if it has a lower likelihood.
is the number of parameters (Burnham and Anderson 2002). Note that the non-clock-like tree and the non-sister convergence–divergence model have the same number of parameters (three edge or epoch length parameters respectively), whereas the clock-like tree has just two height parameters and so may still be preferred by AIC even if it has a lower likelihood.
Exploring the 3-Taxon Case
In one of the earliest articles introducing maximum likelihood to phylogenetics, Felsenstein (1981) proposed that one test of the molecular clock hypothesis would be to compare the likelihood of models where all edges are free to models with a clock imposed. We extend this idea here by adding an extra possible scenario. Convergence–divergence models offer another possibility for explaining apparent violations of the molecular clock (i.e., distances that do not obey the three-point condition, where for any three taxa two of the pairwise distances are equal and no less than the third pairwise distance)—evolution may not be strictly divergent.
From the results of Mitchell (2016), we know that the clock-like tree, non-clock-like tree, and non-sister convergence–divergence model are distinguishable in general. That is, there exist character pattern probabilities that can arise on the non-sister convergence–divergence model that cannot arise on the non-clock-like tree. However, this does not guarantee that the different models will be distinguishable with respect to a particular set of character pattern probabilities.
A question that arises is how to compare the 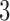 -taxon non-clock-like tree to the 3-taxon clock-like non-sister convergence–divergence model, as both have three parameters, one more than the
-taxon non-clock-like tree to the 3-taxon clock-like non-sister convergence–divergence model, as both have three parameters, one more than the 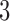 -taxon clock-like tree. We wish to know whether there are any circumstances in which we have a choice of a non-clock-like tree or a clock-like convergence–divergence model. To answer this question, we explored whether character pattern probabilities that arose on the non-clock-like tree could have also arisen on the clock-like convergence–divergence model and whether character pattern probabilities that arose on the clock-like convergence–divergence model could have also arisen on the non-clock-like tree. This involved finding algebraic conditions for the character pattern probabilities expected under a given model and comparing these conditions for different models. This approach has been explored by Klaere and Liebscher (2012), who looked at the conditions for the two-state general Markov model on tripod and quartet trees.
-taxon clock-like tree. We wish to know whether there are any circumstances in which we have a choice of a non-clock-like tree or a clock-like convergence–divergence model. To answer this question, we explored whether character pattern probabilities that arose on the non-clock-like tree could have also arisen on the clock-like convergence–divergence model and whether character pattern probabilities that arose on the clock-like convergence–divergence model could have also arisen on the non-clock-like tree. This involved finding algebraic conditions for the character pattern probabilities expected under a given model and comparing these conditions for different models. This approach has been explored by Klaere and Liebscher (2012), who looked at the conditions for the two-state general Markov model on tripod and quartet trees.
Figure 3 shows an example where particular choices of edge lengths for the non-clock-like tree and epoch lengths for the convergence–divergence model give rise to exactly the same set of character pattern probabilities. Additionally, there are two different non-sister convergence–divergence models that both give rise to the same character pattern probabilities. The same data can be explained either by a violation of the molecular clock, or by supposing convergence between some of the taxa. In some circumstances convergence-divergence models and non-clock-like trees cannot be distinguished for relatively small convergence epochs compared to the second divergence epoch.
Figure 3.
Three biologically different scenarios that are indistinguishable based on the character pattern probabilities that they induce. All edge and epoch lengths are drawn to scale.
An interesting feature of the three scenarios shown in Figure 3 is that in each scenario taxon 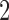 and taxon
and taxon 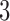 are always diverging. Indeed, the path distance from taxon
are always diverging. Indeed, the path distance from taxon 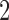 to taxon
to taxon 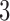 in the non-clock-like tree (
in the non-clock-like tree (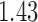 ) is equal to twice the sum of the epoch lengths in both the convergence–divergence models. The distance between taxon
) is equal to twice the sum of the epoch lengths in both the convergence–divergence models. The distance between taxon 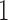 and taxon
and taxon 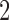 is the smallest but this is achieved in different ways in the two models. In Figure 3b taxon
is the smallest but this is achieved in different ways in the two models. In Figure 3b taxon 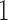 and taxon
and taxon  have only been diverging for a height of
have only been diverging for a height of 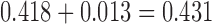 time units, whereas in Figure 3c these taxa have been diverging for a height of
time units, whereas in Figure 3c these taxa have been diverging for a height of 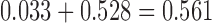 time units, but then have subsequently converged for
time units, but then have subsequently converged for 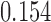 time units.
time units.
Now suppose we fix a 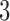 -taxon non-clock-like tree. We wish to determine whether an equivalent set of epoch lengths on a
-taxon non-clock-like tree. We wish to determine whether an equivalent set of epoch lengths on a  -taxon clock-like non-sister convergence–divergence model can be found. That is, we want to find whether there is a set of epoch lengths on the convergence–divergence model, such that all character pattern probabilities for the convergence–divergence model are equal to those for the non-clock-like tree.
-taxon clock-like non-sister convergence–divergence model can be found. That is, we want to find whether there is a set of epoch lengths on the convergence–divergence model, such that all character pattern probabilities for the convergence–divergence model are equal to those for the non-clock-like tree.
We start by finding expressions for the character pattern probabilities in terms of the edge lengths for the non-clock-like tree and in terms of the epoch lengths for the convergence–divergence model. By equating the character pattern probabilities for the non-clock-like tree and the convergence–divergence model, we can find expressions for the epoch lengths of the convergence–divergence model in terms of the edge lengths of the non-clock-like tree. Placing no restrictions on the set of edge lengths for the non-clock-like tree, there will always be one edge length that is less than or equal to the other two edge lengths. If we choose the taxon on this edge to be the taxon on the convergence-divergence model that is both in the cherry and involved in convergence (taxon 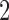 of Fig. 1c) then a set of epoch lengths on the convergence-divergence model can always be found that preserves the character pattern probabilities.
of Fig. 1c) then a set of epoch lengths on the convergence-divergence model can always be found that preserves the character pattern probabilities.
We are free to choose between the two choices of where we will place the remaining two taxa on the convergence–divergence model. The convergence–divergence models will always come in pairs, as seen in the example in Figure 3. Note however, that the epoch lengths on the two convergence–divergence models are not generally equal, but the character pattern probabilities are.
As a consequence, we are always free to choose between two taxon labelings on the convergence–divergence model. We can choose a convergence–divergence model where two lineages split well after the root, with only a short period of convergence between two non-sister taxa at the leaves, as shown in Figure 3b. Alternatively, we can choose a convergence–divergence model where the three lineages split from each other soon after the root, with a long period of convergence between the two non-sister taxa at the leaves, as shown in Figure 3c. These two convergence–divergence models will have identical likelihoods. In some situations there may be strong reasons to prefer one scenario, e.g., sympatric species would have more opportunity to become more similar via introgression than non-sympatric species. In the absence of any guiding information it perhaps seems more parsimonious to prefer the member of the pair that has the shortest convergence period.
We simulated edge lengths from a non-clock-like tree to determine whether there are sets of epoch lengths on the two convergence–divergence models such that all three models have the same character pattern probabilities and likelihoods. The edge lengths for the non-clock-like tree could represent any biological scenario where a non-clock-like tree is appropriate. For all simulations edge length parameters were randomly drawn from a uniform distribution from 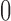 to
to 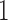 . The character pattern probabilities on this tree were determined and we then checked to see if we could find non-sister convergence–divergence models that achieved the same character pattern probabilities. Again, no specific biological scenario is assumed and the convergence–divergence model could represent any appropriate process.
. The character pattern probabilities on this tree were determined and we then checked to see if we could find non-sister convergence–divergence models that achieved the same character pattern probabilities. Again, no specific biological scenario is assumed and the convergence–divergence model could represent any appropriate process.
Of  random non-clock-like trees, all
random non-clock-like trees, all  gave character pattern probabilities that could be matched on a convergence–divergence model. Although not shown here, it can be proven that a matched convergence–divergence model exists for all choices of edges on the non-clock-like tree. Note that in Mitchell (2016) the potential for character pattern probabilities that could have arisen on the non-clock-like tree, but not on the non-sister convergence–divergence model, was left open. It is now known that these character pattern probabilities do not occur and that character pattern probabilities that arose on a non-clock-like tree can always be matched to character pattern probabilities that arose on a non-sister convergence–divergence model.
gave character pattern probabilities that could be matched on a convergence–divergence model. Although not shown here, it can be proven that a matched convergence–divergence model exists for all choices of edges on the non-clock-like tree. Note that in Mitchell (2016) the potential for character pattern probabilities that could have arisen on the non-clock-like tree, but not on the non-sister convergence–divergence model, was left open. It is now known that these character pattern probabilities do not occur and that character pattern probabilities that arose on a non-clock-like tree can always be matched to character pattern probabilities that arose on a non-sister convergence–divergence model.
We then did a similar simulation, but beginning instead with random choices of epoch lengths on a non-sister convergence–divergence model. The epoch lengths were samples from a uniform distribution from 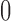 to
to 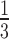 . The arbitrary truncation of epoch lengths at
. The arbitrary truncation of epoch lengths at 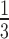 was chosen so that when matched to non-clock-like trees the edge lengths on the non-clock-like trees would on average be similar to the edge lengths on the non-clock-like trees in the first simulation, which were uniform from
was chosen so that when matched to non-clock-like trees the edge lengths on the non-clock-like trees would on average be similar to the edge lengths on the non-clock-like trees in the first simulation, which were uniform from  to
to 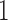 . The character pattern probabilities on the model were determined and we then checked to see if we could find a non-clock-like tree that achieved the same character pattern probabilities. Of
. The character pattern probabilities on the model were determined and we then checked to see if we could find a non-clock-like tree that achieved the same character pattern probabilities. Of  random models,
random models, 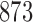 gave character pattern probabilities that could be fit equally well on a non-clock-like tree. Note that this proportion would be different if we chose not to sample epoch lengths from a uniform distribution from
gave character pattern probabilities that could be fit equally well on a non-clock-like tree. Note that this proportion would be different if we chose not to sample epoch lengths from a uniform distribution from 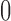 to
to  but instead from a different distribution.
but instead from a different distribution.
These results are consistent with the non-clock-like tree and the convergence–divergence model being distinguishable since there are some character pattern probabilities that could have only arisen on one and not on the other. However, the two models are not always distinguishable with respect to a specific set of character pattern probabilities. There are some character pattern probabilities that could have arisen on either model and some character pattern probabilities that could have only arisen on the convergence–divergence model and not on the non-clock-like tree.
Distances between leaves can be used to determine whether the convergence–divergence model is distinguishable from the clock-like tree or the non-clock-like tree. The distances between pairs of leaves on trees must all satisfy the triangle inequality. That is, the distance between any two leaves must be less than or equal to the sum of the other two distances between leaves. For the convergence–divergence model the triangle inequality is broken when the convergence period is sufficiently large.
Consider the taxon labeling in Figure 1c. One of the distance constraints from the triangle inequality is  .
. 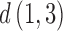 and
and  are simply twice the sum of the relevant epoch lengths since there is no convergence involved. For the triangle inequality to be met on the convergence–divergence model this is equivalent to
are simply twice the sum of the relevant epoch lengths since there is no convergence involved. For the triangle inequality to be met on the convergence–divergence model this is equivalent to 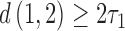 , where
, where  is the length of the epoch starting at the root. When the length of the convergence epoch
is the length of the epoch starting at the root. When the length of the convergence epoch 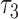 is large in comparison to the second epoch
is large in comparison to the second epoch 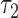 , then
, then 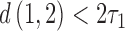 . The triangle inequality is broken and the distances are no longer true distances. Since the triangle inequality must be met for
. The triangle inequality is broken and the distances are no longer true distances. Since the triangle inequality must be met for 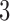 -taxon trees, when the convergence epoch is large enough character pattern probabilities that arose on the convergence–divergence model will not be consistent with any tree. When the amount of convergence is large enough the non-clock-like tree will not be a good fit to the data if the data arose on the convergence–divergence model. Simulated examples are shown in Figures 4 and 5 where the fit of the convergence–divergence model is better than the fit of the non-clock-like tree. In both examples, neither the likelihoods nor the distances between taxa are equal for the convergence–divergence model and the non-clock-like tree.
-taxon trees, when the convergence epoch is large enough character pattern probabilities that arose on the convergence–divergence model will not be consistent with any tree. When the amount of convergence is large enough the non-clock-like tree will not be a good fit to the data if the data arose on the convergence–divergence model. Simulated examples are shown in Figures 4 and 5 where the fit of the convergence–divergence model is better than the fit of the non-clock-like tree. In both examples, neither the likelihoods nor the distances between taxa are equal for the convergence–divergence model and the non-clock-like tree.
Figure 4.
A convergence–divergence model and a non-clock-like tree with different likelihoods despite having optimized edge and epoch lengths. Edge and epoch lengths are not drawn to scale.
Figure 5.
A second convergence–divergence model and a non-clock-like tree with different likelihoods despite having optimized edge and epoch lengths. Edge and epoch lengths are not drawn to scale.
The 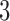 -taxon clock-like tree is nested within both the non-clock-like tree and the convergence–divergence model. As such, if character patterns arose on the clock-like tree they will always be consistent with having arisen on both the non-clock-like tree and the convergence–divergence model as well. The converse is not generally true. Character patterns probabilities that arose on a non-clock-like tree or a convergence–divergence model will not be consistent with having arisen on a clock-like tree unless certain distance constraints are met, such as the convergence epoch being zero. If the convergence epoch is non-zero the three-point condition will not be met, despite the convergence–divergence model still retaining the molecular clock assumption. For three taxa, if the character patterns arose on the non-clock-like tree they will always be consistent with having arisen on the convergence–divergence model. In contrast, if the character patterns arose on the convergence–divergence model they will only sometimes be consistent with having arisen on the non-clock-like tree. These scenarios are summarized in Table 1. Note that character pattern probabilities that arose on a convergence–divergence model are only sometimes consistent with having arisen on a non-clock-like tree.
-taxon clock-like tree is nested within both the non-clock-like tree and the convergence–divergence model. As such, if character patterns arose on the clock-like tree they will always be consistent with having arisen on both the non-clock-like tree and the convergence–divergence model as well. The converse is not generally true. Character patterns probabilities that arose on a non-clock-like tree or a convergence–divergence model will not be consistent with having arisen on a clock-like tree unless certain distance constraints are met, such as the convergence epoch being zero. If the convergence epoch is non-zero the three-point condition will not be met, despite the convergence–divergence model still retaining the molecular clock assumption. For three taxa, if the character patterns arose on the non-clock-like tree they will always be consistent with having arisen on the convergence–divergence model. In contrast, if the character patterns arose on the convergence–divergence model they will only sometimes be consistent with having arisen on the non-clock-like tree. These scenarios are summarized in Table 1. Note that character pattern probabilities that arose on a convergence–divergence model are only sometimes consistent with having arisen on a non-clock-like tree.
Table 1.
Summary of 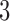 -taxon models, with the number of parameters and the other models that are consistent or possibly consistent with having character patterns arise on them
-taxon models, with the number of parameters and the other models that are consistent or possibly consistent with having character patterns arise on them
| Models | Parameters | Overlap |
|---|---|---|
| Clock-like tree (a) | 2 | b, c |
| Non-clock-like tree (b) | 3 | c |
| Non-sister convergence–divergence model (c) | 3 | b |
Extension to Four Taxa
In cases with four or more taxa the four-point condition can be used to check the distinguishability of convergence–divergence models and tree-like models. For convergence–divergence models the notion of distance is generalized in Mitchell (2016) as follows.  is the distance between leaves
is the distance between leaves 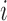 and
and  , where
, where  is the string of
is the string of 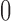 ’s and
’s and 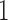 ’s with the
’s with the  ’s in the
’s in the  and
and 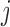 positions and
positions and 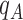 is the corresponding character pattern probability in the Hadamard basis. For example, for four taxa,
is the corresponding character pattern probability in the Hadamard basis. For example, for four taxa,  is the distance between leaves
is the distance between leaves  and
and 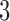 on any tree or convergence–divergence model. The four-point condition states that of the three sums of distances relating four leaves:
on any tree or convergence–divergence model. The four-point condition states that of the three sums of distances relating four leaves: 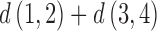 ,
, 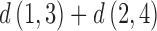 , and
, and  , two are equal and the third is less than or equal to the other two.
, two are equal and the third is less than or equal to the other two.
The four-point condition is satisfied for phylogenetic trees, however, it is not immediately obvious whether it is satisfied for convergence–divergence models. In Mitchell (2016)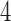 -taxon clock-like trees, convergence–divergence models and the non-clock-like tree were compared under the binary symmetric model with the four-point condition. For simplicity, only convergence–divergence models with convergence immediately before the leaves between two taxa were considered. Convergence between sister taxa was not considered as these models are not identifiable or distinguishable from the clock-like trees that result from removing the convergence.
-taxon clock-like trees, convergence–divergence models and the non-clock-like tree were compared under the binary symmetric model with the four-point condition. For simplicity, only convergence–divergence models with convergence immediately before the leaves between two taxa were considered. Convergence between sister taxa was not considered as these models are not identifiable or distinguishable from the clock-like trees that result from removing the convergence.
Of the four possible convergence–divergence models, three did not satisfy the four-point condition. For these convergence–divergence models the four-point condition could be used to determine whether they are distinguishable from a tree. Interestingly, the convergence–divergence model with an underlying clock-like caterpillar tree shown in Figure 6 also satisfies the four-point condition:
 |
Figure 6.

A  -taxon convergence–divergence model that satisfies the four-point condition, yet is distinguishable from clock-like trees and the non-clock-like tree. There are character pattern probabilities that are consistent with this convergence–divergence model that are not consistent with a tree.
-taxon convergence–divergence model that satisfies the four-point condition, yet is distinguishable from clock-like trees and the non-clock-like tree. There are character pattern probabilities that are consistent with this convergence–divergence model that are not consistent with a tree.
Since all pairs of taxa other than taxa 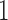 and
and 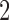 are always diverging,
are always diverging,
 |
where 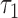 to
to  are the lengths of the epochs starting at the root and moving down. The distance between taxa
are the lengths of the epochs starting at the root and moving down. The distance between taxa  and
and 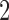 will be
will be
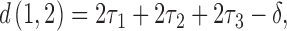 |
where 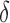 increases from
increases from  to
to 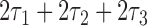 as the convergence period increases from
as the convergence period increases from  to being infinitely long. Then
to being infinitely long. Then
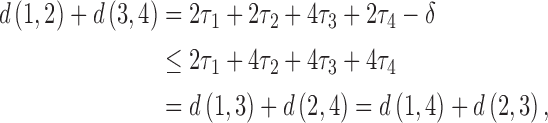 |
and the four-point condition is met for all sets of epoch lengths.
However, this convergence–divergence model is still distinguishable from a clock-like caterpillar tree obtained by removing the convergence since the distances between pairs of leaves sharing the root as the ancestral node are not all equal, with
 |
Similarly, this convergence–divergence model is distinguishable from the non-clock-like tree since  and
and  . For non-clock-like trees, generally the distance between a pair of leaves will not equal the distance between any other pair of leaves since all edge lengths are free to vary. Character pattern probabilities that are consistent with the non-clock-like tree will not generally be consistent with the convergence–divergence model.
. For non-clock-like trees, generally the distance between a pair of leaves will not equal the distance between any other pair of leaves since all edge lengths are free to vary. Character pattern probabilities that are consistent with the non-clock-like tree will not generally be consistent with the convergence–divergence model.
In Mitchell (2016) it is shown that the four 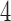 -taxon convergence–divergence models, the non-clock-like tree and the two clock-like trees (caterpillar and balanced) are distinguishable from each other. There are possible character pattern probabilities that could have arisen on one, but not on another.
-taxon convergence–divergence models, the non-clock-like tree and the two clock-like trees (caterpillar and balanced) are distinguishable from each other. There are possible character pattern probabilities that could have arisen on one, but not on another.
Character pattern probabilities that are consistent with one of the  -taxon convergence–divergence models with a non-zero convergence epoch will not be consistent with a clock-like tree since the distance between one pair of leaves has been decreased by the convergence and the three-point condition will not be met. The distance between converging leaves on the
-taxon convergence–divergence models with a non-zero convergence epoch will not be consistent with a clock-like tree since the distance between one pair of leaves has been decreased by the convergence and the three-point condition will not be met. The distance between converging leaves on the 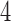 -taxon convergence-divergence model is now less than twice the sum of the relevant epoch lengths, the distance between leaves on a clock-like tree.
-taxon convergence-divergence model is now less than twice the sum of the relevant epoch lengths, the distance between leaves on a clock-like tree.
As in the  -taxon case, character pattern probabilities that are consistent with a
-taxon case, character pattern probabilities that are consistent with a 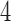 -taxon convergence–divergence model are only sometimes consistent with a non-clock-like tree. For those
-taxon convergence–divergence model are only sometimes consistent with a non-clock-like tree. For those 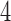 -taxon convergence–divergence models that don’t satisfy the four-point condition, character pattern probabilities will not be consistent with any tree. It is only the
-taxon convergence–divergence models that don’t satisfy the four-point condition, character pattern probabilities will not be consistent with any tree. It is only the 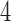 -taxon convergence–divergence model of Figure 6, which satisfies the four-point condition, that may have character pattern probabilities consistent with a non-clock-like tree.
-taxon convergence–divergence model of Figure 6, which satisfies the four-point condition, that may have character pattern probabilities consistent with a non-clock-like tree.
Subject to our restrictions, all of the 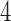 -taxon convergence–divergence models we consider have the
-taxon convergence–divergence models we consider have the 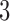 -taxon convergence–divergence model embedded in them. Since there are character pattern probabilities that could have arisen on the
-taxon convergence–divergence model embedded in them. Since there are character pattern probabilities that could have arisen on the 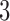 -taxon convergence–divergence model but not on the
-taxon convergence–divergence model but not on the  -taxon non-clock-like tree, the same must be true for the
-taxon non-clock-like tree, the same must be true for the  -taxon case. As in the
-taxon case. As in the  -taxon case, when the convergence epoch of Figure 6 is large enough character pattern probabilities that are consistent with a
-taxon case, when the convergence epoch of Figure 6 is large enough character pattern probabilities that are consistent with a 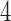 -taxon convergence–divergence model are not consistent with a non-clock-like tree since the triangle inequality is not met. In contrast to the
-taxon convergence–divergence model are not consistent with a non-clock-like tree since the triangle inequality is not met. In contrast to the 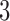 -taxon case, character pattern probabilities that are consistent with a non-clock-like tree will almost always not be consistent with a convergence–divergence model, unless the appropriate distances between pairs of taxa on the non-clock-like tree are equal.
-taxon case, character pattern probabilities that are consistent with a non-clock-like tree will almost always not be consistent with a convergence–divergence model, unless the appropriate distances between pairs of taxa on the non-clock-like tree are equal.
Extension to n Taxa
For 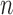 -taxon convergence–divergence models tests of distances between leaves can be used to determine distinguishability from trees. The four-point condition can be used as a simple test to determine distinguishability between convergence–divergence models and all trees. We have shown for
-taxon convergence–divergence models tests of distances between leaves can be used to determine distinguishability from trees. The four-point condition can be used as a simple test to determine distinguishability between convergence–divergence models and all trees. We have shown for 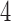 -taxon convergence–divergence models that the four-point condition is sometimes met even though a tree is not present. However, when the four-point condition is met on an
-taxon convergence–divergence models that the four-point condition is sometimes met even though a tree is not present. However, when the four-point condition is met on an 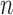 -taxon convergence–divergence model there will still be distances between leaves that are not consistent with a clock-like tree. The distances may also not be consistent with a non-clock-like tree.
-taxon convergence–divergence model there will still be distances between leaves that are not consistent with a clock-like tree. The distances may also not be consistent with a non-clock-like tree.
For clock-like trees the distances between any pair of leaves sharing an ancestral node must be equal. Provided some assumptions are made, this will never be true for convergence–divergence models. We will assume the only convergence epoch is the last epoch in time, no lineage is involved in multiple convergence groups and not all lineages are converging together, such as in Figure 2b. Convergence decreases the distances between some pairs of leaves, while leaving distances between taxa that diverge from each other unchanged. Provided these assumptions are met, convergence–divergence models will be distinguishable from clock-like trees since the three-point condition is not met. Character pattern probabilities that are consistent with convergence–divergence models will not be consistent with clock-like trees provided there is some convergence. On the other hand, character pattern probabilities that are consistent with clock-like trees will be consistent with convergence–divergence models with no convergence.
Subject to these same restrictions, there are always embedded  -taxon convergence–divergence models which have two taxa involved in convergence and one diverging from both of the other two. This is either the convergence–divergence model of Figure 1c or the convergence–divergence model with convergence between taxa
-taxon convergence–divergence models which have two taxa involved in convergence and one diverging from both of the other two. This is either the convergence–divergence model of Figure 1c or the convergence–divergence model with convergence between taxa 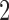 and
and  . Since both convergence–divergence models are distinguishable from the
. Since both convergence–divergence models are distinguishable from the 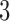 -taxon non-clock-like tree,
-taxon non-clock-like tree,  -taxon clock-like convergence–divergence models must also be distinguishable from
-taxon clock-like convergence–divergence models must also be distinguishable from  -taxon non-clock-like trees. The constraints on the distances involving only these three taxa differ between convergence–divergence models and non-clock-like trees. As in the
-taxon non-clock-like trees. The constraints on the distances involving only these three taxa differ between convergence–divergence models and non-clock-like trees. As in the 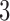 -taxon and
-taxon and  -taxon cases, character pattern probabilities that are consistent with an
-taxon cases, character pattern probabilities that are consistent with an 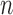 -taxon convergence–divergence model may or may not be consistent with a non-clock-like tree depending on the length of the convergence epoch and whether the four-point condition is met. If the convergence epoch is large enough then the triangle inequality breaks down. Similarly, character pattern probabilities that are consistent with a non-clock-like tree will almost always not be consistent with a convergence–divergence model, unless some distances between pairs of taxa are equal to each other on the non-clock-like tree.
-taxon convergence–divergence model may or may not be consistent with a non-clock-like tree depending on the length of the convergence epoch and whether the four-point condition is met. If the convergence epoch is large enough then the triangle inequality breaks down. Similarly, character pattern probabilities that are consistent with a non-clock-like tree will almost always not be consistent with a convergence–divergence model, unless some distances between pairs of taxa are equal to each other on the non-clock-like tree.
In summary, clock-like convergence–divergence models that meet our restrictions will be distinguishable from all clock-like trees and non-clock-like trees. There will always be some character pattern probabilities that could have arisen on a clock-like convergence–divergence model, but not on a clock-like tree or a non-clock-like tree.
Discussion
Under the assumption of tree-like evolution, the number of structural parameters needed is determined by the number of taxa under consideration (e.g., in a non-clock-like binary tree with  taxa we have
taxa we have 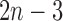 edges). Thus phylogeneticists usually need not think about the number of structural parameters required. However, when we remove the tree assumption we have to think more carefully about parameter selection (Holland 2013).
edges). Thus phylogeneticists usually need not think about the number of structural parameters required. However, when we remove the tree assumption we have to think more carefully about parameter selection (Holland 2013).
It is increasingly apparent that there are many biologically reasonable causes of non-tree-like evolution, so it seems clear that we should consider a broader range of models. In many cases, it is possible to choose between competing scenarios on the basis of AIC, however, an example we give here shows that this will not always be the case. In the scenario presented here we show two competing biologically reasonable scenarios that give identical likelihoods and have the same number of parameters. Which should we prefer? In the end it depends if we believe more in a molecular clock or if we believe more strongly in a divergence-only model. Sometimes we may be able to bring extra information to the problem. For example, to choose between two pairs of models we might know that two species are sympatric and that there is some opportunity for gene-flow, whereas two other species are not. Note, however, that we don’t have a statistical way to choose between models and cannot escape the need for knowledge of the underlying biology/geography. It is possible that this issue could be addressed with Bayesian methods that assign different prior probabilities to different models based on expert opinion of which scenarios are most plausible.
As discussed earlier, Steel (2005) raised two important issues regarding model fit. We want a model that has both enough parameters to be biologically realistic and few enough parameters to not over-fit the data. In the past, phylogeneticists have often rejected models with the molecular clock hypothesis due to their tendency to not have enough parameters to be biologically realistic.
An alternative to the molecular clock assumption is a non-clock-like tree. Removing the molecular clock approximately doubles the number of parameters for large numbers of taxa, which can result in over-fitting the data. If both a clock-like tree under-fits the data and a non-clock-like tree over-fits the data then a model with an intermediate number of parameters may be more appropriate, such as a relaxed clock model of Drummond et al. (2006). Our clock-like convergence–divergence models provide an alternative approach to relaxed clock models when clock-like trees under-fit the data. Any number of extra parameters beyond those on clock-like trees can be introduced. Extra parameters can be added one at a time until there is no statistically significant improvement to the fit of the model to the data, as judged by the AIC. One must take care in the order of introduction of convergence epochs as there are many possible scenarios that could be modeled with convergence–divergence models.
A challenge that arises is determining which convergence–divergence model fits the data best. For a small number of taxa an exhaustive search over all possible convergence–divergence models according to our restrictions is possible. For a large number of taxa we need to be more targeted. One potential approach could be to first optimize the fit for a clock-like tree and then “perturb” the clock-like tree slightly by adding convergence on parts of the tree where the molecular clock appears to be insufficient in explaining all of the variance in the data. It is possible that this approach will not result in the optimal convergence–divergence model, however, it may still result in a convergence–divergence model that fits the data better than a clock-like tree.
Francis and Steel (2015) found that the four-point condition may be satisfied for hybridization and HGT networks. They argued that this is consistent with the four-point condition being met if and only if there is a tree metric, since any distances that satisfy the four-point condition must be consistent with a tree, even if they are also consistent with a hybridization or HGT network. Our convergence-divergence models are fundamentally different to hybridization and HGT networks since the four-point condition can be met for some convergence–divergence models despite the distances not fitting on any tree. The four-point condition is met for all sets of epoch lengths for the convergence–divergence model of Figure 6. However, as we have argued earlier, when the convergence epoch is large enough the character pattern probabilities (and also the distances) will not be consistent with a tree. For  taxa there will be some character pattern probabilities that are consistent with a convergence–divergence model but not with a non-clock-like tree, regardless of whether the four-point condition is met or not.
taxa there will be some character pattern probabilities that are consistent with a convergence–divergence model but not with a non-clock-like tree, regardless of whether the four-point condition is met or not.
Future work will involve exploring more than three and four taxa, as well as examining more biologically realistic Markov models than the binary symmetric model. The Python script supplied in the Supplementary material available on Dryad is capable of comparing models for  taxa, although only
taxa, although only  -taxon and
-taxon and 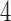 -taxon examples were explored here. The binary symmetric model was chosen to clearly illustrate our salient points, however, in principle the same mathematical techniques can be applied to the general Markov model on any number of states. In particular, the results could be extended to the two-state general Markov model. The two-state general Markov model is of interest because it could be applied to the binary presence/absence data of ddRAD or for morphological data.
-taxon examples were explored here. The binary symmetric model was chosen to clearly illustrate our salient points, however, in principle the same mathematical techniques can be applied to the general Markov model on any number of states. In particular, the results could be extended to the two-state general Markov model. The two-state general Markov model is of interest because it could be applied to the binary presence/absence data of ddRAD or for morphological data.
Acknowledgments
The authors would like to thank the editors and reviewers for their helpful comments.
Supplementary Material
Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.n8m9c.
Funding
This work was supported by the Australian Postgraduate Award, Australian Research Council awards FT100100031 and DP150100088, and the US National Institutes of Health grant R01 GM117590, awarded under the Joint DMS/NIGMS Initiative to Support Research at the Interface of the Biological and Mathematical Sciences.
References
- Allman E.S., Rhodes J.A.. 2008. Identifying evolutionary trees and substitution parameters for the general Markov model with invariable sites. Math. Biosci. 211:18–33. [DOI] [PubMed] [Google Scholar]
- Bandelt H.-J., Dress A.W.. 1992. Split decomposition: a new and useful approach to phylogenetic analysis of distance data. Mol. Phylogenet. Evol. 1:242–252. [DOI] [PubMed] [Google Scholar]
- Bryant D. 2009. Hadamard phylogenetic methods and the n-taxon process. Bull. Math. Biol. 71:339–351. [DOI] [PubMed] [Google Scholar]
- Bryant D., Moulton V.. 2002. Neighbornet: an agglomerative method for the construction of planar phylogenetic networks. In: Guigó, Roderic,, Gusfield, Dan, editors. Algorithms in Bioinformatics. Berlin, Heidelberg: Springer; p. 375–391. [Google Scholar]
- Burnham K.P., Anderson D.R.. 2002. Model selection and multimodel inference: a practical information-theoretic approach. New York: Springer-Verlag. [Google Scholar]
- Drummond A.J., Ho S.Y., Phillips M.J., Rambaut A.. 2006. Relaxed phylogenetics and dating with confidence. PLoS Biol. 4:e88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellstrand N.C., Prentice H.C., Hancock J.F.. 1999. Gene flow and introgression from domesticated plants into their wild relatives. Ann. Rev. Ecol. Syst. 30:539–563. [Google Scholar]
- Emery N.J., Clayton N.S.. 2004. The mentality of crows: convergent evolution of intelligence in corvids and apes. Science. 306:1903–1907. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17:368–376. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 2013. Numerical taxonomy, Vol. 1 Springer-Verlag Berlin Heidelberg. [Google Scholar]
- Francis A.R., Steel M.. 2015. Tree-like reticulation networks when do tree-like distances also support reticulate evolution? Math. Biosci. 259:12–19. [DOI] [PubMed] [Google Scholar]
- Green R.E., Krause J., Briggs A.W., Maricic T., Stenzel U., Kircher M., Patterson N., Li H., Zhai W., Fritz M.H.-Y., et al. et alet al. 2010. A draft sequence of the Neandertal genome. Science. 328:710–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendy M.D. 1989. The relationship between simple evolutionary tree models and observable sequence data. Syst. Zool. 38:310–321. [Google Scholar]
- Hendy M.D., Penny D.. 1989. A framework for the quantitative study of evolutionary trees. Syst. Zool. 38:297–309. [Google Scholar]
- Hey J. 2010. Isolation with migration models for more than two populations. Mol. Biol. Evol. 27:905–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland B.R. 2013. The rise of statistical phylogenetics. Aust. N. Z. J. Stat. 55:205–220. [Google Scholar]
- Holland B.R., Spencer H.G., Worthy T.H., Kennedy M.. 2010. Identifying cliques of convergent characters: Concerted evolution in the cormorants and shags. Syst. Biol. 59:433–445. [DOI] [PubMed] [Google Scholar]
- Huson D.H., Bryant D.. 2005. Application of phylogenetic networks in evolutionary studies. Mol. Biol. Evol. 23:254–267. [DOI] [PubMed] [Google Scholar]
- Jaccoud D., Peng K., Feinstein D., Kilian A.. 2001. Diversity arrays: a solid state technology for sequence information independent genotyping. Nucleic Acids Res. 29:e25–e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin G., Nakhleh L., Snir S., Tuller T.. 2006. Maximum likelihood of phylogenetic networks. Bioinformatics. 22:2604–2611. [DOI] [PubMed] [Google Scholar]
- Klaere S., Liebscher V.. 2012. An algebraic analysis of the two state markov model on tripod trees. Math. Biosci. 237:38–48. [DOI] [PubMed] [Google Scholar]
- Lengyel S., Gove A.D., Latimer A.M., Majer J.D., Dunn R.R.. 2010. Convergent evolution of seed dispersal by ants, and phylogeny and biogeography in flowering plants: a global survey. Perspect. Plant Ecol. Evol. Syst. 12:43–55. [Google Scholar]
- Lepage T., Bryant D., Philippe H., Lartillot N.. 2007. A general comparison of relaxed molecular clock models. Mol. Biol. Evol. 24:2669–2680. [DOI] [PubMed] [Google Scholar]
- Lewis P.O. 2001. A likelihood approach to estimating phylogeny from discrete morphological character data. Syst. Biol. 50:913–925. [DOI] [PubMed] [Google Scholar]
- Liu Y., Cotton J.A., Shen B., Han X., Rossiter S.J., Zhang S.. 2010. Convergent sequence evolution between echolocating bats and dolphins. Curr. Biol. 20:R53–R54. [DOI] [PubMed] [Google Scholar]
- Mitchell J.D. 2016. Distinguishing convergence on phylogenetic networks [PhD thesis]. University of Tasmania https://arxiv.org/abs/1606.07160. [Google Scholar]
- Nakhleh L. 2010. Evolutionary phylogenetic networks: models and issues. In: Heath, Lenwood S.,, Ramakrishnan, Naren, editors. Problem solving handbook in computational biology and bioinformatics. Boston, MA: Springer US; p. 125–158. [Google Scholar]
- Norberg U.M. 1986. Evolutionary convergence in foraging niche and flight morphology in insectivorous aerial-hawking birds and bats. Ornis Scand. 17:253–260. [Google Scholar]
- Reece J.B., Urry L.A., Cain M.L., Wasserman S.A., Minorsky P.V., Jackson R.B.. 2014. Campbell biology. Boston: Pearson Higher Education. [Google Scholar]
- Rhymer J.M., Simberloff D.. 1996. Extinction by hybridization and introgression. Ann. Rev. Ecol. Syst. 27:83–109. [Google Scholar]
- Sage R.F. 2004. The evolution of c4 photosynthesis. New Phytol. 161:341–370. [DOI] [PubMed] [Google Scholar]
- Seehausen O., Takimoto G., Roy D., Jokela J.. 2008. Speciation reversal and biodiversity dynamics with hybridization in changing environments. Mol. Ecol. 17:30–44. [DOI] [PubMed] [Google Scholar]
- Sheppard S.K., McCarthy N.D., Falush D., Maiden M.C.. 2008. Convergence of Campylobacter species: Implications for bacterial evolution. Science. 320:237–239. [DOI] [PubMed] [Google Scholar]
- Sheppard S.K., McCarthy N.D., Jolley K.A., Maiden M.C.. 2011. Introgression in the genus Campylobacter: generation and spread of mosaic alleles. Microbiology. 157:1066–1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steel M. 2005. Should phylogenetic models be trying to ‘fit an elephant’? Trends Genet. 21:307–309. [DOI] [PubMed] [Google Scholar]
- Sumner J., Holland B., Jarvis P.. 2012. The algebra of the general Markov model on phylogenetic trees and networks. Bull. Math. Biol. 74:858–880. [DOI] [PubMed] [Google Scholar]
- Taylor E., Boughman J., Groenenboom M., Sniatynski M., Schluter D., Gow J.. 2006. Speciation in reverse: morphological and genetic evidence of the collapse of a three-spined stickleback (Gasterosteus aculeatus) species pair. Mol. Ecol. 15:343–355. [DOI] [PubMed] [Google Scholar]
- Werdelin L. 1986. Comparison of skull shape in marsupial and placental carnivores. Aust. J. Zool. 34:109–117. [Google Scholar]







