Insights Into Traumatic Brain Injury From MRI of Harmonic Brain Motion

Abstract

Measurements of dynamic deformation of the human brain, induced by external harmonic vibration of the skull, were analyzed to illuminate the mechanics of mild traumatic brain injury (TBI). Shear wave propagation velocity vector fields were obtained to illustrate the role of the skull and stiff internal membranes in transmitting motion to the brain. Relative motion between the cerebrum and cerebellum was quantified to assess the vulnerability of connecting structures. Mechanical deformation was quantified throughout the brain to investigate spatial patterns of strain and axonal stretch. Strain magnitude was generally attenuated as shear waves propagated into interior structures of the brain; this attenuation was greater at higher frequencies. Analysis of shear wave propagation direction indicates that the stiff membranes (falx and tentorium) greatly affect brain deformation during imposed skull motion as they serve as sites for both initiation and reflection of shear waves. Relative motion between the cerebellum and cerebrum was small in comparison with the overall motion of both structures, which suggests that such relative motion might play only a minor role in TBI mechanics. Strain magnitudes and the amount of axonal stretch near the bases of sulci were similar to those in other areas of the cortex, and local strain concentrations at the gray-white matter boundary were not observed. We tentatively conclude that observed differences in neuropathological response in these areas might be due to heterogeneity in the response to mechanical deformation rather than heterogeneity of the deformation itself.

Introduction

Mild traumatic brain injury (mTBI) is a pernicious injury that may have lasting deleterious effects on memory, cognition, and emotion. Football players who experience multiple head impacts over many years are known to be at risk for chronic traumatic encephalopathy (CTE)^1,2—a neurodegenerative disease that is characterized by accumulations of tau protein in specific cortical regions. The Centers for Disease Control and Prevention (CDC) estimates that over 3 million sports-related concussions occur each year in the United States.³

Despite the wide prevalence and medical importance of TBI, the mechanisms that connect the initial mechanical insult (head acceleration) to eventual cognitive and emotional dysfunction remain mysterious even after decades of study. This is due, in part, to the impossibility of observing actual deformation of the brain during injurious impacts and the additional challenge of accurately measuring this deformation. Although head accelerations are now routinely estimated using arrays of external sensors in mouthguards or helmets, head acceleration is only a coarse marker of the actual microscale mechanical events that affect brain function. These likely include rapid stretch of neuronal cell bodies, axons, microvasculature, and other tissue components that may trigger cell death or dysfunction at the microscale.

The measurement challenge in understanding brain deformation associated with TBI is two-fold. First, the brain is completely hidden inside the skull, and, second, researchers must not risk injury to human subjects. Animal studies and in vitro studies are not straightforward to interpret in the context of human TBI because the size, shape, and anatomical structure of the brain are critically important to its mechanical response. In fact, to be useful, cell-level deformations (strains) in animal models and in vitro studies of TBI should replicate strains characteristic of injurious events in humans.

Magnetic resonance elastography (MRE) provides a safe and non-invasive way to visualize and measure dynamic deformation of internal soft tissue in the brain caused by external motion of the skull.⁴ In conventional MRE, these measurements of deformation are “inverted” to estimate the mechanical properties of the tissue, such as its elastic stiffness and viscous damping, in different brain regions.^5–8 However, MRE data sets contain a wealth of additional information about the mechanical behavior of the brain and its mechanical environment. Magnetic resonance elastography raw data consist of three-dimensional (3D) displacement fields throughout the entire brain with voxel resolution of 2 to 3 mm or smaller. Brain motion in MRE can be decomposed into dynamic deformation and bulk motion,^9,10 although this latter term is often discarded. These displacement fields can be analyzed to determine the interactions between external structures (such as the falx) and the brain, between different anatomical components of the brain (cerebellum and cerebrum) or deformations in particular regions in specific directions.

Magnetic resonance elastography data are acquired during steady-state harmonic motion, although injuries typically occur during short (transient) impulsive events, so that MRE is an indirect approach to studying TBI. Although other techniques based on tagged magnetic resonance imaging (MRI) have recently been developed and applied to measure the brain response to transient head acceleration,^11–13 these studies are extremely challenging technically. Only recently has the capability to measure 3D strain fields in the brain been achieved with tagged MRI,¹⁴ and these images still currently have a significantly lower spatial resolution than MRE. In simple mechanical systems, the response to harmonic motion at multiple frequencies can be used to accurately describe the impulse response. In the brain, which exhibits nonlinear behavior, the relationship between harmonic and impulsive motion is not precise, but the harmonic response available through MRE measurements still illuminates fundamental mechanical behavior of the brain.

In this article, we use MRE data to explore three potential deformation mechanisms that may be important in TBI. First, we extract and analyze vector fields of propagation direction for shear waves in the brain to characterize the roles of the stiff internal membranes, the falx cerebri and the tentorium cerebelli, in transmitting skull motion to the brain. Second, the relative motion between cerebrum and cerebellum is quantified as the fiber bundles that couple these structures to each other and to the brainstem are potential injury sites.¹⁵ Finally, we measure deformation (strain) at high resolution throughout the brain during harmonic skull motion. From such strain maps, we seek to assess whether strain magnitude or axonal stretch is higher at the gray matter–white matter boundaries or near the bases of sulci. A number of neuropathology studies have suggested that axonal injury occurs preferentially at the boundaries between gray and white matter and have speculated that this may be due to strain concentrations associated with steep gradients in material properties at this interface.^16,17 Sulcal regions exhibit aggregations of the protein tau associated with CTE.¹⁸ Some authors have speculated that more prominent tau accumulations near sulci may be due to higher strains in these regions,^19,20 but direct evidence of higher strains in these areas remains lacking.

Methods

General methodology for brain MRE

Magnetic resonance elastography of the brain involves 3 steps: (1) generation of harmonic motion in brain tissue by vibration applied externally to the skull; (2) measurement of harmonic tissue motion using an MRI pulse sequence designed to generate images in which the contrast is proportional to displacement; and (3) analysis of dynamic, 3D displacement fields to identify important features of brain motion. Traditionally, this analysis has consisted solely of “inversion” of the wave equations to identify material parameters. Here we analyze other features of the displacement field to gain insight into brain mechanics and TBI.

Experimental methods and data acquisition

Fifteen adult human subjects (10 male, 5 female; age 20-73 years) were scanned using a Siemens Trio 3T scanner. All studies were approved by the Institutional Review Board at Washington University in St. Louis, and subjects provided written informed consent. Subjects lay supine with the head positioned in a 12-channel head coil. Skull vibrations were induced at a frequency of 50 Hz using a mechanical actuator (Resoundant™, Rochester, MN) that generates acoustic frequency pressure waves which are conveyed to a pillow-like actuator (Mayo Clinic, Rochester, MN) positioned under the back of the skull occipital protuberance (Figure 1). In a previous study using the same actuation system, we found that the actuator generated harmonic skull motion amplitudes of 25 to 50 microns, primarily in the anterior-posterior (AP) direction.⁹

Figure 1.

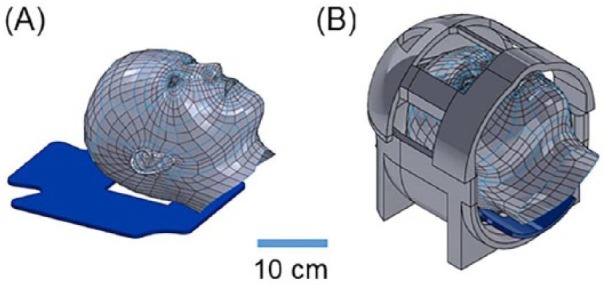
Experimental setup for measurement of skull and brain motion during magnetic resonance elastography (MRE). (A) Pillow actuator. (B) Subject in head coil.

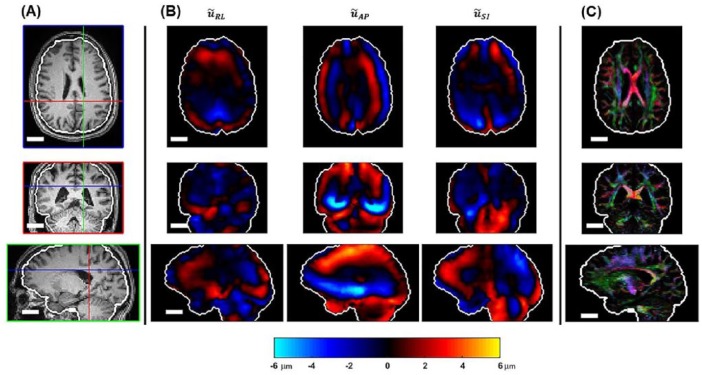
Phase contrast images of the harmonically varying displacement field were obtained in a 240 × 240 × 120 mm³ imaging volume with 2-mm isotropic voxels using a 3D multislab, multishot spiral MRE pulse sequence⁸ with 8 temporal samples acquired per period of harmonic motion. Images were phase unwrapped and temporally Fourier transformed to create complex, full vector displacement fields spanning the entire brain. Expressed in Cartesian components, the position of each voxel is denoted by $X=[x,y,z]$, where $x$ is the coordinate in the right-left (RL) direction, $y$ is the AP coordinate, and $z$ is the coordinate in the inferior-superior (IS) direction. The corresponding displacement vector at each voxel is denoted by $u=[u_{RL},u_{AP},u_{SI}]$. The displacement field may be written as $u(X,t)$ to show explicitly that displacement depends on both position, $X$, and time, $t$. Diffusion tensor imaging (DTI) images were acquired over the same volume and with the same spatial resolution as the MRE images to estimate white matter fiber direction. The DTI scans used a single-shot echo-planar imaging (EPI) acquisition with 30 diffusion directions and b-value of 1000 s/mm². Phase-encoding was in the AP direction; an additional acquisition was obtained without diffusion encoding and the phase-encoding direction reversed (posterior-anterior) for correction of distortion from field inhomogeneity. Diffusion tensor images were corrected for motion and eddy currents with TORTOISE v 1.4,²¹ then corrected for EPI distortion as previously described by Holland et al.²² Nonlinear tensor fitting was performed using RESTORE²³ to provide diffusion tensor metrics such as eigenvectors and eigenvalues for each voxel in the MRE/DTI imaging volume. T₁-weighted MRI image volumes (T1W, 0.9-mm isotropic) were also obtained and the brain was extracted using the TOADS-CRUISE algorithm.²⁴ The resulting brain images were registered to the MRE/DTI image volumes (Figure 2). For voxels in the DTI image volume that had a fractional anisotropy (FA) value greater than a threshold (FA > 0.2), and were segmented as cerebellar or cerebral white matter, the eigenvector corresponding to the direction of maximal diffusivity was considered as the dominant axonal fiber direction.

Figure 2.

Example data set showing (A) T₁-weighted image slices in axial, coronal, and sagittal planes. Crosshair lines indicate location of orthogonal slices. (B) MRE data: $u_{RL},u_{AP},u_{SI}$ wave displacement components corresponding to RL, AP, SI motion, respectively. (C) Directionally encoded DTI color map where colors (red = RL, green = AP, blue = SI) indicate direction of maximum diffusivity and brightness indicates strength of anisotropy. Scale bar equals 4 cm in all images. AP indicates anterior-posterior; DTI, diffusion tensor imaging; MRE, magnetic resonance elastography; RL, right-left; SI, superior-inferior.

Additional MRE experiments were performed to examine strain fields at multiple frequencies. Three adult male subjects (24-35 years) were scanned using a Siemens 3T Prisma scanner with 64-channel head coil, and vibrations were similarly generated using the Resoundant™ actuator and pillow driver. Magnetic resonance elastography data were acquired at 3 separate frequencies—30, 50, and 70 Hz—on each subject in a single scan session using an EPI sequence. Displacement data at each frequency were acquired over the same 240 × 240 × 120 mm³ imaging volume with 2.5-mm isotropic voxels.

Data analysis

Bulk motion and dynamic deformation

The displacement data can then be further separated into bulk (or harmonic rigid body) displacement, $(\overline{u})$, and dynamic deformation $(\tilde{u})$, such that $u(X,t)=\overline{u}(X,t)+\tilde{u}(X,t)$. The bulk motion of the brain was computed by fitting the displacement field in the MRE imaging volume to the equations for translation and rotation of a rigid body. Dynamic deformation was obtained by subtracting the rigid-body motion from the total displacement field.⁹ We refer to dynamic deformation as “wave motion” for the remainder of this work.

Shear wave propagation direction

Amplitude-weighted shear wave propagation directions were estimated by directionally filtering the curl of the displacement field.²⁵ The curl $(\Gamma =\nabla \times u)$ is advantageous to use because it contains no contributions from rigid-body motion or longitudinal waves.

To identify prominent directions of propagation for harmonic waves, the following steps are performed (further mathematical details are in the Supplementary Material).

1. A scalar component of the displacement or curl field, for example,$u(X,t)$, is Fourier transformed in time to extract its Fourier coefficient, $U(X)$, so that $u(X,t)=U\left(X\right)\exp \left(it\right)$.

2. The $U(X)$ field is further decomposed into harmonic functions of space, each with a different 3D wavenumber vector (describing wavelength and propagation direction).

3. A directional spatial filter is used to eliminate wave components outside a conical sector centered on the vector, $n_m$.

4. The result is inverse-Fourier transformed to obtain the filtered displacement component, $U_m(X)$, which is the part of the data explained by propagating waves with wavenumber vectors within the conical sector centered on $n_m$.

5. Then the amplitude-weighted propagation direction at each location is estimated from the formula

$$N^{\left(u\right)}\left(X\right)=\sum _{m=1}^M{n}_m\left|U_m\left(X\right)\right|$$ (1)

Figure 3 depicts the amplitude-weighted propagation direction obtained from the curl field in 1 subject, for shear waves in the brain excited at 70 Hz.

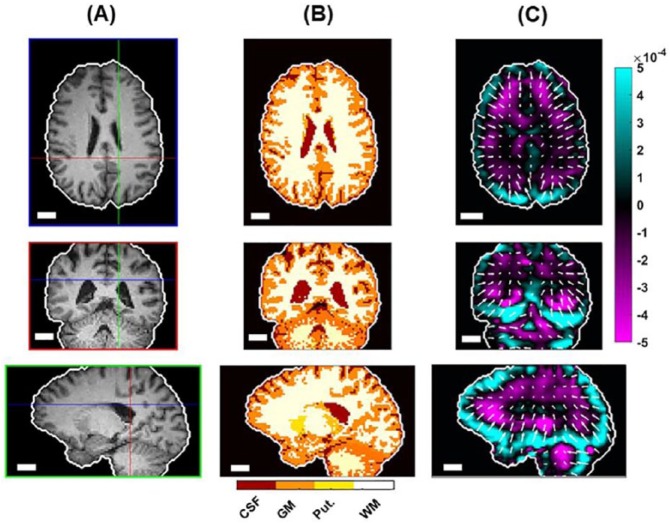
Figure 3.

(A) Brain-extracted and (B) segmented T₁-weighted images showing tissue type segmentation. (C) RL component of curl of the displacement field (isolating shear waves) with arrows showing weighted propagation directions. Scale bar equals 2 cm in all images. CSF indicates cerebrospinal fluid; GM, gray matter; Put., putamen, WM, white matter.

The divergence of the propagation direction vector field indicates the presence of “sources” from which shear waves emerge. The divergence of the propagation direction vector field is a scalar value computed from the vector differential calculus operation

$$\nabla \cdot N=\frac{\partial N_x}{\partial x}+\frac{\partial N_y}{\partial y}+\frac{\partial N_z}{\partial z}$$ (2)

which is performed numerically using the “div” command in MATLAB (MATLAB R2017a, The Mathworks, Natick, MA).

Strain and axonal strain

Strain is a measure of mechanical deformation. It is a second-order tensor, like the diffusion tensor, composed of the spatial derivatives of the displacement field (for details see Supplementary Material). To estimate strain, the three components of the dynamic deformation fields $(\tilde{u}(X,t)=[{\tilde{u}}_{RL},{\tilde{u}}_{AP},{\tilde{u}}_{SI}])$ obtained by MRE were differentiated with respect to spatial coordinates $(X=[x,y,z])$ by analytically calculating the derivatives of polynomial functions fitted to the displacement data.²⁶ A 3 × 3 matrix representation of the strain tensor, $ϵ$²⁷, was constructed at each voxel from the appropriate derivatives at that voxel. The octahedral shear strain (OSS),²⁶ or maximum shear strain, was computed at each voxel. Strain in the axonal fiber direction, ${ϵ}_a$, was estimated from the strain tensor and the unit vector in the fiber direction. The Supplementary Material includes details of the strain, OSS, and axonal strain computations. The median OSS was computed for each subject as a measure of subject-specific motion amplitude and used to normalize values of wave motion, shear strain, and curl to simplify comparisons of these quantities between subjects.

Relative motion between cerebrum and cerebellum

In a previous study, we demonstrated that the vibrations from the pillow actuator give rise to bulk motion in the brain that is largest in the AP direction, with smaller amplitude in the IS direction and very small amplitude in the RL direction.⁹ However, the MRE imaging volume used in that study primarily contained the cerebrum. In this study, we computed bulk motion considering the brain volume as a single rigid body but also considering the portions of the imaging volume corresponding to the cerebrum and cerebellum as separate regions capable of relative bulk motion (eg, sliding). Masks of the cerebrum and cerebellum were created from the segmented T₁-weighted image volumes; these masks were then applied to the MRE image volume (Figure 4). Rigid-body (bulk) motion of the cerebrum and cerebellum was estimated for each region individually by fitting the displacement field in that region to the equations for translation and rotation of a rigid body. Wave motion in each region was obtained by subtracting rigid-body motion from the total displacement field in that region.⁹

Figure 4.

Segmentation of the cerebellum (yellow) and brainstem (pink) from T₁-weighted images for estimation of relative motion.

Atlas registration

Due to differences in subject anatomy, the orientation of the brain relative to the pillow actuator differed modestly between subjects. To facilitate image-based data comparisons between subjects, we performed a 3D rigid registration of each subject’s brain to the MNI T₁-weighted atlas using the using the FLIRT tool within FSL (FMRIB Software Library v.6.0). We applied the translational and rotational components of registration to the unwrapped phase contrast images of the harmonically varying displacement field. The three orthogonal components of the displacement vector were multiplied by the rotation matrix to provide components aligned with RL, AP, and IS directions in the atlas-registered brain. These displacement components were then separated into bulk motion and wave motion, and strain components were calculated as described in section “Bulk motion and dynamic deformation.”

Results

Bulk motion and wave motion

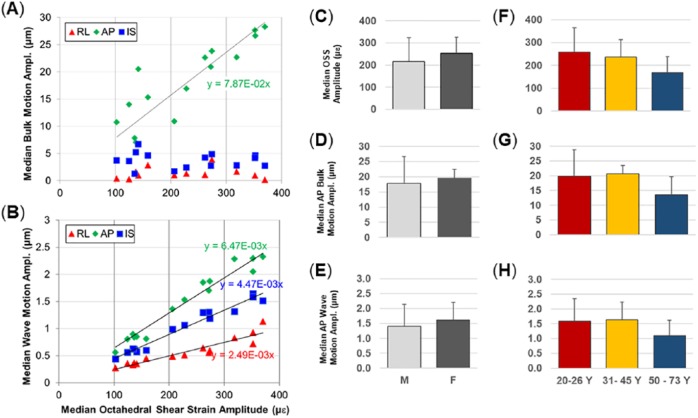
The amplitude of bulk motion was computed for each subject. The bulk motion consisted primarily of AP translation with rotation about the left-right axis with SI translation at a smaller amplitude. The amplitude of OSS varied over a range of 100 to 400 µε. The AP component of bulk motion and all components of wave motion were correlated with median OSS amplitude (Figure 5A and B). Differences in bulk motion between subjects may be due to differences in skull anatomy, neck muscle tone, and the positioning of the pillow actuator below the skull. No consistent trends were observed in these quantities when grouped by sex. Median OSS amplitude was lower in the oldest age group (Figure 5F), but this difference was not significant. When normalized by OSS, the AP wave displacement and AP/RL component of shear strain shows common features for all 15 subjects (Figure 6): decreased shear wave amplitudes toward the center of the brain and symmetry of wave motion with respect to the falx cerebri.

Figure 5.

Comparison of median bulk motion (A) and wave motion (B) amplitudes for each subject as a function of the median OSS for each subject. (C, D, E) Median OSS, AP bulk motion, and AP wave motion amplitudes for male subjects (n = 10) and female subjects (n = 5). (F, G, H) Median OSS, AP bulk motion, and AP wave motion amplitudes for 3 age groups (n = 6, 4, 5, respectively). AP indicates anterior-posterior; OSS, octahedral shear strain.

Figure 6.

Comparison of T₁-weighted axial images (T1W), AP wave displacement normalized by median OSS, and AP/RL component of shear strain normalized by median OSS for 15 subjects: (A) 5 female subjects (20-55 years). (B) 5 male subjects (23-42 years). (C) 5 male subjects (45-73 years). AP indicates anterior-posterior; OSS, octahedral shear strain; RL: right-left.

Propagation direction vector fields

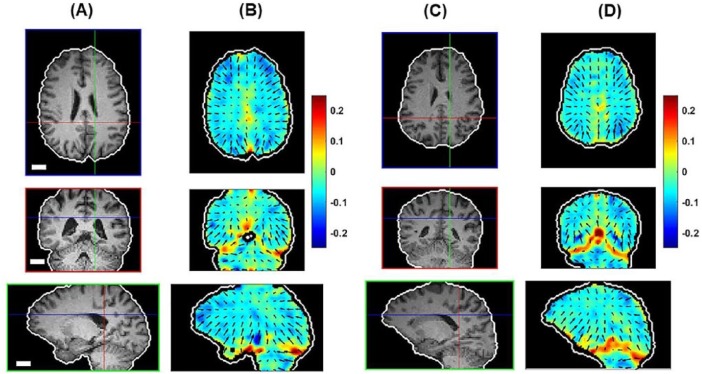
Representative vector fields of shear wave propagation directions are shown for 2 subjects in Figure 7. A common feature is the general propagation inward from the skull into the outer layers of brain parenchyma. Notable exceptions to this inward propagation are visible at the anterior and posterior insertions of the falx cerebri, from which shear waves emanate to the right and left. Also visible are vectors pointing outward from the tentorium. The divergence fields of shear wave propagation (shown in color as the background to the vector fields in Figure 7) show “hot spots” at these locations, verifying their importance as sources of shear waves.

Figure 7.

Shear wave propagation in 2 different subjects: (A, C) brain-extracted T₁-weighted images and (B, D) divergence of propagation direction with superimposed propagation direction vector fields. Regions of positive divergence (red) are sources of shear waves. Scale bar equals 2 cm in all images.

Strain and axonal strain

Strain patterns are shown in Figure 8 for 2 representative subjects. The magnitude of strain in these experiments is near ${10}^{-3},$ which is small relative to brain deformations experienced even in mild head impacts.^11–13,28 Again, some common features are visible including the relatively higher strains near the brain-skull interface, which generally diminish with distance from the skull. Some strain concentrations are visible near anatomical features such as the falx and tentorium.

Figure 8.

Shear strain in 2 different subjects: (A, D) brain-extracted T₁-weighted images overlaid with white matter segmentation; (B, E) OSS magnitude; and (C, F) axonal fiber strain (normalized by median OSS). Scale bar equals 3 cm in all images. OSS indicates octahedral shear strain.

Effects of frequency of excitation

Strain amplitudes are depicted in Figure 9 for a representative subject at 3 different vibration frequencies: 30, 50, and 70 Hz. To compare wave patterns, we have normalized the wave amplitude by the median OSS computed at that frequency. Shear waves clearly attenuate less (penetrate deeper into the brain) at the lowest frequency, 30 Hz, compared with 50 Hz and especially 70 Hz. These trends were observed in all 4 subjects studied as illustrated in Figure 9B and C.

Figure 9.

Shear wave displacement and strain at multiple frequencies for a representative subject: (A) Anatomical images (masked MRE magnitude) with crosshairs indicating location of orthogonal image views. (B) Median OSS at each frequency. Bars show median OSS for representative subject, dashed lines show mean values of median OSS for 4 subjects studied. OSS magnitude at each voxel is normalized by median OSS at corresponding frequency. (C) AP wave displacement. Bars show median amplitude of AP wave displacement for representative subject; dashed line shows mean values of AP wave displacement for 3 subjects studied. AP wave displacement is normalized by median OSS at corresponding frequency. Scale bar equals 2 cm in all images. AP indicates anterior-posterior; MRE, magnetic resonance elastography; OSS, octahedral shear strain.

Relative motion between cerebellum and cerebrum

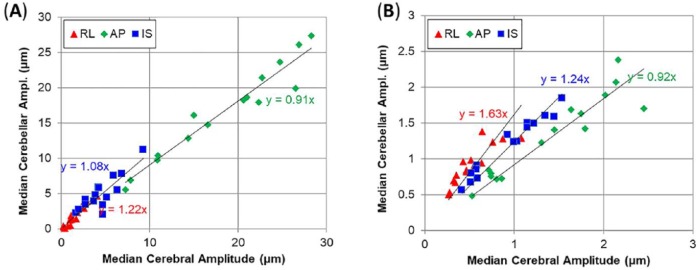
Bulk motion of the brain was primarily in the AP direction, consistent with findings from our previous study.⁹ The bulk motion amplitudes in the cerebrum and cerebellum (Figure 10A) were 10 to 28 µm in the AP direction, and similar between the 2 regions. Median values of AP wave motion were generally smaller in the cerebellum than in the cerebrum of each subject (slope of 0.92), but IS and RL components are larger (slopes of 1.24 and 1.63) as depicted in Figure 10B. The phase and amplitude of AP wave motion differed between the inferior cerebrum and the superior cerebellum. In the cerebrum, shear waves propagate inwards from the skull; in the cerebellum, waves originate from the tentorium and back of the skull (see Figure 7).

Figure 10.

Comparison of median values of (A) bulk motion and (B) dynamic deformation (wave motion) in cerebral and cerebellar volumes. Equations indicate best fit value of slope for 15 subjects. Note the smaller range of motion amplitude for wave motion (B) compared with bulk motion (A). AP indicates anterior-posterior; IS, inferior-superior; RL, right-left.

Discussion

Harmonic displacement and deformation fields were generated by vibration of the skull and imaged using MRE acquisition techniques. The resulting patterns of wave propagation, strain, and relative motion between brain regions were analyzed to illuminate general features of brain biomechanics that may be important in TBI.

Propagation direction vector fields

Shear wave propagation direction fields are qualitatively consistent among the subjects we studied. Shear waves originate from the skull-brain interface at the cortical surface and from the stiff membranes (falx cerebri and tentorium cerebelli) in the interior of the brain. Shear waves penetrate less deeply into the brain as frequency is increased, so that 70 Hz waves induce far less deformation in the corpus callosum and other deep structures than in the cortical regions. This observation highlights the potential importance of lower-frequency components of skull motion in injury to deeper white matter. This may ultimately be relevant to the design of head protection as some helmet designs may reduce peak angular acceleration by decreasing the high-frequency components of skull acceleration. However, if low-frequency components are not decreased (ie, if energy is transferred to lower-frequency modes of deformation), it is possible that injury may be more severe.

Strain and axonal strain

Strain patterns highlight the role of the brain-skull interface in transmitting skull motion to brain deformation. In related work, Yin et al²⁹ noted strain concentrations at boundaries between meningiomas and brain tissue. In this study, we observe that strain magnitudes are generally highest in brain tissue near the interior of the skull or adjacent to the stiff membranes of the falx and tentorium.

These strain measurements, although of much smaller amplitudes than would occur in even mild TBI, may be relevant to common assertions about strain fields in the brain: (1) We do not observe a clear strain concentration at the interface between gray and white matter. It is possible that higher resolution strain measurements might be necessary to see this phenomenon if it exists. (2) We do not observe systematic differences in either the strain magnitude or the magnitude of axonal fiber-oriented strain in the regions below sulcal fundi, compared with regions of comparable depth in gyri. Again, higher resolution measurements could allow more accurate comparisons between these regions. In contrast, strain concentrations are observed at the base of the brain, in and slightly anterior to the brainstem, for example.

Relative motion between cerebrum and cerebellum

Skull vibration induces bulk motion and wave motion in both the cerebrum and cerebellum. The magnitudes of these displacement components are consistent with those observed in prior studies.^9,10 Differences in phase and amplitude of motion on opposite sides of the tentorium indicate sliding motion of these brain structures relative to the tentorium and to each other. Whereas others have noted that damage to structures between cerebellum and cerebrum may be important in TBI,¹⁵ we did not observe large differences in the rigid-body motion of these two regions. Shear waves did appear to propagate into both structures and away from the interface between them. Thus, the interfaces between the cerebellum and cerebrum may be important to injury, potentially because of the stiff tentorial membrane that can impinge on soft brain tissue.

Limitations, future directions, and conclusions

Two primary features of MRE limit the extrapolation of these observations to the case of TBI. First, the deformations are extremely small: strains are at least 2 orders of magnitude smaller than those expected in traumatic injury. The differences are less if compared with the sub-concussive impacts relevant to CTE. Second, the MRE sequences used here involve harmonic motion, as opposed to the impulsive events typical of impacts. However, there are mathematical principles that can be used to predict the response to impulsive loading from the responses to harmonic excitation at different frequencies.³⁰ In addition, only AP excitation was applied. Future MRE studies of the brain should explore a larger frequency range, more excitation directions, and larger amplitudes of deformations, most likely in animal studies.³¹

Overall, we believe that MRE illuminates many features of brain biomechanics, particularly the importance of the brain-skull interface and the stiff internal membranes, and that results of this study and future MRE investigations could be used to guide and evaluate computer models of brain biomechanics.^32–34