Understanding vasopressor intervention and weaning: risk prediction in a public heterogeneous clinical time series database

Abstract

Background: The widespread adoption of electronic health records allows us to ask evidence-based questions about the need for and benefits of specific clinical interventions in critical-care settings across large populations.

Objective: We investigated the prediction of vasopressor administration and weaning in the intensive care unit. Vasopressors are commonly used to control hypotension, and changes in timing and dosage can have a large impact on patient outcomes.

Materials and Methods: We considered a cohort of 15 695 intensive care unit patients without orders for reduced care who were alive 30 days post-discharge. A switching-state autoregressive model (SSAM) was trained to predict the multidimensional physiological time series of patients before, during, and after vasopressor administration. The latent states from the SSAM were used as predictors of vasopressor administration and weaning.

Results: The unsupervised SSAM features were able to predict patient vasopressor administration and successful patient weaning. Features derived from the SSAM achieved areas under the receiver operating curve of 0.92, 0.88, and 0.71 for predicting ungapped vasopressor administration, gapped vasopressor administration, and vasopressor weaning, respectively. We also demonstrated many cases where our model predicted weaning well in advance of a successful wean.

Conclusion: Models that used SSAM features increased performance on both predictive tasks. These improvements may reflect an underlying, and ultimately predictive, latent state detectable from the physiological time series.

BACKGROUND AND SIGNIFICANCE

Decision-making in the intensive care unit (ICU) requires quick response to rapidly changing situations as patients respond to treatment and develop secondary conditions. Treatment decisions are made based on clinicians’ understanding of patients and their own prior experience. However, the efficacy of many interventions remains unquantified,^1,2 and some interventions have even been shown to be ineffective or harmful.³

The widespread adoption of electronic health records allows us to ask evidence-based questions about the need for and benefits of specific interventions in critical-care settings across large populations. Importantly, the vast amounts of data that are collected in ICUs – vital signs, clinical notes, fluids, medications – suggest an opportunity for more data-driven decision-making. Whereas clinicians may struggle to track multiple signals from multiple, rapidly evolving patients at once, algorithms excel at processing large streams of data. Computational tools that summarize relevant parts of these data streams could allow clinicians to focus on decision-making rather than just keeping up with the data.

Open databases such as Multiparameter Intelligent Monitoring in Intensive Care (MIMIC) II,⁴ with information on 26 870 adult hospital admissions, provide an unprecedented opportunity for researchers to build these computational tools. To date, most works have used ICU measurements to predict the mortality of patients in particular disease subgroups.^5–8 However, such risk scores are of limited value to clinicians, who must make decisions on how and when to treat patients regardless of their underlying acuity.

This work takes an important step toward actionable use of ICU data by modeling ICU interventions. We focus on vasopressors, used to elevate mean arterial blood pressure. While vasopressors are commonly used in the ICU, few studies have documented improved outcomes from their use,⁹ and they may even be harmful in some populations.¹⁰ We consider 2 questions regarding vasopressor administration. First, we ask when a patient will require a vasopressor. Knowing who will need a vasopressor even a few hours in advance can help clinical staff plan and execute interventions in a more efficient manner. Second, we ask whether a patient currently on a vasopressor is ready to be weaned from it. Anecdotally, clinicians report being conservative about estimating when the patient is ready for weaning and leaving patients on interventions longer than necessary because they are attending to other patients. However, extended interventions are both costly and detrimental to patient health.¹⁰

Unfortunately, making decisions from data generated in the ICU is challenging: clinical signals are irregularly sampled and are contaminated by interference and human error. Strong modeling assumptions are typically used to clean and impute the signals,^11,12 which introduce their own bias¹³ and often ignore the highly dependent temporal nature of the data.^14–16 Dynamical system models, which impute data by building a model of how the data evolve, provide an alternative to interpolation-based imputation techniques. In this work, we focus on switching-state autoregressive models (SSAMs), which have previously been used to impute signals, identify artifacts, and discover physiological states in a variety of critical settings.^17,18 SSAMs are attractive models for modeling physiologic signals, because they express the notion that the dynamics of the physiologic signal will change depending on some internal patient health state; given the patient's health state, the set of physiological signals the next time depends only on the current signals. This assumption considerably simplifies training of the model, resulting in a more robust predictor. Interpreting SSAMs is also relatively simple, because each time a patient is assigned to exactly 1 discrete hidden state, rather than a more complex embedding.

Unlike prior work, we focus on actionable predictions regarding interventions rather than mortality. We also consider a high-dimensional space of physiological signals and make use of signal discretization to improve performance on downstream tasks.^19,20

Specifically, we

• define 3 clinically actionable prediction tasks: immediate need for an intervention, need for an intervention in the near future, and when a patient is ready to be weaned from an intervention;

• achieve state-of-the-art predictions for intervention-onset tasks using only physiological signals in a large, public ICU dataset; and

• quantify unnecessary extra intervention time.

To our knowledge, ours is the first study to use predictive models to address this question.

MATERIALS AND METHODS

Data

The MIMIC II 2.6 database (MIMIC-III was released after this work began and contains more data for future use) includes retrospective electronic medical records for 26 870 adult hospital admissions recorded between 2001 and 2008.⁴ Creation and use of the MIMIC database was approved by the Institutional Review Boards of both Beth Israel Deaconess Medical Center and the Massachusetts Institute of Technology (IRB Protocol 2001-P- 001699/3). Many ICU patients have a limited chance of survival, regardless of clinical intervention. Therefore, our cohort contains only adult patients on their first ICU stay without orders for reduced care (eg, “comfort measures only,” “do not resuscitate,” “do not intubate,” or “CPR not indicated”). Following prior work by Hug and Szolovits,²³ we also excluded patients with <12 hours of data or >96 hours of data to avoid a group of fundamentally sicker patients. These criteria allowed us to focus on situations in which clinical decisions might have a positive effect, rather than penalizing a classifier for situations where a patient is taken off life support. Applying these filters resulted in an initial cohort of 15 695 patients: 4331 were administered vasopressors (positive class) and 11 364 were not (control class). We extracted the 10 dynamic variables (vital signs and lab results) with the fewest missing entries as well as variables corresponding to vasopressor administration.

Predictive tasks

We considered 3 tasks: predicting imminent vasopressor need, short-term vasopressor need, and wean readiness (see Figure 1 for an illustration).

Figure 1.

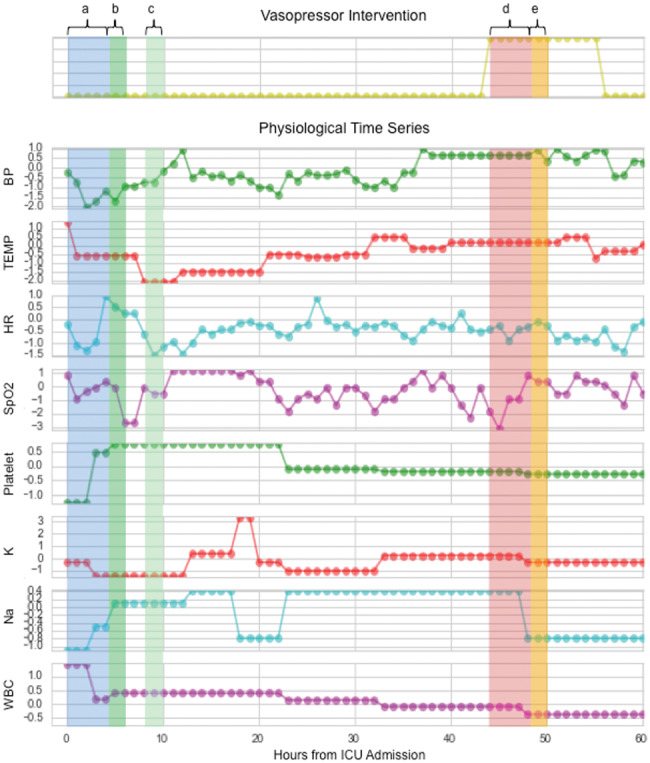
A subset of physiological time series with prediction windows highlighted. Predicting imminent vasopressor need (Task 1) evaluates features from window a on vasopressor need in window b. Predicting short-term vasopressor need (Task 2) evaluates features from window a on vasopressor need in window c. Predicting wean readiness (Task 3) evaluates features from window d on the successful weaning of vasopressors in window e.

Task 1: Imminent vasopressor need. We defined imminent vasopressor need as requiring a vasopressor within the next 2 hours. For each patient, we made predictions every hour until the first vasopressor administration or the end of stay. We only predicted first vasopressor administration because patients with multiple vasopressors are likely to be in fundamentally different physiological situations.

Task 2: Short-term vasopressor need. We defined short-term need as the patient being stable enough not to require vasopressor administration for the next 4 hours but requiring it in the following 2 hours. Predicting who will require vasopressors in the near future, but not now, can help manage ICU logistics and ensure that the patient is ready for the intervention. We made hourly predictions until the first vasopressor administration or the end of stay.

Task 3: Wean readiness. Vasopressors are administered via IV, and patients are weaned by gradually reducing the dose. We defined wean readiness as being able to stop administration completely within 2 hours, and a successful wean as not requiring vasopressors again within 4 hours.

Preprocessing

Numeric trends are generally produced by bedside monitors once per second, but often stored only once every 5–60 minutes. In this work we used nurse-validated vital sign trends from the clinical information system, which are sampled hourly. Variables were discretized using the mean and standard deviation from the training set. As employed in other work, we rounded the resulting z-scores to integer values in −4:4^19,20; we added an extra value for missing values, so each new physiological variable took on 10 discrete values. This discretization procedure helps the model avoid fitting to small variations in the physiological signal and identify global structure in the data. Vasopressor administration variables were post-processed to recover continuous segments of administration; complete data processing details are given in the Supplementary Materials, and cohort characteristics are given in Table 1.

Table 1.

Average population statistics of the cohort

Variable Type	Feature	Pre-Intervention V-	During Intervention V+	Controls (C)
Population distribution	In-Hospital Mortality (%)	5.165	–	2.687
	ICU LoS (days)	1.974	–	1.708
	MICU (%)	15	–	44
	SICU (%)	10	–	30
	CCU (%)	13	–	16
	CSRU (%)	62	–	10
Static data on admission	Age	65.812	–	60.787
	% Male	66	–	56
	Weight	82.229	–	81.767
	SOFA	7.844	–	3.251
	SAPS-I	15.889	–	10.722
	% Pacemaker use	63	–	58
	% ROF	60	–	6
Dynamic data over hospital stay	Mean BP	76.235	74.68	82.12
	TEMP	97.865	98.562	98.371
	HR	83.979	85.251	83.682
	SPO2	97.716	97.283	97.244
	FIO2	0.736	0.53	0.516
	RESP	16.094	18.056	18.286
	GLU	150.657	134.618	138.732
	BICAR	25.09	24.023	24.866
	HCT	29.031	29.903	31.457
	K	4.531	4.244	4.078

Abbreviations: ICU LoS, ICU length of stay in days; MICU, medical care unit; SICU, surgical care unit; CCU, cardiac care unit; CSRU, cardiac-surgery recovery unit. ROF, risk of falls; Mean BP, mean arterial blood pressure; BMI, body mass index; HR, heart rate; SPO2, peripheral capillary oxygen saturation; TEMP, temperature; FIO2, fraction of inspired oxygen; RESP, spontaneous respiration rate; HCT, hematocrit; BICAR, bicarbonate; K, potassium; GLU, glucose. SAPS-I and SOFA are clinical acuity scores calculated at admission.

Feature construction

For each task being evaluated at hour t of patient n, we considered 3 types of input features: raw, SSAM, and combined. The raw features are the previous 4 hours of multidimensional z-scored physiological data at hour t of patient n, appended with the 7 static admissions features. We learned the SSAM features in an unsupervised fashion using the raw features. The combined features were obtained by concatenating the raw and SSAM feature vectors.

We now briefly describe the SSAM (see Supplementary Materials for details). The physiological signals (raw features) xⁿt of a patient n at time t is a vector in R^D of D measurements, some of which may be missing. For each patient n, we observe a sequence {xⁿ1, xⁿ2, xⁿ3,… xⁿT_n} of length Tn. We train an SSAM to learn a hidden sequence of discrete variables {y1ⁿ,y2ⁿ,y3ⁿ,…yTⁿ} that determine the transition dynamics of the observed variables xⁿt. These variables ytⁿ can be interpreted as the physiological state of the patient. Given the physiological state sequence, the observations are generated by an autoregressive model indexed by the hidden state ytⁿ for each dimension d. Importantly, we assume that each dimension d has its own transition function because we expect different variable types to have different dynamics. We compare two classifiers for the autoregressive transition model fx: random forests (RF) and Gaussian Naive Bayes (NB). The random forests maps categorical values to the next set of categorical values directly. The Gaussian NB treats the inputs as continuous variables and the outputs as categorical, closer to reflecting their values before the discretization in the preprocessing. The Gaussian NB was included because while prior work has shown benefits to discretization (Joshi et al.), others have found continuous normalization strategies most beneficial (Che et al.). The Gaussian NB was a simple way to incorporate the ordered nature of the inputs. Our inference alternates between updating 2 sets of latent variables: the hidden physiological state sequences for each patient {y1ⁿ, y2ⁿ, y3ⁿ,…} and the transition parameters for each measurement dimension d and physiological state k.

For each task (administration and weaning), we trained the SSAM on the patients from the positive class only. For vasopressor administration, we used all time points up to vasopressor administration. For weaning, we only considered data immediately after starting administration (negative class) and immediately before weaning (positive class). At time t we computed the probabilities of being in each SSAM state over the last 4 hours for all patients and all times in our cohort and used those as input features. Because there are k states every hour, 4 hours of previous data creates 4k SSAM features.

Each feature was tested with 3 different classifiers: a linear-kernel support vector machine (SVM), naive Bayes (NB), and L2-regularized logistic regression (LR). Standard packages and settings were used for the SVM, NB, and LR classifiers. All analysis was performed in Python 2.7.

RESULTS

We ultimately included 19 variables from the MIMIC II database: 6 nurse-verified vital signs: heart-rate (HR), mean arterial blood pressure (MeanBP), blood oxygenation level (SPO₂), temperature (TEMP), spontaneous respiration rate (RESP), and urine output (URINE); 4 laboratory measurements: hematocrit (HCT), bicarbonate (BICAR), potassium (K), and glucose (GLU); and 7 static variables: admitting age, gender, first simplified acute physiology score (SAPS I),²¹ first sequential organ failure assessment (SOFA) score,²² first weight, use of pacemaker, and whether the patient was noted to be at risk for falls (Table 1).

Predicting vasopressor administration improved by SSAM features

Table 2 compares the performance of all feature sets on Tasks 1 and 2 (imminent and short-term administration prediction) using L2-regularized logistic regression averaged over 5 repetitions. The LR classifiers tended to have the best prediction performance across feature sets; the results with all classification methods can be found in the Supplementary Materials.

Table 2.

Performance of features in vasopressor need tasks using logistic regression classifier

Features Used	Imminent Need Prediction (AUC)	Short-term Need Prediction (AUC)
RAW	0.89 (±1.1e-16)	0.83 (± 0.0040)
SSAM (RF)	0.81 (±0.0584)	0.66 (± 0.0046)
SSAM (NB)	0.87 (±0.0090)	0.83 (± 0.0076)
COMBINED: RAW + SSAM (RF)	0.92 (±0.0008)	0.86 (± 0.0032)
COMBINED: RAW + SSAM (NB)	0.92 (±0.0016)	0.88 (± 0.0061)

Simply using the global SSAM features gives an AUC of 0.87 (±0.009) for imminent need prediction and 0.83 (±0.008) for short-term need prediction. The combined features achieve the best results, and consistently improve AUCs over using only the raw features: AUCs of 0.92 (±0.002) and 0.88 (±0.006) for imminent need and short-term need prediction, respectively.

Imminent need predictions are inherently easier, as the data immediately prior to onset are available. Short-term need predictions are more challenging because they enforce a time gap between observed data and onset of intervention. In general, SSAM features learned with naïve Bayes performed as well as the raw data, and the combination of SSAM features and raw data did better than either alone. In our classification tasks, the latent features learned with NB gave improved performance. This result suggests that discretizatized values may benefit from the use of an ordinal classifier, or that other normalization strategies may be more appropriate for capturing the variations in pre- and post-vasopressor patients.

Predicting vasopressor weaning

Following the best results from administration prediction, we trained a classifier for Task 3 to predict successful weaning on those patients who were alive 30 days post-discharge. The raw features obtained an AUC of 0.67 (±0.008); SSAM (NB) features were AUC 0.63 (±0.021); and raw + SSAM (NB) features were AUC 0.71 (±0.005).

Quantifying unnecessary intervention time prior to a wean

Our quantitative results above discriminate situations in which clinicians may have attempted to wean too early, causing the wean to be unsuccessful. However, clinicians report that patients are often left on interventions for much longer than necessary. We focused on the first time that our classifier predicted a successful wean for each patient in Task 3, and examined the difference in time between the predicted and actual weaning times. As shown in Figure 2, a significant number of patients were successfully weaned at the right time, but the heavy tail depicted suggests that many patients suffered from extended interventions.

Figure 2.

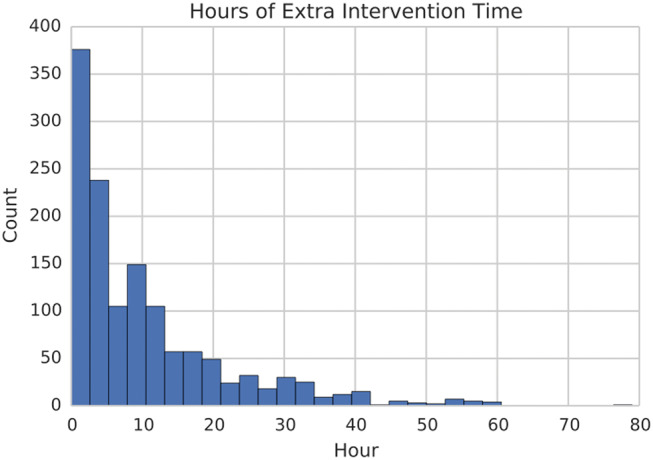
Histogram of excess time for which patients could have been successfully weaned according to the classifier.

We chose 3 patients from different points in the histogram in Figure 2 and examined their medical notes for correspondence to our wean probabilities.

Case 1: Figure 3 shows our probability of a successful wean for a 72-year-old man with coronary artery disease who was put on mechanical ventilation and vasopressors while in the ICU. The probability of a successful wean is low while the patient fails mechanical ventilation weaning early on in his stay and immediately post-extubation. It is explicitly noted in his record at the point of lowest probability of wean that he is dependent on vasopressors. The patient stabilizes as the probability of wean success climbs, and the clinical staff actually begin to wean him near the highest predicted success in our estimates.

Figure 3.

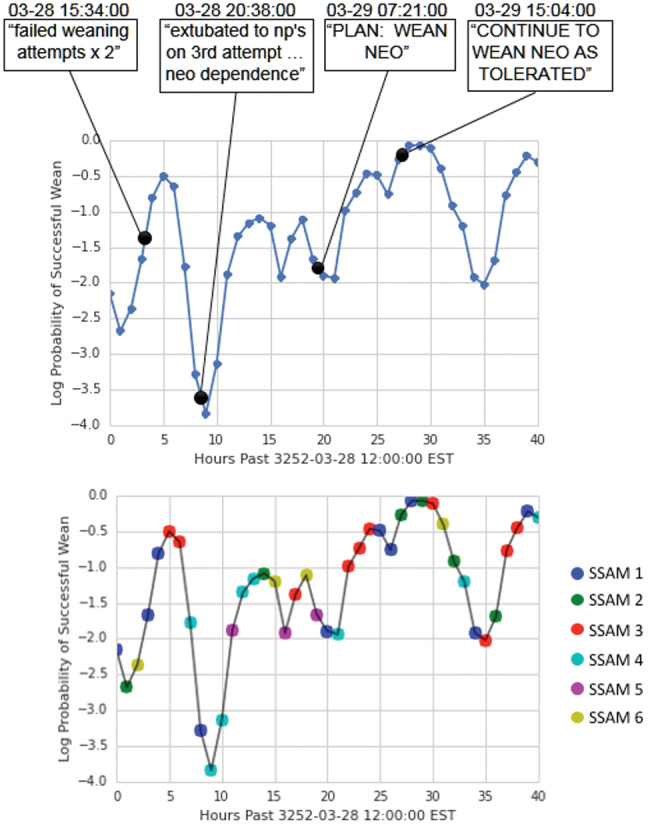
Probabilities of successful weaning and state over time for patient 10 387.

Case 2: Figure 4 shows a similar plot for a 62-year-old male patient with a cardiac catheterization. The probability of successful wean remains low while patient is given a course of treatment and fluids, but he struggles with a low central venous pressure and increasing hematocrit. When the nursing staff notes an increasing need for vasopressors, the corresponding probability of a wean dips further. During recovery, our model’s wean success matches the nurse’s note that the patient should be weaned the following day. In this case, the wean happened almost 10 hours after our model predicted it could be done. However, this was likely due to clinical staff schedules, which vary widely in the ICU. For legal and ethical reasons, there is also a bias toward maintaining interventions in ICU patients rather than withdraw too early, even if a patient seems to be stable.

Figure 4.

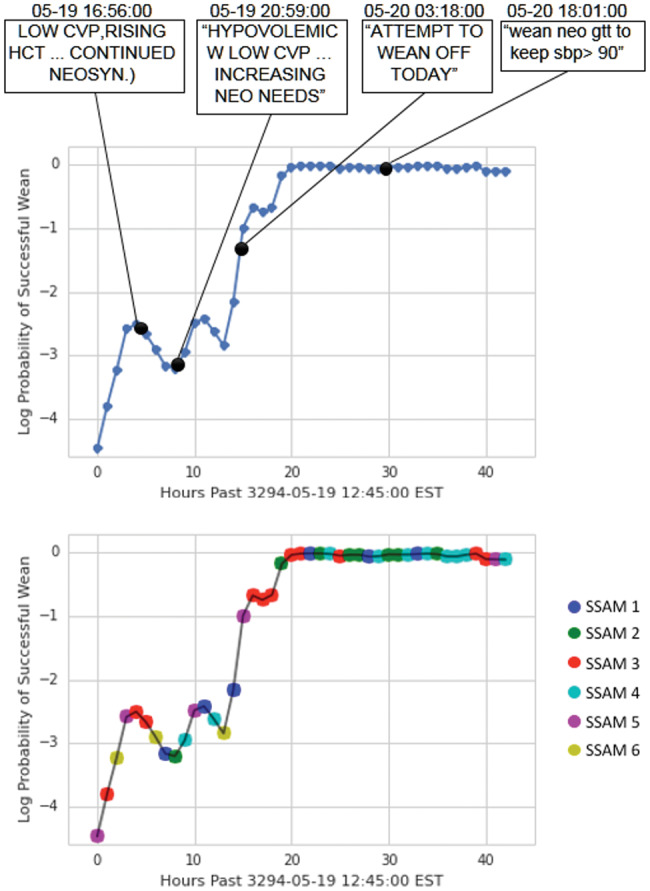
Probabilities of successful weaning and state over time for patient 11 315.

Case 3: Finally, we show a 65-year-old man (Figure 5) who underwent mitral valve replacement and coronary artery bypass graft. The patient tolerated the procedures well and was transferred to the cardiac surgery recovery unit for monitoring, where he maintained a stable condition. Based on the numeric data available, we were unable to find any indication that the patient was weaned, and thus we labeled this case an unsuccessful wean. However, the clinical notes indicate that the patient was successfully weaned from sedation on the same day of his operation. In this case, we correctly predicted that the patient could be successfully weaned (or could be weaned early without any label) prior to his actual weaning, despite an incorrectly labeled example.

Figure 5.

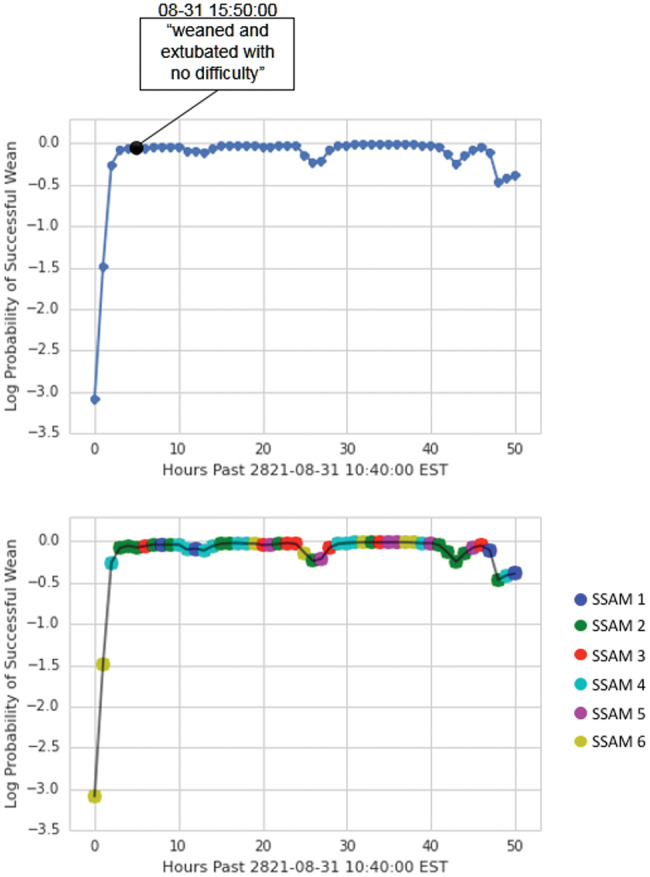
Probabilities of successful weaning and state over time for patient 3194.

Clinical relevance of discovered states

The previous sections show that our SSAM features improved our ability to predict vasopressor administration and weaning. We theorize that this quantitative evidence is due to physiological models that are capturing physiological characteristics relevant to interventions and intervention outcomes but not captured by raw physiological variables.

To investigate this hypothesis, we investigated whether the odds ratios associated with the latent variables were on par with those given to the raw features. In each of the tasks, latent state features were some of the most heavily weighted for logistic regression (see Supplementary Materials). To identify which states were associated with high and low probabilities in weaning prediction, we counted the frequency with which any particular model was associated with correctly predicting successful or unsuccessful weans. Specifically, we looked at which SSAM states generated the highest 1% of successful wean probabilities in cases that were successful weans, and which states generated the lowest 1% of probabilities in unsuccessful cases.

As shown in Figure 6, we see an increase in SSAM states 5 and 6 in those patients who had a high probability of a successful wean. On the other hand, data with a low probability of successful weaning in those patients who were not successful came more often from SSAM states 1 and 3.

Figure 6.

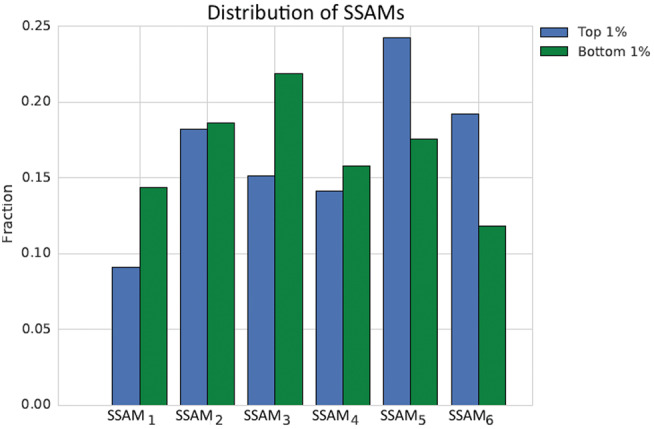
Histograms of the states across patients at time points of high (left) and low (right) probabilities of successful weans.

We then investigated the physiological variables that corresponded to these states by examining the transition probabilities for observed values in SSAM states 3 and 5 (recall that the state of the SSAM governs the dynamics of the observed physiological variables). There are several interesting differences in these probabilities. In SSAM state 5, transition probabilities for blood hematocrit values tended to stabilize from large abnormal values toward normalcy more often (8% vs 5%). This could be indicative of patients who were healthy enough to remove fluid resuscitation, so their hematocrit responded with decreased blood viscosity. In SSAM state 3, we observed that respiration rate tended to stabilize from low values toward normalcy more often (13% vs 11%). This could indicate that state 3 represents patients who eventually require some form of mechanical ventilation, which can cause more unsuccessful weaning patterns.

DISCUSSION

Much literature in clinical prediction has focused on using large numbers of manually defined aggregate features as inputs to a classifier that will predict the risk of clinically significant events.^19,23,24 Switching dynamical systems models have been used to impute signals, identify artifacts, and discover physiological states in a variety of critical settings.^8,17,18 Most of these works have focused on developing models for densely sampled, often one-dimensional data. Our work is distinct in that we consider higher-dimensional data and use discretization and binning to find relevant signals over longer time scales. Other work has applied unsupervised methods to discretized time series to discover anomalies and patient similarities, but without a latent variable representation.^25,26 Time series symbolization creates many opportunities to analyze physiological data with the rich literature of techniques developed for discrete sequences²⁷; our data-processing approach also makes it natural for us to consider rich, nonlinear transition models, such as random forests, rather than the linear dynamical systems approach of the work above.

The most recent prior work on vasopressor prediction used a subset of the MIMIC II patients receiving fluid resuscitation (2944 adult ICU patients), and attempted to predict subsequent vasopressor administration within 2 hours using a general model and 2 disease-based models.²⁸ The general patient model achieved an AUC of 0.79 ± 0.02, and the disease models had AUCs of 0.82 ± 0.02 for pneumonia and 0.83 ± 0.03 for pancreatitis. Our model used a similar short-term prediction approach in the general ICU population and achieved an AUC of 0.88 (±0.0061). To our knowledge, we have the highest reported results for predicting vasopressor administration. These results suggest that the latent states discovered by the SSAM is an effective summary statistic for making predictions about future intervention needs; an increased AUC of 0.05 could affect the treatment of thousands of patients annually in large ICUs.

Predicting weaning success is harder than predicting intervention onset. There is fundamental uncertainty about the right time to wean a patient, and the decision may depend on staffing considerations, clinical judgment, or lack of familial support for intervention removal. In addition, unlike onset, time of weaning is often indicated only in the patient note and not in any structured data source. The most relevant predictive work on vasopressor weaning specifically was done using clinically guided feature engineering over sliding windows of data.²³ In particular, they selected 32 variables from a manually defined set over 438 clinically guided features. They then classified patient segments that preceded successful vasopressor weaning by 1–12 hours (AUC = 0.81) and segments by 6–12 hours (AUC = 0.76). This was improved by looking only at those patients who survived their hospital admission to AUCs of 0.82 and of 0.825, respectively. While our AUCs are lower (0.71 ± 0.005), our approach did not use the large set of hand-engineered features; seeing whether our unsupervised physiological features improve prediction accuracy when combined with these engineered features will be an interesting future direction.

Limitations

Our study has several limitations. The greatest is that our data are retrospective, which prevents us from evaluating causality and answering counterfactual questions such as how a patient might have fared if weaned earlier. While we have some evidence for unnecessary intervention time in our cohort, such a claim must be evaluated in a prospective study. Validating our findings in other ICU databases will help to address the robustness of our methods for different clinical cohorts. Our study also does not consider the dose or duration of vasopressor administration, and our models control for demographics and health state in relatively simple ways (eg, by including SAPS I and SOFA score features). Finally, many of our variables, such as time on vasopressor, were constructed based on both the recorded events in ICU data and input from domain experts on how to process the data correctly. This process could create mislabeled data (eg, an incorrect wean), which would change our results.

Future work

Our predictions of when patients are ready to wean are among several actionable predictions in the area of vasopressor administration. Another important step would be to consider the drug and dosage used for the vasopressor. A multicenter randomized trial comparing the use of dopamine or norepinephrine as first-line vasopressor therapy in 1679 patients with shock found that patients treated with dopamine had significantly more arrhythmic events.²⁹ We could also improve the prediction quality of our model with additional features, such as those used to predict sepsis (sepsis is often preceded by episodes of hypotension, so an early predictor of sepsis could also encompass many of the states that might require vasopressor use).³⁰ Another interesting direction for future work would be to test whether these features assist in stratifying risk for a variety of interventions and intermediate outcomes, such as mechanical ventilation^31,32 and sepsis,³⁰ which, to date, have relied on hand-engineered features.

SSAMs have demonstrated value in detecting physiological states that influence the evolution of clinical measurements along time, and our overall methodology could be used to answer many other clinical questions. In the specific context of vasopressor weaning readiness, the ability to display the probability of a patient’s possible need for an intervention, and the potential for weaning success, are important pieces of information that enable clinicians to view predictions across entire ICU populations, updated on an hourly basis. This information could be further operationalized to create a clinical environment where potential therapies can be evaluated based on their prior performance in diverse populations and settings.

CONCLUSION

We obtained AUCs of 0.92, 0.88, and 0.71 for predicting ungapped vasopressor administration, gapped vasopressor administration, and vasopressor weaning, respectively. Our results for vasopressor use are, to our knowledge, the best achieved, and better results on vasopressor weaning were obtained with feature engineering on a smaller dataset. An important property of our approach is that our SSAM was trained in a completely unsupervised manner, specifically without knowing what the downstream prediction task was to be, and without hand-specification of important features. Our goal in training the SSAM was to model the evolution of symbolized physiological time series, capturing global trends in the dynamics of the measurements that could be interpreted as physiological states. The features derived from our SSAM resulted in improved performance regarding whether a patient would receive a vasopressor (0.79 AUC vs our 0.88 AUC for gapped prediction); we also discovered several features associated with successful weaning from vasopressors, and, to our knowledge, made the first attempt to quantify anecdotal claims about unnecessary intervention time. In summary, our work takes an important step away from hand-engineered, task-specific features and toward features that capture key information about patient health.

Funding

This work was supported by the Intel Science and Technology Center for Big Data, the National Library of Medicine Biomedical Informatics Research Training grant (NIH/NLM 2T15 LM007092-22), and National Science Foundation ACI-1544628.

Competing Interests

The authors have no competing interests to declare.

Contributors

MG and FD designed the experiments and wrote the paper. MW wrote the code for all experiments. MF performed initial data investigation. PS and LC provided clinical and technical expertise in problem and modeling definitions.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.