SUMMARY
Identification of clinically relevant tumor subtypes and omics signatures is an important task in cancer translational research for precision medicine. Large-scale genomic profiling studies such as The Cancer Genome Atlas (TCGA) Research Network have generated vast amounts of genomic, transcriptomic, epigenomic, and proteomic data. While these studies have provided great resources for researchers to discover clinically relevant tumor subtypes and driver molecular alterations, there are few computationally efficient methods and tools for integrative clustering analysis of these multi-type omics data. Therefore, the aim of this article is to develop a fully Bayesian latent variable method (called iClusterBayes) that can jointly model omics data of continuous and discrete data types for identification of tumor subtypes and relevant omics features. Specifically, the proposed method uses a few latent variables to capture the inherent structure of multiple omics data sets to achieve joint dimension reduction. As a result, the tumor samples can be clustered in the latent variable space and relevant omics features that drive the sample clustering are identified through Bayesian variable selection. This method significantly improve on the existing integrative clustering method iClusterPlus in terms of statistical inference and computational speed. By analyzing TCGA and simulated data sets, we demonstrate the excellent performance of the proposed method in revealing clinically meaningful tumor subtypes and driver omics features.
Keywords: Multi-type omics data, Integrative clustering, iCluster, iClusterPlus, iClusterBayes, Latent variable model, Bayesian variable selection
1. Introduction
Cancer is a complex and heterogeneous disease, driven by alterations occurring at multiple levels, namely chromosomal rearrangements, epigenetic changes, somatic mutations, and gene expression. Tumors with similar histopathologic phenotypes but diverse genomic profiles could respond differently to the same treatment, leading to distinct clinical outcomes. Therefore, there is a clinical need to classify tumors into molecular subtypes and to identify driver (causative) molecular alterations that could be targeted for precision medicine. In an effort to comprehensively catalog transcriptomic, genomic and epigenomic alterations of cancers, national and international consortia such as The Cancer Genome Atlas (TCGA) and the International Cancer Genome Consortium (ICGC) have been established to perform large-scale genomic profiling studies, which have been generating an unprecedented amount of data with multiple layers of genomic and genetic information for a variety of cancers. While these large-scale genomic studies have provided integrative data for researchers to discover tumor subtypes and their genomic signatures, most of the clustering analyses are performed at the single data set level and then integrated manually, which is partially due to the relatively slower development of integrative statistical methods and efficient software. It has become increasingly clear that separate analyses of individual genomic data set and a post hoc integration of the clustering results have difficulty capturing the correlated structure of cancer omics data and thus much of the potential for new insight might have gone unrealized. Therefore, there is a great need for developing statistical methods and tools for integrative analysis of omics data from multiple sources.
In an effort to identify clinically relevant tumor subtypes from TCGA data, Shen and others (2009) developed a method called iCluster that uses a Gaussian latent variable model to jointly model continuous genomic data such as gene expression, DNA methylation and copy number data. The latent variables in the iCluster model form a set of principle coordinates spanning a low dimensional subspace that can collectively capture the correlative structure of multi-omics data, and thus can be used for tumor sample clustering and integrated visualization. The iCluster model assumes that each data set is conditionally independent given the latent variables. An optimal number of integrative clusters can be found when the joint likelihood of the genomic data sets is maximized. In the iCluster model, an expectation-maximization (EM) algorithm is used for parameter estimation and a soft-thresholding method is used to induce sparsity in the model parameters in order to achieve better clustering results and distinguish informative features from non-informative features. Shen and others (2013) further extended the iCluster model by employing lasso, elastic net and fused lasso methods to allow feature selection in integrative clustering context. The overall aims of the iCluster method are to obtain a joint clustering of samples and identify cluster-relevant features across data sets. Besides the iCluster method, a few other model-based methods have been developed for integrative clustering analysis although their aims may not be exactly the same as the iCluster method. For example, Kormaksson and others (2012) developed a finite mixture model to perform joint clustering of gene expression and DNA methylation data. In contrast to the iCluster method, the Multiple Dataset Integration (MDI) developed by Kirk and others (2012) does not seek to find joint sample clusters. Instead, it allows different data sets to have different numbers of clusters and the clustering of genes in one data set is influenced by the clustering in another data set. The MDI method focuses more on identifying clusters of genes with shared characteristics in genomic data such as chromatin immunoprecipitation-chip and microarray gene expression. Lock and Dunson (2013) developed the Bayesian consensus clustering (BCC) method to perform both data-specific clustering and consensus clustering. In the BCC framework, individual clustering is not independent and adhere loosely to an overall clustering. The iCluster and MDI methods can perform clustering and feature selection, but the other two aforementioned methods only perform clustering.
The iClusterPlus method developed by Mo and others (2013) is a significant enhancement of the iCluster method that can jointly model multi-type omics data including continuous, count, binary, and multi-categorical data. In the iClusterPlus framework, there is no closed-form solution for estimation of the model parameters. Therefore, a modified Monte Carlo Newton–Raphson algorithm is used to estimate the model parameters and lasso penalty is used to induce sparse estimation. The iClusterPlus method has been used to generate biologically meaningful cancer subtypes in large-scale cancer genomic studies including squamous cell lung cancers, lung adenocarcinoma, endometrial carcinoma and gastric adenocarcinoma studies (TCGA, 2012; 2013; 2014; 2014). Although the iClusterPlus method is widely adopted by research communities, there are two limitations in the statistical model that could limit its usage. First, in order to find an optimal solution for parameter estimation and subtype identification, it needs to tune the model parameters by testing hundreds of 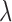 (Lasso shrinkage parameter) values for a few integrated data sets. This requires a lot of computation because it needs to run through all the computationally intensive steps of the modified Monte Carlo Newton–Raphson algorithm for each
(Lasso shrinkage parameter) values for a few integrated data sets. This requires a lot of computation because it needs to run through all the computationally intensive steps of the modified Monte Carlo Newton–Raphson algorithm for each 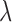 . Second, there is no evaluation of statistical significance for the selected features. A feature is selected if its associated parameter is not 0, according to the Lasso method (Tibshirani, 1996).
. Second, there is no evaluation of statistical significance for the selected features. A feature is selected if its associated parameter is not 0, according to the Lasso method (Tibshirani, 1996).
To address the challenges in integrative analysis of cancer omics data, we have developed a fully Bayesian integrative clustering method named iClusterBayes to model continuous and discrete omics data. This new method overcomes the limitations of the iClusterPlus method and is a valuable tool for cancer research. We organize this article as follows. In Section 2, we provide details for the iClusterBayes framework. In Section 3, we perform simulations to examine the performance of the proposed method. In Section 4, we show that the iClusterBayes method can reveal clinically meaningful cancer subtypes by analyzing TCGA glioblastoma and kidney cancer data. In Section 5, we summarize this article with a brief discussion.
2. Methods
2.1. The integrative clustering framework
The proposed method is designed to integrate continuous and discrete data, which represent the major forms of omics data. Figure 1 shows the core idea of the joint integrative clustering framework. Suppose we have 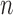 tumor samples and each of them is analyzed by
tumor samples and each of them is analyzed by 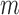 different types of techniques generating
different types of techniques generating 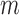 sets of genomic data. For example, microarray-based platforms can generate continuous data for gene expression, DNA copy number and CpG site methylation, while sequencing-based platforms can generate count data for gene expression and binary data for DNA mutation. Let
sets of genomic data. For example, microarray-based platforms can generate continuous data for gene expression, DNA copy number and CpG site methylation, while sequencing-based platforms can generate count data for gene expression and binary data for DNA mutation. Let 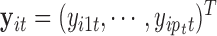 denote a
denote a 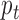 -dimensional data vector. Each element
-dimensional data vector. Each element 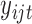 denotes the observed data associated with the
denotes the observed data associated with the 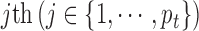 genomic feature in the
genomic feature in the 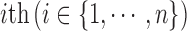 sample of the
sample of the 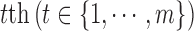 data type. Depending on the type of data, a genomic feature can be a protein coding gene or non-gene-centric elements of interest (e.g., genomic region/location, CpG sites, mRNA, etc.). The
data type. Depending on the type of data, a genomic feature can be a protein coding gene or non-gene-centric elements of interest (e.g., genomic region/location, CpG sites, mRNA, etc.). The  data set can be represented by
data set can be represented by 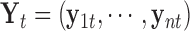 , a matrix with dimension
, a matrix with dimension 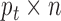 , and all the data sets can be represented by a multi-high dimensional genomic data space
, and all the data sets can be represented by a multi-high dimensional genomic data space 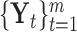 . Assume there are
. Assume there are 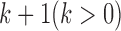 molecular subtypes in the tumor samples, and we hope to identify them from the multi-high dimensional data space
molecular subtypes in the tumor samples, and we hope to identify them from the multi-high dimensional data space 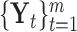 .
.
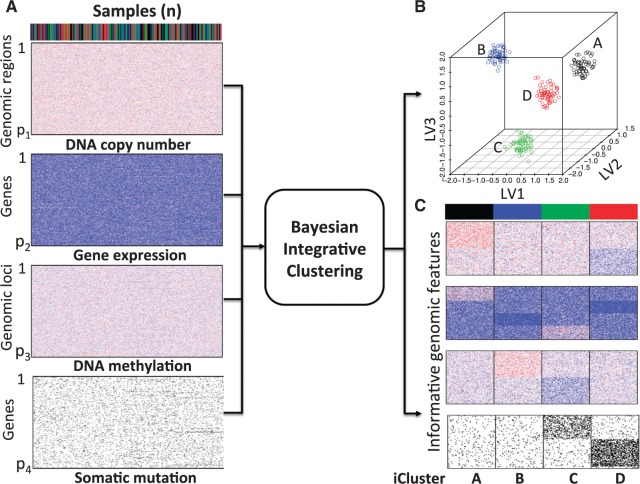
Fig. 1.
The proposed Bayesian integrative clustering framework. Bayesian latent variable regression models are used to jointly model multiple genomic data sets (A) to identify common latent variables that can be used to cluster patient samples in a lower dimensional integrated latent variable space (B). Simultaneously, driver genetic/genomic features (e.g., DNA copy number, gene expression, DNA methylation and somatic mutation) that contribute to sample clustering are identified (C).
The core idea of the integrative clustering framework is to reduce the multi-high dimensional space to a low dimensional subspace that will collectively capture the major variations of the multiple genomic data sets. Therefore, the low-dimensional subspace can be used to cluster the tumor samples. This is similar to principle component analysis (PCA) when there is only one data type in the analysis. In PCA analysis, the high dimensionality of the data is reduced to a low-dimensional space that is represented by a set of new variables called principal components. Usually, the first few principal components (PCs) capture most of the variation in the original data set and thus they can be used to cluster the samples. Different profiling platforms could generate different types of genomic data. The units of measurement vary from one profiling platform to another, and thus it is not appropriate to directly pool them for PCA-like analyses. Borrowing the idea from PCA, we assume that we could project the multi-high dimensional space 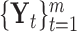 to a low-dimensional integrated subspace
to a low-dimensional integrated subspace 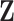 with dimension
with dimension 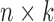 . In other words, we can say that each sample is associated with a latent variable
. In other words, we can say that each sample is associated with a latent variable 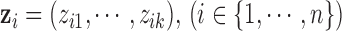 . We assume that
. We assume that 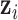 is a continuous variable and follows a standard multivariate normal distribution
is a continuous variable and follows a standard multivariate normal distribution  . The mean zero and identity covariance matrix are necessary constraints to make sure the proposed joint statistical model is identifiable. If there are
. The mean zero and identity covariance matrix are necessary constraints to make sure the proposed joint statistical model is identifiable. If there are 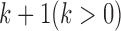 molecular subtypes in the tumor samples, we can separate the samples using the latent variable
molecular subtypes in the tumor samples, we can separate the samples using the latent variable 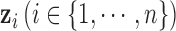 .
.
2.2. Statistical model for continuous data
Microarray-based technologies typically generate continuous data, which are measurements of signal intensities of probe-target hybridization on the microarrays. Through proper transformation, these data can be appropriately normal. Therefore, we first lay out our statistical framework for omics data with continuous measures, which is
| (2.1) |
where 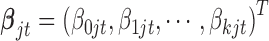 is the coefficient vector associated with the
is the coefficient vector associated with the 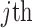 feature in the
feature in the 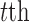 data set;
data set; 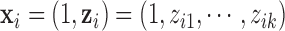 , is a vector in which the first component is 1 and the remaining components are exactly from vector
, is a vector in which the first component is 1 and the remaining components are exactly from vector 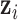 ;
; 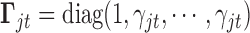 is a diagonal matrix whose first diagonal component is 1 and all the remaining
is a diagonal matrix whose first diagonal component is 1 and all the remaining 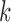 diagonal components are
diagonal components are 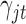 ;
; 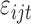 is the random error with mean
is the random error with mean 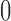 and variance
and variance 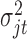 . The constant 1 in
. The constant 1 in 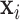 and
and 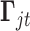 is designed to let the model (2.1) have the intercept
is designed to let the model (2.1) have the intercept 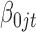 . In the model,
. In the model, 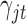 is an indicator variable with value
is an indicator variable with value 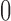 or
or 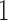 , which is used for Bayesian variable selection (George and McCulloch, 1997). When
, which is used for Bayesian variable selection (George and McCulloch, 1997). When 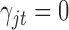 , it indicates that the corresponding
, it indicates that the corresponding 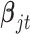 is small and thus the
is small and thus the 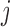 th omics feature in the
th omics feature in the 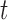 th data set contributes little for the joint clustering. When
th data set contributes little for the joint clustering. When 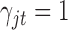 , it indicates that the corresponding
, it indicates that the corresponding  is large and thus the
is large and thus the  th omics feature in the
th omics feature in the 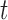 th data set is a contributor for the joint clustering. Let
th data set is a contributor for the joint clustering. Let 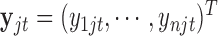 be the data vector of omics feature
be the data vector of omics feature 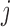 for samples
for samples 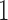 to
to 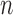 . Let
. Let 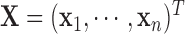 be the design matrix with dimension
be the design matrix with dimension 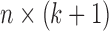 , where row
, where row 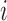 is
is 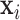 . The model for omics feature
. The model for omics feature 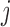 in data set
in data set 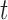 can be written as
can be written as
| (2.2) |
where 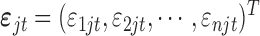 . To perform Bayesian analysis, we assume the following prior distributions for the model parameters
. To perform Bayesian analysis, we assume the following prior distributions for the model parameters
In words, we assume that the coefficient vector 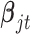 follows multivariate normal distribution with mean
follows multivariate normal distribution with mean 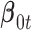 and covariance
and covariance 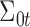 ;
; 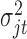 follows inverse-gamma distribution with shape parameter
follows inverse-gamma distribution with shape parameter 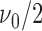 and scale parameter
and scale parameter 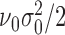 ; indicator variable
; indicator variable 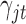 follows Bernoulli distribution with probability of an omics feature being selected as a driving factor for clustering is
follows Bernoulli distribution with probability of an omics feature being selected as a driving factor for clustering is 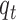 . With these assumptions, we can derive the posterior distributions of the model parameters
. With these assumptions, we can derive the posterior distributions of the model parameters 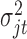 ,
, 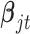 and
and 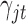 .
.
| (2.3) |
| (2.4) |
| (2.5) |
where 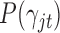 is the prior probability of
is the prior probability of 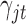 . In words, the posterior distribution of
. In words, the posterior distribution of 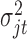 is inverse gamma distribution with scale parameter
is inverse gamma distribution with scale parameter 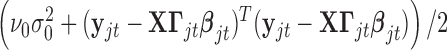 and shape parameter
and shape parameter 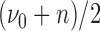 ; the posterior distribution of
; the posterior distribution of 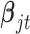 is multivariate normal with mean
is multivariate normal with mean 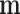 and covariance
and covariance 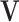 . Since the posterior distributions of
. Since the posterior distributions of 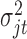 and
and 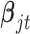 are known, we can use the Gibbs sampling algorithm (Geman and Geman, 1984; Kuo and Mallick, 1998) to obtain samples from their posterior distributions. There is no closed form for parameter
are known, we can use the Gibbs sampling algorithm (Geman and Geman, 1984; Kuo and Mallick, 1998) to obtain samples from their posterior distributions. There is no closed form for parameter 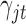 . However, we know its distribution is proportional to the terms on the right side of
. However, we know its distribution is proportional to the terms on the right side of 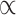 in equation (2.5), thus we can sample from its posterior distribution using the Metropolis–Hasting algorithm (Metropolis and others, 1953; Hastings, 1970; Kuo and Mallick, 1998). There is no closed form for
in equation (2.5), thus we can sample from its posterior distribution using the Metropolis–Hasting algorithm (Metropolis and others, 1953; Hastings, 1970; Kuo and Mallick, 1998). There is no closed form for 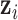 . We will show how to sample from its posterior distribution after we describe our modeling strategy for discrete data in the following sections. The latent variable
. We will show how to sample from its posterior distribution after we describe our modeling strategy for discrete data in the following sections. The latent variable 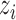 will be used for sample clustering, and omics features with high posterior probability of
will be used for sample clustering, and omics features with high posterior probability of 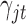 being 1 will be selected as informative features.
being 1 will be selected as informative features.
2.3. Statistical model for binary data
Next generation sequencing is becoming less and less expensive, and more and more sequencing data are being generated, which are usually discrete. For example, exome sequencing data can be represented by binary values indicating mutation or no mutation for genes. RNA-seq often measures gene expression based on read count (the number of reads mapped to a given gene). Therefore, it is not optimal to use the above framework to model these discrete data. Considering the nature of these data, we propose the following model for the discrete data. If 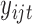 is a binary variable (e.g., mutation or no-mutation), we model the data with the classical logistic regression,
is a binary variable (e.g., mutation or no-mutation), we model the data with the classical logistic regression,
| (2.6) |
where 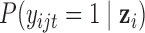 is the probability of gene
is the probability of gene 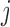 being mutant in sample
being mutant in sample 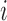 given the value of the latent variable
given the value of the latent variable 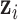 ;
; 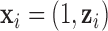 is the same design vector as the one in model (2.1);
is the same design vector as the one in model (2.1); 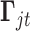 and
and 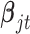 have the same components as those in model (2.1) while data type
have the same components as those in model (2.1) while data type 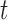 refers to binary. We assume the prior distributions of
refers to binary. We assume the prior distributions of 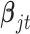 and
and 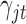 follow
follow 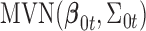 and
and 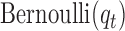 , respectively. Therefore, the posterior distributions of
, respectively. Therefore, the posterior distributions of 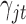 and
and 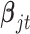 given the data and the other parameters in model (2.6) are
given the data and the other parameters in model (2.6) are
| (2.7) |
| (2.8) |
In words, the posterior distributions of 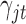 and
and 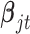 are proportional to the terms on the right side of
are proportional to the terms on the right side of  , respectively.
, respectively.
2.4. Statistical model for count data
When 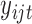 is a count variable (e.g., RNA-seq gene expression data), we model the data with the following Poisson regression
is a count variable (e.g., RNA-seq gene expression data), we model the data with the following Poisson regression
| (2.9) |
where 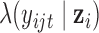 is the predicted mean of
is the predicted mean of 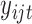 conditional on the latent variable
conditional on the latent variable  ;
; 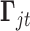 and
and 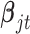 are the corresponding indicator variable and parameter for the count data type as those for the continuous and binary cases. To perform Bayesian analysis, we use a multivariate prior
are the corresponding indicator variable and parameter for the count data type as those for the continuous and binary cases. To perform Bayesian analysis, we use a multivariate prior 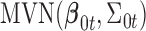 for
for 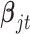 and
and 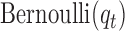 for
for 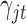 . Therefore the posterior distributions of
. Therefore the posterior distributions of 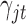 and
and 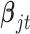 given the data and the other parameters in the Poisson regression model (2.9) are
given the data and the other parameters in the Poisson regression model (2.9) are
| (2.10) |
| (2.11) |
There is no closed form for the posterior distributions of  and
and 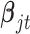 when the data are binary or count values, but we know they are proportional to some functions respectively. Therefore, we can use the Metropolis–Hasting algorithm to jointly sample
when the data are binary or count values, but we know they are proportional to some functions respectively. Therefore, we can use the Metropolis–Hasting algorithm to jointly sample  from their posterior distributions for statistical inference (Savitsky and others, 2011).
from their posterior distributions for statistical inference (Savitsky and others, 2011).
2.5. The joint likelihood
As it can be seen from the above models, each of them has a common 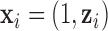 , which is the key to our modeling strategy. We let sample
, which is the key to our modeling strategy. We let sample 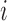 be associated with latent variable
be associated with latent variable 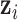 . Through joint modeling,
. Through joint modeling, 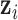 will collectively capture the major biological variations across the omics data of the cancer samples and provide a basis for predicting if an omics feature
will collectively capture the major biological variations across the omics data of the cancer samples and provide a basis for predicting if an omics feature 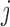 in a given data set
in a given data set 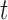 is a driver for sample clustering. The joint model for the data types described above can be written as
is a driver for sample clustering. The joint model for the data types described above can be written as
| (2.12) |
where the multiplication is due to the conditional independence assumption of 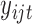 given
given 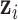 ;
; 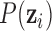 is the density function of the standard multivariate normal distribution
is the density function of the standard multivariate normal distribution 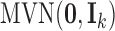 ; the conditional density function
; the conditional density function 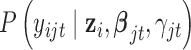 has the form of normal, Bernoulli or Poisson depending on the type of omics data. More specifically,
has the form of normal, Bernoulli or Poisson depending on the type of omics data. More specifically,
The latent variable 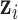 is not observable, thus we also need to use the Markov Chain Monte Carlo (MCMC) method to obtain samples from its posterior distribution for statistical inference. The exact posterior distribution of
is not observable, thus we also need to use the Markov Chain Monte Carlo (MCMC) method to obtain samples from its posterior distribution for statistical inference. The exact posterior distribution of 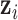 is not known. However, we know it is proportional to the product of the density of
is not known. However, we know it is proportional to the product of the density of 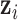 and the joint likelihood of the data as the following,
and the joint likelihood of the data as the following,
| (2.13) |
Therefore, the Metropolis–Hasting algorithm will be used to sample from its posterior distribution for statistical inference (Metropolis and others, 1953; Hastings, 1970). The mean value of the latent variables are used for sample clustering. Specifically, following a general principle for separating 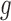 clusters among
clusters among 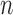 data points, we use
data points, we use 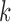 -means clustering to divide the
-means clustering to divide the 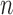 samples into
samples into 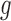 clusters in the latent variable space, where
clusters in the latent variable space, where 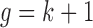 (Mo and others, 2013).
(Mo and others, 2013).
3. Simulation studies
To demonstrate the feasibility of the integrative model, we performed simulation studies. We assumed there were 240 cancer samples analyzed by array comparative genomic hybridization (aCGH), RNA sequencing, DNA methylation assay and whole-exome sequencing (see Figure 1). These analyses generated DNA copy number, gene expression, DNA methylation and somatic mutation data, which were presented as continuous, count, continuous and binary data types, respectively. We assumed that these cancer samples belonged to four subtypes (A, B, C, and D) and each of the subtypes had 60 samples. We let each data set have 2000 genomic features and 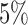 of them were informative features that defined the subtypes. More specifically, we let subtype A be characterized by 50 genomic regions with amplification, which made 50 genes increase their expression. Subtype B was characterized by hypermethylation of 50 genomic loci, which decreased the expression of 50 genes. Subtype C was characterized by hypomethylation of 50 genes, which increased the expression of 50 genes. Subtype D was characterized by 50 genomic regions with deletion, which led to decreased expression of 50 genes. In addition, subtypes C and D had relatively high somatic mutation rates in 50 genes, respectively. The simulated data were generated according to these hypothesized biological events. Specifically, the DNA copy number data for genomic regions with normal copy number were randomly generated from a standard normal distribution
of them were informative features that defined the subtypes. More specifically, we let subtype A be characterized by 50 genomic regions with amplification, which made 50 genes increase their expression. Subtype B was characterized by hypermethylation of 50 genomic loci, which decreased the expression of 50 genes. Subtype C was characterized by hypomethylation of 50 genes, which increased the expression of 50 genes. Subtype D was characterized by 50 genomic regions with deletion, which led to decreased expression of 50 genes. In addition, subtypes C and D had relatively high somatic mutation rates in 50 genes, respectively. The simulated data were generated according to these hypothesized biological events. Specifically, the DNA copy number data for genomic regions with normal copy number were randomly generated from a standard normal distribution 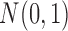 and the data for genomic regions with amplification and deletion were randomly generated from
and the data for genomic regions with amplification and deletion were randomly generated from 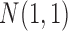 and
and 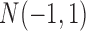 , respectively. The normal gene expression data were randomly generated from
, respectively. The normal gene expression data were randomly generated from 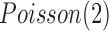 (Poisson distribution with mean of 2), and the increased and decreased expression data were randomly generated from
(Poisson distribution with mean of 2), and the increased and decreased expression data were randomly generated from 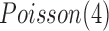 and
and 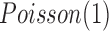 , respectively. By appropriate transformation (e.g., logit transformation of beta-values), the methylation data can be approximately normal. Thus, we used the data randomly generated from
, respectively. By appropriate transformation (e.g., logit transformation of beta-values), the methylation data can be approximately normal. Thus, we used the data randomly generated from 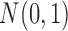 as the normal methylation data, and the data randomly generated from
as the normal methylation data, and the data randomly generated from 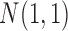 and
and 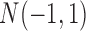 as the hypermethylation and hypomethylation data, respectively. For the somatic mutation data, we assumed the genes selected for analysis have a back ground mutation rate of 0.05, and the informative genes in subtypes C and D have mutation rates of 0.3 and 0.5, respectively. The mutation data were generated from Bernoulli distribution with the assumed mutation rates. The heatmaps of the four data sets are shown in Figure 1A. It can be seen that the patterns defining the subtypes are not clearly revealed on the heatmaps without clustering analysis.
as the hypermethylation and hypomethylation data, respectively. For the somatic mutation data, we assumed the genes selected for analysis have a back ground mutation rate of 0.05, and the informative genes in subtypes C and D have mutation rates of 0.3 and 0.5, respectively. The mutation data were generated from Bernoulli distribution with the assumed mutation rates. The heatmaps of the four data sets are shown in Figure 1A. It can be seen that the patterns defining the subtypes are not clearly revealed on the heatmaps without clustering analysis.
In all the simulation and real data analyses reported in the paper, we set the priors for 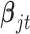 to the standard multivariate normal distribution
to the standard multivariate normal distribution 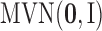 , the priors for
, the priors for 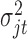 to
to 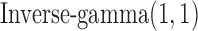 , which are uninformative priors for the model parameters. For the the indicator variable
, which are uninformative priors for the model parameters. For the the indicator variable  , we used
, we used 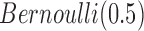 as the prior for each variable. If we know the proportion of informative features, we can choose to use an informative prior, which is the case in the simulation study. In fact, we found there was very little effect on the results by choosing the prior in the range of 0.05–0.5. In our model,
as the prior for each variable. If we know the proportion of informative features, we can choose to use an informative prior, which is the case in the simulation study. In fact, we found there was very little effect on the results by choosing the prior in the range of 0.05–0.5. In our model, 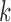 is the dimension of the latent variable
is the dimension of the latent variable 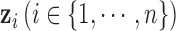 . For a given
. For a given 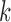 , the samples can be divided into
, the samples can be divided into 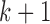 clusters. In real data analysis, we usually don’t know the number of subtypes. Therefore, we need to try a sequence of small integers and check how well the model fits the data under different values. In this simulation study, we let
clusters. In real data analysis, we usually don’t know the number of subtypes. Therefore, we need to try a sequence of small integers and check how well the model fits the data under different values. In this simulation study, we let 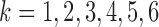 and for each
and for each 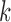 we ran 22 000 MCMC iterations, of which the first 10 000 were discarded as burn-in.
we ran 22 000 MCMC iterations, of which the first 10 000 were discarded as burn-in.
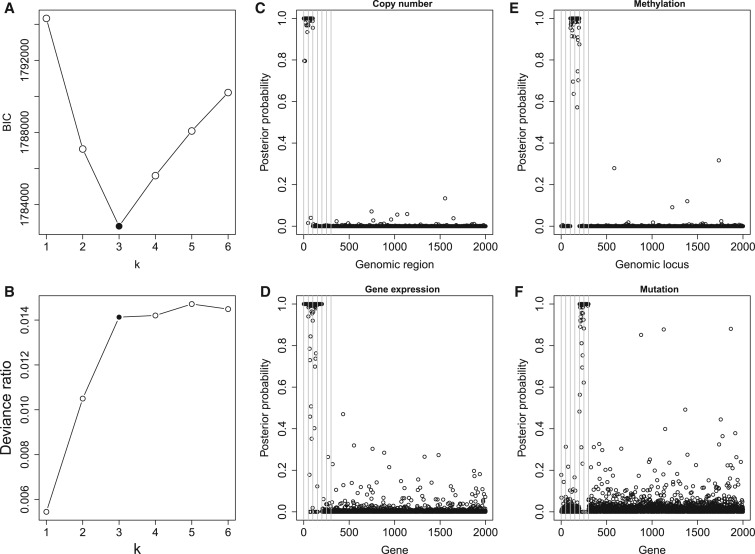
Figure 2A and B shows the deviance ratios and Bayesian information criterion (BIC) values for the selected  . We can see the BIC value reaches the minimum and the deviance ratio reaches a plateau when
. We can see the BIC value reaches the minimum and the deviance ratio reaches a plateau when 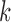 is equal to 3, which indicates the model fits the data best when the samples are divided into 4 subtypes. Therefore, BIC or deviance ratio can be used as a criterion for selecting an appropriate value for
is equal to 3, which indicates the model fits the data best when the samples are divided into 4 subtypes. Therefore, BIC or deviance ratio can be used as a criterion for selecting an appropriate value for 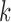 , which defines an optimal number of clusters for the samples. Figure 2C-F shows the posterior probabilities of the genomic features. A high posterior probability suggests that the corresponding genomic feature is more likely to be a driver (informative) feature, which contributes to the integrative clustering. As it can be seen on Figure 2C-F, more than
, which defines an optimal number of clusters for the samples. Figure 2C-F shows the posterior probabilities of the genomic features. A high posterior probability suggests that the corresponding genomic feature is more likely to be a driver (informative) feature, which contributes to the integrative clustering. As it can be seen on Figure 2C-F, more than 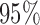 of the informative features have posterior probabilities greater than 0.5 and more than
of the informative features have posterior probabilities greater than 0.5 and more than 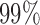 of the uninformative features have posterior probabilities less than 0.5. This demonstrates that the proposed method can achieve a high sensitivity and specificity in distinguishing informative features from uninformative features. In addition, all the samples cluster according to their subtypes in the three-dimensional latent variable space (Figure 1B). The genomic expression patterns of the subtypes were revealed by presenting the identified genomic features on the heat maps (Figure 1C). We also analyzed the simulated data sets using the iClusterPlus software which uses a MCMC algorithm to sample the latent variable and the
of the uninformative features have posterior probabilities less than 0.5. This demonstrates that the proposed method can achieve a high sensitivity and specificity in distinguishing informative features from uninformative features. In addition, all the samples cluster according to their subtypes in the three-dimensional latent variable space (Figure 1B). The genomic expression patterns of the subtypes were revealed by presenting the identified genomic features on the heat maps (Figure 1C). We also analyzed the simulated data sets using the iClusterPlus software which uses a MCMC algorithm to sample the latent variable and the  -norm penalized regression to induce sparsity in the model parameters. The iClusterPlus correctly clustered the samples. However, it was about 200 times slower than iClusterBayes using six cores of a Mac Pro computer for the computation (see supplementary material available at Biostatistics online.).
-norm penalized regression to induce sparsity in the model parameters. The iClusterPlus correctly clustered the samples. However, it was about 200 times slower than iClusterBayes using six cores of a Mac Pro computer for the computation (see supplementary material available at Biostatistics online.).
Fig. 2.
Model and variable selection for the simulated data sets. (A) BIC and (B) deviance ratio at k = 1, 2, 3, 4, 5, and 6. The model fits the data best when k = 3. (C-F): Posterior probabilities of genomic features when k = 3. For easy comparison, the informative genomic features are arranged in the neighborhood of each other on the x-axes, which have high posterior probabilities of being the driver for the sample clustering. Copy number: genomic regions 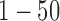 and
and 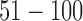 are gain and loss regions, respectively. Methylation: genomic loci
are gain and loss regions, respectively. Methylation: genomic loci 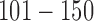 and
and 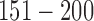 are hypermethylated and hypomethylated, respectively. Gene expression: genes
are hypermethylated and hypomethylated, respectively. Gene expression: genes 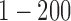 are up- or down-regulated in response to the copy number and methylation alterations. Mutation: genes
are up- or down-regulated in response to the copy number and methylation alterations. Mutation: genes 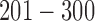 are hypermutated.
are hypermutated.
4. Case studies
4.1. TCGA glioblastoma data application
We first applied our method to TCGA glioblastoma (GBM) data sets. GBM was the most common brain tumor in adults and was the first cancer chosen for genomic characterization by TCGA (TCGA, 2008). The GBM data sets were downloaded from TCGA data portal (https://tcga-data.nci.nih.gov/tcga/) and the cBio Cancer Genomics Portal (http://cbioportal.org/) at the Memorial Sloan-Kettering Cancer Center. The data sets consisted of 84 samples that were measured by somatic mutation, DNA copy number and mRNA expression. The somatic mutation data were obtained by sequencing analysis of 601 selected genes in matched tumor-normal sample pairs. The data were summarized in a binary matrix (1: mutation, 0: no mutation) with the rows and columns corresponding to the samples and genes, respectively. We filtered out genes with mutation rate 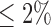 . DNA copy number alterations (CNAs) measured by the Agilent 244k microarrays were used for clustering analysis. The level 3 normalized and segmented data were condensed to non-redundant regions as described by (Mo and others, 2013). Gene expression was measured by three microarray platforms (Affymetrix Human Exon 1.0 ST GeneChips, Affymetrix HT-HG-U133A GeneChips, and custom designed Agilent 244K array). For each gene, a unified gene expression was generated by integrating the measurements from the three platforms as described by (Verhaak and others, 2010). The 1740 most variable genes were used for our clustering analysis. Therefore, the GBM mutation, copy number and gene expression data were presented as binary, continuous, and continuous data types, respectively.
. DNA copy number alterations (CNAs) measured by the Agilent 244k microarrays were used for clustering analysis. The level 3 normalized and segmented data were condensed to non-redundant regions as described by (Mo and others, 2013). Gene expression was measured by three microarray platforms (Affymetrix Human Exon 1.0 ST GeneChips, Affymetrix HT-HG-U133A GeneChips, and custom designed Agilent 244K array). For each gene, a unified gene expression was generated by integrating the measurements from the three platforms as described by (Verhaak and others, 2010). The 1740 most variable genes were used for our clustering analysis. Therefore, the GBM mutation, copy number and gene expression data were presented as binary, continuous, and continuous data types, respectively.
In this integrative clustering analysis, we used the prior 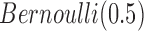 for the indicator variable
for the indicator variable 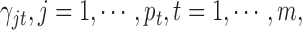 and tested the cluster number parameter
and tested the cluster number parameter 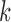 from 1 to 6. For each
from 1 to 6. For each 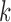 , we ran 30 000 MCMC iterations, of which the first 18 000 were discarded as burn-in. Supplementary material available at Biostatistics online shows the BIC and deviance ratio at each
, we ran 30 000 MCMC iterations, of which the first 18 000 were discarded as burn-in. Supplementary material available at Biostatistics online shows the BIC and deviance ratio at each 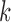 . We can see that the BIC as well as the deviance ratio reaches a transition point beyond which dividing samples into more clusters no longer provides significant improvement for model fitting. Therefore, we thought that
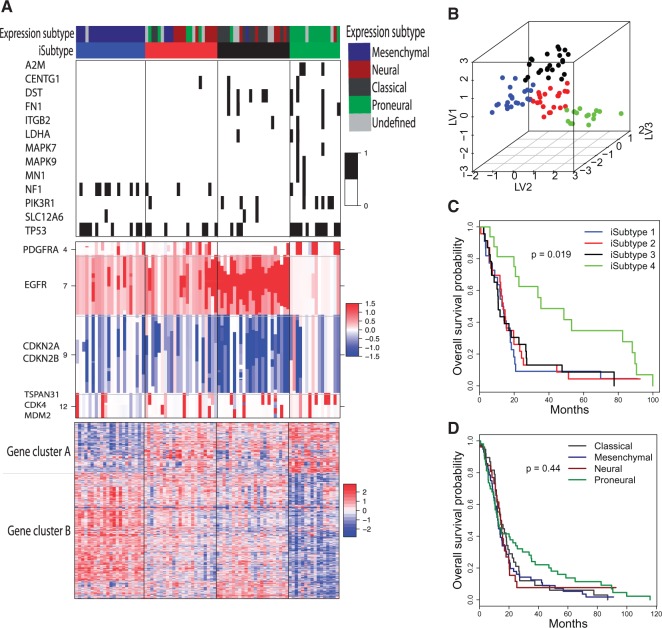
. We can see that the BIC as well as the deviance ratio reaches a transition point beyond which dividing samples into more clusters no longer provides significant improvement for model fitting. Therefore, we thought that 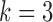 was an optimal parameter for the cluster number at which the samples could be divided into 4 clusters (subtypes). Figure 3B shows the 84 samples clustered in the three-dimensional latent variable space where the subtypes
was an optimal parameter for the cluster number at which the samples could be divided into 4 clusters (subtypes). Figure 3B shows the 84 samples clustered in the three-dimensional latent variable space where the subtypes 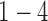 are indicated by blue, red, black and green colors respectively. Interestingly, the patients in the subtype 4 had significantly better survival than the other three subtypes (p-value = 0.019, Log-rank test; Figure 3C). In contrast, the overall survivals for the previously reported gene expression subtypes were not significantly different (p-value = 0.44, Log-rank test; Figure 3D) (Verhaak and others, 2010).
are indicated by blue, red, black and green colors respectively. Interestingly, the patients in the subtype 4 had significantly better survival than the other three subtypes (p-value = 0.019, Log-rank test; Figure 3C). In contrast, the overall survivals for the previously reported gene expression subtypes were not significantly different (p-value = 0.44, Log-rank test; Figure 3D) (Verhaak and others, 2010).
Fig. 3.
GBM integrative subtypes. (A): Heatmaps of the genes and genomic regions with posterior probability 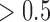 . The genomic patterns for the mutation (black, mutated; white, not mutated), copy number (red, amplification; white, normal; blue, deletion), and gene expression (red, high-level expression; blue, low-level expression) are shown on the top, middle and bottom panels, respectively. (B): GBM samples clustered in the three-dimensional latent variable space. (C): K–M survival curves for the four clusters (iSubtypes). (D): K–M survival curves for the previously reported gene expression subtypes (Verhaak and others, 2010). LV: latent variable.
. The genomic patterns for the mutation (black, mutated; white, not mutated), copy number (red, amplification; white, normal; blue, deletion), and gene expression (red, high-level expression; blue, low-level expression) are shown on the top, middle and bottom panels, respectively. (B): GBM samples clustered in the three-dimensional latent variable space. (C): K–M survival curves for the four clusters (iSubtypes). (D): K–M survival curves for the previously reported gene expression subtypes (Verhaak and others, 2010). LV: latent variable.
Besides identifying the four biologically meaningful subtypes, we also identified important genes and genomic regions that contributed to the sample clustering. Figure 3A shows the genes and genomic regions with posterior probability greater than 0.5 from the three data sets. The mutated genes contributing to the subtype classification included tumor suppressor genes (NF1, TP53, MN1), genes involved in intracellular signaling cascades (NF1, TP53, MAPK9, MAPK7,PIK3R1), and genes involved in inflammatory and defense responses (A2M, ITGB2, FN1). These genes play important roles in controlling cell division and proliferation and immune response. It is well known that the accumulated mutations in these genes could lead to tumor initiation and progression. There were 161 genomic regions located on chromosomes 4, 7, 9, and 12 identified as the drivers for the subtype classification, which had distinct patterns of copy number alterations across the 4 subtypes (Figure 3A, the middle panel). These regions contain important tumor suppressor genes (e.g., CDKN2A and CDKN2B on chr9) and oncogenes that play an important role in the regulation of cell activation, division, and proliferation (e.g., PDGFRA on chr4; EGFR on chr7; TSPAN31, CDK4 and MDM2 on chr12). Deletion of tumor suppressor genes and amplification of oncogenes could lead to tumorigenesis and tumor growth. In the gene expression data set, A set of 711 genes were identified as the drivers for the subtype classification. These genes were grouped into two clusters, A and B (Figure 3, the bottom panel). Gene cluster A consisted of 204 genes whose top enriched gene ontology (GO) terms included nervous system development, neurogenesis, gliogenesis, neuron differentiation, development and projection. Gene cluster B was made up of 507 genes whose top enriched GO terms included immune, wound, defense and inflammatory responses, cell activation, proliferation, migration and adhesion.
Using the unified expression data of the 1740 most variable genes, Verhaak and others (2010) clustered the GBM samples into 4 expression subtypes: Proneural, Neural, Classical and Mesenchymal. The integrative subtypes (iSubtypes) 1, 2, 3, and 4 were highly overlapped with the expression subtypes Mesenchymal, Neural, Classical and Proneural, respectively (See the color bars on Figure 3 A). For that reason, the iSubtypes may be named as those used for the expression subtypes. However, the iSubtypes contained more information than the expression subtypes. Figure 3A shows the four iSubtypes with distinct genomic patterns. The iSubtype 1 (Mesenchymal) was characterized by relatively high mutation rates of NF1 and TP53, low-mutation rates of the other genes, moderate-level amplification of EGFR, moderate-level loss of CDKN2A and CDKN2B, low-level expression of gene cluster A, and high-level expression of gene cluster B. The iSubtype 2 (Neural) had a similar mutation and copy number patterns as the iSubtype 1, but it had a different expression pattern. The iSubtype 3 (Classical) was characterized by relatively low mutation rates of the genes including A2M, MAPK7, MAPK9, MN1 and NF1, high-level amplification of EGFR, high-level loss of CDKN2A and CDKN2B. The iSubtype 4 (Proneural) was a hypermutated subtype, but it had the lowest degree of copy number alteration of EGFR, CDKN2A and CDKN2B. In addition, it had high-level expression of gene cluster A and low-level expression of gene cluster B, which were negatively correlated with the expression patterns of the iSubtype 1 (Mesenchymal).
4.2. TCGA kidney cancer data application
Clear cell renal cell carcinoma (CCRCC) is the most common type of renal cell carcinoma (RCC), or kidney cancers. Recently, TCGA analyzed more than 400 CCRCC samples using multiple genomic platforms and reported 4 mRNA subtypes (m1–m4) and 4 miRNA subtypes (mi1-mi4) respectively. Although there were samples overlapping between mRNA and miRNA subtypes, coordinated genomic patterns across the genomic data sets were not self-evident. We hypothesized that an integrative clustering analysis would be more powerful in revealing coordinated genomic, epigenomic, and transcriptomic patterns in CCRCC subtypes. To this end, we performed an integrative clustering analysis of 241 CCRCC samples that had somatic mutation, copy number, mRNA expression, methylation, and miRNA expression data using our method. All the data used for the analysis were the Level 3 data, which were downloaded from http://firebrowse.org. Specifically, the somatic mutation data were generated by DNA sequencing and the mutation calls including deletion, insertion, missense, nonsense, RNA, splice site and translation start site mutations were summarized in the mutation annotation format (MAF). A gene by sample matrix of binary values (1, mutation; 0, no mutation) was generated from the mutation data. Genes with mutation rate 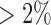 were used for clustering. For the copy number data, the normalized and segmented data based on Affymetrix SNP Array 6.0 were used. The segmented data were further condensed to 4470 non-redundant copy number regions using the method described in Mo and others (2013). The gene expression data were generated by RNA sequencing and the level 3 expression data were the log2-transformed normalized count values. We used the top
were used for clustering. For the copy number data, the normalized and segmented data based on Affymetrix SNP Array 6.0 were used. The segmented data were further condensed to 4470 non-redundant copy number regions using the method described in Mo and others (2013). The gene expression data were generated by RNA sequencing and the level 3 expression data were the log2-transformed normalized count values. We used the top 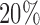 (4106) most-variable genes for the clustering analysis. The DNA methylation level was measured using Illumina DNA methylation arrays and the methylation level at each CpG locus was summarized as a
(4106) most-variable genes for the clustering analysis. The DNA methylation level was measured using Illumina DNA methylation arrays and the methylation level at each CpG locus was summarized as a 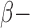 value ranging from 0 to 1, which can be interpreted as the percentage of methylation. We performed logit transformation for the
value ranging from 0 to 1, which can be interpreted as the percentage of methylation. We performed logit transformation for the  values and then used the top
values and then used the top 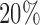 (3955) most-variable CpG sites that had the minimum correlation with the mRNA-seq data for the clustering analysis. The miRNA expression data were generated by miRNA sequencing and the level 3 data were the normalized count values represented as reads per million miRNA precursor reads (RPM). The data were log2 transformed and the bottom
(3955) most-variable CpG sites that had the minimum correlation with the mRNA-seq data for the clustering analysis. The miRNA expression data were generated by miRNA sequencing and the level 3 data were the normalized count values represented as reads per million miRNA precursor reads (RPM). The data were log2 transformed and the bottom 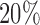 least-variable were removed from the clustering analysis. In summary, the CCRCC mutation data were modeled as binary data types, and the other data were modeled as continuous data types.
least-variable were removed from the clustering analysis. In summary, the CCRCC mutation data were modeled as binary data types, and the other data were modeled as continuous data types.
As we analyzed the GBM data sets, we used the prior 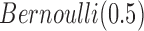 for the indicator variable
for the indicator variable 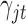
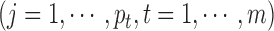 and tested the parameter
and tested the parameter 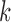 from 1 to 6. For each
from 1 to 6. For each 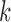 , we ran 30 000 MCMC iterations including the initial 18 000 burn-in iterations. In our initial analysis, we included the DNA copy number data. However, we found that the copy number data contributed little to the integrative clustering because all the regions had low posterior probability (
, we ran 30 000 MCMC iterations including the initial 18 000 burn-in iterations. In our initial analysis, we included the DNA copy number data. However, we found that the copy number data contributed little to the integrative clustering because all the regions had low posterior probability (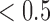 ). Therefore, we excluded the copy number data and only used the remaining four data sets for the final integrative analysis. Supplementary material available at Biostatistics online shows the BIC and deviance ratio for each
). Therefore, we excluded the copy number data and only used the remaining four data sets for the final integrative analysis. Supplementary material available at Biostatistics online shows the BIC and deviance ratio for each 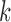 , respectively. We can see that the BIC is the minimum and the deviance ratio is the maximum when
, respectively. We can see that the BIC is the minimum and the deviance ratio is the maximum when 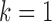 . Therefore, we thought that
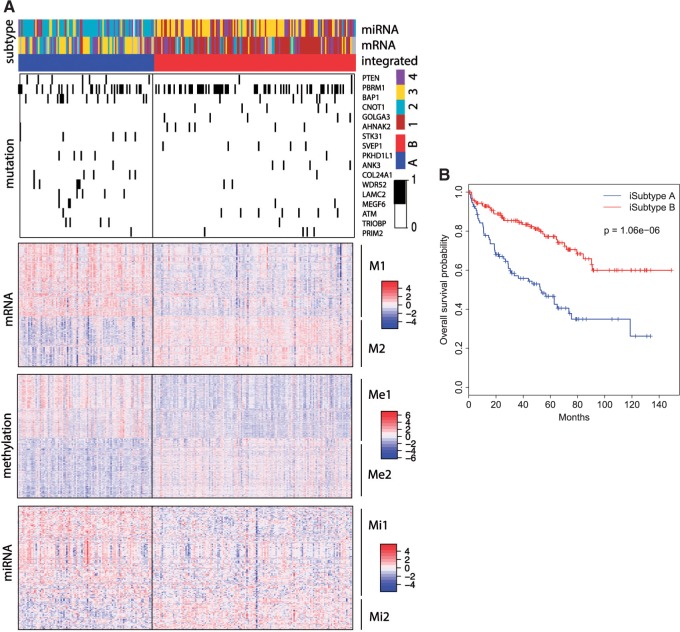
. Therefore, we thought that 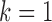 was an optimal parameter for the integrative clustering, which implied that it was optimal to divide the samples into 2 iSubtypes. The iSubtype A was mainly overlapped with TCGA miRNA subtype 2 and mRNA subtype 3, and the iSubtype B was mainly overlapped with TCGA miRNA subtype 3 and mRNA subtype 1. The two iSubtypes showed different survival functions: the patients in the iSubtype B had significantly better survival than the patients in the iSubtype A (p-value = 1.06e–06, Log-rank test; Figure 4B).
was an optimal parameter for the integrative clustering, which implied that it was optimal to divide the samples into 2 iSubtypes. The iSubtype A was mainly overlapped with TCGA miRNA subtype 2 and mRNA subtype 3, and the iSubtype B was mainly overlapped with TCGA miRNA subtype 3 and mRNA subtype 1. The two iSubtypes showed different survival functions: the patients in the iSubtype B had significantly better survival than the patients in the iSubtype A (p-value = 1.06e–06, Log-rank test; Figure 4B).
Fig. 4.
CCRCC integrative subtypes. (A): Heatmaps of the genomic features with posterior probability 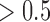 . The TCGA miRNA and mRNA subtypes are shown on the top of the heatmaps. For the mutation heatmap, black and white represent mutation and no mutation, respectively. For the mRNA, miRNA and methylation heatmaps, blue, white, and red represent low, middle, and high level of expression or methylation, respectively. The feature clusters are labeled as M1 and M2 for mRNA, Me1, and Me2 for methylation, and Mi1 and Mi2 for miRNA, respectively. (B): K–M survival curves for iSubtypes A and B.
. The TCGA miRNA and mRNA subtypes are shown on the top of the heatmaps. For the mutation heatmap, black and white represent mutation and no mutation, respectively. For the mRNA, miRNA and methylation heatmaps, blue, white, and red represent low, middle, and high level of expression or methylation, respectively. The feature clusters are labeled as M1 and M2 for mRNA, Me1, and Me2 for methylation, and Mi1 and Mi2 for miRNA, respectively. (B): K–M survival curves for iSubtypes A and B.
Figure 4A shows distinct patterns of alterations in the two iSubtypes. There were 17 mutated genes identified as the drivers for the iSubtype classification, which showed different mutation rates in the two iSubtypes. The mutated genes include tumor suppressor PTEN, chromatin remodeler PBRM1 and BAP1 that can act as tumor suppressors by regulating gene expression through chromatin remodeling, transcription regulator CNOT1, Serine/Threonine kinases STK31 and ATM. Notably, ATM is an important cell cycle checkpoint kinase that regulates a variety of downstream targets including tumor suppressors BRCA1 and p53, cell cycle checkpoint proteins RAD17 and RAD9, checkpoint kinase CHK2 and DNA repair protein NBS1 (http://www.genecards.org). There were 2064 mRNAs, 2077 CpG sites and 229 miRNAs identified as the major contributors for the iSubtype classification. The genomic features in each of the three data sets appeared to form two clusters whose expression or methylation levels were relatively higher in one iSubtype and lower in the other iSubtype. These feature clusters were labeled as mRNA clusters M1 and M2, methylation clusters Me1 and Me2, and miRNA clusters Mi1 and Mi2, respectively (Figure 4A). Gene functional enrichment analysis using DAVID bioinformatics tools showed that gene ontology (GO) terms related to cell adhesion, immune, defense, inflammatory and wound responses were among the top enriched GO terms in the negatively correlated mRNA cluster M1 and methylation cluster Me2. GO terms related to cell motion and morphogenesis, regulation of cell migration and motion, positive regulation of DNA-dependent transcription and RNA metabolic process, and response to hormone, endogenous and extracellular stimuli were among the top enriched GO terms in the negatively correlated feature clusters M2 and Me1. The miRNAs contributing to the iSubtype classification also had important functions related to immune response, inflammation, apoptosis, cell proliferation, differentiation, death, and motility.
5. Discussion
In the past years, an unprecedented amount of omics data have been generated by national and international cancer genome consortia, which have provided great resources for researchers to study cancer biology and to identify clinically relevant subtypes and biomarkers for precision medicine. These omics data are usually presented in different data types that pose a challenge for integrative analysis. For example, mutation data can be summarized in binary format with 1 and 0 indicating mutation and normal, respectively; microarray data are usually continuous; RNA-seq gene expression data are usually presented as count format. Different data types have different sources of variation, and need to be modeled differently. However, there is still a lack of data type flexible and computationally efficient methods for integrative analysis of multi-type omics data. In this article, we present a fully Bayesian latent variable model that can model any combination of major omics data including continuous, binary and count data for integrative clustering analysis. In our method, the latent variable designed to capture the inherent structure of multi-type omics data is used as the hub for statistical modeling. Conditioning on the latent variable, different types of data are assumed to be independent. Therefore, they can be modeled separately and then are integrated through the latent variable. In order to identify the features that drive the integrative clustering, Bayesian variable selection methods are naturally incorporated in the model. This new modeling approach has two advantages over the iClusterPlus method. First, it provides posterior probability estimation for each omics feature, which can be used as a criterion for feature selection. In contrast, the iClusterPlus method doesn’t provide statistical inference (e.g., p-value or confidence interval) for variable selection due to the limitation of lasso-type penalized regression. Second, it significantly reduce the computational time, which make it possible to perform integrative clustering analysis on a single computer workstation. For example, it took iClusterBayes about 2 h to analyze the simulated data sets using 6 cores of a 2.62 GHz 12-core Mac Pro computer. However, it took the iClusterPlus about 391 h (see supplementary material available at Biostatistics online).
Through simulation studies, we demonstrated that our new method precisely identified the samples’ subtypes and subtype-specific driver features. Using the TCGA GBM, and CCRCC data sets, we demonstrated that our new method was able to identify clinically relevant cancer subtypes and driver genes. For example, integrative clustering of the TCGA GBM data revealed four iSubtypes with distinct genomic patterns (Figure 3A). Interestingly, the GBM patients in the iSubtype 4 tended to have a better survival than the patients in the other three iSubtypes. Known disease-associated genes including TP53, PIK3R1, NF1, MN1, MAPK9, MAPK7, FN1, DST, and A2M were found to be the driver genes, which shown different mutation frequencies among the four iSubtypes. Tumor suppressor genes CDKN2A and CDKN2B, and oncogenes PDGFRA and EGFR were identified as driver genes that showed different copy number alteration patterns among the four iSubtypes. These genes are potential therapeutic targets for the subgroup of patients with abnormal expression or mutation. For the TCGA CCRCC data sets, we discovered two CCRCC iSubtypes that showed distinct mutation, methylation, mRNA and miRNA expression patterns (Figure 4A). These two iSubtypes were also clinically meaningful because their overall survivals were significantly different (Figure 4B). Brannon and others (2010) reported two gene expression subtypes named ccA and ccB. In terms of survival, the ccA and ccB are similar to the iSubtype A and B, respectively. Tumor suppressor genes including PTEN, PBRM1 and BAP1, and cell cycle checkpoint kinase ATM showed different mutation frequencies between the two iSubtypes, which could be potential therapeutic targets for subtype-specific therapy. In addition, a set of genes involved in immune response, transcription regulation, and cell adhesion and motion had different expression patterns between the two iSubtypes, which can also be potential therapeutic targets.
In summary, we have developed a fully Bayesian method for integrative clustering analysis of multi-type omics data. This new method significantly improved on the iClusterPlus method in terms of statistical computation. In addition, it provides a posterior probability estimation for each omics feature, which is a great advantage over the iClusterPlus method. It will provide researchers a powerful tool for deconvolution of cancer omics data and identification of clinically meaningful cancer subtypes and potential therapeutic targets.
6. Software
The iClusterBayes method was implemented in C language and wrapped in R code. User-friendly functions will be included in the iClusterPlus package https://www.bioconductor.org/packages/devel/bioc/html/iClusterPlus.html.
Supplementary Material
Acknowledgments
The authors thank the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources. Conflict of Interest: None declared.
Supplementary Material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
This work is supported by a seed grant to Q.M. from the Computational and Integrative Biomedical Research (CIBR) Center at Baylor College of Medicine, Houston, TX, USA. Q.M. and S.G.H. are supported in part by the cancer center support grant CA125123. Q.M. and K.C. are supported in part by R01 CA175397. R.S. is supported in part by P30-CA008748, P01-CA129243, CA195365, Movember Foundation-PCF Challenge Award GC226463. M.V. is supported in part by T32 CA096520.
References
- Brannon A. R., Reddy A., Seiler M., Arreola A., Moore D. T., Pruthi R. S., Wallen E. M., Nielsen M. E., Liu H., Nathanson K. L., Ljungberg B., Zhao H.. and others (2010). Molecular stratification of clear cell renal cell carcinoma by consensus clustering reveals distinct subtypes and survival patterns. Genes Cancer 1, 152–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geman S. and Geman D. (1984) Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence 6, 721–741. [DOI] [PubMed] [Google Scholar]
- George E. I. and McCulloch R. E. (1997) Approaches of bayesian variable selection. Statistica Sinica 7, 339–373. [Google Scholar]
- Hastings W. K. (1970) Monte carlo sampling methods using markov chains and their applications. Biometrika 57, 97–109. [Google Scholar]
- Kirk P., Griffin J. E., Savage R. S., Ghahramani Z. and Wild D. L. (2012) Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 28, 3290–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kormaksson M., Booth J. G., Figueroa M. E. and Melnick A. (2012) Integrative model-based clustering of microarray methylation and expression data. Annals of Applied Statistics 6, 1327–1347. [Google Scholar]
- Kuo L. and Mallick B. K. (1998) Variable selection for regression models. Sankhya: The Indian Journal of Statistics. Series B 60, 65–81. [Google Scholar]
- Lock E. F. and Dunson D. B. (2013) Bayesian consensus clustering. Bioinformatics 29, 2610–2616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H. and Teller E. (1953) Equations of state calculations by fast computing machines. Journal of Chemical Physics 21, 1087–1092. [Google Scholar]
- Mo Q., Wang S., Seshan V. E., Olshen A. B., Schultz N., Sander C., Powers R. S., Ladanyi M. and Shen R. (2013) Pattern discovery and cancer gene identification in integrated cancer genomic data. Proceedings of the National Academy of Sciences 110, 4245–4250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savitsky T., Vannucci M. and Sha N. (2011) Variable selection for nonparametric gaussian process priors: Models and computational strategies. Statistical Science 26, 130–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen R., Olshen A. B. and Ladanyi M. (2009) Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 25, 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen R., Wang S. and Mo Q. (2013) Sparse integrative clustering of multiple omics data sets. Annals of Applied Statistics 7, 269–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA. (2008). Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature 455, 1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA. (2012). Comprehensive genomic characterization of squamous cell lung cancers. Nature 489, 519–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA. (2013). Integrated genomic characterization of endometrial carcinoma. Nature 497, 67–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA. (2014a). Comprehensive molecular characterization of gastric adenocarcinoma. Nature 513, 202–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA. (2014b). Comprehensive molecular profiling of lung adenocarcinoma. Nature 511, 543–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 58, 267–288. [Google Scholar]
- Verhaak R. G. W., Hoadley K. A., Purdom E., Wang V., Qi Y., Wilkerson M. D., Miller C. R., Ding L., Golub T., Mesirov J. P.. and others (2010). Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in pdgfra, idh1, egfr, and nf1. Cancer Cell 17, 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.