Robust network-based analysis of the associations between (epi)genetic measurements

Abstract

With its important biological implications, modeling the associations of gene expression (GE) and copy number variation (CNV) has been extensively conducted. Such analysis is challenging because of the high data dimensionality, lack of knowledge regulating CNVs for a specific GE, different behaviors of the cis-acting and trans-acting CNVs, possible long-tailed distributions and contamination of GE measurements, and correlations between CNVs. The existing methods fail to address one or more of these challenges. In this study, a new method is developed to model more effectively the GE-CNV associations. Specifically, for each GE, a partially linear model, with a nonlinear cis-acting CNV effect, is assumed. A robust loss function is adopted to accommodate long-tailed distributions and data contamination. We adopt penalization to accommodate the high dimensionality and identify relevant CNVs. A network structure is introduced to accommodate the correlations among CNVs. The proposed method comprehensively accommodates multiple challenging characteristics of GE-CNV modeling and effectively overcomes the limitations of existing methods. We develop an effective computational algorithm and rigorously establish the consistency properties. Simulation shows the superiority of the proposed method over alternatives. The TCGA (The Cancer Genome Atlas) data on the PCD (programmed cell death) pathway are analyzed, and the proposed method has improved prediction and stability and biologically plausible findings.

1. Introduction

For complex diseases, profiling studies have been extensively conducted, collecting data on multiple types of omics measurements. Different types of omics measurements are interconnected, for example with molecular changes at the DNA/epigenetic level and microRNAs regulating gene expressions. Studying the associations between different types of omics measurements can lead to a better understanding of disease biology and clinically useful models. In this study, we analyze the association between GE (gene expression) and CNV (copy number variation), which have one of the first known regulation relationships and have attracted extensive attention. The proposed approach is also potentially applicable to other types of omics measurements and other high-dimensional problems.

Modeling the GE-CNV association is challenging. Both GE and CNV measurements are high-dimensional. The expression level of a specific gene can be affected by both the cis-acting and trans-acting CNVs [6], with the set of relevant CNVs usually unknown. Some studies, such as [17], are limited by conducting the “one GE versus one CNV” analysis on only the cis-acting CNVs. Cis-acting and trans-acting CNVs behave differently, with the cis-acting CNVs usually having dominant effects. Further Figure A.1 in the Online Supplement and those alike suggest that the effects of cis-acting CNVs can be nonlinear. Many of the existing studies, such as [9, 16], are limited by assuming linear effects. There are a few studies that consider nonlinear modeling [12] and suggest the limitations of linear modeling. However, they are under different contexts, and there is still a lack of large-scale regression analysis.

In data analysis, many GEs have been observed to have long-tailed distributions. In addition, various technical problems can cause data contamination [21]. In Figure A.2 (Online Supplement), the long-tailed characteristic of GE distributions is clearly seen. Most of the existing studies adopt non-robust estimation, which, with such distribution, may result in biased model parameter estimation and false variable selection. The existing studies are also limited by lacking attention to the correlations among CNVs, which are commonly observed in data analysis. Studies in other contexts have shown that effectively accommodating the correlations among variables leads to more accurate selection and estimation. However, this has not been pursued in the GE-CNV analysis.

Although multiple studies have been conducted on modeling the GE-CNV associations, they fail to address one or more of the aforementioned challenges. In this article, we develop a new and more effective analysis approach, which can directly overcome the limitations of existing analyses. The primary analysis goal is to identify CNVs that are relevant for GEs and estimate their effects. For a specific GE, we jointly model the effects of multiple candidate CNVs and data-dependently search for the important ones. A partially linear model is adopted, with a nonlinear effect for the cis-acting CNV and linear effects for the trans-acting CNVs. A robust loss function is adopted to accommodate long-tailed distributions and data contamination. Penalization is used for estimation and variable selection. We describe the correlations among CNVs using a network structure and accommodate it in estimation. It is remarkable that with multiple advancements over the existing alternatives, the proposed method is still statistically and numerically manageable.

In Section 2, we introduce the data and model settings. The proposed method is described in Section 3. We develop an effective computational algorithm and rigorously establish the consistency properties. Simulation is conducted in Section 4. We analyze the TCGA (The Cancer Genome Atlas) data on the PCD (programmed cell death) pathway in Section 5. Additional technical details and numerical results are provided in an online supplement.

2. Data and model settings

Consider a random sample of size n, each with p GE and k CNV measurements. Let $Y=(y^1,\dots ,y^p)$ denote the n × p matrix of GEs with $y^m={(y_1^m,\dots ,y_n^m)}^{\top }$, for all $m\in \{1,\mathrm{...},p\}$, and let $X=\left(X_1,\dots ,X_k,X_{k+1}\right)$ be the n × (k + 1) matrix of CNVs with $X_t={\left(X_{t1},\dots ,X_{tn}\right)}^{\top }$, for all $t\in \left\{1,\dots ,k\right\}$ and the n × 1 vector $X_{k+1}={\left(1,\dots ,1\right)}^{\top }$ for intercept. For simplicity of notation, consider data with matched GE and CNV measurements. For the ith sample and mth GE, we consider

$$y_i^m=f_m\left(X_{mi}\right)+\underset{t=1}{\overset{k+1}{\mathrm{\Sigma }}}{X}_{ti}{\alpha }_t^m\mathbf{1}\left(t\ne m\right)+{\epsilon }_i^m.$$ (1)

where the f_ms are unknown smooth functions, with the consideration that most biological processes are continuous. In practice, some datasets may have not fully matched GEs and CNVs. This can be easily accommodated by making minor modifications to the proposed method and will not be further discussed.

For identifiability, we impose the constraint $f_m\left(X_{m1}\right)+\cdots +f_m\left(X_{mn}\right)=0$ in estimation. Let ${\alpha }^m={\left({\alpha }_1^m,\dots ,{\alpha }_{m-1}^m,{\alpha }_{m+1}^m,\dots ,{\alpha }_{k+1}^m\right)}^{\top }$ denote the k × 1 regression coefficient vector, and ${\epsilon }_i^m$ be the random error. Also denote $X={\left(x_1,\dots ,x_n\right)}^{\top }$, where $x_i^{\top }$ is the ith row of X. For the random error, assume that $\text{Pr}\left({\epsilon }_i^m\le 0|x_i\right)=1/2.$ Note that strict moment assumptions, which are commonly needed in the existing studies, are not made on ${\epsilon }_i^m$.

Under the smoothness condition, we approximate f_m using the basis expansion

$$f_m\left(X_{mi}\right)\approx {\displaystyle \sum _{\ell =1}^L{\gamma }_{m\ell }{B}_{m\ell }\left(X_{mi}\right),}$$

where L is the number of basis functions, ${\gamma }_m={\left({\gamma }_{m1},\dots ,{\gamma }_{mL}\right)}^{\top }$ is the spline coefficient vector, and $B_m\left(X_{mi}\right)={\left(B_{m1}\left(X_{mi}\right),\dots ,B_{mL}\left(X_{mi}\right)\right)}^{\top }$ is the set of normalized B-spline basis. Denote $\alpha ={\left({\alpha }^{1\top },\dots ,{\alpha }^{p\top }\right)}^{\top }$ and $\gamma ={\left({\gamma }_1^{\top },\dots ,{\gamma }_p^{\top }\right)}^{\top }$.

In the literature, there are multiple strategies for modeling trans-acting CNV effects. Some describe their effects through their regulating genes and model across-gene effects. Some studies suggest that such a strategy is “more direct” and may have a strong biological basis. However, this strategy can be mathematically challenging, since GEs are on both sides of the regression and dynamic network analysis may be needed. In this study, we directly regress GEs on CNVs. This strategy has been adopted in multiple recent studies, including [20, 26, 30], and generated scientifically and statistically interesting results. It is beyond the scope of this article to compare different modeling strategies. Model (1) jointly describes the effects of all candidate CNVs, includes that with a single CNV as a special case, and is more flexible. It is a partially linear model and allows the cis-acting CNV to contribute to GE in a nonlinear way. It is possible to also allow nonlinear effects for trans-acting CNVs. However, their effects are comparatively smaller, and it is reasonable to “pay more attention” to the cis-acting CNV with a larger effect. In addition, excessive nonlinear modeling leads to high computational cost and unstable estimation. Model (1) also includes the multivariate linear model as a special case.

3. Robust network-based penalized estimation

Robust estimation is needed when the random error has a long-tailed distribution or contamination. Consider the LAD (least absolute deviation) loss function

$$Q\left(\alpha ,\gamma \right)=\frac{1}{n}{\displaystyle \sum _{m=1}^p{\displaystyle \sum _{i=1}^n\left|y_i^m-{\displaystyle \sum _{\ell =1}^L{\gamma }_{m\ell }{B}_{m\ell }\left(X_{mi}\right)}-{\displaystyle \sum _{t=1}^{k+1}{X}_{ti}{\alpha }_t^m\mathbf{1}\left(t\ne m\right)}\right|.}}$$ (2)

The LAD loss is a special case of the popular quantile regression.

To accommodate the high data dimensionality, and to select relevant CNVs, we consider the penalized estimate

$$\left(\widehat{\alpha },\widehat{\gamma }\right)=\underset{\alpha ,\gamma }{\text{arg}\text{min}}\left\{Q\left(\alpha ,\gamma \right)+P\left(\alpha ,\gamma ;\lambda ,\zeta \right)\right\},$$ (3)

where $\alpha ={\left({\alpha }^{1\top },\dots ,{\alpha }^{p\top }\right)}^{\top }$, $\gamma ={\left({\gamma }_1^{\top },\dots ,{\gamma }_p^{\top }\right)}^{\top }$, and λ and ζ are tuning parameters. A nonzero component of the estimate suggests an association between the corresponding GE and CNV. For penalty, we first consider

$$P_A\left(\alpha ,\gamma ;{\lambda }_1,{\lambda }_2,\zeta \right)={\displaystyle \sum _{m=1}^p{\displaystyle \sum _{t=1}^{k+1}\varphi \left({\alpha }_t^m;{\lambda }_1,\zeta \right)\mathbf{1}\left(t\ne m\right)}}+{\displaystyle \sum _{m=1}^p\varphi \left({\Vert {\gamma }_m\Vert }_1;{\lambda }_2,\zeta \right)\equiv P_1+P_2},$$ (4)

where $\varphi \left(s;\lambda ,\zeta \right)=\lambda {\displaystyle {\int }_0^{\left|s\right|}{\left(1-x/\left(\lambda \zeta \right)\right)}_{+}dx}$ is the Minimax Concave Penalty (MCP, [29]) with tuning parameter λ and regularization parameter ζ. For trans-acting CNVs, penalties are imposed on their regression coefficients. For cis-acting CNVs , their effects are represented by vectors of regression coefficients, and penalties are imposed on the group norms of these vectors. We adopt the ℓ₁ group norm, which leads to similar statistical properties as the ℓ₂ group norm but simplifies computation. The proposed analysis imposes the same tuning parameters across all GEs and CNVs, which ensures that they are analyzed on the same ground. This is reasonable as no GE/CNV is “special” compared to others. In addition, having a smaller number of tunings (compared to allowing for GE-/CNV-specific tunings) significantly reduces computational cost.

A limitation of P_A is that it does not accommodate the (sometimes high) correlations among CNVs. To solve this problem, we first adopt a network structure to describe the correlations among CNVs. In the CNV network, a node corresponds to a CNV, and two nodes are connected if the corresponding CNVs are correlated. To construct adjacency, which quantifies the network connection between any two nodes, we consider the following approach [28]. For nodes i and j, let r_ij be their correlation coefficient. Let A = (a_ij : 1 ≤ i, j ≤ k) be the adjacency matrix. Consider $a_{ij}=r_{ij}^{\varrho }\mathbf{1}\left\{\left|r_{ij}\right|>r\right\}.$ In subsequent numerical studies, we set ϱ = 5, which retains the sign of r_ij, down-weighs weak correlations (which are possibly noises), and keeps the strong ones. Choosing the power transformation and the specific value of ϱ follows the published literature [8, 28]. The cutoff r leads to a sparse network and is calculated from the Fisher transformation [4] as $r=\left\{\text{exp}\left(2c/\sqrt{n-3}\right)-1\right\}/\left\{\text{exp}\left(2c/\sqrt{n-3}\right)+1\right\}$, where c = 1.96 is determined from the standard normal distribution. We refer to [8, 28] for more discussions on network construction. There are other ways of defining network adjacency. For example, some approaches use biological (such as pathway) information. It is expected that they are equally applicable. As our goal is not to compare different network constructions, we focus on this specific network structure without further discussing others.

To accommodate the CNV network, we propose the penalty

$$\begin{gathered} P_B\left(\alpha ,\gamma ;\tilde{\lambda },\zeta \right)=P_A\left(\alpha ,\gamma ;{\lambda }_1,{\lambda }_2,\zeta \right)+{\lambda }_3{\displaystyle \sum _{m=1}^P{\displaystyle \sum _{1\le j<t\le k}\left|a_{jt}\right|\times \left|{\alpha }_j^m-\text{sgn}\left(a_{jt}\right){\alpha }_t^m\right|\mathbf{1}\left(j,t\ne m\right)}} \\ \equiv P_1+P_2+P_3, \end{gathered}$$ (5)

where $\tilde{\lambda }=\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$, and sgn is the sign function. The newly added P₃ has been motivated by the following considerations. When two CNVs are highly correlated, it encourages their regression coefficients to have similar magnitudes. The “directions” of estimates and “degree of encouragement” are adjusted by a_jt. A similar strategy has been developed in the literature under different contexts [14]. The ℓ₁ penalty is adopted to be “consistent” with the loss function, which significantly simplifies computation. The tuning parameters are data-dependently adjusted to effectively avoid over shrinkage.

The proposed P₃ shares some similarity with the Laplacian penalty [8], contrasted penalty [19], and others in shrinking the differences of regression coefficients but also has notable differences. First it is noted that the application context is significantly different. In addition, different from the Laplacian penalty, it is based on the ℓ₁ norm. The fused Lasso is defined on the differences of consecutive coefficients and demands a “spatial lining-up”, which differs from the considered network structure. Also different from the existing methods, penalties are only imposed on trans-acting CNVs, not all CNVs. Cis- and trans-acting CNVs behave differently, and shrinking the difference between a linear and a nonlinear effect is insensible. In the literature, there are also methods that incorporate the networks of both GEs and CNVs [20]. The numerical study in [20] suggests that, after incorporating the CNV network structure, further accommodating the GE network leads to incremental improvements but significant computational cost. In addition, the goal of penalization is to select and estimate the coefficients of CNV effects. It thus seems “more direct” to build the penalty on the correlations (network) of CNVs.

3.1. Computation

With fixed tunings, optimization with different GEs can be conducted separately in a parallel manner. For each GE, the proposed penalty has an “MCP+ℓ₁” form, both of which have been well studied in the literature. Overall, optimization can be achieved by adopting and modifying existing techniques. Specifically, we develop an effective computational algorithm based on the MM (majorize minimization) and CD (coordinate descent) techniques.

The MM step: Denote ${\theta }_{s_0}\left(s\right)$ as the majorization function of $\varphi \left(s;\lambda ,\zeta \right)$ at s₀. In the proposed iterative algorithm, we use the superscript “(d)” to denote the dth iteration. Denote ${\varphi }^{\prime }\left(\left|{\alpha }_t^m\right|+;\lambda ,\zeta \right)$ as the limit of ${\varphi }^{\prime }\left(\left|s\right|;\lambda ,\zeta \right)$ as $s\to {\alpha }_t^m$ from above. Then we have

$${\theta }_{{\alpha }_t^{m\left(d-1\right)}}\left(\left|{\alpha }_t^m\right|\right)={\varphi }^{\prime }\left(\left|{\alpha }_t^{m\left(d-1\right)}\right|+;\lambda ,\zeta \right)\left[\left|{\alpha }_t^m\right|-\left|{\alpha }_t^{m\left(d-1\right)}\right|\right]+\varphi \left(\left|{\alpha }_t^{m\left(d-1\right)}\right|;\lambda ,\zeta \right)$$ (6)

as the majorization function of $\varphi \left(\left|{\alpha }_t^m\right|;\lambda ,\zeta \right).$

The CD step: With the assistance of MM, minimization can be solved using the CD approach. In the dth iteration, for $m\in \left\{1,\dots ,p\right\}$ and $t\in \left\{1,\dots ,k+1\right\}$.

Step 1. Minimize the majorized penalized objective function with respect to ${\gamma }_m$, with the other parameters fixed at their current estimates. Consider only terms relevant to ${\gamma }_m$:

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|y_i^m-{\displaystyle \sum _{t=1}^{k+1}{X}_{ti}{\alpha }_t^{m}1\left(t\ne m\right)}-{\displaystyle \sum _{\ell =1}^L{\gamma }_{m\ell }{B}_{m\ell }\left(X_{mi}\right)}\right|}+{\varphi }^{\prime }\left({\Vert {\gamma }_m^{d-1}\Vert }_1+;{\lambda }_2,\zeta \right){\Vert {\gamma }_m\Vert }_1.$$

With the assistance of slack variables, this optimization problem can be casted as a linear programming problem, viz.

$$\underset{\xi ,{\gamma }_m}{\text{minimize}}\frac{1}{n}{\displaystyle \sum _{i=1}^n\left({\xi }_i^{+}+{\xi }_i^{-}\right)+{\varphi }^{\prime }\left(\Vert {\gamma }_m^{\left(d-1\right)}\Vert +;{\lambda }_2,\zeta \right)}{\displaystyle \sum _{\ell =1}^L\left({\gamma }_{m\ell }^{+}+{\gamma }_{m\ell }^{-}\right)}$$

$$\text{subject to}{\xi }_i^{+}-{\xi }_i^{-}=y_i^m-{\displaystyle \sum _{t=1}^{k+1}{X}_{ti}{\alpha }_t^m\mathbf{1}\left(t\ne m\right)}-{\displaystyle \sum _{\ell =1}^L{\gamma }_{m\ell }{B}_{m\ell }\left(X_{mi}\right)};$$ (7)

$${\xi }_i^{+}\ge 0,{\xi }_i^{-}\ge 0\text{for}\text{all}i\in \left\{1,\dots ,n\right\},$$

where $a^{+}=a\mathbf{1}\left(a\ge 0\right)$ and $a^{-}=-a\mathbf{1}\left(a\le 0\right)$. This can be solved using existing software.

Step 2. Minimize the majorized penalized objective function with respect to ${\alpha }_j^m$, with the other parameters fixed at their current estimates. It is equivalent to minimizing

$$\begin{gathered} \frac{1}{n}{\displaystyle \sum _{i=1}^n\left|y_i^m-{\displaystyle \sum _{\ell =1}^L{\gamma }_{m\ell }{B}_{m\ell }\left(X_{mi}\right)-{\displaystyle \sum _{t=1}^{k+1}{X}_{ti}{\alpha }_t^m\mathbf{1}\left(t\ne j,m\right)-X_{ji}{\alpha }_j^m}}\right|} \\ +{\varphi }^{\prime }\left(\left|{\alpha }_j^{m\left(d-1\right)}\right|+;{\lambda }_1,\zeta \right)\left|{\alpha }_j^m\right|+{\lambda }_3{\displaystyle \sum _{t=j+1}^k\left|a_{jt}\right|\times \left|{\alpha }_j^m-\text{sgn}\left(a_{jt}\right){\alpha }_t^m\right|\mathbf{1}\left(j,t\ne m\right)} \\ =\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|X_{ji}\right|\times \left|v_{ij}^m\right|+{\varphi }^{\prime }\left(\left|{\alpha }_j^{m\left(d-1\right)}\right|+;{\lambda }_1,\zeta \right)}\left|{\alpha }_j^m\right|+{\lambda }_3{\displaystyle \sum _{t=j+1}^k\left|a_{jt}\right|\times \left|{\alpha }_j^m-\text{sgn}\left(a_{jt}\right){\alpha }_t^m\right|\mathbf{1}\left(j,t\ne m\right)}, \end{gathered}$$

where

$$v_{ij}^m=\frac{1}{X_{ji}}\left\{y_i^m-{\displaystyle \sum _{\ell =1}^L{\gamma }_{m\ell }{B}_{m\ell }\left(X_{mi}\right)}-{\displaystyle \sum _{t=1}^{k+1}{X}_{ti}{\alpha }_t^m\mathbf{1}\left(t\ne j,m\right)}\right\}-{\alpha }_j^m,$$

for all $i\in \left\{1,\dots ,n\right\}$. Minimizing the above objective function can be further formulated as a weighted median regression with $n+k-j+1$ pseudo-observations

$$\underset{{\alpha }_j^m}{\text{arg}\text{min}}\left\{\frac{1}{n+k-j+1}{\displaystyle \sum _{i=1}^{n+k-j+1}{w}_{ij}\left|{\tilde{v}}_{ij}^m\right|}\right\},$$ (8)

Where

$${\tilde{v}}_{ij}^m=\{\begin{array}{l}{v}_{ij}^m\text{if}\text{i}\in \left\{1,\dots ,n\right\},\\ {\alpha }_j^m\text{if}\text{i}\text{=}\text{n+1}\\ {\alpha }_j^m-\text{sgn}\left(a_{jt}\right)a_t^m\text{if}\text{i}\in \left\{n+2,\dots ,n+k-j+1\right\},\end{array}$$

and

$$w_{ij}^m=\{\begin{array}{l}\left|X_{ji}\right|/n\text{if}\text{i}\in \left\{1,\dots ,n\right\},\\ {\varphi }^{\prime }\left(\left|{\alpha }_j^{m\left(d-1\right)}\right|+;{\lambda }_1,\zeta \right)\text{if}\text{i}\text{=}\text{n+1}\\ {\lambda }_3\left|a_{jt}\right|\text{if}\text{i}\in \left\{n+2,\dots ,n+k-j+1\right\}.\end{array}$$

The minimizer of (8) is the weighted median of the $n+k-j+1$ pseudo-observations.

The overall algorithm can be summarized as follows.

Algorithm: The two-step coordinate descent algorithm
Initialize d = 0, ${\gamma }^{(d)}$ = 0, and ${\alpha }^{(d)}$ = 0
Repeat
for $m\in \left\{1,\dots ,p\right\}$ do
for $j\in \left\{1,\dots ,k+1\right\}$ do
Update ${\gamma }_m^{\left(d+1\right)}\left(j=m\right)$ via (7);
Update ${\alpha }_j^{m\left(d+1\right)}\left(j\ne m\right)$ via (8);
end
end
$d=d+1$;
until the difference between two consecutive estimates is less than a cutoff (set as 10−4 in our numerical study); Return the estimate of (α, γ) at convergence.

The LAD approach is a special case of quantile regression. For the nonconvex penalized quantile regression, Peng and Wang [15] established convergence to a stationary point. Convergence properties for fused Lasso type penalties have been examined in Friedman et al. [5]. It should be noted that, in the aforementioned studies, the penalties have much simpler forms. The newly added P₃ does not have a separable form, whereas most studies that are able to establish convergence to global optimizers have separable penalties. With the proposed algorithm, the value of the penalized objective function decreases at each iteration and is bounded below. It is conjectured that, following [5, 15, 22], the proposed algorithm converges to a coordinate-wise minimum, which is also a stationary point. Our literature search does not suggest a way to establish convergence to the global optimizer for the proposed approach (and under what conditions). We postpone rigorous research on convergence to future studies. In our numerical studies, convergence is achieved in a small to moderate number of iterations.

Tuning parameter selection:

The tuning/regularization parameters have similar implications as in the literature and are selected using commonly adopted approaches. Specifically, we set ${\lambda }_2=\sqrt{L}{\lambda }_1$ and impose comparable penalization to linear and nonlinear effects. λ₁ (and so λ₂) and λ₃ control the degree of shrinkage and are selected using V-fold cross validation (V = 5 in our numerical study). The regularization parameter ζ balances between unbiasedness and concavity. Breheny and Huang [1], Zhang [29] and other studies suggest experimenting with a few values (including 1.8, 3, 4.5, 6, and 10) or fixing its value. In our numerical study, we examine this sequence and find that the results are not sensitive to the value of ζ and set ζ = 3. In practice, to be prudent, ζ values other than 3 should also be examined. There are many publications on tuning parameter selection with splines. In our numerical study, we choose cubic splines and ~ n^1/5 equally spaced interior knots.

Implementation:

To facilitate data analysis, we implement the above procedure in R. The code is available at https://github.com/shuanggema.

3.2. Consistency properties

Theoretical study of penalized robust regression under high-dimensional settings is limited [25]. Compared with the existing ones, this study is more complicated with the partially linear modeling and introduction of the network-based penalty. In addition, the proposed method involves simultaneously estimating a large number of high-dimensional models, which brings significantly more challenges than estimating a single high-dimensional model. Our theoretical study not only provides a strong basis for the proposed method but also sheds light on several existing methods and has independent value.

Recall that X = (X₁,..., X_k, X_k+1) = (x₁,...,x_n)^⊤ is the n × (k + 1) design matrix. Define x_i,_I as the subvector of x_i indexed by I ⊆ {1,...,k + 1}. Let I^c and |I| denote the complement and cardinality of set I, respectively. Then the model can be rewritten, for all m ∈ {1,..., p} and I ∈{1,...,n}, as

$$y_i^m=f_m\left(X_{mi}\right)+x_{i,m^{\text{C}}}^{\top }{\alpha }_{m^{\text{C}}}^m+{\epsilon }_i^m,$$ (9)

where $x_{i,m^{\text{C}}}$ denotes x_i with the mth element removed, and ${\alpha }_{m^{\text{C}}}^m$ is the regression coefficient vector associated with $x_{i,m^{\text{C}}}$ for the mth GE.

Let $\left\{B_{m\ell }\left(x\right)=\sqrt{L}\left(S_{\ell }\left(x\right)-{\displaystyle {\sum }_{i=1}^n{S}_{\ell }\left(X_{mi}\right)/n}\right):\ell =1,\dots ,L\right\}$ be the set of normalized basis functions, where ${\{S_{\ell }(x)\}}_{\ell =1}^L$ is the set of B-spline basis. With basis expansion, one has, for all m ∈ {1,..., p} and i ∈ {1, ... ,n},

$$y_i^m\approx B_m{\left(X_{mi}\right)}^{\top }{\gamma }_m+x_{i,m^{\text{C}}}^{\top }{\alpha }_{m^{\text{C}}}^m+{\epsilon }_i^m.$$

With a slight abuse of notation, we also denote ${\alpha }_m^m={\gamma }_m$. Denote the true value of regression coefficients as ${\alpha }^{*}=\left({\alpha }_t^{m\ast }\right)$. Then ${\gamma }_m^{*}$ , the true value of ${\gamma }_m$, is also labeled as ${\alpha }_t^{m\ast }$. Let $f_m^{*}$ be the true value of $f_m$. Denote $\mathcal{S}=\left\{\left(t,m\right):{\alpha }_t^{m*}\ne 0\right\}$, which is the union of $\mathcal{F}=\left\{\left(m,m\right):{\alpha }_m^{m*}\ne 0\right\}$ and $\mathcal{C}=\left\{\left(t,m\right):{\alpha }_t^{m*}\ne 0,t\ne m\right\}$. Let $\mathcal{D}=\left\{m:f_m^{*}\ne 0\right\}$ be the set of important nonparametric effects. For m =∈ {1,…, p}, define ${\mathcal{S}}_m=\{t:\left(t,m\right)\in \mathcal{S}\}$ and ${\mathcal{C}}_m=\{t:\left(t,m\right)\in \mathcal{C}\}.$ Let ${\Vert \cdot \Vert }_q$ be the ${\ell }_q$ norm for vectors and C^ν([a, b]) be the space of ν-times continuously differentiable functions defined on [a, b].

Let ${\alpha }_s=\left\{{\alpha }_t^m:\left(t,m\right)\in \mathcal{S}\right\}$, ${\gamma }_{\mathcal{D}}=\{{\gamma }_m:m\in \mathcal{D}\}$, and ${\alpha }_{\mathcal{C}}=\left\{{\alpha }_t^m:\left(t,m\right)\in \mathcal{C}\right\}$. First consider

$$\begin{gathered} {\mathcal{O}}_n\left({\alpha }_S\right)=\frac{1}{n}{\displaystyle \sum _{m=1}^P{\displaystyle \sum _{i=1}^n\left|y_i^m-B_m{\left(X_{mi}\right)}^{\top }{\gamma }_m\mathbf{1}\left(m\in \mathcal{D}\right)-x_{i,{\mathcal{C}}_m}^{\top }{\alpha }_{{\mathcal{C}}_m}^m\right|}} \\ +{\lambda }_3{\displaystyle \sum _{m=1}^p\left\{{\displaystyle \sum _{\left(j,t\right)\in {\mathcal{A}}_{1m}}\left|a_{jt}\right|\times \left|{\alpha }_j^m-\text{sgn}\left(a_{jt}\right){\alpha }_t^m\right|+}{\displaystyle \sum _{\left(j,t\right)\in {\mathcal{A}}_{1m}}\left|a_{jt}\right|\times \left|{\alpha }_i^m\right|}\right\}}, \end{gathered}$$ (10)

Where ${\mathcal{A}}_{1m}=\{(j,t):j,t\in {\mathcal{C}}_m,j<t\le k;a_{jt}\ne 0\}$ and ${\mathcal{A}}_{2m}=\left\{(j,t):j\in {\mathcal{C}}_m,t\notin {\mathcal{C}}_m,j<t\le k;a_{jt}\ne 0\right\}$. ${\mathcal{O}}_n\left({\alpha }_{\mathcal{S}}\right)$ is the oracle counterpart of the proposed objective function. Define

$$U_{i,m}=\{\begin{array}{l}{\left(B_m{\left(X_{mi}\right)}^{\top },x_{i,C_m}^{\top }\right)}^{\top }\text{if}m\in D,\\ x_{i,C_m}\text{if}m\notin D.\end{array}$$

The following conditions are needed to establish the asymptotic properties.

• (C1)The cardinality of 𝒟, denoted as d₀, is fixed. For m ∈ 𝒟, $f_m^{*}\in C^v([a,b])$ .
• (C2)X_i has a compact support on [a,b], for $i\in \left\{1,\dots ,k\right\}$. There exist positive constants M1 < M2 such that $M_1\le {\lambda }_{\min }(n^{-1}{\displaystyle {\sum }_{i=1}^n{U}_{i,m}{U}_{i,m}^{{}^{\top }}})\le {\lambda }_{\max }(n^{-1}{\displaystyle {\sum }_{i=1}^n{U}_{i,m}{U}_{i,m}^{{}^{\top }}})\le M_2$ for all m, where ${\lambda }_{\min }$ and ${\lambda }_{\max }$ denote the smallest and largest eigenvalues, respectively.
• (C3)Denote the density function of ${\epsilon }_i^m$ conditional on $U_{i,m}$ as $g_{i,m}$($\cdot |U_{i,m}$). Uniformly over i and m, in a neighborhood of zero, g_i,m(·|U_i,m) is bounded away from zero and infinity and has a bounded first order derivative.

These conditions are mild, and comparable ones have been assumed in the literature; see, e.g., [3, 13]. Conditions (C2) and (C3) also imply that, for all m, there exist positive constants M₃ < M₄ such that

$$M_3\le {\lambda }_{\text{min}}\left\{n^{-1}{\displaystyle \sum _{i=1}^n{g}_{i,m}\left(0|U_{i,m}\right)U_{i,m}{U}_{i,m}^{\top }}\right\}\le {\lambda }_{\max }\left\{n^{-1}{\displaystyle \sum _{i=1}^n{g}_{i,m}\left(0|U_{i,m}\right)U_{i,m}{U}_{i,m}^{\top }}\right\}\le M_4.$$ (11)

Consider the estimator ${\tilde{\alpha }}_S=\text{arg}\text{min}{\mathcal{O}}_n\left({\alpha }_S\right)$. Let s_m = |𝒞_m| and $J={\text{max}}_m{\displaystyle {\sum }_{t\ne m}^k\left|a_{mt}\right|}$. The following theorem establishes the consistency of ${\tilde{\alpha }}_{\mathcal{S}}$.

Theorem 1. Assume that (C1)–(C3) hold and that κ_n → ∞ as n → ∞. In addition, L → ∞, (L + s_m)²κⁿ/n → 0 (m ∈ 𝒟), $s_m^2{k}_n/n\to 0\left(m\in \mathcal{D}\right)$, and λ₃J →0, where C₁,...,C_p are large constants. With probability at least

$$1-{\displaystyle \sum _{m\in \mathcal{D}}\text{exp}\left\{-\left(L+s_m\right)k_n/8\right\}}-{\displaystyle \sum _{m\notin \mathcal{D}}\text{exp}\left(-s_m{k}_n/8\right)}$$

the estimator ${\tilde{\alpha }}_s=\left\{{\tilde{\alpha }}_t^m:\left(t,m\right)\in \mathcal{S}\right\}$ satisfies

For $m\in \mathcal{D},\left|{\tilde{f}}_m\left(x\right)-f_m^{*}\left(x\right)\right|+{\Vert {\tilde{\alpha }}_{{\mathcal{C}}_m}^m-{\alpha }_{{\mathcal{C}}_m}^{m*}\Vert }_2\le {\delta }_m,$ where ${\delta }_m=C_m\left\{\sqrt{\left(L+s_m\right)k_n/n}+L^{-v}+{\lambda }_{3}J\right\}$ and ${\tilde{f}}_m\left(x\right)=B_m{\left(x\right)}^{\top }{\tilde{\gamma }}_m$ for any x ∈ [a, b].

For $m\notin \mathcal{D},{\Vert {\tilde{\alpha }}_{{\mathcal{C}}_m}^m-{\alpha }_{{\mathcal{C}}_m}^{m*}\Vert }_2\le {\delta }_m,$ where ${\delta }_m=C_m\left(\sqrt{s_m{k}_n/n}+{\lambda }_{3}J\right).$The tail probability in Theorem 1 is exponentially small. In other words, the proposed method is able to accom-modate high-dimensional data with ln $p=o\left(k_n{\text{min}}_{m\notin D}{s}_m\right).$ Consider the oracle estimator ${\widehat{\alpha }}^o=\left\{{\widehat{\alpha }}_S,{\widehat{\alpha }}_{S^{\text{C}}}\right\}$, where ${\widehat{\alpha }}_S={\tilde{\alpha }}_S$ and ${\widehat{\alpha }}_{S^{\text{C}}}=0$. Let

$$b_l\left({\lambda }_1,{\lambda }_3\right)=\underset{j,m}{\text{max}}\left[-{\lambda }_1-{\lambda }_3\left\{{\displaystyle \sum _{t\in m^{\text{C}}-{\mathcal{C}}_m}\left|a_{jt}\right|-{\displaystyle \sum _{t\in {\mathcal{C}}_m}{a}_{jt}\text{sgn}\left({\alpha }_t^{m*}\right)}}\right\}\right],$$

$$b_u\left({\lambda }_1,{\lambda }_3\right)=\underset{j,m}{\text{min}}\left[{\lambda }_1+{\lambda }_3\left\{{\displaystyle \sum _{t\in m^{\text{C}}-{\mathcal{C}}_m}\left|a_{jt}\right|-{\displaystyle \sum _{t\in {\mathcal{C}}_m}{a}_{jt}\text{sgn}\left({\alpha }_t^{m*}\right)}}\right\}\right].$$

The following additional conditions are needed.

• (C4)b(λ₁,λ₃) = min {−b_l(λ₁,λ₃),b_u(λ₁,λ₃)} > 0, nb(λ₁,λ₃) → ∞.
• (C5)${\left({\text{max}}_m{\delta }_m\right)}^{-1}{\text{min}}_{\left(t,m\right)\in \mathcal{C}}\left|{\alpha }_t^{m*}\right|\to \infty$ and ${\left({\mathrm{m}\mathrm{a}\mathrm{x}}_{m\in \mathcal{D}}{\delta }_m\right)}^{-1}{\mathrm{m}\mathrm{i}\mathrm{n}}_{m\in \mathcal{D}}{\displaystyle {\sum }_{i=1}^n{f}_m^{*}{\left(X_{mi}\right)}^2/n}\to \infty$, where δm is defined in Theorem 1.
• (C6)max_m δ_m ≤ λ₁ and max_m∈𝒟 δ_m ≤ λ₂.

Condition (C4) requires that the smallest signal does not decay too fast. Comparable conditions have been assumed in Wang et al. [24] and others.

Theorem 2. Assume that (C1)–(C6) and conditions in Theorem 1 hold. If ln $p=o\left(k_n{\text{min}}_{m\notin \mathcal{D}}{s}_m\right),$ ${\text{max}}_m\sqrt{L+s_m}{\delta }_m=o\left\{b\left({\lambda }_1,{\lambda }_3\right)\right\},$ $\left({\text{max}}_m{s}_m\text{v}L\right)\text{ln}n+\ln k+\ln p=o\left\{nb\left({\lambda }_1,{\lambda }_3\right)\right\}$ and $ma{x}_{m<\mathcal{D}}{s}_m$ ln $n+lnk+lnp=o({\lambda }_2)$, then with probability converging to 1, ${\widehat{\alpha }}^o$ is a local minimizer of the penalized LAD objective function with penalty (5).

This theorem establishes that the proposed estimator enjoys the same asymptotic consistency as the oracle estima-tor with probability approaching one. This property holds under ultrahigh dimensions without restrictive (for example, moment) conditions on the random errors. The proofs are presented in an Online Supplement.

4. Simulation

We set (n, k, p) = (200, 200, 200). Note that although k and p may seem modest, the number of unknown effects ((k + 1) × p) is in fact very large. The analysis is even more challenging with the basis expansion for nonlinear effects. An important component of the proposed method is to accommodate the connections among CNVs. In practice, the number of highly correlated CNVs is not expected to be large. As to be shown in data analysis, this simulation setting mimics that of a pathway. GEs/CNVs in the same pathway are more likely to have related functions and correlated measurements and are sensible to be analyzed together, whereas different pathways are largely different and can be analyzed separately.

In TCGA and other data, the processed CNV data marginally have unimodal continuous distributions close to normal. Here we simulate the CNVs to have a multivariate normal distribution with marginal means zero and a block diagonal covariance structure. There are 40 blocks, with 5 CNVs per block. CNVs within the same block have correlation coefficient ρ, and those in different blocks are uncorrelated. Three levels of correlation are considered.

To generate the parametric parameters, we first simulate the 200×200 matrix M = diag(U₁ ∗ I₁,…, U₄₀ ∗ I₄₀), where “∗” denotes the element-wise product between the 5 × 5 matrices U_s and I_s with s ∈ {1,…, 40}. Each entry of I_s is generated from a Bernoulli distribution with a success probability of 0.8. For s ∈ {2,…, 10}, the entries in the odd and even columns of U_s are simulated from 𝓤(0.8, 1) and 𝓤(−1, −0.8), respectively. For s ∈ {12,…, 20}, the entries in the odd and even columns of U_s are simulated from 𝓤(−1, −0.8) and 𝓤(0.8, 1), respectively. For s ∈ {1, 11} and s > 20, all components of U_s are 0. The diagonal elements of M are then set as zero. For each GE, the parametric parameters correspond to a row of M. Under this setup, trans-acting CNVs with nonzero effects belong to the same block as the cis-acting CNVs and are correlated. This is motivated by the presence of small functional groups, each of which consists of a small number of correlated CNVs and coregulated GEs [31].

For the effects of cis-acting CNVs, set f_m(x) = 2 sin(xπ/2) for m ∈ {1,…, 5, 11,…, 55, 61,…, 100} and = 0 otherwise. For blocks 1 and 11, GEs are regulated by cis-acting CNVs only. For blocks 2 and 12, GEs are regulated by trans-acting CNVs only. For the rest of the blocks with s ≤ 20, GEs are regulated by both types of CNVs. For blocks with s ∈ {21,…, 40}, there is no detectable regulation. The settings thus comprehensively cover all possible scenarios. The true parametric effects are generated randomly. By expectation, there are 288 of them. There are 90 true nonparametric effects. The intercepts are set as zero. Consider three random error distributions: N(0, 1) (Error 1), 0.85 N(0, 1)+0.15 Cauchy (Error 2), and 0.75 N(0, 1)+0.25 Cauchy (Error 3), which have different contamination levels.

Beyond the proposed method, we also consider seven alternatives (Table A.1, Online Supplement): (A₂) The partially linear modeling is adopted, and P₁ + P₂ is applied. There is no accommodation of the network structure. (A₃) All CNV effects are assumed to be linear, P₁ is used for estimation and selection, and the network structure is accommodated using P₃. (A₄) All CNV effects are assumed to be linear, and there is no accommodation of the network structure. Methods A₅–A₈ are parallel to A₁–A₄ but adopt the non-robust LS (least squares) loss. Although there are other alternatives, these seven have an analysis framework closest to that of the proposed method and can directly establish the merit of the proposed partially linear modeling, robust loss, and accommodation of the CNV network structure.

When evaluating the proposed and alternative methods, we mainly focus on selection. If CNVs that are relevant to GEs can be accurately identified, there are multiple ways of generating satisfactory estimation. Summary results are presented in Tables 1 and 2. The means and standard deviations of true and false positives are computed for the parametric and nonparametric effects separately based on 100 replicates. The main findings are as follows:

Table 1:

Simulation: summary based on 100 replicates. In each cell, mean (sd). TP1/FP1 and TP2/FP2: number of true/false positives for parametric and nonparametric effects.

	ρ		TP1	FP1	TP2	FP2
Error 1	0.1	A1	283.1 (2.9)	0.0 (0.0)	90.0 (0.0)	0.1 (0.2)
		A2	283.1 (2.7)	0.0 (0.0)	90.0 (0.0)	0.1 (0.2)
		A3	246.3 (9.6)	0.0 (0.0)	81.7 (2.6)	0.0 (0.0)
		A4	246.8 (9.5)	0.0 (0.0)	81.7 (2.6)	0.0 (0.0)
	0.5	A1	287.6 (0.7)	2.5 (1.6)	90.0 (0.0)	0.0 (0.0)
		A2	287.6 (0.6)	2.4 (1.7)	90.0 (0.0)	0.0 (0.0)
		A3	232.7 (3.4)	1.5 (1.0)	50.9 (0.8)	2.3 (1.3)
		A4	232.2 (3.7)	1.6 (0.9)	50.8 (0.8)	2.4 (1.3)
	0.9	A1	285.0 (2.4)	147.6 (14.3)	90.0 (0.0)	0.1 (0.3)
		A2	286.2 (1.5)	179.9 (16.1)	90.0 (0.0)	0.1 (0.3)
		A3	219.8 (3.1)	60.6 (9.7)	49.6 (0.7)	8.6 (0.6)
		A4	222.1 (4.4)	64.6 (8.9)	49.4 (0.9)	8.5 (0.6)
Error 2	0.1	A1	278.1 (4.6)	0.1(0.3)	89.7 (0.5)	0.2 (0.4)
		A2	278.4 (4.4)	0.1 (0.3)	89.7 (0.5)	0.3 (0.5)
		A3	227.9 (9.3)	0.1 (0.3)	78.9 (2.9)	0.0 (0.0)
		A4	228.0 (8.8)	0.1 (0.3)	78.9 (3.0)	0.0 (0.0)
	0.5	A1	286.8 (1.4)	3.1 (1.7)	89.5 (0.7)	0.2 (0.5)
		A2	286.9 (1.5)	3.0 (1.5)	89.5 (0.8)	0.2 (0.5)
		A3	234.2 (3.6)	1.7 (1.1)	51.2 (1.0)	2.5 (1.3)
		A4	233.2 (3.3)	1.6 (1.2)	51.2 (1.0)	2.6 (1.4)
	0.9	A1	283.3 (2.8)	162.0 (12.0)	89.7 (0.5)	0.3 (0.6)
		A2	284.8 (2.5)	190.3 (12.4)	89.7 (0.6)	0.3 (0.5)
		A3	222.3 (4.1)	81.7 (8.6)	49.4 (0.7)	9.0 (0.5)
		A4	223.6 (5.0)	85.9 (12.5)	49.4 (0.9)	8.8 (0.6)
Error 3	0.1	A1	279.2 (4.7)	0.0 (0.0)	89.4 (0.9)	0.2 (0.5)
		A2	279.0 (4.7)	0.0 (0.0)	89.4 (0.9)	0.2 (0.5)
		A3	218.8 (8.9)	0.0 (0.0)	76.3 (2.9)	0.0 (0.0)
		A4	218.7 (8.4)	0.1 (0.2)	76.5 (2.8)	0.0 (0.0)
	0.5	A1	286.5 (1.4)	3.9 (1.3)	89.3 (0.9)	0.3 (0.6)
		A2	286.7 (1.2)	4.2 (1.5)	89.4 (0.9)	0.3 (0.6)
		A3	233.7 (3.4)	2.0 (1.5)	50.8 (0.9)	2.9 (1.3)
		A4	233.3 (3.5)	2.0 (1.3)	51.0 (0.9)	2.9 (1.2)
	0.9	A1	282.4 (2.9)	162.9 (14.6)	89.6 (0.9)	0.4 (0.7)
		A2	283.8 (2.2)	202.1 (19.1)	89.6 (0.9)	0.5 (0.6)
		A3	223.2 (3.9)	79.4 (13.2)	49.6 (0.5)	9.1 (0.6)
		A4	221.6 (3.5)	74.1 (9.7)	49.6 (0.7)	9.0 (0.6)

Table 2:

Simulation: summary based on 100 replicates. In each cell, mean (sd). TP1/FP1 and TP2/FP2: number of true/false positives for parametric and nonparametric effects.

	ρ		TP1	FP1	TP2	FP2
Error 1	0.1	A5	288 (0)	0.1 (0.2)	90.0 (0.0)	0.0 (0.0)
		A6	288 (0)	0.1 (0.2)	90.0 (0.0)	0.0 (0.0)
		A7	288 (0)	1.6 (1.2)	90.0 (0.0)	0.0 (0.0)
		A8	288 (0)	1.6 (1.2)	90.0 (0.0)	0.0 (0.0)
	0.5	A5	283.6 (2.1)	2.4 (1.5)	90.0 (0.0)	0.0 (0.0)
		A6	283.2 (1.9)	2.4 (1.5)	90.0 (0.0)	0.0 (0.0)
		A7	287.2 (0.8)	2.4 (1.6)	88.8 (1.1)	0.0 (0.0)
		A8	287.2 (0.9)	2.4 (1.6)	88.8 (1.0)	0.0 (0.0)
	0.9	A5	247.6 (3.8)	35.0 (4.6)	89.9 (0.3)	0.0 (0.0)
		A6	171.6 (4.9)	16.9 (2.3)	89.9 (0.3)	0.0 (0.0)
		A7	262.7 (6.9)	41.0 (11.6)	50.2 (1.3)	0.3 (0.5)
		A8	204.7 (9.4)	6.5 (2.6)	43.0 (2.5)	0.0 (0.0)
Error 2	0.1	A5	287.0 (1.7)	196.5 (157.9)	89.9 (0.4)	0.4 (0.7)
		A6	287.1 (1.3)	198.1 (158.0)	89.9 (0.3)	0.4 (0.7)
		A7	287.3 (1.4)	201.5 (155.4)	89.5 (0.7)	0.3 (0.6)
		A8	287.3 (1.4)	199.0 (155.4)	89.5 (0.7)	0.3 (0.6)
	0.5	A5	274.5 (11.1)	171.7 (85.0)	87.9 (2.4)	0.6 (0.7)
		A6	273.8 (11.5)	173.8 (86.9)	87.8 (2.6)	0.6 (0.7)
		A7	274.6 (11.0)	176.0 (88.4)	78.3 (9.5)	0.33 (0.6)
		A8	273.5 (12.0)	174.9 (89.9)	78.4 (9.1)	0.37 (0.6)
	0.9	A5	242.1 (17.2)	182.6 (104.4)	88.6 (5.4)	0.9 (1.1)
		A6	158.8 (23.4)	159.6 (115.3)	80.3 (12.3)	0.7 (0.9)
		A7	227.6 (31.8)	160.1 (83.6)	45.4 (4.9)	0.6 (0.7)
		A8	159.7 (39.8)	149.1 (116.0)	35.9 (7.7)	0.3 (0.6)
Error 3	0.1	A5	286.5 (1.9)	262.7 (133.7)	89.5 (0.7)	1.1 (0.8)
		A6	286.7 (1.7)	265.4 (141.7)	89.4 (0.9)	1.0 (0.8)
		A7	285.5 (1.9)	262.8 (134.0)	89.5 (0.7)	1.1 (0.8)
		A8	286.7 (1.7)	263.8 (141.0)	89.4 (0.9)	1.0 (0.8)
	0.5	A5	269.8 (11.2)	281.7 (126.5)	87.3 (3.0)	1.1 (1.0)
		A6	269.0 (11.5)	288.6 (144.6)	87.4 (2.7)	1.1 (1.0)
		A7	268.2 (9.9)	279.3 (147.5)	73.6 (2.6)	0.5 (0.7)
		A8	264.1 (11.8)	268.9 (135.0)	72.1 (8.1)	0.6 (0.7)
	0.9	A5	225.7 (21.0)	279.8 (154.9)	87.1 (6.7)	1.7 (1.4)
		A6	145.1 (20.4)	253.6 (194.2)	74.8 (12.6)	1.4 (1.4)
		A7	211.3 (33.3)	250.8 (142.9)	43.3 (4.9)	1.2 (0.9)
		A8	139.8 (31.0)	233.6 (171.5)	32.4 (6.3)	1.0 (1.0)

• (a)Simulation shows the advantage of partially linear modeling. For example with Error 1 and ρ = 0.5, TP1 and TP2 under A₁ are 287.6 and 90.0, respectively. In comparison, TP1 and TP2 under A₃ are 232.7 and 50.9, respectively.
• (b)When there is no contamination and correlation is weak to moderate, the non-robust methods can have satisfactory performance. However, with contamination, the robust methods outperform. For example with Error 2 and ρ = 0.5, TP1 and TP2 under A₁ are 286.8 and 89.5, respectively. TP1 and TP2 under A₅ are 274.5 and 87.9, respectively, which are also very satisfactory. However, the price is that A₅ has a large number of false positives with FP1 = 173.8.
• (c)When there exist moderate to strong CNV correlations, it pays off to accommodate the network structure. For example with Error 2 and ρ = 0.9, A₁ and A₂ have FP1 162.0 and 190.3, respectively. We note that with strong correlations, the proposed method may have more false positives. This observation is reasonable. The network-based penalty shrinks the differences between regression coefficients. When an unimportant variable is correlated with an important one (within the same block in this simulation), this penalty tends to “pull” their coefficients together, also select the unimportant one, and increase false positives. Overall, across the whole spectrum of simulations, we observe superior performance of the proposed method.

In the second set of simulation, we examine whether the superiority of the proposed method over the alternatives depends on signal level. Specifically, under Error 2, we reduce the signal levels to 0.8 of those described above. Results are shown in Table A.2 (Online Supplement). A₁ outperforms A₂–A₄ in a similar way as observed above. Results on the non-robust methods, which have inferior performance, are omitted.

In the third set of simulation, we examine if performance of the proposed method depends on the number of signals. Specifically, the expected number of parametric effects is doubled, and the number of nonparametric effects remains at 90. Other settings are similar to those under the first set of simulation. Results of the robust methods are shown in Table A.3 (Online Supplement). We draw similar conclusions as those from Tables 1 and 2.

In the fourth set of simulation, we consider more realistic CNV distributions. Specifically, we use the real data analyzed in the next section. For each simulation replicate, we randomly sample 200 subjects from the TCGA data, each with 426 observed CNV measurements. The parametric coefficient matrix is generated in a similar way as under the first set of simulation. The same nonlinear f_m’s and error distributions are adopted. Results are summarized in Table A.4 (Online Supplement). With more complex CNV distributions, all methods perform worse than in the first three sets. However, the patterns are similar, with the proposed method significantly outperforming the alternatives.

As in many other studies, the simulated CNV distributions in the first three sets may be much simpler than practically encountered. Luckily, this is “compensated” by the last set. The simulated settings have comprehensively covered different numbers and strengths of signals and correlations. Similar settings have been adopted in the literature [20]. In the literature, research on nonlinear cis-acting CNV effects is limited. It is sensible to start with simple forms, which have been extensively adopted in semiparametric modeling. As in any other study, the simulation set-tings have limitations. However, the superiority of the proposed method is clearly seen. We have also experimented with a few other settings and drawn similar conclusions (results omitted).

With the robust loss function and more complicated penalty, the proposed method has higher computational cost than some alternatives. However, simulation suggests that it is still computationally affordable. Specifically, with fixed tunings, the analysis of one replicate in the first set of simulation takes 5.1 (A₁), 3.4 (A₂), 4.7 (A₃), 2.0 (A₄), 3.9 (A₅), 1.8 (A₆), 3.1 (A₇), and 1.3 (A₈) minutes on a desktop with standard configurations. We have also observed that, when sample size and data dimensionality increase, computational cost increases moderately (details omitted). The current code is written in R. Computer time may be much reduced if the computational core is written in C and parallel computing is adopted.

5. Analysis of TCGA data

We analyze the TCGA data on cutaneous melanoma. In our analysis, the processed level 3 data are downloaded from the TCGA portal. Details on data collection and processing are available at TCGA website. Briefly, the GE data were collected using the Illumina Hiseq 2000 RNA-SEQ Ver 2 platforms. The processed data are the robust Z-scores, which have been lowess-normalized, log-transformed, and median-centered. The measurements indicate the under- or over-expression of genes in tumor with respect to normal tissues. The CNV data were collected using the Affymetrix SNP 6.0 platforms. Data went through segmentation analysis and were transformed into segment mean values, with amplified regions having positive values and deletions having negative values.

In principle, the proposed method can accommodate whole-genome data. However that would involve estimating a huge number of nonparametric effects and a giant coefficient matrix. In addition, as previously described, it is sensible to analyze different pathways separately. Specifically, we analyze the PCD (programmed cell death) pathway, which is well known for resistance to induction of apoptosis. The PCD pathway is related to the regulated cell suicide process where cells go through death to prevent themselves from proliferating or in response to certain signals to cells, such as stress or DNA damage. Genes within this pathway are identified using the annotation package in GSEA (http://www.broadinstitute.org/gsea). A total of 428 CNV and 426 GE measurements are available on 333 subjects. We remove the two CNVs that are not matched to GEs, resulting in 426 pairs of CNV and GE measurements. Under the proposed model, there are a total of 181,050 parametric parameters, 426 intercepts, and 426 nonparametric parameters.

Summary analysis results are presented in Table 3. The proposed method identifies 2260 parametric and 307 nonparametric effects. Each GE is found to be regulated by at least one CNV. Since a large number of effects are iden-tified, it is infeasible to present all results. For the identified parametric effects, we calculate the median as −0.025, and interquartile range as (−0.115, 0.099). For the identified nonlinear effects, we compute the normalized `₁ norms, which have median 1.029, and interquartile range (0.714, 1.668). In Figure 1, for four representative GEs, we show the estimated cis-acting CNV effects. For BCL2 and SNCA, we observe an overall decreasing and increasing trend, respectively. The “bumps” close to the boundaries need to be interpreted cautiously, as the numbers of observations are small in these regions. For IL2RA and TXNL1, the effects are mostly constants in the middle, but differences are observed for regions with high levels of deletions/amplifications. Such results suggest that the commonly adopted linear modeling may be insufficient. The deviation from linear can be caused by interactions, other regulating mech-anisms (microRNAs, methylation, etc.), and others. Mechanistic studies will be needed to fully validate and interpret the identified nonlinear trends.

Table 3:

Analysis of TCGA data. Numbers of identified nonzero parametric (P) and nonparametric (NP) effects, and sum of absolute prediction errors (PE).

	P	NP	PE
A1	2260	307	282.02
A2	2088	299	293.16
A3	2735		307.67
A4	2748		308.12
A5	2491	70	549.99
A6	2648	76	538.14
A7	2784		438.62
A8	2293		436.58

Figure 1:

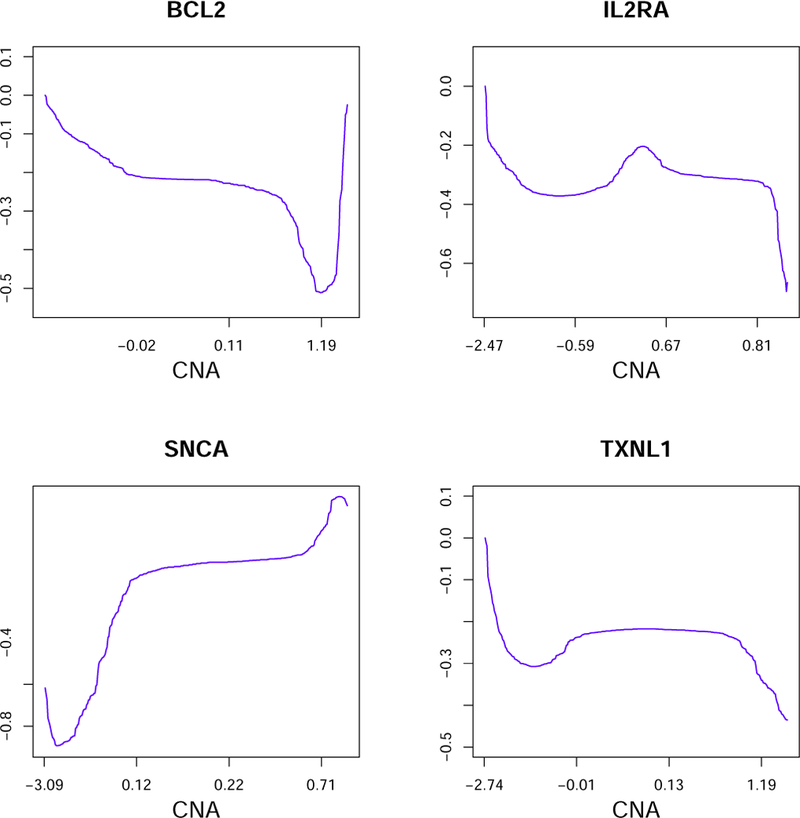
Analysis of the TCGA data: estimated cis-acting CNV effects for four genes.

To complement the above analysis, we implement a resampling-based method [7], use part of the data for iden-tification/estimation, make prediction for the rest, and compute the absolute prediction errors. As shown in Table 3, the proposed method has prediction performance slightly better than A₂ but much better than the other alternatives. It is noted that the non-robust methods have inferior prediction, which partly justifies the necessity of robust analysis. Also using the resampling approach, we compute the probability of a specific effect being identified, which provides a way of assessing stability. For effects identified using full data, the mean probabilities (of being identified) are 59% (A₁), 45% (A₂), 46% (A₃), and 41% (A₄), respectively. The probabilities are lower for non-robust methods.

As a representative example, we take a closer look at gene BCL2, which is a confirmed biomarker for melanoma etiology and prognosis. In the process of apoptosis, the BCL2 protein plays an important role in inhibiting cell death and promoting cell survival. Elevated BCL2 gene expressions have been associated with the presence of ulceration and poorer survival. Using the proposed method, the cis-acting CNV is identified as having a nonlinear effect (Figure 1). The parametric effects identified using different methods are presented in Tables A.5 and A.6 (Online Supplement). Different methods generate significantly different findings. In Figure A.3 (Online Supplement), we show the network connection of CNVs identified using different methods. The proposed method identifies a tightly connected module composed of six CNVs: PPARD, RIPK1, SERPINB9, TNF, TXNDC5, and VEGFA. The corresponding genes are all located on chromosome 6p. The instability of chromosome 6 has been associated with melanoma progression. The proposed method also identifies two other connected CNVs: PMAIP1 and SERPINB2. The corresponding genes are located closely on the chromosome (18q21.33), with PMAP1 on18q21.32 and SERPINB2 on 18q21.3. Two isolated CNVs are also identified, with one located on chromosome 2 and the other on the X chromosome. The other robust methods also identify connected CNVs but not the six-CNV module. The non-robust methods do not identify connected CNVs.

In studies with a much smaller scale (with a few GEs and CNVs), the identified GE-CNV relationship can be functionally validated. The proposed analysis involves a large number of GEs and CNVs, and it may be unrealistic to validate all results. If there is an interest, subsets of the results can be examined in greater details. The improvement observed in simulation and improved prediction and stability provide support to the validity of analysis.

6. Discussion

In recent studies, multiple types of omics measurements have been collected, making it possible to study their regulation relationships. The regulation of GE by CNV is one of the first known regulating mechanisms and has attracted special attention. In this article, we have developed a new analysis approach for modeling the GE-CNV regulation. With the partially linear modeling, the proposed approach can more accurately describe the dominant cis-acting CNV effects. The proposed estimation also has notable advantages: the robust loss function accommodates long-tailed GE distributions and contamination; the simultaneous analysis ensures that all GEs are analyzed on the same ground; and the correlations among CNVs are effectively accommodated using a network structure and a shrinkage penalty. It is remarkable that with significant methodological advancements, the proposed method is still theoretically and computationally manageable. Under a variety of simulation settings, it significantly outperforms seven direct competitors. In the analysis of TCGA data, it leads to biologically plausible findings and improved prediction and stability.

The proposed approach is not limited to GE-CNV analysis. In omics studies, other regulation relationships (for example, proteins by GEs, GEs by methylation and microRNAs) are also of significant interest. In addition, data with both high-dimensional responses and high-dimensional covariates also arise in other fields. It is noted that with other data, there may not be a simple match between responses and covariates. More carefully examining the proposed approach (methodology, computation, and theory) suggests that there is actually no need for matching, and it can accommodate multiple nonlinear effects per response. Determining which covariate effects should be nonlinear is a “classic” statistical problem and has been examined in multiple studies. The proposed approach can be coupled with the techniques for determining nonlinear effects and have broader applications.