The Effects of Demography and Genetics on the Neutral Distribution of Quantitative Traits

Abstract

Neutral models for quantitative trait evolution are useful for identifying phenotypes under selection. These models often assume normally distributed phenotypes. This assumption may be violated when a trait is affected by relatively few variants or when the effects of those variants arise from skewed or heavy tailed distributions. Molecular phenotypes such as gene expression levels may have these properties. To accommodate deviations from normality, models making fewer assumptions about the underlying genetics and patterns of variation are needed. Here, we develop a general neutral model for quantitative trait variation using a coalescent approach. This model allows interpretation of trait distributions in terms of familiar population genetic parameters because it is based on the coalescent. We show how the normal distribution resulting from the infinitesimal limit, where the number of loci grows large as the effect size per mutation becomes small, depends only on expected pairwise coalescent times. We then demonstrate how deviations from normality depend on demography through the distribution of coalescence times as well as through genetic parameters. In particular, population growth events exacerbate deviations while bottlenecks reduce them. We demonstrate the practical applications of this model by showing how to sample from the neutral distribution of $Q_{ST}$, the ratio of the variance between subpopulations to that in the overall population. We further show it is likely impossible to distinguish sparsity from skewed or heavy tailed mutational effects using only sampled trait values. The model analyzed here greatly expands the parameter space for neutral trait models.

NEUTRAL models of quantitative traits provide a null distribution against which goodness-of-fit tests can be used to test for natural selection (Lande 1976; Leinonen et al. 2013). Neutral models also clarify the effects of purely neutral forces such as genetic drift and mutation on trait distributions (Lynch and Hill 1986). Common approaches model phenotypes as normally distributed among offspring within a family, among members of a population, or among species (Turelli 2017). Indeed, it has been suggested that the normality assumption is the defining characteristic of quantitative genetics (Rice 2004). This is approximately true if phenotypes are influenced by a large number of sufficiently independent Mendelian factors (Fisher 1918) and selection is weak (Turelli and Barton 1990).

The goal of neutral models for quantitative traits is to ask to whether phenotypic differentiation between groups can be reasonably explained by processes other than natural selection. On macroevolutionary time scales, models stemming from Lande (1976) have used Brownian motion to describe the evolution of the mean value of a quantitative trait in a population. These models are used in tests for extreme trait divergence between species (Turelli et al. 1988), test for phylogenetic signal in trait distributions (Freckleton et al. 2002), and correct for phylogenetic dependence when calculating correlations between traits (Felsenstein 1985). On shorter time scales, multivariate normality of neutral trait values also underlie tests for spatially varying selection in structured populations such as the method developed by Ovaskainen et al. (2011). Other neutral models for quantitative traits have not assumed normality (Chakraborty and Nei 1982; Lynch and Hill 1986; Lande 1992), and the dynamics of phenotypic evolution are examined forward in time as a balance between mutation creating variance, migration spreading variance among subpopulations, and fixation removing it. However, these studies were limited to simple models of population structure and history. Backward-in-time, coalescent models would allow for more general demographic scenarios.

Under normality, trait dynamics are modeled without concern for the number of causal loci, genealogies at these loci, or the distribution of mutational effects (the distribution that mutations at causal loci draw their effects from). However, heritable phenotypic variation is ultimately due to discrete mutations at discrete loci, and how the variation arising from these mutations is distributed depends on individual genealogies. The distribution of genealogies in the genome might be influenced by recent population growth and the distribution of mutational effects could be skewed for due to the details of a particular developmental pathway. When a large number of mutations affect a trait, the central limit theorem ensures that the distributions of genealogies and mutational effects can be ignored, but a full model of phenotypic variation would have to include them. Importantly, deviations from normality may affect the outcomes of goodness-of-fit tests that necessarily aim to identify outliers from a normal model.

A more expansive neutral model of phenotypic variation would consider genealogies at causal loci. The principle modeling framework for genealogical variation is the coalescent (Wakeley 2008), but few studies have connected the coalescent to quantitative genetics. Whitlock (1999) used coalescent theory to argue that measures of phenotypic $\left(Q_{ST}\right)$ and genetic $\left(F_{ST}\right)$ differentiation have the same expected value in general models of population subdivision. Using coalescent simulations, Griswold et al. (2007) investigated the effects of shared ancestry and linkage disequilibrium on the genetic covariance matrix for a set of traits (G matrix). They found that linkage disequilibrium and small numbers of causal loci can cause phenotypic covariance not predicted by mutational covariance. Mendes et al. (2018) also used a coalescent-based model to show that using a species tree based on population split times increases false positive rates in phylogenetic comparative methods, among other problems. Although not explicitly connected, Ovaskainen et al. (2011) developed a test for spatially varying selection that assumes the genetic covariance between individuals depends only on pairwise coancestry coefficients, which have a clear interpretation under the coalescent (Slatkin 1991).

Two studies have asked how the shape of the distribution of mutational effect sizes, beyond just the variance, impacts trait distributions. Khaitovich et al. (2005) modeled the evolution of gene expression on phylogenetic trees assuming a single nonrecombining causal locus but allowed for an arbitrary distribution of mutational effects. This model detected deviations from normality consistent with asymmetries in the mutational distribution of gene expression in great apes. More recently, Schraiber and Landis (2015) developed a similar model for trait evolution within populations based on the coalescent and allowing for any number of causal loci. They derived the characteristic function for the distribution of phenotypes in a sample and showed how they can deviate from normality when the number of loci is small or the mutational distribution has heavy tails.

Schraiber and Landis (2015) derived their results for a panmictic, constant-size population. Natural populations rarely have stable population sizes and show considerable spatial structure. It is unclear how these violations of the constant-size, panmictic model influence deviations from normality. We take advantage of the ability of coalescent theory to handle nonequilibrium demographies and population structure to relax these modeling assumptions.

Extending coalescent models of quantitative traits to structured populations is important because the analysis of structured populations provides an opportunity to infer the incidence of local adaptation or stabilizing selection. In structured populations, the neutral divergence in suitably normalized trait values among subpopulations has approximately the same expectation and variance as the neutral divergence in allele frequency at a single site (Rogers and Harpending 1983; Whitlock 2008). The $Q_{ST}/F_{ST}$ paradigm was developed to test whether trait divergence in structured populations could be explained by genetic drift alone (Spitze 1993; Whitlock 2008; Leinonen et al. 2013). $Q_{ST}$, defined as the ratio of the trait variance between subpopulations to the total trait variance, is compared to $F_{ST}$, which measures the same property for genetic variation at neutral markers. It is concluded that natural selection has acted if the observed $Q_{ST}$ is sufficiently far from the neutral expectation. Ovaskainen et al. (2011) developed a modern extension of the $Q_{ST}/F_{ST}$ paradigm for genetic values measured in breeding experiments, and Berg and Coop (2014) also extended the paradigm to make use of genetic values computed from GWAS summary statistics. Understanding the neutral distribution of trait values is necessary for the development of goodness-of-fit tests that are applicable to populations with complicated histories and traits with sparse genetic architectures.

We generalize the work of Schraiber and Landis (2015) by deriving the form of the mgf for arbitrary distributions of coalescent times, and, therefore, arbitrary population histories. The key result of Schraiber and Landis (2015), the characteristic function of the distribution of trait values, is a special case of this general result. We then show how a normal model arises by taking an infinitesimal limit where the effect size per mutation becomes small as the number of loci potentially affecting the trait becomes large. We then calculate the third and fourth central moments of the trait distribution in panmictic populations to illustrate how departures from normality depend both on genetic parameters and genealogical distributions. For instance, in exchangeable populations the expected third central moment is proportional to the third noncentral moment of the mutational distribution times the expected time to the first coalescent event in a sample of size n = 3.

Finally, we discuss the consequences of these results for $Q_{ST}$ tests and the inference of genetic parameters. We find that using the normal distribution that arises in the infinitesimal limit gives an improved null distribution of $Q_{ST}$. Additionally, we show that it is likely not possible to infer useful features of the mutational distribution using only sampled trait values. Future work will be necessary to develop tests for selection that take into account both demography and genetic parameters, but the model developed here provides the groundwork for such an undertaking.

Model

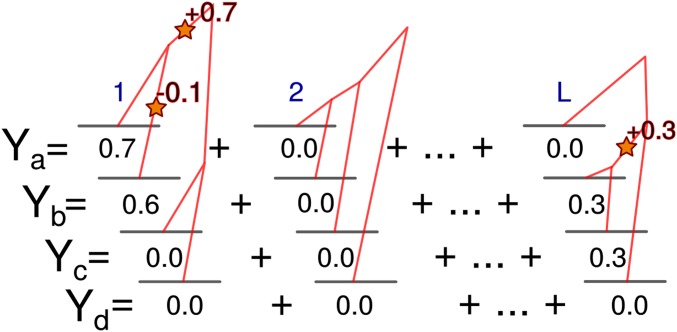
We consider a trait controlled by L potentially causal loci (shown schematically in Figure 1). Loci are unlinked and the effects of recombination are not explored. Following Kimura (1969), an infinite number of mutations are possible within each locus (though the number of loci is finite) and mutations affecting the trait (causal mutations) arise at rate $\frac{\theta }{2}$. That is, $\frac{\theta }{2}$ is the rate for one entire locus and not per nucleotide. An approximation restricting the number of mutations per locus to at most one is considered below. Mutations receive values from a distribution of effect sizes. This distribution is described by its mgf, ψ, and its noncentral moments, $m_i$. Individuals are haploid and their trait values are determined by summing, both within and between loci, the effects of all mutations occurring since the most recent common ancestor. Environmental effects are not included. An extension to diploidy would be straightforward but is not considered here.

Figure 1.

How trait distributions arise from genealogical and mutational processes under the model. L causal loci potentially affect the trait in a set of individuals and have independent genealogies. Mutations occur within loci as a Poisson process and act additively to determine individual trait values. Many loci with the potential to affect the trait may receive no mutations.

The genealogy at a locus is represented by the random vector of branch lengths, $T$. An element $T_{\omega }$ of $T$ is the branch length subtending only individuals in the set ω. For example, $T_{\left\{a,b\right\}}$ is the length of the branch ancestral only to individuals a and b. If such a branch does not exist for a given genealogy, $T_{\left\{a,b\right\}}$ is set to zero. In this way, $T$ encodes both the branch lengths and topology of a genealogy. $\text{Ω}$ is the set of all possible branches. For three sampled individuals, a, b, and c, $\text{Ω}=\left\{\left\{a\right\},\left\{b\right\},\left\{c\right\},\left\{a,b\right\},\left\{a,c\right\},\left\{b,c\right\}\right\}$ and $T=\left(T_{\left\{a\right\}},T_{\left\{b\right\}},T_{\left\{c\right\}},T_{\left\{a,b\right\}},T_{\left\{a,c\right\}},T_{\left\{b,c\right\}}\right)$. The distribution of genealogies is also described by its mgf, ${\varphi }_T$. Genealogies are independent between loci because of the lack of linkage.

Phenotypic trait values are random quantities of ultimate interest, and are hereafter referred to simply as trait values. The vector of trait values in the sampled individuals is $Y$. If we had sampled individuals a, b, and c, then $Y=\left(Y_a,Y_b,Y_c\right)$. The contribution to the trait values from a single locus is the change relative to the value in the most recent common ancestor (MRCA) of the sample at that locus. $Y$ is the sum over contributions from L loci, each measured with respect to an arbitrary ancestral value. Since we do not know the ancestral value, we cannot directly observe $Y$. However, $Y$ determines measurable quantities such as differences in trait values between individuals as well as the sample variance. The distribution of trait values is also studied through its mgf, ${\varphi }_Y$.

We call those quantities not influenced by the genealogical process $\left(L,\hspace{0.17em}\frac{\theta }{2},\hspace{0.17em}\text{and}\hspace{0.17em}\psi \right)$ the genetic parameters of the trait. Another quantity useful for describing a trait is its sparsity. Sparsity should reflect the number of segregating mutations that influence the trait, with a more “sparse” trait being affected by fewer segregating mutations. Formally, we measure sparsity as the average number of pairwise differences between two randomly chosen haplotypes at loci affecting the trait. A trait with fewer causal pairwise differences is more sparse. Sparsity thus depends both on the genetic parameters through the mutation rate and the number of potentially causal loci, and on demography through the distribution of coalescence times. A trait with fewer causal loci in a larger population may therefore have lower sparsity than a trait with more causal loci in a smaller population.

In populations of exchangeable individuals, a useful way to summarize the distribution of genealogies is through the moments of ${\mathrm{핋}}_{k,n},$ which denotes the amount of time that k lineages remain in the genealogy of a sample of size n. The pairwise coalescent time between a lineage in individual a and a lineage in individual b is written as ${\mathcal{T}}_{a,b}$. When considering structured populations, ${\mathcal{T}}_{a,b}$ is also used to denote the coalescence time between a randomly chosen lineage from subpopulation a and a randomly chosen lineage from subpopulation b. Table 1 provides a reference for the notation used in this article.

Table 1. Notation used in this article.

Type of quantity	Symbol	Description
Genetic parameter	ψ	Mgf of the mutational effect size distribution
	$\frac{\theta }{2}$	Per-locus mutation rate in units of coalescent time
	$m_i$	$i\mathrm{th}$ noncentral moment of the mutational effect size distribution
	$\frac{\theta }{2}{\mu }_1$	Rate that mutational bias shifts trait values in the infinitesimal limit
	$\frac{\theta }{2}{\mu }_2$	Rate that variance accumulates in the infinitesimal limit
	L	Number of potentially causal loci
Genealogy value	$\text{Ω}$	Set of all possible branches in the genealogy of a given sample
	ω	A particular branch in a genealogy, defined by all individuals that branch subtends
	$T$	Random vector of branch lengths representing the entire genealogy at a locus
	$T_{\omega }$	Length of branch ω
	$T_{MRCA}$	Time to the most recent common ancestor at a particular locus
	${\varphi }_T\left(s\right)$	Mgf of the genealogy distribution
	$s$	Vector of dummy variables for the length of each possible branch
	$s_{\omega }$	Dummy variable for branch length $T_{\omega }$
	${\mathrm{T}}_{k,n}$	For a sample of exchangeable lineages, the amount of time that k lineages remain in a sample of size n
	${\mathcal{T}}_{a,b}$	Pairwise coalescent time between a lineage sampled from a and a lineage sampled from b, depending on the context, a and b may be either individuals or subpopulations
	${\tau }_{a+b}$	Sum of all branches ancestral to individuals a and b
Trait value	$Y$	Random vector of trait values
	$Y_a$	Trait value of individual a
	${\varphi }_Y\left(k\right)$	Mgf of the trait value distribution
	$k$	Vector of dummy variables for each individual trait value
	$k_a$	Dummy variable for the trait value of individual a
	$M_i$	$i\mathrm{th}$ central moment of the trait value distribution in the entire population
	$CVV$	Coefficient of variation of trait variance over evolutionary realizations of a population

Data availability

All code used in computer algebra, simulation, and figure generation for this paper is available at https://github.com/emkoch/trait_mgf_math. Supplemental material available at Figshare: https://figshare.com/s/f8f38ce72d0218aa34c6

Results

The mgf for the distribution of trait values

We first derive the mgf of the distribution of trait values, following closely the approach of Khaitovich et al. (2005) and Schraiber and Landis (2015), but generalizing to arbitrary demographies and population structure. We consider the distribution of trait values over evolutionary realizations of the combined random processes of drift and mutation. The probability distribution for a trait is complex in its general form. There is a point mass at zero corresponding to the possibility that no mutations occur, and mutational effects could be drawn from discrete or continuous distributions. Correlations between individuals arise because of shared history in genealogies at individual loci. Deriving the cumulative distribution function for trait values may be possible in some instances, but the difficulty of integrating over mutational configurations makes it practically impossible for most cases.

However, we can use the mgf approach to study the distribution of trait values. Following the definition of the mgf for a vector-valued random variable (Ross 2010), the mgf for a trait controlled by a single nonrecombining locus is

$${\varphi }_Y\left(k\right)=\text{E}\left[e^{k\cdot y}\right]={\displaystyle \int e^{k\cdot Y}}\text{P}\left(Y=y\right)\text{d}y.$$ (1)

The vector $k$ contains dummy variables for each individual, and the whole operation is an integral transform of the probability distribution of trait values. Equation 1 can be rewritten by conditioning on the genealogy to give

$${\varphi }_Y\left(k\right)={\displaystyle {\int }_Y{e}^{k\cdot y}{\displaystyle {\int }_T\text{P}\left(Y=y|T=t\right)\text{P}\left(T=t\right)\text{d}t\text{d}y}}={\displaystyle \int \int e^{k\cdot y}\text{P}\left(Y=y|T=t\right)\text{d}y\text{P}\left(T=t\right)\text{d}t.}$$ (2)

To proceed, assumptions about the mutational process must be made. The first is that mutations occur as a Poisson process along branches, and the second is that mutations at a locus are additive. The changes in the trait value along each branch are then conditionally independent given the branch lengths. Khaitovich et al. (2005) and Schraiber and Landis (2015) noted that this describes a compound Poisson process. The mgf of a compound Poisson process with rate λ over time t is $\text{exp}\hspace{0.17em}\left(\lambda t\left(\psi \left(k\right)-1\right)\right),$ where ψ is the mgf of the distribution of jump sizes caused by events in the Poisson process (Kingman 1992). Here, jump sizes are the effects on the trait value caused by new mutations. Using the mgf of a compound Poisson process, along with the fact that the mgf of the joint distribution of two perfectly correlated random variables with the same marginal distribution is ${\varphi }_{X_1,X_2}\left(k_1,k_2\right)={\varphi }_{X_1}\left(k_1+k_2\right)$, we can rewrite Equation 2 as

$${\varphi }_Y\left(k\right)={\displaystyle \int {{\displaystyle {\displaystyle \prod _{\omega \in \text{Ω}}\text{exp}}}}^{\text{}}}\left(\frac{\theta }{2}{t}_{\omega }\left(\psi \left({\displaystyle \sum _{a\in \omega }{k}_a}\right)-1\right)\right)\text{P}\left(T=t\right)\text{d}t.$$ (3)

Equation 3 is the mgf of $T$ with the dummy variable $s_{\omega }$ for branch $T_{\omega }$ set to $\frac{\theta }{2}\left(\psi \left({\displaystyle {\sum }_{a\in \omega }{k}_a}\right)-1\right)$. This implies that

$${\varphi }_T\left(s\right)|{}_{s_{\omega }=\frac{\theta }{2}\left(\psi \left({\displaystyle {\sum }_{a\in \omega }{k}_a}\right)-1\right)}.$$ (4)

Thus, if the mgf of the distribution of branch lengths is known, Equation 3 allows us to obtain the mgf of the trait values through a substitution. When the trait is controlled by L independent loci, the full mgf is obtained by raising Equation 4 to the power L. This result obviates the need for separate derivations for particular models of population history and structure. Lohse et al. (2011) derived the mgf of the genealogy in various population models including migration and splitting of subpopulations. Using their result for a single population we can obtain equation (1) of Schraiber and Landis (2015) using equation (4) and equation (5) of Lohse et al. (2011) (see Appendix A).

The infinitesimal limit

This model converges to a normal distribution when we take an infinitesimal limit. We accomplish this by substituting Taylor series for the genealogical and mutational distributions in Equation 3 and taking appropriate limits. The infinitesimal limit lets mutation effect sizes become small as the number of loci becomes large. The resulting distribution of a trait value Y is multivariate normal with expectation $\text{E}\left[T_{\text{MRCA}}\right]\frac{\theta }{2}{\mu }_1$ and variance $\text{E}\left[T_{\text{MRCA}}\right]\frac{\theta }{2}{\mu }_2$. The covariance between trait values in individuals a and b is $\text{E}\left[{\tau }_{a+b}\right]\frac{\theta }{2}{\mu }_2$, where ${\tau }_{a+b}$ is the shared branch length between a lineage sampled from individual a and a lineage from individual b. $\text{E}\left[T_{\text{MRCA}}\right]$ is the expected time to the most recent common ancestor. $\frac{\theta }{2}{\mu }_1$ is the per genome rate that mutational bias shifts the mean, and $\frac{\theta }{2}{\mu }_2$ is the rate per genome that variance accumulates. The infinitesimal limit requires that the products of L, and moments of the mutational distribution ≥ 3, go to zero. This can be thought of as requiring the mutational distribution to not be extremely skewed or heavy tailed. Derivation details are given in Appendix B.

Interestingly, the rate of variance accumulation is proportional to the second moment of the mutational distribution instead of the variance. We can see the intuition for this by considering a degenerate distribution where each mutation has the same effect. We still expect variation among individuals due to differences in the mutation count each individual receives, even though the variance of the mutational distribution is zero. The variance among individual trait values thus has one component due to differences in the number of mutations and an additional component due to differences in the effects of these mutations. The first component is proportional to the square of the mean mutational effect, while the second is proportional to the mutational variance. Therefore, the sum of the two components is proportional to $m_2$, the mean squared effect.

Since the trait values are normally distributed, any linear combination of sampled trait values will be as well. This includes observable quantities like the differences in trait values from a reference individual or from a sample mean. The distribution of trait differences between individuals is multivariate normal with mean zero and covariance between any pair of trait differences given by

$$\text{Cov}\left[Y_a-Y_b,Y_c-Y_d\right]={\mu }_2\frac{\theta }{2}\left(\text{E}\left[{\mathcal{T}}_{a,d}\right]+\text{E}\left[{\mathcal{T}}_{b,c}\right]-\text{E}\left[{\mathcal{T}}_{a,c}\right]-\text{E}\left[{\mathcal{T}}_{b,d}\right]\right),$$ (5)

where ${\mathcal{T}}_{a,b}=0$ if $a=b$. Classical theory in quantitative genetics uses a univariate normal distribution of phenotypes in a panmictic population. We can recover this by considering a population of exchangeable individuals. In this case, $\text{E}\left[{\mathcal{T}}_{a,b}\right]=\text{E}\left[{\mathrm{핋}}_{2,2}\right]$ for all pairs $a\ne b$. Multivariate normal theory can be used to show that individual trait values are then conditionally independent given the mean value in the population and are normally distributed with variance $\text{E}\left[{\mathrm{핋}}_{2,2}\right]\frac{\theta }{2}{\mu }_2$ (see Appendix B).

The normal model in the infinitesimal limit provides additional theoretical justification for studies using normal models to look for differences in selection on quantitative traits between populations (Ovaskainen et al. 2011; Praebel et al. 2013; Robinson et al. 2015). Additionally, Equation 5 implies that a covariance matrix based on mean pairwise coalescent times rather than population split times should be used in phylogenetic models of neutral trait evolution (Mendes et al. 2018).

Low-mutation-rate approximation

A useful simplification of the model is to ignore the possibility of more than one mutation per locus, thus breaking the infinite sites assumption within loci. This approximation is reasonable as long as nucleotide positions affecting the trait are loosely linked throughout the genome. The mgf of the trait distribution is greatly simplified by grouping terms of order two and above in Equation 3:

$${\varphi }_Y\left(k\right)\approx {\left[1+\frac{\theta }{2}{\displaystyle \sum _{\omega \in \text{Ω}}\text{E}\left[T_{\omega }\right]}\left(\psi \left({\displaystyle \sum }_{a\in \omega }{k}_a\right)-1\right)+O\left({\theta }^2\right)\right]}^L\cdot$$ (6)

Derivation details are given in Appendix C. Ignoring the $O\left({\theta }^2\right)$ terms corresponds to allowing at most one mutation per locus. Conveniently, the mgf of the trait then depends only on the expected branch lengths $\text{E}\left[T_{\omega }\right]$, whereas Equation 3 requires higher order moments of branch lengths (e.g., $\text{E}\left[T_{{\omega }_1}{T}_{{\omega }_2}\right]$). It is therefore no longer necessary to know the mgf of the genealogical distribution, and we can express moments of the trait distribution using expected branch lengths calculated from coalescent models.

Moments of the trait distribution

For most population genetic models and for sample sizes greater than n = 3, the recursive nature of ${\varphi }_Y$ makes it computationally infeasible to obtain general solutions. However, it is possible to derive moments of the trait distribution in terms of moments of branch lengths and mutational effects without an expression for the full mgf. Under the low mutation rate approximation, moments can be calculated by differentiating Equation 6. Even without this approximation, moments can be calculated using Equation 2 and only considering terms in a Taylor expansion contributing to the desired moment’s order. We implemented a symbolic math program to calculate trait moments, which can be found at https://github.com/emkoch/trai_mgf_math. Details of the procedure are given in Appendix D. The normal distribution is completely defined by its first two moments, and the extent to which a trait distribution deviates from normality can be measured by the extent to which its moments deviate from those of a normal distribution with the same mean and variance.

Considering the distribution over evolutionary realizations, the expectation of $Y_a$ is $L\frac{\theta }{2}{m}_1\text{E}\left[T_{\text{MRCA}}\right]$, and the variance is $L\frac{\theta }{2}{m}_2\text{E}\left[T_{\text{MRCA}}\right]+L{\left(m_1\frac{\theta }{2}\right)}^2\text{Var}\left[T_{\text{MRCA}}\right]$. Although simple to derive using computer algebra, expressions for the higher central moments of $Y_a$ are complicated even under the low mutation rate approximation, and not much is gained by showing them here.

In a given evolutionary realization, there will be a distribution of trait values within the entire population, which can also be described by its moments. Since this distribution is itself random, the moments of the within-population distribution are random as well. Since $Y_a$ is defined relative to an unobservable value, the expected central moments within the whole population offer more insight. We are particularly interested in how trait distributions deviate from normality. Schraiber and Landis (2015) computed the expected first four central moments of a constant-size population. We derive the same expectations for an arbitrary demographic history,

$$\text{E}\left[M_2\right]=L\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{2,2}\right]m_2$$ (7a)

$$\text{E}\left[M_3\right]=L\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{3,3}\right]m_3$$ (7b)

$$\text{E}\left[M_4\right]=3{\left(L\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{2,2}\right]m_2\right)}^2+3L{\left(\frac{\theta }{2}{m}_2\right)}^2\text{Var}\left[{\mathrm{핋}}_{2,2}\right]+\frac{1}{3}L{\left(\frac{\theta }{2}{m}_2\right)}^2\left(\frac{11}{9}\text{E}\left[{\mathrm{핋}}_{2,4}^2\right]-\frac{1}{3}\text{E}\left[{\mathrm{핋}}_{2,4}{\mathrm{핋}}_{3,4}\right]-\frac{1}{4}\text{E}[{\mathrm{핋}}_{3,4}^2]\right)+L{m}_4\frac{\theta }{2}\left(\text{E}\left[{\mathrm{핋}}_{4,4}\right]+\frac{1}{3}\text{E}\left[{\mathrm{핋}}_{3,4}\right]+\frac{2}{9}\text{E}\left[{\mathrm{핋}}_{2,4}\right]\right).$$ (7c)

In the infinitesimal limit, Equation 7b and the second two lines of Equation 7c go to zero. To give more insight into Equation 7, some moment calculations done by hand under the low mutation rate approximation are presented in Appendix F.

Equation 7a gives the expected variance in the population, but this will vary over realizations of the evolutionary process. The variation in the population variance depends on the expected sparsity of the trait $\left(L\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{2,2}\right]\right)$ and the number of causal loci. The variation in the variance can be quantified using its coefficient of variation (CVV): the SD of the variance divided by its expectation. For a constant-size, panmictic population

$$\text{CVV}=\sqrt{\frac{4}{3}\frac{1}{L}+\frac{1}{6}\frac{m_4/m_2^2}{L\theta \text{E}\left[{\mathrm{핋}}_{2,2}\right]}}.$$ (8)

Equation 8 has a contribution due to linked mutations occurring at a single locus $\left(\frac{4}{3}\frac{1}{L}\right)$ and a contribution due to sparsity and mutation $\left(\frac{1}{6}\frac{m_4/m_2^2}{L\theta \text{E}\left[{\mathrm{핋}}_{2,2}\right]}\right)$. Even when the sparsity is low, i.e., when a large number of variants affect the trait, if the trait is controlled by only a single locus there will be considerable variation in the within-population variance $\left(\text{CVV}=\sqrt{\frac{4}{3}}\right)$. On the other hand, the CVV of a sparse trait controlled by many loci will depend on the ratio of the fourth and squared second noncentral moments of the mutational distribution $\left(m_4/m_2^2\right)$.

Comparison to normal distribution

Deviations of the within-population distribution from normality depend on the distribution of coalescent times and the genetic parameters. One natural way to quantify a distribution’s deviation from normality is using its kurtosis. The kurtosis, defined as $M_4/M_2^2$, measures the tendency of a distribution to produce outliers (Westfall 2014). However, since the kurtosis is a ratio of two random variables, its expectation is challenging to calculate. Rather than attempt this calculation, we compare the expected fourth central moment itself to that expected under normality. This approach qualitatively identifies the factors influencing deviations from normality.

Using the low mutation rate approximation, the ratio of the expected fourth moment to that under normality simplifies to

$$\frac{\text{E}\left[M_4\right]}{3{\left(L\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{2,2}\right]m_2\right)}^2}\approx 1+\underset{\text{mutation}}{\underbrace{\frac{m_4}{m_2^2}}}\underset{\text{sparsity}}{\underbrace{{\left(6L\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{2,2}\right]\right)}^{-1}}}\underset{\text{demography}}{\underbrace{\left(\frac{2\text{E}\left[{\mathrm{핋}}_{4,4}\right]+\frac{2}{3}\text{E}\left[{\mathrm{핋}}_{3,4}\right]+\frac{4}{9}\text{E}\left[{\mathrm{핋}}_{2,4}\right]}{\text{E}\left[{\mathrm{핋}}_{2,2}\right]}\right)}}$$ (9)

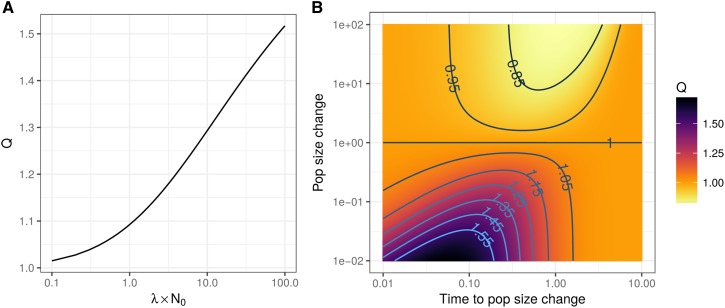
The expected excess in $M_4$, relative to normality, increases with sparsity and with $m_4/m_2^2$. $m_4/m_2^2$ is equal to the kurtosis of the mutational effect distribution when mutations are unbiased and reflects its propensity to produce large effect mutations. The excess depends on demography through the factor $Q=\frac{2\text{E}\left[{\mathrm{핋}}_{4,4}\right]+\frac{2}{3}\text{E}\left[{\mathrm{핋}}_{3,4}\right]+\frac{4}{9}\text{E}\left[{\mathrm{핋}}_{2,4}\right]}{\text{E}\left[{\mathrm{핋}}_{2,2}\right]}$. The extent to which demography increases or decreases deviations from normality can be investigated by calculating Q in different models. In a constant-size, panmictic population, Q = 1. In unstructured populations, $\text{E}\left[{\mathrm{핋}}_{k,n}\right]$ can be calculated numerically using expressions from Griffiths and Tavaré (1998) or Polanski and Kimmel (2003). Values of Q in an exponentially growing population are shown in Figure 2A. Holding sparsity and the mutational distribution constant, a population that underwent exponential growth will have a greater expected deviation from normality in its trait distribution. Another example demography is a population that goes through a step change at some point in the past. Figure 2B shows that when the population size increased at some point in the past, Q is increased similarly to the exponential growth scenario. When the population experiences a bottleneck, Q is decreased to < 1. Q also appears more sensitive to population growth than to decline.

Figure 2.

The effects of demography on deviations of the expected fourth central moment of the population trait distribution from normality. Q measures the effect due to demography on the expected fourth central moment (Equation 9). (A) Q increases as the exponential growth rate increases relative to the current population size. λ is the growth rate and $N_0$ is the initial effective population size. (B) Q values when the population undergoes an instantaneous step change at some point in the past. The time and magnitude of this change are given in units of the current effective population size. Q increases when the population grows and decreases when it declines.

For a more concrete example, we consider the differences in the expected fourth moment produced by demographic histories in different human populations. In the demographic model fit by Tennessen et al. (2012), the generic European population experiences an out-of-Africa bottleneck followed by recent growth, while the generic African population experiences a more stable history, also with recent growth. Differences in demographic history between the two populations has resulted in a lower heterozygosity in European populations due to the out-of-Africa bottleneck (Yu et al. 2002).

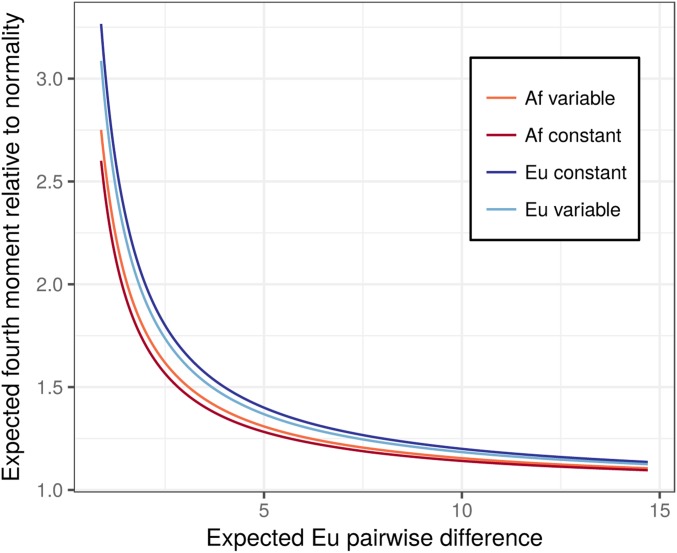
For a given sparsity, the African population model predicts a smaller deviation from normality than the European model (Figure 3). The expected fourth moment in constant-size populations with the same heterozygosity as the African and European models is lower for the African model and higher for the European model. This is because the African model is dominated by population growth that leads to a Q >1, while the European model is dominated by a bottleneck event that leads to a Q <1 (Figure 2). However, differences due to demography are small and deviations from normality are driven mostly by differences in sparsity.

Figure 3.

A comparison between the expected fourth moment at different levels of sparsity in the African and European demographic models fit by Tennessen et al. (2012). Trait sparsity is varied by changing the expected number pairwise differences at sites affecting the trait in the European model. The mutational kurtosis is set to six. The darker lines show the predicted relationship for populations with the same heterozygosity as the European and African models but with constant size.

Even though recombination is not modeled, we can speculate on how linkage impacts deviations from normality. Line two of Equation 7c corresponds to the contribution from two mutations occurring at a single locus. The first quantity indicates that the expectation of the fourth moment increases with the variance of the pairwise coalescence time. The second part does not have a clear interpretation. If the sum of these two terms is positive this agrees with the intuition that linkage disequilibrium increases deviations from normality by reducing the effective number of independent loci.

Simulations of the kurtosis itself show substantial variance, with about a quarter of simulated populations having a value <3 (that of a normal distribution) even as the mean kurtosis increases to almost 9 (see Appendix E and Supplemental Material, Figure S1). This high variance in the kurtosis is likely due to a high variance in both the variance and fourth moment. This, along with the fact that deviations from the infinitesimal model inflate the fourth moment (Equation 9), leads to a situation where the kurtosis increases with trait sparsity but the variance is high across evolutionary realizations.

Trait divergence in structured populations

To demonstrate the utility of the normal distribution arising in the infinitesimal limit (Equation 5), we use simulating from the null distribution of $Q_{ST}$, a measure of divergence in trait values between groups in structured populations. $Q_{ST}$ is defined as the variance between group means divided by the total variance in the population (Spitze 1993). In a haploid model, $Q_{ST}=\frac{V_{\text{between}}}{V_{\text{between}}+V_{\text{within}}}$, where

$$V_{\text{between}}=\frac{1}{K}{\displaystyle \sum }_i{\left({\overline{Y}}_i-\overline{Y}\right)}^2$$

and

$$V_{\text{within}}=\frac{1}{{{\displaystyle \sum }}_k{N}_k}{\displaystyle \sum }_i{{\displaystyle \sum _j\left(Y_{i,j}-{\overline{Y}}_i\right)}}^2.$$

Here, $Y_{i,j}$ is the trait value of individual j in population i, K is the number of subpopulations, and $N_k$ is the size of subpopulation k.

Since all $Y_{i,j}$ are normally distributed, ${\overline{Y}}_i-\overline{Y}$ and $Y_{i,j}-{\overline{Y}}_i$ are as well. When population sizes are large, individual deviations from population means are nearly uncorrelated, as are $V_{\text{between}}$ and $V_{\text{within}}$. $V_{\text{within}}$ is nearly constant across evolutionary realizations and is approximately ${\displaystyle \sum _k{N}_{k}E\left[{\mathcal{T}}_{k,k}\right]}/{\displaystyle {\sum }_k{N}_k}$ because the within population variances are approximately uncorrelated and constant. While we do not have an explicit form for the density function of the between-group variance, we can simulate from its distribution by drawing ${\overline{Y}}_i-\overline{Y}$ values from a multivariate normal distribution with mean zero and covariance

$$\text{Cov}\left[{\overline{Y}}_a-\overline{Y},{\overline{Y}}_b-\overline{Y}\right]={\mu }_2\frac{\theta }{2}\left(\text{E}\left[{\mathcal{T}}_{a,\cdot }\right]+\text{E}\left[{\mathcal{T}}_{b,\cdot }\right]-\text{E}\left[{\mathcal{T}}_{\cdot ,\cdot }\right]-\text{E}\left[{\mathcal{T}}_{a,b}\right]\right)$$ (10)

between populations a and b. To simulate from the null distribution of $Q_{ST}$, ${\mu }_2$ and $\frac{\theta }{2}$ are unnecessary because the scale of the trait cancels in the $Q_{ST}$ ratio. All that is needed to simulate $Q_{ST}$ are the relative expected coalescent times within and between populations, which can be estimated using pairwise nucleotide differences. No further information about population structure, history, or mutation rate is needed.

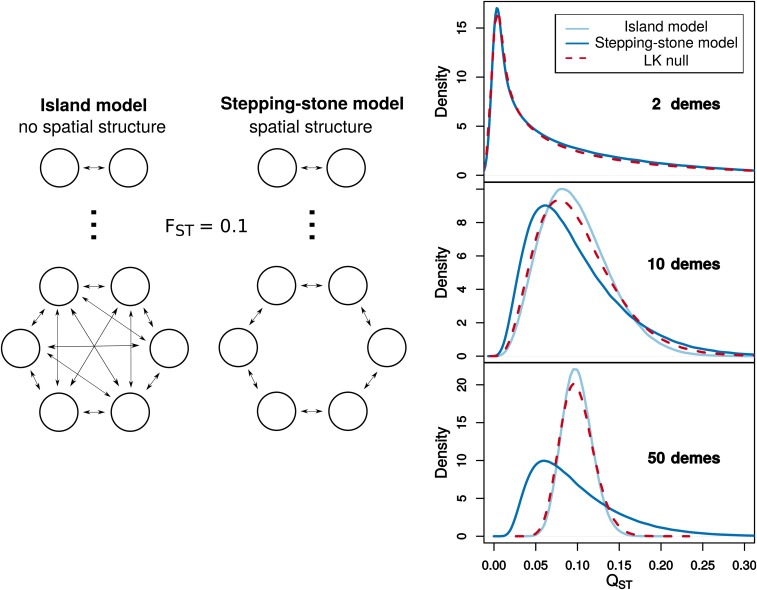
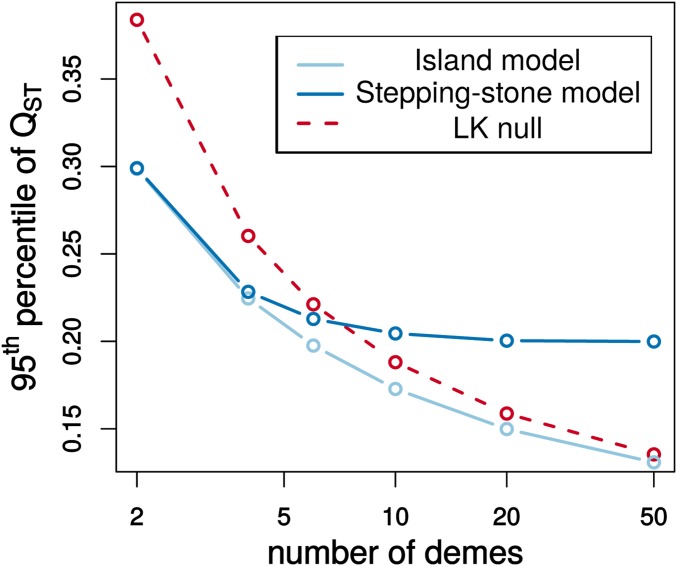
This simulation procedure could be useful in testing whether an observed $Q_{ST}$ is unlikely under neutrality. Current goodness-of-fit tests either compare $Q_{ST}$ to an empirical distribution of $F_{ST}$ values or to a ${\mathrm{\chi }}^2$ distribution (Leinonen et al. 2013). In the second case, a distribution developed by Lewontin and Krakauer (1973) for single-locus neutrality tests is used as the null distribution for $Q_{ST}$. The ${\mathrm{\chi }}^2$ testing procedure was suggested by Whitlock and Guillaume (2009), and is implemented in the program QstFstComp (Gilbert and Whitlock 2015). The Lewontin-Krakauer (LK) distribution assumes independence between subpopulations and provides a good approximation in populations without spatial structure, such as in a symmetric island model (Figure 4). When subpopulations are strongly correlated, such as in a one-dimensional stepping-stone model, the LK distribution is a poor approximation. Even when the distributions appear qualitatively similar, there are substantial differences in tail probabilities (Figure 5).

Figure 4.

A comparison of neutral sampling distributions for $Q_{ST}$ at the population level. The LK distribution for $Q_{ST}$ is compared to the null distribution in the infinitesimal limit for cases with (the stepping-stone model) and without (the island model) spatial structure. The case with no spatial structure assumes the migration rate is equal between all subpopulations. The case with spatial structure arranges subpopulations in a ring with migration only between neighboring subpopulations. Migration rates and subpopulation sizes are uniform and are set such that $F_{ST}=0.1$ as the number of subpopulations increases (Slatkin 1991). $Q_{ST}$ values for these models are simulated by drawing vectors from a multivariate normal distribution parameterized using the expected pairwise coalescence times given by Slatkin (1991). Under the LK distribution, $Q_{ST}$ is distributed as $F_{ST}/\left(n_d-1\right)$ times a chi-square distribution with $n_d-1$ degrees of freedom $\left(Q_{ST}\sim F_{ST}{\chi }_{n_d-1}^2/\left(n_d-1\right)\right)$, where $n_d$ is the number of subpopulations. The neutral distributions for $Q_{ST}$ become increasingly different as the number of subpopulations over which the genetic divergence is spread increases.

Figure 5.

Differences in the $95\mathrm{th}$ percentile of different neutral sampling distributions for $Q_{ST}$ at the population level. The LK distribution is compared to neutral null distributions for structured populations with and without a spatial component using the normal model arising in the infinitesimal limit.

Nearly identical issues to these were raised with the LK test (Nei and Maruyama 1975; Robertson 1975). However, while the neutral distribution for $F_{ST}$ depends on the precise details of population structure and history, the $Q_{ST}$ distribution depends only on coalescence times within and between subpopulations. The point here is not that the LK distribution is particularly bad, but rather that an improved neutral distribution is easily obtained using the infinitesimal limit. This distribution is similar to the extension of the LK test developed by Bonhomme et al. (2010) to account for the correlation structure between subpopulations. The Bonhomme et al. (2010) method treats allele frequencies as multivariate normal with covariance matrix parameterized by coancestry coefficients. Ovaskainen et al. (2011) and Berg and Coop (2014) use normal models for phenotypes also with covariance matrices based on coancestry coefficients. When phenotypic and genetic divergence is mostly driven by changes in allele frequency, the coalescent and coancestry based models should be very similar. However, the coalescent model is ultimately preferable since it is the correct neutral model at any scale of population divergence in the infinitesimal limit. A coancestry model is the only option if only allele frequency data are available, but it is still better to use the full matrix of coancestry than to use a single value of $F_{ST}$.

Treating $Q_{ST}$ as a random variable also lets us reexamine the classic result in evolutionary quantitative genetics that $Q_{ST}=F_{ST}$ (Whitlock 1999). $F_{ST}$, in this context, refers to a population parameter. In particular, $F_{ST}=\frac{\overline{t}-{\overline{t}}_0}{\overline{t}}$, where $\overline{t}$ is the expected coalescent time for two loci sampled at random from the entire population, and ${\overline{t}}_0$ is the expected coalescent time for two loci sampled within a subpopulation (Slatkin 1991). This value is constant over realizations of the evolutionary process. $Q_{ST}$ can refer to either the state of the population or to an estimate of this state. $Q_{ST}$, as a state of the population, varies across evolutionary realizations. Thus, there is no sense in which $Q_{ST}$ can be defined as a constant parameter in the way that $F_{ST}$ can. The expectation of $V_{\text{between}}$ is $\overline{t}-{\overline{t}}_0$, and the expectation of $V_{\text{within}}$ is ${\overline{t}}_0$. $\frac{\text{E}\left[V_{\text{between}}\right]}{\text{E}\left[V_{\text{between}}\right]+\text{E}\left[V_{\text{within}}\right]}$ is equal to $F_{ST}$. Due to Jensen’s inequality, the expectation of this ratio $\left(\text{E}\left[Q_{ST}\right]\right)$ is never greater than $F_{ST}$. This was previously shown by Edge and Rosenberg (2015) for a slightly different trait model.

Inferring genetic parameters

Schraiber and Landis (2015) suggested the possibility of estimating moments of the distribution of mutational effects for traits that deviate from normality. These moments would be informative about the shape of the mutational distribution. Using the expected trait moments (Equation 7), we can attempt to derive a method of moments estimator for the moments of the mutational distribution. The system of equations for the first three central moments is

$${\widehat{M}}_2={\widehat{D}}_{2,2}L{m}_2$$

$${\widehat{M}}_3=\frac{1}{3}{\widehat{D}}_{3,3}L{m}_3$$

$${\widehat{M}}_4=3{\widehat{M}}_2^2+\left({\widehat{D}}_{4,4}+\frac{1}{3}{\widehat{D}}_{3,4}+\frac{2}{9}{\widehat{D}}_{2,4}\right)L{m}_4,$$ (11)

where ${\widehat{D}}_{k,n}$ is an estimator of $\frac{\theta }{2}\text{E}\left[{\mathrm{핋}}_{k,n}\right]$, and the low mutation rate approximation has been used. The moments of the trait distribution only enter through products with the number of loci potentially affecting the trait $\left(L{m}_i\right)$. If we have the estimates $\widehat{L{m}_2}$, $\widehat{L{m}_3}$, and $\widehat{L{m}_4}$, it is possible to estimate the ratios $m_2/m_4$ and $m_3/m_4$ for the mutational distribution. These ratios are meaningless on their own because any value could be obtained by changing the measurement scale of the trait. The identifiable quantity in this system of equation is the compound parameter $\frac{m_3^2}{m_2{m}_4}$. This quantity reflects the degree of mutational skew relative to the spread of the distribution, but it is not possible to distinguish sparsity from skewed or heavy-tailed distributions of mutational effects.

Discussion

Neutral models of quantitative trait evolution are important for establishing a baseline against which to test for selection. Schraiber and Landis (2015) recently analyzed a neutral model of trait evolution that made few assumptions about the number of loci potentially affecting the trait and the distribution of mutational effects. However, they only derived results for constant-size, panmictic populations. We extend their results to populations with arbitrary distributions of coalescent times and therefore arbitrary demographic histories and spatial structures. A key result of Schraiber and Landis (2015) is the characteristic function of the distribution of trait values in a sample. We work instead with the mgf, but the two approaches are interchangeable as long as the mgf of the mutational distribution exists (which it will if the moments of the mutational distribution are all finite). Our main result (Equation 4) shows that the characteristic function from Schraiber and Landis (2015) is a special outcome of a general procedure whereby the mgf for a trait can be obtained by making a simple substitution into the mgf for a distribution over genealogies. The mgfs for many demographies of interest, and for sample sizes greater than n = 3 are complex recursions that are impractical to solve (Lohse et al. 2011). However, progress can still be made by deriving moments of trait distributions in terms of moments of the genealogical and mutational distributions.

This result extends previous work using coalescent theory to investigate neutral models of quantitative traits (Whitlock 1999; Schraiber and Landis 2015). Ours is the most general model yet analyzed. As a natural first step, we show that the infinitesimal limit suggested by Fisher (1919) leads to a model where phenotypes are normally distributed as the number of loci becomes large and the magnitude of effect sizes becomes small. In the limiting distribution, the variance of the difference between two individuals is proportional to the expected pairwise coalescent time between them, and the covariance between a pair of differences is $\text{Cov}\left[Y_a-Y_b,Y_c-Y_d\right]\propto \text{E}\left[{\mathcal{T}}_{a,d}\right]+\text{E}\left[{\mathcal{T}}_{b,c}\right]-\text{E}\left[{\mathcal{T}}_{a,c}\right]-\text{E}\left[{\mathcal{T}}_{b,d}\right]$. The resulting covariance matrix completely specifies the neutral distribution in the infinitesimal limit. This is similar to classic models in evolutionary quantitative genetics for the neutral divergence of trait values after population splits (Lande 1976; Lynch 1989) but holds regardless of the precise details of population structure and history. Schraiber and Landis (2015) derive essentially the same distribution using a central limit theorem argument.

Mendes et al. (2018) point out several problems caused by incomplete lineage sorting when a covariance matrix based on species split times is used in phylogenetic comparative methods. The normal model arising in the infinitesimal limit is not subject to these problems because it is explicitly based in the coalescent. A matrix based on average pairwise coalescence times takes into account the effects of all lineages at causal loci, even those that do not follow the species topology. The covariances specified by Equation 5 could also be used to generate within-species contrasts in a similar manner to the method suggested by Felsenstein (2002).

We derived the first four expected central moments of sparse traits and compared them to those expected under normality. This showed how demography and genetics separately influence the expected deviation from normality. For a fixed expected sparsity, population growth produces greater deviations in the fourth central moment while population bottlenecks produce lower deviations (Figure 2). However, for realistic demographic scenarios, we find that the effects attributable to demography are small (Figure 3). We only analyzed cases with exchangeable individuals, but adding population structure would increase deviations from normality as drifting trait means between subpopulations can yield multimodal distributions.

We next investigated two simple problems where a coalescent perspective on the neutral distribution of a quantitative trait provides useful intuition. The first is the question of the appropriate null distribution for $Q_{ST}$ at the population level. We show how to easily simulate from the null distribution in the infinitesimal limit, providing a much better approximation when subpopulations are correlated than previous approaches (Whitlock and Guillaume 2009) (Figure 4). For the second we show that the shape of the mutational distribution is largely confounded with the number of loci affecting the trait, with only one compound parameter identifiable. This makes it unlikely that mutational parameters could be inferred from trait values sampled from a population.

Even though we have broadened the model space for neutral traits, many features of real populations have not yet been incorporated. Linked loci are a particular concern as there is substantial linkage disequilibrium between causal SNPs (Bulik-Sullivan et al. 2015). Lohse et al. (2011) derived the form of the mgf for genealogies at linked loci and future work will attempt to incorporate recombination using Equation 4. In particular, it will be important to show how linkage affects the distribution in the infinitesimal limit. Diploidy, dominance, and epistasis have also been ignored thus far. The qualitative effects described here should hold under additive diploidy, but having trait values within individuals summed over loci from two copies of the genome will decrease deviations from normality. Dominance will also produce a normal distribution within populations because individual trait values are generated by summing genotypic effects from many independent loci. A relationship between dominance and mutational effects can skew the distribution of trait values at individual loci, thereby slowing convergence, but the central limit theorem will ultimately ensure a normal marginal distribution of individual trait values. The same argument used for the haploid model also shows that the within-population distribution will be normal under dominance (see Appendix B). Analogous to the haploid within-population variance of $\text{E}\left[{\mathrm{핋}}_{2,2}\right]\frac{\theta }{2}{\mu }_2$, the diploid variance also depends on the genealogical, mutational, and dominance distributions, and could be derived with an approach similar to that used here. An analysis of dominance in the infinitesimal limit would be a useful next step as previous work has found that dominance decreases mean $Q_{ST}$ (Goudet and Büchi 2006).

Barton et al. (2017) recently performed a deep mathematical investigation of a more formal “infinitesimal model.” They proved conditions under which the trait values of offspring within a family are normally distributed with a covariance matrix conditionally independent of the parental trait values given the pedigree. Interestingly, they found normality still holds under pairwise epistasis if it is not too extreme. It may therefore be possible to include epistasis in the infinitesimal limit considered here, and thus study how epistasis affects neutral trait divergence. In a commentary on Barton et al. (2017), Turelli (2017) noted that at least three infinitesimal models have been used. The first stems from Fisher (1918), and states that a large number of Mendelian factors each make a small contribution to the genetic variance. The second is the model studied by Barton et al. (2017) that descendants are Gaussian with variance independent of parental phenotypes. The third assumes that trait values are Gaussian within a population and has been used to study selection (Bulmer 1971). The infinitesimal limit considered here fits all three definitions: (1) the limit corresponds to Fisher’s notion of a large number of Mendelian factors; (2) the descendants within a family have a Gaussian distribution of trait values, as shown rigorously by Barton et al. (2017); and (3) the distribution of trait values is Gaussian in panmictic populations.

Although GWAS of many traits have shown them to be controlled by large numbers of loci (Boyle et al. 2017), this is not necessarily the case for every trait of interest to biologists. It has been suggested, for instance, that gene expression levels have a sparse genetic architecture (Wheeler et al. 2016). Since there is much interest in testing whether natural selection has acted on gene expression levels (Gilad et al. 2006; Whitehead and Crawford 2006; Yang et al. 2017), well-calibrated goodness-of-fit tests will need to take into account the complications that arise when trait distributions deviate from normality (Khaitovich et al. 2005). Direct measurements of mutational distributions (Gruber et al. 2012; Metzger et al. 2016) could aid calibrations. Generally, more work is needed to develop neutrality tests robust to the details of genetics and population history, and to investigate whether anything about mutational processes can be learned using statistical models that share information across multiple traits.

Appendix

Appendix A: Rederivation of Equation (1) of Schraiber and Landis

This appendix shows how the main mathematical result of this study connects to previous work by Lohse et al. (2011) and Schraiber and Landis (2015). Lohse et al. (2011) showed how the probability distribution of genealogies at a locus can be represented using a generating function. Schraiber and Landis (2015) took a similar approach to a different problem, and derived the characteristic function for the distribution of quantitative traits in a panmictic population. Equation 4 of this paper demonstrates a fundamental connection between the mgfs of traits and of genealogies. If this connection holds we should be able to reproduce equation (1) of Schraiber and Landis (2015) (the panmictic trait mgf) using Equation 4 of this paper and equation (5) of Lohse et al. (2011) (the genealogy mgf).

We go through this derivation rewriting equations in the notation of this paper. Equation (5) of Lohse et al. (2011) is a recursion for finding the mgf of a sample of size n lineages from a panmictic population:

$${\varphi }_T^n\left(s,\mathrm{\Upsilon }\right)=\frac{1}{\left(\frac{n}{2}\right)+{\displaystyle {\sum }_{\omega \in \mathrm{\Upsilon }}{s}_{\omega }}}{\displaystyle \sum _{\left({\omega }_i,{\omega }_j\right)\in \mathrm{\Upsilon }}{\varphi }_T^{n-1}\left(s,\mathcal{C}\left(\mathrm{\Upsilon },{\omega }_i,{\omega }_j\right)\right)}.$$ (12)

Here, $\mathrm{\Upsilon }$ is the set of all external branches of the genealogy, and $\mathcal{C}\left(\mathrm{\Upsilon },{\omega }_i,{\omega }_j\right)$ is an operator that removes ${\omega }_i$ and ${\omega }_j$ from $\mathrm{\Upsilon }$ and adds ${\omega }_i\cup {\omega }_j$. Following Equation 4, we make the substitution $s_{\omega }=\frac{\theta }{2}\left(\psi \left({\displaystyle {\sum }_{i\in \omega }{k}_i}\right)-1\right)$ to get

$${\varphi }_Y^n\left(k\right)=\frac{2}{n\left(n-1\right)+\theta \left({\displaystyle {\sum }_{u=1}^n\psi \left(k_u\right)-n}\right)}{\displaystyle {\sum }_{\left({\omega }_i,{\omega }_j\right)\in \mathrm{\Upsilon }}{\varphi }_T^{n-1}\left(s,\mathcal{C}\left(\mathrm{\Upsilon },{\omega }_i,{\omega }_j\right)\right)}|{}_{s_{\omega }=\frac{\theta }{2}\left(\psi \left({\displaystyle {\sum }_{i\in \omega }{k}_i}\right)-1\right)}.$$ (13)

Next we can write

$${\varphi }_T^{n-1}\left(s,\mathcal{C}\left(\mathrm{\Upsilon },{\omega }_i,{\omega }_j\right)\right)|{}_{s_{\omega }=\frac{\theta }{2}\left(\psi \left({\displaystyle {\sum }_{i\in \omega }{k}_i}\right)-1\right)}={\varphi }_Y^{n-1}\left(\mathcal{C}\left(k,i,j\right)\right).$$ (14)

The operator $\mathcal{C}\left(k,i,j\right)$ removes the $i\mathrm{th}$ and $j\mathrm{th}$ elements of $k$ and adds the term $k_i+k_j$. We can use this simple operator because the order of elements in $k$ does not matter for a panmictic population. This yields

$${\varphi }_Y^n\left(k\right)=\frac{2}{n\left(n-1\right)+\theta \left({\displaystyle {\sum }_{u=1}^n\psi \left(k_u\right)-n}\right)}{\displaystyle \sum _{i,j\le n,i\ne j}{\varphi }_Y^{n-1}\left(\mathcal{C}\left(k,i,j\right)\right)}.$$ (15)

This recursive expression is equivalent to equation (1) in Schraiber and Landis (2015).

The complicated appearance of Equation 15 is mostly due to the need for novel notation. A simple example for a sample of three lineages shows how the substitution process works, and better demonstrates the utility of Equation 4. The mgf for a genealogy of sample size three from a panmictic population is

$$\begin{array}{l}{\varphi }_T=\frac{1}{3-s_{\left\{a\right\}}-s_{\left\{b\right\}}-s_{\left\{c\right\}}}\\ \times \left(\frac{1}{1-s_{\left\{a,b\right\}}-s_{\left\{c\right\}}}+\frac{1}{1-s_{\left\{a,c\right\}}-s_{\left\{b\right\}}}+\frac{1}{1-s_{\left\{b,c\right\}}-s_{\left\{a\right\}}}\right),\end{array}$$

and the mgf for the trait distribution after substitution is

$${\varphi }_Y=\left(\frac{1}{3-\frac{\theta }{2}\left(\psi \left(k_a\right)+\psi \left(k_b\right)+\psi \left(k_c\right)-3\right)}\times \left(\begin{array}{l}\frac{1}{1-\frac{\theta }{2}\left(\psi \left(k_a+k_b\right)+\psi \left(k_c\right)-2\right)}+\frac{1}{1-\frac{\theta }{2}\left(\psi \left(k_a+k_c\right)+\psi \left(k_b\right)-2\right)}\\ +\frac{1}{1-\frac{\theta }{2}\left(\psi \left(k_b+k_c\right)+\psi \left(k_a\right)-2\right)}\end{array}\right)\right)$$

Appendix B: The Infinitesimal Limit

This appendix describes in detail how taking an infinitesimal limit where the number of loci becomes large as the effect size per mutation becomes small, yields a multivariate normal distribution of individual trait values. The resulting normal model leads to Equation 5, which gives the covariance in individual trait differences. Equation 5 is later used to simulate from the null distribution of $Q_{ST}$ in the main text section on trait divergence in structured populations. The first section of this appendix describes a full central limit theorem argument for obtaining the means, variances, and covariances that are given in the main text section on the infinitesimal limit. The second section provides a heuristic derivation of the same means, variances and covariances. The third section explains how these results for the joint trait distribution in the infinitesimal limit relate to trait distributions in panmictic populations where individuals are exchangeable.

A central limit theorem derivation

The mgf for the distribution of trait values from a single locus is

$${\varphi }_Y\left(k\right)={\displaystyle \int \text{exp}}\left({\displaystyle \sum _{\omega \in \text{Ω}}{s}_{\omega }{t}_{\omega }}\right)\text{P}\left(T=t\right)\text{d}t|{}_{s_{\omega }=\frac{\theta }{2}\left(\psi \left({\displaystyle {\sum }_{a\in \omega }{k}_a}\right)-1\right)}.$$

If we substitute in the Taylor series expansions for the mgf of the trait value distribution we get

$${\displaystyle \int {\displaystyle \prod _{\Omega }\text{exp}\left[t_{\omega }\frac{\theta }{2}\left({\displaystyle \sum _{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}}{\left({\displaystyle \sum _{a\in \omega }{k}_a}\right)}^n\right)\right]\text{P}\left(T=t\right)\mathrm{d}\mathbf{t}\mathrm{.}}}$$

If we then write the Taylor series of each exponential function we get

$${\displaystyle \int {\displaystyle \prod _{\text{Ω}}\left[{\displaystyle \sum _{j=0}^{\mathrm{\infty }}\frac{t_{\omega }^j}{j!}{\left(\frac{\theta }{2}\right)}^j}{\left({\displaystyle \sum _{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}}{\left({\displaystyle \sum _{a\in \omega }{k}_a}\right)}^n\right)}^j\right]\text{P}\left(T=t\right)\text{d}t,}}$$

which is equivalent to

$$1+{\displaystyle \sum _{\text{Ω}}\text{E}}\left[T_{\omega }\right]\frac{\theta }{2}{\displaystyle \sum _{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}}{\left({\displaystyle \sum _{a\in \omega }{k}_a}\right)}^2+{\displaystyle \sum _{\text{Ω}\times \text{Ω}}\frac{1}{2}}E\left[T_{{\omega }_1}{T}_{{\omega }_2}\right]{\displaystyle \sum _{n=1}^{\mathrm{\infty }}\frac{\theta }{2}\frac{m_n}{n!}}{\left({\displaystyle \sum _{a\in {\omega }_1}{k}_a}\right)}^n{\displaystyle \sum _{n=1}^{\mathrm{\infty }}\frac{\theta }{2}}\frac{m_n}{n!}{\left({\displaystyle \sum _{a\in {\omega }_2}{k}_a}\right)}^n+\dots$$

This is raised to the power L for a trait controlled by L loci. We want the limit as the number of loci increases while the size of mutational effects decreases. This can be expressed by the limits $L{m}_1\to {\mu }_1$, $L{m}_2\to {\mu }_2$ and $L{m}_i\to 0$ for $i>2$ as $L\to \mathrm{\infty }.$ Knowing we will not be retaining $m_3$ and above we can rewrite the mgf as

$${\left(1+{\displaystyle \sum _{\text{Ω}}\text{E}\left[T_{\omega }\right]\frac{\theta }{2}}\left(m_1{\displaystyle \sum _{a\in \omega }{k}_a}+\frac{m_2}{2}{\left({\displaystyle \sum _{a\in \omega }{k}_a}\right)}^2\right)\right)}^L.$$

The result of taking these limits is

$$\text{exp}\left({\displaystyle \sum _{\omega \in \text{Ω}}\text{E}\left[T_{\omega }\right]\frac{\theta }{2}}\left({\mu }_1{\displaystyle \sum _{a\in \omega }{k}_a}+\frac{{\mu }_2}{2}{\left({\displaystyle \sum _{a\in \omega }{k}_a}\right)}^2\right)\right).$$ (16)

This is multivariate normal distribution with mean equal to $\text{E}\left[T_{\text{MRCA}}\right]\frac{\theta }{2}{\mu }_1$, variance equal to $\text{E}\left[T_{\text{MRCA}}\right]\frac{\theta }{2}{\mu }_2$, and covariance between $Y_a$ and $Y_b$ equal to $\text{E}\left[{\tau }_{a+b}\right]\frac{\theta }{2}{\mu }_2$. This can be seen from Equation 16 by noting that in the mgf for a multivariate normal distribution the coefficient in the exponential of $k_a$ is the mean of $Y_a$ and the coefficient of $k_a{k}_b$ is $2\text{Cov}\left[Y_a,Y_b\right]$ if $a\ne b$ and $\text{Var}\left[Y_a\right]$ if $a=b$.

These Y values are not directly observed because in the theory presented here they are measured as the sum of differences since the $T_{\text{MRCA}}$s at the causal loci affecting the trait. Rather, differences between individual trait values are what analyses would be based on. Since the Y are normally distributed differences between trait values such as $Y_a-Y_b$ will be as well.

$$\begin{array}{l}\text{Var}\left[Y_a-Y_b\right]=Var\left[Y_a\right]+\text{Var}\left[Y_b\right]-2\text{Cov}\left[Y_a,Y_b\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=2\left(\text{E}\left[T_{\text{MRCA}}\right]-\text{E}\left[{\tau }_{a+b}\right]\right){\mu }_2.\end{array}$$

The same argument is used to arrive at Equation 5 in the main text. The covariance between all pairs of differences in trait values determines any observable statistics in the infinitesimal limit.

A heuristic derivation:

A much simpler heuristic derivation of the limiting normal distribution can be done by calculating the variance and covariance at a single locus. This derivation is very similar to that done by Schraiber and Landis (2015). Using the law of total variance we can write

$$\text{Var}\left[Y\right]=\text{E}\left[\text{Var}\left[\left[Y\right]|T\right]\right]+\text{Var}\left[\text{E}\left[Y|T\right]\right]$$

The variance conditional on T can be calculated again using the law of total variance and conditioning on the number of mutations at the locus.

$$\begin{array}{l}\text{Var}\left[Y|T\right]=\text{E}\left[\text{Var}\left[Y|M\right]|T\right]+\text{Var}\left[E\left[Y|M\right]|T\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\text{E}\left[M\left(m_2-m_1^2\right)|T\right]+\text{Var}\left[M{m}_1|T\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\frac{\theta }{2}T\left(m_2-m_1^2\right)+\frac{\theta }{2}T{m}_1^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\frac{\theta }{2}T{m}_2\end{array}$$

$$\text{E}\left[Y|T\right]=\frac{\theta }{2}T{m}_1$$

$$\text{Var}\left[\frac{\theta }{2}T{m}_1\right]={\left(\frac{\theta }{2}{m}_1\right)}^2\text{Var}\left[T\right]$$

Therefore we have

$$\text{Var}\left[T\right]=\frac{\theta }{2}{m}_2\text{E}\left[T_{\text{MRCA}}\right]+{\left(\frac{\theta }{2}{m}_1\right)}^2\text{Var}\left[T_{\text{MRCA}}\right].$$ (17)

The same procedure can be done for the covariance.

$$\text{Cov}\left[Y_a,Y_b\right]=\text{E}\left[\text{Cov}\left[Y_a,Y_b|T\right]\right]+\text{Cov}\left[E\left[Y_a|T\right],E\left[Y_b|T\right]\right]$$

We can break $Y_a$ and $Y_b$ into a shared part, $Y_S$ and unshared parts for each, $Y_{\delta a}$ and $Y_{\delta b}$.

$$\text{Cov}\left[Y_S+Y_{\delta a},Y_S+Y_{\delta b}|T\right]=\text{Var}\left[Y_s|T\right]=\frac{\theta }{2}{\tau }_{a+b}{m}_2.$$

$$E\left[\frac{\theta }{2}{\tau }_{a+b}{m}_2\right]=\frac{\theta }{2}{m}_2\text{E}\left[{\tau }_{a+b}\right]$$

$$\text{Cov}\left[E\left[Y_a|T\right],E\left[Y_b|T\right]\right]=\text{Cov}\left[\frac{\theta }{2}T{m}_1,\frac{\theta }{2}T{m}_1\right]={\left(\frac{\theta }{2}{m}_1\right)}^2\text{Var}\left[T_{\text{MRCA}}\right]$$

Therefore we have

$$\text{Cov}\left[Y_a,Y_b\right]=\frac{\theta }{2}{m}_2\text{E}\left[{\tau }_{a+b}\right]+{\left(\frac{\theta }{2}{m}_1\right)}^2\text{Var}\left[T_{\text{MRCA}}\right].$$ (18)

The terms proportional to the variance of the $T_{\text{MRCA}}$ disappear because $L{m}_1^2\to 0$ as $L\to \mathrm{\infty }$

Within-population trait distributions

The above theory considers the distribution of trait values over realizations of the neutral evolutionary process and shows that this is multivariate normal. As discussed in the main text section on the infinitesimal limit, we also intuitively expect that the distribution of trait values within a randomly mating population will be univariate normal. These two perspectives are easily reconciled using multivariate normal theory. In a population of size N, the trait values $Y=\left(Y_1,\dots ,Y_N\right)$ are exchangeable normal random variables. They are therefore jointly multivariate normal with a common mean $\mathrm{ℳ}$, common variance $\mathcal{V}$, and common covariance $\mathcal{D}$ (Tong 1990). If the mean value in the population is $\overline{Y}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{Y}_i}$, then

$$\text{E}\left[Y_i-\overline{Y}\right]=0,$$ (19)

$$\text{Var}\left[Y_i-\overline{Y}\right]=\mathcal{V}-2\frac{\left(N-1\right)\mathcal{D}+\mathcal{V}}{N}+\frac{N\left(N-1\right)\mathcal{D}+N\mathcal{V}}{N^2}\approx \mathcal{V}-\mathcal{D},$$ (20)

and

$$\text{Cov}[Y_i-\overline{Y},Y_j-\overline{Y}]=\mathcal{D}-2\frac{\left(N-1\right)\mathcal{D}+\mathcal{V}}{N}+\frac{N\left(N-1\right)\mathcal{D}+N\mathcal{V}}{N^2}\approx 0.$$ (21)

The within-population trait value are therefore approximately i.i.d. normal around the population mean. In the infinitesimal limit we have $\mathcal{V}=\text{E}[T_{\text{MRCA}}]\frac{\theta }{2}{\mu }_2$ and $\mathcal{D}=\text{E}[{\tau }_{a+b}]\frac{\theta }{2}{\mu }_2$. The within-population variance is therefore $\text{E}[T_{MRCA}]\frac{\theta }{2}{\mu }_2-\text{E}[{\tau }_{a+b}]\frac{\theta }{2}{\mu }_2=\text{E}[{\mathrm{핋}}_{2,2}]\frac{\theta }{2}{\mu }_2$.

The reasoning here applies to any situation where the marginal trait values are normal and individuals are exchangeable. As mentioned in the discussion, a situation of particular interest is the case of dominance. In a diploid model with dominance we would also get a marginal normal distribution when summing over independent loci. Equation 20 would therefore still apply and we would get a within-population variance analogous to $\text{E}[{\mathrm{핋}}_{2,2}]\frac{\theta }{2}{\mu }_2$ that depends on moments of the genealogical, mutational, and dominance distributions.

Appendix C: Derivation of the Low-Mutation-Rate Approximation

This appendix gives the derivation of the low-mutation-rate approximation to the trait mgf given in Equation 6. This approximate mgf is derived starting with Equation 3 and only allowing for the possibility of one or zero mutations at each locus.

Using Equation 3, and taking a Taylor series approximation to the exponential function, we get

$${\varphi }_Y(k)={{\displaystyle \int }}^{\text{}}{\displaystyle \prod }_{\omega \in \text{Ω}}[1+\frac{\theta }{2}{t}_{\omega }(\psi ({\displaystyle \sum }_{a\in \omega }{k}_a)-1)+O({\theta }^2)]\text{P}(T=t)\text{d}t.$$ (22)

The $O\left({\theta }^2\right)$ term captures events where more than one mutation occurs on the same branch of the genealogy. Events corresponding to more than one mutation occurring on different branches can also be absorbed into this term to give

$${\varphi }_Y(k)=1+\frac{\theta }{2}{\displaystyle \sum }_{\omega \in \text{Ω}}\text{E}[T_{\omega }](\psi ({\displaystyle \sum }_{a\in \omega }{k}_a)-1)+O({\theta }^2))$$ (23)

This is the mgf for a trait controlled by only a single locus, and raising it to the power L to account for multiple independent loci gives the Equation 6 given in the main text.

Appendix D: Automatic Moment Derivations

Equations 7a–c in the full text were derived using a symbolic math program written using sympy (Meurer et al. 2017). This appendix describes the basic idea behind this program. A python module and ipython notebook used to make calculations are available at https://github.com/emkoch/trait_mgf_math.

Moments of the trait distribution can be calculated by differentiating Equation 3. To derive moments for an arbitrary distribution of coalescent times we take a Taylor series of the mgf of the mutational distribution to get

$${({{\displaystyle \int }}^{\text{}}{\displaystyle \prod }_{\text{Ω}}\text{exp}[t_{\omega }\frac{\theta }{2}({\displaystyle \sum }_{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}{({\displaystyle \sum }_{a\in \omega }{k}_a)}^n)]\text{P}(T=t)\text{d}t)}^L.$$ (24)

We then also Taylor expand the exponential function appearing in this integral to get

$${\left(1+{\displaystyle \sum }_{\text{Ω}}\text{E}[T_{\omega }]\frac{\theta }{2}{\displaystyle \sum }_{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^n+\frac{1}{2}\text{E}[{\left({\displaystyle \sum }_{\text{Ω}}{T}_{\omega }\frac{\theta }{2}{\displaystyle \sum }_{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^n\right)}^2]+\frac{1}{6}\text{E}[{\left({\displaystyle \sum }_{\text{Ω}}{T}_{\omega }\frac{\theta }{2}{\displaystyle \sum }_{n=1}^{\mathrm{\infty }}\frac{m_n}{n!}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^n\right)}^3]+\dots \right)}^L.$$ (25)

Of course, the infinite sums appearing in this expression pose a problem. To calculate a particular moment, we only consider terms that will contribute terms of that moment’s order when Equation 25 is differentiated and zero is substituted for all dummy variables. For example, to calculate $E[Y_a{Y}_b{Y}_c]$ we only want terms that contain an order three product of k when the polynomial in Equation 25 is expanded. For a moment of order m, we only need consider terms of size m and less in the series expansion of the exponential, and within the expansions of the mutational mgf we only need consider terms up to order $m-m_t+1$ where $m_t$ is the order of the exponential term being considered.

Appendix E: Kurtosis Simulations

This appendix investigates how the kurtosis, rather than the expected fourth moment of the within-population trait distribution responds to demography and sparsity. Equations 7a–c and Figure 2 only show the response of the fourth moment. The kurtosis proves difficult to deal with analytically. A first order approximation proves to be poor and simulations show high variance of the within-population kurtosis.

Entire populations were simulated using msprime (Kelleher et al. 2016) and mutations were assigned effects from a standard normal or Laplace distribution. The effective population size and mutation rate were kept constant and the expected number of pairwise difference was increased by increasing the number of loci affecting the trait.

A first order approximation to the kurtosis is

$${\kappa }_Y^{\left(1\right)}=3+\frac{m_4/m_2^2\frac{\text{E}[{\mathrm{핋}}_{4,4}]-\frac{1}{6}\text{E}[{\mathrm{핋}}_{3,4}]-\frac{1}{9}\text{E}[{\mathrm{핋}}_{2,4}]}{\text{E}[{\mathrm{핋}}_{2,2}]}}{L\frac{\theta }{2}\text{E}[{\mathrm{핋}}_{2,2}]+m_4/m_2^2\frac{\frac{1}{9}\text{E}[{\mathrm{핋}}_{2,4}]+\frac{1}{6}\text{E}[{\mathrm{핋}}_{3,4}]}{\text{E}[{\mathrm{핋}}_{2,2}]}}.$$ (26)

Although this expression suggests that the expected ${\kappa }_Y$ will be greater than under normality when external branches are longer $\left(\text{E}[{\mathrm{핋}}_{4,4}]>\frac{1}{6}\text{E}[{\mathrm{핋}}_{3,4}]+\frac{1}{9}\text{E}[{\mathrm{핋}}_{2,4}]\right)$ and less than under normality when they are longer $\left(\text{E}[{\mathrm{핋}}_{4,4}]<\frac{1}{6}\text{E}[{\mathrm{핋}}_{3,4}]+\frac{1}{9}\text{E}[{\mathrm{핋}}_{2,4}]\right)$, simulations show that the approximation is actually quite poor (Figure S1).

Appendix F: Additional Moment Derivations

This appendix provides full derivations of some moments of trait distributions to show how things would proceed without the assistance of computer algebra. The first section derives the variance and kurtosis of a single trait value, $Y_a$. This is the variance and kurtosis that would result if we were to rerun the evolutionary history leading to that individual many times. The second section derives the expected fourth central moments of the within-population trait distribution under the low-mutation-rate approximation. This result should be compared with that in Equation 7c.

First and second trait moments

We can use the low-mutation-rate approximation to the mgf to calculate moments of the distribution of trait values. In what follows, let ${\tau }_{a+b}$ be the sum of all branches ancestral to both a and b, and ${\tau }_{a/b}$ be the sum of all branches ancestral to a but not b. Extensions of this for more than two individuals are also used. The same notation is used when referring to sets of branch indices. So ${\text{Ω}}_{a+b}$ and ${\text{Ω}}_{a/b}$ would be the sets of branches added to get ${\tau }_{a+b}$ and ${\tau }_{a/b}$, respectively.

We will start by calculating the first and second moments. First, as was done when deriving the normal distribution, substitute the Taylor series of the mutational mgf:

$${\varphi }_Y\left(k\right)\approx {[1+{\displaystyle \sum }_{\omega \in \text{Ω}}\text{E}[T_{\omega }]\frac{\theta }{2}\left(m_1{\displaystyle \sum }_{a\in \omega }{k}_a+\frac{m_2}{2!}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^2+\frac{m_3}{3!}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^3+\frac{m_4}{4!}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^4\dots \right)]}^L.$$ (27)

We can expand this out using multinomial coefficients to get

$$\begin{array}{l}{\varphi }_Y\left(k\right)\approx 1+L\frac{\theta }{2}{\displaystyle \sum }_{\omega \in \mathcal{O}}\text{E}[T_{\omega }]\left(m_1{\displaystyle \sum }_{a\in \omega }{k}_a+\frac{m_2}{2}{\left({\displaystyle \sum }_{a\in \omega }{k}_a\right)}^2+\dots \right)\\ +\frac{L\left(L-1\right)}{2}{(\frac{\theta }{2})}^2{\displaystyle \sum }_{\omega \in \text{Ω}}E{[T_{\omega }]}^2{(m_1{\displaystyle \sum }_{a\in \omega }{k}_a+\frac{m_2}{2}{({\displaystyle \sum }_{a\in \omega }{k}_a)}^2+\dots )}^2\\ +L\left(L-1\right){\left(\frac{\theta }{2}\right)}^2{\displaystyle \sum }_{{\omega }_1,{\omega }_2\in \text{Ω}}\text{E}[T_{{\omega }_1}]\text{E}[T_{{\omega }_2}]\left(m_1{\displaystyle \sum }_{a\in {\omega }_1}{k}_a+\dots \right)\left(m_1{\displaystyle \sum }_{a\in {\omega }_2}{k}_a+\dots \right)+\dots .\end{array}$$ (28)

The first coefficient is $\left(\begin{array}{c}L\\ L-1,1,0\end{array}\right)$, the second is $\left(\begin{array}{c}L\\ L-2,2,0\end{array}\right)$, and the third is $\left(\begin{array}{c}L\\ L-2,1,1,0\end{array}\right)$. To calculate the moments of this distribution one takes the partial derivatives of the mgf and sets the dummy variables to zero.

$$\text{E}[Y_1^{r_1}\dots Y_n^{r_n}]=\frac{{\partial }^{r_1+\dots +r_n}}{\partial k_1^{r_1}\dots \partial k_n^{r_n}}{\varphi }_Y\left(k\right){|}_{k=0}$$ (29)

Using this to calculate the first moment of the trait distribution, we get

$$\text{E}[Y_a]\approx L\frac{\theta }{2}{m}_1{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }].$$ (30)

The second moment is more complicated because there are $k_a^2$ terms in all three lines of Equation 28.

$$\begin{array}{l}\text{E}[Y_a^2]\approx L\frac{\theta }{2}{m}_2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}E[t_{\omega }]\\ +\frac{L\left(L-1\right)}{2}{\left(\frac{\theta }{2}\right)}^2{m}_1^2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}2\text{E}{[T_{\omega }]}^2\\ +L\left(L-1\right){\left(\frac{\theta }{2}\right)}^2{m}_1^2{\displaystyle \sum }_{{\omega }_1,{\omega }_2\in {\text{Ω}}_{a+b}}2\text{E}[T_{{\omega }_1}]E[T_{{\omega }_2}]\end{array}$$ (31)

Terms with ${\left(\frac{\theta }{2}\right)}^2$ are kept because they also include a second order term of L in front of them. We can now calculated the variance using $\text{Var}[Y]=\text{E}[Y^2]-\text{E}{[Y]}^2$. The squared first moment can be written as

$$\begin{array}{l}{\left(L\frac{\theta }{2}{m}_1{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[t_{\omega }]\right)}^2=L^2{\left(\frac{\theta }{2}\right)}^2{m}_1^2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}{[T_{\omega }]}^2+L^2{\left(\frac{\theta }{2}\right)}^2{m}_1^2{\displaystyle \sum }_{{\omega }_1,{\omega }_2\in {\text{Ω}}_{a+b}}\text{E}[T_{{\omega }_1}]\text{E}[T_{{\omega }_2}].\end{array}$$ (32)

Subtracting this from the second moment gives

$$\begin{array}{l}\text{Var}[Y_a]\approx L\frac{\theta }{2}{m}_2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]\\ -L{\left(\frac{\theta }{2}\right)}^2{m}_1^2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}{[T_{\omega }]}^2\\ -2L{\left(\frac{\theta }{2}\right)}^2{m}_1^2{\displaystyle \sum }_{{\omega }_1,{\omega }_2\in {\text{Ω}}_{a+b}}\text{E}[T_{{\omega }_1}]\text{E}[T_{{\omega }_2}]\\ =L\frac{\theta }{2}{m}_2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]-L{\left(\frac{\theta }{2}{m}_1{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]\right)}^2\\ =L\frac{\theta }{2}{m}_2\text{E}[T_{MRCA}]-L{\left(\frac{\theta }{2}{m}_1\text{E}[T_{MRCA}]\right)}^2\\ \approx L\frac{\theta }{2}{m}_2\text{E}[T_{MRCA}].\end{array}$$ (33)

Due to the large number of terms we only derive the fourth moment of the trait value distribution for the case when the mean mutational effect is zero. The terms of (27) appearing in the fourth moment after we apply (29) are

$$L(\frac{\theta }{2})\frac{m_4}{24}{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]{({\displaystyle \sum }_{a\in \omega }{k}_a)}^4$$

for the fourth moment along one branch,

$$\left(\begin{array}{c}L\\ L-2,2,\mathbf{0}\end{array}\right){(\frac{\theta }{2})}^2{(\frac{m_2}{2})}^{2}24{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}{[T_{\omega }]}^2{({\displaystyle \sum }_{a\in \omega }{k}_a)}^4$$

for the second moment of the same branch chosen twice, and

$$\left(\begin{array}{c}L\\ L-2,1,1,\mathbf{0}\end{array}\right){(\frac{\theta }{2})}^2{(\frac{m_2}{2})}^{2}24{\displaystyle \sum }_{{\omega }_1,{\omega }_2\in {\text{Ω}}_{a+b}}\text{E}[T_{{\omega }_1}]\text{E}[T_{{\omega }_2}]{({\displaystyle \sum }_{a\in {\omega }_1}{k}_a)}^2{({\displaystyle \sum }_{a\in {\omega }_2}{k}_a)}^2$$

for the second moments on two different branches. Taking the fourth derivatives of these in terms of the desired branch, we get

$$\begin{array}{l}\text{E}[Y_a^4]=L\frac{\theta }{2}{m}_4\text{E}[T_{\text{MRCA}}]\\ +\frac{L\left(L-1\right)}{2}{\left(\frac{\theta }{2}\right)}^2{\left(\frac{m_2}{2}\right)}^{2}24{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}{[t_{\omega }]}^2\\ +L\left(L-1\right){\left(\frac{\theta }{2}\right)}^2{\left(\frac{m_2}{2}\right)}^{2}24{\displaystyle \sum }_{{\omega }_1,{\omega }_2\in {\text{Ω}}_{a+b}}\text{E}[T_{{\omega }_1}]\text{E}[T_{{\omega }_2}]\\ =L\frac{\theta }{2}{m}_4\text{E}[T_{\text{MRCA}}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2{\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]\right)}^{2}x\\ =L\frac{\theta }{2}{m}_4\text{E}[T_{\text{MRCA}}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\text{E}[T_{\text{MRCA}}]\right)}^2\\ \approx L\frac{\theta }{2}{m}_4\text{E}[T_{\text{MRCA}}]+3{\left(L\frac{\theta }{2}{m}_2\text{E}[T_{\text{MRCA}}]\right)}^2.\end{array}$$ (34)

The variance and the fourth moment derived in Equations 33 and 34 can be used to derive the kurtosis of $Y_a$. The kurtosis of a random variable X is defined as

$$\text{Kurt}[X]=\frac{\text{E}[{(X-\text{E}[X])}^4]}{\text{E}{[\left(X-\text{E}[X]\right)]}^2{]}^2}.$$

This is the fourth central moment divided by the variance. It is possible to calculate the kurtosis of a single trait value over evolutionary realization. For ease of calculation, we will examine this in the case where the mean mutation effect (and therefore trait value) is zero. If we plug (33) and (34) into the expression for the kurtosis we get

$$\begin{array}{l}\text{Kurt}[Y_a]=\frac{L\frac{\theta }{2}{m}_4\text{E}[T_{\text{MRCA}}]}{{\left(L\frac{\theta }{2}{m}_2\text{E}[T_{\text{MRCA}}]\right)}^2}+\frac{3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\text{E}[T_{\text{MRCA}}]\right)}^2}{{\left(L\frac{\theta }{2}{m}_2\text{E}[T_{\text{MRCA}}]\right)}^2}\\ =\frac{m_4}{L\frac{\theta }{2}{m}_2^2\text{E}[T_{\text{MRCA}}]}+\frac{3\left(L^2-L\right)}{L^2}\\ =\frac{\kappa }{L\frac{\theta }{2}\text{E}[T_{\text{MRCA}}]}+3\left(1-\frac{1}{L}\right).\end{array}$$

The expected fourth central moment of the within-population trait distribution under the low-mutation-rate approximation

To derive the expected fourth central moment of the within-population trait distribution, we first calculate some additional moments that have less clear interpretations but which are necessary. The first of these is $\text{E}[Y_a^3{Y}_b]$. The terms of (27) appearing in this are

$$L\left(\frac{\theta }{2}\right)\frac{m_4}{24}4k_a^3{k}_b{\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b}}\text{E}[T_{\omega }]$$

and

$$L\left(L-1\right){\left(\frac{\theta }{2}\frac{m_2}{2}\right)}^2{k}_a^2\times 2k_a{k}_b\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b}}\text{E}[T_{\omega }]\right)\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]\right).$$

This ultimately gives

$$E[Y_a^3{Y}_b]=L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[T_{MRCA}]\text{E}[{\tau }_{a+b}].$$ (35)

The next fourth moment of interest is $\text{E}[Y_a^2{Y}_b{Y}_c]$. The terms of (27) are

$$L\frac{\theta }{2}\frac{m_4}{24}12k_a^2{k}_b{k}_c{\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b+c}}\text{E}[T_{\omega }],$$

$$L\left(L-1\right){\left(\frac{\theta }{2}\frac{m_2}{2}\right)}^2{k}_a^2\times 2k_b{k}_c\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_a}\text{E}[T_{\omega }]\right)\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b}}\text{E}[T_{\omega }]\right),$$

and

$$L\left(L-1\right){\left(\frac{\theta }{2}\frac{m_2}{2}\right)}^{2}2k_a{k}_b\times 2k_a{k}_c\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b}}\text{E}[T_{\omega }]\right)\left({\displaystyle \sum }_{\omega \in {\omega }_{b+c}}\text{E}[T_{\omega }]\right).$$

Taking the appropriate derivatives of these gives

$$L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b+c}]+L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[T_{MRCA}]\text{E}[{\tau }_{b+c}]+2L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[{\tau }_{a+b}]\text{E}[{\tau }_{a+c}].$$ (36)

Individuals in the population are exchangeable as long as it is not structured. The pairwise expected shared branch lengths are, in that case, all equal, and we can write (36) as

$$L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b+c}]+L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[T_{MRCA}]\text{E}[{\tau }_{a+b}]+2L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}{[{\tau }_{a+b}]}^2.$$ (37)

The final moment we will look at is $\text{E}[Y_a{Y}_b{Y}_c{Y}_d]$ which has relevant terms

$$L\frac{\theta }{2}\frac{m_4}{24}24k_a{k}_b{k}_c{k}_d{\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b+c+d}}\text{E}[T_{\omega }],$$

$$L\left(L-1\right){\left(\frac{\theta }{2}\frac{m_2}{2}\right)}^{2}2k_a{k}_b\times 2k_c{k}_d\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+b}}\text{E}[T_{\omega }]\right)\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{c+d}}\text{E}[T_{\omega }]\right),$$

$$L\left(L-1\right){\left(\frac{\theta }{2}\frac{m_2}{2}\right)}^{2}2k_a{k}_c\times 2k_b{k}_d\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+c}}\text{E}[T_{\omega }]\right)\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{b+d}}\text{E}[T_{\omega }]\right),$$

and

$$L\left(L-1\right){\left(\frac{\theta }{2}\frac{m_2}{2}\right)}^{2}2k_a{k}_d\times 2k_b{k}_c\left({\displaystyle \sum }_{\omega \in {\text{Ω}}_{a+d}}\text{E}[T_{\omega }]\right)\left({\displaystyle \sum }_{\omega \in {\omega }_{b+c}}\text{E}[T_{\omega }]\right).$$

When the appropriate fourth order partial derivatives are taken, we get

$$\begin{array}{l}L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b+c+d}]\\ +L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[{\tau }_{a+b}]\text{E}[{\tau }_{c+d}]\\ +L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[{\tau }_{a+c}]\text{E}[{\tau }_{b+d}]\\ +L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[{\tau }_{a+d}]\text{E}[{\tau }_{b+c}].\end{array}$$

We can again simplify this expression for populations if we assume that individual are exchangeable. This gives

$$L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b+c+d}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}{[{\tau }_{a+b}]}^2.$$ (38)

The expected kurtosis in the population is a quotient of random variables and calculating a second order approximation requires calculating eight order moments of the trait distribution. Instead, we will calculate the expected fourth central moment.

$$\text{E}[M_{4,Y}]=\text{E}[\frac{1}{N}{{\displaystyle \sum }}^{\text{}}{\left(Y_i-\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}\right)}^4].$$ (39)

Examining the sum inside the expectation, we see that

$$\begin{array}{l}\text{E}[{\left(Y_i-\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}\right)}^4]=\text{E}[Y_i^4]-4\text{E}[Y_i^3\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}]+6\text{E}[Y_i^2{\left(\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}\right)}^2]-4\text{E}[Y_i{\left(\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}\right)}^3]+{\left(\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}\right)}^4\\ =\text{E}[Y_i^4]-\frac{4}{N}{\displaystyle \sum }_j\text{E}[Y_i^3{Y}_j]+\frac{6}{N^2}{\displaystyle \sum }_{j,k}\text{E}[Y_i^2{Y}_j{Y}_k]-\frac{4}{N^3}{\displaystyle \sum }_{j,k,l}\text{E}[Y_i{Y}_j{Y}_k{Y}_l]+\frac{1}{n^4}{\displaystyle \sum }_{j,k,l,d}\text{E}[Y_j{Y}_k{Y}_l{Y}_d].\end{array}$$ (40)

In calculating these expectations, we have to remember that the value depends only on the number of times each variable appears in the expectation. That is, $\text{E}[Y_1^2{Y}_2{Y}_3]$ is equivalent to $\text{E}[Y_1{Y}_2^3{Y}_3]$ as long as all individuals in the population are exchangeable. The resulting expansion of (40) can be simplified by only considering terms of order one. Other terms can be ignored since we are assuming there are a large number of individuals in the population. This yields

$$\begin{array}{l}\text{E}[{\left(Y_i-\frac{{{\displaystyle \sum }}^{\text{}}{Y}_j}{N}\right)}^4]=\text{E}[Y_i^4]-\frac{4\left(n-1\right)}{n}\text{E}[Y_i^3{Y}_j]+\frac{6\left(n-1\right)\left(n-2\right)}{n^2}\text{E}[Y_i^3{Y}_j{Y}_k]\\ -\frac{4\left(n-1\right)\left(n-2\right)\left(n-3\right)}{n^3}\text{E}[Y_i{Y}_j{Y}_k{Y}_l]\\ +\frac{\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)}{n^4}\text{E}[Y_j{Y}_k{Y}_l{Y}_d]+O\left(n^{-1}\right)\\ \approx \text{E}[Y_i^4]-4\text{E}[Y_i^3{Y}_j]+6\text{E}[Y_i^2{Y}_j{Y}_k]-3\text{E}[Y_i{Y}_j{Y}_k{Y}_l].\end{array}$$ (41)

The first term, $\text{E}[Y_i^4]$ was derived in Equation 34 as

$$L\frac{\theta }{2}{m}_4\text{E}[T_{\text{MRCA}}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\text{E}[T_{\text{MRCA}}]\right)}^2.$$

The second term, $\text{E}[Y_i^3{Y}_j]$ was derived in Equation 35 as

$$L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[T_{\text{MRCA}}]E[{\tau }_{a+b}].$$

The third term, $\text{E}[Y_i^2{Y}_j{Y}_k]$ was derived in Equation 36 as

$$L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b+c}]+L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}[T_{\text{MRCA}}]\text{E}[{\tau }_{a+b}]+2L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}{[{\tau }_{a+b}]}^2.$$

The fourth term, $\text{E}[Y_i{Y}_j{Y}_k{Y}_l]$ was derived in Equation 38 as

$$L\frac{\theta }{2}{m}_4\text{E}[{\tau }_{a+b+c+d}]+3L\left(L-1\right){\left(\frac{\theta }{2}{m}_2\right)}^2\text{E}{[{\tau }_{a+b}]}^2.$$

Plugging these into (41) we get

$$\begin{array}{l}\text{E}[M_4]\approx L\frac{\theta }{2}{m}_4\left(\text{E}[T_{\text{MRCA}}]-4\text{E}[{\tau }_{a+b}]+6\text{E}[{\tau }_{a+b+c}]-3\text{E}[{\tau }_{a+b+c+d}]\right)\\ +3{\left(L\frac{\theta }{2}{m}_2\right)}^2{\left(\text{E}[T_{\text{MRCA}}]-\text{E}[{\tau }_{a+b}]\right)}^2.\end{array}$$ (42)

With some simple manipulation this can be rewritten in terms of ${\mathrm{핋}}_{k,n}$ to give

$$\begin{array}{l}\text{E}[M_4]=3{\left(L\frac{\theta }{2}\text{E}[{\mathrm{핋}}_{2,2}]m_2\right)}^2+L{m}_4\frac{\theta }{2}\left(\text{E}[{\mathrm{핋}}_{4,4}]+\frac{1}{3}\text{E}[{\mathrm{핋}}_{3,4}]+\frac{2}{9}\text{E}[{\mathrm{핋}}_{2,4}]\right).\end{array}$$ (43)

This expression should be compared to Equation 7c in the main text. We get the same result if we ignore terms of order $L{\left(\frac{\theta }{2}\right)}^2$