Complex Trait Prediction from Genome Data: Contrasting EBV in Livestock to PRS in Humans

Genomic estimated breeding values (GEBVs) in livestock and polygenic risk scores (PRS) in humans are conceptually similar; however, the between-species differences in linkage disequilibrium (LD) provide a fundamental point of distinction that impacts approaches to data analyses...

Abstract

In this Review, we focus on the similarity of the concepts underlying prediction of estimated breeding values (EBVs) in livestock and polygenic risk scores (PRS) in humans. Our research spans both fields and so we recognize factors that are very obvious for those in one field, but less so for those in the other. Differences in family size between species is the wedge that drives the different viewpoints and approaches. Large family size achievable in nonhuman species accompanied by selection generates a smaller effective population size, increased linkage disequilibrium and a higher average genetic relationship between individuals within a population. In human genetic analyses, we select individuals unrelated in the classical sense (coefficient of relationship <0.05) to estimate heritability captured by common SNPs. In livestock data, all animals within a breed are to some extent “related,” and so it is not possible to select unrelated individuals and retain a data set of sufficient size to analyze. These differences directly or indirectly impact the way data analyses are undertaken. In livestock, genetic segregation variance exposed through samplings of parental genomes within families is directly observable and taken for granted. In humans, this genomic variation is under-recognized for its contribution to variation in polygenic risk of common disease, in both those with and without family history of disease. We explore the equation that predicts the expected proportion of variance explained using PRS, and quantify how GWAS sample size is the key factor for maximizing accuracy of prediction in both humans and livestock. Last, we bring together the concepts discussed to address some frequently asked questions.

IN this Review we contrast polygenic risk score (PRS) used in human genetics (Wray et al. 2007; Evans et al. 2009; Purcell et al. 2009; Chatterjee et al. 2016; Torkamani et al. 2018) to the estimated breeding values (EBVs) used in livestock genetics (Henderson 1975; Meuwissen et al. 2001; Brotherstone and Goddard 2005; de los Campos et al. 2010). Our intended target audiences are researchers from either field, and we try to provide the key information that, from our experience, bridges the knowledge between experts from either domain. Our livestock focus is dairy cattle, but the points raised mostly transfer across species. Understanding the between-species differences in linkage disequilibrium (LD, the local correlation structure within the genome) is the fundamental point of distinction, and this is driven by differences in effective population size, which, in turn reflect differences in family size. We provide a brief history of PRS and EBV methods, and contrast the difference in approaches for estimating SNP effect sizes. Next, we consider accuracy of out-of-sample prediction of PRS for which we find the theoretical expectations of prediction accuracy under-recognized by practitioners. Last, we discuss the concept of within-family variation, which despite being an essential feature of the conceptualization of polygenic traits since Fisher (1918), and despite being the key force underlying selection paradigms in crops and livestock, seems to us to be underappreciated in human genetics as the driving force of polygenic variation across generations. Traditionally, genetically informative data sets have been larger for livestock than human data sets, but this is starting to change. Taken together our perspective leads to a discussion of four frequently asked questions (FAQ).

A Brief History of PRS and genomic EBV

The breeding value (BV) of an individual for a given trait is its aggregate additive genetic value, of which the individual passes, on average, half to his or her offspring (“half,” because the offspring only receive a random exact half of the parent’s DNA complement; “on average,” because the genetic value associated with the inherited DNA may deviate from the average based on the segregation sampling). In theory, this could be computed from the genotypes of the individual at all loci affecting the trait using knowledge of the average effect of each allele at these loci. That is, it is a linear function of the genotypes (x = 0,1,2 trait increasing alleles) multiplied by average effect of the trait increasing effect of each allele (b), i.e., $BV= {\displaystyle \sum _i{b}_i{x}_i}$.

In practice, we do not know the loci that affect a trait, nor their effect sizes, so we must estimate the breeding value of each individual. In livestock genetics, traditionally this was done by using the phenotype of the individual together with phenotypes of its relatives. Now that SNP chip data have become available, these pedigree EBVs can be supplemented with information from genomic data, generating genomic EBVs (GEBVs). The GEBV can be calculated as a linear function of the SNP genotypes weighted by the apparent effect of each genotype on the trait. It is not assumed that the polymorphisms assayed by the SNP chip cause variation in the trait, but that they are correlated (in LD) with unknown causal variants.

A PRS is the same as a GEBV, that is, it is a linear function of the SNP genotypes (or other DNA variants), each weighted by the apparent effect of that SNP. In humans, interest mostly focuses on disease traits, hence the “risk” paradigm. The apparent effect of each DNA variant can be estimated from an association analysis in a discovery sample of individuals that have been assayed for the DNA variants and recorded for the phenotype. Since we want the PRS to reflect as much genetic variation as possible, SNP effect sizes are estimated in genome-wide association studies (GWAS).

There is a fundamental difference in purpose between prediction in humans and in livestock: in humans the purpose is to predict the future phenotype of an individual, whereas in livestock the purpose is (usually) to predict the average value of an animal’s genetic material to its offspring. Inherently therefore, understanding of EBV or GEBV focuses on the average of a group, i.e., the average of the offspring of the individual. The units of EBV/GEBVs are the units of the trait, e.g., deviation of liters of milk expected in the offspring compared to the offspring from the base or reference population. PRS could be presented in trait units, but are mostly presented in SD units of an unselected or control sample. In human genetics, although the goal for PRS is prediction of the phenotype, the accuracy of prediction for an individual is low (see below); hence, the value of PRS is, like in livestock genetics, best interpreted at the group level. The area under the receiver operator characteristic curve (AUC) is one statistic used to evaluate the accuracy of PRS for disease. AUC ranges from 0.5 (random prediction) to 1 (perfect prediction) and can be interpreted as the probability that a randomly selected disease-affected individual ranks higher than a randomly selected nonaffected individual. For example, the AUC for coronary artery disease (CAD) based on PRS was estimated as 0.81 [95% confidence interval (CI) 0.80–0.81], with the top 10% based on PRS having 2.89-fold the risk of the average risk of the rest of the population (Khera et al. 2018). It is noteworthy that these results also include age, sex, genotyping array, and four ancestry informed principal components (PCs) in the predictive model. Another study also generated PRS for CAD based on similar GWAS summary statistics data, and, like the study of Khera et al. (2018), used the UK Biobank cohort (but subsetted slightly differently) to evaluate efficacy (Inouye et al. 2018). They quantified AUC as 0.79, which was a 2.8% gain over a baseline model that included sex, baseline age, genotyping array, and 10 PCs.

The concepts that underpin what we now call PRS and GEBV were published in two landmark GENETICS papers. Russell Lande and Robin Thompson (Lande and Thompson 1990) recognized that genome-wide LD between measured DNA variants (markers) and loci causally influencing variation between individuals (quantitative trait loci or QTL) could be exploited for selection. They introduced the concept of a “molecular score,” as the sum of the additive effects on the character associated with the markers (i.e., GEBV or PRS). At that time, the measurable DNA variants were restriction fragment length polymorphisms (RFLPs), yet the authors introduced the concepts of GWAS followed by selection of the most associated markers. They discussed the need for unbiased estimates of effect sizes (since effect size estimates from GWAS of the most significantly associated loci are always overestimated owing to what is referred to as winner’s curse in human genetics or the Beavis effect in livestock genetics). Lande and Thompson estimated how many markers would be needed to represent the variation in the genome when LD is created by drift (as a result of finite effective population size), which provides theoretical justification for the very different numbers of SNPs included on human (500,000–1,000,000) compared to cattle (50,000) SNP chip arrays. In cattle, denser SNP arrays are needed for crossbreed prediction.

The second landmark paper, a decade later from Meuwissen et al. (2001), provided additional theory and predicted the arrival, and implications for use, of dense SNP arrays. They considered methods to estimate SNP effects, acknowledging issues of winner’s curse, and the problem of estimability, because the number of markers is usually greater than the number of individuals. They considered least squares (without P-value thresholding), best linear unbiased prediction (BLUP), and Bayesian methods to estimate marker effects and considered different genetic architectures in simulation scenarios.

The Illumina Bovine SNP50 chip became available in 2008. The rate of uptake of so-called genomic selection in the dairy industry has been astounding, and, by 2015, over 1 million Holstein cattle (black and white) had been genotyped, and by 2018 this exceeded 2.2 million (https://queries.uscdcb.com/Genotype/counts.html). Evaluation of the 7-year implementation of genomic breeding values in the US found that annual genetic improvement had increased by ∼100% for milk production traits and 300–400% for low heritability fertility traits (García-Ruiz et al. 2016). These changes reflect reduced generation interval (e.g., from 7 to <2.5 years for sires of bulls) achieved through the ability to use DNA variants to select between 1-year old bulls based on GEBVs before they have daughters whose milk yield can be assessed. That is, the GEBV accurately predict which of the sons have received the best combination of DNA variants in the genetic segregation sampling from their parents.

In human genetics, the GWAS era is benchmarked by the Wellcome Trust Case Control Consortium study (Wellcome Trust Case Control Consortium 2007) published in 2007. In the months before its publication, there was great excitement and expectation about what this study would deliver; the sample sizes of 2000 cases per disease with 3000 controls were unprecedented. At this time, we (based on our understanding of polygenic traits from nonhuman species) were less confident about what GWAS would deliver in terms of individual variant discovery, but hypothesized about the value of PRS for community health disease prevention programs (Wray et al. 2007, 2008). We conducted a simulation study (Wray et al. 2007) to investigate the use of PRS prediction for common disease, concluding “Our study shows that prediction of genetic risk is possible, even if there are hundreds of risk variants each of small effect.” and “The value of these predictive SNPs could be reaped long before the causal mechanism of each contributing variant can be determined.” Others (Collins et al. 2003; Bell 2004; Khoury et al. 2006; Kathiresan et al. 2008; Pharoah et al. 2008) had introduced the concept of multi-SNP genetic profiling, but the only previous study that considered genome-wide profiling (Janssens et al. 2006) assumed in simulations that all risk loci are known, and hence the key determinant of the efficacy of risk prediction was missing (i.e., the need to estimate effect sizes). Given the number of DNA variants in the genome, the accuracy of PRS depends on the accuracy with which effect sizes are estimated, and the extent to which true and false positives are separated.

Methods of Estimating the Apparent Effect of DNA Variants

A GEBV is like a multiple regression equation with a very large number of predictors (i.e., SNPs or other DNA variants), which is currently often larger than the number of individuals in the discovery dataset. These effects can be estimated by fitting them all jointly but treating the effects as random variables drawn from some specified distribution. If all the effect sizes are assumed to be drawn from the same normal distribution, then the method is BLUP. Other commonly used distributions are a mixture of normal distributions including a proportion with zero effect. These mixture models are usually included in Bayesian models implemented by Markov chain Monte Carlo methods (Habier et al. 2011).

By contrast, the effect sizes for a PRS are commonly estimated by fitting one SNP at a time, ignoring all other SNPs. When we conducted our 2007 simulation study (Wray et al. 2007), we made decisions that we knew were not optimal, but our approach was very different from the thinking of the time. One decision was to use a fairly stringent association P-value threshold for selection of SNPs for use in calculation of PRS. However, when the first opportunity arose to apply the method to real GWAS data (Purcell et al. 2009), we investigated much more relaxed P-value thresholds for generating PRS. We (led by Shaun Purcell) (Purcell et al. 2009) showed by simulation that the optimum P-value threshold to impose on the discovery sample, depends on its sample size and the genetic architecture of the trait (see figure S8 of Purcell et al. 2009). The now “standard” PRS method follows that initial application, and is based on selecting SNPs from a GWAS analysis based on LD pruning/clumping and P-value thresholding. However, both the clumping and thresholding steps are somewhat arbitrary, and reporting the results from the P-value threshold that maximizes out-of-sample prediction in a single cohort is a form of Winner’s curse. Ideally, out-of-sample prediction results should report average results across many cohorts, e.g., (Schizophrenia Working Group of the Psychiatric Genomics Consortium 2014; Wray et al. 2018). In 2007, we knew [based on results from Meuwissen et al. (2001)] that standard human GWAS one-SNP-at-a-time regression was not the optimal way to estimate SNP effects for use in prediction. The reason one-SNP-at-a-time regression is used in human genetics is because the primary goal of GWAS is the identification of trait-SNP associations to better understand the underlying biology of the trait; SNPs that are highly correlated to each other all have similar effect sizes. In BLUP, individual SNP effect estimates may be small if there are many SNPs in high LD with each other and the causal variant, as the effect of the causal variant is “shared” across the correlated variants. Other methodologies for estimating PRS, such as those commonly used for GEBVs, have been investigated (de los Campos et al. 2013; Abraham et al. 2014; Golan and Rosset 2014; Moser et al. 2015; Vilhjálmsson et al. 2015). In real and simulated human and livestock data, the methods that fit all SNPs simultaneously usually generate more accurate out-of-sample prediction than those fitting one SNP at a time, and the Bayesian mixture models are usually better than BLUP. However, the increases in accuracy are sometimes small, except when the trait has some variants of larger effect. Accuracy can also be increased by methods that increase discovery sample size by “borrowing” sample size from correlated GWAS of larger sample size (Li et al. 2014; Maier et al. 2015, 2018; Turley et al. 2018). Multivariate approaches have been used for decades in livestock, particularly in the context of selection based on an index of many traits predicting a trait of economic importance (Hazel 1943).

Accuracy of Out-of-Sample Prediction

The ultimate aim of the PRS is to predict a phenotype in individuals who do not have a recorded phenotype, or who have not yet had the opportunity to experience the phenotype. The efficacy of PRS is evaluated using a group of individuals that were not included in the discovery dataset but have the phenotype recorded. The efficacy of a PRS is well understood from theory (Daetwyler et al. 2008; Visscher et al. 2010; Wray et al. 2013; Dudbridge 2013; Pasaniuc and Price 2017), yet understanding the expected increase in the proportion of variance explained $\left(R^2\right)$ in out-of-sample prediction seems less well recognized in human genetics applications compared to livestock genetics. $R^2$ is defined here as the squared correlation between a phenotype $\left(y\right)$ and a predictor of the phenotype $\left(\widehat{y}\right)$, i.e., the PRS,

$$R^2= \frac{cov{\left(y,\widehat{y}\right)}^2}{var\left(y\right)var\left(\widehat{y}\right)}$$

It has been shown (Daetwyler et al. 2008; Visscher et al. 2010; Wray et al. 2013; Pasaniuc and Price 2017) that expected $R^2, E\left(R^2\right)$, depends on sample size (N), the number of independent SNPs whose effect sizes are estimated (M), and the proportion of phenotypic variance associated with those SNPs, $h_M^2$.

$$E\left(R^2\right)\approx \frac{h_M^2}{1+M/\left(N{h}_M^2\right)}$$ (1)

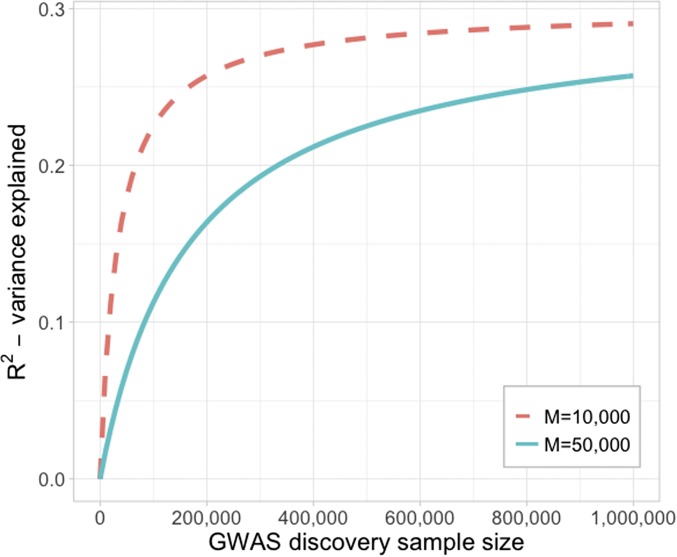
Let us explore this relationship in detail. First, as N increases $M/\left(N{h}_M^2\right)$ tends to zero, so $R^2$ tends to $h_M^2$, providing an upper bound for $R^2$; hence, PRS are not fully accurate diagnostic predictors for individuals (as they only predict the component of phenotype captured by the SNPs). If the predictor is built from all genome-wide SNPs then M is the number of independent SNPs (or the effective number of SNPs). M can be estimated as the total number of SNPs divided by the mean LD score of the SNPs (Yang et al. 2011b), where LD score for a SNP is defined as the sum of LD r² with other SNPs, including itself (usually calculated within a defined genomic distance window). Assuming SNPs have frequency >1%, then M∼50,000 in humans (compared to only ∼5000 in dairy cattle), and $h_M^2$ is the SNP-based heritability. The SNP-based heritability is the proportion of phenotypic variance captured by SNPs in LD with the causal mutations affecting the phenotype (as discussed below, this is a more difficult concept in livestock than in human genetics because of the high LD across the genome). Hence, while heritability is the theoretical upper bound for the $R^2$ of a genetic predictor, SNP-based heritability is the upper limit of $R^2$ for PRS based on common SNPs. Even when SNP-based heritability is high, out-of-sample prediction $R^2$ is expected to be low, unless discovery sample sizes are massive. As shown in the derivations for the estimate of SNP-based heritability using LD Score method (Bulik-Sullivan et al. 2015), SNP-based heritability can be approximately estimated as a regression between association test statistics and LD scores of each SNP. This regression coefficient can be estimated with a high degree of accuracy because so many SNPs contribute to the estimate of a single statistic. However, for out-of-sample prediction, individual SNP effects need to be estimated with accuracy. We need to estimate effect sizes of all SNPs, both those truly associated (i.e., causal variants and SNPs correlated with causal variants) and those that are not. For example, when $h_M^2$ = 0.3 and discovery sample size is N = 50,000 then the expected $R^2$ in out-of-sample prediction is only ∼7%. Doubling the discovery sample size to 100,000 increases the $R^2$ to 11% (Figure 1). Very large sample sizes are needed to achieve $R^2$ that approach $h_M^2$, because the massive number of SNPs in the genome whose effects sizes must be estimated, i.e., M. P-value thresholding, or statistical methods that attempt to exploit genetic architecture to reduce the number of SNPs used to generate the PRS, e.g., LDpred (Vilhjálmsson et al. 2015), can be interpreted as ways to reduce M. However, in such approaches, some of the true signal tagged by the SNPs will be lost so that the $h_M^2$ is also reduced. Hence, these methods can be interpreted as trying to find a M vs. $h_M^2$ combination that maximizes $R^2$. A common pitfall is to substitute into Equation 1 the estimate of the causal number of SNPs, but this overlooks the key difficulty in real data analysis, which is the accurate estimation of SNP effect sizes for both truly associated and truly not associated variants.

Figure 1.

Variance explained in out of sample prediction. Using Equation 1, we assume $h_M^2$ = 0.3 associated with common variants of frequency >0.1. In humans, the effective number of markers whose effect sizes are estimated is M∼50,000. Discovery sample GWAS of >1 million people are needed to achieve out-of-sample that achieves $R^2$ approaching the upper limit of $h_M^2$. The red line bench marks out of sample prediction for M∼10,000, representative of a species with a smaller effective population size, or if, in humans, we achieve statistical methodologies that allow identification of a smaller number of DNA variants associated with the same $h_M^2$.

Whole genome sequence (WGS) data will become cheaper to generate. As a result, we expect that estimates of $h_M^2$ will increase as the minor allele frequency threshold for SNP inclusion decreases, but accompanied by an even greater increase in the M contributing to it. We can make an informed guess (based on unpublished analyses) that WGS data in human populations may imply M as high as 500,000, i.e., a 10-fold increase compared to common SNP array data. This increased representation of genomic variation likely increases the associated genetic variation captured, such that $h_M^2$ might approach heritability estimated from family phenotypic records. So in our example above for SNP-array data, we used $h_M^2$ = 0.3, which, with WGS data, might be $h_M^2$ = 0.6. Then, for the sample size of 100,000 people, using Equation 1, we expect $R^2$ to decrease from 11% to 6% from use of SNP-array to WGS data! These calculations are made under the infinitesimal model. Hence, to take advantage of the increased $h_M^2$ captured by WGS, we will need methods that reduce the number of variants whose effect sizes are estimated, i.e., reduce M, while maintaining high $h_M^2$, for example, using genomic annotation, e.g., LD-pred-funct (Marquez-Luna et al. 2018).

For case-control studies, Equation 1 is a good approximation for liability $R^2$ using the effective sample size equivalent to having equal numbers of cases and controls, i.e., N = 4*P(1−P)N_TOT (where N_TOT is the sum of numbers of cases and controls and P is the proportion of cases) (Yang et al. 2010b), but more accurate equations have been derived (Lee and Wray 2013). Predictions from Equation 1 agree well with the observed results. For example, for height: N = 700,00, $h_M^2$ = 0.246, M = 50,000, $R^2$ expected is 0.19, and the observed out-of-sample $R^2$ = 0.19, (reported as R = 0.44) (Yengo et al. 2018). Similarly, for schizophrenia: 36,989 cases and 113,075 controls, N_TOT = 111,487, $h_M^2$ = 0.23 (Cross-Disorder Group of the Psychiatric Genomics Consortium et al. 2013), M = 50,000, $R^2$ expected is 0.08, observed out-of-sample liability $R^2$ = 0.07 (Schizophrenia Working Group of the Psychiatric Genomics Consortium 2014).

In human genetics applications, in evaluation of the efficacy of PRS it is important to check that the test sample is independent of the sample that is used for GWAS discovery, as sample overlap (direct or through relatives) will inflate the variance explained in out-of-sample prediction. However, when applying PRS in out-of-sample prediction when the phenotype is unknown, having relatives in the discovery sample is desirable as this will improve the prediction for an individual (Lee et al. 2017). Indeed, for disease traits, family history of disease can be used as an additional predictor, as this may incorporate genetic and nongenetic factors not captured by the PRS (Do et al. 2012; Inouye et al. 2018). In livestock data sets, it is not usually possible for the target sample to be independent of the discovery sample because of the small effective population size. In livestock GEBV evaluations, individuals without phenotypes are included in the mixed model equations, connected to those with phenotypes through the genomic relationship matrix that describes the variance–covariance structure between breeding/genetic values. In human genetics applications this approach is unlikely to be adapted, since the largest discovery samples for diseases will only be available as GWAS summary statistics.

The Consequences of Recent Effective Population Size

The fundamental difference between livestock and human genomes is the difference in effective population size (N_e). In most livestock populations in developed countries most individuals make no long-term genetic contribution to the population. Instead, nearly all the genes in the future population come from a small nucleus leading to small N_e. This breeding structure is easy to implement if family sizes are large. In dairy cattle, for example, as a consequence of artificial insemination, bulls can have 100,000s of offspring [Toystory (https://en.wikipedia.org/wiki/Toystory_(bull)] sired >500,000 daughters], having been selected for their genetic merit for milk production traits (which, of course, are traits they do not even express themselves). Traditionally, EBVs were calculated based on records of daughters and other female relatives. Given the large number of daughters with milk production records, EBVs can be a very accurate representation of the bull’s genetic value. EBVs have been used for decades to identify which individuals should be chosen as the parents of the next generation. Even high-producing elite cows can have large numbers of offspring through egg harvesting and in vitro fertilization technology. Hence, the number of parents needed is small relative to the population census, leading to high selection intensities. For example, the international black and white Holstein dairy cattle population is ∼25 million but the current effective population size (N_e) is estimated to be only ∼50 (Kim and Kirkpatrick 2009) to ∼100 (Bovine HapMap Consortium et al. 2009).

The large family size and small N_e in livestock species has a number of knock-on effects relevant to comparisons with humans. First, haplotype blocks are large. For dairy cattle, they are about double the length of human LD (26 kb vs. 8–14 kb) (Kim and Kirkpatrick 2009) [within breed LD in dairy cattle stretches to 0.5 Mb (Bovine HapMap Consortium et al. 2009), and generates LD across chromosomes], and this impacts on all aspects of analyses of genomic data. Second, the concept of SNP-based heritability is different in livestock (Jensen et al. 2012). In human genetic analyses where interest is understanding genetic architecture of a trait and the additive genetic contribution to variation, we select individuals unrelated in the classical sense (coefficient of relationship from the genomic relationship matrix (GRM) estimates from SNP data <0.05) and use these individuals to determine the proportion of variance associated with common genome-wide SNPs (i.e., SNP-based heritability) (reflecting LD between common SNPs and causal variants). SNP-based heritability is conceptually different from (and smaller than) heritability estimated from family/pedigree data, as the latter includes contributions to variation from genetic variants that are less common in the population (not tagged by common SNPs), but are shared between relatives. SNP-based heritability estimated from summary statistics using LD Score regression (Bulik-Sullivan et al. 2015) also only captures the genetic signal associated with common variants. In analyses of livestock data, all animals within a breed are to some extent “related” and so it is not usual (or possible) to try to select unrelated individuals for an analysis. An alternative is to fit two genetic effects in the statistical model, one described by the GRM and one described by pedigree relationships (Haile-Mariam et al. 2013; Zaitlen et al. 2013; Kemper et al. 2015). When this is done, 80–90% of the genetic variance in milk yield is explained by the SNPs (Haile-Mariam et al. 2013; Kemper et al. 2015). The higher proportion of genetic variance explained by SNPs in livestock than in humans is due to the greater LD in livestock.

Big Data in Humans and Livestock

For human research, we are entering a disruptive data era, for example, the 500,000 UK Biobank (Sudlow et al. 2015) is an unprecedented resource for genetics and epidemiology research. The All of Us study (https://allofus.nih.gov/) aims to collect data on 1 million people. In livestock, even larger datasets have been common for several decades, but until recently they did not include DNA data. The desire to obtain EBVs for dairy bulls for female-linked milk production traits was a catalyst for complex worldwide data collection systems for milk production records. This was painstakingly paper-based when first introduced [in 1908 in the US (https://www.aipl.arsusda.gov/aipl/history/hist_eval.htm)], but is now very high tech, with each cow tagged with a transponder that directly records milk production and activity, and controls access to food on some farms. Farm managers can review herd and individual records from their smart phones. The US Council of Dairy Cattle Breeding has ∼60 years of records on 31 million cows for use in evaluation (https://queries.uscdcb.com/Genotype/counts.html), and a number of other countries have databases of similar magnitude. The long-term, longitudinal, and high-tech data collection systems to which we aspire for improved population health have already underpinned advanced statistical analyses. The masses of data available in livestock evaluations, and with close relatives found across different environmental settings, means that genetic and nongenetic factors can be well-separated in linear mixed models, and a complex array of covariates can be fitted. Maternal and cytoplasmic/mitochondrial effects models (Southwood et al. 1989), and random regression models (Kirkpatrick et al. 1990) for repeated-measure longitudinal data have been used for many years (Meyer 1998) (including complexities of annual milk production distributions based on daily recordings). Recognizing that so-called environmental covariates are themselves complex traits, reaction norm models have been used to model jointly genotype-environment interaction and genotype-environment correlation (Meyer 1998). Such analyses can now be attempted with data sets like the UK biobank (Robinson et al. 2017; Beaumont et al. 2018; Ni et al. 2018), but it will be a long time before we have human complex disease data sets that can really benefit from these statistical methods. Human researchers sometimes assume that livestock are measured in environmentally controlled conditions, and can be surprised that livestock data sets can encompass complex environmental measures. In contrast, researchers not familiar with human data can be taken aback that often the only covariates in such data sets are age and sex. On the other hand, human disease data sets bring challenges not arising in livestock analyses, resulting from binary case/control data with oversampling of cases. In the fields of both human and livestock genetics, there are discussions about whether deep phenotyping of smaller samples is preferential to shallower phenotyping in large samples, but, in general, technologies allow both large samples and adequate phenotyping. The UK Biobank (UKB) study has demonstrated the value of having a single large cohort collected in a consistent way. For example, published meta-analyses of 257,000 people for height (Wood et al. 2014) and 339,000 people for body mass index (BMI) (Locke et al. 2015) identified 594 and 82 independent genome-wide significant loci, respectively. In contrast, GWAS of the UKB cohort using 250,000 people identified 850 and 160 GWS loci, for height and BMI, respectively (Yengo et al. 2018).

While, traditionally, livestock data sets have been bigger and phenotypically richer than human data sets, SNP array data sets are of more comparable sizes. As biobank and crowd-sourced studies accumulate recruited participants, and exploit smart phone data collection, human data sets will overtake livestock data sets in size, phenotypic depth and longitudinal breadth. The user-friendly tools developed in human genetics [e.g., Principal Component analysis software (Price et al. 2006), PLINK (Purcell et al. 2007), GCTA (Yang et al. 2011a)] are already being actively used by the livestock genetics community. Methodology for exploiting association summary statistics (Pasaniuc and Price 2017) has been a fertile field of research in human genetics recently, and allows prediction gain from large discovery samples without the need to share primary level data. The key feature is that the association results can be interpreted by superimposing a genomic LD correlation structure derived from an external reference sample. These methods are computationally efficient and avoid problems associated with sharing of primary level data (which depends on privacy and consent in human populations, and commercial sensitivity in livestock populations). There has been little interest, to date, in livestock genetics with regard to use of summary statistics, but this may be a fruitful area for future research, at least in some species.

Understanding and Appreciating Within Family Segregation Variance

The genetic variance among offspring achieved through the random samplings of their parents’ genomes is the key source of variation exploited in agricultural selection programs. Since family sizes can be large in livestock (and crop) breeding programs, variation among offspring within a family is observed and tangible. However, in human genetics, it seems to us, that this key source of variation is not fully recognized, despite being an essential part of the biometric model used since Fisher (1918), perhaps because human family sizes are relatively small. It goes without saying that each child receives exactly half of its genetic material from each parent, and that each child receives a different sample of each parent’s genome. Hence, we can attribute the genetic value of a child $\left(A_{\text{child}}\right)$ as the mean genetic value of its parents $\left(\left(A_{\text{dad}}+A_{\text{mum}}\right)/2\right)$, plus a deviation from the mean that is specific to that child $\left(A_{\text{seg}}\right)$

$$A_{\text{child}}=\left(A_{\text{dad}}+A_{\text{mum}}\right)/2+A_{\text{seg}}$$

We can then consider the variance of genetic values of the generation of children as,

$$V\left(A_{\text{child}}\right)=V\left(A_{\text{dad}}\right)/4+V\left(A_{\text{mum}}\right)/4+V\left(A_{\text{seg}}\right)$$ (2)

There are no covariance terms, because for simplicity we assume random mating so $A_{\text{dad}}$ and $A_{\text{mum}}$ are independent, and the segregation term (as a deviation from the parental average) is also independent. Next, we can assume that the genetic variance among the individuals of the children’s generation is the same as among their parents, and genetic variance among the mothers is the same as among the fathers. Moreover, all variances are simply the additive genetic variance of the population, $V\left(A\right)$, i.e., $V\left(A_{\text{child}}\right)=V\left(A_{\text{dad}}\right)=V\left(A_{\text{mum}}\right)=V\left(A\right)$.

Then, substituting these into Equation 2 and rearranging, gives

$$V\left(A_{\text{seg}}\right)=V\left(A\right)/2$$

This well-known result is fundamental to understanding genetic variation in populations. Half the genetic variance in populations is derived from segregation of genomes within families, this seems underappreciated, but is jaw-dropping for its implications. Let us consider the properties of segregation variance. First, it is not reduced by selection of the parents [which reduces V$\left(A_{\text{dad}}\right)$ and V$\left(A_{\text{mum}}\right)$ in Equation 2]. In other words, however strong the selection is on parents, a pair of parents still generate a lot of genetic variation among their offspring. Segregation variance is reduced a little by inbreeding (in a population it reduces proportionally by a factor of (1−F), where F is the mean inbreeding coefficient in the parent generation in the population), but this is counter-balanced, in part, by new mutations. It is noteworthy that some model species have been inbred to the extent that no within family segregation variance remains, except where this has been generated by new mutations. The lack of between-individual variation is a key reason why the relevance of mouse models for human disease is being increasingly questioned (Cavanaugh et al. 2014). From an experimental design perspective, inbred lines remove uncontrolled variation, and hence reduce sample sizes needed for powered studies. However, in humans, the essence of polygenic disease is that many variants contribute to risk, and that there are many combinations of DNA variants that lead to the same disease diagnosis. Research paradigms are needed that embrace the nature of polygenic disease. In the past, such paradigms were difficult to achieve, but technological advances mean that new avenues are opening.

Selection Experiments Demonstrate the Power of Segregation Variance

For almost a century, the nature of genetic variation was described statistically, but could not be directly measured. Selection experiments became the tool to verify the validity of the statistical models. Observed responses could be compared to those expected by inference from the statistical theory. Documented selection experiments began in 1896 for maize and the early 20th century for chickens (Hill 2011) and became a standard tool in genetics research midcentury. In 1980, Bill Hill laid down (Hill 1980) the many motivations for selection experiments, and then, 30 years later (Hill 2011), asked “Can more be learned from selection experiments of value in animal breeding programmes? Or is it time for an obituary?.” He concluded, that while “There can be little argument that selection experiments have greatly added to our understanding of quantitative genetic and selection principles,” that the lessons had been learned and that it was indeed time for an obituary. We agree with the conclusion, but highlight this work to increase exposure to those lessons.

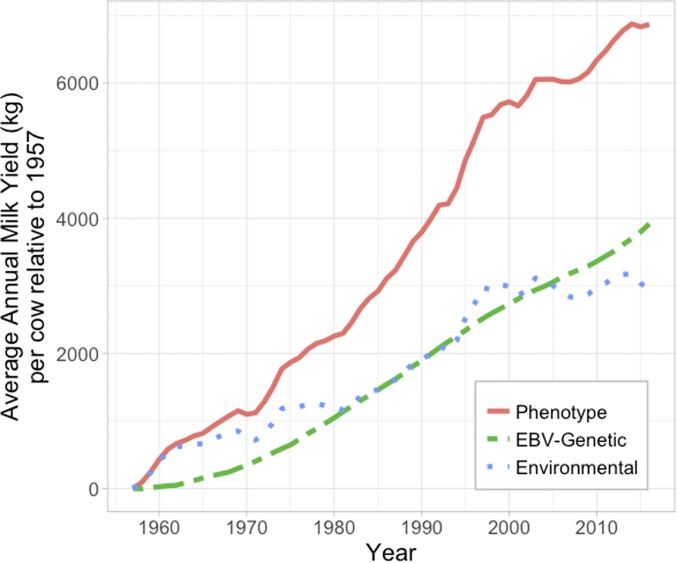
Selection programs shed light on many aspects of theory and genetic architecture (Hill 1980, 2011; Hill and Caballero 1992; Brotherstone and Goddard 2005). A key lesson of selection programs and selection experiments is the clear demonstration of the importance of segregation variance. While segregation variance has been studied in humans to estimate genetic variance based by relating phenotypic differences between full-sibs with their coefficients of relationship estimated from genome-wide SNP data (which range from ∼0.4 to ∼0.6) (Visscher et al. 2006; Kong et al. 2018), the studies are few because of the large sample sizes needed to achieve acceptable SE of estimates. The results of selection programs provide powerful demonstrations of the contributions of segregation variance to variation in the population. In humans, segregation variance is harder to appreciate because family sizes are small. Understanding segregation variance is key to understanding why absolute risks of disease are small in first degree relatives of diseases individuals even in diseases of high heritability, and to understand PRS variation between family members. To demonstrate the lessons from selection programs, Figure 2 shows the response to selection in dairy cattle for milk yield (red line), which has also been accompanied by increases attributable to nongenetic factors (e.g., improved management and feed, green line). In 1957 the SD in milk yield was ∼600 kg (∼600 liters). The genetic value for milk production of an average dairy cow today is >6.5 genetic SD above the mean milk production in 1957 (achieved despite the relatively long generation intervals). In 1957, only 0.1% of cows would have produced >9600 kg of milk, now >50% of cows achieve this! Selection programs/experiments have demonstrated that very little of this change can be attributed to new mutations [see reviews cited in Hill and Caballero (1992)], but rather reflects the selection of combinations of variants. Under a polygenic architecture few variants become fixed, and selection experiments have shown that reverse selection can return population mean levels to their preselection levels (Dunnington and Siegel 1996). In broiler chickens, short generation intervals and high selection intensities led to massive changes in body weight, with 56 day weight increasing ∼3.4 kg or ∼ >20 phenotypic SD, with >80% of the change attributed to genetic selection (Zuidhof et al. 2014); figure 1 in Zuidhof et al. (2014) reproduced as figure 1.1 in Walsh and Lynch (2018) is worth checking out for a visualization of this spectacular increase (Walsh and Lynch 2018). These data were also published in the Economist (Anon 2019).

Figure 2.

Increase in milk yield in black and white Holstein cattle since 1957. The mean EBV has increased by 3916 kg or 66 kg per cow per year. The phenotypic and genetic SD of milk yield in 1957 were ∼1200 and ∼600 kg. Hence, the genetic contribution to milk yield has increased by ∼6.5 genetic SD since 1957. Source: Council on Dairy Cattle Breeding (https://queries.uscdcb.com/eval/summary/trend.cfm)

The GWAS era in human genetics has demonstrated the polygenic genetic architecture of common disease. Hence, we can interpret results from selection in the light of complex disease. For example, the ongoing incidence of schizophrenia in populations is considered a conundrum in the context of the reduced fecundity in those with schizophrenia (Keller and Miller 2006; Power et al. 2013). The impact of reduced fecundity in schizophrenia induces extremely weak selection pressure (reduced fecundity in 1% of the population) compared to intense selection in livestock (only 1% of males have offspring in cattle), in which we still observe masses of genetic variation in the offspring generation. We urge readers to read the summaries of selection experiments to better appreciate the power of the variation hidden in genomes and exposed through segregation variation.

Frequently Asked Questions

This Review brings together some important points, a few of which we previously explored in detail (Kemper and Goddard 2012). The selected topics provide the background needed to respond to four common frequently asked questions.

• Q1: Why is SNP-based heritability lower when estimated from human compared to from livestock data?

• A1: The difference is explained by understanding the differences in recent effective population size. The small effective population size in livestock means that the average coefficient of relationship between pairs of individuals is high and common SNPs tag causal variants at much greater physical distance, compared to in humans, and including across chromosomes.

• Q2: Why is the proportion of variance explained in out of sample prediction so low compared to SNP-based heritability, and what increase is expected as we increase GWAS discovery sample size?

• A2: Equation 1 provides this explanation. Although well known in PRS theory, it seems underappreciated in PRS practice, particularly the definition of M, the effective number of SNPs (use M∼50,000 in humans for common variants). GWAS were originally designed to detect specific associated variants to better understand the functional biology of a disease or trait. Now that the number of identified variants is of the order of hundreds to thousands for many traits, the need to increase GWAS sample size has been questioned. However, a key outcome of the GWAS era will be the application of PRS in prevention medicine, and larger GWAS are still needed to maximize the accuracy of PRS.

• Q3: What is the difference between PRS in humans and GEBV in livestock?

Both PRS and GEBV are estimates of the additive genetic value of a trait of an individual. In principle, the same methodology can be used to estimate both. In practice, the structure of the data (measured covariates, ascertainment, LD) lead to different approaches [e.g., single SNP regression in humans (Purcell et al. 2007; Chang et al. 2015; Loh et al. 2015) vs. GBLUP (Meuwissen et al. 2001) or BayesC (Habier et al. 2011) in cattle]. In livestock, the purpose of the GEBV is to select the parents of the next generation, and the efficacy is measured as the change in mean GEBV over time. Small changes are cumulative each generation, and, hence, use of GEBV has been highly successful, with the key gain compared to EBV calculated without DNA variant data coming from reduced generation interval (García-Ruiz et al. 2016). In humans, the PRS is used to predict future phenotype of the individual. The efficacy of a genetic predictor (measured by $R^2$) has a theoretical upper limit dependent on the heritability of the trait, and has a practical upper limit dependent on the variance tagged by the measured SNPs, $h_M^2$. While PRS can be calculated at birth to predict a phenotype in adulthood, the predictor can become more accurate over time by adding in prediction contributions from measurable risk factors reported as the individual ages.

• Q4: What is the relationship between PRS and family history for risk of common disease?

PRS is an estimate of the aggregate genetic value of an individual, tracking only the genetic contribution to the trait tagged by common DNA polymorphisms. Family history reflects the phenotypes of relatives of the individual. Those phenotypes depend partly on genetic factors (tracking polymorphisms of all frequencies in the population), and, hence, the importance of family history to an individual depends on the heritability of the trait. We have shown previously that common disease is more-often-than-not expected to occur in the absence of family history (Yang et al. 2010a). For example, for a disease with lifetime risk 1% (typical of a common human disease) and high heritability of 80%, even with full knowledge of three generations of family history, ∼70% of those affected are expected to have no family history of disease. For full understanding of this result, we refer readers to that paper, but a key to its understanding is to recognize the masses of genetic variation between full-siblings within families. Hence, although there is an increased risk in those with known family history, random samplings of genomes of parents generate the genetic lottery. Hence, children of both affected and unaffected parents can receive a polygenic burden of risk loci that leads to increased risk of disease in that individual. In practice, prevention strategies such as earlier or more frequent disease screening that are available to those with known family history, should also be made available to those with high PRS. High PRS will identify a different (partially overlapping) set of individuals that are similarly deserving of prevention interventions available to those with family history (Khera et al. 2018). The expected $R^2$ from family history is $h^4/2$, whereas the limit on $R^2$ from Equation 1 is $h_M^2,$ achieved when GWAS discovery sample is very large. Hence, $R^2$ in a sample estimated from PRS will be more accurate than that estimated from family history alone when $\frac{h_M^2}{h^2}>\frac{h^2}{2}$, and whether this is achievable depends on genetic architecture; i.e., if $h^2$ is 0.6, PRS can be more accurate than family history when $h_M^2$ > 0.18.