Fast Estimation of Recombination Rates Using Topological Data Analysis

Abstract

Accurate estimation of recombination rates is critical for studying the origins and maintenance of genetic diversity. Because the inference of recombination rates under a full evolutionary model is computationally expensive, we developed an alternative approach using topological data analysis (TDA) on genome sequences. We find that this method can analyze datasets larger than what can be handled by any existing recombination inference software, and has accuracy comparable to commonly used model-based methods with significantly less processing time. Previous TDA methods used information contained solely in the first Betti number (${\beta }_1$) of a set of genomes, which aims to capture the number of loops that can be detected within a genealogy. These explorations have proven difficult to connect to the theory of the underlying biological process of recombination, and, consequently, have unpredictable behavior under perturbations of the data. We introduce a new topological feature, which we call ψ, with a natural connection to coalescent models, and present novel arguments relating ${\beta }_1$ to population genetic models. Using simulations, we show that ψ and ${\beta }_1$ are differentially affected by missing data, and package our approach as TREE (Topological Recombination Estimator). TREE’s efficiency and accuracy make it well suited as a first-pass estimator of recombination rate heterogeneity or hotspots throughout the genome. Our work empirically and theoretically justifies the use of topological statistics as summaries of genome sequences and describes a new, unintuitive relationship between topological features of the distribution of sequence data and the footprint of recombination on genomes.

RECOMBINATION is a fundamental source of genetic variation in many natural populations. By bringing existing mutations into novel genomic backgrounds, recombination can accelerate the rate at which adaptation occurs, as well as prevent the buildup of deleterious variants that occurs in asexuals via Muller’s ratchet (Felsenstein 1974; Hill and Roberston 2007; McDonald et al. 2016). It is therefore critical to measure the rates of recombination in order to understand rates of adaptation. Resolution along the genome is also an important factor, as recombination rates are known to vary substantially along chromosomes. In particular, hotspots of recombination have been found associated with a variety of sequence and structural motifs in natural populations (Coop et al. 2008; Baudat et al. 2010; McVean and Myers 2010; Parvanov et al. 2010; Comeron et al. 2012). In addition to hotspot detection, better estimation techniques for recombination rates can also improve our understanding of observed levels of linkage disequilibrium in genome data (Stumpf and McVean 2003), and, consequently, the expected signatures of various evolutionary phenomena such as selective sweeps (Neher and Shraiman 2009).

In practice, detecting genome-wide heterogeneity in recombination rates is challenging. Empirical approaches require building linkage maps through involved procedures such as sperm typing or multi-generational genetic crosses (Hubert et al. 1994). While these are often the most powerful methods for detecting recombination, they are costly and time consuming. With the recent influx of large-scale sequencing data, alternative algorithmic approaches to inferring recombination rates from bulk genomic data have become a focus of attention. These methods, while often faster, come with their own set of technical challenges. In order to detect patterns and rates of recombination along a genome, model-based algorithms infer properties of the ancestral recombination graph (ARG)—an exercise which can be prohibitively computationally expensive on large datasets (Fearnhead and Donnelly 2001). This problem has driven the development of methods that use either a variety of summary statistics built on quantities such as the distribution of pairwise differences (Wakeley 1997), or only compute partial or composite likelihoods, such as LDhat and its sister LDhelmet—two of the most widely used model-based methods (Auton and McVean 2007; Chan et al. 2012). Even with this relaxation, these methods can take a matter of days to run on realistically sized sequence data.

In this paper, we present a method that takes advantage of novel summary statistics based on topological features of the genomes in a given sample to quickly and accurately provide estimates of recombination rate heterogeneity. Our method differs from existing model-based methods in that it is based solely on distances between sequences and consequently scales significantly better on large datasets. We find that a topological data analysis (TDA)-based approach greatly increases feasibility of the inference problem and implicitly ties genetic distances to modern models of population genetics via the coalescent (see Coalescent Intuition for Topological Statistics).

Recently, Camara et al. (2016) demonstrated the utility and efficiency of TDA to inference of recombination rates, benchmarked against the methods of Hudson and Kaplan (1985), Myers and Griffiths (2003), and Chan et al. (2012). They focused on a topological feature known as the first Betti number (${\beta }_1$, explained in Motivation for TDA), which captures the number of cycles in an ARG, the canonical graphical representation of recombination events. We have found that another topological feature of lower dimension, which we call ψ, is a better predictor of recombination rate in genomes. Moreover, ψ and ${\beta }_1$ used in tandem provide much more accurate estimates than previous TDA-based methods. We investigate these two topological features and their relationships to evolutionary quantities of interest—including recombination rate as well as coalescent tree length—and describe a method of estimating recombination rates from genome samples using these features. We then compare the performance of our estimator on whole-genome data to LDHelmet; we find that our results justify the use of the TDA estimator as a rapid approximation method.

Motivation for TDA

We are interested in accessing information about the structure of the ancestral recombination graph held in the Hamming distances between sampled sequences, given that we can only sample lineages at the present time.

This structure has a natural connection to TDA—a new branch of statistics that applies tools from algebraic topology to describe the shape of data (Carlsson 2009; Zomorodian 2009; Edelsbrunner and Harer 2010; Ghrist 2014; Chazal et al. 2016). Here, we will provide a brief motivation for this technique, with a precise discussion in Appendix A: Background on TDA. TDA has been applied successfully to a range of applications in biology, including the study of breast cancer transcriptional data for the discovery of a cancer subgroup (Nicolau et al. 2011), the construction of phylogenetic trees for analyzing tumor evolutionary patterns (Zairis et al. 2014), and the detection of intrinsic structure in neural activity (Giusti et al. 2015).

In particular, we use a mathematical invariant called persistent homology, which quantifies the connected components, holes, and higher dimensional voids at different “resolutions,” or filtrations of the data. This is analogous to expanding spheres around each of the points in a dataset and considering the properties of the object generated by the union of these spheres at different radii.

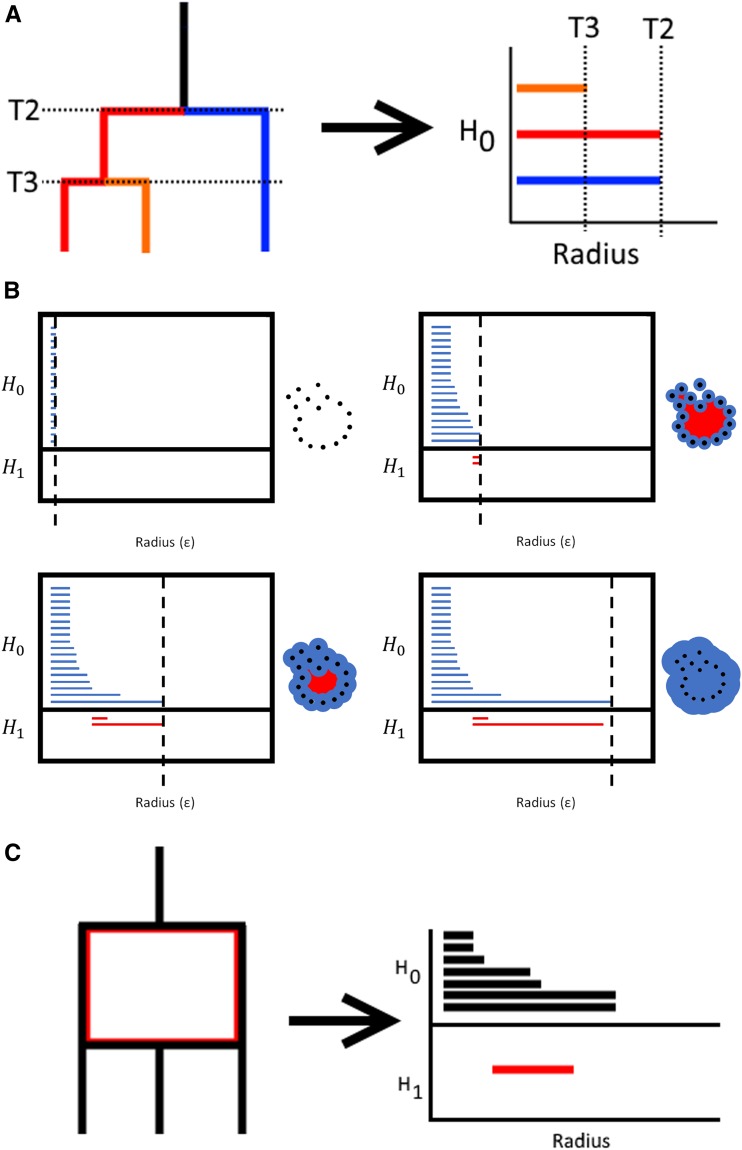
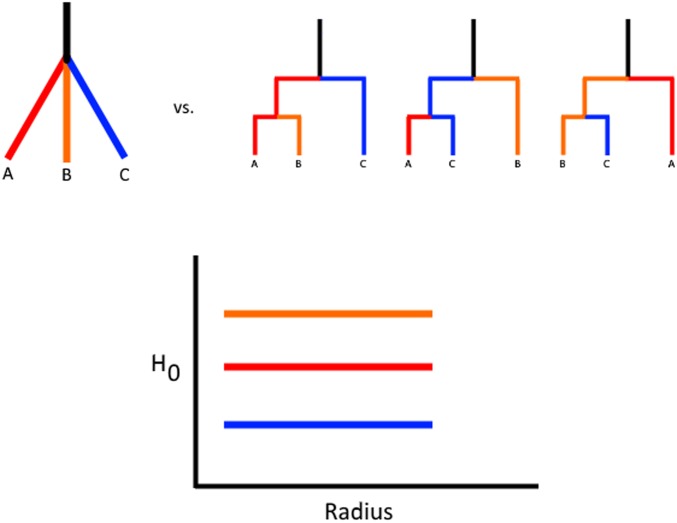
This process has a direct coalescent interpretation in the case of a single genealogy—as we expand spheres around our sampled sequences, we are exploring the possible ancestral states along a coalescent tree, with the contact point between the spheres corresponding to the most parsimonious sequence of the common ancestor of the samples in question. Just as we lose a lineage backward in time at each coalescent event, we lose a distinct connected component in our graph of persistent homology (see Figure 1a). This process of keeping track of the “lifetime” of these components is represented using a barcode diagram, a collection of bars associated to each of the features with length equal to the difference between the radii at which it appears and is lost (see Figure 1b). These bars can be sorted by the dimensionality of their corresponding homology group. We focus on $H_0$, the zeroth homology group or set of connected components, and $H_1$, the first homology group or the number of holes in the data. The counts of the elements in each homology group are captured by the Betti numbers, defined such that ${\beta }_i$ is the number of bars in a barcode diagram of $H_i$. Note that dimension 0 persistent homology is closely related to single linkage clustering, where ${\beta }_0$ corresponds to the number of points and the lengths of the bars in the resulting barcode diagram of $H_0$ correspond to the branch lengths in the clustering dendrogram (Carlsson 2009).

Figure 1.

Persistent homology applied to genealogies in the absence and presence of recombination. (a) Sample genealogy without recombination and corresponding dimension-0 barcode diagram for sequences at the terminals, with the time to a coalescence event given three and two remaining lineages labeled. (b) A sequence of complexes for increasing distance parameter choices on a set of arbitrary data. (c) Sample ARG with recombination event represented by the loop in red, and corresponding dimension 0 and dimension 1 barcode diagrams, assuming sampling throughout the graph rather than just at the terminals. We note that the $H_0$ bar lengths no longer have a straightforward coalescent interpretation under this sampling scheme.

When there are multiple gene genealogies within the sample, as is the case when there is recombination, the relationship between coalescent and topological quantities changes as the distances between sequences are now averages over multiple trees. In addition, $H_1$ will now show features loosely corresponding to loops in the ARG (see Figure 1c). This has particular consequences for how we expect TDA-based summaries to behave when recombination occurs, which are detailed in Coalescent Intuition for Topological Statistics.

Methodological Overview

We sought to identify topological summary statistics (using ${\beta }_1$ as a baseline for comparison) that can serve as features for algorithms to perform recombination rate inference. Utilizing simulated data, we computed a variety of topological summaries of dimensions 0, 1, and 2 from the Hamming distance matrix between sequences.

The results of our LASSO regression indicated that the topological features with the highest predictive power for recombination rate are, in order: (1) the average dimension 0 barcode length (ψ), (2) the first Betti number (${\beta }_1$), and (3) the variance of the dimension 0 barcode lengths ($\text{Φ}$). We then used a nonlinear combination of these three topological statistics to build a novel TDA-based model for recombination rate inference, the Topological REcombination Estimator (TREE). We used simulated data to perform an initial validation of the model. For a more serious validation, we applied TREE to 22 full genome assemblies from the RG Drosophila population (Pool et al. 2012) (see Methods for more details) and compared its performance to ${\rho }_{ph}$, the recombination rate estimator introduced by Camara et al. (2016), and to LDhelmet. We also benchmarked TREE on a much larger dataset of Arabidopsis genomes, consisting of 1135 individuals and up to 50k SNPs.

Notation and symbols

Throughout the text, we refer to various quantities. We list them here (Table 1) in addition to where they are first defined.

Table 1. Symbols used throughout the text.

Symbol	Meaning
ρ	population-scaled recombination rate
$\widehat{\rho }$	TREE estimate of ρ
${\rho }_{ph}$	Camara et al.’s estimate of ρ
ψ	Mean bar length in dimension 0
${\beta }_i$	$i^{th}$ Betti number
θ	Watterson’s population mutation rate
$H_i$	$i^{th}$ homology group
$\text{Φ}$	variance in ψ

Coalescent Intuition for Topological Statistics

The main topological statistics of interest here are ${\beta }_1$, the first Betti number, and ψ, the mean bar length in the dimension 0 barcode diagram. In order to relate these to the biological process of recombination, we will use the language of coalescent theory. For a detailed introduction to the field, see Wakeley (2009). We note that our approach differs from the recent considerations of Lesnick et al. (2018) in that we consider a coalescent model with branch lengths and model $H_0$ behavior. Furthermore, we assume a more restrictive sampling regime where only sequences at contemporaneous terminals of the graph are known, as opposed to sequences all along the genealogy.

Explaining $\mathit{\psi }$:

We provide a heuristic argument that the value of ψ is elevated in the presence of recombination by demonstrating the desired behavior at the recombination rate extremes. First, we claim that in the absence of recombination, the distribution of $H_0$ feature lengths corresponds to the mutation scaled distribution of branch lengths in the coalescent tree of the sample, as shown in Figure 1a. Since there is a single, fixed genealogy that describes all positions within the sequence, it is sufficient to calculate the expected length of the coalescent tree and divide by the sample size. Assuming a large idealized diploid population of size N, from which we sample K individuals with K sufficiently small relative to N, the expected waiting time between coalescence events is $\frac{4N}{k\left(k-1\right)}$ generations (Watterson 1975; Tavaré 1984), where k is the number of remaining lineages. The full coalescent tree is then made of each $k^{th}$ interval k times, for the number of remaining lineages at that time. Summing over all these segments and dividing by the sample size gives us the following:

$$E\left|\psi \right|=\frac{4N\mu }{K}{\displaystyle \sum }_{k=1}^{K-1}\frac{1}{k}=\mathcal{O}\left(\frac{\text{log}\left(K\right)}{K}\right),$$

where μ is the per-generation mutation rate. Notably, this is equivalent to the expected number of segregating sites divided by the sample size per Watterson’s estimator (Watterson 1975).

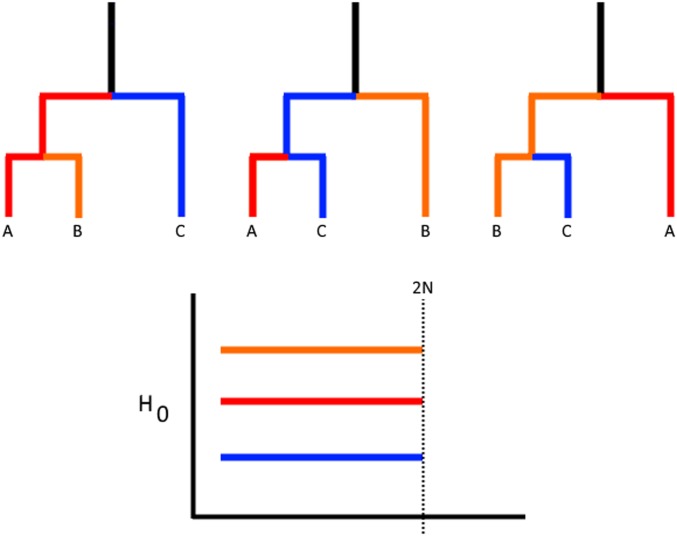
We now show that in the infinite recombination limit, the expectation for ψ is strictly larger than in the case where there is a single fixed genealogy. If there is free recombination, every site in the sample has an independent genealogy, which we will average over, so all the bars must be of the same length (Figure 2). In other words, the expected value of ψ becomes the scaled average coalescence time for two randomly sampled individuals in the current generation. This is simply $2\mu N$. All that remains is to show that $\frac{2}{K}{{\displaystyle {\displaystyle {\sum }_{k=1}^{K-1}\frac{1}{k}}}}^{\text{}}$ is <1. Since the partial sum is bounded by $\text{log}\left(K-1\right)+1,$ this holds for all values of K >5. This additionally suggests that the variance in the length of the $H_0$ barcodes features should decrease as the recombination rate increases, which we observe in simulations. By integrating information about both the length of the coalescent tree and the distribution of pairwise differences averaged over multiple topologies, ψ can be viewed as capturing distortions in the expected amount of independent evolution between samples that occurs when sequences contain multiple discordant gene genealogies.

Figure 2.

By averaging over multiple genealogies, the barcode of $H_0$ features approaches identical bars of length equal to the expected pairwise coalescence time. (a) The C̆ech complex for these points at the drawn radius is a graph with a cycle (shown with the dotted lines), as the triple intersection is empty. (b) An ARG with lineage b inheriting p proportion of its genome from the lineage leading to a.

Explaining ${\mathit{\beta }}_1$:

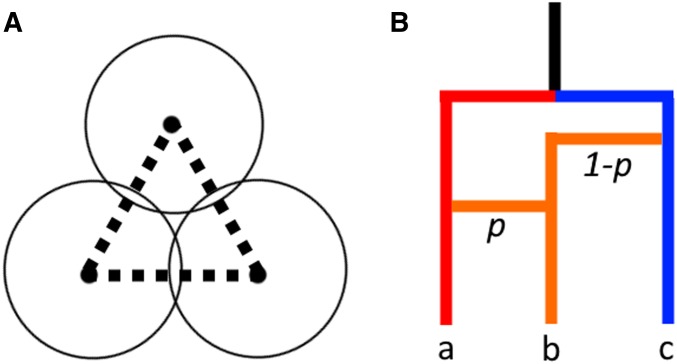
We suggest, in addition, that the standard intuition for the use of ${\beta }_1$ to detect cycles in the ARG [presented in Chan et al. (2013), Camara et al. (2016), as well as here in Appendix A: Background on TDA], potentially oversimplifies the relationship between recombination events and features in the $H_1$ barcode. For this, we will consider C̆ech complexes, rather than Vietoris-Rips complexes (which we use in the actual analyses). These are closely related (Ghrist 2014), but the C̆ech complex construction allows holes to be formed given only three points (see Figure 3a), which lets us consider only three terminals. Given the graph in Figure 3b, it is clear that if one were to sample the sequences at every node, there would be an $H_1$ feature observed that corresponds precisely to the hole in the graph. However, in many genetic studies, samples of the common ancestors of present-day sequences do not exist. If we restrict our data to the sequences at the terminals, single cycle detection with ${\beta }_1$ becomes a function of mutation heterogeneity along the graph, and any single recombination event cannot be detected if we are given only the true coalescent distances between samples along the genealogy. To see this, take terminals a and c from the graph. By hypothesis, the amount of time between them and their most recent common ancestor (MRCA) is the same, which we will call L. It follows that the minimum radius such that balls around these points would intersect is L. Then, for the triple intersection of balls around the terminals to be empty, b must be a distance greater than L from the MRCA. However, each portion of its genome has certainly experienced the same amount of time since the MRCA regardless of recombination history. Therefore, we require that there be a more than expected amount of mutations generated along the path to b in order for this event to be detected, given the actual sequence data.

Figure 3.

Given the true coalescent distances between the terminals $a,b,c$, a recombination cycle will not be detected in the manner shown in (a), and so will not generate an $H_1$ feature in the C̆ech complex at any radius. This example motivates the need for topological summaries beyond ${\beta }_1$ for recombination estimation.

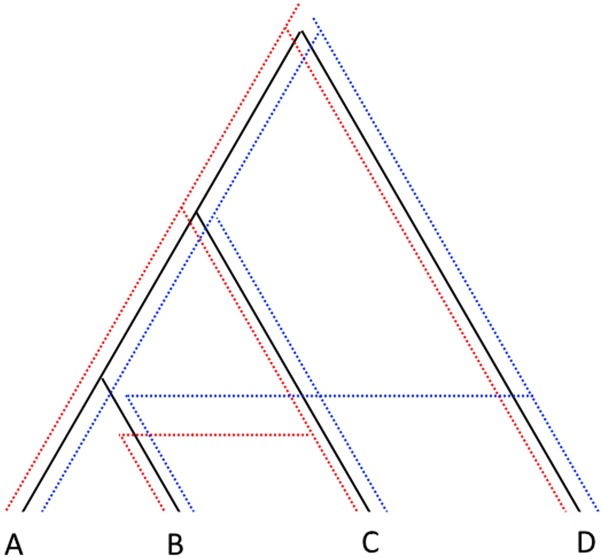
However, if we take into account multiple recombination events, certain configurations of multiple events will generate $H_1$ features even if we know the true coalescent distances. This is because we can now introduce additional independent evolution in one of the tips by having recombination occur both within a clade and with an outgroup lineage (see Figure 4). We note that ${\beta }_1$ is nonzero only in the presence of recombination events, assuming no sequence convergence and infinite sites, but the sampling reality may bias ${\beta }_1$ detection in subtle ways. This also implies that the length of the $H_1$ bar will not necessarily be indicative of features of the actual cycle in the graph, as it will increase in length as additional mutations are placed on the lineage leading to b, even if the cycle itself is untouched. We find via simulations (see Supplemental Material, Supplement S1 section Filtering ${\mathit{\beta }}_1$) that filtering small $H_1$ bars only hurts our inference capabilities, as we would then expect.

Figure 4.

A genealogy with two recombination events, with the three resulting gene trees overlaid. A loop will be formed in the C̆ech complex of $A,B,C$ when the radius is equal to the time to the MRCA for A and C, since B is now further from that node than either A or C.

Combining $\mathit{\psi }$ and ${\mathit{\beta }}_1$:

These explanations for the behavior of ψ and ${\beta }_1$ also implies differences in behavior between ψ and ${\beta }_1$ under different population models. For example, while rapid demographic changes, such as exponential population growth, will distort ψ-based estimation (Figure 5), ${\beta }_1$ counts features generated by recombination at a rate independent of the underlying tree structure, since the relative distances to the MRCA are unchanged with multifurcations. On the other hand, we find empirically that ψ is very robust (especially compared to ${\beta }_1$) to perturbations in the form of missing data, which serve only to minorly rescale the $H_0$ bars on average. These differences suggest that a reliable predictor should incorporate both features. A more formal follow-up to the behavior of these statistics under different models of demography and selection, as well as further characterization of the behavior of ψ using the sequentially Markov coalescent (SMC) model (McVean and Cardin 2005) will be conducted in future work.

Figure 5.

Exponential population expansion creates multiple-merger events and shrinks internal branches. This can give a similar signal in $H_0$ as increased recombination, but does not change cycle detectability via ${\beta }_1$ in the ARG.

Methods

Topological data analysis

We created a pipeline that takes as input a sequence file in FASTA format, computes a Hamming distance matrix $D_H$, uses $D_H$ to extract the corresponding dimension 0 and dimension 1 persistent homology barcodes, and then calculates barcode summary statistics. The barcodes were computed using Ripser, a publicly available C++ package for computing Vietoris-Rips persistence barcodes, and all other computations were performed in Python 2.7 (Bauer 2016). The scripts are compatible with Python 2.7 and 3.0 and are available on our Github page at: https://github.com/MelissaMcguirl/TREE.

Simulations

We simulated over 50,000 datasets of genetic sequence data with known recombination rates, each of length 1000 bp, using the programs ms and seq-gen (Rambaut and Grassly 1997). Given an idealized population, we varied the parameters for the population recombination rate $\rho =4N_{e}r$, sample size n, and population mutation rate $\theta =4N_e\mu$ to capture a variety of mutation-recombination regimes in the data. The datasets had recombination rates varying from 0 to 1000 (that is, no recombination up to free recombination between all sites under the population recombination model $\rho =1000$).

For each population we computed dimension-0 and dimension-1 persistent homology barcodes using Ripser (Bauer 2016). We ran regression analyses to discover topological predictors for recombination and then confirmed that our method predicts ρ directly and does not predict a covariate such as θ.

Model selection

Initially, we applied polynomial regression of degree two, linear regression, LASSO regression, polynomial LASSO regression, and exponential regression using several different combinations of barcode statistics as inputs for predicting recombination rate using Scikit-learn (Pedregosa et al. 2011). We sought the most parsimonious model that was able to predict recombination rate with high accuracy.

Each model was trained on a randomly selected subset of the input data, whose size was chosen to be 30% of the total dataset. The model was then tested on the remaining 70% of the input data, where $R^2$ values were computed to access the goodness-of-fit of the resulting model. This process was repeated several times to test the robustness of the learned parameters with respect to different training sets.

Based on the $R^2$ values, we were able to focus on just three barcode statistics, ψ (average dimension 0 bar length), ${\beta }_1$ (first Betti number), and $\text{Φ}$ (variance of dimension 0 bar lengths), as inputs for an exponential regression model of the form

$$\rho =\text{exp}\left(\alpha \mathrm{\ast }{\psi }^2+\beta \mathrm{\ast }{\beta }_1^2+\gamma \mathrm{\ast }\psi +\delta \mathrm{\ast }{\beta }_1+\mathit{ϵ}\mathrm{\ast }\text{Φ}+\zeta \right).$$

The coefficients $\left(\alpha ,\beta ,\gamma ,\delta ,\mathit{ϵ},\zeta \right)$ were determined via ordinary least squares from simulated training data in scikit-learn Python 2.7.

This model was tested on input data consisting of 53,461 barcode statistic files corresponding to simulations of varying sample size, mutation rate, and recombination rate. Fivefold cross validation was preformed for different sample sizes, and for the complete dataset.

Empirical analysis

We obtained 22 full genome assemblies from the publicly available RG population (from the African survey of Drosophila melanogaster) for our analyses. These sequences were collected from independently bred isofemale lines, and sequenced using Illumina GA IIx. The genomes in this sample are homozygous/haploid, so phasing was not necessary.

With these assemblies, we ran LDhelmet and TDA in parallel and compared the mean estimates of recombination rate ρ in sliding windows of 500 SNPs. Since LDhelmet provides estimates of ρ between any two SNPs, whereas our method computes ρ within windows of 500 SNPs, we take the mean of every 500 ρ estimates from LDhelmet to compare to our windows. Moreover, since LDhelmet estimates $\rho =2\times N_e\times r$ per base pair, and TREE predicts $\rho =4\times N_e\times r$, where $N_e$ is the population size and r is the probability of a crossover event from ms, then we apply a uniform normalization of $\frac{1}{2\times \#\left(\text{base pairs}\right)}=\frac{1}{2\times 500}=\frac{1}{1000}$ to the TREE predictions for comparison to LDHelmet.

We also ran Camara et al.’s model using only ${\beta }_1$ as a predictor within our sliding window framework to compare this to our method and LDhelmet. We looked at the results in three different ways: (1) in terms of absolute estimates compared to each other, (2) in terms of concordance in the change in ρ across windows (i.e., do both methods predict an increase or decrease in ρ in the same window), and (3) in terms of concordance of estimates above the 75th and 90th percentiles of the distribution of estimates.

We additionally included an analysis of 1135 publicly available Arabidopsis genomes. We converted the raw VCF file to FASTA using a combination of bcftools and VCF-kit’s phylo fasta function, subsampling up to 50k SNPs in order to run the software within the 48 hr time limit of the Texas Advanced Computing Center’s Stampede2 cluster. We ultimately used this dataset to benchmark the computational efficiency of TREE over LDhelmet due to impractical runtimes for LDhelmet on the larger dataset.

Data availability

The authors affirm that descriptions and results for all the simulations necessary for confirming the conclusions of the article are present within the article, figures, and tables. The sequence data used are available from the 1001 Genomes (doi: 10.1016/j.cell.2016.05.063) and the RG population of the Drosophila Population Genomics (doi: 10.1371/journal.pgen.1003080) projects. Supplemental File S1 contains additional experiments and results concerning the robustness of ψ with missing data, population structure, and random noise. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.7744814.

Results

Coalescent simulations

We simulated data for an idealized population of fixed size $N_e$, with per-generation crossover rate r and mutation rate μ. Given this, we ran regression analyses to discover relationships between various topological summary statistics and $\rho =4N_{e}r,$ the population recombination rate. The topological statistics included were: (1) the mean and median bar lengths; (2) the variance of bar lengths; (3) the total number of bars; and (4) the number of bars above varying noise-filtering thresholds for dimensions 0, 1, and 2.

Our intention was to test various topological features as predictors of known recombination rates, and to demonstrate comparable performance of these features to a comparator method, LDhelmet. However, given the computational bottlenecks inherent to LDhelmet, we were unable to run this software over the full set of >3600 alignments. We are nevertheless satisfied in that the parameters to be estimated are known from simulation, and so we save the use of LDhelmet for our empirical analyses where the truth is unknown.

As a preliminary analysis, the weight vectors of LASSO regression models provided insight into which barcode statistics were the strongest predictors of ρ. The results of this analysis showed that two key topological features, ${\beta }_1$ and the mean dimension 0 bar length, which we will denote as ψ, correlate strongly with ρ given a constant sample size $n>10$. Thus, these topological summaries became the main foci of our work. Moreover, we found no correlation between our barcode statistics and $\theta =4N_e\mu ,$ the population mutation rate, as expected, since changes in θ with a constant $N_e$ only linearly rescale the distances.

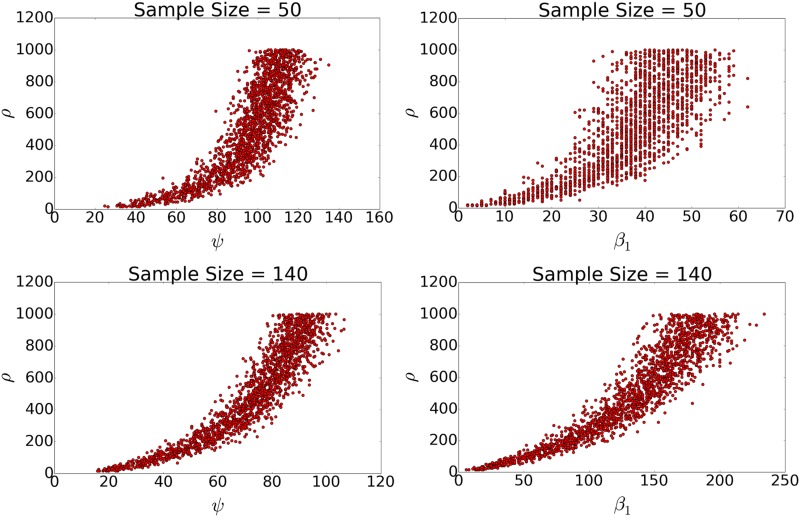
In studying the information content of these various statistics, we found that ψ stood out as an even better predictor of recombination rate than ${\beta }_1$, and performed better on its own in predicting recombination rates from simulated datasets. Figure 6 demonstrates the relationships between ρ and ${\beta }_1$, and between ρ and ψ for sample sizes $n=50$ and $n=140$. We note that both topological summaries exhibit an exponential relationship with recombination rate, and that the relationship is tighter for ψ than ${\beta }_1$, especially for smaller sample size.

Figure 6.

The relationship between ψ and recombination rate (left), and ${\beta }_1$ and recombination rate (right) for a simulated dataset with fixed sample size $n=50$ (top) and $n=140$ (bottom).

As a baseline, we fit our simulated data with a fixed sample size of 160 to the ${\beta }_1$ based model of Camara et al. (2016), ${\rho }_{ph}$ (the “ph” stands for persistent homology). This model is given by the equation

$${\rho }_{ph}=g[{(1+\frac{1}{f})}^{{\beta }_1}-1],$$

where the parameters g and f are coefficients related to sample size and are independently calculated for a given dataset. The best fit over the simulated range of recombination rates simulated is $R^2=0.86$. We found a relationship between ρ and ψ with $R^2=0.90$, suggesting that this new parameter has comparable or greater power for predicting population recombination rates.

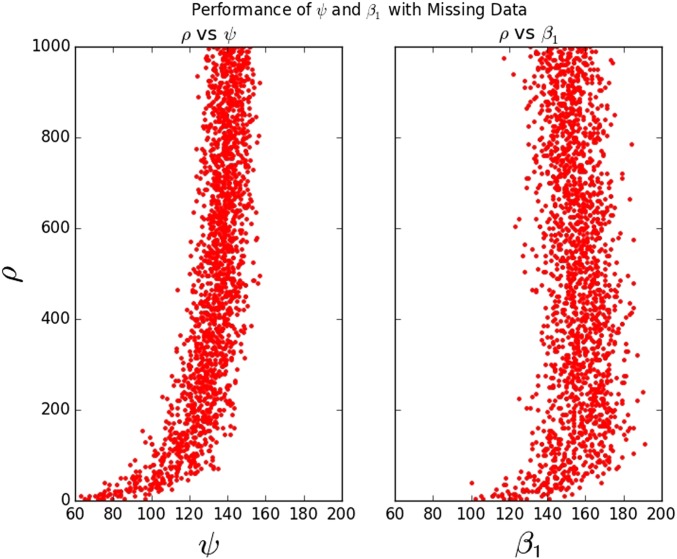
We demonstrated that the two parameters ψ and ${\beta }_1$ are differentially stable under violations of assumptions about the data. Notably, ψ is robust to large amounts of missing data, whereas ${\beta }_1$ is robust to rapid changes in population size. The former we show empirically: ψ maintains its relationship with ρ with $R^2=0.76$ with 10% of each sequence missing as a tandem indel, while ${\beta }_1$ loses this relationship quickly with $R^2=0.036$ under the same missing data scheme. These results are shown in Figure 7.

Figure 7.

ψ continues to be accurate under a missing data scenario ($R^2=0.76$with 10% of the data missing in large blocks) while the accuracy of ${\beta }_1$ under the same scenario drops to $R^2=0.036$.

The assumption of 10% missing data are somewhat conservative; next-generation sequencing data sets have less missing data, but this figure is realistic for many older sequencing data sets. As one would expect, we note that performance of each method declines as missing data become more prevalent (See Supplement S1 section Missing Data). However, if missing data are located randomly throughout the genome, it is unlikely to bias relative measures of recombination rates within a dataset. While ${\beta }_1$ is expected to be robust to rapid changes in population size since this does not change the number of cycles in the ARG, ψ will be more sensitive to these changes as rapid demographic expansion generates multifurcations in the genealogy which converge to the same branch lengths as in the infinite recombination case.

TREE model

We implemented several machine learning and regression models to build an accurate and robust model relating topological summaries to ρ, including LASSO, polynomial regression, exponential regression, and linear regression. We varied model parameters and input features (subsets of the aforementioned barcode statistics) across each learning algorithm.

A subset of model comparison results are presented in Table 2, where we show the $R^2$, or goodness-of-fit measure, values for the model $\rho =\text{exp}\left(a^T\overrightarrow{x}\right)$, where $\overrightarrow{x}$ corresponds to a vector of different barcode statistics and $a^T$ is the transposed vector of coefficients. We ran the model separately on datasets generated with varying sample sizes, as well as on a dataset consisting of simulations of varying population size. An $R^2$ value close to 1 signifies a nearly perfect model, whereas $R^2$ near 0 indicate that the model has low predictive power.

Table 2. $R^2$ values for the exponential regression model for different feature inputs and sample sizes.

Sample size	ψ	${\beta }_1$	$\left({\psi }^2,{\beta }_1^2,\psi ,{\beta }_1,\text{Φ}\right)$
25	0.724	0.456	0.792
50	0.847	0.749	0.894
75	0.883	0.827	0.927
95	0.898	0.862	0.941
140	0.909	0.887	0.959
Mixed	0.414	0.164	0.851

The results show that ψ is an overall stronger predictor than ${\beta }_1$, and, as expected, recombination rate is predicted more accurately for higher sample sizes. Importantly, ${\beta }_1$ fails as a predictor in the case of small sample size, while ψ maintains decent predictive power for sample size as low as 25.

A thorough comparison of the different model outputs showed that an exponential model in ${\psi }^2$, ${\beta }_1^2$, ψ, ${\beta }_1$, and the variance of the dimension 0 bar lengths, which we will denote $\text{Φ}$, is the best predictor for ρ. While we also tested more topological features as inputs to different models, the increase in $R^2$ values was negligible in comparison to the increased risk of over-fitting.

Summarizing, we propose the following TREE model:

$$\rho =\text{exp}\left(\alpha \mathrm{\ast }{\psi }^2+\beta \mathrm{\ast }{\beta }_1^2+\gamma \mathrm{\ast }\psi +\delta \mathrm{\ast }{\beta }_1+\mathit{ϵ}\mathrm{\ast }\text{Φ}+\zeta \right),$$

where

$$\left(\begin{array}{c}\alpha \\ \beta \\ \gamma \\ \delta \\ \mathit{ϵ}\\ \zeta \end{array}\right)=\left(\begin{array}{c}-1.797\times {10}^{-4}\\ -5.934\times {10}^{-5}\\ 5.530\times {10}^{-2}\\ 1.813\times {10}^{-2}\\ -3.744\times {10}^{-4}\\ 2.248\end{array}\right)$$

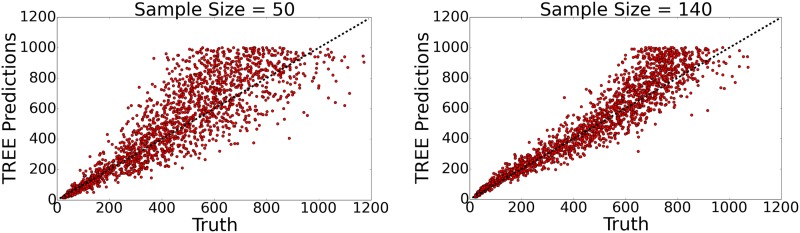
Figure 8 shows TREE’s performance on blind testing sets for sample sizes of 50 and 140. While the model preforms best when restricted to datasets corresponding to high sample size, TREE was trained on mixed sample size data in an attempt to make the model as robust and have as little bias as possible.

Figure 8.

TREE predictions on testing sets compared to the true recombination rate for sample size = 50 (left) and sample size = 140 (right). The dotted line corresponds to perfect predictions.

To analyze the robustness of the model, we performed fivefold cross validation. The results, presented in Table 3, show that the model maintains high accuracy regardless of the training set.

Table 3. Fivefold cross validation $R^2$ values for the full model.

Sample Size	$k=1$	$k=2$	$k=3$	$k=4$	$k=5$
25	0.797	0.769	0.738	0.696	0.786
50	0.857	0.901	0.905	0.884	0.881
75	0.901	0.934	0.906	0.925	0.928
95	0.938	0.934	0.944	0.936	0.952
140	0.956	0.963	0.949	0.958	0.961
Mixed	0.849	0.847	0.849	0.852	0.858

Empirical analysis

We compared the performance of TREE on empirical datasets to a widely used estimator, LDhelmet v1.9. We first benchmarked each method on a large genomic dataset from the Arabidopsis 1000 Genomes project consisting of 1135 samples. We used subsets of 1k, 10k, and 50k SNPs in 100 SNP windows from the total dataset in order to test the computational speed of each program. We found that LDhelmet was not able to process >50 samples from these datasets, failing to complete the first step of the likelihood table computations for the smallest of these datasets. However, TREE was able to process each dataset in full within a reasonable time frame (Table 4). By subsampling these data, we can illustrate one advantage of TREE’s ability to analyze this quantity of individuals. We find that as the number of samples is increased from 20 to 50–100% of the full set, the distribution of recombination events along the genome shifts such that the top $10\%$ of windows contain 17.4, 19.8, and 23.9% of events, respectively, as the signal of hotspots grows more pronounced. In addition, the importance of efficiency is underscored by the fact that as more samples are included, more SNPs are realized in the data, and more windows are required for a full analysis. As we could not compare recombination estimates on the full Arabidopsis genome due to LDhelmet’s processing times, we turned to a smaller Drosophila dataset with 22 samples and >22 Mbp. For these datasets, LDhelmet takes on the order of hours to complete a run over a single chromosome, whereas TREE terminates on the order of minutes and in all cases finished running in under 1 hr.

Table 4. Benchmarking TREE’s runtime on a large dataset (1135 Arabidopsis individuals).

Number of SNPs	Runtime (hr)
1k	0.521
10k	5.556
50k	27.866

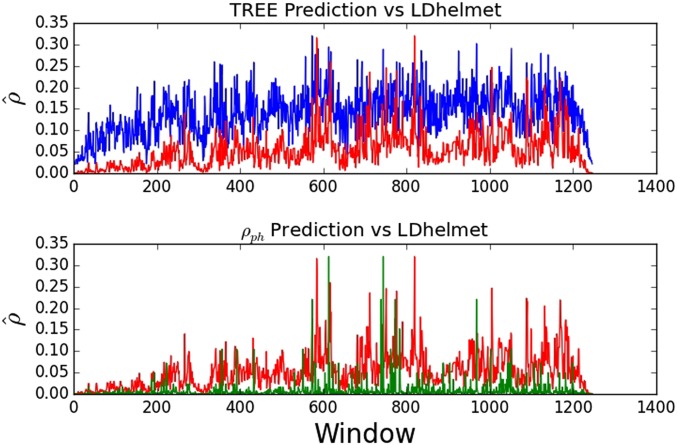
Figure 9 presents the relative accuracy of TREE and Camara’s ${\rho }_{PH}$ with respect to LDhelmet. To quantify the results, we first take a broad look at the relative performance of TREE to LDhelmet on genomic datasets, looking for concordance in predicting an increase, decrease, or no change between each window of our analysis. We find that TREE is concordant with LDhelmet in 69.2% of cases where ρ increases, and in 69% of cases where ρ decreases. We note that, since LDhelmet applies a smoothing while TREE does not, we cannot directly compare the accuracy with which TREE generates adjacent windows of identical recombination rate (Table 7 and Table 8).

Figure 9.

Relative accuracy of TREE and Camara’s ${\rho }_{ph}$ with respect to LDhelmet. The blue line plot represents TREE, the red represents LDhelmet, and the green in the second panel represents ${\rho }_{ph}$. Because ${\rho }_{ph}$ suggests orders of magnitude more rate variation than LDHelmet, we rescale the estimate given by ${\rho }_{ph}$ to the exact range of LDHelmet. For TREE, we only multiply by a uniform window length conversion factor of $\frac{1}{1000}$.

Table 7. Comparison of the change in ρ in adjacent windows between TREE and LDhelmet.

Chr	Increase	Decrease
2L	283/408 (69.4%)	278/394 (64.3%)
2R	407/560 (72.7%)	406/568 (71.5%)
3L	425/637 (66.7%)	427/635 (67.2%)
3R	454/632 (71.8%)	485/680 (71.3%)
X	358/546 (65.6%)	365/568 (64.3%)

Table 8. Comparison of the change in ρ in adjacent windows between ${\rho }_{ph}$ and LDhelmet.

Chr	Increase	Decrease	No Change
2L	199/408 (48.77%)	215/394 (54.57%)	8/116 (6.90%)
2R	133/560 (23.8%)	128/568 (22.5%)	64/118 (54.2%)
3L	290/637 (45.5%)	283/635 (44.6%)	12/204 (5.8%)
3R	298/632 (47.2%)	321/680 (47.2%)	3/78 (3.8%)
X	243/546 (44.5%)	262/568 (46.1%)	30/411 (7.3%)

To characterize TREE’s behavior in these cases, we looked at the magnitude of the difference between TREE’s prediction and LDhelmet’s. We found that in the cases where LDhelmet predicts no change in ρ, 72.5% of the time TREE’s predicted change is <0.05, 18.1% of the time TREE’s predicted change is <0.01, and 1.8% of the time TREE’s predicted change is <0.001. These results suggest that TREE is good at detecting large changes in recombination rate, and is thus well-suited for hotspot detection. However, it can have difficulty differentiating between subtler changes in recombination rate ranging in magnitude between 0 and 0.01.

Finally, we looked directly at the correlation between the absolute predicted values of TREE and LDhelmet for the most fine-grained comparison (Table 5). We used two measures of correlation: the Kendall-Tau rank test and Spearman’s Rho. With the exception of chromosome arm 2L, Kendall’s Tau between TREE estimates and LDhelmet estimates ranges between 0.067 and 0.241 with P-values <0.0001. Similarly, Spearman’s Rho ranges between 0.097 and 0.346 with P-values <0.0002. These positive correlation coefficients and low P-values suggests global agreement between LDhelmet’s and TREE’s rankings of recombination rates across sliding windows, indicating that TREE is useful in detecting global hotspots of recombination.

Table 5. Comparison of TREE to LDhelmet’s ρ estimates.

Chr	Kendall’s Tau	P-value	Spearman’s Rho	P-value
2L	0.026	0.230	0.039	0.237
2R	0.178	5.7e−21	0.260	8.7e−21
3L	0.241	7.5e−44	0.346	1.1e−42
3R	0.225	1.8e−36	0.326	6.1e−36
X	0.067	8.0e−05	0.097	1.6e−4

The correlation coefficients for Chromosome X and arm 2L are substantially lower and associated P-values substantially higher than the remaining chromosome arms in the dataset (Table 5). Despite attempts to discover why these two chromosomes are outside of the average ranges of performance, we were unable to find a compelling reason. It may be that each of these chromosomes have many more cases of subtle recombination rate changes between 0 and 0.1, such that LDhelmet’s estimates are most different from TREE’s.

We also compared the model of Camara et al. (2016) to LDhelmet in the same framework to discover its relative performance and to test whether the addition of the feature ψ is necessary for greater accuracy. We found that the ${\rho }_{ph}$ model in ${\beta }_1$ alone is dramatically less concordant with LDhelmet estimates across all windows than is TREE (Table 6). For each chromosome arm analyzed using ${\rho }_{ph}$, the rank coefficients of Kendall’s Tau or Spearman’s Rho are <0.01, sometimes negative, and not statistically significant. This indicates poor concordance between the two methods, and, in some cases, disagreement, suggesting that the addition of ψ to an estimator of recombination rate substantially improves accuracy as well as computation time compared to LDhelmet. We see evidence of the differences in prediction between TREE and LDhelmet as well as ${\rho }_{ph}$ in Figure 9, which shows that TREE approximates the estimates of LDhelmet across the entire span of the chromosome without rescaling, whereas ${\rho }_{ph}$ fails to capture similar detail to TREE and requires an informed recentering to the range of LDHelmet to be competitive.

Table 6. Comparison of ${\rho }_{ph}$ to LDhelmet’s ρ estimates.

Chr	Kendall’s Tau	P-value	Spearman’s Rho	P-value
2L	0.017	0.446	0.02	0.430
2R	−0.104	4.1e−8	−0.154	5.0e−8
3L	0.005	0.754	0.008	0.745
3R	−0.002	0.879	−0.003	0.918
X	0.013	0.449	0.019	0.435

Discussion

We have discovered a new feature, which we denote ψ, of the distribution of genomes in Hamming space that improves the performance of topological estimators of recombination. While the field of TDA is in its infancy, our work provides a novel demonstration of the power of persistent homology-based estimators for fundamental questions in evolutionary biology. Notably, our feature is related to biologically meaningful quantities in coalescent models; this is some of the first work we are aware of to make such a tight connection between TDA estimators and coalescent theory.

Our ψ-based approach to recombination rate inference is able to quickly scan large genomic datasets for regions of recombination rate heterogeneity. Due to its speed, it can serve as a first-pass estimate of recombination rate variation prior to targeted use of much more computationally expensive inference methods. While ψ itself can potentially be influenced by distortions to the genealogical structure of a sample, it is naturally complemented by higher dimensional topological features (namely ${\beta }_1$) of the data explored in prior work (Chan et al. 2013; Camara et al. 2016), while maintaining accuracy in the face of missing data which confounds ${\beta }_1$-only methods.

Similar to how ψ can supplement and guide the usage of evolutionary-model-driven methods, ψ can also add a degree of finer-scale detection and biological intuition to topology-driven methods, bringing us closer to bridging the gap between population genetics and persistent homology. The distinct behaviors of $H_0$ and $H_1$ derived statistics on genomic data also point toward the potential of TDA as a source for summary statistics that can tease apart the signatures of demography, selection, or population structure, a fundamental goal of population genetics. The behavior of ψ also suggests that topological quantities could be merged with a fully coalescent model of recombination, as a more rigorous SMC-based modeling could make explicit predictions for the distribution of the effect sizes of a single recombination events on ψ. In addition, the ordering of the $H_0$ features by duration of persistence hints at additional connections between barcodes and the look-down construction of the coalescent (Donnelly and Kurtz 1999; Pfaffelhuber and Wakolbinger 2006). We will explore these avenues in a future theoretical treatment of these statistics.

Summarizing, we have shown that a combination of TDA and machine learning techniques can detect recombination rate heterogeneity in biological data faster than previously possible and with greater accuracy than previous TDA-based approaches. We demonstrate that while the behavior of 0-dimensional barcodes has been previously ignored with respect to genealogical inference problems, these features are robust and increase the overall accuracy of inference compared to using one-dimensional barcodes alone. Our coalescent analyses also suggest a promising future endeavor: building a fully coalescent-motivated model explaining the behavior of Betti numbers on distributions of genome sequences.

Appendix A: Background on TDA

Topology is a branch of mathematics that concerns itself with classifying spaces or objects that have the same “shape.” Spaces are considered to be topologically equivalent if you can deform one into the other without breaking, tearing, or gluing. A topological invariant of interest in algebraic topology is the homology. Note that herein, homology refers to a mathematical concept rather than a biological one.

Homology can be thought of as a family of ways to associate a vector space to a geometric object. For the scope of this paper it suffices to restrict ourselves to homology with $\mathrm{\mathbb{Z}}/2\mathrm{\mathbb{Z}}$ coefficients in dimensions 0,1, and 2. For simplicity, we can think of the dimension 0 homology group as a representative of the connected components of a topological space, the dimension 1 homology group as a representative of the loops within a topological space, and the dimension 2 homology group as a representative of the voids within a topological space. That is, the 0-th dimension homology group of an object is a vector space whose dimension is the number of connected components of that object, and similarly for higher dimensions.

The rank of the $i^{th}$ dimensional homology group is known as the $i^{th}$ Betti number, denoted ${\beta }_i$, and, roughly speaking, it encodes the number of i-dimensional holes in the dataset (Carlsson 2009; Chazal et al. 2016; Edelsbrunner and Harer 2010; Ghrist 2014; Zomorodian 2009). For example, a Figure 8 consists of a single connected component (all the points in the boundary of the figure are connected) and two loops, so for this shape ${\beta }_0=1$, ${\beta }_1=2$, and ${\beta }_k=0$ for $k>1$ [see Figure 1a in Camara et al. (2016)]. In contrast, a basketball is one connected component (all points on the surface are connected) with one hollow sphere and no loops so its associated Betti numbers are ${\beta }_0=1$, ${\beta }_1=0$, ${\beta }_2=1$, and ${\beta }_k=0$ for $k>2$. To see why ${\beta }_1=0$ for this example, consider any loop on the basketball and fix some point p on the surface of the ball. Without breaking the loop, it is possible to slide the loop in a continuous manner (while remaining on the ball) toward p until eventually the loop contracts to p. Consequently all loops on the basketball are trivially equivalent to a point, i.e. ${\beta }_1=0$.

TDA lies at the intersection of algebraic topology, statistics, and data science. The main goal of TDA is to extract descriptive topological features from large, high-dimensional data sets, and one of the primary tools for doing so is called persistent homology. In this section, we briefly review the relevant TDA methodology that we apply to the study of recombination. [For a more detailed review of TDA applications in genomics, see Blumberg and Rabadan (2017).]

While shapes and surfaces have well-defined homology groups, computing the homology of data is less straightforward. Let X be a data set consisting of N data points living in some metric space $\left(S,d_S\right)$. Observe, X itself is simply a discrete set of points and thus it has no interesting homological properties beyond dimension 0. However, if each data point $x\in X$ is replaced by a ball $B_r\left(x\right)=\left\{y:d_S\left(x,y\right)\le r\right\}$ of radius $r>0$ centered at x, then the union of these balls over all points $x\in X$ yields a new topological space with nontrivial homology. Repeating this for a sequence of r values yields a sequence of topological spaces for which the homology can be computed. Analyzing how the homology changes across this sequence of topological spaces is the main idea behind persistent homology.

Algorithmically, this procedure is carried out by assigning a combinatorial model of a space, called a simplicial complex, to the data for an increasing sequence of r values. Here, we will focus on defining the Vietoris-Rips simplicial complex. For any $k=0,1,\dots$, we define a k-simplex as the convex hull of k + 1 affinely independent points, i.e., the k-simplex of $k+1$ affinely independent points is the convex polygon whose vertices are precisely the $k+1$ affinely independent points [Ghrist (2014), Edelsbrunner and Harer (2010)]. For example, a 0 simplex is a point, a 1 simplex is an edge, and 2 simplex is a triangle, and so on. Denote a k-simplex corresponding to the convex hull of $\left(x_{i_0},x_{i_1},\dots ,x_{i_k}\right)$ as ${\sigma }_k\left(x_{i_0},x_{i_1},\dots ,x_{i_k}\right)$. Then, the Vietoris-Rips complex of X with respect to r is the union of all k-simplices ${\sigma }_k\left(x_{i_0},\dots ,x_{i_k}\right)$ such that $B_R\left(x_{i_l}\right)\cap B_R\left(x_{i_j}\right)\ne \mathrm{\varnothing }$ for all $l,j=0,1,\dots ,k$. Note, another common simplicial complex is the C̆ech complex (mentioned in Coalescent Intuition for Topological Statistics), which instead requires nonempty mutual intersections of the k-simplices rather than nonempty pair-wise intersection.

The homology is computed on the simplicial complex representation of $\underset{x\in X}{{{\displaystyle \mathrm{\cup }}}^{\text{}}}{B}_r\left(x\right)$ instead of the original union. Simplicial complexes are easier to work with computationally, and there exist theoretical guarantees that make it feasible to compute the homology of simplicial complex instead of $\underset{x\in X}{{{\displaystyle \mathrm{\cup }}}^{\text{}}}{B}_r\left(x\right)$ [See Nerve theorem in Edelsbrunner and Harer (2010)].

Lastly, we take a sequence of parameters ${\left\{r_i\right\}}_{j=1}^N$, build the simplicial complex of X with respect to $r_j$ and compute its homology for all j. This yields a sequence of a families of vector spaces associated to X, known as the persistent homology of X.

We represent the persistent homology of X with a barcode diagram ${\mathrm{ℬ}}_i$ for each dimension i [Carlsson et al. (2005)]. A bar $\left(b,d\right)\in {\mathrm{ℬ}}_i$ represents a generator of homology in dimension i. The birth time b of the bar corresponds to the r value at which the homological feature first appeared and the death time d of the bar corresponds to the r value at which the homological feature collapsed. Bars with longer bar length (d–b) are of particular interest since they persist throughout the sequence of simplicial complexes.

Note, in the above construction, computing the homology of data only requires that the data of interest lie in a metric space. Topological changes will occur at discrete values of ϵ when the data lie in a Hamming space or other discrete metric space, whereas topological features may appear and disappear continuously in a continuous metric space. Regardless, persistent homology is suitable for any metric space and thus is a useful tool for summarizing genomic data [Camara et al. (2016), Blumberg and Rabadan (2017), Lesnick et al. (2018)].

In this work, X is a collection of genomes and we use the Hamming distance $d_H$ to build Vietoris Rips representations of sampled populations using $B_r\left(x\right)=\left\{y:D_H\left(x,y\right)\le r\right\}$. We then compute the persistent homology of X and extract statistics from the corresponding dimension-0 and dimension-1 barcode diagrams as input for the TREE.

One can think of persistent homology as an extension of hierarchical clustering for higher dimension homology groups, where dimension 0 persistent homology is analogous to single linkage clustering [Carlsson (2009)]. See Figure 1b for an example of persistent homology applied to an arbitrary dataset via the Vietoris-Rips complex.

Intuitively, in the presence of recombination events, the genealogy contains loops that correspond to dimension 1 homological features. This hypothesis was explored in certain cases in Camara et al. (2016); the loops do not appear in the absence of recombination, and, consequently, ${\beta }_1$ can be used to predict recombination rate. This is illustrated in Figure 1c (although we note that in the context of standard coalescent assumptions, this connection is more complicated than it appears; see Explaining ${\mathit{\beta }}_1$ for details). One of the main discoveries we describe is that in fact the mean barcode length in dimension 0, denoted ψ, is an even more accurate predictor of recombination rate than ${\beta }_1$. We note that each bar in the dimension 0 barcode diagram corresponds to an individual in the sample population, and the bar lengths correlate with distance between the individual, or cluster of individuals, and its closest neighbor in Hamming space.