Potential Mean Force from Umbrella Sampling Simulations: What Can We Learn and What Is Missed?

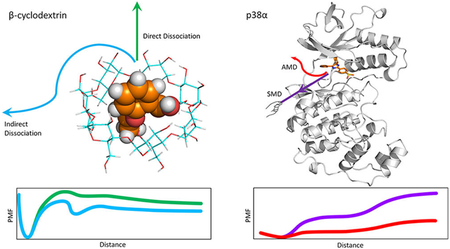
Abstract

Changes in free energy provide valuable information for molecular recognition, including both ligand–receptor binding thermodynamics and kinetics. Umbrella sampling (US), a widely used free energy calculation method, has long been used to explore the dissociation process of ligand–receptor systems and compute binding free energy. In existing publications, the binding free energy computed from the potential of mean force (PMF) with US simulation mostly yielded “ball park” values with experimental data. However, the computed PMF values are highly influenced by factors such as initial conformations and/or trajectories provided, the reaction coordinate, and sampling of conformational space in each US window. These critical factors have rarely been carefully studied. Here we used US to study the guest aspirin and 1-butanol dissociation processes of β-cyclodextrin (β-CD) and an inhibitor SB2 dissociation from a p38α mitogen-activated protein kinase (MAPK) complex. For β-CD, we used three different β-CD conformations to generate the dissociation path with US windows. For p38α, we generated the dissociation pathway by using accelerated molecular dynamics followed by conformational relaxing with short conventional MD, steered MD, and manual pulling. We found that, even for small β-CD complexes, different β-CD conformations altered the height of the PMF, but the pattern of PMF was not affected if the MD sampling in each US window was well-converged. Because changing the macrocyclic ring conformation needs to rotate dihedral angles in the ring, a bound ligand largely restrains the motion of cyclodextrin. Therefore, once a guest is in the binding site, cyclodextrin cannot freely change its initial conformation, resulting in different absolute heights of the PMF, which cannot be overcome by running excessively long MD simulations for each US window. Moreover, if the US simulations were not converged, the important barrier and minimum were missed. For ligand–protein systems, our studies also suggest that the dissociation trajectories modeled by an enhanced sampling method must maintain a natural molecular movement to avoid biased PMF plots when using US simulations.

Graphical Abstract:

INTRODUCTION

Free energy is an important quantity that characterizes chemical and biological processes. The change in free energy governs the directionality and extent of binding and unbinding kinetics. For these reasons, one central task for the computational chemist is to achieve accurate calculation of free energy, especially the free energy profile along a chemical or biological Process.^1–3

A variety of free energy calculation methods developed in the past decades include perturbation theory,^4,5 thermodynamic integration,⁶ umbrella sampling (US),^7,8 partition function from density of states,⁹ and MM/PBSA-type methods.¹⁰ US is one of the most popular methods that efficiently and reliably computes the potential of mean force (PMF) based on rigorous probability calculations along a given coordinate.⁷ It requires a well-defined reaction coordinate (RC) represented by one or a few variables.^11–13 Intensive conformational sampling is performed by enforcing external restraints at the conformations along the RC within a series of successive overlapping windows. Finally, the PMF can be constructed by removing the external restraints.

US is particularly suitable for computing the PMF of noncovalent ligand–receptor association/dissociation processes. It has long been used to calculate binding affinity of various receptor–ligand systems, ranging from small chemical molecular systems^14,15 to large biological systems.^16–18 By computing local energy barriers along a binding/unbinding path, a PMF can provide thermodynamic details for molecular recognition. However, US itself does not provide the dissociation path. Therefore, enhanced sampling methods, such as steered molecular dynamics simulation (SMD),^19,20 adaptive biasing force (ABF),²¹ and metadanamics,²² are often used to provide the dissociation pathway that can be used as an initial conformation for the intensive biased sampling for US.

A number of methods have been proposed to improve the accuracy of US, such as the use of constrained schemes to alleviate sampling limitation,^12,23,24 replica exchange umbrella sampling,^25–27 or combination with other methods such as the Markov model to improve the convergence.²⁸ Although US has been widely applied to various systems for computing binding free energy and a PMF along an RC, results that can potentially be affected by initial conformations, trajectories, or RC with US have rarely been studied. Here we investigated the influential factors of US by computing PMFs for ligand dissociation from β-cyclodextrin (β-CD) complexes and p38α mitogen-activated protein kinase (MAPK).

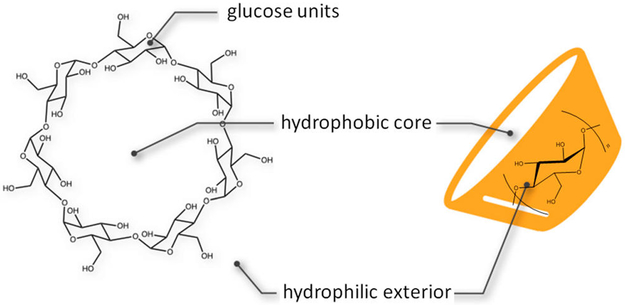
β-CD is a cyclic oligosaccharide containing seven glucopyranose units linked via 1,4 α glycosidic bonds, thus forming a truncated conical structure. With a hydrophobic inner surface and hydrophilic rims containing primary and secondary hydroxyl groups, β-CD is able to accommodate small hydrophobic molecules, thereby enhancing the solubility and bioavailability of such molecules (Figure 1). The cavity of β-CD also resembles a protein binding site, which makes it a good host molecule to study ligand–receptor binding. Because of these properties, β-CD and its derivatives have been well-studied and widely applied in drug-delivery, pharmaceutical, food, and chemical industries.²⁹ The guest–β-CD systems also serve as good model systems to study ligand–receptor binding thermodynamics and kinetics and to examine the accuracy of force-field parametrization.^15,30,31

Figure 1.

Structure of β-CD. β-CD consists of seven glucopyranose units with a hydrophobic core and hydrophilic exterior.

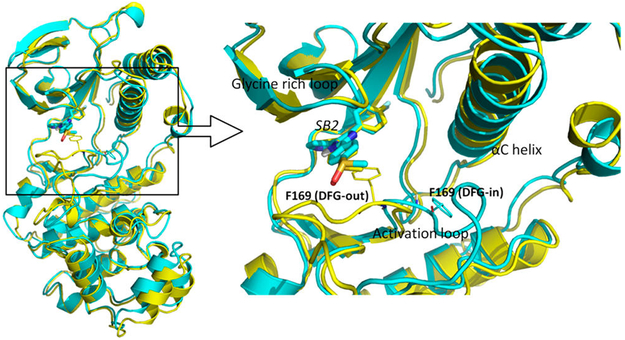
p38α is the major isoform of p38, belonging to the MAPKs, a superfamily of enzymes that regulate a variety of biological processes, such as proliferation, gene expression, differentiation, and apoptosis.^32,33 p38α is a drug target for treating various inflammatory diseases, including rheumatoid arthritis, asthma, and cardiovascular disease.^34–40 Like all protein kinases, p38α contains a N-terminal domain and C-terminal domain that are connected via a hinge.⁴¹ The activation loop that carries a DFG (Asp-Phe-Gly) motif determines the opening or closing of the binding cavity, where adenosine triphosphate (ATP) binds during the activation process. The conformational change of activation loop can be characterized by different orientations of its Phe side chain. In the active conformation, Phe is buried in the αC helix (DFG-in), whereas in the inactive conformation, Phe rotates away from the αC helix and projects into the ATP binding pocket (DFG-out). Of note, inhibitors binding to DFG-in or DFG-out loop conformations may have the same binding affinity with profoundly different kinetic behavior, and ligands binding to p38α with the DFG-out loop position can be orders of magnitude slower than those binding with the DFG-in loop conformation.⁴² NMR and computation studies showed that DFG-in and DFG-out conformations have equal populations in the apo p38α^43,44 and ligand SB2, which binds to the ATP binding site, while the activation loop adopts the DFG-in or DFG-out conformation⁴³ (Figure 2). NMR study also showed that SB2 binding does not interfere with the conversion between DFG-in and DFG-out conformations of the activation loop. Therefore, we chose SB2 binding to both DFG-in and DFG-out loop conformations as our model system to investigate the PMF computed by US.

Figure 2.

Comparison of the bound structures of SB2 in DFG-in and DFG-out conformations. (left) The structure alignment of DFG-in (cyan, PDB 1A9U) and DFG-out (yellow, PDB 3GCP) conformations bound with ligand SB2. (right) The binding site structure of the p38α–SB2 complex. The Phe169 from the DFG motif is shown as a thin licorice structure, and ligand SB2 is shown as a bold licorice structure.

In this work, we investigated how the PMF from US is affected by subtle changes in the initial structures of a receptor. We also used protein–ligand dissociation trajectories obtained by different enhanced sampling methods. We examined aspirin and 1-butanol unbinding processes from β-CD and various p38α-SB2 dissociation trajectories sampled from accelerated MD (AMD), SMD, and manual pulling of SB2. By using different β-CD conformations as a starting point for US, we found that the host conformation can essentially change the depth of the PMF from US, and the influence of initial conformation can barely be eliminated by running well-converged biased MD simulations for each window, even though a β-CD complex is a reasonably small system. We found that changing the macrocyclic ring of β-CD needs to rotate dihedral angles in the macrocyclic ring; a bound ligand largely restrains the motion of β-CD. Therefore, once a guest is in the binding site, β-CD cannot freely change its conformation from one to another because our three different initial β-CD conformations have different ring puckers. Different β-CD conformation has different conformation energy, which results in different absolute heights of the PMF, which cannot be overcome by running excessively long MD simulations for each US window. Although the absolute values of PMF may not be identical when using different β-CD conformations, the patterns of PMF that illustrate local energy barriers and minima are the same. Our study also showed that in sampling ligand–protein dissociation trajectories, the pathways cannot have abrupt ligand/protein movement during ligand unbinding. Postprocessing by classical MD simulations using frames saved from an enhanced sampling method such as AMD can effectively smooth the trajectories for US simulations. We also suggest that directly applying forces using SMD to drag SB2 from the binding site can produce unnatural movements of protein side chains that bias the computed PMF when using US simulations.

MATERIALS AND METHODS

Structure Preparation and Parameters.

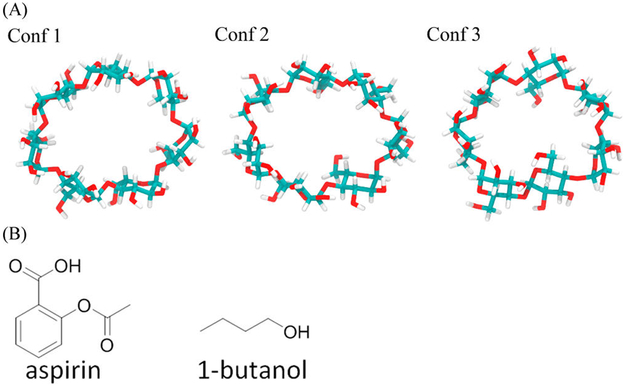
β-CD. Because the ligand and β-CD cocrystal structures are not available, structures of each ligand bound to β-CD were obtained from previous MD simulations.⁴⁵ Two ligands, namely, aspirin and 1-butanol, were selected for performing US along manually built dissociation pathways as detailed later (Figure 3). The structures of these two ligands were taken from previous work by using the minimized structures for MD simulations. The partial charges and parameters of β-CD–aspirin and β-CD–1-butanol complexes were taken from the same previous work.⁴⁵ The structures of the three initial β-CD conformations were conformations with high populations from existing MD simulations⁴⁵ and with low computed free energy.⁴⁶

Figure 3.

Structures of ligands and three β-CD conformations. (A) Three different conformations of β-CD. The plots of their conformation fingerprint angles (defined in Figure S1) along trajectories are in Supporting Information Figure S1. (B) Structures of aspirin and 1-butanol.

p38α. SB2 is a ligand of the p38α system that binds to both DFG-in and DFG-out conformations. We obtained the p38α DFG-in conformation (PDB ID: 1A9U)⁴⁷ and DFG-out conformation (PDB ID: 3GCP)⁴⁸ from the protein databank (PDB). We built the missing activation loop (residues 173 to 184) of 3GCP by using the conformation from a previous MD simulation of free DFG-out p38α.^13,44 Amber 99SB force field was used for proteins, and GAFF was used for ligand SB2.⁴⁹

Preparation of Dissociation Paths for US.

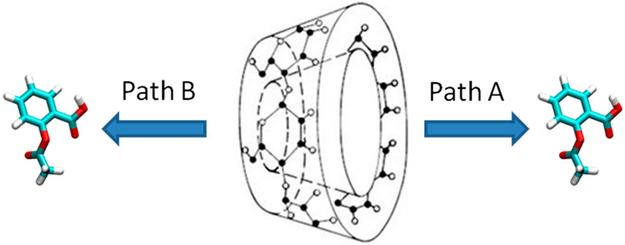
For β-CD, we manually placed the ligands along the dissociation path. First, we put the center of mass (COM) of β-CD at the origin (0, 0, 0) and aligned its principal axes along X, Y, and Z axes, so that the primary cavity of β-CD faces the positive direction of the X-axis. Then, we manually located the ligand so that its COM was also aligned at the origin. By using this artificial bound conformation, we gradually moved the ligand along the positive and negative X-axis with 0.1 Å every step for 26 Å in both directions, until the ligand was fully dissociated. In this way, we obtained paths A and B for ligand dissociation along the primary and secondary cavity of β-CD (Figure 4). We repeated this procedure for aspirin and 1-butanol in the three β-CD conformations.

Figure 4.

Dissociation pathways of β-CD complexes. Path A is from the primary cavity, and path B is from the secondary cavity of β-CD.

For the p38α–SB2 system, we constructed the dissociation paths by using three methods–AMD, SMD, and manual pulling as used for β-CD. We obtained two paths from AMD (path1 and 2), one path from SMD, one path from manual pulling for the DFG-in conformation, and one path from AMD for the DFG-out conformation.

Accelerated MD Simulation.

AMD introduces a continuous non-negative bias boost potential function ΔV(r) to the potential energy surface when the system potential is below a reference energy, to enhance the conformational sampling of biological systems, thereby lowering the local barriers to accelerate the calculation.⁵⁴ AMD uses the following equations to alleviate the energy barriers

$$\begin{gathered} V^{\ast }(r)=V(r)+\Delta V(r) \\ \Delta V(r)=\{\begin{array}{cc}0\hfill & V(r)\ge E\hfill \\ \frac{(E-V(r){)}^2}{\alpha +(E-V(r))}\hfill & V(r)<E\hfill \end{array}\phantom{\}} \end{gathered}$$

where V(r) is the original potential, E is the reference energy, and V*(r) is the modified potential. ΔV(r) is the boost potential, and α is the acceleration factor.

The boost potential ΔV(r) can be applied to dihedrals with input parameters (Ed, αD) and overall potential energy terms with input parameters (Ep, αP)

$$\Delta V(r)=\frac{(\text{Ep}-V(r){)}^2}{(\alpha \mathrm{P}+\text{Ep}-V(r))}+\frac{(\text{Ed}-Vd(r){)}^2}{(\alpha \mathrm{D}+\text{Ed}-Vd(r))}$$

For simulations of p38α, we applied both potential-boost and dihedral-boost.

Steered MD Simulation.

SMD simulation uses a time-dependent external force to drive the system to move in a predefined way.⁵⁵ The external force V(t) can be described as follows, V(t) = k[x – x₀(t)]², where x and x₀(t) are the variables in simulation and the predefined time-dependent track of the variables, respectively, and k is a harmonic force constant. We selected the distances between Cα of Arg173 and CC2 of SB2 (Figure S2), which is also used to describe the RC in US, as the variables used. Arg173 has the smallest root-mean-square fluctuation (RMSF) value computed from our classical MD simulations among the alpha carbons of residues in the alpha C helix (from Ile63 to His77), which makes Arg173 the most stable dissociation reference. The CC2 atom of ligand SB2 is the geometric center of the ligand. In addition, the vector of the α carbon of Arg173 and CC2 of the ligand is generally consistent with the dissociation directions when comparing with our multiple AMD runs that we performed earlier (data not shown). Therefore, we chose the vector between the α carbon of Arg173 and CC2 of the ligand as the direction for both steered MD and manual pulling. x₀(t) was set to move by 1.75 Å/ns and with a maximum at 33 Å. The force constant k was set to 10 kcal/mol·Å². We ran the bound state conformation for 100 ns by using conventional MD, then performed SMD for 10 ns at 300 K and 1 bar in the NPT ensemble. Temperature was maintained by a Langevin thermostat.

Manual Pulling.

In manual pulling, the crystal structure of SB2 bound to p38α (1A9U) was used as a reference conformation. Ligand SB2 was gradually moved along the vector of Cα of Arg173 and CC2 of SB2 toward the outside of the cavity at a speed of 0.25 Å every step for 16.75 Å, until SB2 was fully dissociated.

Umbrella Sampling.

US^56,57 was performed to compute the free energy along the dissociation pathway. In US, a series of windows is evenly located along RC, and intensive sampling in these windows is achieved by enforcing an external biasing potential. The samplings in each window must overlap with adjacent windows, so that the unbiased PMF can be reproduced by removing the biasing potential. The external biasing potential u_i at window i is a harmonic function u_i = k_i(r – r_i)², where r_i is the reference position, and k_i is the harmonic force constant. All biased MD simulations were performed with Amber14.⁵⁸ We used WHAM⁵⁹ and MBAR⁶⁰ to remove the biasing potential and reconstruct the PMF. Both methods resulted in highly similar PMF, and figures generated from WHAM are reported here.

For β-CD, the distance between the COMs of the heavy atoms of β-CD and the ligand was selected to represent the RC. As described in the previous section, a total of 260 windows with 0.1 Å spacing along the RC were used for biased MD simulations. We minimized the initial conformation for each window for 1500 steps by using the generalized Born implicit solvation model⁶¹ to remove clashes from manual pulling. Then we solvated the β-CD–ligand complex with a 30 Å rectangular box of TIP3P water molecules by using the tleap module in AMBER14.⁶² After minimizing the system for 1000 steps, we equilibrated the water molecules at 298 K for 1 ns with a 1 fs time step and heated the entire system at 200, 250, and 298 K for 150 ps. In the minimization and equilibration steps, a harmonic force constant of 1000 kcal/mol·Å² was used to restrain the ligand at the correct window. Finally, we performed a 2.5 ns production run at 298 K with restraint by using the harmonic force constant of 100 kcal/mol·Å². In WHAM, the bin size was set to 0.05 Å. The tolerance for iteration was set to 0.0001. The temperature was set to 298 K.

For p38α, the distance between Cα of Arg173 and CC2 of SB2 was selected as the RC. We prepared five trajectories from manual pulling, AMD, and SMD simulations for computing PMF by using US. Although AMD provided dissociation pathways, the frames saved every 1 ps sometimes were not continuous enough to smoothly connect each window. Therefore, we used 10 ns conventional MD simulations on the conformations along the two DFG-in and one DFG-out paths produced from AMD before we used them as initial conformations in each window for US (Figure S2). Although ligand SB2 mostly stayed in the same position during a short 10 ns classical MD simulation, in some cases SB2 moved toward the inside or outside of the cavity, which allowed for building a smooth dissociation pathway. Protein conformations obtained from two to three 10 ns MD simulations were superimposed, and we measured the root-mean-square deviation (RMSD) value for different classical MD frames of SB2. We selected the frames with the smallest RMSD but 0.25 Å apart along the RC as initial structures for each US window. No short 10 ns MD simulations were performed for frames from SMD. Frames from SMD were superimposed, and again we selected the frames with the smallest RMSD but 0.25 Å apart along the RC as initial structures for each US window. For the manual pulling path, because the system is not optimized or solvated, we performed the following steps on the conformations we obtained before proceeding to biased MD sampling. We optimized the conformations along the path by minimizing the hydrogen atom, side chains, and entire complex for 500, 5000, and 5000 steps, respectively, for the same reason as for β-CD. Next, we solvated the conformation by using the TIP3P water model,⁶² so that the edge of the water box is at least 12 Å away from the solutes. We also added Na⁺ ions to neutralize the system. We optimized the water molecules and the entire system for 10 000 and 20 000 steps, respectively. After equilibrating the solvate for 40 ps at 298 K in NPT, we heated the system from 250 to 300 K gradually. In the minimization and equilibration process, the external force constant was 500 kcal/mol·Å². In total, 62 windows from SMD, 68 windows from path1, 2 and manual pulling, and 71 windows from the DFG-out path were evenly located every 0.25 Å along the RC. For all five sets of conformations, we performed a production run for 10 ns at 300 K with an external restraint of 5 kcal/mol·Å². In WHAM, the bin size was set to 0.2 Å, the tolerance for iteration to 0.0001, and the temperature to 300 K.

For both β-CD and protein system, we ran excessively long MD simulations, several times longer than the reported length here, for selected consecutive windows, to test the convergence. We also tested the harmonic force constant, the bin size, and the tolerance to ensure that all the PMF plots are well-converged for each provided pathway.

All trajectories and input and output files are available upon request.

RESULTS AND DISCUSSION

PMF of Aspirin and 1-Butanol Unbinding from β-CD with Different Conformations.

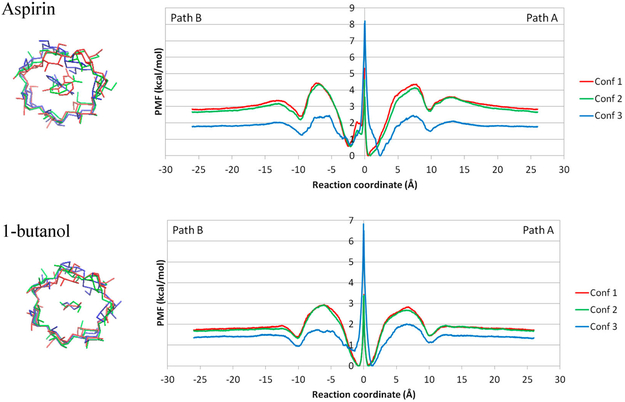
As illustrated in Figure 4, ligands aspirin and 1-butanol can dissociate from the primary cavity (path A) or the secondary cavity of β-CD (path B). Therefore, the PMF is constructed for both unbinding paths. The combined PMFs for β-CD–aspirin and β-CD-1–butanol from both paths are shown in Figure 5. Comparing conformations (confs) 1 and 2 with conf3 of the β-CD, clearly, host conformations had a remarkable impact on the absolute values of free energy shown in the PMF. Importantly, the overall shape of the plot with the three conformations is similar, with one major energy barrier during ligand dissociation. Because the primary and secondary cavities of β-CD are not identical, paths A and B are highly similar but not identical. For aspirin, the binding affinity, ΔG, of conf1 and 2 is −2.8 and −2.7 kcal/mol, which are similar, whereas the binding affinity of conf3 is only −1.8 kcal/mol. The binding affinities of conf1 and 2 are 1 kcal/mol less favorable than the experimental value, −3.77 kcal/mol. For 1-butanol, the binding affinities of conf1, 2, and 3 are −1.7, −1.7, −1.3 kcal/mol, respectively. The binding affinities of conf1 and 2 agree with experimental value (−1.67 kcal/mol). We considered only three representative β-CD conformations, but in reality, β-CD can adopt many more conformations in the ligand association and dissociation. Another β-CD conformation could result in the ΔG of aspirin being closer to the experimental value; however, it was not selected in this study. Notably, in US, the harmonic potential was applied to only the direction of the RC, which is the COM distance between the ligand and β-CD. The ligand is free to move on the sphere with a radius of the COM distance in that window, which results in unrestrained deviation from the X-axis.

Figure 5.

PMF of dissociation of aspirin and 1-butanol from β-CD. Path A and Path B are combined in the same plot for conformation (conf) 1, 2, and 3 of β-CD–aspirin and β-CD-1–butanol complexes. The three initial conformations were aligned using the heavy atoms of glucose rings with the smallest RMSD, the bottom part of the conformation plot. Note that a ligand cannot pass through the origin of the reaction coordinate, and the energy barrier in the middle point should be ignored. Motions of cyclodextrin are restrained by a bound ligand; therefore, initial confs 1, 2, and 3 cannot switch to another initial conformation while the ligand is in the bound state.

The difference in barrier heights between different ligands provides accurate information in terms of which ligand can associate/dissociate faster or slower from β-CD. Because the PMFs from confs1 and 2 are highly similar, here we focus on PMFs constructed from conf1. When a ligand is binding to conf1 of β-CD, the PMFs (Figure 5) suggested that the association energy barriers of aspirin and 1-butanol are 1.5 and 1.1 kcal/mol, respectively. The similar association energy barriers of aspirin and 1-butanol agree with these two ligands having similar association rate constants (Table 1). Although the twofold faster association rate constant for aspirin implies a smaller association energy barrier and the computed value is actually larger than for 1-butanol, the difference in the barrier is less than 0.6 kcal/mol and can be considered variation from the β-CD conformation and errors due to thermal fluctuation. The computed dissociation energy barriers for aspirin and 1-butanol from conf1 are 4.4 and 2.8 kcal/mol, respectively. This observation agrees with the relative experimental dissociation rate constants.

Table 1.

Experimental Kinetics and Thermodynamics Data for Aspirin and 1-Butanol Complexed with β-CD, and SB2 Complexed with p38α^a

complex system	KD (M)	kon (M−1 s−1)	koff (s−1)	ΔGexp (kcal/mol)
β-CD–aspirin	1.81 × 10−3	7.20 × 108	1.30 × 106	−3.77
β-CD-1–butanol	1.36 × 10−1	2.80 × 108	3.80 × 107	−1.67
p38α-SB2	11.5 × 10−9	1.5 × 107	1.8 × 10−1	−10.90

^aK_D, k_on, and k_off data for complexes were taken from refs 50–52. The ΔG_exp, for the β-CD–1-butanol complex was taken from ref 53. The ΔG_exp for the β-CD–aspirin and p38α–SB2 complexes were calculated as ΔG_exp = RT ln K_D.

The PMFs in Figure 5 unambiguously indicates that the ligands bind preferentially to the primary cavity of β-CD. The ligand binds to β-CD from −3 to +3 Å in depth, with a huge energy barrier in the middle of the plots. By close investigation of the population plot (Figure S3), we noticed that this energy barrier near the origin of the RC was an artifact (Supporting Information Section Artifact of Restraints). Classical MD simulations showed that, due to geometry constraints, when aspirin or 1-butanol is binding to β-CD via the primary cavity, it will dissociate from the same site and vice versa.⁴⁵ Therefore, this energy barrier at the origin of the RC should be ignored. By looking at the PMFs without this energy barrier, we observed that the free energy of the primary side is consistently 0.6 kcal/mol more favorable than the secondary side, with one exception of 1-butanol in confs1 and 2. The primary side of the β-CD cavity is more open and allows the aspirin to better fit into it. Because of the small size of 1-butanol, it can fit into both primary and secondary sides of the β-CD cavity in conf1 and 2. In conf3, the size of the cavity shrinks because of the flipping of two of the glucopyranose units of β-CD; therefore, 1-butanol prefers to bind to the larger primary side of the β-CD cavity (Figure 3).

Notably, although we would wish a system could sample all possible configuration for each window if adequate simulation length is provided and result in a well-converged ΔG, it is not possible for many bound complex conformations. Changing the β-CD conformation may need to rotate dihedral angles in the macrocyclic ring, and a bound ligand largely restrains the motion of β-CD. Because our three different initial β-CD conformations have different ring puckers, once aspirin or 1-butanol is in the binding site, β-CD cannot freely change its initial conformation. Because different β-CD conformation has different conformation energy (Table S1 in Supporting Information), it is reason to yield different absolute heights of the PMF and ΔG. Running excessively long MD simulations or applying enhanced sampling techniques for each US window cannot overcome this limitation, because the ligand must leave the binding site for β-CD to alter a ring pucker. The restricted cyclodextrin motions when a ligand is in the binding cavity have been discussed in previous publication.⁶³

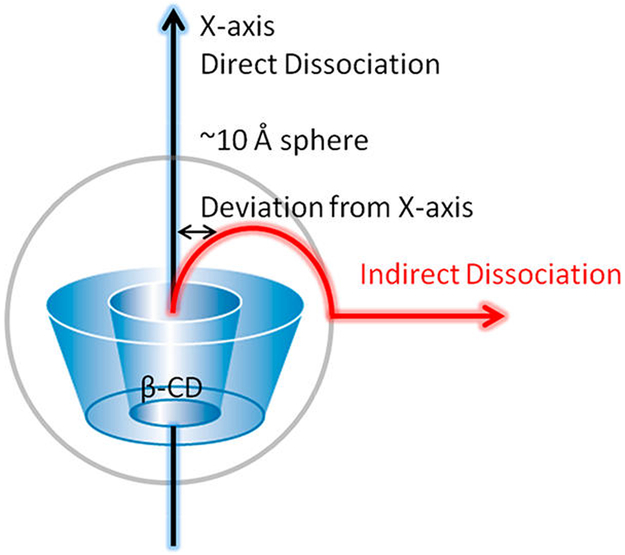
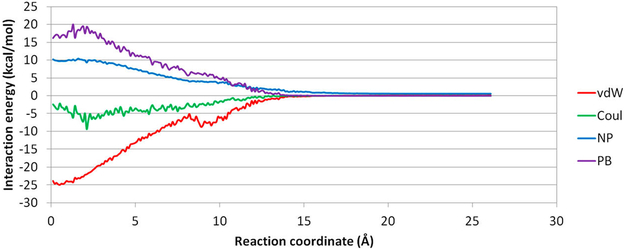
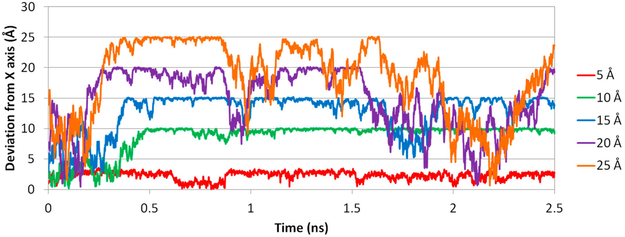
Because we only put restraints on the RC represented by the COM distance between the host and guest, we did not restrain the position of the ligand. For example, in the window where the COM distance is 10 Å, the ligand can adopt positions anywhere on a sphere with a radius of ~10 Å. When there are no intermolecular interactions between the ligand and β-CD, the ligand should have equal population in all positions on the 10 Å sphere. In reality, the intermolecular attractions alter the distribution of the ligand on such a sphere and significantly deviate the ligand from the initial positions, despite the initial positions being placed along the X-axis (Figure 6). In our simulation for aspirin, the ligand more or less followed the X-axis dissociation pathway within 7 Å on the RC because of the geometrical restraints from the β-CD cavity. The ligand is free from the geometrical restraints and can diffuse on the spherical space under control of intermolecular interactions in windows above 7 Å and within 13 Å. Note that, between 10 and 13 Å, the ligand can form favorable van der Waals (vdW) interactions if the ligand is far away from the X-axis and sticks to the outer surface of β-CD (Figure 7). Hence, the ligand deviates from the initial path along the X-axis remarkably in that region (Figure 8). Apparently, even at the same COM distance of 10 Å, the ligand naturally tends to stay closer to β-CD when it is on the outer surface of β-CD with stronger attractions than when it is aligned to the X-axis, where no stronger attraction can be formed. This situation will certainly affect the shape of the PMF. When the RC is beyond 15 Å, the two molecules do not form strong interactions any more, and the ligand is totally free to diffuse in the spherical space in the simulation for one US window. With this concern, it is interesting to investigate how PMF will be affected by the direct dissociation along X-axis and the indirect dissociation when the ligand diffuses to the outer surface of β-CD and then dissociates.

Figure 6.

Direct and indirect ligand dissociation paths from β-CD. In the direct dissociation, the ligand moves out of the binding site along the X-axis. In the indirect dissociation, the ligand first diffuses to the outer surface of β-CD, which is ~10 Å from the X-axis, then dissociates from there. Notably, during US, the initial position of a ligand for each window is placed along the X-axis, which presents a direct dissociation.

Figure 7.

Plot of averaged MM/PBSA energy at each US window. van der Waals energy (vdW), Coulombic energy (Coul), nonpolar solvation energy (NP), and PB solvation energy (PB) of aspirin from β-CD in Conf1 along path A were averaged in the biased MD for each window.

Figure 8.

Deviation of aspirin from the X-axis at different RC distances. Deviations at 5, 10, 15, 20, and 25 Å during the dissociation process of aspirin from β-CD in conf1 along path A are shown in red, green, cyan, purple, and orange, respectively.

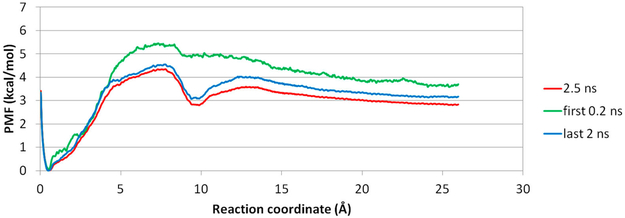
As illustrated in Figure 6, the initial position of a ligand for each window is placed along the X-axis, which presents a direct dissociation. Because of intermolecular attractions, after MD is run for longer than 0.2 ns, the position of a ligand starts to deviate from its initial location (Figure 8). Therefore, we used data from the first 0.2 ns and last 2.0 ns MD runs to construct PMFs for a direct or indirect dissociation pathway, respectively (Figure 9). When aspirin dissociates directly to the solvent, all intermolecular attractions quickly diminish, and the PMF shows a high dissociation energy barrier at ~7 Å in the RC, with no obvious local energy minima during the unbinding process. In contrast, when US simulations are allowed for longer MD simulation lengths, aspirin is able to find positions with optimized intermolecular attractions within each window and does not dissociate into the solvent directly. This indirect dissociation process results in a PMF with a smaller free energy barrier and local energy minima at 10 Å along the RC. Thus, providing an adequate MD simulation length for each US window is critical. For large biomolecular systems, a few nanoseconds of MD simulation may not be able to allow the system to thoroughly explore the conformational space in each window,^16,64 and methods have been developed to improve the conformational sampling for each window during US sampling ^26,28,65

Figure 9.

Three PMF plots for aspirin dissociating from β-CD in conf1 along path A. (red) Complete 2.5 ns biased MD for US. (green) First 0.2 ns biased MD for US. (blue) Last 2.0 ns biased MD for US.

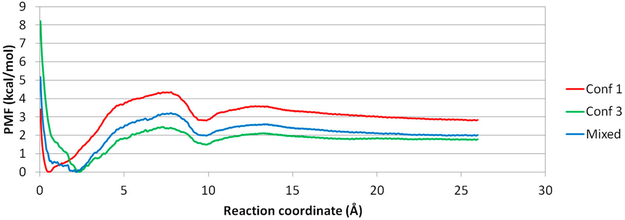
To further explore how the β-CD may affect the PMF plots from US simulations, we randomly chose data along the RC from β-CD conf1, 2, and 3 to construct a PMF. In this way, we introduced an ensemble of β-CD conf1, 2, and 3 conformations when we performed US simulations. As anticipated, when using data from β-CD conf1 and 3, the new PMF situates between the two plots (Figure 10). The overall shape was preserved, with a local energy minimum near 10 Å along the RC. However, the dissociation energy barrier differed. Therefore, the initial conformation chosen to run US simulations for a molecular system can greatly influence the absolute values of the barrier height and binding free energy ΔG, even the system can thoroughly explore its conformational space for each umbrella window. However, the overall shape of the PMF plot, such as the location of free energy barriers and minima along a RC, should be highly similar. As a result, with careful setups so that the MD runs for each window are well-converged, the PMF plots from US simulations can still yield accurate information regarding where the barriers are along the provided RC.

Figure 10.

Aspirin PMFs using Conf1, Conf3, and a mixture of conf1 and 3 along path A. The mixed PMF in conf1 and 3 locates between the PMF of conf1 and 3.

Unbinding Process of p38α Complex System.

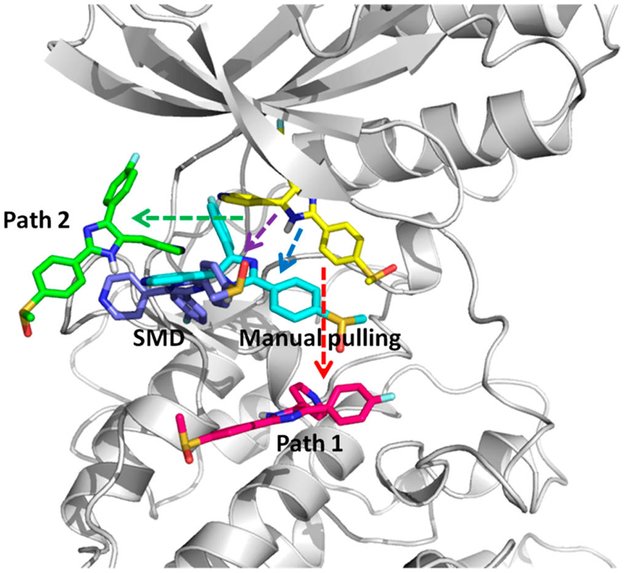
Ligand–protein association or dissociation pathways bring insights into molecular recognition and binding kinetics; however, the trajectories are usually descriptive without energy information. US sampling used to construct a PMF for an available association or dissociation pathway is particularly useful to calculate the free energy along the given pathway or RC. Modeling ligand–protein dissociation typically needs enhanced sampling methods because of longer than millisecond processes, so classical MD simulations are impractical. Different enhanced sampling techniques may bring different artificial biases that can result in different ligand–protein dissociation behaviors. To examine the PMF constructed from dissociation paths from different pathways by using different enhanced sampling methods, we prepared five dissociation paths of a ligand SB2 from the p38α complex with AMD, SMD, and manual pulling. Path1 and 2 were obtained by using AMD to sample SB2 dissociating from p38α with a DFG-in conformation. The directions of path1 and 2 are different, as indicated in Figure 11. In path1, SB2 quickly moves to the solvent (Figure S4). However, in path2, SB2 stays the hinge region of p38α and diffuses on the surface of the hinge area, until it eventually moves away from the protein surface. Path3 also uses AMD to sample the SB2 dissociation but from the SB2–p38α complex, where the protein has a DFG-out loop conformation. SB2 ligand in SMD and manual pulling are dissociated from different directions, between the two sampled dissociation pathways from path1 and 2. Notably, the original AMD trajectories were saved every 1 ps, and frames sometimes were not continuous enough to smoothly connect two consecutive windows. Therefore, we performed 10 ns conventional MD simulations for many selected frames to further smooth the AMD trajectories, as detailed in Methods. We suggest thoroughly inspecting every trajectory obtained from enhanced sampling techniques and carefully removing any discontinuous motion before using the trajectory to construct a PMF.

Figure 11.

Four dissociation paths for the SB2–p38α complex with the DFG-in conformation. (yellow) Crystal bound conformation of SB2. (red) Path1, where SB2 direct moves toward the outside. (green) Path2, where SB2 diffuses on the surface of the hinge region until moving out. (cyan) Manual pulling path. (purple) SMD path. SB2 in manual pulling and SMD paths moves out along directions between the two directions of path1 and 2.

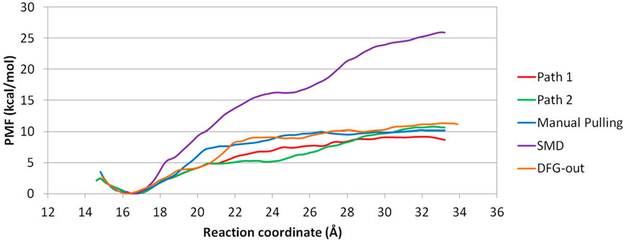
PMF plots of the five paths of SB2 dissociation are shown in Figure 12. Of note, except for the PMF from SMD, the other PMF plots predict similar binding affinities, ΔG, which are ~8 to 10 kcal/mol. The binding affinities from these paths somehow fall into the common range of ΔG for drug-like compounds⁶⁶ and close to the experimental value (Table 1), regardless of the diversity of behaviors of energy barriers along the dissociation pathway and protein conformations. However, US using the SMD path predicts a binding affinity of ~25 kcal/mol, which is apparently large, so either each window is far from well-converged or the dissociation trajectory is very unfavorable. Notably, we used a simple RC in this study–the distance between Cα of Arg173 and CC2 of SB2. This simplified RC may not be able to accurately reveal the free energy profile during SB2 dissociation. Moreover, although many dissociation pathways can be obtained by steered MD, we use this pathway to illustrate possible results from SB2 direct dissociation.

Figure 12.

PMF plots of the SB2–p38α complex. (red, green) Path1 and 2 from the AMD path with conformation relaxed using short conventional MD. (cyan) Manual pulling. (purple) SMD. (orange) AMD path with conformation relaxed with short conventional MD for dissociation of SB2 from the DFG-out conformation.

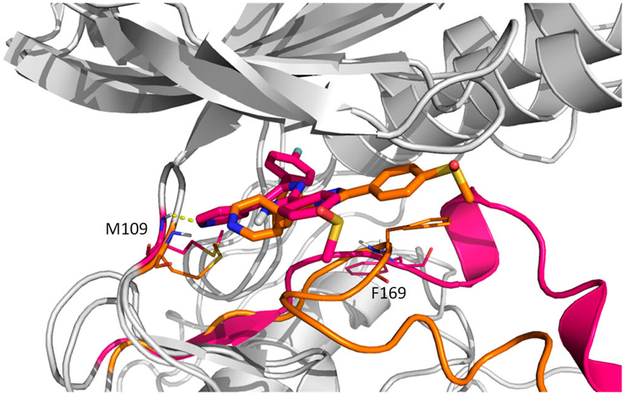
NMR spectrum showed that binding of SB2 does not affect the slow exchange between the DFG-in and DFG-out loop conformations, and SB2 can bind to p38α with either loop conformation equally well.⁴³ The binding affinities computed by using path1 and 2 are −8.7 and −10.6 kcal/mol, respectively, and ΔG of SB2 with a DFG-out conformation is −11.2 kcal/mol. The PMF reproduced experimental ΔG and agreed with experiments that SB2 can bind to both loop conformations equally well. Although we used a very simple RC, the PMF can capture interesting phenomena of a dissociation pathway. For example, in path2, SB2 diffuses on the surface of the hinge region during dissociation, so the free energy stops increasing but rather plateaus between 21 and 24 Å. In the DFG-out conformation, after SB2 breaks its hydrogen bond with Met109, the 4-methylsulfinylphenyl group can rotate back inside the cavity. The phenyl ring then forms a stacking interaction with Phe169, which also appears when SB2 binds to p38α with a DFG-in loop conformation (Figure 13). The study suggests that, although the RC used here is very simple, the PMF from the three trajectories can provide valuable information for SB2 dissociation and yield experimental ΔG.

Figure 13.

DFG-out path (orange) VS path1 (red). During dissociation of SB2 from the DFG-out conformation, the 4-methylsulfinylphenyl group rotates back inside the cavity and forms a stacking interaction with the side chain of Phe169. Hydrogen bonds between SB2 and Met109 are shown in a dash line.

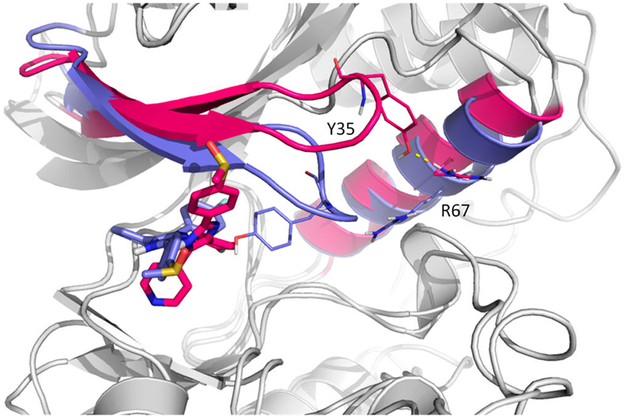
Because of the complex dynamical nature of ligand–protein systems, simulations from AMD, SMD, and manual pulling cannot cover all large-scale protein motions and side-chain movements. However, modeled dissociation pathways must capture key interactions and movements during ligand unbinding. For example, crystal structures showed that Tyr35 of free p38α formed a hydrogen bond with Arg67, and in the bound complex, Tyr35 formed a hydrogen bond with the 4-methylsulfinylphenyl group of SB2. To leave the binding pocket, a ligand needs to break key interactions with the protein, which is seen in AMD simulations that the hydrogen bond between Tyr35 and SB2 breaks to allow SB2 unbinding. AMD simulations also show that once Tyr35 lost the hydrogen bond with SB2, it quickly reformed a hydrogen bond with Arg67, shown in another crystal structure. However, in SMD, due to the artificial pulling force applied to SB2 instead of thermal fluctuation used in AMD, Tyr35 did not rotate away after breaking the hydrogen bond with SB2 (at 24 Å in RC shown in Figure 12) but rather moved with SB2 and then formed another interaction with the fluorobenzene group of SB2. The interaction was kept until ~29 Å in RC (Figure 14). This situation yields a much larger energy barrier, as compared with PMFs built from other paths. Interestingly, trajectory prepared by manual pulling showed that, after the hydrogen bond was broken between Tyr35 and SB2, Tyr35 remained in the same position without forming interactions with other atoms of SB2 or protein side chains. Although many dissociation pathways are possible, a trajectory must be carefully examined to ensure no unrealistic or discontinuous motions before performing biased harmonic potential of MD simulations for each window for PMF calculation. If pulling forces are applied to guide ligand dissociation, such as using SMD for ligand dissociation, improved methods such as the forward–reverse strategy can be used to provide reliable conformational sampling.⁶⁷

Figure 14.

SMD path (purple) and VS path1 (red). Tyr35 rotates away in path1 to form a hydrogen bond (shown in dash line) with Arg67 and breaks the stacking interaction with SB2, while Tyr35 in SMD follows SB2.

CONCLUSION

We used US to investigate the free energy changes during ligand unbinding from three different β-CD conformations and five SB2–p38α trajectories modeled by AMD, SMD, and manual pulling. We examined the effect of the computed PMF due to β-CD conformations, SB2 dissociation pathways, and data point selections in US. Different β-CD conformations can change the height of the energy barrier significantly, which suggests that the initial conformations of a molecular system can influence free energy values in PMF and the computed ΔG. However, the overall shape of PMFs hold if the US simulations converge. We tested a less-likely ligand dissociation pathway of the β-CD system, the direct dissociation, and the PMF showed no free energy barrier and no energy minimum, which suggests that US simulations can accurately provide insights for different dissociation pathways.

Notably, running excessively long MD for each US window cannot overcome the influence of different β-CD conformations to the computed ΔG, because ligand binding can restrict the receptor to sample all possible conformations along a reaction coordinate. To obtain a more accurate ΔG and free energy profile for ligand association/dissociation using US, one may sample multiple pathways with high population and use a partition function to reconstruct a PMF and ΔG from these pathways. However, it may be challenging to estimate the population of each pathway, and using the same association/dissociation coordinate may not be applicable to all the pathways. We anticipate that, by combining additional theoretical work and sampling techniques, US will provide more accurate ΔG and the binding/unbinding free energy profile by considering multiple pathways.

For large protein–ligand systems, a predefined dissociation pathway needs to be used for US simulations, and various sampling techniques can be used to model protein–ligand dissociation. SMD is one of the most popular methods that efficiently pulls a ligand out of the binding cavity of the protein. However, a very simple artificial force may produce an unrealistic dissociation process, which results in an inaccurate free energy profile for ligand unbinding. This work also studied dissociation pathways sampled by AMD with short MD simulations to further smooth the trajectories. Except for the trajectory from SMD that used a simple artificial force without an improved SMD setting, other trajectories resulted in a similar PMF using the same RC. Notably, we used the distance between Cα of Arg173 and CC2 of SB2 as the RC in our study, but using a simple RC may not be able to capture all important physical properties during ligand unbinding. However, we showed that US can be a reliable method for computing PMF, if a reasonable trajectory is provided and the biased MD used in each umbrella window is well-converged. Various biased sampling techniques are typically applied to model ligand dissociation. We suggest careful examination of a trajectory to ensure no unrealistic or discontinuous motions during ligand dissociation before constructing a PMF using US simulations.

ABBREVIATIONS:

US

umbrella sampling

MD

molecular dynamics

AMD

accelerated molecular dynamics

SMD

steered molecular dynamics

β-CD

β-cyclodextrin

PMF

potential of mean force

RC

reaction coordinate

COM

center of mass

RMSD

root-mean-square deviation

ABF

adaptive biasing force

MAPK

mitogen-activated protein kinase

DFG

Asp-Phe-Gly