Simulating Water Exchange to Buried Binding Sites

Abstract

Traditional molecular dynamics (MD) simulations of proteins, which rely on integration of Newton’s equations of motion, cannot efficiently equilibrate water occupancy for buried cavities in proteins. This leads to slow convergence of thermodynamic averages for such systems. We have addressed this challenge by efficiently integrating standard Metropolis Monte Carlo (MC) translational water moves with MD in the AMBER simulation package. The translational moves allow water to easily enter or exit buried sites in a thermodynamically correct way during a simulation. To maximize efficiency, the algorithm avoids moves that only interchange waters within the bulk around the protein, instead focusing on moves that can transfer water between bulk and the protein interior. In addition, a steric grid allows avoidance of moves that would lead to obvious steric clashes, and a fast grid-based energy evaluation is used to reduce the number of expensive full energy calculations. The potential energy distribution produced using MC/MD was found to be statistically indistinguishable from that of control simulations using only MD, and the algorithm effectively equilibrated water across steric barriers and into binding pockets that are not accessible with pure MD. The MC/MD method introduced here should be of increasing utility for applications spanning protein folding, the elucidation of protein mechanisms, and free energy calculations for computer-aided drug design. It is available in version 18 release of the widely disseminated AMBER simulation package.

Graphical Abstract:

2. INTRODUCTION

Many proteins contain buried cavities large enough to accommodate a buried water molecule.¹ Such cavities may open and allow water exchange only rarely, particularly if they are deeply buried.² As a consequence, standard molecular dynamics (MD) simulations, that integrate Newton’s equations of motion, do not efficiently sample water occupancy states in buried cavities³. Because water occupancy of a buried site influences the conformational distribution of the protein, standard MD simulations may be inefficient at sampling protein conformations in a manner that accounts for both occupied and unoccupied states of buried cavities. Thus, the conformational distribution provided by even a long MD simulation may not accurately follow the Boltzmann distribution associated with the force field and the conditions (e.g. solvent composition and temperature) of the simulation. The challenge of equilibrating water in buried sites also has important implications for the calculation of protein-ligand binding free energies and hence for computer-aided drug design.^3,4 For example, it may be difficult to converge an alchemical relative binding free energy calculation⁵ that modifies a ligand in a buried site in a manner that requires entry or exit of a buried water molecule. Similarly, binding affinity calculations by the double-decoupling method,⁶ in which the ligand is gradually decoupled from the binding site, require that water be free to enter and occupy the site. This may pose serious convergence issues if the site is deeply buried.⁷ The kinetics of water penetration may be a bottleneck to convergence of other types of molecular systems as well, such as membranes and porous materials.

Several prior works have addressed this important problem by integrating grand canonical Monte Carlo (MC) steps with MD simulations,^3,4,8 so that water molecules can be added to or removed from random locations in the system in a manner that preserves the Boltzmann distribution of states for a given chemical potential of water. Thus, water molecules can enter or leave a buried cavity even if the cavity remains closed to the outside solvent. This elegant method solves the problem, but it adds algorithmic complexity, and variations in the total numbers of water molecules during a simulation can require substantial changes in the tools used to analyze the results.

Here, we describe a simpler yet rigorous solution, where standard MD steps are supplemented with translational MC steps executed within a rectangular region that overlaps with the protein interior and part or all of the bulk solvent around the protein. The total number of water molecules in the system remains constant, and application of the Metropolis accept/reject criterion means the method yields a valid Boltzmann distribution, as required for the calculation of protein properties and binding thermodynamics. Detailed balance is preserved without the need for reweighting because the rectangular region is both the origin and destination of all water moves, only the waters within this region are selected for moves, their candidate destination sites are also within this region, and the waters and sites are sampled with uniform probability. Hence the algorithm does not lead to preferential sampling.⁹ It is worth noting that the present method has a different purpose than algorithms whose aim is to efficiently identify stable water-binding sites in protein crystal structures.^10–15 Such methods are valuable tools to initialize a simulation in a likely hydration state, but they do not yield a Boltzmann distribution and are not integrated into simulations. It is also important to distinguish the present work from methods like WaterMap,^16,17 GIST,^18,19, and STOW,²⁰ which are ways of analyzing water distributions from MD, not of generating the water distribution. In fact, our development of the present method is motivated in part by the aim of generating valid water distributions for analysis by such methods. The following subsections detail the method and its implementation in the widely used AMBER simulation package,^21,22 and present a series of tests that validate the resulting conformational ensemble and the ability of the method to equilibrate water across barriers and into buried sites.

3. METHODS

We introduce a method to integrate standard Metropolis Monte Carlo (MC) translational water moves with MD, allowing water molecules to enter and exit buried sites during the course of a simulation and thus to generate an equilibrium distribution.

3.1. WORKFLOW

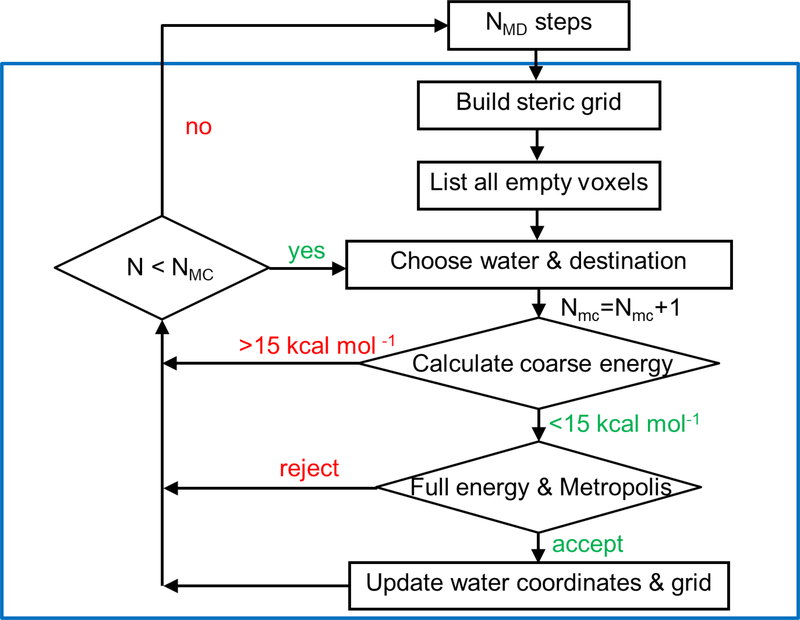
The basic approach is to iteratively alternate a block of N_MC move attempts with a block of N_MD time steps (Figure 1). Each block of MD starts from the configuration present at the end of the prior MC block, and vice versa. The velocities of all the atoms in the system at the start of each MD block are the same as those at the end of the prior MD block; i.e., a moved water molecule carries its velocities. In addition, the orientation of a moved water is not modified, as the orientation of waters in the bulk is randomized by the MD blocks. Trajectory snapshots (atomic coordinates and velocities and system properties such as energy) are saved during the MD block, but not during the MC block. The MD and the full Particle Mesh Ewald (PME) energy calculation are performed on the GPU when using AMBER18’s GPU-accelerated PMEMD simulation code.^23–26 The MC part is performed on the CPU.

Figure 1:

Flowchart of the Monte Carlo/molecular dynamics procedure. The blue frame marks the MC part. See text for details.

Although this procedure is valid, in the sense of generating a Boltzmann distribution of configurations for whatever force field is used, implementing it in a naïve manner would be inefficient, for two main reasons. First, for the condensed phase systems, which are of greatest interest here, most move attempts would lead to steric overlaps and hence to Metropolis rejections that do not advance the goal of sampling new water positions. Nonetheless, each failed move attempt would still require a costly energy calculation. Second, for simulations of a protein in water, many of the water moves would merely move water molecules from place to place in the bulk around the protein and thus would not serve the purpose of equilibrating water between the bulk and the protein interior; and MD is already highly effective at equilibrating water in the bulk. We have addressed these inefficiencies by a combination of methods, as now described.

3.1.1. FOCUSING MOVE ATTEMPTS WITH A STERIC GRID

An MC move attempt involves tentatively relocating a water molecule from its initial position within the rectangular sampling region to a target position also in the rectangular sampling region. If the target position would lead to gross steric overlap of the moved water with nearby atoms, it would generate a very high energy change, so the move attempt would be rejected with near certainty. Hence making such move attempts, computing the resulting high energies, and then rejecting them, is essentially equivalent to not trying them at all. The present method takes advantage of this equivalence by only attempting moves to target positions that will not generate a gross steric overlap, thus avoiding many needless energy calculations. This procedure does not require any adjustment in configuration weights because configurations are not saved during the MC procedure. The only role of the MC block is to deliver a new starting configuration for the following block of MD moves.

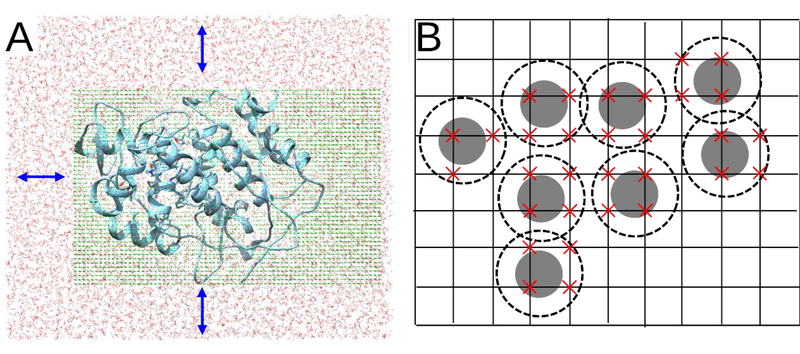
To accomplish this, and to reduce the number of uninteresting move attempts where both the initial and target locations are in the bulk, we set up a “steric grid” within the rectangular sampling region that includes at least part of the protein interior and that extends into the surrounding bulk water (Figure 2b). This region is defined by the input variable shift (default 10 Å). The origin of the grid is therefore positioned at (shift, shift, shift), where the origin of the simulation box is at (0,0,0). The maximal coordinates of the grid along the x and y axes are the size of the periodic box minus shift. The maximum z-coordinate of the grid is the maximum z-coordinate of the simulation box minus 3 Å. Thus, the grid can be sized to just encompass the protein along the x- and y-axes while extending into bulk solvent along the z-axis (see Figure 2).

Figure 2:

A) Diagram of the steric grid inside the simulation box. Only waters within the box are moved by the MC steps, and only to unblocked (empty) grid points in the box. Blue arrow indicates the shift of the grid from the edges of the simulation box (see section 3.3). B) Two-dimensional representation of the steric grid. The gray disks represent the atoms, and the dashed circles account for the radius of water. A red X represents a grid point that is sterically blocked, and trial water moves are directed to target positions within ±0.1 Å of an empty grid point.

At the start of each MC block, each grid point is marked to indicate whether it is sterically blocked, as detailed below. A move attempt then involves choosing a water whose oxygen atom is within the steric grid and moving it to an unblocked target position anywhere on the grid. A water molecule in bulk can thus jump to an unoccupied site in the protein interior and vice versa. After each accepted move, the steric grid is updated to account for the move.

The 0.2 Å resolution steric grid is constructed as follows. It is initialized by assigning a zero overlap count to each grid point. The algorithm (Figure 1) then loops over all atoms in the system and increments the overlap count at each grid point by 1 for every atom that overlaps it (Figure 2B). Each atom is considered to overlap a spherical region of radius r_vdw +r_wat, where r_vdw is the atom’s van der Waals radius, based on elements,27 and r_wat an effective steric radius for a water molecule. We found empirically that using r_wat = 0.9 Å provided good efficiency and negligible risk of treating an accessible site as occupied. Thus, if a grid point is covered by 3 atoms, (van der Waals radius plus added water radius; see Figure 2B), the value of this grid point will be 3. Grid points with the value zero then lie within cavities in which a water molecule can be placed without causing major steric clashes with the existing atoms. We make a list of all these empty grid points for use in choosing target positions for water moves.

To execute a move, the algorithm randomly selects a water molecule that lies within the rectangular region covered by the grid and moves it to a target position in the immediate neighborhood of a grid point randomly selected from the list of empty grid points. The target position is generated by allowing random shifts of up to a half grid unit (0.1 Å) from the selected grid point along all three axes. The move is then either accepted or rejected, as detailed in Section 3.1.2. If the move is accepted, the water’s coordinates are shifted to the target position, and the steric grid is updated by: a) decrementing by 1 the overlap count of the grid points that the atom previously overlapped; and b) incrementing by 1 the overlap count of the grid points it overlaps after the move. Grid points that had been covered by only this water molecule now have an overlap count of 0 and thus are accessible for the next move attempt, while grid points that had an overlap count of zero but now are overlapped by the moved water are inaccessible for the next move attempt. This approach is similar but not identical to the cavity-bias algorithm used in a number of grand canonical MC implementations.^3,8,28–31

3.1.2. FILTERING MOVES BASED ON HYDROGEN CLASHES AND A FAST ENERGY ESTIMATOR

We observed that even moves generated using the steric grid often have very high energies. This results partly from the requirement of using a small value of r_wat to avoid excluding close hydrogen-bonded configurations, and partly from the fact that the steric grid does not effectively deal with polar hydrogen atoms, due to their small Lennard-Jones radii. We therefore developed filters that efficiently reject trial moves with very high energies and thus reduce the number of costly full Particle Mesh Ewald (PME) energy calculations. First, a move is immediately rejected if it leads to a hydrogen-hydrogen distance <0.5 Å. Second, the algorithm estimates the energy change due to the trial move by computing the interaction energy of the water with only its neighboring atoms before and after the move and examining the difference between these two energies. If the difference is highly unfavorable (>15 kcal mol⁻¹), the move is rejected. Otherwise, a full energy calculation is performed and the Metropolis criterion³² is used to decide whether to accept or reject the move. The validity of this procedure is demonstrated in Results.

The interaction energy calculations are accelerated by using a grid-based neighbor list. Thus, at the start of each MC block, a second grid, which covers the entire simulation box, is set up, with a coarse spacing defined as half the user-defined AMBER variable cutoff, which is the distance cutoff used for nonbonded interactions. Each coarse grid point is then assigned a list of the atoms in its corresponding voxel. To evaluate a trial move, the algorithm calculates the interactions of the water molecule with only the atoms that are in the neighboring two coarse voxels in each direction.

3.2. EVALUATION

We verified that the present method yields a proper Boltzmann distribution and then evaluated its ability to sample hydration changes in buried cavities. These tests are detailed in the following subsections.

3.2.1. MAINTAINING THE BOLTZMANN DISTRIBUTION

We tested the method on a system that is less dense than liquid water and so has a high MC acceptance rate, so that any error introduced by the MC procedure would easily become apparent. We chose a system with 612 gas phase water molecules at 500 K in a constant volume box about 113 Å along each axis. The rectangular sampling region, with its steric grid, covered the entire simulation box. The MC acceptance rate was 45% for this system. The SHAKE algorithm^33,34 was used with the default tolerance of 0.00001. The integration time step was set to 0.2 fs in both the pure MD and the MCMD calculations to minimize deviations from the Boltzmann ensemble due to the use of a finite time-step. This maximized compatibility with the MC steps, for which there are no finite time-step errors. The reference MD simulation was run for 20 ns and the MD energy was recorded every 10 steps, resulting in 10⁷ full energy calculations. For the MCMD calculation, we ran 2.5×10⁶ cycles, with N_MC=N_MD=10, and the energy was recorded immediately following each MC component of the cycle.

3.2.2. HYDRATING AND DEHYDRATING INACCESSIBLE SITES

We used several systems to test the ability of the MC/MD method to allow water exchange between otherwise inaccessible regions.

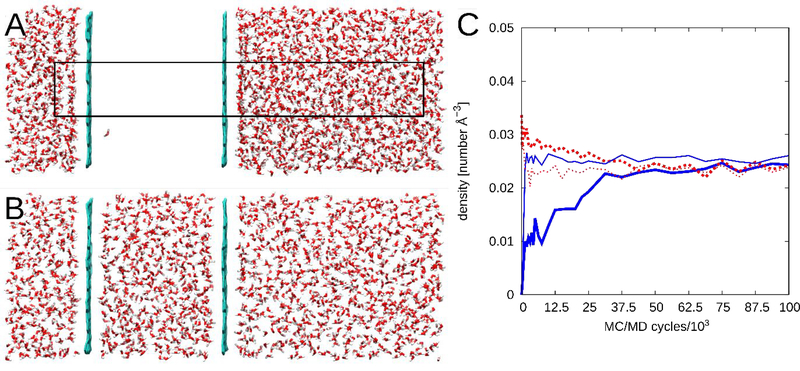
The first test system was a ~30×30×85 Å rectangular box partitioned into two regions by planar graphene sheets at Z ≈ 42 Å and 70 Å (Figure 5A). The outer sides of the system were initially populated with water molecules at normal liquid density, whereas the middle region was initially populated with a single water molecule. The simulations were performed at 500 K in boxes of constant volume. The expectation was that pure MD would not allow water to exchange between the two regions, while MC/MD should allow the densities to equalize. In one calculation, the rectangular sampling and steric grid covered the entire simulation box. In a second calculation the sampling region and grid spanned only a thin elongated rectangle (10<X<20;10<Y<20;10<Z<82 Å) which crossed the graphene walls. (Figure 5A).

Figure 5:

The wall test system, A) before starting the MC/MD run, where the black rectangle diagrams the asymmetric grid to scale, and B) after using MC/MD. C) the water densities between the 2 walls (blue) and outside the walls (red). Thick lines represent the system in which the grid covered the entire simulation box, and thin lines represent results with the asymmetric grid. Each MC/MD cycle comprises 25,000 MD steps and 25,000 MC trial moves.

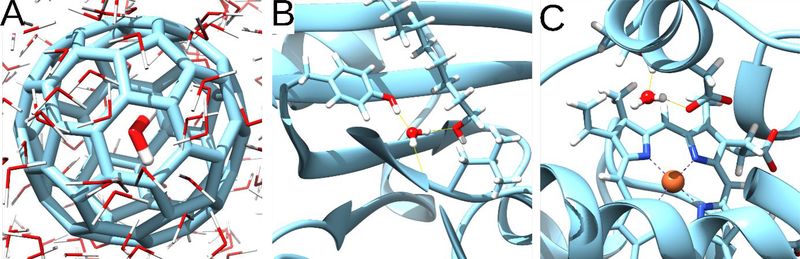
The second test system started with a water molecule trapped inside a C₆₀ buckyball (Figure 6A). As this water molecule forms no hydrogen bonds with any of the surrounding carbons, it is energetically unstable relative to a water in bulk. The buckyball was solvated in 11 Å of water molecules in all directions, forming a cubic simulation box (Figure 6A). The simulation was performed at constant volume at 300 K.

Figure 6:

A) is the C60 Buckyball with a trapped water molecule in the middle of the structure. B), the occluded hydration site of the MUP. C) the occluded hydration site of the CcP.

The third and fourth test systems were proteins with buried water sites. Major Urinary Protein (MUP)³⁵ contains a buried crystallographic water molecule which bridges between the ligand (nonan-1-ol) and Tyr120 (Figure 6B), while Cytochrome c Peroxidase (CcP)³⁶ has a trapped crystallographic water molecule which binds to the Glu229 (Figure 6C). Here we removed the buried water molecules and compared the ability of pure MD and MC/MD to reoccupy these cavities. To focus on the water exchanges, the Cα atoms and the MUP ligand atoms were restrained during the simulation with positional restraints of 5 kcal/mol-Ų. For the MUP and CcP, the simulations included bulk water to a thickness of 11 and 10 Å respectively in all directions, in a cubic simulation box, and the shift variable (Section 3.1.1) was set to 11 Å.

3.3. USING THE MC/MD METHOD IN AMBER

The MC/MD method is invoked and controlled with several keywords in the AMBER input file: mcwat invokes the MC/MD method when set to 1 (default=0); N_MC sets N_MC (default=1,000); N_MD sets N_MD (default=1,000); and mcboxshift sets the value of shift, the gap between the sides of the grid box and the sides of the simulation box (Section 3.1.1 and Figure 1; default=10Å). If the system is prepared with cubic periodic boundary conditions with an equal amount of solvent padding along all three axes, it is recommended that this value be set to the thickness of the padding. The input variable mcresstr is the name of the water residue e.g. WAT or HOH.

3.4. SIMULATION DETAILS

Following equilibration at constant pressure and temperature, production MD was performed at constant volume using the TIP3P water model³⁷, the ff14SB^38,39 force field for the protein, and GAFF⁴⁰ for the ligand of MUP. The CcP was prepared as described by Balius et al.⁴¹ The particle mesh Ewald (PME) method⁴² was used for periodic boundary conditions. The SHAKE algorithm^33,34 was used to constrain hydrogen bond lengths. The cutoff used for non-bonded interactions was 12Å. The time step was 2 fs for the 300 K simulations, and 0.2 fs for the gas phase (500 K) simulations. The MC blocks were run at a matching temperature and constant volume.

4. RESULTS

4.1. ACCURACY OF THE FAST ENERGY ESTIMATOR

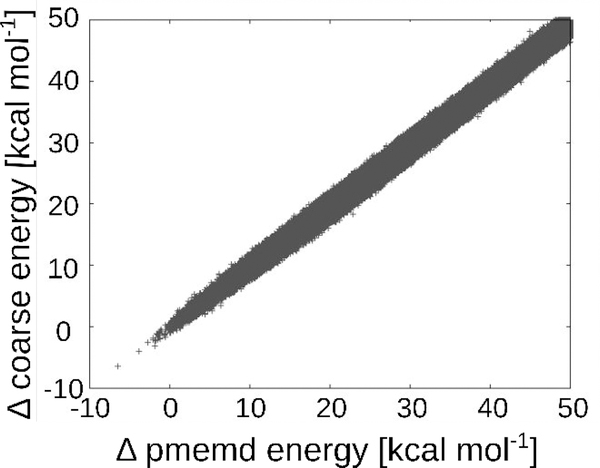
We evaluated the accuracy of the fast energy estimator (Section 3.1.2) by comparing the energy differences it provides for 10⁷ MC trial moves in the CcP system (Section 3.2.2) with energy differences computed with the full PME method. The agreement and correlation are excellent (Figure 3), with a root-mean-squared deviation of 0.91 kcal mol⁻¹, coefficient of determination (R²) of 1.00, and linear regression y = 1.00x + 0.68. Using the fast energy estimator resulted in a 2-fold speed up compared to the full energy. These results support the utility of the fast estimator as a filter to reduce the number of full energy calculations that must be performed during the MC procedure.

Figure 3:

Correlation between approximate and full energies. Graph shows only energy differences less than 50 kcal mol⁻¹ by both methods.

4.2. MAINTAINING THE BOLTZMANN DISTRIBUTION

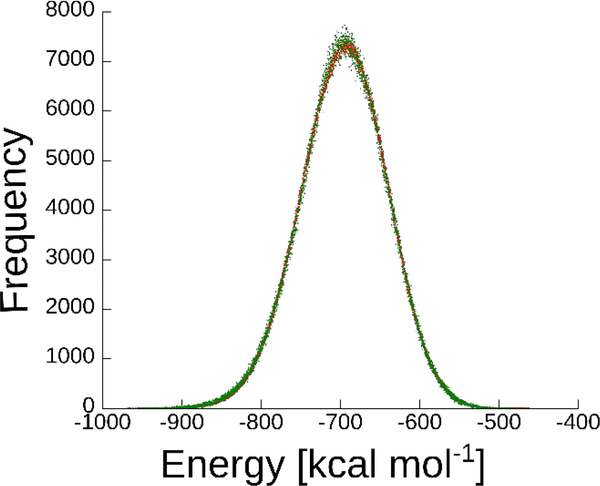
We checked whether the MC/MD procedure maintains a proper Boltzmann distribution for a gas phase test system where ~45% of MC attempted moves are accepted, so that the MC steps contribute heavily to the distribution of states. As shown in Figure 4, the potential energy distribution provided by the MC/MD method agrees closely with that provided by a pure MD simulation of the same system. For MC/MD, the mean potential energy over 2.5×10⁶ energy evaluations was −696.53 kcal mol⁻¹, with a standard error of the mean (SEM) by blocking analysis ⁴³ of 1.55 kcal mol⁻¹, while the mean and SEM for 10⁷ pure MD steps was −695.85 kcal mol⁻¹ with SEM 1.52 kcal mol⁻¹. The good agreement between MC/MD and pure MD supports the validity of the MC/MD method and its correct maintenance of detailed balance.

Figure 4:

Histogram of the energy distribution of MD (red, 10⁷ pme energy calculations), and MC/MD (green, 2.5*10⁶ pme energy calculations). The energies were divided to bins of 0.1 kcal mol⁻¹, and normalized according to the MD.

4.3. HYDRATING AND DEHYDRATING INACCESSIBLE SITES

Further tests of the MC/MD procedure started with two relatively artificial test cases. The first tests the ability of the MC/MD procedure to equilibrate water density across impermeable graphene barriers (Figure 5A), so that an initially nonuniform distribution of water in two regions of the simulation box may become uniform. As expected, based on the construction of the system, standard MD does not allow water to populate the empty region, due to the barriers (data not shown). In contrast, the translational MC moves in the MC/MD method smoothly equalizes the densities in the two regions, as intended, both with a rectangular sampling region covering the entire simulation box and with a much smaller sampling region that spans the graphene walls asymmetrically (Figure 5B & 5C). The fact that the asymmetric grid equalizes the densities faster probably results from the fact that a smaller fraction of its volume is in the region with high initial density, so, during the equilibration phase, it generates more moves into the region with initial low-density. The second test system starts with a buckyball containing one water molecule (Figure 6A). With MD, the water is trapped, while with MC/MD, the water returns to the surrounding bulk water and the buckyball remains unoccupied thereafter. This outcome is not unexpected, given that the trapped water is unable to form stabilizing polar interactions with the nonpolar carbon atoms of the buckyball.

We then examined buried water sites in two proteins, the Major Urinary Protein (Figure 6B) and Cytochrome c Peroxidase (Figure 6C). In both cases, we artificially removed the crystallographic water from the site and simulated the proteins immersed in bulk water, using pure MD and the MC/MD procedure. In both cases, 10 μs of pure MD simulation failed to transfer a water into the empty sites, while MC/MD simulations successfully hydrated them. Following hydration of the sites, no MC moves were accepted that emptied them again. For these two test cases, the CPU time required to carry out 1,000 MC steps followed by 1,000 MD steps results is currently ~5 times greater than that to carry out just the 1,000 MD steps, but this computational cost is accompanied by a clear improvement in conformational sampling.

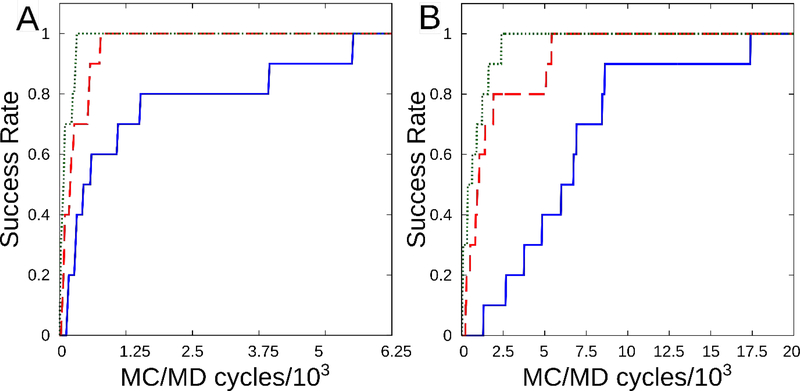
We also examined how the number of MC steps in each block, N_MC, affects the rate of water transfer from bulk to each site, by carrying out runs with N_MC = 1,000, 5,000 and 10,000; N_MD = 1,000 in all cases. Ten replicates, with different random number seeds, were run for each value of N_MC. As shown in Figure 7, increasing N_MC consistently shortens the number of MC/MD cycles required for a given fraction of the replicates to become hydrated. Over all runs, the mean number of MC steps required to reach a 50% probability of occupation is 7 × 10⁵ for MUP and 5 × 10⁶ for CcP. Note that these statistics depend, in general, on the dimensions of the steric grid.

Figure 7:

Mean fraction of 10 replicate simulations in which the water site has become hydrated, for N_MC= 1,000 (solid blue), 5,000 (dashed red), and 10,000 (dotted green). A) Major urinary protein. B) cytochrome C peroxidase. N_MD=1,000 in all cases.

5. DISCUSSION

The hybrid MC/MD approach described here accelerates configurational sampling during simulations by allowing large translational water moves during the MC component of each MC/MD cycle. These moves allow water molecules to jump in and out of buried cavities without any need to wait for the protein to sample conformations in which the cavities are connected by a channel to the bulk. The method yields the same Boltzmann distribution of states expected from a sufficiently long MD simulation, so it can be used to compute thermodynamic averages and properties, such as conformational distributions and free energies. This characteristic differentiates the method from more targeted algorithms aimed only at finding high-occupancy water sites, rather than at sampling both occupied and unoccupied states according to the potential function (force field) being used in the simulation. The present method is more closely related to ones that combine MD with grand canonical Monte Carlo steps, in which water molecules may be introduced to or removed from the simulation in a manner that preserves a Boltzmann distribution.^3,44 However, the full grand canonical machinery is not needed to achieve our goal of equilibrating between buried sites and bulk, and it may be simpler to interpret and analyze simulation results in which the number of water molecules remains constant and integer, as in the present approach.

The present method, which is available in the AMBER simulation package as of version 18,²¹ should be useful to accelerate calculations of thermodynamic averages in any setting where water equilibration is rate-limiting for pure MD simulations. We anticipate that it will be particularly valuable in calculating protein-ligand binding free energies where the binding site is isolated from bulk solvent, as it will allow water occupancy to change when a ligand is alchemically modified^45–47 or fully decoupled from the binding site.⁶ It may also speed equilibration of protein conformation ensembles for proteins, such as BPTI,^48,49 which form cavities large enough to bind water in their folded state. By the same token, it should be noted that the present method is not designed to generate the correct kinetics for the Hamiltonian being simulated, as the MC steps that speed equilibration are nonphysical.

Key parameters of the method are the dimensions and position of the steric grid and the numbers of MC and MD steps in each cycle. For the protein cases studied here, we have used a steric grid which covers the entire protein, but in many applications, a smaller grid will be advantageous. For example, if one wishes to speed the equilibration of waters between a specific ligand-binding site and the bulk, then a small, focused steric grid just large enough to cover the site and extend into bulk may suffice and should greatly increase efficiency by focusing the MC move attempts on the site of interest. It may also be appropriate to adjust N_MC and N_MD to suit the application. For example, if the goal is to determine the hydration state of a cavity for a fairly well-defined protein structure, one might set N_MC>>N_MD. This scenario may be particularly relevant for analyses of water structure with methods like WaterMap^16,17 and GIST.^18,19 On the other hand, if the goal is to explore the conformational space of the protein, a 1:1 ratio may be more useful. In all cases, we suggest setting N_MC ≥1,000, because the steric grid is rebuilt for every cycle, and it is favorable to amortize this computational cost across a large number of MC steps.

We foresee opportunities to further accelerate these calculations in the future. For example, porting the MC cycles to the GPU would reduce the amount of costly communication between GPU and CPU. It should also be possible to evaluate MC energy changes not by recomputing the full energy but instead by computing the change in the interactions of the moved water with all other atoms, while properly accounting for the Ewald summation of Coulombic interactions. Thus, the MC/MD paradigm introduced here should be of increasing utility for applications spanning protein folding, the elucidation of protein mechanisms, and free energy calculations for computer-aided drug design, as well as for a broader range of molecular systems with cavities that are not directly accessible to bulk water.