Bone-Cancer Assessment and Destruction Pattern Analysis in Long-Bone X-ray Image

Abstract

Bone cancer originates from bone and rapidly spreads to the rest of the body affecting the patient. A quick and preliminary diagnosis of bone cancer begins with the analysis of bone X-ray or MRI image. Compared to MRI, an X-ray image provides a low-cost diagnostic tool for diagnosis and visualization of bone cancer. In this paper, a novel technique for the assessment of cancer stage and grade in long bones based on X-ray image analysis has been proposed. Cancer-affected bone images usually appear with a variation in bone texture in the affected region. A fusion of different methodologies is used for the purpose of our analysis. In the proposed approach, we extract certain features from bone X-ray images and use support vector machine (SVM) to discriminate healthy and cancerous bones. A technique based on digital geometry is deployed for localizing cancer-affected regions. Characterization of the present stage and grade of the disease and identification of the underlying bone-destruction pattern are performed using a decision tree classifier. Furthermore, the method leads to the development of a computer-aided diagnostic tool that can readily be used by paramedics and doctors. Experimental results on a number of test cases reveal satisfactory diagnostic inferences when compared with ground truth known from clinical findings.

Introduction

X-ray image analysis provides one of the cheapest primary screening tools for the diagnosis of bone cancer. As reported in the medical literature [16], a primary bone tumor usually appears with unsuspecting symptoms such as fracture of a bone, swelling around a bone, a new bone growth, or swelling in the soft tissues surrounding a bone. Oftentimes, an X-ray image of cancer-affected bone appears different from its surrounding healthy bones and flesh region. The X-ray absorption rate of bone cells in the cancer-affected region differs from that in healthy bone cells [16]. As a result, the image of cancer-affected bones appears in the form of a “ragged” surface (permeative bone destruction), tumor (geographic bone destruction), or holes (moth-eaten pattern of bone destruction) [7].

Grading of bone cancer and identification of the underlying bone-destruction pattern are two essential components needed for treatment of the disease. The stage and grade of bone cancer represent a measure of the severity of the disease. Progressive identification of destruction pattern in a cancer-affected bone also helps doctors to estimate the rapidity of growth of the disease, or prognosis of the treatment. Hence, automated classification of bone-cancer stage, grade, and destruction pattern will be useful to medical practitioners in order to plan for the course of treatment.

In the past few years, researchers have proposed different approaches for bone-tumor detection. Conventional image-analysis techniques such as thresholding, region growing, classifiers, and Markov random field model have been used for the detection of tumor region in X-ray and MRI¹ images [11]. Frangi et al. [12] have used multi-scale analysis of MRI perfusion images for bone-tumor segmentation. They proposed a two-stage cascaded classifier for hierarchical classification of healthy and tumor tissues, and subsequently, to discriminate viable and non-viable tumors. Ping et al. [23] have proposed an approach based on intensity analysis and graph description for the detection and classification of bone tumor from clinical X-ray images. The method analyzes a graph representation to locate the suspected tumor area. It can also classify the benign and malignant tumor depending on the number of pixels extracted from the analysis of brightness values.

Bone CT images have also been widely used for fracture detection and disease diagnosis. A fusion between CT² and SPECT³ images is proposed for the identification of cancerous regions in bone image [22]. Yao et al. [28] have designed an automated lytic bone metastasis detection system. The procedure uses adaptive thresholding, morphology, and region growth for the segmentation of spine region. An approach based on watershed model is used for the detection of lytic bone lesions, and a support vector machine (SVM) classifier is used for feature classification and to diagnose the affected lesions. Automated diagnosis of secondary bone cancer from a CT image of bone vertebrae was proposed by Huang et al. [18]. Their technique involves texture-based classifiers and an artificial neural network (ANN), which are used for the detection of abnormality. Fuzzy-possibilistic classification and variational model are also utilized for multimodal bone cancer detection from CT and MRI images [6]. Most of the researchers have focused on the identification of bone tumor or cancer-affected region from CT or MRI. To the best of our knowledge, no automated method for determining the destruction pattern caused by bone cancer along with classification of its stage and grade is yet known.

In this paper, we have proposed a computer-aided diagnostic method that can perform an automated analysis of bone X-ray images and identify the cancer-affected region. Our method can be used to localize the destruction pattern and to assess the severity of the disease based on its stage and grade.

The rest of the paper is organized as follows. “Methods” discusses various phases of the proposed method and the features used for bone cancer detection. An algorithm for localizing the cancer-affected zone is presented in “Localization of Cancer-Affected Region.” Procedures for classifying stage and grade of the disease are described in “Cancer Severity Analysis.” Results on test cases and performance of the proposed method are reported in “Identification of Bone-Destruction Pattern.” Discussions of test results and concluding remarks appear in “Results” and “Discussion,” respectively.

Methods

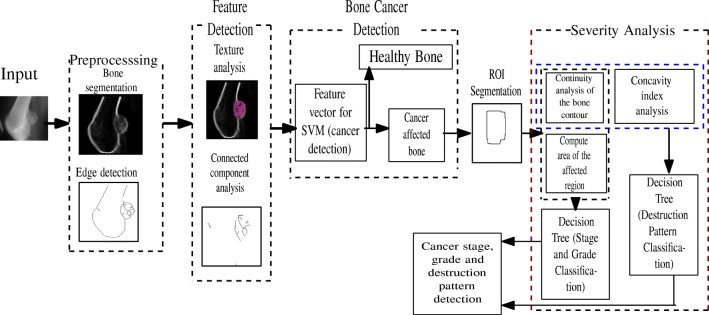
The method described in this work has three major components: (i) diagnosis of bone cancer in an X-ray image, if any, (ii) localization of the affected zone, and (iii) estimation of severity of the disease. Figure 1 depicts different phases of the proposed model. In order to detect the presence of bone cancer, certain diagnostic features are extracted from a pre-processed X-image based on the analysis of connected components and bone texture. Next, we make use of a support vector machine [8, 27] to localize cancer-affected portions in an X-ray image. The exact boundary of the cancerous zone is determined using the concept of isothetic ortho-convex covering [21]. Various feature parameters such as area of the affected zone (in pixel count), concavity index [3], and continuity attributes of the zone boundary are extracted. Finally, given these features as input, a classifier based on decision tree [9] is used to recognize bone-destruction pattern, stage, and grade of the disease.

Fig. 1.

Block diagram of the proposed technique

Preprocessing

The first step in our analysis is to segment the bone region from its surrounding tissues and muscles. In cancer-affected bone X-ray image, pixels appear with heterogeneous intensity values. In order to segment the affected region, the proposed method relies on a method based on entropy-standard deviation discrimination [4].

The entropy of an image represents the uncertainty associated with the pixel values belonging to a region. The value of local entropy in the image is larger for a heterogeneous region compared to that of a homogeneous region. Thus, transition regions will have higher local entropy compared to other homogeneous regions. If local entropy for each pixel of the image is multiplied by local standard deviation of intensity values (for n × n window), the resulting product becomes significantly high at transition regions, and this fact can be used to identify bone-boundaries from the surrounding homogeneous regions comprising flesh and tissues.

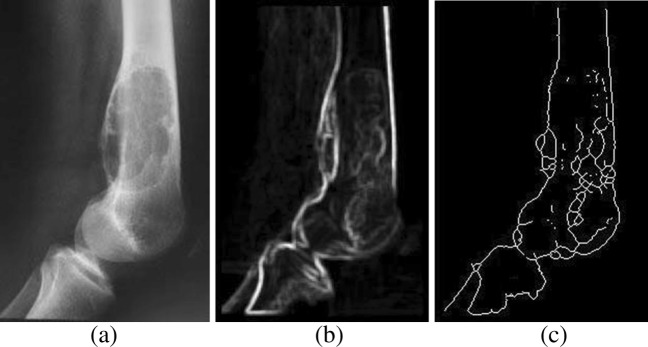
In the proposed approach, entropy-standard deviation product (E-S) image is produced to locate the affected region along with the bone boundary. A window size of 9 × 9 is chosen for computation of local entropy. A smaller window size (5 × 5 or 7 × 7) increases the computation time at the cost of marginal improvement in the quality of a segmented image. Hence, we have used 9 × 9 as the window size for computing local entropy. Figure 2a shows the bone X-ray image. The entropy-standard deviation (E-S) image (with 9 × 9 window) corresponding to the input X-ray image is shown in Fig. 2b and the contour of the segmented bone image is shown in Fig. 2c. Histogram-based intensity thresholding and morphological thinning are applied on the E-S image to generate the single-pixel binary image.

Fig. 2.

Bone contour generation. a Bone X-ray image. b E-S image of (a). c Single-pixel contour of (b)

Feature Extraction

With the development of bone cancer, the contour of the bone and the texture of the bone surface get affected [16]. The deformity of the bone contour and the changed texture are analyzed to identify the features to be used for decision making.

Bone Contour Analysis

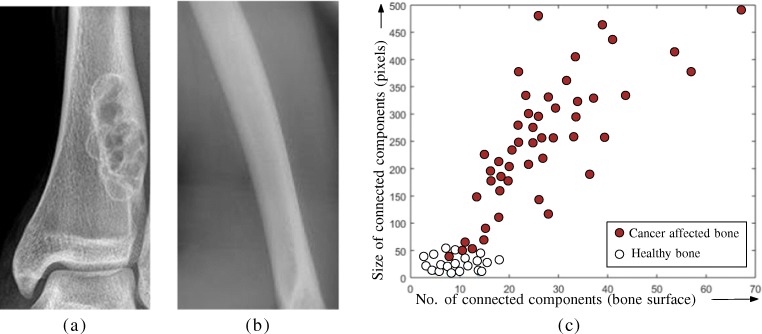
The presence of multiple connected components in the left and right sides of bone contour or on the bone surface indicates abnormality in the bone. We perform connected component analysis (CCA) [10] of the single-pixel image of the bone contour. Our analysis on training-set images shows that a healthy long bone contains very few edges on the bone surface, whereas cancer-affected bones have multiple connected components (Fig. 3c).

Fig. 3.

aX-ray of cancer-affected bone with ragged surface, b Healthy bone X-ray. c Variation of number of connected components on bone surface with total component size (pixels) for healthy and cancer-affected bone images

According to the medical literature [16], cancer-affected region appears with a different structure compared to the healthy bone in its X-ray image. The affected area may have ragged surface (Fig. 3a), small holes on the surface, or a giant hollow region at the interior of the bone. In some cases, the hollow region expands and corrupts bone boundaries. In such situations, few edges may appear on the bone surface. Figure 3c shows the distribution of total number of surface lines (connected components on bone surface) and their total size (pixel) for healthy and cancer-affected images. Thus, the multiplicity of connected components on the bone surface of an X-ray image can be utilized to identify the presence of cancer in the bone.

Runs-Test for Bone Texture Analysis

The cancer-affected bone surface exhibits an irregular texture where structural and geometrical texture analysis approaches may not be very useful in such a situation as the texture has no specific pattern. It is observed that the pixels have homogeneous intensity distribution in the healthy bone region and heterogeneous intensity distribution in the cancer-affected regions. Hence, they can be differentiated on the basis of a measure that reflects the randomness of pixel intensities. Here, the runs-test [19] is applied to detect the randomness of intensity values in cancer-affected regions.

The distribution of different data items in a data set can be tested for randomness in their order by using one-sample runs-test. A run is a sequence of data with the same characteristics. The sequence can be preceded and followed by data with different characteristics, or by no data. If R be the observed number of runs, μ_R be the expected number of runs, n₁ be the number of occurrences of data item 1 with characteristic 1, and n₂ be the number of occurrences of data item 2 with characteristic 2, then the test statistics can be represented as

$$Z=\frac{R-{\mu }_R}{S_R}$$ 1

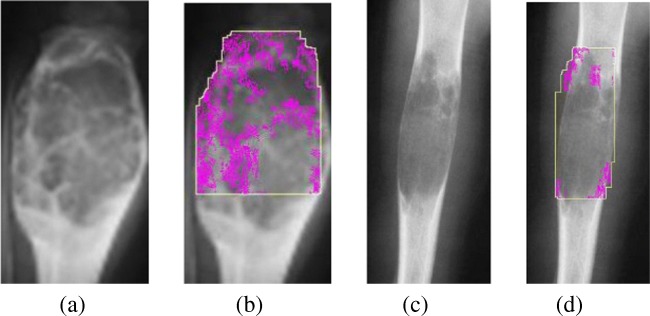
where S_R denotes the standard deviation of the number of runs. The mean of R statistics μ_R and standard deviation S_R can be computed as ${\mu }_R=\frac{2n_1{n}_2}{n_1+n_2}+1$ and $S_R^2=\frac{2n_1{n}_2(2n_1{n}_2-n_1-n_2)}{{(n_1+n_2)}^2(n_1+n_2-1)}$. The null hypothesis is that the sequence of occurrences of data item 1 (n₁) and data item 2 (n₂) in an observation appears in random order, against the alternative that the occurrence is not random. The runs-test rejects null hypothesis if |Z| > Z_1−α/2 where α = 5% significance level. In a gray scale image, a pixel can have any intensity value lying between 0 and 255. The intensity distribution will be random in the case of a heterogeneous intensity region and uniform in the region of homogeneous intensity. The proposed method uses runs-test to detect the region that has heterogeneous intensity distribution on the bone surface of the pre-processed image (as shown in Fig. 4). It divides the entire ROI (identified using CCA) in small blocks (5 × 5) and performs runs-test for pixels in each of these blocks. To determine the nature of intensity distribution in a small block, the median of pixel-intensity values therein is considered as the threshold. Intensities below the threshold value are grouped as Characteristic 1 and those above the threshold are grouped as Characteristic 2. The number of occurrences of Characteristic 1 (n₁) and Characteristic 2 (n₂) are used to calculate μ_R and S_R. The rejection of null hypothesis (RH) indicates the presence of homogeneous intensity distribution in the ROI, whereas the acceptance of the hypothesis (AH) implies heterogeneous distribution of pixel intensities in the ROI. Table 1 shows the results of runs-test performed on ROI of different cancer-affected bone images. This table shows the percentage of pixels that reject the null hypothesis (RH), and the percentage of pixels that accept the null hypothesis (AH) within ROI. Experiments on several cancer-affected X-ray images (Fig. 11) show that healthy regions exhibit homogeneous intensity distribution on the bone surface, whereas cancer-affected regions show heterogeneous intensity distribution in the affected area.

Fig. 4.

Randomness detection of intensity. a Bone X-ray image. b Heterogeneous pixel-intensity distribution (colored pixels) detected via runs-test

Table 1.

Results on runs-test

Figure no.a	ROI (pixels)	RHb (%)	AHc (%)
Figure 11(a1)	3500	31.51	76.31
Figure 11(c1)	4387	13.83	51.62
Figure 11(d1)	12285	17.53	56.77
Figure 11(e1)	19313	5.23	15.45
Figure 11(f1)	26499	17.41	41.45
Figure 11(c5)	25764	16.47	55.8
Figure 11(a3)	15435	24.63	59.75
Figure 11(b3)	18981	14.83	44.41
Figure 11(d3)	17934	18.81	57.02
Figure 11(d5)	12654	23.66	19.75

^a Figure 11 is given in “Results”

^b RH, rejection of null hypothesis (implies homogeneous intensity distribution)

^c AH, acceptance of null hypothesis (implies heterogeneous intensity distribution)

Fig. 11.

(a) Column-1, column-3, and column-5: input X-ray image. (b) Column-2, column-4, and column-6: ortho-convex cover of affected region with heterogeneous pixels marked by runs-test

Detection of Bone Cancer

In this work, we have used a support vector machine to detect the presence of cancer-affected region in the X-ray image. SVM is a machine learning tool that is widely used for data analysis and pattern recognition [27]. SVM was originally developed as two-class pattern recognition problem, and later it was extended to multi-class recognition problem [8, 20].

Let a vector x denote the pattern to be classified, and y (scalar for binary classification and vector for multi-class classification) denote the class labels. If {(x_i,y_i), i = 1,2,3,…,l} represents a set of training examples, then SVM constructs a classifier with a suitable decision function f(x) that can correctly classify an input pattern x. In binary classification, for a new pattern $x\in {ℝ}^n$, the classifier predicts the corresponding class y ∈{± 1}. SVM creates a non-linear decision boundary by projecting the data through a non-linear function ϕ to higher dimension. The objective function of SVM classifier can be represented by the following minimization problem:

$$\mathit{min}\left[J\right(w,\xi \left)\right]=\frac{1}{2}\left(w^{T}w\right)+C\sum _{i=1}^l{\xi }_i$$ 2

subject to $y_i\left(w^T\varphi \left(x_i\right)+b\right)\ge 1-\xi$, $\xi \ge 0$, i = 1,2,…,l where w is the weight vector and b is the bias. C is a user-specified, positive, regularization parameter that determines the trade-off between maximizing the margin, and the number of training data points within that margin. A very high value of C (C →∞) represents a “hard margin” (constraints hard to ignore, narrow separation gap), and a finite small value of C represents the “soft margin” (constraints easy to ignore, large separation gap) among the training data.

While working with binary SVM classifier with “linear” kernel function and “soft margin” (here, we choose C = 1), we performed fivefold 6cross validation (CV) and computed the average classification accuracy to evaluate the proposed method. In each iteration of fivefold CV, the database is divided into training data T_i and test data t_i [14, 17]. This process is applied to avoid over-fitting problem due to small size of the dataset. The feature parameters used in the SVM are taken from the results of CCA and texture analysis (runs-test). The number of connected components (s) present on the surface of the bone image is considered as one of the feature parameters. The percentage of ROI pixels with heterogeneous intensity distribution (h) is used as another feature parameter.

Localization of Cancer-Affected Region

Localization of the cancer-affected region is essential to detect the stage and grade of the disease. CCA and the bone texture analysis, discussed earlier, help to locate the cancer-affected region in the bone X-ray image. The segmentation of ROI mandates identification of a contour that tightly encloses the pixel clusters of cancer-affected region along with islands of healthy portion surrounded by cancer-affected regions. In this work, we have utilized the property of ortho-convex polygon and proposed a method to generate 4-staircase ortho-convex cover that encloses the cancer-affected region on the bone surface.

Required Definitions

Isothetic Curve

An isothetic curve is a rectilinear path consisting of alternating horizontal and vertical line segments. An isothetic curve is a monotonically rising staircase (R-stair) if for all pairs of points α = (x_α,y_α) and β = (x_β,y_β) and on the curve, x_α ≤ x_β implies y_α ≤ y_β. Similarly, in a monotonically falling staircase (F-stair), for all pairs of points α = (x_α,y_α) and β = (x_β,y_β) and on the curve, x_α ≤ x_β implies $y_{\alpha }\ge y_{\beta }$ [21].

Ortho-Convex Polygon

An isothetic polygon P is said to be ortho-convex if for any horizontal or vertical line l, the number of intersections of P with l is either 0 or 2. In other words, l intersects no edge or exactly two edges of P.

An ortho-convex polygon is bounded by two R-stairs R_tl (left-to-top boundary) and R_br (bottom-to-right boundary), and two F-stairs F_tr (top-to-right boundary) and F_bl (bottom-to-left boundary). Figure 5a shows rising stair (R-stair), and Fig. 5b shows falling stair (F-stair) in an ortho-convex polygon. Figure 5c shows the ortho-convex polygon with a pair of R-stair and F-stair with black dots that represent the object pixels.

Fig. 5.

Staircase in an ortho-convex polygon. a Rising stair. b Falling stair. c Ortho-convex cover

Ortho-Convex Covering of ROI

An ortho-convex cover, by inherent constitution, not only tightly covers the ROI but also encloses the concave portions appearing on its boundary, as desired. The proposed method is as follows.

From the set of marked pixels (with heterogeneous intensity distribution detected using runs-test), $\mathcal{ℳ}$, we determine the sets of topmost, leftmost, bottommost, and rightmost pixels stored in the arrays υ_t, υ_l, υ_b, and υ_r respectively (Fig. 5). Note that there can be several pixels in each such υ. Now, in order to generate the R-stair, say R_tl, the leftmost points in each row of $\mathcal{ℳ}$ starting from the topmost point in υ_l to the leftmost point in υ_t are noted (termed as boundary pixels). These pixels along with the topmost point of υ_l and leftmost point of υ_t form the array $R_{\mathrm{tl}}^{\prime }$. Then, the array $R_{\mathrm{tl}}^{\prime }$ is lexicographically sorted in the ascending order of x-coordinates. To generate R_tl, we process as follows: for each $p_i\in R_{\mathrm{tl}}^{\prime }$, if y_i+ 1 > y_i and $x_{i+1}\ge x_i$, then all the pixels starting from p(x_i,y_i) to p(x_i,y_i+ 1) and those from p(x_i,y_i+ 1) to p(x_i+ 1,y_i+ 1) are added to R_tl. Otherwise, p_i+ 1 is removed from $R_{\mathrm{tl}}^{\prime }$ and no pixel is added to R_tl. Using the same principle, R_br, F_bl, and F_tr can be obtained. The cover points υ_t and υ_b (υ_l and υ_r) are augmented by adding all the pixels lying between the leftmost and the rightmost pixel (bottommost and the topmost) in each of them, respectively. Finally, the arrays υ_t, R_tl, υ_l, F_bl, υ_b, R_br, υ_r, and F_tr are merged together to output the ortho-convex cover of the ROI (Fig. 5c).

The proposed method uses CCA and runs-test analysis to mark the pixels in the ROI and use this pixel cluster to compute the ortho-convex cover for the cancer-affected region (Fig. 6b). The ortho-convex cover delineates the cancer-affected region.

Fig. 6.

a Bone X-ray image with ragged surface. b Ortho-convex cover for“ragged” bone surface. c Bone X-ray image with hollow surface. d Ortho-convex cover for “hollow” bone surface

Cancer Severity Analysis

Severity of bone cancer depends on the stage and grade of the disease. Bone-destruction patterns also provide information regarding severity of the disease [7]. In the proposed approach, the severity of bone cancer is estimated by identifying proper feature parameters of the X-ray image and feeding them in a decision tree. The proposed approach aids automated estimation of stage, grade, and destruction pattern caused by bone cancer.

Feature Selection for Analysis

In order to classify the stage, grade, and destruction pattern of the bone cancer, we have used a few feature parameters. According to the medical literature [11], the stage of the bone cancer is decided based on the spread of the disease in bone whereas grading of cancer indicates the severity of the disease. Low-grade cancer has slightly abnormal cells and high-grade cancer shows rapid growth which results in bone destruction. Hence, the width of the affected area and gap (discontinuity) in bone boundary play important roles in cancer stage and grade detection. Classification of bone-destruction pattern is based on the change in texture and shape of the bone surface. Cancer-affected bone X-ray image appears with ragged bone surface. This abnormality in texture of the bone surface appears as spurious edges during edge detection process. Hence, the presence of edges on the bone surface indicates change in bone texture. The change in bone contour curvature implies the abnormality in the shape of long bone and helps to classify different bone destruction patterns. In view of these scenarios, we have selected the following feature parameters in our analysis:

• (a) Width of the affected area (w). We compute the maximum width (W ) of the ortho-convex cover enclosing the cancer-affected region on the bone surface. The width of the affected region (w) is represented as the ratio of W to the total bone width (B) (in %). As $w=\frac{W}{B}$ represents the proportion of width of the affected region with respect to the total bone width, it does not depend on the bone size (wide or narrow) or size of the X-ray image. It is used as a feature parameter for cancer stage and grade detection.

• (b) Contour gap (c). It represents the discontinuity of bone contour around the affected area. High-grade bone cancer usually spreads up to the bone boundary and causes boundary destruction. Hence, a fragmented bone contour indicates a high-grade extra-compartmental situation. The presence of multiple components in left and right sides of the bone contour when observed during connected component labeling, indicates fragmented bone boundary. The proposed method computes the gap C (in pixels) between fragments present in each side (left or right). The pixel counts for the left and right contour indicate the gap (discontinuity) present in the respective side of the contour. The ratio of the gap C to the total contour length L (in %), i.e., $c=\frac{C}{L}$, is used as a feature parameter.

• (c) Concavity change rate (Δ_CI). The concavity index represents a geometric property of a digital curve (DC), which can be computed during its traversal. The direction of traversal of pixels in a DC is represented using chain code (values 0 … 7 for 8 possible directions of move) [5, 13]. While traversing an image contour, each point p_i is assigned a concavity index, α_i where α₀ and α₁ are initialized to 0 and 1, respectively.

  α_i+ 1 = α_i + (d_i+ 1 − d_i)mod 8 (for clockwise traversal)

  α_i+ 1 = α_i − (d_i+ 1 − d_i)mod 8 (for counter-clockwise traversal)

  On the other hand, if the curve continues in the same direction, the concavity index remains unchanged. The count of change in concavity index (Δ_CI) with respect to the total number of pixel traversed (n) can be represented as

  $${\mathrm{\Delta }}_{\mathit{CI}}=\frac{{\sum }_{i=1}^n\mathit{coun}{t}_{\delta }}{n}$$ 3

  where δ = α_i+ 1 − α_i and δ≠ 0. It is observed that for a smooth contour curvature, α_i changes between {0,1,− 1} over a short traversal whereas for any abnormality in shape, this change occurs over a long traversal (with large value of n). Hence, a small value of Δ_CI indicates some sudden and abnormal change in the contour curvature.

  In this work, we traverse the left and right side of the contour of the segmented bone image while computing concavity change rate (Δ_CI).

• (d) Surface edge length (e_l). The maximum length of the connected component on the bone surface (apart from contour) represents the longest portion of the cancer-affected region. We use e_l as a feature parameter.

• (e) Number of edges (e_n). The total number of connected component on the bone surface (apart from contour) represents the edges detected in the heterogeneous region (cancer-affected). This is also used as a feature-parameter.

We use a set of training images to compute the feature parameters mentioned above. We have computed information gain (I_G) and entropy (H) [15] for each feature parameter set. Information gain (I_G) of a feature parameter measures the amount of information that it can provide about the class prediction, if the only information available is the presence of that feature in the corresponding class distribution [2, 26]. The entropy (uncertainty associated with a random feature) of a system reduces when the elements are homogeneous and increases when the elements are heterogeneous. Hence, information gain measures the reduction in entropy for each feature. It estimates the dependence between features and class labels. I_G between the i-th feature f_i and the class labels $\mathcal{C}$ as

$$I_G(f_i,\mathcal{C})=H\left(f_i\right)-H\left(f_i\right|\mathcal{C})$$ 4

where H(f_i) is the entropy of f_i and $H\left(f_i\right|\mathcal{C})$ is the entropy of f_i after observing $\mathcal{C}$.

$$\begin{array}{rcl}H\left(f_i\right)& =& \sum _j-p\left(x_j\right)\mathit{lo}{g}_2\left(p\right(x_j\left)\right),\\ H\left(f_i\right|\mathcal{C})& =& \sum _k-p\left(c_k\right)\sum _j-p\left(x_j\right|c_k\left)\mathit{lo}{g}_2\right(p\left(x_j\right|c_k\left)\right)\end{array}$$ 5

We select the features with high information gain as the nodes of the decision tree.

Cancer Stage and Grade Detection

The stage and grade of bone cancer play an important role in the treatment of the disease. Among the two different staging systems (Enneking system and AJCC classification) [11], the proposed method uses the former system, and assesses the severity of cancer based on that. In this work, we have focused on the primary bone cancer that originates in bone. In secondary bone cancer, the disease spreads in bone from other parts of the body (may be from lungs, prostate, or elsewhere).

The Enneking staging system grades cancer in G0, G1, and G2, where G0 is non-cancerous tumor, G1 is low-graded cancer, and G2 is high-graded cancer. The stage of cancer is categorized as Stage 1, Stage 2, and Stage 3, where Stage 1 is low grade and Stage 2 and Stage 3 represent higher grades. Stage 3 means metastasized situation where cancer has spread in bone from other parts of the body. In most of the such cases, cancer originates in other regions of the body and then spreads to bone in a later stage. As such cases are clinically identified as secondary bone cancer [16], we have considered only Stage 1 and Stage 2 in this study. The proposed method categorizes cancer severity based on the stages mentioned in Table 2. In this table, intra-compartmental implies the situation when the affected region is completely confined within the bone boundary, and extra-compartmental indicates the scenario where cancer has grown out of the area (compartment) of the bone [1].

Table 2.

Cancer stages and grades (Enneking System)

Stage	Description	Grade
Stage 1A	Intra-compartmental and low grade	G1
Stage 1B	Extra-compartmental and low grade	G1
Stage 2A	Intra-compartmental and high grade	G2
Stage 2B	Extra-compartmental and high grade	G2

The stage of bone cancer describes the size of the affected region and whether and how far it has spread. This information is important to doctors as they plan their treatment according to the stage of the disease. The geometry of cancer-affected bone region can be estimated from the maximum width of the affected region and the extent of spread of the disease outside the bone, as seen from an X-ray image. We compute information gain with respect to the features such as width of the affected area (w), concavity rate change (Δ_CI), surface edge number (e_l), contour gap (c), and surface edge length (e_n). Table 3 shows that the information gain of the feature set (affected area, contour gap) is more prominent compared to other features. So this feature set is selected for stage and grade identification.

Table 3.

Feature selection for stage and grade analysis

Width of	Concavity	Contour	Surface	Surface	Information
affected	change rate	gap (c)	edge no.	edge length	gain
area (w)	(ΔCI)		(en)	(el)	(IG)
√	√	×	×	×	0.7589
√	×	√	×	×	0.9163
√	×	×	√	×	0.2706
√	×	×	×	√	0.1663

Identification of Bone-Destruction Pattern

An X-ray image of cancer-affected bone may reveal different bone-destruction patterns such as geographic, moth-eaten, and permeative. The presence of giant cyst or calcification may also occur in some cases [7]. Each of these bone-destruction patterns can be identified by certain geometric feature parameters present in the image. Figure 7 shows different types of destruction patterns that can be found in cancer-affected bones. Table 4 shows the mapping of each pattern with geometric feature parameters. In this work, we have used the training-set images to learn the behavior of feature parameters and calculate the information gain for different feature sets. Features with high information gain (concavity change rate, surface edge length, and the number of surface edges) are selected as decision tree features to identify the specific bone-destruction pattern present in the input X-ray image.

Fig. 7.

Cancer-affected bones. a Geographic pattern. b Moth-eaten pattern. c Permeative pattern. d Calcification. e Giant cyst

Table 4.

Bone-destruction characteristics

Destruction property	Clinical feature (X-ray image)	Image feature (X-ray image after pre-processing)
Geographic pattern (Fig. 7a)	1. Abnormal bone contour shape	∙ Multiple (≥ 3) connected components in left or right contour line
	2. Small zone of transition	∙ Low-valued concavity change rate on left or right contour line
		∙ Few long surface lines
		∙ Small length of spread
Moth-eaten pattern (Fig. 7b)	1. Area of destruction with ragged border	∙ Multiple (≥ 3) connected components with in-between gap in left or right contour line
	2. Multiple scattered holes	∙ High concavity change rate value for left and right contour line
	2. Longer transition zone	∙ Multiple small surface lines
		∙ Wide length of spread
Permeative pattern (Fig. 7c)	1. Poorly demarcated border	∙ Single or multiple (≥ 2) connected components with very small in-between gap in left or right contour line
	2. Numerous elongated holes	∙ High concavity change rate value for left and right contour line
	3. Long transition zone spread parallel to long-bone axis	∙ Few small surface lines
		∙ Wide length of spread parallel to bone axis
Presence of calcification (Fig. 7d)	1. Flecks of calcification appear	∙ Single connected component in left and right contour line
	2. Small transition zone	∙ High concavity change rate value for left or right contour line
		∙ Few long surface lines
		∙ Small length of spread
Presence of giant cyst (Fig. 7e)	1. Irregular or fragmented bone contour	∙ Multiple (≥ 3) connected component in left and right contour line
	2. Large affected area appears as transparent to X-ray	∙ High concavity change rate value for left and right contour line
		∙ Very few (≤ 5) small surface lines
		∙ Wide length of spread

We have used contour fragment count (cf), concavity change rate (Δ_CI), the number of edges on the bone surface (e_n), length of the surface edges (e_l), and width of the affected region (w) as feature parameters and form the decision tree using training X-ray images (Fig. 8). Each leaf node in the decision tree represents a particular classification of test images. The root node and all internal nodes represent feature values used to train the sample images.

Fig. 8.

Decision tree for classifying bone-destruction patterns

Results

Data Collection

The proposed method has been evaluated on the data sets of cancer-affected long-bone X-ray images. Most of the images are collected from different publicly available datasets and websites such as TCIA dataset (https://wiki.cancerimagingarchive.net/display/Public/Wiki), website of Radiology Assistant (www.radiologyassistant.nl), Radiopedia (http://radiopaedia.org), and Bone and Spine (http://boneandspine.com/bone-tumors-images-and-xrays/). Clinical findings and comments available with these images are used as ground truth for respective image. The complete database for all these images used in this work can be accessed from the webpage (https://drive.google.com/open?id=0B5M6Y0ylgFnSalduRnJJNG5QQlE). It consists of a set of 150 long-bone X-ray images (50 for healthy persons and 100 for cancer-affected patients). We have used fivefold cross-validation strategy to evaluate the average accuracy of the classifier. In the data selection process, we have performed stratified sampling to maintain an equal proportion of healthy and diseased images in each selected set. In our experiments, we have used gray-tone X-ray images. Table 5 shows the severity level of bone cancer in the X-ray images shown in Fig. 11.

Table 5.

Detection of cancer stage (S), grade (G), and destruction patterns (P)

Figure no.	Diagnosis (CAD)			Diagnosis (clinical)			Remarks
	S	G	P	S	G	P	S	G	P
Figure 11(a1)	S1A	G1	Calcification	S1A	G1	Calcification	√	√	√
Figure 11(b1)	S2A	G2	Permeative	S2A	G2	Permeative	√	√	√
Figure 11(c1)	S2A	G2	Geographic	S2B	G2	Geographic	×	√	√
Figure 11(d1)	S2A	G2	Geographic	S2B	G2	Geographic	×	√	√
Figure 11(e1)	S2B	G2	Cyst	S2B	G2	Cyst	√	√	√
Figure 11(a3)	S2A	G2	Geographic	S2A	G2	Geographic	√	√	√
Figure 11(b3)	S1A	G1	Calcification	S1B	G1	Calcification	×	√	√
Figure 11(c3)	S1B	G1	Moth-eaten	S1B	G1	Calcification	√	√	×
Figure 11(d3)	S2A	G2	Moth-eaten	S2A	G2	Moth-eaten	√	√	√
Figure 11(e3)	S2A	G2	Moth-eaten	S2A	G2	Cyst	√	√	×
Figure 11(a5)	S2A	G2	Permeative	S2A	G2	Permeative	√	√	√
Figure 11(b5)	S2B	G2	Geographic	S2A	G2	Moth-eaten	√	√	×
Figure 11(c5)	S2B	G2	Moth-eaten	S2B	G2	Moth-eaten	√	√	√
Figure 11(d5)	S2B	G2	Cyst	S2B	G2	Cyst	√	√	√
Figure 11(e5)	S1A	G1	Calcification	S1A	G1	Calcification	√	√	√

Note: Entries in Bold indicate the cases where diagnosis using proposed approach differs from clinical diagnosis

Classification of Healthy and Cancer-Affected Bones

We have trained the binary SVM with healthy and cancer-affected X-ray image dataset and use the test dataset for diagnosis. The number of connected components (s) present on the surface of the bone image and the percentage of ROI pixels with heterogeneous intensity distribution (h) are used as feature parameter of the binary SVM model. Figure 9 shows the distribution of training images in the feature space. Each (s,h) pair in the feature space represents a bone X-ray image from our medical database. The points marked with the red circle represent correctly classified test images.

Fig. 9.

SVM (binary) for bone cancer diagnosis (points in rectangle represent misclassification)

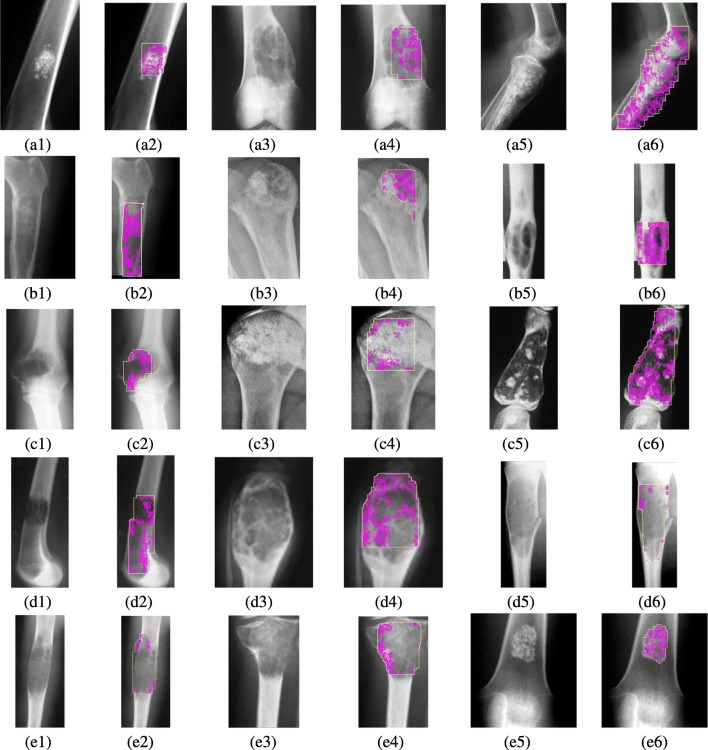
Figure 11 shows the images generated by the proposed approach with the cancer-affected region enclosed by the ortho-convex cover. Several types of bone cancer X-ray images have been used for validating the proposed technique. In Fig. 11, the first and third columns show the input bone X-ray images and the second and fourth columns show the final output images. In these images, the pixels (with heterogeneous intensity values) belonging to cancer-affected area, as identified by runs-test, are marked with purple color. The ortho-convex cover enclosing the affected region is also shown (in blue) in each output image.

Results of Caner Severity Analysis

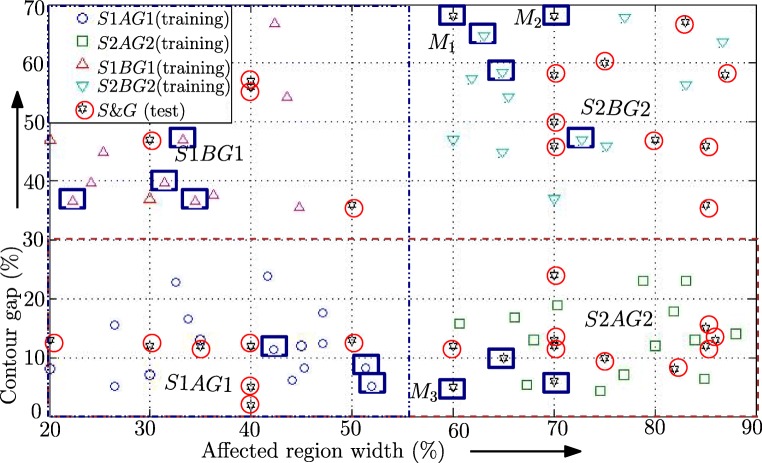
Diseased bone images identified by SVM are used for cancer severity analysis. This analysis is performed in two phases. In the first phase, stage and grade of the disease are identified using decision tree classifier. Width of affected area (w) and contour gap (c) are used as the feature parameters for this classification. Figure 10 shows the distribution of w and c for cancer-affected bone images (training set) and test images in the feature space. Here, each (w,c) pair represents the X-ray image of a cancer-affected bone (from medical database). The images in the training set are classified in four stage-grade combinations: S1AG1, S2AG2, S1BG1, and S2BG2 (as mentioned in Table 2). Test images are classified by the decision tree. Note that 90% of the test images have been classified correctly (shown by “S&G” marker). The misclassified test images (Fig. 11(c1, d1, b3)) are marked with blue rectangular boxes (M1, M2, and M3).

Fig. 10.

Stage and grade classification using decision tree (points in rectangle represent misclassification)

In the second phase of cancer severity analysis, we have used decision tree classifier to identify the bone-destruction patterns. Features such as concavity change rate, surface edge length, and the number of surface edges are used for this classification.

The stage, grade, and bone-destruction pattern of the different input images, as determined by the proposed method, are shown in Table 5. Note that in most of the cases, the cancer stage and grade have been correctly identified. While detecting the bone-destruction pattern, misclassification occurs in three scenarios (Fig. 11(c3, e3, b5)). A lower value of concavity change rate identifies the bone-destruction pattern as geographic (Fig. 11(c1, d1, a3)), whereas an increase in surface-edge-count identifies the situation as calcification (Fig. 11(a1, b3)). The presence of few surface edges indicates the possibility of single giant cyst in the bone (Fig. 11(e1, d5)). In permeative-destruction pattern, cancer spreads along the long-bone axis. Thus, a longer surface edge implies the presence of permeative pattern (Fig. 11(b1, a5)). Moth-eaten destruction pattern creates small holes on the bone surface. Hence, the presence of multiple small length surface edges with medium concavity-difference indicates the possibility of moth-eaten pattern (Fig. 11(c5, d3)). The image shown in Fig. 11(c1) shows that one side of the bone wall is deformed due to tumor and hole. The proposed method detects the stage wrongly as being intra-compartmental. In Fig. 11(b5), though the bone boundary has become thin due to the tumor and hole, it is not totally disconnected. Thus, the actual stage of cancer is intra-compartmental. Our method identifies this case wrongly as being extra-compartmental. However, the grade of the disease for each of these cases is detected correctly.

Discussion

The efficiency of the proposed approach is evaluated by computing the receiver operating characteristic curve (ROC) [25] for SVM result (bone cancer detection), decision tree result for cancer stage and grade detection, and decision tree result for bone-destruction pattern (Fig. 12). We have selected the classifier parameters that maximize the area under the ROC curve (AUC). For every classification scenario, we have considered all true positive (TP), true negative (TN), false positive (FP), and false negative (FN) cases to generate the mean ROC [29]. In the case of stage and grade detection, ROC curve (Fig. 12b) shows higher AUC for grade B images compare to grade A cases. As larger bone area gets affected in grade B cases, the proposed approach detects those cases more accurately than grade A images. Figure 12c shows the ROC curve for bone destruction pattern. Various performance parameters used for classification such as accuracy, sensitivity, specificity, precision, and F-measure [24] are listed in Table 6. The observations are based on test samples obtained using fivefold cross validation on 150 X-ray images. The same procedure is applied while analyzing stage and grade of the disease and bone-destruction patterns.

Fig. 12.

a Mean ROC curve for bone cancer detection (using SVM). b Mean ROC curve for cancer stage and grade detection (using decision tree). c Mean ROC curve for bone-destruction pattern detection (using decision tree)

Table 6.

Performance matrix for different classifications

Classification type	Accuracy	Sensitivity	Specificity	F-measure
Bone cancer	0.84	0.87	0.8	0.88
Bone cancer (stage and grade)	0.85	0.88	0.82	0.86
Bone-destruction pattern	0.83	0.86	0.81	0.87

We have also developed a graphical user’s interface (GUI) where a demonstration with four different X-ray images can be viewed. The display boxes for viewing the output image are also provided. The tool allows the user to select a demonstration option among four available examples. After selection, the user may click on the “show demonstration” button. This will initiate the background process and display the input image in the leftmost box. As the execution continues, the entropy-standard deviation image and bone contour are shown on the GUI platform. Finally, the cancer-affected region is identified, enclosed in the ortho-convex cover, and displayed on the screen. The GUI developed for the proposed automated bone cancer detection technique is available in the linked page https://drive.google.com/folderview?id=0B5M6Y0ylgFnSbHRMUUZJU0Q4d00&usp=sharing.

Conclusions

In this work, we have proposed a technique for automated long-bone cancer diagnosis for the first time that is solely based on the analysis of an input X-ray image. The proposed method integrates several interdisciplinary concepts such as statistical runs-test, local entropy- and standard deviation-based tools, digital-geometric analysis, SVM classification, and decision tree. The notion of ortho-convex cover of a cluster of marked pixels is used for convenient visualization and diagnosis of the disease and for grading the severity of cancer-affected regions. The use of digital-geometric tools leads to a fast estimation of the area of ROI as the required computation needs only integer-domain operations. Experimental results on a medical database of healthy and cancer-affected X-ray images reveal that the proposed method is fairly accurate as AUC for bone cancer detection is more than 0.85. Further, in 85% of cases, the bone-destruction pattern, stage, and grade of cancer predicted by the automated tool correctly match with the actual findings as judged by the doctors and medical professionals.