Abstract
Biological systems integrate dynamics at many scales, from molecules, protein complexes and genes, to cells, tissues and organisms. At every step of the way, mechanics, biochemistry and genetics offer complementary approaches to understand these dynamics. At the tissue scale, in vitro monolayers of epithelial cells provide a model to capture the influence of various factors on the motions of the tissue, in order to understand in vivo processes from morphogenesis, cancer progression and tissue remodelling. Ongoing efforts include research aimed at deciphering the roles of the cytoskeleton, of cell-substrate and cell-cell adhesions, and of cell proliferation–the point we investigate here. We show that confined to adherent strips, and on the time scale of a day or two, monolayers move with a characteristic front speed independent of proliferation, but that the motion is accompanied by persistent velocity waves, only in the absence of cell divisions. Here we show that the long-range transmission of physical signals is strongly coupled to cell density and proliferation. We interpret our results from a kinematic and mechanical perspective. Our study provides a framework to understand density-driven mechanisms of collective cell migration.
1. Introduction
The role of mechanics was first understood clearly for single cells, where observables like deformations, velocities, forces, viscosities and elasticities have been correlated with molecular kinetics and genetic pathways1,2. The macroscopic mechanical aspects and the more microscopic biochemical aspects are united in concepts such as mechanosensing or mechanotransduction, which are now paramount to our understanding of cell biology3,4. More recently, the same perspective has served to better understand the dynamics of collections of cells organized as cohesive tissues5,6. For single cells, in vitro studies of models like that of cell spreading have been essential to the integration of mechanics in our understanding of the dynamics of the cell7. For tissues, the monitoring of the motions of monolayers of cells confined to various geometries is serving the same purpose5,6.
Studies on single cells have provided a roadmap for the integration of mechanics to biological processes. In particular, the influence of the cytoskeleton8–10 and of its coupling with the substrate through adhesion complexes11 is known to be crucial for single cell migration but also for collective cell movements5. For instance, it is known that cells, individually or collectively can move differentially depending on the rigidity of the substrate12,13 and its well functioning or impaired sensing, from integrins to actomyosin5. Nevertheless, the roadmap is only partial, since collections of cells necessarily introduce new aspects. Cells can now interact with each other, and a lot of research has been devoted to the mechanosensing and mechanotransduction pathways associated with cell-cell contacts, for instance those mediated by cadherins5. Maybe more prosaically, collections of cells also bring in the number of cells as a new variable. For monolayers, the density n (number of cells per unit area), has been shown to be of great importance for the behavior of the tissue5,6,14–16.
To some extent, the density can be used as the principal control parameter determining the ‘state of the tissue’. High density leads to jamming, trapping the tissue in a state comparatively more solid than at lower densities15,17. In vivo, changes in what one could call the ‘state’ of the tissue are indeed observed, for instance in the well studied epithelial to mesenchymal transition14. Jamming at high densities is well documented, but there remain many interrogations pertaining to the dynamics of tissues at lower densities5,6. Although jamming may also occur at moderate constant density due to an increase in cortical tension18, the jamming threshold is expected to depend on density. Below the jamming threshold, tissues are more fluid and we aim here at a better understanding of the properties of their flows. By definition, the density can vary in two ways: either the number of cells can evolve via cell divisions and cell death or extrusions, or the area can change via swelling and migration of the cells. It is unclear how these two factors (proliferation and migration) contribute to the dynamics of tissues. For instance, cells could migrate as a consequence of proliferation, preventing an increase in cell density19. Conversely, if migration is too slow, proliferation could stop due to contact inhibition20,21. These are just two examples of the ways in which proliferation and migration could interact.
Here, we will study tissues by recording their motions restricted to a simplified geometry. We will see that proliferation has no impact on the global migration speed of the monolayer, but has an impact on the density distribution and on the emergence of velocity waves propagating away from the leading edge. We will then propose an explanation for the existence of these waves and their speed, first from kinematics, and then from a mechanical perspective. Finally, we will discuss how these waves may be similar to others already reported in vitro22–25 and in silico23,26–28, and how they can be used to better understand the mechanical properties of tissues.
2. Materials and methods
To facilitate comparison with the existing literature on monolayers, we use Madin-Darby canine kidney (MDCK) cells29, marked with Histone GFP in order to easily measure the local density of cells by tracking the nuclei30. A day prior to the start of an experiment, a fraction of cells are taken from their culture environment and seeded onto a micropatterned substrate. The motion of cells is restricted to rectangular strips of fibronectin (75 μg/μL), printed onto a thin layer of rigid PDMS on a plastic Petri dish, according to a standard soft lithography technique31. The strips have a width w = 200 μm, and a length L = 1 cm.
Cells are initially cultured overnight in a small segment of about 2 or 3 mm, restricted to one end of the strip by a block of PDMS. Once the desired cell density is reached (overnight) the block is removed and cells progressively invade the newly available space, as illustrated in Fig. 1a and b, and in the supplementary movie†. Samples are rinsed and placed under the microscope. This intermediate step takes about two hours after which the motion of cells is monitored by live microscopy with an image every 6 or 10 minutes, and for durations ranging from 20 to 30 hours. The sub-fields taken by the microscope are stitched together using the stitching plugin on ImageJ32. As long as the initial density is sufficient (see section 3.3.6), by the end of the experiment, the back of the monolayer is still dense enough to fill the strip. For experiments where divisions are restricted, 10μg/mL of mitomycin C is added just after the removal of the PDMS block30. It is incubated for an hour and rinsed before the beginning of recording.
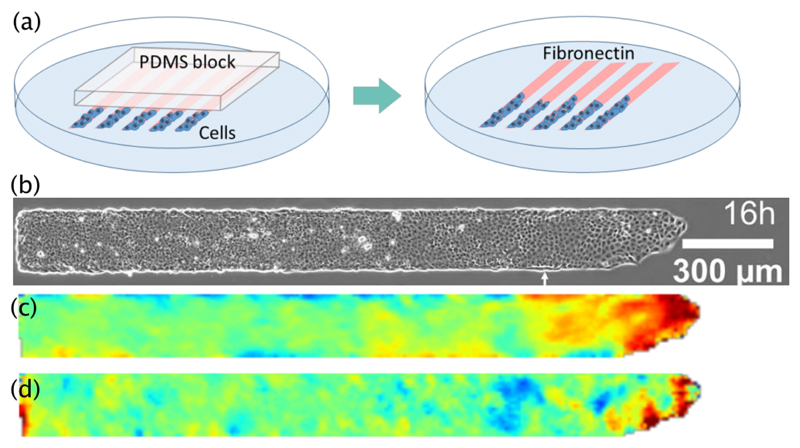
Fig. 1.
(a) Schematic representation of the protocol. Cells are first cultured overnight on a segment of the micropatterned lines restricted by a block of PDMS (left), and then the block is removed and the cells are free to invade the fibronectin substrate. (b) Snapshot of a monolayer 16 hours after the start of the experiment. The white arrow indicates the location of the front at t = 0, that is when recording starts. (c and d) Maps showing the velocity components along x (c) and y (d), averaged over an hour around the instant shown in (b). The color scales are linear between blue and red, ranging from -0.6 μm/min to 0.6 μm/min for (c), and from -0.3 μm/min to 0.3 μm/min for (d).
The position of the leading edge of the monolayer as it moves forward on the strip can be tracked reliably using the phase contrast images to obtain a front speed U averaged across the width of the strip. Velocity fields within the monolayer are computed by particle image velocimetry using MatPIV33. The PIV windows are 32 × 32 pixels with an overlap of 50%, generating a velocity field with one measurement every 16 pixels, that is every 10.24μm, with the magnification used on the microscope. Density within the monolayer is measured by counting the number of nuclei in the same windows. Because cells are larger than the PIV windows, this measurement of the density suffers from a higher error. Nevertheless, this error can be mitigated by averaging along y, that is by counting cells on larger windows, as described in section 3.1.
In the following, we will often make use of a different measure of cell density n, involving the local mean radius of cells R. The inverse of the density n gives the typical area covered by a cell in the region where the density is evaluated. Then, the mean radius of cells in this region is given by the square root of this area:
3. Experimental results
3.1. From three to one spatial dimension
In general, tissues can be three-dimensional collections of cells, which can move in all three directions (x, y, z). For monolayers, the dimensionality is reduced and motions are essentially confined to a plane (x, y). The third direction, along z, corresponds to the thickness of the monolayer. The thickness h(x, y) may vary a little, but in our experiments it does not seem to change substantially. In the following, we will assume a constant average thickness H = 9 ± 1 μm†.
If L and w are the characteristic dimensions of the monolayer along x and y, we are always in the limit where H ≪ w and H ≪ L. This limit corresponds to the geometric conditions of a so-called lubrication approximation34. Within this limit, the volumetric viscosity associated with changes in volume can be neglected in comparison to the shear viscosity associated with changes in shape34,35. When we turn to the modeling of the monolayer motion in section 4, we will see how the lubrication approximation can be used more specifically.
Without further constraint on L and w, monolayers can have non-trivial dynamics along both x and y. The vectorial velocity field, u(x, y,t), and the density field, n(x, y,t), depend on the two spatial coordinates plus time. For instance, recent studies have shown that vortices can form in various geometries29,33. In our set-up, such dynamics seem to be prevented, probably by the additional geometric constraint that w ≪ L, and the absence of obstacles, or entry effects between a reservoir and the strip29,33,36,37. The flows do have components along y, but with a zero mean since there is no net flux along y, and with smaller magnitude, as seen in Fig. 1d. In the flowing region near the front, the velocity component along x usually follows a plug profile38, and the component along y is negligible in comparison. Further away from the front, where the mean flow along x becomes negligible, we often observe a shear localized near the wall, as shown on an example in Fig. 1c. Such shear was reported recently in another cell type39. We differ to a further study the description of its properties in our case. The density n(x, y,t) has an even weaker dependence on the coordinate y. The density is constant along y, except at the wall, where it is usually slightly larger. Overall, we will neglect the component of velocity along y and we will focus on the velocity component along x (we just call it u) and the density n.
In the following the velocity field u(x,t) and density field n(x,t) are assumed to depend only on time and on the coordinate x along the strip length. We obtain u(x,t) and n(x,t) by averaging all values of u(x, y,t) and n(x, y,t) along y. That is, instead of computing velocities and densities in the original PIV boxes of 10.24μm×10.24μm, we compute them in rectangles with dimensions 10.24μm×200μm. In this way, we also reduced the error on the density mentioned earlier.
3.2. Proliferation and number of cells
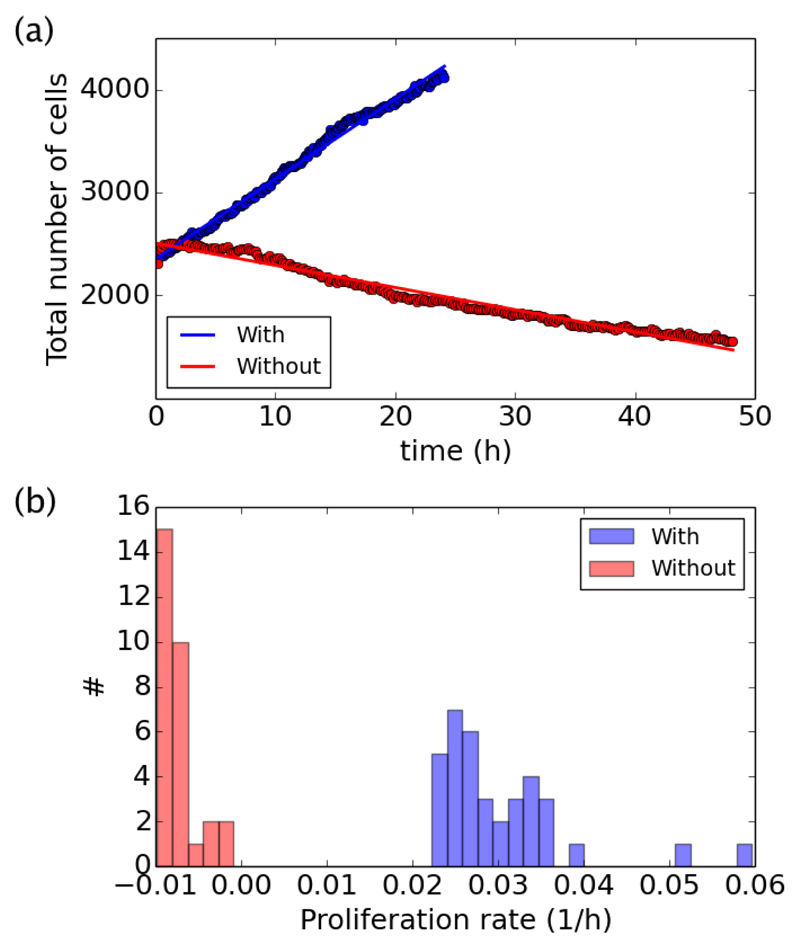
In control conditions, the number of cells can increase by cell divisions and it can decrease by cell death and extrusion. The addition of mitomycin C prevents cell division, such that the number of cells can only decrease. By counting the nuclei throughout the course of each experiment, we can follow the evolution of the number of cells, as shown on two examples (with or without divisions) in Fig. 2a. In both cases, the total number of cells N(t) either decreases or increases linearly, and it can be fitted to extract the initial number of cells N0 and the proliferation rate by cell, K, which is given by the ratio between the slope of the fit and the initial number N0. The proliferation rate K can be positive in control conditions, or negative in the absence of cell division. The histogram of K across experiments, with (# = 36) or without divisions (# = 30), is given in Fig. 2b. With divisions we found an average 〈K〉 = 0.030 ± 0.001 h−1, and without divisions we found 〈K〉 = −0.0072 ± 0.0004 h−1, where the ranges give standard errors (if not otherwise specified). The initial number of cells, with or without cell divisions is distributed around an average 〈N0〉 = 2400 ± 100.
Fig. 2.
Measure of the proliferation rate with (blue) and without (red) divisions. (a) Evolution of the total number of cells N(t) for two representative examples. Solid lines give the best linear fit to the data. (b) Histogram of the positive or negative proliferation rates for all experiments with or without divisions.
3.3. Main flow properties
3.3.1. Constant front speed
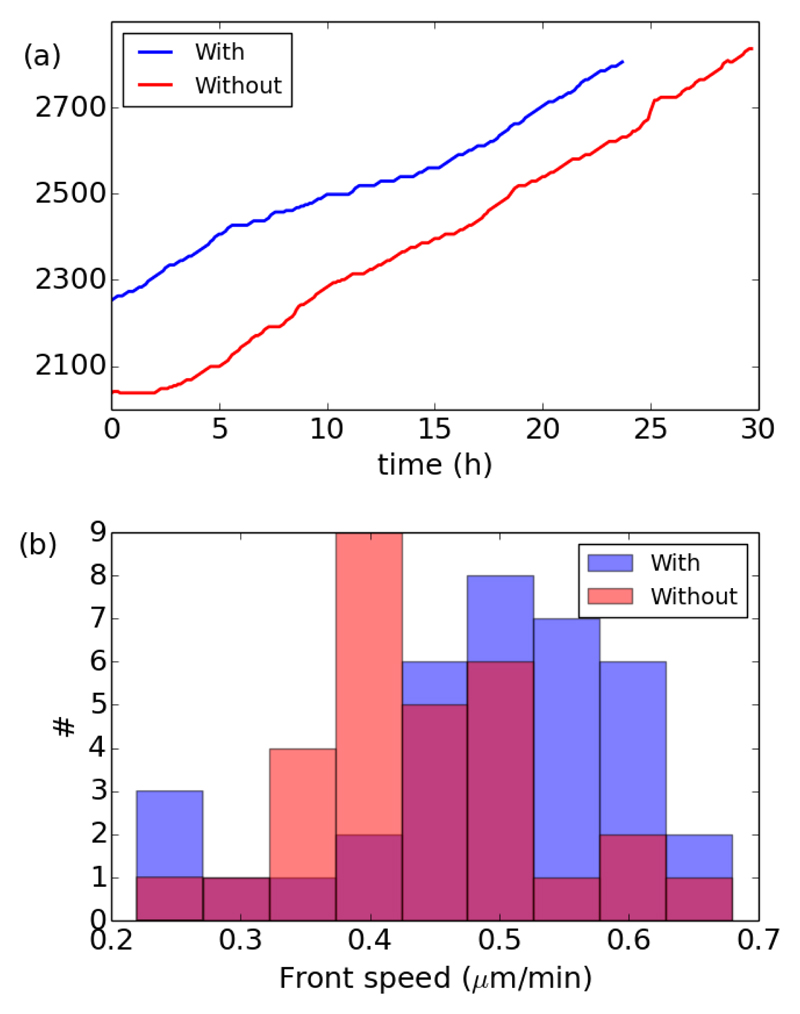
The first and somewhat surprising result is that the front speed is independent of proliferation. The addition of mitomycin C to prevent cell divisions does not modify the value of the front speed, as seen on two representative examples in Fig. 3a, where the slope of the position of the front is essentially similar with or without divisions. Note that we chose to display two experiments where the initial location of the front is slightly different so the curve would not overlap. Nevertheless, on average the initial extent of the monolayer L0 was the same, with 〈L0〉 = 2650 ± 100 μm (# = 36 + 30). With or without divisions, the position L(t) of the front advances roughly linearly with time. Thus, we calculated the front speed as the slope of the front position over the entire experiment. More local computations of the speed give similar results. Fig. 3b gives the histogram of front speed with or without divisions. Across experiments, with divisions (# = 36) we found a front speed 〈U〉 = 0.49 ± 0.03 μm/min, and without divisions (# = 30) we found 〈U〉 = 0.44 ± 0.03 μm/min. Both values are essentially similar.
Fig. 3.
Front speed with (blue) and without (red) divisions. (a) Advancement of the position of the front of the monolayer for two representative examples. (b) Histogram of the front speed for all experiments with or without divisions.
3.3.2. Gradient of velocity in the flow direction
Differences between the proliferating and non-proliferating cases set in when one looks at the gradient of velocity behind the front. The velocity is maximum at the front and decreases toward the bulk, where the flow of cells eventually comes to a stop, as seen in Fig. 4a for two representative examples with or without divisions. Although the velocity at the front are the same, the gradient of velocity is steeper with divisions.
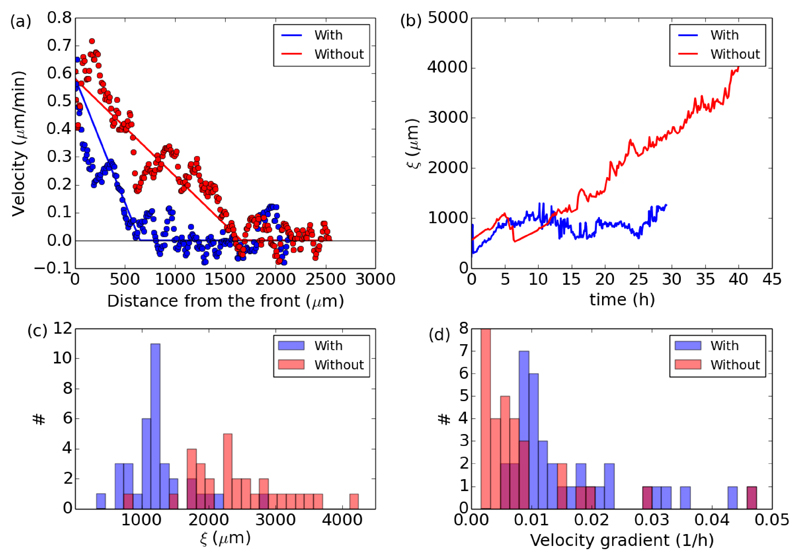
Fig. 4.
Gradient of velocity in the flow direction with (blue) and without (red) divisions. (a) Instantaneous velocity profiles behind the front for two representative examples. The solid lines represent the best piecewise fit used to extract the extent ξ of the flowing region. (b) Evolution of ξ(t) for two representative examples. The jumps in the data are due to the oscillations visible on the profiles in panel a. The piecewise fit can intermittently land on one side or the other at the crossover between the linear and constant part. (c) Histogram of the final values of ξ for all experiments with or without divisions. (d) Corresponding histograms of the velocity gradient in the flowing region.
With or without divisions, the velocity gradient in the flowing region can be approximated at any time by the ratio between the front speed and the extent of the moving part of the epithelium: Instantaneous velocity profiles like those in Fig. 4a can be fitted by a piecewise function comprised of a linearly decreasing part and a constant null part, in order to extract the distance ξ and the gradient Even if the front speed does not change significantly during the course of experiments, the velocity gradient tends to decrease† as the extent of the moving part (ξ) increases, as shown on two examples in Fig. 4b. Based on these time series we can extract the final value of ξ after tf = 24 hours (averaged over the last hour), and the corresponding velocity gradient The histogram shown in Fig. 4c confirms that in the absence of divisions, the flowing region extends further behind the moving front, with an average final length 〈ξ(tf)〉 = 2400 ± 130 μm (# = 30) in contrast to an average of 〈ξ(tf)〉 = 1200 ±75 μm (# = 36) in the presence of divisions. In turn, as shown in Fig. 4d, the velocity gradient is smaller in the absence of divisions, with an average in contrast with in the proliferating case.
3.3.3. Cell size and density gradient
Since the number of cells increases in the proliferating case and decreases in the absence of cell divisions, and since the front otherwise moves with a speed independent of proliferation, the density of cells n ends up being larger in the proliferating case. Conversely, the mean cell radius R ends up larger in the absence of cell divisions. For single experiments, at any time, the cell radius can be averaged on the entire epithelium by dividing the area covered by the epithelium by the number of cells at this time:
| (1) |
where the bar over R denotes the spacial averaging over the entire epithelium. The expression involving the ratio of L(t) and N(t) (first line) can be computed directly from the independent experimental data exemplified in Fig. 2a and Fig. 3a†. Such computations yield a linear increase of in the absence of divisions, and a linear decrease in the presence of divisions. This linear trend can be understood if one calls on the linear approximations for the progression of the front and for the cell number discussed respectively in section 3.3.1 and 3.2, and uses the Taylor expansion of the root justified by the fact that Kt and are small (third line). Whereas K represents the rate of proliferation through the modification in the number of cells, represents the rate of expansion through the advancement of the front.
The initial mean radius was roughly the same across experiments. We found for experiments with divisions (# = 36), and without divisions (# = 30)†. The rate of expansion was similarly constant, since U and L0 have about the same values regardless of proliferation. We found for all experiments with or without divisions†. The final mean radius can be computed directly from the data using the first line in Eq. 1, or it can be estimated by using the formula on the second line and the average values of K obtained in section 3.2. Both methods give similar results. Taking t = 24 hours, this gives with divisions and without divisions†. In other words, in the proliferating case cells become globally more packed than initially even though the front is advancing, whereas in the absence of divisions cells have more and more space available.
Besides the general trend we outlined by averaging R on the entire epithelium, we can can also look at the values of R at various locations within the epithelium. As the front moves forward, this gives more space to the cells behind it, thus decreasing the local density. Such rarefaction is apparent if one plots the profile of cell density or cell size in the flow direction. As shown on two examples (with or without divisions) in Fig. 5a and b, the profile of cell size R(x) in the flow direction is analogous to the velocity profile. Schematically, the larger the cells (i.e. the lower their density) the larger their velocity. Thus, the length associated with the gradient of density in the flow direction is actually the same as the length ξ we introduced for the velocity gradient This proportionality between cell radius and cell speed is what we will turn to now.
Fig. 5.
Connection between the instantaneous velocity and cell radius profiles, for two representative examples with (a-blue) and without (b-red) divisions.
3.3.4. Velocity-radius relation
Since we measure the flow speed u(x,t) and mean cell radius R(x,t) at any time and any location behind the front, we can actually compare their values systematically. We reported previously that in the absence of proliferation, the velocity u(x,t) can be linearly related to the typical size of the cells R(x,t), at the same location within the monolayer, as long as R > Rj, where Rj is a critical size under which cells are jammed and their motion virtually stops30. We here qualify this result and extend it to cases where proliferation has its course. With or without proliferation, we found that the velocity along the strip direction follows a linear relationship with the cell size for radii between the jamming radius we identified earlier, and a larger critical radius Rc over which the proportionality breaks down. Over this last radius, the velocity levels off (or may decrease a little), as shown on an example in Fig. 6a. On average, the cell velocity in the strip direction schematically follows:
| (2) |
where u and R depend on the same spatio-temporal coordinates (x,t), and where the time τv and the jamming and critical radii are constant parameters. Such schematic relation between cell velocity and radius holds well across all experiments, but as shown in Fig. 6b, the parameters of the relation between speed and radius are different with or without proliferation. In the absence of cell divisions, both the jamming and critical radii and the time τv are larger. The histograms of Rj and τv for each experiment with or without proliferation are given in Fig. 6c and d. They give the following average values: 〈Rj〉 = 7.3 ±0.1 μm and 〈τv〉 = 10.2 ±0.8 min with divisions, and 〈Rj〉 = 8.8 ±0.2 μm and 〈τv〉 = 22 ± 2 min without divisions. The average values of critical radii follow a similar trend†, with 〈Rc〉 = 10.9 ± 0.1 μm and 14.4 ± 0.5 μm, for the cases with and without divisions respectively.
Fig. 6.
Relation between speed and cell radius with (blue) and without (red) divisions. (a) Relation between speed u(x,t) and cell radius R(x,t) for all positions and times (x,t) for one experiment with divisions, representative of all experiments (with high enough initial density). Each data point corresponds to a region of interest in the monolayer, at a single time. The regions of interest have the width of the strip (200μm), and a length of 100μm. The black curve represent the average velocity-radius curve, constructed by averaging the speed for all data points within consecutive intervals of radius spaced by increments of 0.2μm. The error bars represent the associated standard deviation. (b) Overall average velocity-radius curves for all experiments with or without divisions. The error bars represent the standard error of the mean of the individual velocity-radius curves. (c and d) Histograms of the jamming radius and time τv extracted by fitting the individual velocity-radius curves for each experiment by the piecewise function in Eq. 2.
Note that within this broader context, the front speed U is usually larger than the maximum velocity of the curve u(R). Indeed, the maximum velocity of the curve incorporates values from large cells at the front as well as further behind, where velocities are smaller. Nevertheless, the two quantities remain in a linear relationship†.
3.3.5. Influence of the cytoskeleton
To further study the potential impact of cell polarity on these movements, we sought to perturb actin polymerization. To do so, we performed a series of experiments under the influence of the drug CK666, an inhibitor of the Arp2/3 complex40. In these experiments, cell divisions where inhibited by the use of mitomycin. Cells were allowed to migrate in the band for 24 hours, after which the drug CK666 was added at a concentration of 100μM41, and their subsequent motion was recorded for another 24 hours. For each of these experiments (# = 30), the front speed and the characteristics of the velocity-radius relation were computed, before and after the addition of the drug. Overall we found that the inhibition of actin polymerization substantially reduced the front speed, from an average of 〈U〉 = 0.50 ± 0.02 μm/min before the addition of the drug, to 〈U〉 = 0.16 ± 0.01 μm/min after. As for the parameters of the velocity-radius relation, we found no influence of the drug on the values of the jamming and critical radii (〈Rj〉 = 9.7 ± 0.2 μm and 〈Rc〉 = 13.4 ± 0.3 μm), but a substantial difference in the time scale, with 〈τv〉 = 10 ± 1 min and 〈τv〉 = 25±4 min, respectively before and after the drug addition†. Therefore, it seems that contrary to proliferation, which has no effect on front speed but an effect on all three parameters of the velocity-radius relation, actin polymerization affects the front speed and the time scale τv.
3.3.6. Motion for low initial density
For all the experiments described so far, with (# = 36) or without (# = 30) proliferation, the initial number of cells and the initial area covered by the monolayer are similar, they correspond to an average initial radius of cells 〈R0〉 = 8.5 ± 0.1 μm. This value roughly corresponds to the jamming radius, so the subsequent rarefaction near the front immediately leads to a motion driven by the proportionality between the cell radius and its speed. Nevertheless, since we know that this proportionality breaks down above a second critical radius Rc, we performed a few experiment at very low initial densities, to test if the subsequent dynamics was different in that case. For these experiment (# = 8), the initial number of cells is much smaller, with 〈N0〉 = 135 ± 18. Given how small this number is, the number of divisions is negligible over the course of the experiment, and we pulled together data with (# = 3) or without (# = 5) mitomycin C. The initial average cell radius in these experiments was very large†, with a mean value 〈R0〉 = 18.3 ± 1.4 μm, which is above the critical radius Rc, regardless of proliferation. Under such initial conditions, the mean front speed is 〈U〉 = 0.4 ± 0.1 min, comparable to the other experiments, but the proportionality between size and speed in the bulk broke down†.
3.4. Proliferation-dependent velocity waves
3.4.1. Spatio-temporal evolution of the velocity
Returning to our standard protocol with sufficiently high initial density and without alteration of the cytoskeleton, we did notice a difference of behavior between proliferating and non proliferating conditions if we precisely studied the spatiotemporal variations of the velocity within the monolayer. We found that without proliferation, waves of velocity propagating away from the front were reproducibly observed throughout the duration of the experiments, whereas they were strongly damped or absent when cells could divide normally. The presence or absence of waves is most evident on space-time diagrams as illustrated in Fig. 7a and b. On these diagrams, representative of the conditions with or without divisions, the magnitude of the velocity u is color-coded and given as a function of the two coordinates x and t. Without proliferation, waves are clearly visible as streaks tilted in the opposite direction than the front motion, signifying a propagation from the leading edge to the back of the monolayer, on distances growing with time. With proliferation, the waves are not visible. Beyond the surprising constance of the front speed, this dichotomous result was the most salient feature of our experiments.
Fig. 7.
Spatiotemporal diagrams (kymographs) of the velocity and mean cell radius. (a) Representative example of velocity diagram with divisions. (b) Representative example of velocity diagram without divisions. (c and d) Corresponding diagrams of mean cell radius.
From the streaks visible on the space-time plots, we measured the speed c of the waves and their period Tw. The histograms of their values for all experiments without divisions (# = 30) are given in Fig. 8a and b. We found an average wave speed 〈c〉 = 3.1 ± 0.3 μm/min, and an average period 〈Tw〉 = 195 ± 5 min. This gives an average spatial wavelength 〈λ〉 = 605 ± 74 μm, considering a linear dispersion relation λ = cTw. As seen in Fig. 8c, the dispersion relation may not actually be linear, as revealed if one plots the measured wave speed versus the wavelength λ = cTw, computed from the independent measurements of c and Tw for each experiment. In order to connect the properties of the waves and the properties of the main flow, we plot the wave speed versus the velocity of the front in Fig. 8d. Here again, we found a correlation that seems to be more subtle than a simple proportionality. The dimensionless ratio of front speed to wave speed is by definition a Mach number, Ma = U/c, and on average we found 〈Ma〉 = 0.14 ± 0.02.
Fig. 8.
Properties of the velocity waves observed in the absence of divisions (# = 30). (a) Histogram of wave speed c. (b) Histogram of wave period Tw. (c) Plot of the wave speed versus the wavelength. Error bars reflect our estimated error on our measurements of c and Tw. (d) Wave speed versus front speed. Dots take into account a front speed averaged on the last five hours of each experiment. The associated horizontal error bars give the standard deviation of this speed over the last five hours. Star symbols take into account the global front speed used in Fig. 3.
Beyond the standard experimental conditions, we also studied the existence or absence of waves in the presence of the drug CK666 altering the cytoskeleton, and for low initial densities. For low initial densities, we could not identify the waves we described here†. After addition of CK666, waves were still present, but we noticed a longer period
3.4.2. Spatio-temporal evolution of the density/radius
As for the velocity, we can construct space-time maps of the density from the counting of cell nuclei. As done in previous sections, we measure the density of cells by computing the average local radius R. The greater the value of this radius, the lower the density. Two representative space-time maps of the radius are given in Fig. 7c and d. They correspond respectively to the velocity maps in Fig. 7a and b, for cases with and without divisions. In the presence of proliferation, the mean cell radius decreases everywhere in the bulk. Only in a strip of about ξ ≃ 1000μm does it stay constant or increases. Comparing with the velocity map in Fig. 7a, the relation between velocity and radius sketched in Eq. 2 is everywhere apparent. In the flowing strip near the front, velocities are larger where radii are larger, and further back in the bulk the flow stops since the radius falls below the jamming threshold. In contrast, in the absence of divisions, the density decreases everywhere, that is the radius increases everywhere. Nevertheless, part of the rarefaction is evidently generated by the moving front and only located in its vicinity. In Fig. 7d, it is apparent that the rarefied region of high radii (say R ≃ 12μm and higher) grows substantially in length during the course of the experiment. In turn, on the velocity map in Fig. 7b, the growing rarefied part of the epithelium near the front corresponds to the flowing region where waves are observed.
Throughout experiments without divisions (# = 30) we noticed that where waves are observed on the velocity map, they are not visible on the radius map, as observed in a previous study30. This can be explained from the continuity equation (Eq. 3), which we will discuss soon. Basically, it is expected that the dimensionless amplitude of the waves in the radius signal is related to the amplitude of the waves in the velocity signal by If we estimate the amplitude of the waves in the velocity from Fig. 7b to be about unity (u′/u0 ≃ 1), then Assuming R0 ≃ 10μm, this gives an amplitude R′ ≃ 0.7μm, which is actually comparable to our estimated error on R. In other words, our measure of R is not precise enough to detect the waves in density.
4. Modelization
4.1. Kinematic description
4.1.1. Continuity equation
To understand further the nature of the velocity waves, we turn to our other principal observable, n(x,t), the density of cells. With or without proliferation, the density of cells follows a continuity equation connecting the local temporal variations in density to the flux (u.n) of cells, and to the sources and sinks generated by the cell divisions and the cell deaths/extrusions:
| (3) |
where the aggregated rate K is the only parameter, and combines the positive rate of division and the negative rate of cell death (K = K+ −K−). When proliferation is not restrained, it leads to K > 0. In contrast, if divisions are prevented, it leads to K < 0. For each experiment, we saw that the value of K can be obtained by tracking the total number of cells within the monolayer over time. Indeed, integrated on the whole surface of the monolayer, the continuity equation becomes:
| (4) |
where N(t) is the total number of cells. If the rate K is independent of N, this equation leads to an exponential solution, N = N0 exp(Kt). For all experiments we have |K|t < 1, the total duration of the experiment remains short in comparison to the inverse source/sink rate. In this regime, we can approximate the exponential by a linear function: N ≃ N0(1 + Kt), and easily extract the slope KN0, as done in Fig. 2.
4.1.2. Kinematic waves
Why is it that if K < 0, waves are observed, whereas they are strongly damped or absent if K > 0? To approach this question we can note that the continuity equation (Eq. 3) together with the relation between the cell velocity and the mean cell radius (Eq. 2) can be combined to yield an equation for the cell velocity u. Indeed, we know that in regions where the monolayer is moving, and where Rj < R < Rc, the velocity is related to the density by that is where Conversely So the density can be replaced by the velocity in the continuity equation, to reach:
| (5) |
where ur = Rj/τv. Within this limit, we can use this equation to predict the emergence of waves if K < 0. Indeed, if we add a small harmonic perturbation to the velocity u = u0 + u′ exp i(qx − ωt), the linearized equation for the perturbation leads to a complex solution for ω = ωr + iωi, with:
| (6) |
Thus, this linear stability analysis of Eq. 5 suggests that waves with a typical speed can emerge if ωi > 0, that is if If the initial profile u0 is such that the highest velocities are at the front the growth rate of the instability can only be positive if K < 0, i.e. in the non-proliferating case. Nevertheless, this condition is necessary but not sufficient, since for the instability to grow the death rate K must actually be smaller than the slope of the initial velocity profile. We have seen that on average, over experiments without divisions, the velocity gradient is whereas the proliferation rate is 〈K〉 = −0.0072 ± 0.0004 h−1. Both are comparable and so the linear stability criterion could be fulfilled. Nevertheless, our measure of the gradient involved a simplified linear description of the velocity profile, and so it may not really reflect the gradient in the stability analysis. For instance, in Fig. 5b, it is apparent that the velocity gradient near the front may be smaller than the one calculated by fitting a piecewise profile. Furthermore, if we take the front speed, 〈U〉 ≃ 0.44 μm/min, as characteristic of the main flow u0, and ur ≃ 〈Rj/τv〉 ≃ 0.65 μm/min, this predicts that the waves should move backward at a speed c0 ≃ 0.1 μm/min, which is much smaller than what we observe (〈c〉 ≃ 3 μm/min).
Overall, the essential piece of information we gathered from the linear stability analysis is more qualitative than quantitative: it is that K < 0 is a necessary condition for the emergence of waves, if cells in the front move faster than the ones in the back. Note that this kinematic approach to the waves is similar to the one found in studies on the dynamics of cars on highway42,43. The emergence of waves in monolayers is akin to the emergence of traffic jams in highway systems (without bottleneck). For traffic flows as well as for cells within tissues, agent-based models and vertex models can also be used44–46. In this context, the speed of cells can also be made to scale with the cell radius, with a coefficient of proportionality given by a frequency connected to friction as well as stiffness46.
The parallel with the dynamics of cars should also warrant caution. Indeed, if the linear stability analysis can give us a hint as to the origin of the instability and its connection to the value of K, it is known that non-linear equations like Eq. 5 can lead to the growth of patterns going well beyond the linear regime of the stability analysis43.
4.2. Mechanical description
4.2.1. Inertialess flow
To understand further the nature of the waves we now turn to a more mechanical approach on the problem. Eq. 5 gave us an informative example of equation on the velocity u that could be obtained from the continuity equation on n. Alternatively, we could try to obtain an equation for the velocity from the momentum balance:
| (7) |
where ρ is the volumetric mass density (in kg/m3), Σxx is the (pressure-like) normal component of the stress, and Σxz is the shear component–yet unspecified.
Note that even if the left-hand side of this equation is very similar to that of Eq. 5, such convective derivative on the velocity cannot come from here, since monolayers are well within the creeping flow limit, where inertial effects associated with ρ can be neglected and where the momentum equation reduces to a balance between pressure and shear47:
| (8) |
Then, where are the inertia-like terms of the left-hand side of Eq. 5 coming from? One possibility is that these terms come from a viscoelastic rheology for the stresses Σxz and Σxx. The convective derivative of the velocity may actually indirectly come from a convective derivative on the stress.
4.2.2. Example of a viscoelastic fluid
To illustrate how inertia-like convective terms can emerge from a viscoelastic rheology, let us consider a Maxwellian model, a simple viscoelastic model with a long-time viscous response, which is often used to model the mechanical properties of cells and tissues48,49. Note that with such choice, all of the activity of the stress must be factored in as a boundary condition. For our purpose, it is not necessary to specify it. In a Maxwellian model, the stress in the bulk follows the following dynamics47,50:
| (9) |
where η is the viscosity, is the symmetric part of the velocity gradient, τe is the viscoelastic relaxation time, and is the material derivative of the stress, which guaranties frame invariance47,50. The precise form of this derivative may vary, but a range of formulations can be encompassed by the so-called Gordon-Schowalter derivative51,52. For the shear and normal components of the stress it reads:
| (10) |
| (11) |
where we have considered that the flow has no component along y nor z. The convected derivative is D/Dt = ∂/∂t + u∂/∂x. The dimensionless parameter a (sometimes called ‘slip parameter’) is usually taken to vary between -1 and 1. The classical upper-convected formulation corresponds to a = 152.
A Maxwellian equation like Eq. 9 can be read as giving an elastic correction (second term on the right-hand side) to the long-time viscous response. Indeed, in the limit where τe/t ≪ 1, the stress is Newtonian with a small correction. At order the stresses are:
| (12) |
| (13) |
At the next order the stresses are†:
| (14) |
| (15) |
Enforcing the lubrication approximation by only keeping terms of order 1/z2, the stress gradients are:
| (16) |
| (17) |
Note that the lubrication approximation selects a term of order rather than as the leading term for the normal stress53. Then, the force balance is:
| (18) |
Note that the velocity u in these equations is now a function of both x and z. Strictly speaking, the velocity we discussed so far with respect to our experimental measurements was the velocity seen from the top of the monolayer. In the absence of experimental data on the variations of the flow field along the thickness of the monolayer we can hypothesize that the velocity at the top can be used to estimate the gradients. Then, to see how such viscoelastic stress can lead to an equation on the velocity like Eq. 5, we can consider that the gradient along z involves a characteristic length h, which does not vary (∂/∂z ≃ 1/h). Under such assumption, the momentum balance gives:
| (19) |
Note the similarity with the kinematic equation (Eq. 5). From the factor of the gradient on the left-hand side we can gather that the wave speed would be c0 = 2(1 − 3a)u0. Thus, waves move backward if and only if a > 1/3.
From the right-hand side of Eq. 19, we can infer that†:
| (20) |
Such scaling (τe ~ K−1) between the viscoelastic relaxation time and the proliferation rate was indeed predicted a few years ago by a rheological model of monolayers48. Our contribution suggests that the value of the slip parameter a is actually connected to the proliferation rate. Indeed, since τe is always positive, K > 0 if and only if a < 1/6.
As an example, the upper-convected derivative (a = 1) necessarily corresponds to a condition without cell divisions (K < 0 since a > 1/6), and leads to a wave speed c0 = −4u0 and a relaxation time τe = (5|K|)−1. Note that the wave speed is still lower than the observed value. Moreover, the theoretical inequality τe/t < 1 that we used to simplify the expressions of the stress components would only be true if t > (5|K|)−1, which is about 28.5 h, using the average of K for all experiments without divisions. Refinements of the approximation of the velocity gradient along z could lift some of these discrepancies†. Our purpose here is not to resolve these issues, but rather to highlight the fact that even this simple viscoelastic mechanical approach leads to convective terms similar to the kinematic approach.
5. Discussion and conclusion
The purpose of our study was to understand more precisely how proliferation and migration could interact in the dynamics of epithelial monolayers. By studying two sets of conditions, with or without divisions, we obtained three main results. The first result was that the front speed was independent of proliferation. The second result was that the cell speed varied linearly with the cell size in a range of radii comprised between a jamming radius Rj and a critical radius Rc. Proliferation had an impact on the values of the radii, as well as on the time scale τv in the proportionality regime. In contrast, altering actin polymerization only impacted τv. The third result was the existence of velocity waves, which were consistently observed to travel from the front toward the back of the epithelium, only in the absence of divisions.
From the perspective of the velocity-radius relation, the constance of the front speed may be a manifestation of the fact that cells at the front maintain a fairly constant size, close to Rc. In the absence of divisions, Rc is larger, but τv is larger too, such that the compounded speed is similar to the proliferating case†. This results could also be explained by potential antagonist effects of tissue proliferation and slowing down of velocities around cell division events. Throughout the article, we often took the point of view that cells could grow in size due to the advancement of the front, but the advancement of the front could very well be a consequence of the growing cell size. The velocity-radius relation provides a correlation between velocity and radius but does not set a direction of causality. At any rate, we expect that the constancy of the front speed is largely relying on the fact that we only studied time scales that were short in comparison to the cell cycle time K−1. It is expected that in the subsequent regime, where |K|t > 1, the behavior of the front may be different. First, in the absence of divisions, the mean cell size may eventually grow to a value beyond Rc and the epithelium may even tear up, creating new front inside, as seen in our experiments at very low initial density. Conversely, in the presence of divisions, if |K|t > 1 the mean radius may fall bellow Rj, and the front may move forward at a rhythm dictated by the increasing number of cells, but only up to a maximal velocity. Such behavior was indeed observed in a recent study conducted on initially small circular colonies over 10 days19. In this study, the maximal velocity was 0.25μm/min, which is in the same range as our typical front velocity. The slightly lower value may be due to a different fibronectin concentration54.
The velocity-radius relation was the dominant feature of our experiments, and many questions pertaining to the dynamics of epithelium can be re-framed according to it. The piecewise approximation of this relation can be used to ask whether various factors–such as proliferation, the well functioning of the cytoskeleton, adhesion between cells and the substrates, etc–can be factored into expressions for Rj, Rc and τv, which are yet to be determined. Beyond the piecewise approximation, it would be stimulating to move toward a fuller understanding of the velocity-radius relation, and to investigate where it comes from and what are its limits. In particular, in geometries where the motion of cells is fully bi-dimensional, it would be interesting to extend the relation to a vectorial velocity. From a mechanical perspective, the Maxwellian model we used as an example shows that the velocity-radius relation can be understood as a consequence of a viscoelastic rheology in a lubrication context, and as long as the relaxation time is connected to the cell cycle time K−1. To be more precise, the Maxwellian model suggested that the relation between stress relaxation and proliferation may also be connected to the specifics of stress advection via the ‘slip parameter’ a52. This slip parameter introduces the possibility for so-called ‘shear localization’ along z (also called ‘shear-banding’ 52), which in the context of epithelium may be connected to the fact that cells may advance by use of cryptic lamellipodium55, where the cell speed is concentrated on heights much smaller than the epithelium thickness.
Lastly, we observed very persistent backward velocity waves, only in the absence of proliferation. The wave speed was typically ten times larger than the front speed, with a non-trivial dependence between the two. By combining the continuity equation in the number of cells with the experimental velocity-radius relation we arrived at a linear instability criterion predicting the emergence of waves when the proliferation rate was smaller than velocity gradient in the direction of motion, that is In theory, waves could be observed in the presence of divisions, but only if they are rare in comparison to cell deaths and extrusions, and/or if cells are not faster at the front that in the bulk (i.e. if ). This caveat could explain why waves are sometimes observed restricted to a small strip behind the front in the presence of divisions, whereas they could extend on distances greater than 1 mm in the absence of divisions. Indeed, previous in vitro research did report similar behaviors22–25. The kinematic approach to the waves–in analogy with traffic flows43–benefits from its simplicity, since it is the direct product of a very well grounded balance equation (the continuity equation) and a very reproducible experimental fact (the velocity-radius relation). Moreover it discriminates naturally between the proliferating and non-proliferating case, and does not invoke additional fields such as the concentration of a chemical species or a polarity23,26–28. Contrary to all previous approaches, our experiments and kinematic model place proliferation at the center of our understanding of the waves. The compressibility/extensibility induced by proliferation is paramount to the existence of the waves. Nevertheless, other processes may affect the waves, and their disappearance may be connected to a more refined picture of how cell divisions and cell death disturb the dynamic organization of monolayers56,57.
Despite its value the kinematic approach has some limitations. To some extent, the stability criterion depends on the precise choice of velocity-radius function, and many could fit our data†. Maybe more importantly, the predicted wave speed is smaller than the observed one. These limitations motivated us to sketch a more mechanical perspective. We showed that a viscoelastic fluid rheology was compatible with the observed velocity-radius relation, but this choice should in no way be interpreted as definitive. It should just provide a roadmap to design rheological models that do not contradict the experimental velocity-radius relation. In short, the essential ingredient of a candidate rheology should be some kind of advection of the stress (and/or deformation), that could be translated into an advection of velocity by simplifying assumptions, be they that of lubrication or others. It is this advection that takes the place of the inertial advection more often encountered in hydrodynamics problems, and at the center of more well known wave propagations, like sound. It is customary to express wave speeds in terms of a volumetric density ρ⋆ and an elasticity G⋆, as c ~ (G⋆/ρ⋆)1/2. For waves driven by inertia, the volumetric density is just the regular mass density ρ. For waves in the creeping flow limit, where inertia is negligible, this volumetric density must involve some type of effective inertia6,23. As shown in many other hydrodynamic contexts, viscoelasticity is a good candidate for such effective inertia 58. Dimensional arguments then suggests that the effective density is ρ⋆ ~ ητe/d2, where the distance d could be connected to R as well as h. Then, since η = Gτe, the wave speed scaling could be expressed as c ~ (G⋆/G)1/2(d/τe). Making this result precise enough to compare with experiments will require a better grasp at the nature of the distance d, as well as an understanding of the contributions of normal and shear components to the effective elasticity G⋆. The first objective is rather geometric and will require a better reading at the shape of cells in the vertical direction as well as in the horizontal plane, an endeavor that is on the way22,54,55. The second objective echoes the long standing goal to measure the stress within epithelia and to relate it to density and velocities22,59–61.
Overall, our results show how collective behaviors depend on cell proliferation and cell density. They shed a new light on how collective cell migration should be reinterpreted depending on cell-cell interactions and tissue dynamics.
Supplementary Material
† Electronic Supplementary Information (ESI) available: [details of any supplementary information available should be included here]. See DOI: 10.1039/b000000x/
Acknowledgements
The authors acknowledge members of the IJM team ‘Cell mechanics and Adhesion’. The authors thank Philippe Marcq and François Graner for helpful discussions. The authors gratefully acknowledge financial supports from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no 617233, the LABEX ‘Who am I?’, and the French National Research Agency (ANR) (‘POLCAM’ (ANR-17- CE13-0013 and ‘MechanoAdipo’ ANR-17- CE13-0012).
Footnotes
Conflicts of interest
There are no conflicts to declare.
Notes and references
- 1.Alberts B. Molecular Biology of the Cell. CRC Press; 2017. [Google Scholar]
- 2.Lim C, Zhou E, Quek S. Journal of biomechanics. 2006;39:195–216. doi: 10.1016/j.jbiomech.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 3.Vogel V, Sheetz M. Nature reviews Molecular cell biology. 2006;7:265. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- 4.Goldmann WH. Progress in molecular biology and translational science. Vol. 126. Elsevier; 2014. pp. 75–102. [DOI] [PubMed] [Google Scholar]
- 5.Ladoux B, Mège R-M. Nature Reviews Molecular Cell Biology. 2017;18:743. doi: 10.1038/nrm.2017.98. [DOI] [PubMed] [Google Scholar]
- 6.Trepat X, Sahai E. Nature Physics. 2018:671–682. [Google Scholar]
- 7.Raucher D, Sheetz MP. J Cell Biol. 2000;148:127–136. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rafelski SM, Theriot JA. Annual review of biochemistry. 2004;73:209–239. doi: 10.1146/annurev.biochem.73.011303.073844. [DOI] [PubMed] [Google Scholar]
- 9.Mitchison T, Cramer L. Cell. 1996;84:371–379. doi: 10.1016/s0092-8674(00)81281-7. [DOI] [PubMed] [Google Scholar]
- 10.Bugyi B, Carlier M-F. Annual review of biophysics. 2010;39:449–470. doi: 10.1146/annurev-biophys-051309-103849. [DOI] [PubMed] [Google Scholar]
- 11.Mitra SK, Hanson DA, Schlaepfer DD. Nature reviews Molecular cell biology. 2005;6:56. doi: 10.1038/nrm1549. [DOI] [PubMed] [Google Scholar]
- 12.Lo C-M, Wang H-B, Dembo M, Wang Y-l. Biophysical journal. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sunyer R, Conte V, Escribano J, Elosegui-Artola A, Labernadie A, Valon L, Navajas D, García-Aznar JM, Muñoz JJ, Roca-Cusachs P, et al. Science. 2016;353:1157–1161. doi: 10.1126/science.aaf7119. [DOI] [PubMed] [Google Scholar]
- 14.Revenu C, Gilmour D. Current opinion in genetics & development. 2009;19:338–342. doi: 10.1016/j.gde.2009.04.007. [DOI] [PubMed] [Google Scholar]
- 15.Marchetti MC, Joanny J-F, Ramaswamy S, Liverpool TB, Prost J, Rao M, Simha RA. Reviews of Modern Physics. 2013;85:1143. [Google Scholar]
- 16.Kocgozlu L, Saw TB, Le AP, Yow I, Shagirov M, Wong E, Mège R-M, Lim CT, Toyama Y, Ladoux B. Current Biology. 2016;26:2942–2950. doi: 10.1016/j.cub.2016.08.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Angelini TE, Hannezo E, Trepat X, Marquez M, Fredberg JJ, Weitz DA. Proceedings of the National Academy of Sciences. 2011;108:4714–4719. doi: 10.1073/pnas.1010059108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bi D, Lopez J, Schwarz J, Manning ML. Nature Physics. 2015;11:1074. [Google Scholar]
- 19.Puliafito A, Hufnagel L, Neveu P, Streichan S, Sigal A, Fygenson DK, Shraiman BI. Proceedings of the National Academy of Sciences. 2012;109:739–744. doi: 10.1073/pnas.1007809109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Abercrombie M. National Cancer Institute Monograph. 1967;26:249–277. [PubMed] [Google Scholar]
- 21.Heckman CA. Journal of cellular physiology. 2009;220:574–575. doi: 10.1002/jcp.21775. [DOI] [PubMed] [Google Scholar]
- 22.Serra-Picamal X, Conte V, Vincent R, Anon E, Tambe DT, Bazellieres E, Butler JP, Fredberg JJ, Trepat X. Nature Physics. 2012;8:628. [Google Scholar]
- 23.Notbohm J, Banerjee S, Utuje KJ, Gweon B, Jang H, Park Y, Shin J, Butler JP, Fredberg JJ, Marchetti MC. Biophysical journal. 2016;110:2729–2738. doi: 10.1016/j.bpj.2016.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yang TD, Kim H, Yoon C, Baek S-K, Lee KJ. New Journal of Physics. 2016;18 103032. [Google Scholar]
- 25.Xi W, Sonam S, Saw TB, Ladoux B, Lim CT. Nature communications. 2017;8 doi: 10.1038/s41467-017-01390-x. 1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Banerjee S, Utuje KJ, Marchetti MC. Physical review letters. 2015;114 doi: 10.1103/PhysRevLett.114.228101. 228101. [DOI] [PubMed] [Google Scholar]
- 27.Yabunaka S, Marcq P. Soft matter. 2017;13:7046–7052. doi: 10.1039/c7sm01172e. [DOI] [PubMed] [Google Scholar]
- 28.Blanch-Mercader C, Casademunt J. Soft matter. 2017;13:6913–6928. doi: 10.1039/c7sm01128h. [DOI] [PubMed] [Google Scholar]
- 29.Vedula SRK, Leong MC, Lai TL, Hersen P, Kabla AJ, Lim CT, Ladoux B. Proceedings of the National Academy of Sciences. 2012;109:12974–12979. doi: 10.1073/pnas.1119313109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tlili S, Gauquelin E, Li B, Cardoso O, Ladoux B, Delanoë-Ayari H, Graner F. Royal Society open science. 2018;5 doi: 10.1098/rsos.172421. 172421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vedula SRK, Ravasio A, Anon E, Chen T, Peyret G, Ashraf M, Ladoux B. Methods in cell biology. Vol. 120. Elsevier; 2014. pp. 235–252. [DOI] [PubMed] [Google Scholar]
- 32.Preibisch S, Saalfeld S, Tomancak P. Bioinformatics. 2009;25:1463–1465. doi: 10.1093/bioinformatics/btp184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Petitjean L, Reffay M, Grasland-Mongrain E, Poujade M, Ladoux B, Buguin A, Silberzan P. Biophysical journal. 2010;98:1790–1800. doi: 10.1016/j.bpj.2010.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hamrock BJ, Schmid SR, Jacobson BO. Fundamentals of fluid film lubrication. CRC press; 2004. [Google Scholar]
- 35.Landau L, Lifshitz E. Fluid Mechanics. Elsevier Science; 2013. [Google Scholar]
- 36.Kim JH, Serra-Picamal X, Tambe DT, Zhou EH, Park CY, Sadati M, Park J-A, Krishnan R, Gweon B, Millet E, et al. Nature materials. 2013;12:856. doi: 10.1038/nmat3689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tarle V, Gauquelin E, Vedula S, DÕAlessandro J, Lim C, Ladoux B, Gov NS. Physical biology. 2017;14 doi: 10.1088/1478-3975/aa6591. 035001. [DOI] [PubMed] [Google Scholar]
- 38.Marel A-K, Zorn M, Klingner C, Wedlich-Söldner R, Frey E, Rädler JO. Biophysical journal. 2014;107:1054–1064. doi: 10.1016/j.bpj.2014.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Duclos G, Blanch-Mercader G, Yashunsky V, Salbreux G, Joanny J-F, Prost J, Silberzan P. Nature Physics. 2018:728–732. doi: 10.1038/s41567-018-0099-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nolen B, Tomasevic N, Russell A, Pierce D, Jia Z, Mc-Cormick C, Hartman J, Sakowicz R, Pollard T. Nature. 2009;460:1031. doi: 10.1038/nature08231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Harris AR, Daeden A, Charras GT. J Cell Sci. 2014 doi: 10.1242/jcs.142349. jcs–142349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lighthill MJ, Whitham GB. Proc R Soc Lond A. 1955;229:317–345. [Google Scholar]
- 43.Helbing D. Reviews of modern physics. 2001;73:1067. [Google Scholar]
- 44.Xi W, Saw TB, Delacour D, Lim CT, Ladoux B. Nature Reviews Materials. 2019;4:23–44. [Google Scholar]
- 45.Kabla AJ. Journal of The Royal Society Interface. 2012;9:3268–3278. doi: 10.1098/rsif.2012.0448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lin S-Z, Li B, Xu G-K, Feng X-Q. Journal of Biomechanics. 2017;52:140–147. doi: 10.1016/j.jbiomech.2016.12.035. [DOI] [PubMed] [Google Scholar]
- 47.Bird RB, Armstrong RC, Hassager O. Dynamics of polymeric liquids Vol 1: Fluid mechanics. 1987. [Google Scholar]
- 48.Ranft J, Basan M, Elgeti J, Joanny J-F, Prost J, Jülicher F. Proceedings of the National Academy of Sciences. 2010 doi: 10.1073/pnas.1011086107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gupta M, Sarangi BR, Deschamps J, Nematbakhsh Y, Callan-Jones A, Margadant F, Mège R-M, Lim CT, Voituriez R, Ladoux B. Nature communications. 2015;6 doi: 10.1038/ncomms8525. 7525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Morozov A, Spagnolie SE. Complex Fluids in Biological Systems. Springer; 2015. pp. 3–52. [Google Scholar]
- 51.Gordon R, Schowalter W. Transactions of the Society of Rheology. 1972;16:79–97. [Google Scholar]
- 52.Fardin M-A, Ober T, Gay C, Grégoire G, McKinley G, Lerouge S. Soft Matter. 2012;8:910–922. [Google Scholar]
- 53.Zhang R, Li XK. Journal of Engineering Mathematics. 2005:1–13. [Google Scholar]
- 54.Ravasio A, Le AP, Saw TB, Tarle V, Ong HT, Bertocchi C, Mège R-M, Lim CT, Gov NS, Ladoux B. Integrative Biology. 2015;7:1228–1241. doi: 10.1039/c5ib00196j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Farooqui R, Fenteany G. J Cell Sci. 2005;118:51–63. doi: 10.1242/jcs.01577. [DOI] [PubMed] [Google Scholar]
- 56.Rossen NS, Tarp JM, Mathiesen J, Jensen MH, Oddershede LB. Nature communications. 2014;5 doi: 10.1038/ncomms6720. 5720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Saw TB, Doostmohammadi A, Nier V, Kocgozlu L, Thampi S, Toyama Y, Marcq P, Lim CT, Yeomans JM, Ladoux B. Nature. 2017;544:212. doi: 10.1038/nature21718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fardin M, Perge C, Taberlet N. Soft Matter. 2014;10:3523–3535. doi: 10.1039/c3sm52828f. [DOI] [PubMed] [Google Scholar]
- 59.Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA, Butler JP, Fredberg JJ. Nature physics. 2009;5:426. [Google Scholar]
- 60.Nier V, Jain S, Lim CT, Ishihara S, Ladoux B, Marcq P. Biophysical journal. 2016;110:1625–1635. doi: 10.1016/j.bpj.2016.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Du Roure O, Saez A, Buguin A, Austin RH, Chavrier P, Siberzan P, Ladoux B. Proceedings of the National Academy of Sciences. 2005;102:2390–2395. doi: 10.1073/pnas.0408482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.