Management strategies for pancreatic pseudocysts

Abstract

Background

Pancreatic pseudocysts are walled‐off peripancreatic fluid collections. There is considerable uncertainty about how pancreatic pseudocysts should be treated.

Objectives

To assess the benefits and harms of different management strategies for pancreatic pseudocysts.

Search methods

We searched the Cochrane Central Register of Controlled Trials (CENTRAL) in The Cochrane Library 2015, Issue 9, and MEDLINE, EMBASE, Science Citation Index Expanded, and trials registers until September 2015. We also searched the references of included trials and contacted trial authors.

Selection criteria

We only considered randomised controlled trials (RCTs) of people with pancreatic pseudocysts, regardless of size, presence of symptoms, or aetiology. We placed no restrictions on blinding, language, or publication status of the trials.

Data collection and analysis

Two review authors independently identified trials and extracted data. We calculated the odds ratio (OR) and mean difference (MD) with 95% confidence intervals (CI) with RevMan 5, based on an available‐case analysis for direct comparisons, using fixed‐effect and random‐effect models. We also conducted indirect comparisons (rather than network meta‐analysis), since there were no outcomes for which direct and indirect evidence were available.

Main results

We included four RCTs, with 177 participants, in this review. After one participant was excluded, 176 participants were randomised to endoscopic ultrasound (EUS)‐guided drainage (88 participants), endoscopic drainage (44 participants), EUS‐guided drainage with nasocystic drainage (24 participants), and open surgical drainage (20 participants). The comparisons included endoscopic drainage versus EUS‐guided drainage (two trials), EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage alone (one trial), and open surgical drainage versus EUS‐guided drainage (one trial). The participants were mostly symptomatic, with pancreatic pseudocysts resulting from acute and chronic pancreatitis of varied aetiology. The mean size of the pseudocysts ranged between 70 mm and 155 mm across studies. Although the trials appeared to include similar types of participants for all comparisons, we were unable to assess this statistically, since there were no direct and indirect results for any of the comparisons.

All the trials were at unclear or high risk of bias, and the overall quality of evidence was low or very low for all outcomes. One death occurred in the endoscopic drainage group (1/44; 2.3%), due to bleeding. There were no deaths in the other groups. The differences in the serious adverse events were imprecise. Short‐term health‐related quality of life (HRQoL; four weeks to three months) was worse (MD ‐21.00; 95% CI ‐33.21 to ‐8.79; participants = 40; studies = 1; range: 0 to 100; higher score indicates better) and the costs were higher in the open surgical drainage group than the EUS‐guided drainage group (MD 8040 USD; 95% CI 3020 to 13,060; participants = 40; studies = 1). There were fewer adverse events in the EUS‐guided drainage with nasocystic drainage group than in the EUS‐guided drainage alone (OR 0.20; 95% CI 0.06 to 0.73; participants = 47; studies = 1), or the endoscopic drainage group (indirect comparison: OR 0.08; 95% CI 0.01 to 0.61). Participants with EUS‐guided drainage with nasocystic drainage also had shorter hospital stays compared to EUS‐guided drainage alone (MD ‐8.10 days; 95% CI ‐9.79 to ‐6.41; participants = 47; studies = 1), endoscopic drainage (indirect comparison: MD ‐7.10 days; 95% CI ‐9.38 to ‐4.82), or open surgical drainage group (indirect comparison: MD ‐12.30 days; 95% CI ‐14.48 to ‐10.12). The open surgical drainage group had longer hospital stays than the EUS‐guided drainage group (MD 4.20 days; 95% CI 2.82 to 5.58; participants = 40; studies = 1); the endoscopic drainage group had longer hospital stays than the open drainage group (indirect comparison: ‐5.20 days; 95% CI ‐7.26 to ‐3.14). The need for additional invasive interventions was higher for the endoscopic drainage group than the EUS‐guided drainage group (OR 11.13; 95% CI 2.85 to 43.44; participants = 89; studies = 2), and the open drainage group (indirect comparison: OR 23.69; 95% CI 1.40 to 400.71). The differences between groups were imprecise for the other comparisons that could be performed. None of the trials reported long‐term mortality, medium‐term HRQoL (three months to one year), long‐term HRQoL (longer than one year), time‐to‐return to normal activities, or time‐to‐return to work.

Authors' conclusions

Very low‐quality evidence suggested that the differences in mortality and serious adverse events between treatments were imprecise. Low‐quality evidence suggested that short‐term HRQoL (four weeks to three months) was worse, and the costs were higher in the open surgical drainage group than in the EUS‐guided drainage group. Low‐quality or very low‐quality evidence suggested that EUS‐guided drainage with nasocystic drainage led to fewer adverse events than EUS‐guided or endoscopic drainage, and shorter hospital stays when compared to EUS‐guided drainage, endoscopic drainage, or open surgical drainage, while EUS‐guided drainage led to shorter hospital stays than open surgical drainage. Low‐quality evidence suggested that there was a higher need for additional invasive procedures with endoscopic drainage than EUS‐guided drainage, while it was lower in the open surgical drainage than in the endoscopic drainage group.

Further RCTs are needed to compare EUS‐guided drainage, with or without nasocystic drainage, in symptomatic patients with pancreatic pseudocysts that require treatment. Future trials should include patient‐oriented outcomes such as mortality, serious adverse events, HRQoL, hospital stay, return‐to‐normal activity, number of work days lost, and the need for additional procedures, for a minimum follow‐up period of two to three years.

Plain language summary

Treatment methods for people with pancreatic pseudocysts (fluid collections around the pancreas)

Review question

How should people with pancreatic pseudocysts be treated?

Background

The pancreas is an abdominal organ that secretes several digestive enzymes (substances that enable and speed up chemical reactions in the body) into the pancreatic ductal system, which empties into the small bowel. It also contains the Islets of Langerhans, which secrete several hormones, including insulin (that helps to regulate blood sugar). Pancreatic pseudocysts are fluid collections around the pancreas. They arise due to sudden or long‐standing inflammation of the pancreas. While some will disappear when the inflammation of the pancreas settles down, others remain and cause symptoms such as abdominal pain, indigestion, vomiting, and weight loss. Treatments of pancreatic pseudocysts include conservative treatment (watchful monitoring), surgical drainage, which can be performed through a standard cut (open surgical drainage) or by key‐hole surgery (laparoscopic surgical drainage), or endoscopic drainage. In endoscopic drainage, a tube (stent) is inserted with the help of an endoscope (a tube passed through the mouth into the stomach, usually to visualise the abdominal organs from inside the body), that connects the pseudocyst to the stomach or the upper part of the small intestine. The insertion may be further helped by using an endoscopic ultrasound (an ultrasound probe attached to the endoscope; EUS‐guided drainage). Endoscopic ultrasound‐guided drainage may be further assisted by passing a tube through the nose and inserting it into the cyst during EUS‐guided drainage (EUS‐guided drainage with nasocystic drainage). The best way to treat pancreatic pseudocysts is not clear. We sought to resolve this by searching for existing studies on the topic. We included all randomised controlled trials whose results were reported up to 8 September 2015. Apart from using standard Cochrane methods, which allow comparison of only two treatments at a time (direct comparison), we used advanced methods, which allow individual comparison of the different treatments compared in the trials (indirect comparison).

Study characteristics

We included four trials, with 177 participants, in the review, 176 of whom were included in the analyses. The treatments compared in the four trials included endoscopic drainage (without EUS guidance), EUS‐guided drainage, EUS‐guided drainage with nasocystic drainage, and open surgical drainage. The participants were mostly people with pancreatic pseudocysts resulting from sudden onset or long‐term inflammation of the pancreas, from different causes.

Key results

One death occurred in the endoscopic drainage group, due to bleeding. The differences in the serious complications were imprecise. Short‐term health‐related quality of life (HRQoL; four weeks to three months) was worse, and the costs were higher in the open surgical drainage group than in the EUS‐guided drainage group. There were fewer complications of any severity (such as bleeding) that required additional treatment in the EUS‐guided drainage with nasocystic drainage group than in the EUS‐guided drainage alone or endoscopic drainage groups. Those who received EUS‐guided drainage with nasocystic drainage also had a shorter hospital stay compared to those who received EUS‐guided drainage alone, endoscopic drainage, or open surgical drainage. Those who received EUS‐guided drainage alone had shorter hospital stays than those with open surgical drainage. There was a higher need for additional invasive treatments to completely drain the pseudocyst with endoscopic drainage than EUS‐guided drainage alone. The differences for the other comparisons were imprecise. None of the trials reported long‐term deaths, medium‐term or long‐term HRQoL, time‐to‐return to normal activities, or time‐to‐return to work.

Quality of the evidence

The overall quality of evidence was low or very low for all the outcomes, because the trials were small and at high risk of bias (for example, prejudice of people who conduct the trial, and trial participants who prefer one treatment over another). As a result, further studies are required on this topic. Such studies should compare EUS‐guided drainage with or without nasocystic drainage in people who have symptoms from their pancreatic pseudocysts and need treatment. Such trials should measure patient‐oriented outcomes for a minimum follow‐up period of two to three years.

Summary of findings

Summary of findings for the main comparison. Management strategies for pancreatic pseudocysts: primary outcomes.

Management strategies for pancreatic pseudocysts: a network meta‐analysis
Patient or population: patients with pancreatic pseudocysts Settings: secondary or tertiary care Intervention: management strategies for pancreatic pseudocysts
Outcomes	Illustrative comparative risks* (95% CI)		Relative effect (95% CI)	No of Participants (studies)	Quality of the evidence (GRADE)
	Assumed risk	Corresponding risk
	EUS‐guided drainage	Other methods of drainage
Short‐term mortality
Endoscopic drainage versus EUS‐guided drainage	1 per 1000	3 per 1000 (0 to 74)	OR 3 (0.11 to 79.91)	89 (2 studies)	⊕⊝⊝⊝ very low1,2,3
EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage	not estimable since there was no short‐term mortality in either group		Not estimable	47 (1 study)	⊕⊝⊝⊝ very low1,2,3
Open surgical drainage versus EUS‐guided drainage	not estimable since there was no short‐term mortality in either group		Not estimable	40 (1 study)	⊕⊝⊝⊝ very low1,2,3
Serious adverse events
Endoscopic drainage versus EUS‐guided drainage	31 per 1000	72 per 1000 (16 to 268)	OR 2.42 (0.51 to 11.46)	89 (2 studies)	⊕⊝⊝⊝ very low1,2,3
Open surgical drainage versus EUS‐guided drainage	31 per 1000	208 per 1000 (13 to 845)	OR 8.2 (0.4 to 169.9)	40 (1 study)	⊕⊝⊝⊝ very low1,2,3
Health‐related quality of life (4 weeks to 3 months)
Open surgical drainage versus EUS‐guided drainage Scale from: 0 to 100. Higher indicates better	The mean health‐related quality of life in the EUS‐guided drainage was 71.4	The mean health‐related quality of life in the open surgical drainage was 21 lower (33.21 to 8.79 lower)		40 (1 study)	⊕⊕⊝⊝ low1,2
Serious adverse events were not reported for the comparison of EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage. Health‐related quality of life (4 weeks to 3 months) was not reported for the comparisons of EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage and open surgical drainage versus EUS‐guided drainage. None of the trials reported long‐term mortality, health‐related quality of life at 3 months to 1 year, or health‐related quality of life at more than one year.
*The basis for the assumed risk was the mean control group proportion for all outcomes other than short‐term mortality. For short‐term mortality, a short‐term mortality of 0.1% was used since there was no mortality in the control group. The corresponding risk (and its 95% confidence interval) is based on the assumed risk in the comparison group and the relative effect of the intervention (and its 95% CI). CI: Confidence interval; OR: Odds ratio.
GRADE Working Group grades of evidence High quality: Further research is very unlikely to change our confidence in the estimate of effect. Moderate quality: Further research is likely to have an important impact on our confidence in the estimate of effect and may change the estimate. Low quality: Further research is very likely to have an important impact on our confidence in the estimate of effect and is likely to change the estimate. Very low quality: We are very uncertain about the estimate.

¹ Risk of bias was unclear or high in the trial(s).
 ² Sample size was small.
 ³ Confidence intervals overlapped clinically important differences.

Summary of findings 2. Management strategies for pancreatic pseudocysts: a network meta‐analysis.

Management strategies for pancreatic pseudocysts: a network meta‐analysis
Patient or population: patients with pancreatic pseudocysts Settings: secondary or tertiary care Intervention: management strategies for pancreatic pseudocysts
Outcomes	Illustrative comparative risks* (95% CI)		Relative effect (95% CI)	No of Participants (studies)	Quality of the evidence (GRADE)
	Assumed risk	Corresponding risk
	EUS‐guided drainage	Other methods of drainage
Adverse events
Endoscopic drainage versus EUS‐guided drainage	171 per 1000	333 per 1000 (95 to 703)	OR 2.42 (0.51 to 11.46)	89 (2 studies)	⊕⊝⊝⊝ very low1,2,3
EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage	171 per 1000	40 per 1000 (12 to 131)	OR 0.2 (0.06 to 0.73)	47 (1 study)	⊕⊕⊝⊝ low1,2
Open surgical drainage versus EUS‐guided drainage	171 per 1000	698 per 1000 (104 to 979)	OR 11.18 (0.56 to 222.98)	40 (1 study)	⊕⊝⊝⊝ very low1,2,3
Hospital stay
Endoscopic drainage versus EUS‐guided drainage	The median hospital stay in the EUS‐guided drainage group was 2.65 days	The mean hospital stay in the endoscopic drainage was 1 day less (2.53 less to 0.53 higher)		29 (1 study)	⊕⊝⊝⊝ very low1,2,3
EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage	The median hospital stay in the EUS‐guided drainage group was 2.65 days	The mean hospital stay in the EUS‐guided drainage with nasocystic drainage was 8.1 days less (9.79 to 6.41 less)		47 (1 study)	⊕⊕⊝⊝ low1,2
Open surgical drainage versus EUS‐guided drainage	The median hospital stay in the EUS‐guided drainage group was 2.65 days	The mean hospital stay in the open surgical drainage was 4.2 days more (2.82 to 5.58 more)		40 (1 study)	⊕⊕⊝⊝ low1,2
Need for additional drainage
Endoscopic drainage versus EUS‐guided drainage	62 per 1000	424 per 1000 (159 to 742)	OR 11.13 (2.85 to 43.44)	89 (2 studies)	⊕⊝⊝⊝ very low1,2,4
Open surgical drainage versus EUS‐guided drainage	62 per 1000	30 per 1000 (3 to 273)	OR 0.47 (0.04 to 5.69)	40 (1 study)	⊕⊝⊝⊝ very low1,2,3
Costs
Open surgical drainage versus EUS‐guided drainage	The mean costs in the EUS‐guided drainage were 7010 US dollars	The mean costs in the open surgical drainage were 8040 higher (3020 to 13,060 higher)		40 (1 study)	⊕⊕⊝⊝ low1,2
Need for additional drainage was not reported for the comparison of EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage. Costs were not reported for the comparisons of EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage and open surgical drainage versus EUS‐guided drainage. None of the trials reported time‐to‐return to normal activity, or time‐to‐return to work.
*The basis for the assumed risk was the mean control group proportion. The corresponding risk (and its 95% confidence interval) was based on the assumed risk in the comparison group and the relative effect of the intervention (and its 95% CI). CI: Confidence interval; OR: Odds ratio;
GRADE Working Group grades of evidence High quality: Further research is very unlikely to change our confidence in the estimate of effect. Moderate quality: Further research is likely to have an important impact on our confidence in the estimate of effect and may change the estimate. Low quality: Further research is very likely to have an important impact on our confidence in the estimate of effect and is likely to change the estimate. Very low quality: We are very uncertain about the estimate.

¹ Risk of bias was unclear or high in the trial(s).
 ² Sample size was small.
 ³ Confidence intervals overlapped clinically important differences.
 ⁴ There was moderate inconsistency as evidenced by I‐square, tau‐square, and lack of significant overlap of confidence intervals.

Background

Description of the condition

The pancreas is an abdominal organ that secretes several digestive enzymes into the pancreatic ductal system that empties into the small bowel. It also lodges the Islets of Langerhans, which secrete several hormones, including insulin (NCBI 2014). Pancreatic pseudocysts are fluid collections in the peripancreatic tissues, although they may be partly or wholly intra‐pancreatic (Banks 2013). They are surrounded by a well‐defined wall and contain only fluid, with little or no solid material (Banks 2013). They can arise after an episode of acute pancreatitis, sudden worsening of chronic pancreatitis, or pancreatic trauma (Cannon 2009). However, the development of a pancreatic pseudocyst is rare in acute pancreatitis (Banks 2013). Most fluid collections previously called pseudocysts after an episode of acute pancreatitis are now called acute peripancreatic fluid collections (which do not have well‐defined walls), acute necrotic collections (which do not contain a wall and contain solid material because of necrosis), or walled‐off necrosis (which have solid material because of necrosis; Banks 2013). Pancreatic pseudocysts are believed to arise from a disruption of the main pancreatic duct or its branches without any recognisable pancreatic parenchymal (pancreatic cellular tissue) necrosis (indicated by solid necrotic material), resulting in leakage of pancreatic juice into the retroperitoneum or the peripancreatic tissues, which leads to a persistent, localised fluid collection (Banks 2013; Cannon 2009). Occasionally, a pseudocyst may also arise in people with acute necrotising pancreatitis (inflammation of the pancreas with presence of necrosis in the pancreas or peripancreatic tissues) when the pancreatic parenchymal necrosis of the neck or body of the pancreas isolates a still‐functioning distal (left‐sided) pancreatic remnant (‘disconnected duct syndrome’; Banks 2013). Rarely, a pseudocyst may be evident many weeks after surgical debridement (removal of necrotic tissue) for acute pancreatic necrosis (necrosectomy), due to localised leakage of the disconnected duct into the necrosectomy cavity. Since the necrosis has been removed, the walled‐off cavity contains only fluid and hence, is called a pseudocyst (Banks 2013). The pancreatic pseudocystic fluid is usually rich in pancreatic amylase (Banks 2013; Cannon 2009). Diagnoses of pancreatic pseudocysts are made on the basis of the presence of cystic collection in the peripancreatic tissues with a well‐defined wall and with little or no solid material on an imaging modality, such as contrast‐enhanced computed tomography (CECT), magnetic resonance imaging (MRI), or an ultrasound (Banks 2013).

The true incidence of pancreatic pseudocysts is difficult to determine, because many of the previous studies calculating the incidence in acute pancreatitis might have included acute peripancreatic fluid collections, acute necrotic collections, or walled‐off necrosis. Symptoms related to pancreatic pseudocysts include persistent abdominal pain, gastric (stomach) outlet obstruction, jaundice (yellowish discolouration of the skin and dark urine), dyspepsia (indigestion), weight loss, and persistent fevers. They are believed to arise from the local mass effect (pressure on the surrounding structures) of the pseudocyst or the associated inflammatory response (Cannon 2009; Cheruvu 2003). Potential complications related to pancreatic pseudocysts include infection of the pseudocyst, bile duct or gastric outflow obstruction, free rupture of the pseudocyst into the peritoneal cavity, portal or splenic vein thrombosis leading to sinistral (left‐sided) portal hypertension, pseudocyst erosion into adjacent (nearby) vessels resulting in pseudoaneurysm formation, or even catastrophic haemorrhage into the gastrointestinal tract or peritoneal cavity (Cannon 2009; Vitas 1992). However, the frequency of these complications is not known, since the natural history of pancreatic pseudocysts is not well understood (Cannon 2009).

See Appendix 1 for a glossary of terms.

Description of the intervention

The main purpose of treatment is for the relief of symptoms related to pancreatic pseudocysts and to avoid the complications related to pseudocysts. The various treatment options include: conservative management; surgical management (cystogastrostomy or cystoenterostomy); radiological management (percutaneous drainage); endoscopic management (transpapillary), when the pancreatic pseudocyst communicates with the main pancreatic duct, transenteric approach, when an endoluminal bulge (within the cavity of the stomach or small intestine), or endoscopic ultrasound evidence of adherence between the gastric or duodenal wall and the cyst without associated necrosis, which can be achieved with or without an endoscopic ultrasound and with or without nasocystic drainage; Cannon 2009; Cheruvu 2003; Johnson 2009; Varadarajulu 2008; Varadarajulu 2013; Yuan 2015). Some of the treatment‐related complications include bleeding that requires additional treatment, and pancreatic stricture (Varadarajulu 2008; Varadarajulu 2013).

How the intervention might work

The interventions may work by decompressing the fluid, relieving the pressure of the pancreatic pseudocyst on the surrounding structures, relieving the inflammatory response that causes symptoms, and allowing an alternative route for the pancreatic juice to reach the small bowel, thereby allowing digestion and relieving pain that arises because of indigestion.

Why it is important to do this review

Currently, treatment of pseudocysts is only indicated in symptomatic patients (Cannon 2009). The traditional management of symptomatic pancreatic pseudocysts is open surgical drainage. The roles of laparoscopic drainage, endoscopic drainage using an oesophagoduodenoscope or an endoscopic ultrasound, percutaneous management, and conservative management are not clear. Multiple treatment comparison or network meta‐analysis allows the comparison of several treatments simultaneously and provides information on the relative effect of one treatment versus another, even when no direct comparison has been made. There is no Cochrane network meta‐analysis on this topic. This systematic review and network meta‐analysis will identify the relative effects of different treatments and identify any research gaps.

Objectives

To assess the benefits and harms of different management strategies for pancreatic pseudocysts.

Methods

Criteria for considering studies for this review

Types of studies

We included randomised controlled trials (RCTs). We included studies reported as full text, those published as abstract only, and unpublished data.

Types of participants

We included adults with pancreatic pseudocysts, regardless of the cause for the pseudocyst (acute pancreatitis, chronic pancreatitis, or trauma), the presence of symptoms, or the size and location of the cyst.

When an incidental pancreatic cyst is noted (i.e., people undergo a scan for other reasons and a pancreatic cyst is noted), there may be difficulty in distinguishing a pancreatic pseudocyst, arising in the background of chronic pancreatitis, from pancreatic cystic neoplasms (premalignant or malignant) that may cause local inflammation (Cannon 2009). Sometimes, it may not be possible to establish a clear diagnosis based on additional imaging, cytology of the fluid, or tumour marker levels in the fluid (Cannon 2009). In such situations, resection of the cyst and histopathological examination (examination under the microscope) may be performed purely to ensure that premalignant or malignant lesions are not missed. We excluded such participants from this review as they were not our main focus.

Types of interventions

We had planned to include trials comparing any of the following interventions with another intervention in the list, provided that the only difference between the randomised groups was the management intervention or interventions being assessed.

1. Open surgical drainage;

2. Laparoscopic surgical drainage;

3. Percutaneous radiological drainage;

4. Endoscopic drainage;

5. Endoscopic drainage with guidance from endoscopic ultrasound (EUS‐guided drainage);

6. EUS‐guided drainage with nasocystic drainage;

7. Conservative management.

Types of outcome measures

Primary outcomes

1. Mortality.

   1. Short‐term mortality (in‐hospital mortality or mortality within three months);

   2. Long‐term mortality (at maximum follow‐up).

2. Serious adverse events (within three months). We accepted the following definitions of serious adverse events:

   1. International Conference on Harmonisation ‐ Good Clinical Practice guideline (ICH‐GCP 1996): Serious adverse events, defined as any untoward medical occurrence that results in death, is life‐threatening, requires inpatient hospitalisation or prolongation of existing hospitalisation, results in persistent or significant disability, incapacity, or both;

   2. Other variations of ICH‐GCP classifications such as Food and Drug Administration (FDA) classification (FDA 2006), Medicines and Healthcare products Regulatory Agency (MHRA) classification (MHRA 2013);

   3. Clavien‐Dindo classification (Clavien 2009; Dindo 2004): Grade III or more;

   4. Individual complications that could be clearly classified as Grade III or more with Clavien‐Dindo classification or as a serious adverse event with ICH‐GCP classification.

3. Health‐related quality of life (HRQoL), using any validated scale.

   1. Short‐term (four weeks to three months);

   2. Medium‐term (three months to one year);

   3. Long‐term (longer than one year).

Secondary outcomes

1. Adverse events (within three months). We accepted all adverse events reported by the study author regardless of the severity of the event.

2. Measures of decreased complications and earlier recovery (within three months).

   1. Length of hospital stay (including the index admission for intervention and any disease‐related or intervention‐related readmissions);

   2. Time‐to‐return to normal activity (return to pre‐intervention mobility without additional caregiver support);

   3. Time‐to‐return to work (for those who were previously employed).

3. Need for additional invasive intervention, such as drainage or reoperation in the case of surgical interventions, and redrainage or surgical intervention in the case of other interventions (long‐term).

4. Costs (within three months).

The choice of these clinical outcomes is based on the necessity to assess whether the interventions are safe and effective in the treatment of pancreatic pseudocysts. The costs provide an indication of resource requirement.

We did not regard the reporting of the outcomes listed here as an inclusion criterion for the review.

Search methods for identification of studies

Electronic searches

We conducted a literature search to identify all published and unpublished randomised controlled trials in all languages. We had planned to translate the non‐English language papers and fully assess them for potential inclusion in the review as necessary.

We searched the following electronic databases:

• Cochrane Central Register of Controlled Trials (CENTRAL; The Cochrane Library 2015, Issue 9; Appendix 2);

• MEDLINE (1966 to September 2015; Appendix 3);

• EMBASE (1988 to September 2015; Appendix 4); and

• Science Citation Index (1982 to September 2015; Appendix 5).

We also searched ClinicalTrials.gov (Appendix 6) and the World Health Organization International Clinical Trials Registry Platform (WHO ICTRP) on 8 September 2015 (Appendix 7).

Searching other resources

We checked reference lists of all primary studies and review articles for additional references. We attempted to contact authors of identified trials and asked them to identify other published or unpublished studies.

We searched for errata or retractions from eligible trials www.ncbi.nlm.nih.gov/pubmed on 4 January 2016.

Data collection and analysis

Selection of studies

Two review authors (KG and EP) independently screened titles and abstracts of all the potential studies we identified, and coded them as 'retrieve' (eligible or potentially eligible or unclear) or 'do not retrieve'. We retrieved the full‐text study reports, and two review authors (KG and EP) independently screened them and identified studies for inclusion; we identified and recorded reasons for exclusion of the ineligible studies. We resolved disagreements through discussion. We identified and excluded duplicates, and collated multiple reports of the same study, so that each study, rather than each report, was the unit of interest in the review. We had planned to contact the authors of trials of unclear eligibility. We recorded the selection process in sufficient detail to complete a PRISMA flow diagram and a 'Characteristics of excluded studies' table.

Data extraction and management

We used a standard data collection form for study characteristics and outcome data, which had been piloted on at least one study in the review. Two review authors (KG and EP) extracted the following study characteristics:

1. Methods: study design, total duration of study and run in, number of study centres and location, study setting, withdrawals, date of study.

2. Participants: number (N), mean age, age range, gender, presence of symptoms, average size of the pancreatic pseudocyst, inclusion criteria, exclusion criteria.

3. Interventions: intervention, comparison, concomitant interventions, number of participants randomised to each group.

4. Outcomes: primary and secondary outcomes specified and collected, time points reported. For binary outcomes, we obtained the number of participants with events and the number of participants included in the analysis in each group. For continuous outcomes, we obtained the unit or scale of measurement, mean, standard deviation, and the number of participants included in the analysis for each group. For count outcomes, we had planned to obtain the number of events and the number of participants included in the analysis in each group. For time‐to‐event outcomes, we had planned to obtain the proportion of people with events, the average duration of follow‐up of participants in the trial, and the number of participants included in the analysis for each group.

5. Notes: funding for trial, notable conflicts of interest of trial authors.

Two review authors (KG and EP) independently extracted outcome data from the included studies. If outcomes had been reported at multiple time points, we would have extracted the data for all time points. We obtained information on the number of participants with adverse events (or serious adverse events) and the number of such events, where applicable. We extracted costs, using the currency reported by trial authors and had planned to convert them to US dollars at the conversion rates on the day of the analyses. We extracted data for every trial arm that was an included intervention. If outcome data were reported in an unusable way, we attempted to contact the trial authors to obtain usable data. If we were unable to obtain usable data, we had planned to summarise the unusable data in an appendix. We resolved disagreements by consensus. One review author (KG) copied the data from the data collection form into the Review Manager 5 file. We double‐checked that the data were entered correctly by comparing the study reports with the data in the systematic review.

Assessment of risk of bias in included studies

Two review authors (KG and EP) independently assessed the risk of bias for each study, using the criteria outlined in the Cochrane Handbook for Systematic Reviews of Interventions (Higgins 2011). We resolved disagreement by discussion. We assessed the risk of bias according to the following domains:

1. Random sequence generation;

2. Allocation concealment;

3. Blinding of participants and personnel;

4. Blinding of outcome assessment;

5. Incomplete outcome data;

6. Selective outcome reporting;

7. Other potential bias.

We classified each potential source of bias as high, low, or unclear, and provided a quote from the study report, together with a justification for our judgement, in the 'Risk of bias' table. We summarised the risk of bias judgements across all studies for each of the domains listed. We had planned to consider blinding separately for different key outcomes where necessary, e.g., for unblinded outcome assessment, risk of bias for all‐cause mortality may be very different than for a participant‐reported pain scale. Where information on risk of bias related to unpublished data or to correspondence with a trial author, we had planned to note this in the 'Risk of bias' table. We had planned to present the risk of bias in each pair‐wise comparison in separate tables. However, there were only four trials and all the trials were considered to be at unclear or high risk of bias, so, we did not present this information.

When considering treatment effects, we took into account the risk of bias for the studies that contributed to that outcome by completing a sensitivity analysis.

Assesment of bias in conducting the systematic review

We conducted the review according to the published protocol, and have reported any deviations from it in the 'Differences between protocol and review' section of the review (Gurusamy 2014).

Measures of treatment effect

For dichotomous variables, such as short‐term mortality, proportion of participants with adverse events, requirement for additional interventions, we planned to calculate the odds ratio (OR) with a 95% credible interval (CrI). For continuous variables, such as length of hospital stay, time‐to‐return to normal activity, time‐to‐return to work, and costs, we had planned to calculate the mean difference (MD) with a 95% CrI. We had planned to use the standardised mean difference (SMD) with a 95% CrI for quality of life if different scales were used. For count outcomes, such as the number of adverse events, we had planned to calculate the rate ratio (RaR) with a 95% CrI. For time‐to‐event data, such as long‐term mortality, and a requirement for additional invasive intervention, such as reoperation in the case of surgical interventions, and surgical intervention in the case of other interventions, we had planned to use the hazard ratio (HR) with a 95% CrI. However, we did not perform a Bayesian network analysis and performed a simple indirect comparison using frequentist methods. So, we calculated the above treatment effects when data was available with 95% confidence intervals. Please see 'Data synthesis' for the reason for not performing the network meta‐analysis.

A common way that trial authors indicate that they have skewed data is by reporting medians and interquartile ranges. When we encountered this, we had planned to report the median and interquartile range in a table.

Unit of analysis issues

The unit of analysis was individual participants with a pancreatic pseudocyst. As anticipated, there were no cluster‐randomised trials for this comparison, but if we had identified any, we had planned to obtain the effect estimate adjusted for the clustering effect. If this was not available from the report or from the trial authors, we had planned to exclude the trial from the meta‐analysis.

In multi‐arm trials, the models account for the correlation between trial‐specific treatment effects from the same trial.

Dealing with missing data

We attempted to contact investigators or study sponsors in order to verify key study characteristics, and obtain missing numerical outcome data, where possible (e.g., when a study was identified as an abstract only). For binary, count, and time‐to‐event outcomes, we had planned to perform an intention‐to‐treat analysis whenever possible (Newell 1992). If this was not possible, we would have performed an available‐case analysis, but had planned to assess the impact of 'best‐best', 'best‐worst', 'worst‐best', 'worst‐worst' scenario analyses on the results for binary outcomes. For continuous outcomes, we performed an available‐case analysis. if we were unable to obtain the information from the investigators or study sponsors, we imputed the mean from the median (i.e., considered the median as the mean) and the standard deviation from the standard error, interquartile range, or P values, according to the Cochrane Handbook for Systematic Reviews of Interventions (Higgins 2011); we assessed the impact of including such studies in a sensitivity analysis, as indicated. If we had been unable to calculate the standard deviation from the standard error, inter‐quartile range, or P values, we had planned to impute the standard deviation as the highest standard deviation in the remaining trials included in the outcome, being fully aware that this method of imputation would decrease the weight of the studies in the meta‐analysis of mean difference and that it would shift the effect towards no effect for standardised mean difference. We had planned to assess the impact of including such studies by performing sensitivity analyses.

Assessment of heterogeneity

We assessed the heterogeneity in each pair‐wise comparison by assessing the Higgins I² (Higgins 2003), the Chi² test with significance set at a P value less than 0.10, and visual inspection, whenever applicable. We also used the Tau² statistic to measure heterogeneity among the trials in each analysis. The Tau² statistic provides a measure of the variability of the effect estimate across studies in a random‐effects model (Higgins 2011). If we had identified substantial heterogeneity, we had planned to explore it by performing a meta‐regression.

Assessment of reporting biases

We attempted to contact trial authors, asking them to provide missing outcome data. Where this was not possible, and the missing data were thought to introduce serious bias, we had planned to explore the impact of including such studies in the overall assessment of results with a sensitivity analysis. 

If we had been able to pool more than 10 trials for a specific comparison, we had planned to create and examine a funnel plot to explore possible publication bias. We had planned to use Egger's test to determine the statistical significance of the reporting bias (Egger 1997). We had planned to consider a P value of less than 0.05 statistically significant of reporting bias.

Data synthesis

We undertook meta‐analyses only where this was meaningful, i.e., if the treatments, participants and the underlying clinical question were similar. In general, we favoured performing a meta‐analysis, and had planned to clearly highlight the reason for not performing one if we decided against it. We had planned to conduct network meta‐analyses to compare multiple interventions simultaneously for each of the primary and secondary outcomes whenever applicable. Network meta‐analysis combines direct evidence within trials and indirect evidence across trials (Mills 2012).

We had planned to obtain network plots to ensure that the trials were connected by treatments using Stata/IC 11 (StataCorp LP; please see Appendix 8 for the Stata command we had planned to use). We had planned to apply network meta‐analysis to each connected network, and conduct a Bayesian network meta‐analysis using the Markov chain Monte Carlo method in WinBUGS 1.4. We had planned to model the treatment contrast (e.g., log OR for binary outcomes and MD for continuous outcomes) for any two interventions ('functional parameters') as a function of comparisons between each individual intervention and an arbitrarily selected reference group ('basic parameters'; Lu 2004). We had planned to use EUS‐guided drainage as the reference group. We had planned to perform the network analysis as per the guidance from the National Institute for Health and Clinical Excellence Decision Support Unit (NICE DSU) documents (Dias 2013).

Further details of the codes used and the technical details of how we planned to perform the analysis are shown in Appendix 9 and Appendix 10. In short, we had planned to use three non‐informative priors, a burn‐in of 30,000 simulations to ensure convergence (we planned to use longer burn‐in if the models did not converge in 30,000 simulations), and obtain the posterior estimates after a further 100,000 simulations. We had planned to use the fixed‐effect and random‐effects models (assuming homogeneous between‐trial variance across comparisons) for each outcome. We had planned to choose the fixed‐effect model if results were an equivalent or better fit (assessed by residual deviances, number of effective parameters, and deviance information criterion (DIC)) than the random‐effects model. A lower DIC indicates a better model fit. We had planned to use the random‐effects model if it resulted in a better model fit, as indicated by a DIC lower than that of the fixed‐effect model by at least three. In addition, we had planned to perform a treatment‐by‐design random‐effects inconsistency model (Higgins 2012; White 2012). We had planned to consider that the inconsistency model was a better model than the random‐effects consistency model (standard random‐effects network meta‐analysis model) if the model fit of the inconsistency model (as indicated by the DIC) was at least three lower than the random‐effects consistency model.

For multi‐arm trials, one can enter the data from all arms in a trial. This is entered as the number of people with events and the number of people exposed to the event, using the binomial likelihood and logit link for binary outcomes; the mean and standard error using the normal likelihood and identity link for continuous outcomes requiring calculation of the mean difference; the mean and standard error of the treatment differences using the normal likelihood and identity link for continuous outcomes requiring calculation of the standardised mean difference; the number of events and the number of people exposed to the event using the Poisson likelihood and log link for count outcomes; and follow‐up time in the study, number of people with the event and the number of people exposed to the event using the binomial likelihood and cloglog link for time‐to‐event outcomes. However, we did not encounter any multi‐arm trials.

We had planned to report the treatment contrasts (e.g., log ORs for binary outcomes and MDs for continuous outcomes) of the different treatments in relation to the reference treatment (i.e., EUS‐guided drainage), the residual deviances, the number of effective parameters, and the DIC for a fixed‐effect model and a random‐effects model for each outcome. We had also planned to report the parameters used to assess the model fit (i.e., residual deviances, number of effective parameters, and DIC) for the inconsistency model for all the outcomes, and the between‐trial variance for the random‐effects model (Dias 2012a; Dias 2012b; Higgins 2012; White 2012). If the inconsistency model had resulted in a better model fit than the consistency models, the transitivity assumption was likely to be untrue and the effect estimates obtained may not have be reliable. We had planned to highlight such outcomes where the inconsistency model resulted in a better model fit than the consistency models. We had planned to perform a separate network meta‐analysis for different subgroups to assess the inconsistency again. If there was no evidence of inconsistency in the revised analysis, we had planned to present the results of the analysis for different subgroups separately. If there was persistent evidence of inconsistency, we had planned to present the results from the direct comparison in the 'Summary of findings' table.

We had planned to calculate the 95% CrIs of treatment effects (e.g. ORs for binary outcomes, MDs for continuous outcomes, and so on) in the Bayesian meta‐analysis, which is similar in use to the 95% confidence intervals in the Frequentist meta‐analysis. These are the 2.5^th percentile and 97.5^th percentiles of the simulations. We had planned to report the mean effect estimate and the 95% CrI for each pair‐wise comparison in a table. We had also planned to estimate the probability that each intervention ranked at one of the possible positions and would have presented this information in graphs. It should be noted that one should not conclude that a treatment is the best one for an outcome if the probability of being the best is less than 90% (Dias 2012a). We had also planned to present the cumulative probability of the treatment ranks (i.e., the probability that the treatment is within the top two, the top three, etc.) in graphs. We had also planned to plot the probability that each treatment was best for each of the different outcomes (rankograms), which are generally considered more informative (Dias 2012a; Salanti 2011). However, because of sparse data, trials with zero events and lack of direct and indirect evidence for any comparisons, we only performed indirect comparisons, using methods described by Bucher, et al (Bucher 1997). Although we had planned to perform the direct comparisons using the same codes, we used the RevMan statistical algorithm for direct comparisons, which allowed us to present information in the standard Cochrane way.

In the presence of adequate data, where authors reported the outcomes of participants at multiple follow‐up time points, we had planned to follow the methods suggested by Lu 2007 to perform the meta‐analysis.

'Summary of findings' table

We created a 'Summary of findings' table that reported on all the outcomes. We used the five GRADE considerations (study limitations, consistency of effect, imprecision, indirectness and publication bias) to assess the quality of the body of evidence as it related to the studies that contributed data to the meta‐analyses for the prespecified outcomes. We had planned to use methods and recommendations described in the GRADE Working Group approach for rating the quality of treatment effect estimates from network meta‐analysis (Puhan 2014). However, since the network meta‐analysis was not performed, we only presented the results of direct and indirect comparisons. We justified all decisions to down‐ or upgrade the quality rating of the evidence using footnotes, and made comments to aid the reader's understanding of the review where necessary. We considered whether there was any additional outcome information that we were not able to incorporate into meta‐analyses and noted this in the comments.

Subgroup analysis and investigation of heterogeneity

We had planned to assess the differences in the effect estimates between the following subgroups using meta‐regression, with the help of the code shown in Appendix 6, when at least one trial was included in each subgroup.

1. Symptomatic versus asymptomatic participants.

2. Reason for pancreatic pseudocyst (acute pancreatitis, chronic pancreatitis, trauma).

3. Mean size of the pseudocyst. Although size is not the main reason for the treatment, observational studies have found that the mean size of pseudocysts was higher in people who required surgery after conservative management, compared to those who did not require surgery after conservative management (7 cm versus 5 cm) (Vitas 1992).

We had planned to calculate the interaction term (Dias 2012c). If the 95% CrI of the interaction term did not overlap zero, we had planned to consider this statistically significant.

Sensitivity analysis

We had planned to perform the following sensitivity analyses defined a priori to assess the robustness of our conclusions. 

1. Excluding trials at unclear or high risk of bias (one or more of the risk of bias domains classified as unclear or high).

2. Excluding trials in which either the mean, the standard deviation, or both were imputed.

3. Imputation of binary outcomes under 'best‐best', 'best‐worst', 'worst‐best', and 'worst‐worst' scenarios.

Reaching conclusions

We based our conclusions only on findings from the quantitative or narrative synthesis of included studies for this review. We avoided making recommendations for practice, and our implications for research give the reader a clear sense of the remaining uncertainties, and where future research in this area should focus.

Results

Description of studies

Results of the search

We identified 2467 references through electronic searches of Cochrane (Wiley; N = 200), MEDLINE (OvidSP; N = 1262), EMBASE (OvidSP; N = 736), Science Citation Index expanded (N = 255), ClinicalTrials.gov (N = 1), and WHO Trials register (N = 13). After removing duplicate references, there were 2052 references remaining. We excluded 2041 clearly irrelevant references by reading titles and abstracts. One reference was identified by reference searching. The full publication of 12 references were retrieved for further detailed assessment. One reference was excluded since it was a comment on an included study (Sauer 2010). One reference was an ongoing study from the WHO ICTRP trial register (NCT02041793). Although it appears to have completed recruitment, we were unable to find any written record of the results. In total, ten references describing four trials fulfilled the inclusion criteria (Characteristics of included studies). The reference flow is shown in Figure 1.

1.

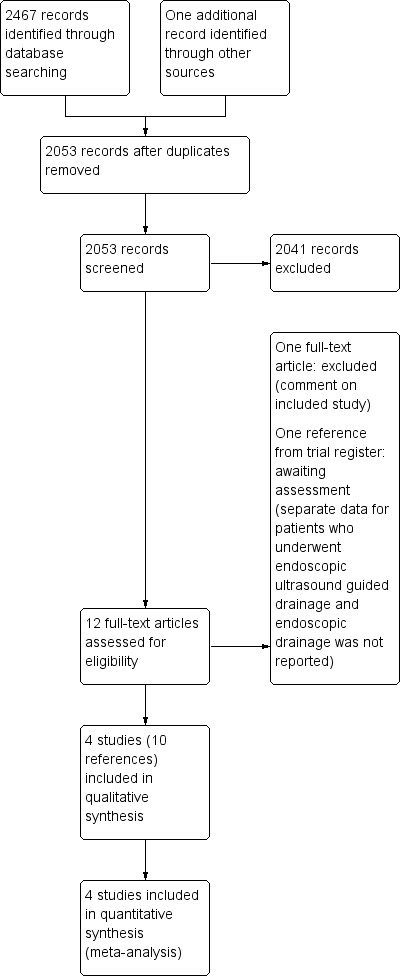
Study flow diagram.

Included studies

Four randomised controlled trials (RCT) were included in this review; they were all two‐armed trials (Park 2009; Varadarajulu 2008; Varadarajulu 2013; Yuan 2015). Three trials included only symptomatic patients with pseudocysts (Park 2009; Varadarajulu 2008; Varadarajulu 2013). This information was not available in Yuan 2015. Two studies reported that they included patients with pseudocysts from acute and chronic pancreatitis due to various aetiologies (Park 2009; Varadarajulu 2013). However, these studies did not report the data separately for people with acute and chronic pancreatitis. The remaining two trials did not report information on whether the pseudocyst was associated with acute or chronic pancreatitis. The mean size of the pseudocysts across studies ranged between 70 mm and 155 mm. No separate data were available for pseudocysts of different sizes. Infected pseudocysts were excluded in two trials (Park 2009; Varadarajulu 2008). This information was not available in the remaining two trials (Varadarajulu 2013; Yuan 2015).

A total of 177 participants were randomised in the four trials. One trial excluded a participant with suspicion of a pancreatic adenoma, leaving a total of 176 participants (Varadarajulu 2008). The interventions and length of follow‐up were as follows; all were compared to EUS‐guided drainage:

1. Park 2009: Endoscopic drainage (29 participants) versus EUS‐guided drainage (31 participants). Follow‐up: minimum six months.

2. Varadarajulu 2008: Endoscopic drainage (15 participants) versus EUS‐guided drainage (14 participants). Follow‐up: minimum six weeks.

3. Yuan 2015: EUS‐guided drainage with nasocystic drainage (24 participants) versus EUS‐guided drainage (23 participants). Follow‐up: minimum 24 months.

4. Varadarajulu 2013; Open surgical drainage (20 participants) versus EUS‐guided drainage (20 participants). Follow‐up: minimum 24 months.

Pseudocysts were drained into the stomach in two trials (Varadarajulu 2013; Yuan 2015), and into the stomach or duodenum in two trials (Park 2009; Varadarajulu 2008). Routine stent removal was reported in two trials (Varadarajulu 2008; Varadarajulu 2013). In Varadarajulu 2008, the stents were removed after six weeks in those with successful resolution of cysts in both groups. In Varadarajulu 2013, the stents were removed after eight weeks in the EUS‐guided drainage group following CT scan confirmation of the successful resolution of the cysts. The timing of stent removal in either group was not reported in the remaining trials.

Study details of the population, interventions, outcomes and risk of bias are listed in the Characteristics of included studies table and Table 3.

1. Characteristics table (arranged according to comparisons).

Study name Inclusion and exclusion criteria	Number of people in intervention group	Number of people in control group	Risk of bias
			Random sequence generation	Allocation concealment	Blinding of participants and personnel	Blinding of outcome assessment	Incomplete outcome data	Selective reporting	Other bias
Endoscopic drainage versus EUS guided drainage
Park 2009	31	29	Low	Unclear	High	High	Low	Low	Unclear
Inclusion criteria 1. History of pancreatitis. 2. Symptomatic pseudocysts with duration of longer than 4 weeks. Exclusion criteria 1. Age less than 18 years. 2. A pancreatic pseudocyst more than 4 cm in size and communicating with the pancreatic duct. 3. A suggested pancreatic abscess or necrosis, shown by computed tomography (CT). 4. A moderate thickness (> 10 mm) from the cyst wall to the intramural wall, shown by EUS. 5. Portal hypertension or coagulopathy.
Varadarajulu 2008	14	15	Low	Low	High	Unclear	High	Low	Unclear
Inclusion criteria 1. History of pancreatitis. 2. Symptomatic pseudocysts. Exclusion criteria 1. CT findings were suggestive of pathology other than a pseudocyst. 2. Pseudocyst was ≤ 4 cm in size. 3. Patients younger than 18 years of age. 4. Patients with pancreatic abscess or necrosis by CT.
EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage
Yuan 2015	23	24	Unclear	Low	Unclear	Unclear	Unclear	High	Unclear
Inclusion criteria 1. Ages 16 to 70 years. 2. Clinical presentation with abdominal distension with or without upper gastrointestinal obstruction. 3. Radiological findings suggestive of a pancreatic pseudocyst > 10 cm. Exclusion criteria 1. Cysts without adherence to the gastric wall. 2. Distance between pseudocyst and gastric wall greater than 1 cm. 3. Pseudocyst communication with the main pancreatic duct. 4. Pregnancy. 5. Pancreatic tumors. 6. Risk for anaesthesia and surgery. 7. Contraindications to magnetic resonance cholangiopancreatography and endoscopic retrograde cholangiopancreatography. 8. Liver cirrhosis. 9. Previous history of abdominal surgery (e.g. gastrectomy). 10. Inability to give informed consent.
Open surgical drainage versus EUS‐guided drainage
Varadarajulu 2013	20	20	Low	Low	High	High	Low	Low	Low
Inclusion criteria 1. Diagnosis of pancreatic pseudocyst based on CT criteria. 2. Pseudocyst measuring >= 6 cm in size and located adjacent to the stomach. 3. Documented history of acute or chronic pancreatitis. 4. Persistent pancreatic pain requiring narcotics or analgesics. 5. Symptomatic gastric outlet or bile duct obstruction induced by the pseudocyst. Exclusion criteria 1. Age < 18 or > 80 years. 2. Contraindications to surgery: ASA class IV, severe portal hypertension. 3. Contraindication to endoscopic drainage: gastrectomy with Billroth II reconstruction, gastric bypass surgery, prior surgery for pancreas‐related complications. 4. Pregnancy. 5. Associated pancreatic necrosis on CT. 6. Pseudocyst not adjacent to the stomach. 7. Multiloculated pseudocyst or multiple pseudocysts.

Excluded studies

One reference was excluded since this was a comment on an included study (Sauer 2010).

Risk of bias in included studies

None of the included trials were at low risk of bias. The risk of bias in the individual domains are summarised in Figure 2 and Figure 3.

2.

Risk of bias graph: review authors' judgements about each risk of bias item presented as percentages across all included studies.

3.

Risk of bias summary: review authors' judgements about each risk of bias item for each included study.

Allocation

Two trials reported the allocation sequence generation and allocation concealment adequately and are at low risk of selection bias (Varadarajulu 2008; Varadarajulu 2013). The remaining trials did not report the allocation sequence generation (Yuan 2015), or allocation concealment (Park 2009) and hence are at unclear risk of selection bias.

Blinding

It is not possible to blind the endoscopist or surgeons performing the procedures. However, it is possible to blind the participants (except for the comparison between endoscopic and surgical methods) and outcome assessors, endoscopists or surgeons who make clinical decisions after the procedure. None of the trials reported on blinding of the participants or outcome assessors. Hence, all the trials were at unclear risk of performance bias and unclear risk of detection bias for all outcomes other than mortality. All‐cause mortality was reported and it was unlikely that the lack of blinding introduced bias in the assessment of mortality.

Incomplete outcome data

Three trials reported the participant flow clearly (Park 2009; Varadarajulu 2008; Varadarajulu 2013). Of these, there were no post‐randomisation drop‐outs in two trials (Park 2009; Varadarajulu 2013). So, these two trials are at low risk of attrition bias. In one trial, one participant randomised to EUS‐guided drainage group was excluded from analysis since the EUS revealed septae in the cyst, leading to a suspicion of pancreatic adenoma (Varadarajulu 2008). However, identifying septae is only possible with EUS‐guided drainage and is a potential advantage of the procedure. Hence, the overall benefit of EUS‐guided drainage may have been underestimated. Nevertheless, the exclusion of this patient was unlikely to result in bias for any of the reported outcomes. So, this trial was also considered to be at low risk of attrition bias. The fourth trial was considered to be at unclear risk of attrition bias since it did not report the participant flow (Yuan 2015).

Selective reporting

None of the trials had a pre‐published protocol. Three trials reported the clinical outcomes that were likely to be measured in such clinical trials and were considered to be at low risk of selective reporting (Park 2009; Varadarajulu 2008; Varadarajulu 2013). Yuan 2015 did not report morbidity clearly and was considered to be at risk of selective outcome reporting bias.

Other potential sources of bias

One trial advised they had no external funding (Varadarajulu 2013). The source of funding in the remaining trials was not reported. There was no other bias noted in the remaining trials.

Effects of interventions

See: Table 1; Table 2

The effects of interventions have been summarised in Table 1 and Table 2, None of the trials reported the following outcomes: long‐term mortality, quality of life at medium‐term (three months to one year) or long‐term (more than one year), time‐to‐return to normal activity, and time‐to‐return to work.

Only one comparison (endoscopic drainage versus EUS‐guided drainage) was examined in more than one trial. So, heterogeneity and random‐effects model are only presented for this comparison, when both trials reported the outcome (Park 2009; Varadarajulu 2008).

Primary outcomes

1. Short‐term mortality

All four trials reported short‐term mortality (Park 2009; Varadarajulu 2008; Varadarajulu 2013; Yuan 2015). There was only one death reported in the endoscopic drainage group, due to major bleeding (Varadarajulu 2008). A direct comparison using the RevMan statistical algorithm revealed no statistically significant difference between the EUS‐guided drainage and endoscopic drainage groups (OR 3.00; 95% CI 0.11 to 79.91; participants = 89; studies = 2; Analysis 1.1). Since there was only one death in one arm of one study, a network meta‐analysis was not performed and the issues of fixed‐effect model versus random‐effects model and heterogeneity did not arise. The absolute proportions of short‐term mortality in different interventions are as follows.

1.1. Analysis.

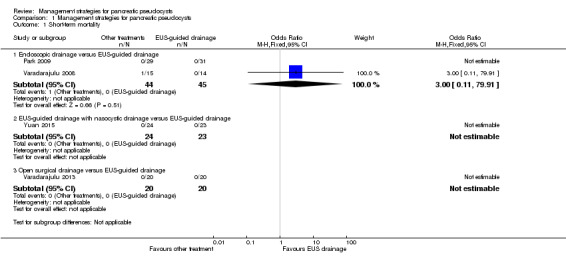
Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 1 Short‐term mortality.

1. EUS‐guided drainage 0% (0/88);

2. Endoscopic drainage 2.3% (1/44);

3. EUS‐guided drainage with nasocystic drainage 0% (0/24);

4. Open surgical drainage 0% (0/20).

Long‐term mortality

None of the trials reported long‐term mortality.

2. Serious adverse events

Three trials (129 participants) reported serious adverse events, which included: bleeding requiring additional intervention, pneumoperitoneum, stent migration, difficulty in eating requiring surgical placement of feeding tube, and pancreatic stricture requiring distal pancreatectomy (Park 2009; Varadarajulu 2008; Varadarajulu 2013).

Direct comparison

As shown in Analysis 1.2, there were no statistically significant differences in any of the direct comparisons (endoscopic drainage versus EUS‐guided drainage: OR 2.42; 95% CI 0.51 to 11.46; participants = 89; studies = 2; open surgical drainage versus EUS‐guided drainage: OR 8.20; 95% CI 0.40 to 169.90; participants = 40; studies = 1). There was no evidence of heterogeneity in the endoscopic drainage versus EUS‐guided drainage comparison (I² = 0; Chi² test for heterogeneity = 0.53), and no difference in the interpretation of results using either the fixed‐effect or random‐effects models.

1.2. Analysis.

Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 2 Serious adverse events.

The absolute unadjusted proportions of people with serious adverse events in different interventions were:

1. EUS‐guided drainage: 3.1% (2/65);

2. Endoscopic drainage: 11.4% (5/44);

3. Open surgical drainage: 15.0% (3/20).

Indirect comparison

As shown in Figure 4, there was no statistically significant difference in the proportion of people with serious adverse events between endoscopic drainage and open surgical drainage (OR 0.30; 95% CI 0.01 to 8.87).

4.

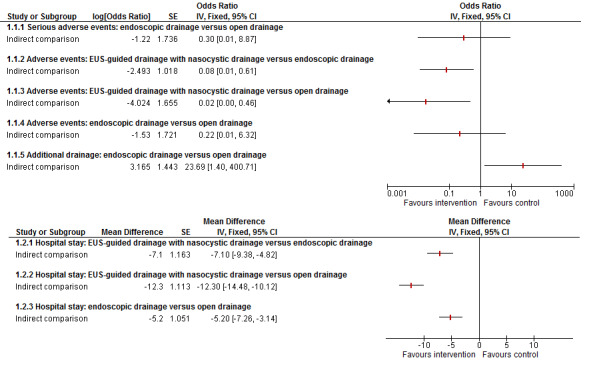
Indirect comparisons for adverse events and length of hospital stay

3. Health‐related quality of life (HRQoL)

Short‐term: four weeks to three months

Only one trial reported HRQoL, using the SF‐36 scale (Varadarajulu 2013). Data for general health perception were obtained to compare the HRQoL results (range of scores: 0 to 100, with 100 indicating maximum health). Health‐related quality of life was statistically significantly worse in the open surgical drainage group than in the EUS‐guided drainage group, using the RevMan statistical algorithm (MD ‐21.00; 95% CI ‐33.21 to ‐8.79; participants = 40; studies = 1; Analysis 1.3). Since this was the only trial reporting the outcome, a network meta‐analysis was not performed and the issues of fixed‐effect model versus random‐effects model and heterogeneity did not arise.

1.3. Analysis.

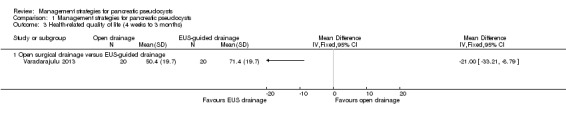
Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 3 Health‐related quality of life (4 weeks to 3 months).

Medium term: three months to one year and long‐term: more than one year

None of the trials reported HRQoL at medium‐term (three months to one year) or long‐term (more than one year).

Secondary outcomes

1. Adverse events

All four trials (176 participants) reported adverse events of any severity (Park 2009; Varadarajulu 2008; Varadarajulu 2013; Yuan 2015).

Direct comparison

As shown in Analysis 1.4, the proportion of people with any adverse events was statistically significantly lower with EUS‐guided drainage with nasocystic drainage compared to EUS‐guided drainage (OR 0.20; 95% CI 0.06 to 0.73; participants = 47; studies = 1). There were no statistically significant differences in any of the remaining direct comparisons (endoscopic drainage versus EUS‐guided drainage: OR 2.42; 95% CI 0.51 to 11.46; participants = 89; studies = 2; open surgical drainage versus EUS‐guided drainage: OR 11.18; 95% CI 0.56 to 222.98; participants = 40; studies = 1). There was no evidence of heterogeneity in the comparison of endoscopic drainage versus EUS‐guided drainage (I² = 0; Chi² test for heterogeneity = 0.53; Tau² statistic = 0; or visual inspection). There was no difference in the interpretation of results using fixed‐effect or random‐effects models.

1.4. Analysis.

Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 4 Adverse events.

The absolute unadjusted proportions of people with adverse events in different interventions are:

1. EUS‐guided drainage 17.0% (15/88);

2. Endoscopic drainage 11.4% (5/44);

3. EUS‐guided drainage with nasocystic drainage 20.8% (5/24);

4. Open surgical drainage 20.0% (4/20).

Indirect comparison

As shown in Figure 4, those who received EUS‐guided drainage with nasocystic drainage had fewer adverse events when compared to endoscopic drainage (OR 0.08; 95% CI 0.01 to 0.61) or open drainage (OR 0.02; 95% CI 0.00 to 0.46). There was no statistically significant differences in the proportion of people with adverse events between the endoscopic drainage and open drainage groups (OR 0.22; 95% CI 0.01 to 6.32).

2. Measures of decreased complications and earlier recovery (within three months)

2a. Length of hospital stay

Three trials (116 participants) reported length of hospital stay (Varadarajulu 2008; Varadarajulu 2013; Yuan 2015).

Direct comparison

As shown in Analysis 1.5, the length of hospital stay was statistically significantly shorter in the EUS‐guided drainage with nasocystic drainage compared to EUS‐guided drainage (MD ‐8.10 days; 95% CI ‐9.79 to ‐6.41; participants = 47; studies = 1), and statistically significantly longer in the open surgical drainage group compared to the EUS‐guided drainage group (MD 4.20 days; 95% CI 2.82 to 5.58; participants = 40; studies = 1). There was no statistically significant difference in the comparison between endoscopic drainage and EUS‐guided drainage (MD ‐1.00 days; 95% CI ‐2.53 to 0.53; participants = 29; studies = 1). Since there was only one study for the different comparisons, the issues of heterogeneity and fixed‐effect versus random‐effects model did not arise. Exclusion of one trial in which the mean was imputed from the median, and the standard deviation was calculated from the P value did not alter the interpretation of results, other than there was no information available in the comparison of hospital stays between the endoscopic drainage and EUS‐guided drainage groups (Varadarajulu 2008).

1.5. Analysis.

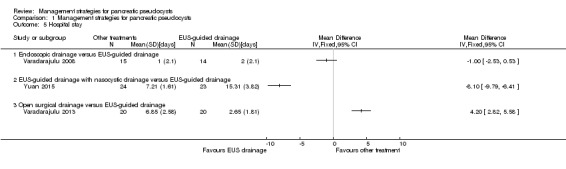
Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 5 Hospital stay.

Indirect comparison

As shown in Figure 4, the EUS‐guided drainage with nasocystic drainage group had a shorter hospital stay compared to the endoscopic drainage group (MD ‐7.10 days; 95% CI ‐9.38 to ‐4.82), or open surgical drainage group (MD ‐12.30 days; 95% CI ‐14.48 to ‐10.12). The endoscopic drainage group had a shorter hospital stay than the open drainage group (MD ‐5.20 days; 95% CI ‐7.26 to ‐3.14).

2b & 2c.Time‐to‐return to normal activity and time‐to‐return to work

None of the trials reported either the time‐to‐return to normal activity or the time‐to‐return to work.

3. Need for additional invasive intervention

Three trials (129 participants) reported that additional invasive interventions were required for drainage (Park 2009; Varadarajulu 2008; Varadarajulu 2013).

Direct comparison

As shown in Analysis 1.6, the proportion of people requiring additional invasive intervention for drainage was statistically significantly higher with endoscopic drainage than EUS‐guided drainage (OR 11.13; 95% CI 2.85 to 43.44; participants = 89; studies = 2). There was moderate heterogeneity (I² = 44%; Chi² test for heterogeneity = 0.18; Tau² statistic = 1.21; and visual inspection), but the heterogeneity appeared to be in the magnitude rather than direction of effect. There was no difference in the interpretation of results using either fixed‐effect or random‐effects models for this comparison. There were no statistically significant differences in the need for additional drainage between the open surgical and EUS‐guided drainage groups (OR 0.47; 95% CI 0.04 to 5.69; participants = 40; studies = 1).

1.6. Analysis.

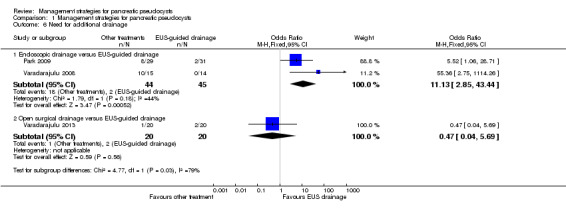
Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 6 Need for additional drainage.

The absolute unadjusted proportions of need for additional drainage in different interventions were:

1. EUS‐guided drainage 6.2% (4/65);

2. Endoscopic drainage 40.9% (18/44);

3. Open surgical drainage 5.0% (1/20).

Indirect comparison

As shown in Figure 4, the proportion of people requiring additional drainage was statistically significantly more in the endoscopic drainage group than in the open surgical drainage group (OR 23.69; 95% CI 1.40 to 400.71).

4. Costs

Only one trial reported costs (Varadarajulu 2013). Treatment costs were statistically significantly higher in the open surgical drainage group compared to the EUS‐guided drainage group, using the RevMan statistical algorithm (MD 8040 USD; 95% CI 3020 to 13,060; participants = 40; studies = 1; Analysis 1.7). Since this was the only trial reporting the outcome, we did not perform a network meta‐analysis, and the issues of fixed‐effect versus random‐effects model and heterogeneity did not arise.

1.7. Analysis.

Comparison 1 Management strategies for pancreatic pseudocysts, Outcome 7 Costs.

Subgroup analysis

We did not perform any of the planned subgroup analyses. Three trials included only symptomatic patients with pseudocysts (Park 2009; Varadarajulu 2008; Varadarajulu 2013). This information was not available in Yuan 2015. Two studies included patients with a pseudocyst from acute or chronic pancreatitis due to various aetiologies, but did not report the data separately (Park 2009; Varadarajulu 2013). The remaining two trials did not report whether the pseudocyst was associated with acute or chronic pancreatitis. None of the trials provided separate data for pseudocysts of different sizes.

Sensitivity analyses

We did not perform the sensitivity analysis of excluding trials at unclear or high risk of bias, since all the trials fell into this category. We did not perform a sensitivity analysis of imputation of binary outcomes under 'best‐best', 'best‐worst', 'worst‐best', or 'worst‐worst' scenarios because we did not consider that the exclusion of one patient due to pancreatic adenoma would result in attrition bias (please see 'Incomplete outcome data (attrition bias)'). The sensitivity analysis of excluding trials in which the mean, standard deviation, or both were imputed has been presented under the individual outcomes.

Reporting bias

We did not explore reporting bias using a funnel plot because we had fewer than 10 trials for each comparison.

Discussion

Summary of main results

We included four randomised controlled trials that included 176 participants and compared different methods of draining pseudocysts with EUS‐guided drainage (Park 2009; Varadarajulu 2008; Varadarajulu 2013; Yuan 2015). Network meta‐analysis provided inferior quality of evidence than direct comparison for all comparisons that used EUS‐guided drainage as the control group because of the indirectness it introduces, particularly since we were unable to assess the transitivity assumption. However, it provided the effect estimates for other pair‐wise comparisons when direct comparison was not available, the reliability of such effect estimates when the transitivity assumption could not be tested formally is not known.

There were no statistically significant differences between the treatments in short‐term mortality or the proportion of people with serious adverse events. Short‐term (four weeks to three months) health‐related quality of life (HRQoL) was worse and the costs were higher in the open surgical drainage group than in the EUS‐guided drainage group. Participants who received EUS‐guided drainage with nasocystic drainage had fewer adverse events when compared to those who received either EUS‐guided or endoscopic drainage. Participants who received EUS‐guided with nasocystic drainage also had shorter hospital stays when compared to EUS‐guided drainage, endoscopic drainage, or open surgical drainage, while those who received open surgical drainage had longer hospital stays than those who received EUS‐guided drainage. The need for additional invasive interventions was significantly higher with endoscopic drainage than with EUS‐guided drainage, while it was statistically significantly lower in those who received open surgical drainage than in those who received endoscopic drainage. There were no statistically significant differences in the other comparisons.

None of the trials reported on long‐term mortality, medium‐term HRQoL (three months to one year), long‐term HRQoL (longer than one year), time‐to‐return to normal activities, or time‐to‐return to work.

Overall completeness and applicability of evidence

Three trials only included symptomatic patients with pseudocysts (Park 2009; Varadarajulu 2008; Varadarajulu 2013), while Yuan 2015 did not state whether asymptomatic patients were included. So, the results of this study are only applicable for symptomatic patients with pseudocysts. Two trials clearly stated that they included pseudocysts that had resulted from acute or chronic pancreatitis due to various aetiologies (Park 2009; Varadarajulu 2013). The remaining two trials did not report on this association. Nevertheless, it appears that the results are applicable to patients with pseudocysts resulting from acute and chronic pancreatitis, the major causes of pseudocysts. The mean size of the pseudocysts ranged between 70 mm and 155 mm across all included studies. Thus, the results of this review are applicable for moderate to large pseudocysts. Infected pseudocysts were excluded in two trials (Park 2009; Varadarajulu 2008). This information was not available in the remaining two trials (Varadarajulu 2013; Yuan 2015). So, the results of this review are only applicable for non‐infected pseudocysts.

Quality of the evidence

The overall quality of evidence was low or very low for all the outcomes. There was no blinding of outcome assessors for any of the comparisons. All statistically significant outcomes were subjective outcomes and may be influenced by the lack of blinding. As a result, the risk of bias was unclear or high for most of the outcomes. It was not possible to assess the consistency of evidence since two comparisons, EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage and open surgical drainage versus EUS‐guided drainage had only one trial. There was no evidence of inconsistency in the comparison of endoscopic drainage with EUS‐guided drainage for serious adverse and adverse events, while there was moderate inconsistency for the need for additional drainage for the same comparison. However, the inconsistency in the need for additional drainage appears to be in the magnitude, rather than in the direction of effect. We were unable to assess the consistency for length of hospital stay since only one of the two trials comparing endoscopic drainage with EUS‐guided drainage reported it (Varadarajulu 2008). Another major issue was the small sample size in the trials, which resulted in imprecise results.

Potential biases in the review process

We followed the guidance in the NICE DSU documents and the Cochrane Handbook for Systematic Reviews of Interventions for the direct comparisons in the review (Dias 2013; Higgins 2011). Two people selected studies and extracted data, reducing the errors in data collection. We used formal search strategies to identify trials. While the likelihood of missing trials from identified references is low, the search strategy included the time‐frame before the mandatory trial registration era and it is possible that some trials were not reported in journals because of their results. However, one has to be pragmatic and accept that this is the best evidence that is currently available.

We imputed the mean and calculated the standard deviation for length of hospital stay for one trial from the median and P value (Varadarajulu 2008). Excluding this trial altered the conclusions by withdrawing information on the length of hospital stay for those who received endoscopic drainage.

While network meta‐analysis has its advantages in combining direct and indirect evidence (resulting in more precise evidence) and Bayesian network meta‐analysis allows the calculation of the probability of best treatments, these advantages were limited in this review because of the sparse data. All comparisons had at least one trial that had no events in one arm, disallowing direct and indirect evidence for a single comparison. So, we conducted direct comparisons using the Frequentist methods and conducted indirect comparisons using the methods described in Bucher 1997. The effect estimates of indirect comparisons and network meta‐analysis assume that the transitivity assumption is met. While the participants appeared to be similar across trials of various comparisons, we were unable to verify this using statistical methods, since none of the comparisons had direct and indirect evidence. So, we were not able to verify the transitivity assumption statistically. This decreases the confidence in indirect estimates.

Agreements and disagreements with other studies or reviews

This is the first systematic review of randomised controlled trials on pancreatic pseudocysts. There has been one previous review comparing open surgical drainage with endoscopic or EUS‐guided drainage for pancreatic pseudocysts, but this review included non‐randomised studies (Zhao 2016). The review authors concluded that the endoscopic group (endoscopic drainage or EUS‐guided drainage) was associated with a shorter length of hospital stay and lower hospital costs compared to the surgical group. We do not agree with this conclusion, since there is significant uncertainty in these statements due to the small sample size in the trials, and the lack of replication of the findings in two or more studies. In addition, only one trial included the costs of stent removal. None of the trials included the complications and length of hospital stay resulting from stent removal. Although stent removal can be considered a relatively minor procedure compared to the treatments, it does incur costs and may cause complications and longer hospital stays.

Authors' conclusions

Implications for practice.

Very low‐quality evidence suggested that the differences in mortality and serious adverse events between treatments were imprecise. Low‐quality evidence suggested that short‐term health‐related quality of life (four weeks to three months) was worse and the costs were higher in the open surgical drainage group than in the EUS‐guided drainage group. Low‐quality or very low‐quality evidence suggested that the EUS‐guided drainage with nasocystic drainage group had fewer adverse events compared to the EUS‐guided drainage or endoscopic drainage groups, and shorter hospital stays compared to those who received EUS‐guided drainage, endoscopic drainage, or open surgical drainage, while those who received EUS‐guided drainage had shorter hospital stays than those with open surgical drainage. Low‐quality evidence suggested that the need for additional invasive intervention was higher with endoscopic drainage than EUS‐guided drainage, while it was lower in the open surgical drainage than in the endoscopic drainage group.

Implications for research.

Further randomised controlled trials are needed in patients with symptomatic pancreatic pseudocysts requiring treatment. The most effective interventions in this review appear to be EUS‐guided drainage with or without nasocystic drainage, so, it is reasonable to start here. Other possible interventions include variations of EUS‐guided drainage (with or without nasocystic drainage) using self‐expanding stents (Huggett 2015), or EUS‐guided drainage with nasocystic drainage compared with laparoscopic drainage. Future trials should include patient‐oriented outcomes, such as mortality, serious adverse events, health‐related quality of life, length of hospital stay, return‐to‐normal activity, and the number of work days lost. All outcomes should be measured at least until the end of the draining procedure and the removal of the stent, with a minimum follow‐up period of two to three years, to ensure there are no recurrences of pseudocysts.

What's new

Date	Event	Description
13 September 2016	Amended	A typographic error in the Plain Language Summary was corrected.

Appendices

Appendix 1. Glossary of terms

Acute: sudden.

Aetiology: cause.

Amylase: an enzyme that breaks down carbohydrates.

Aspiration cytology: inserting a hollow needle into the body to obtain cells from an organ and examining the cells under microscopy to determine presence of cancer.

Cystoenterostomy: opening between the pseudocyst and small intestine.

Cystogastrostomy: opening between the pseudocyst and stomach.

Distal pancreatectomy: removal of body and tail of the pancreas.

Duodenal: relating to the first part of the small intestines.

Endoscopic: with the help of an endoscope, a tube inserted into the body (in this context, through the mouth and into the stomach and upper part of the small intestine).

Enzyme: substances that enable and speed up chemical reactions that are necessary for the normal functioning of the body.

Epigastric pain: upper central abdominal pain.

Gastric: related to stomach.

Gastrointestinal tract: digestive tract.

Haemorrhage: bleeding.

Insulin: substance which helps regulate blood sugar.

Intrapancreatic: within the pancreas.

Morbidity: illness (in this context, it means complications)

Mortality: death

Necrosis: death and decomposition of living tissue, usually caused by lack of blood supply, but can be caused by other pathological insult.

Neoplasm: tumour.

Oesophagoduodenoscope: inserting an endoscope, a tube inserted into the food pipe and stomach to view them internally (in this context).

Pathologic insult: substance or mechanism that causes the condition.

Percutaneous drainage: drainage carried out by insertion of a drain from the external surface of the body, usually guided by an ultrasound or CT (computed tomography) scan.

Peripancreatic tissues: tissues surrounding the pancreas.

Peritoneal cavity: abdominal cavity (tummy).

Portal vein: vein that transports the blood from the intestines to the liver.

Pneumoperitoneum: inflation of the abdomen (tummy) with gas, in this context, because of a hole in the bowel.

Pseudoaneurysm: false aneurysm (blood clot outside the arterial wall formed by a leak through a hole in the artery; the leak is contained by the surrounding tissues).

Protease: an enzyme that digests protein.

Retroperitoneum: behind the abdominal cavity.

Serum: clear fluid that separates out when blood clots.

Sinistral portal hypertension: left‐sided portal hypertension (high pressure in the portal vein)

Splenic vein: vein that drains the spleen.

Stricture: narrowing of a passage within the body.

Thrombosis: blood clot.

Transenteric endoscopic management: drainage of the pseudocyst through the intestines.

Transient: temporary.

Transpapillary endoscopic management: drainage of the pseudocyst through the papilla (ampulla of Vater) which is formed by the union of the pancreatic duct and the common bile duct.

Appendix 2. CENTRAL search strategy

#1 MeSH descriptor: [Pancreatic Pseudocyst] this term only

#2 (pancrea* near/2 pseudocyst*)

#3 MeSH descriptor: [Pancreatitis, Chronic] this term only and with qualifier(s): [Complications ‐ CO]

#4 MeSH descriptor: [Constriction, Pathologic] this term only and with qualifier(s): [Complications ‐ CO, Diagnosis ‐ DI, Etiology ‐ ET]

#5 MeSH descriptor: [Abscess] this term only

#6 pancrea*

#7 #5 and #6

#8 ((peri‐pancreatic or peripancreatic or pancrea*) near/2 (abscess or fluid))

#9 #1 or #2 or #3 or #4 or #7 or #8

Appendix 3. MEDLINE search strategy

1. Pancreatic Pseudocyst/

2. (pancrea* adj2 pseudocyst*).mp.

3. Pancreatitis, Chronic/co [Complications]

4. Constriction, Pathologic/co, di, et [Complications, Diagnosis, Etiology]

5. Abscess/

6. pancrea*.mp.

7. 5 and 6

8. ((peri‐pancreatic or peripancreatic or pancrea*) adj2 (abscess or fluid)).mp.

9. 1 or 2 or 3 or 4 or 7 or 8

10. randomized controlled trial.pt.

11. controlled clinical trial.pt.

12. randomized.ab.

13. placebo.ab.

14. drug therapy.fs.

15. randomly.ab.

16. trial.ab.

17. groups.ab.

18. 10 or 11 or 12 or 13 or 14 or 15 or 16 or 17

19. exp animals/ not humans.sh.

20. 18 not 19

21. 9 and 20

Appendix 4. EMBASE search strategy

1. Pancreatic Pseudocyst/

2. (pancrea* adj2 pseudocyst*).mp.

3. Pancreatitis, Chronic/co [Complications]

4. common bile duct obstruction/

5. common bile duct stenosis/

6. pancreas duct stenosis/

7. ((peri‐pancreatic or peripancreatic or pancrea*) adj2 (abscess or fluid)).mp.

8. pancreas abscess/

9. pancreas juice/

10. 1 or 2 or 3 or 4 or 5 or 6 or 7 or 8 or 9

11. Clinical trial/

12. Randomized controlled trial/

13. Randomization/

14. Single‐Blind Method/

15. Double‐Blind Method/

16. Cross‐Over Studies/

17. Random Allocation/

18. Placebo/

19. Randomi?ed controlled trial*.tw.

20. Rct.tw.

21. Random allocation.tw.

22. Randomly allocated.tw.

23. Allocated randomly.tw.

24. (allocated adj2 random).tw.

25. Single blind*.tw.

26. Double blind*.tw.

27. ((treble or triple) adj blind*).tw.

28. Placebo*.tw.

29. Prospective study/

30. or/11‐29

31. Case study/

32. Case report.tw.

33. Abstract report/ or letter/

34. or/31‐33

35. 30 not 34

36. 10 and 35

Appendix 5. Science Citation Index search strategy

# 1 TS=((pancrea* near/2 pseudocyst*) OR ((peri‐pancreatic or peripancreatic or pancrea*) near/2 (abscess or fluid)))

# 2 TS=(random* OR rct* OR crossover OR masked OR blind* OR placebo* OR meta‐analysis OR systematic review* OR meta‐analys*)

# 3 #2 AND #1

Appendix 6. ClinicalTrials.gov search strategy

"Interventional" [STUDY‐TYPES] AND pseudocyst [DISEASE] AND ( "Phase 2" OR "Phase 3" OR "Phase 4" ) [PHASE]

Appendix 7. WHO ICTRP search strategy

pseudocyst

Appendix 8. Stata code for network plot

networkplot t1 t2, labels(T1 T2 T3 ...)

Appendix 9. Winbugs code

Source of code:

Consistency models: Dias 2014

Inconsistency models: White 2012 (modifications were performed for continuous, count, and time‐to‐event outcomes)

Binary outcome

Binary outcome ‐ fixed‐effect model

# Binomial likelihood, logit link
 # Fixed effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dbin(p[i,k],n[i,k]) # binomial likelihood
 # model for linear predictor
 logit(p[i,k]) <‐ mu[i] + d[t[i,k]] ‐ d[t[i,1]]
 # expected value of the numerators
 rhat[i,k] <‐ p[i,k] * n[i,k]
 #Deviance contribution
 dev[i,k] <‐ 2 * (r[i,k] * (log(r[i,k])‐log(rhat[i,k]))
 + (n[i,k]‐r[i,k]) * (log(n[i,k]‐r[i,k]) ‐ log(n[i,k]‐rhat[i,k])))
 }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 }
 totresdev <‐ sum(resdev[]) # Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 
 # pairwise ORs and LORs for all possible pair‐wise comparisons, if nt>2
 for (c in 1:(nt‐1)) {
 for (k in (c+1):nt) {
 or[c,k] <‐ exp(d[k] ‐ d[c])
 lor[c,k] <‐ (d[k]‐d[c])
 }
 }
 # ranking on relative scale
 for (k in 1:nt) {
 # rk[k] <‐ nt+1‐rank(d[],k) # assumes events are “good”
 rk[k] <‐ rank(d[],k) # assumes events are “bad”
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Binary outcome ‐ random‐effects model

# Binomial likelihood, logit link
 # Random effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dbin(p[i,k],n[i,k]) # binomial likelihood
 logit(p[i,k]) <‐ mu[i] + delta[i,k] # model for linear predictor
 rhat[i,k] <‐ p[i,k] * n[i,k] # expected value of the numerators
 #Deviance contribution
 dev[i,k] <‐ 2 * (r[i,k] * (log(r[i,k])‐log(rhat[i,k]))
 + (n[i,k]‐r[i,k]) * (log(n[i,k]‐r[i,k]) ‐ log(n[i,k]‐rhat[i,k]))) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific LOR distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of LOR distributions (with multi‐arm trial correction)
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of LOR distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment for multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) # Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 
 # pairwise ORs and LORs for all possible pair‐wise comparisons, if nt>2
 for (c in 1:(nt‐1)) {
 for (k in (c+1):nt) {
 or[c,k] <‐ exp(d[k] ‐ d[c])
 lor[c,k] <‐ (d[k]‐d[c])
 }
 }
 # ranking on relative scale
 for (k in 1:nt) {
 # rk[k] <‐ nt+1‐rank(d[],k) # assumes events are “good”
 rk[k] <‐ rank(d[],k) # assumes events are “bad”
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 
 } # *** PROGRAM ENDS

Binary outcome ‐ inconsistency model (random‐effects)

# Binomial likelihood, logit link, inconsistency model
 # Random effects model
 # Treatment by design interactions
 # ns = number of studies, nt = number of treatments, A = total number of treatment arms in all trials, and D = the number of designs have to be stated.
 # The main data are arranged with one record per arm: d and study indicate which design and study that arm belongs to, t indicates its treatment, and b indicates the first treatment in that design. r and n are the numbers of events and individuals in the arm. The supplementary data offset and offset.design list the rows in which the first arm of each trial and of each design is found.
 model {
 for(i in 1:ns) {
 eff.study[i, b[offset[i]], b[offset[i]]] <‐0
 for(k in (offset[i] + 1):(offset[i + 1]‐1)) {
 eff.study[i,t[k],b[k]] <‐eff.des[d[k],t[k]] + RE[i,t[k]] ‐ RE[i,b[k]]
 }
 }
 # Random effects for heterogeneity
 for(i in 1:ns) {
 RE[i,1] <‐0
 RE[i,2:nt] ˜ dmnorm(zero[], Prec[,])
 }
 # Prec is the inverse of the structured heterogeneity matrix
 for(i in 1:(nt‐1)) {
 for(j in 1:(nt‐1)){
 Prec[i,j] <‐2*(equals(i,j)‐1/nt)/(tau*tau)
 }
 }
 for(i in 1:A) {
 logit(p[i]) <‐mu[study[i]] + eff.study[study[i],t[i],b[i]]
 r[i] ˜ dbin(p[i],n[i])}
 # For computing DIC
 for(i in 1:A) {
 rhat[i] <‐p[i] * n[i]
 dev[i] <‐2 * (r[i] * (log(r[i])‐log(rhat[i])) + (n[i]‐r[i]) * (log(n[i]‐r[i]) ‐ log(n[i]‐
 rhat[i])))
 }
 devs <‐sum(dev[])
 # Priors
 for(i in 1:ns) {
 mu[i] ˜ dnorm(0,0.01)
 }
 tau ˜ dunif(0,2)
 } # *** PROGRAM ENDS

Continuous outcome (mean difference)

Continuous outcome (mean difference) ‐ fixed‐effect model

# Normal likelihood, identity link
 # Fixed effect model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 var[i,k] <‐ pow(se[i,k],2) # calculate variances
 prec[i,k] <‐ 1/var[i,k] # set precisions
 y[i,k] ˜ dnorm(theta[i,k],prec[i,k])
 # model for linear predictor
 theta[i,k] <‐ mu[i] + d[t[i,k]] ‐ d[t[i,1]]
 #Deviance contribution
 dev[i,k] <‐ (y[i,k]‐theta[i,k])*(y[i,k]‐theta[i,k])*prec[i,k]
 }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for control arm
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 # ranking on relative scale
 for (k in 1:nt) {
 rk[k] <‐ rank(d[],k) # assumes lower is better
 # rk[k] <‐ nt+1‐rank(d[],k) # assumes lower outcome is worse
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Continuous outcome (mean difference) ‐ random‐effects model

# Normal likelihood, identity link
 # Random effects model for multi‐arm trials
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 var[i,k] <‐ pow(se[i,k],2) # calculate variances
 prec[i,k] <‐ 1/var[i,k] # set precisions
 y[i,k] ˜ dnorm(theta[i,k],prec[i,k])
 theta[i,k] <‐ mu[i] + delta[i,k] # model for linear predictor
 #Deviance contribution
 dev[i,k] <‐ (y[i,k]‐theta[i,k])*(y[i,k]‐theta[i,k])*prec[i,k]
 }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific MD distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of MD distributions, with multi‐arm trial correction
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of MD distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment, multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for control arm
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 # ranking on relative scale
 for (k in 1:nt) {
 rk[k] <‐ rank(d[],k) # assumes lower is better
 # rk[k] <‐ nt+1‐rank(d[],k) # assumes lower outcome is worse
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Continuous outcome (mean difference) ‐ inconsistency model (random‐effects)

# Normal likelihood, identity link, inconsistency model
 # Random effects model
 # Treatment by design interactions
 # ns = number of studies, nt = number of treatments, A = total number of treatment arms in all trials, and D = the number of designs have to be stated.
 # The main data are arranged with one record per arm: d and study indicate which design and study that arm belongs to, t indicates its treatment, and b indicates the first treatment in that design. y, se, and n are the mean, standard error, and number of individuals in the arm. The supplementary data offset and offset.design list the rows in which the first arm of each trial and of each design is found.
 model {
 for(i in 1:ns) {
 eff.study[i, b[offset[i]], b[offset[i]]] <‐0
 for(k in (offset[i] + 1):(offset[i + 1]‐1)) {
 eff.study[i,t[k],b[k]] <‐eff.des[d[k],t[k]] + RE[i,t[k]] ‐ RE[i,b[k]]
 }
 }
 # Random effects for heterogeneity
 for(i in 1:ns) {
 RE[i,1] <‐0
 RE[i,2:nt] ˜ dmnorm(zero[], Prec[,])
 }
 # Prec is the inverse of the structured heterogeneity matrix
 for(i in 1:(nt‐1)) {
 for(j in 1:(nt‐1)){
 Prec[i,j] <‐2*(equals(i,j)‐1/nt)/(tau*tau)
 }
 }
 for(i in 1:A) {
 var[i] <‐ pow(se[i],2) # calculate variances
 prec[i] <‐ 1/var[i] # set precisions
 y[i] ˜ dnorm(theta[i],prec[i]) # normal likelihood
 theta[i] <‐mu[study[i]] + eff.study[study[i],t[i],b[i]] # model for linear predictor
 }
 # For computing DIC
 for(i in 1:A) {
 dev[i] <‐ (y[i]‐theta[i])*(y[i]‐theta[i])*prec[i]
 }
 devs <‐sum(dev[])
 # Priors
 for(i in 1:ns) {
 mu[i] ˜ dnorm(0,0.01)
 }
 tau ˜ dunif(0,2)
 for(i in 1:D) {
 for(k in (offset.design[i] + 1):(offset.design[i] + num.ests[i])) {
 eff.des[i,t[k]] ˜ dnorm(0,0.01)
 }
 }
 } # *** PROGRAM ENDS

Continuous outcome (standardised mean difference)

The standardised mean difference and its standard error for each treatment comparison will be calculated using the statistical algorithms used by RevMan (RevMan 2014).

Continuous outcome (standardised mean difference) ‐ fixed‐effect model

# Normal likelihood, identity link
 # Trial‐level data given as treatment differences
 # Fixed effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns2) { # LOOP THROUGH 2‐ARM STUDIES
 y[i,2] ˜ dnorm(delta[i,2],prec[i,2]) # normal likelihood for 2‐arm trials
 #Deviance contribution for trial i
 resdev[i] <‐ (y[i,2]‐delta[i,2])*(y[i,2]‐delta[i,2])*prec[i,2]
 }
 for(i in (ns2+1):(ns2+ns3)) { # LOOP THROUGH THREE‐ARM STUDIES
 for (k in 1:(na[i]‐1)) { # set variance‐covariance matrix
 for (j in 1:(na[i]‐1)) {
 Sigma[i,j,k] <‐ V[i]*(1‐equals(j,k)) + var[i,k+1]*equals(j,k)
 }
 }
 Omega[i,1:(na[i]‐1),1:(na[i]‐1)] <‐ inverse(Sigma[i,,]) #Precision matrix
 # multivariate normal likelihood for 3‐arm trials
 y[i,2:na[i]] ˜ dmnorm(delta[i,2:na[i]],Omega[i,1:(na[i]‐1),1:(na[i]‐1)])
 #Deviance contribution for trial i
 for (k in 1:(na[i]‐1)){ # multiply vector & matrix
 ydiff[i,k]<‐ y[i,(k+1)] ‐ delta[i,(k+1)]
 z[i,k]<‐ inprod2(Omega[i,k,1:(na[i]‐1)], ydiff[i,1:(na[i]‐1)])
 }
 resdev[i]<‐ inprod2(ydiff[i,1:(na[i]‐1)], z[i,1:(na[i]‐1)])
 }
 for(i in 1:(ns2+ns3)){ # LOOP THROUGH ALL STUDIES
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 var[i,k] <‐ pow(se[i,k],2) # calculate variances
 prec[i,k] <‐ 1/var[i,k] # set precisions
 delta[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]]
 }
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 # ranking on relative scale
 for (k in 1:nt) {
 rk[k] <‐ nt+1‐rank(d[],k) # assumes higher HRQoL is “good”
 #rk[k] <‐ rank(d[],k) # assumes higher outcome is “bad”
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Continuous outcome (standardised mean difference) ‐ random‐effects model

# Normal likelihood, identity link
 # Trial‐level data given as treatment differences
 # Random effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns2) { # LOOP THROUGH 2‐ARM STUDIES
 y[i,2] ˜ dnorm(delta[i,2],prec[i,2]) # normal likelihood for 2‐arm trials
 #Deviance contribution for trial i
 resdev[i] <‐ (y[i,2]‐delta[i,2])*(y[i,2]‐delta[i,2])*prec[i,2]
 }
 for(i in (ns2+1):(ns2+ns3)) { # LOOP THROUGH THREE‐ARM STUDIES
 for (k in 1:(na[i]‐1)) { # set variance‐covariance matrix
 for (j in 1:(na[i]‐1)) {
 Sigma[i,j,k] <‐ V[i]*(1‐equals(j,k)) + var[i,k+1]*equals(j,k)
 }
 }
 Omega[i,1:(na[i]‐1),1:(na[i]‐1)] <‐ inverse(Sigma[i,,]) #Precision matrix
 # multivariate normal likelihood for 3‐arm trials
 y[i,2:na[i]] ˜ dmnorm(delta[i,2:na[i]],Omega[i,1:(na[i]‐1),1:(na[i]‐1)])
 #Deviance contribution for trial i
 for (k in 1:(na[i]‐1)){ # multiply vector & matrix
 ydiff[i,k]<‐ y[i,(k+1)] ‐ delta[i,(k+1)]
 z[i,k]<‐ inprod2(Omega[i,k,1:(na[i]‐1)], ydiff[i,1:(na[i]‐1)])
 }
 resdev[i]<‐ inprod2(ydiff[i,1:(na[i]‐1)], z[i,1:(na[i]‐1)])
 }
 for(i in 1:(ns2+ns3)){ # LOOP THROUGH ALL STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 var[i,k] <‐ pow(se[i,k],2) # calculate variances
 prec[i,k] <‐ 1/var[i,k] # set precisions
 }
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific SMD distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of random effects distributions, with multi‐arm trial correction
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of random effects distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment, multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 # ranking on relative scale
 for (k in 1:nt) {
 rk[k] <‐ nt+1‐rank(d[],k) # assumes higher HRQoL is “good”
 # rk[k] <‐ rank(d[],k) # assumes higher outcome is “bad”
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Continuous outcome (standardised mean difference) ‐ inconsistency model (random‐effects)

# Normal likelihood, identity link
 # Trial‐level data given as treatment differences
 # Random effects model
 model {
 for(i in 1:ns) {
 eff.study[i, t[i,1], t[i,1]] <‐0
 for(k in 2:na[i]) {
 eff.study[i,t[i,k],t[i,1]] <‐eff.des[design[k],t[i,k]] + RE[i,t[i,k]] ‐ RE[i, t[i,1]]
 }
 }
 # Random effects for heterogeneity
 for(i in 1:ns) {
 RE[i,1] <‐0
 RE[i,2:nt] ˜ dmnorm(zero[], Prec[,])
 }
 # Prec is the inverse of the structured heterogeneity matrix
 for(i in 1:(nt‐1)) {
 for(j in 1:(nt‐1)){
 Prec[i,j] <‐2*(equals(i,j)‐1/nt)/(tau*tau)
 }
 }
 
 
 for(i in 1:ns2) { # LOOP THROUGH 2‐ARM STUDIES
 y[i,2] ˜ dnorm(delta[i,2],prec[i,2]) # normal likelihood for 2‐arm trials
 #Deviance contribution for trial i
 resdev[i] <‐ (y[i,2]‐delta[i,2])*(y[i,2]‐delta[i,2])*prec[i,2]
 }
 for(i in (ns2+1):(ns2+ns3)) { # LOOP THROUGH THREE‐ARM STUDIES
 for (k in 1:(na[i]‐1)) { # set variance‐covariance matrix
 for (j in 1:(na[i]‐1)) {
 Sigma[i,j,k] <‐ V[i]*(1‐equals(j,k)) + var[i,k+1]*equals(j,k)
 }
 }
 Omega[i,1:(na[i]‐1),1:(na[i]‐1)] <‐ inverse(Sigma[i,,]) #Precision matrix
 # multivariate normal likelihood for 3‐arm trials
 y[i,2:na[i]] ˜ dmnorm(delta[i,2:na[i]],Omega[i,1:(na[i]‐1),1:(na[i]‐1)])
 #Deviance contribution for trial i
 for (k in 1:(na[i]‐1)){ # multiply vector & matrix
 ydiff[i,k]<‐ y[i,(k+1)] ‐ delta[i,(k+1)] + eff.study[i,t[i,k],t[i,1]]
 z[i,k]<‐ inprod2(Omega[i,k,1:(na[i]‐1)], ydiff[i,1:(na[i]‐1)])
 }
 resdev[i]<‐ inprod2(ydiff[i,1:(na[i]‐1)], z[i,1:(na[i]‐1)])
 }
 
 for(i in 1:(ns2+ns3)){ # LOOP THROUGH ALL STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 var[i,k] <‐ pow(se[i,k],2) # calculate variances
 prec[i,k] <‐ 1/var[i,k] # set precisions
 }
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific SMD distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of random effects distributions, with multi‐arm trial correction
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of random effects distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment, multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 for(i in 1:D) {
 for(k in (offset.design[i] + 1):(offset.design[i] + num.ests[i])) {
 eff.des[i,t[i,k]] ˜ dnorm(0,0.01)
 }
 }
 }
 } # *** PROGRAM ENDS

Count outcome

Count outcome ‐ fixed‐effect model

# Poisson likelihood, log link
 # Fixed effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dpois(theta[i,k]) # Poisson likelihood
 theta[i,k] <‐ lambda[i,k]*E[i,k] # failure rate * exposure
 # model for linear predictor
 log(lambda[i,k]) <‐ mu[i] + d[t[i,k]] ‐ d[t[i,1]]
 #Deviance contribution
 dev[i,k] <‐ 2*((theta[i,k]‐r[i,k]) + r[i,k]*log(r[i,k]/theta[i,k])) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 
 # pairwise RRs and LRRs for all possible pair‐wise comparisons, if nt>2
 for (c in 1:(nt‐1)) {
 for (k in (c+1):nt) {
 rater[c,k] <‐ exp(d[k] ‐ d[c])
 lrater[c,k] <‐ (d[k]‐d[c])
 }
 }
 # ranking on relative scale
 for (k in 1:nt) {
 # rk[k] <‐ nt+1‐rank(d[],k) # assumes events are “good”
 rk[k] <‐ rank(d[],k) # assumes events are “bad”
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Count outcome ‐ random‐effects model

# Poisson likelihood, log link
 # Random effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dpois(theta[i,k]) # Poisson likelihood
 theta[i,k] <‐ lambda[i,k]*E[i,k] # failure rate * exposure
 # model for linear predictor
 log(lambda[i,k]) <‐ mu[i] + d[t[i,k]] ‐ d[t[i,1]]
 #Deviance contribution
 dev[i,k] <‐ 2*((theta[i,k]‐r[i,k]) + r[i,k]*log(r[i,k]/theta[i,k])) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific LOR distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of LOR distributions (with multi‐arm trial correction)
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of LOR distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment for multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) # Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 
 # pairwise ORs and LORs for all possible pair‐wise comparisons, if nt>2
 for (c in 1:(nt‐1)) {
 for (k in (c+1):nt) {
 or[c,k] <‐ exp(d[k] ‐ d[c])
 lor[c,k] <‐ (d[k]‐d[c])
 }
 }
 # ranking on relative scale
 for (k in 1:nt) {
 # rk[k] <‐ nt+1‐rank(d[],k) # assumes events are “good”
 rk[k] <‐ rank(d[],k) # assumes events are “bad”
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 
 } # *** PROGRAM ENDS

Count outcome ‐ inconsistency model (random‐effects)

# Poisson likelihood, log link, inconsistency model
 # Random effects model
 # Treatment by design interactions
 # ns = number of studies, nt = number of treatments, A = total number of treatment arms in all trials, and D = the number of designs have to be stated.
 # The main data are arranged with one record per arm: d and study indicate which design and study that arm belongs to, t indicates its treatment, and b indicates the first treatment in that design. r and E are the numbers of successes and exposures in the arm. The supplementary data offset and offset.design list the rows in which the first arm of each trial and of each design is found.
 model {
 for(i in 1:ns) {
 eff.study[i, b[offset[i]], b[offset[i]]] <‐0
 for(k in (offset[i] + 1):(offset[i + 1]‐1)) {
 eff.study[i,t[k],b[k]] <‐eff.des[d[k],t[k]] + RE[i,t[k]] ‐ RE[i,b[k]]
 }
 }
 # Random effects for heterogeneity
 for(i in 1:ns) {
 RE[i,1] <‐0
 RE[i,2:nt] ˜ dmnorm(zero[], Prec[,])
 }
 # Prec is the inverse of the structured heterogeneity matrix
 for(i in 1:(nt‐1)) {
 for(j in 1:(nt‐1)){
 Prec[i,j] <‐2*(equals(i,j)‐1/nt)/(tau*tau)
 }
 }
 for(i in 1:A) {
 
 r[i] ˜ dpois(theta[i]) # Poisson likelihood
 theta[i] <‐ lambda[i]*E[i] # failure rate * exposure
 
 log(lambda[i]) <‐mu[study[i]] + eff.study[study[i],t[i],b[i]] # model for linear predictor
 }
 # For computing DIC
 for(i in 1:A) {
 
 dev[i] <‐ 2*((theta[i]‐r[i]) + r[i]*log(r[i]/theta[i]))
 }
 devs <‐sum(dev[])
 # Priors
 for(i in 1:ns) {
 mu[i] ˜ dnorm(0,0.01)
 }
 tau ˜ dunif(0,2)
 for(i in 1:D) {
 for(k in (offset.design[i] + 1):(offset.design[i] + num.ests[i])) {
 eff.des[i,t[k]] ˜ dnorm(0,0.01)
 }
 }
 } # *** PROGRAM ENDS

Time‐to‐event outcome

Time‐to‐event outcome ‐ fixed‐effect model

# Binomial likelihood, cloglog link
 # Fixed effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dbin(p[i,k],n[i,k]) # Binomial likelihood
 # model for linear predictor
 cloglog(p[i,k]) <‐ log(time[i]) + mu[i] + d[t[i,k]] ‐ d[t[i,1]]
 rhat[i,k] <‐ p[i,k] * n[i,k] # expected value of the numerators
 #Deviance contribution
 dev[i,k] <‐ 2 * (r[i,k] * (log(r[i,k])‐log(rhat[i,k]))
 + (n[i,k]‐r[i,k]) * (log(n[i,k]‐r[i,k]) ‐ log(n[i,k]‐rhat[i,k]))) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for control arm
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 # ranking on relative scale
 for (k in 1:nt) {
 # rk[k] <‐ rank(d[],k) # assumes lower is better
 rk[k] <‐ nt+1‐rank(d[],k) # assumes lower outcome is worse
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Time‐to‐event outcome ‐ random‐effects model

# Binomial likelihood, cloglog link
 # Random effects model
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dbin(p[i,k],n[i,k]) # Binomial likelihood
 # model for linear predictor
 cloglog(p[i,k]) <‐ log(time[i]) + mu[i] + delta[i,k]
 rhat[i,k] <‐ p[i,k] * n[i,k] # expected value of the numerators
 #Deviance contribution
 dev[i,k] <‐ 2 * (r[i,k] * (log(r[i,k])‐log(rhat[i,k]))
 + (n[i,k]‐r[i,k]) * (log(n[i,k]‐r[i,k]) ‐ log(n[i,k]‐rhat[i,k]))) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific LOR distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of LOR distributions, with multi‐arm trial correction
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of LOR distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment, multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) #Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 # vague priors for treatment effects
 for (k in 2:nt){ d[k] ˜ dnorm(0,.0001) }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 # ranking on relative scale
 for (k in 1:nt) {
 # rk[k] <‐ rank(d[],k) # assumes lower is better
 rk[k] <‐ nt+1‐rank(d[],k) # assumes lower outcome is worse
 best[k] <‐ equals(rk[k],1) #calculate probability that treat k is best
 for (h in 1:nt){ prob[h,k] <‐ equals(rk[k],h) } # calculates probability that treat k is h‐th best
 }
 } # *** PROGRAM ENDS

Time‐to‐event outcome ‐ inconsistency model (random‐effects)

# Binomial likelihood, cloglog link, inconsistency model
 # Random effects model
 # Treatment by design interactions
 # ns = number of studies, nt = number of treatments, A = total number of treatment arms in all trials, and D = the number of designs have to be stated.
 # The main data are arranged with one record per arm: d and study indicate which design and study that arm belongs to, t indicates its treatment, and b indicates the first treatment in that design. r ,n, and time are the numbers of events, individuals, and follow‐up time in the arm. The supplementary data offset and offset.design list the rows in which the first arm of each trial and of each design is found.
 model {
 for(i in 1:ns) {
 eff.study[i, b[offset[i]], b[offset[i]]] <‐0
 for(k in (offset[i] + 1):(offset[i + 1]‐1)) {
 eff.study[i,t[k],b[k]] <‐eff.des[d[k],t[k]] + RE[i,t[k]] ‐ RE[i,b[k]]
 }
 }
 # Random effects for heterogeneity
 for(i in 1:ns) {
 RE[i,1] <‐0
 RE[i,2:nt] ˜ dmnorm(zero[], Prec[,])
 }
 # Prec is the inverse of the structured heterogeneity matrix
 for(i in 1:(nt‐1)) {
 for(j in 1:(nt‐1)){
 Prec[i,j] <‐2*(equals(i,j)‐1/nt)/(tau*tau)
 }
 }
 for(i in 1:A) {
 r[i] ˜ dbin(p[i],n[i]) # Binomial likelihood
 cloglog(p[i]) <‐ log(time[i]) + mu[study[i]] + eff.study[study[i],t[i],b[i]] # model for linear predictor
 }
 # For computing DIC
 for(i in 1:A) {
 
 dev[i] <‐ 2 * (r[i] * (log(r[i])‐log(rhat[i]))+ (n[i]‐r[i]) * (log(n[i]‐r[i]) ‐ log(n[i]‐rhat[i])))
 }
 devs <‐sum(dev[])
 # Priors
 for(i in 1:ns) {
 mu[i] ˜ dnorm(0,0.01)
 }
 tau ˜ dunif(0,2)
 for(i in 1:D) {
 for(k in (offset.design[i] + 1):(offset.design[i] + num.ests[i])) {
 eff.des[i,t[k]] ˜ dnorm(0,0.01)
 }
 }
 } # *** PROGRAM ENDS

Appendix 10. Technical details of network meta‐analysis

The posterior probabilities (effect estimates or values) of the treatment contrast (i.e., log odds ratio, mean difference, standardised mean difference, rate ratio, or hazard ratio) may vary depending upon the initial values to start the simulations. In order to control the random error due to the choice of initial values, we performed the network analysis for three different initial values (starting values) as per the guidance from The National Institute for Health and Care Excellence (NICE) Decision Support Unit (DSU) documents (Dias 2013). If the results from three different initial values were similar and stable (convergence), then the results are reliable. It is important to discard the results of the initial simulations, as they can be significantly affected by the choice of the initial values, and only include the results of the simulations obtained after the convergence. The discarding of the initial simulations is called 'burn in'. We had planned to run the models for all outcomes for 30,000 simulations for 'burn in' for three different chains (a set of initial values). We had planned to run the models for another 100,000 simulations to obtain the effect estimates. We had planned to obtain the effect estimates from the results of all the three chains (different initial values). We had planned to ensure that the results in the three different chains were similar in order to control for random error due to the choice of priors. We had planned to do this in addition to the visual inspection of convergence obtained after simulations in the 'burn in'.

We had planned to run three different models for each outcome. A fixed‐effect model assumes that the treatment effect is the same across studies. The random‐effects consistency model assumes that the treatment effect is distributed normally across the studies, but assumes that the transitivity assumption is satisfied (i.e., the population studied, the definition of outcomes, and the methods used were similar across studies and that there is consistency between the direct comparison and indirect comparison). A random‐effects inconsistency model does not make the transitivity assumption. If the inconsistency model resulted in a better model fit than the consistency model, the results of the network meta‐analysis could be unreliable and so should be interpreted with extreme caution. If there was evidence of inconsistency, we had planned to identify areas in the network where substantial inconsistency might be present in terms of clinical and methodological diversities between trials, and when appropriate, we had planned to limit network meta‐analysis to a more compatible subset of trials.

We had planned to base the choice of the model between fixed‐effect and random‐effects on the model fit as per the guidelines of the NICE TSU (Dias 2013). The model fit was assessed by deviance residuals and Deviance Information Criteria (DIC) according to NICE TSU guidelines (Dias 2013). A difference of three or five in the DIC is not generally considered important (Dias 2012c). We had planned to use the simpler model, i.e., the fixed‐effect model, if the DIC were similar between the fixed‐effect and the random‐effects models. We had planned to use the random‐effects model if it resulted in a better model fit, as indicated by a DIC that was lower than the fixed‐effect model by at least three.

We had planned to calculate the effect estimates of the treatment and the 95% credible intervals using the following additional code:
 # pairwise ORs and MD for all possible pairwise comparisons, if nt > 2
 for (c in 1:(nt‐1)) {
 for (k in (c+1):nt) {
 OR[c,k] <‐ exp(d[k] ‐ d[c])
 #MD[c,k] <‐ (d[k]‐d[c])
 }
 }

where c indicates control group, k indicates intervention group, OR indicates odds ratio or other ratios, and MD indicates mean difference or other differences.

Appendix 11. Winbugs code for subgroup analysis

Source of code: Dias 2012c

Categorical covariate

Only the code for random‐effects model for a binary outcome is shown. The differences in the code are underlined. We had planned to make similar changes for other outcomes.

# Binomial likelihood, logit link, subgroup
 # Random effects model for multi‐arm trials
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dbin(p[i,k],n[i,k]) # binomial likelihood
 # model for linear predictor, covariate effect relative to treat in arm 1
 logit(p[i,k]) <‐ mu[i] + delta[i,k] + (beta[t[i,k]]‐beta[t[i,1]]) * x[i] 
 rhat[i,k] <‐ p[i,k] * n[i,k] # expected value of the numerators
 #Deviance contribution
 dev[i,k] <‐ 2 * (r[i,k] * (log(r[i,k])‐log(rhat[i,k]))
 + (n[i,k]‐r[i,k]) * (log(n[i,k]‐r[i,k]) ‐ log(n[i,k]‐rhat[i,k]))) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific LOR distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of LOR distributions (with multi‐arm trial correction)
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of LOR distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment for multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) # Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 beta[1] <‐ 0 # covariate effect is zero for reference treatment 
 for (k in 2:nt){ # LOOP THROUGH TREATMENTS
 d[k] ˜ dnorm(0,.0001) # vague priors for treatment effects
 beta[k] <‐ B[k] # exchangeable covariate effect 
 B[k] ˜ dnorm(0,.0001) # vague prior for covariate effect 
 }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 # treatment effect when covariate = z[j]
 for (k in 1:nt){ # LOOP THROUGH TREATMENTS
 for (j in 1:nz) { dz[j,k] <‐ d[k] + (beta[k]‐beta[1])*z[j] }
 }
 # *** PROGRAM ENDS

Continuous covariate

# Binomial likelihood, logit link, continuous covariate
 # Random effects model for multi‐arm trials
 model{ # *** PROGRAM STARTS
 for(i in 1:ns){ # LOOP THROUGH STUDIES
 w[i,1] <‐ 0 # adjustment for multi‐arm trials is zero for control arm
 delta[i,1] <‐ 0 # treatment effect is zero for control arm
 mu[i] ˜ dnorm(0,.0001) # vague priors for all trial baselines
 for (k in 1:na[i]) { # LOOP THROUGH ARMS
 r[i,k] ˜ dbin(p[i,k],n[i,k]) # binomial likelihood
 # model for linear predictor, covariate effect relative to treat in arm 1
 logit(p[i,k]) <‐ mu[i] + delta[i,k] + (beta[t[i,k]]‐beta[t[i,1]]) * (x[i]‐mx) 
 rhat[i,k] <‐ p[i,k] * n[i,k] # expected value of the numerators
 #Deviance contribution
 dev[i,k] <‐ 2 * (r[i,k] * (log(r[i,k])‐log(rhat[i,k]))
 + (n[i,k]‐r[i,k]) * (log(n[i,k]‐r[i,k]) ‐ log(n[i,k]‐rhat[i,k]))) }
 # summed residual deviance contribution for this trial
 resdev[i] <‐ sum(dev[i,1:na[i]])
 for (k in 2:na[i]) { # LOOP THROUGH ARMS
 # trial‐specific LOR distributions
 delta[i,k] ˜ dnorm(md[i,k],taud[i,k])
 # mean of LOR distributions (with multi‐arm trial correction)
 md[i,k] <‐ d[t[i,k]] ‐ d[t[i,1]] + sw[i,k]
 # precision of LOR distributions (with multi‐arm trial correction)
 taud[i,k] <‐ tau *2*(k‐1)/k
 # adjustment for multi‐arm RCTs
 w[i,k] <‐ (delta[i,k] ‐ d[t[i,k]] + d[t[i,1]])
 # cumulative adjustment for multi‐arm trials
 sw[i,k] <‐ sum(w[i,1:k‐1])/(k‐1)
 }
 }
 totresdev <‐ sum(resdev[]) # Total Residual Deviance
 d[1]<‐0 # treatment effect is zero for reference treatment
 beta[1] <‐ 0 # covariate effect is zero for reference treatment 
 for (k in 2:nt){ # LOOP THROUGH TREATMENTS
 d[k] ˜ dnorm(0,.0001) # vague priors for treatment effects
 beta[k] <‐ B[k] # exchangeable covariate effect 
 B[k] ˜ dnorm(0,.0001) # vague prior for covariate effect 
 }
 sd ˜ dunif(0,5) # vague prior for between‐trial SD
 tau <‐ pow(sd,‐2) # between‐trial precision = (1/between‐trial variance)
 # treatment effect when covariate = z[j] (un‐centring treatment effects)
 for (k in 1:nt){
 for (j in 1:nz) { dz[j,k] <‐ d[k] ‐ (beta[k]‐beta[1])*(mx‐z[j]) }
 }
 # pairwise ORs and LORs for all possible pair‐wise comparisons, if nt>2
 for (c in 1:(nt‐1)) {
 for (k in (c+1):nt) {
 # at mean value of covariate
 or[c,k] <‐ exp(d[k] ‐ d[c])
 lor[c,k] <‐ (d[k]‐d[c])
 # at covariate=z[j]
 for (j in 1:nz) {
 orz[j,c,k] <‐ exp(dz[j,k] ‐ dz[j,c])
 lorz[j,c,k] <‐ (dz[j,k]‐dz[j,c])
 }
 }
 }
 } # *** PROGRAM ENDS

Data and analyses

Comparison 1. Management strategies for pancreatic pseudocysts.

Outcome or subgroup title	No. of studies	No. of participants	Statistical method	Effect size
1 Short‐term mortality	4		Odds Ratio (M‐H, Fixed, 95% CI)	Subtotals only
1.1 Endoscopic drainage versus EUS‐guided drainage	2	89	Odds Ratio (M‐H, Fixed, 95% CI)	3.0 [0.11, 79.91]
1.2 EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage	1	47	Odds Ratio (M‐H, Fixed, 95% CI)	0.0 [0.0, 0.0]
1.3 Open surgical drainage versus EUS‐guided drainage	1	40	Odds Ratio (M‐H, Fixed, 95% CI)	0.0 [0.0, 0.0]
2 Serious adverse events	3		Odds Ratio (M‐H, Fixed, 95% CI)	Subtotals only
2.1 Endoscopic drainage versus EUS‐guided drainage	2	89	Odds Ratio (M‐H, Fixed, 95% CI)	2.42 [0.51, 11.46]
2.2 Open surgical drainage versus EUS‐guided drainage	1	40	Odds Ratio (M‐H, Fixed, 95% CI)	8.2 [0.40, 169.90]
3 Health‐related quality of life (4 weeks to 3 months)	1		Mean Difference (IV, Fixed, 95% CI)	Totals not selected
3.1 Open surgical drainage versus EUS‐guided drainage	1		Mean Difference (IV, Fixed, 95% CI)	0.0 [0.0, 0.0]
4 Adverse events	4		Odds Ratio (M‐H, Fixed, 95% CI)	Subtotals only
4.1 Endoscopic drainage versus EUS‐guided drainage	2	89	Odds Ratio (M‐H, Fixed, 95% CI)	2.42 [0.51, 11.46]
4.2 EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage	1	47	Odds Ratio (M‐H, Fixed, 95% CI)	0.20 [0.06, 0.73]
4.3 Open surgical drainage versus EUS‐guided drainage	1	40	Odds Ratio (M‐H, Fixed, 95% CI)	11.18 [0.56, 222.98]
5 Hospital stay	3		Mean Difference (IV, Fixed, 95% CI)	Totals not selected
5.1 Endoscopic drainage versus EUS‐guided drainage	1		Mean Difference (IV, Fixed, 95% CI)	0.0 [0.0, 0.0]
5.2 EUS‐guided drainage with nasocystic drainage versus EUS‐guided drainage	1		Mean Difference (IV, Fixed, 95% CI)	0.0 [0.0, 0.0]
5.3 Open surgical drainage versus EUS‐guided drainage	1		Mean Difference (IV, Fixed, 95% CI)	0.0 [0.0, 0.0]
6 Need for additional drainage	3		Odds Ratio (M‐H, Fixed, 95% CI)	Subtotals only
6.1 Endoscopic drainage versus EUS‐guided drainage	2	89	Odds Ratio (M‐H, Fixed, 95% CI)	11.13 [2.85, 43.44]
6.2 Open surgical drainage versus EUS‐guided drainage	1	40	Odds Ratio (M‐H, Fixed, 95% CI)	0.47 [0.04, 5.69]
7 Costs	1		Mean Difference (IV, Fixed, 95% CI)	Totals not selected
7.1 Open surgical drainage versus EUS‐guided drainage	1		Mean Difference (IV, Fixed, 95% CI)	0.0 [0.0, 0.0]

Characteristics of studies

Characteristics of included studies [ordered by study ID]

Park 2009.

Methods	Randomised controlled trial
Participants	Country: South Korea. Number randomised: 60. Post‐randomisation drop‐outs: not stated. Revised sample size: 60. Average age: 48 years. Females: 13 (21.7%). Symptomatic patients: 60 (100%). Acute pancreatitis: 27 (45%). Chronic pancreatitis: 28 (46.7%). Infected pseudocyst: 0 (0%). Mean size of pseudocyst in mm: 78 Follow‐up time: minimum 6 months Concomitant interventions: not stated Inclusion criteria 1. History of pancreatitis. 2. Symptomatic pseudocysts with duration of longer than 4 weeks. Exclusion criteria 1. Age less than 18 years. 2. A pancreatic pseudocyst more than 4 cm in size and communicating with the pancreatic duct. 3. A suggested pancreatic abscess or necrosis, shown by computed tomography (CT). 4. A moderate thickness (> 10 mm) from the cyst wall to the intramural wall, shown by EUS. 5. Portal hypertension or coagulopathy.
Interventions	Participants were randomly assigned to two groups. Group 1: Endoscopic EUS‐guided drainage (N = 31). Group 2: Endoscopic drainage (N = 29).
Outcomes	The outcomes reported were short‐term mortality, adverse events, and requirement for additional procedures.
Notes	Source of funding: not stated.
Risk of bias
Bias	Authors' judgement	Support for judgement
Random sequence generation (selection bias)	Low risk	Quote: "...randomly assigned by means of computer‐generated numbers to undergo….".
Allocation concealment (selection bias)	Unclear risk	Comment: This information was not available.
Blinding of participants and personnel (performance bias) All outcomes	High risk	Quote: "... because this study was non‐blinded, the inherent possibility of bias may exist. However, blinding of an investigator to any technique to which patients are randomly assigned is impractical".
Blinding of outcome assessment (detection bias) All outcomes	High risk	Quote: "... because this study was non‐blinded, the inherent possibility of bias may exist. However, blinding of an investigator to any technique to which patients are randomly assigned is impractical".
Incomplete outcome data (attrition bias) All outcomes	Low risk	Comment: There were no post‐randomisation drop‐outs.
Selective reporting (reporting bias)	Low risk	Comment: All important outcomes were reported.
Other bias	Low risk	Comment: No other source of bias.

Varadarajulu 2008.

Methods	Randomised controlled trial
Participants	Country: USA. Number randomised: 30. Post‐randomisation drop‐outs: 1 (3.3%). Revised sample size: 29. Average age: 47 years. Females: 11 (37.9%). Symptomatic patients: 29 (100%). Acute pancreatitis: not stated Chronic pancreatitis: not stated Infected pseudocyst: 0 (0%). Mean size of pseudocyst in mm: 70 Follow‐up time: minimum 6 weeks Concomitant interventions: not stated Inclusion criteria 1. History of pancreatitis. 2. Symptomatic pseudocysts. Exclusion criteria 1. CT findings were suggestive of pathology other than a pseudocyst. 2. Pseudocyst was ≤ 4 cm in size. 3. Patients younger than 18 years of age. 4. Patients with pancreatic abscess or necrosis by CT.
Interventions	Participants were randomly assigned to two groups. Group 1: Endoscopic EUS‐guided drainage (N = 14). Group 2: Endoscopic drainage (N = 15).
Outcomes	The outcomes reported were short‐term mortality, adverse events, length of hospital stay, and requirement for additional procedures.
Notes	Reasons for post‐randomisation drop‐outs: had septae on EUS and so the diagnosis was revised to pancreatic adenoma rather than pseudocyst, and patient underwent surgery. Source of funding: not stated.
Risk of bias
Bias	Authors' judgement	Support for judgement
Random sequence generation (selection bias)	Low risk	Quote: "After ERCP, an endoscopy nurse opened a sealed envelope that contained computer‐generated randomization assignments".
Allocation concealment (selection bias)	Low risk	Quote: "After ERCP, an endoscopy nurse opened a sealed envelope that contained computer‐generated randomization assignments".
Blinding of participants and personnel (performance bias) All outcomes	High risk	Quote: "Furthermore, the blinding of an investigator to the technique to which the patient was randomized is neither feasible nor practical, and therefore, it is difficult to exclude the possibility of bias completely". Comment: It is impossible to blind the healthcare providers.
Blinding of outcome assessment (detection bias) All outcomes	Unclear risk	Comment: This information was not available.
Incomplete outcome data (attrition bias) All outcomes	Low risk	Comment: There was one post‐randomisation drop‐out in the EUS‐guided drainage group since septae were noted and the diagnosis was revised to pancreatic adenoma. This is an inherent advantage of EUS‐guided drainage and exclusion of the patient may have underestimated the overall benefit of EUS‐guided drainage. However, this is unlikely to influence any of the reported outcomes.
Selective reporting (reporting bias)	Low risk	Comment: All important outcomes were reported.
Other bias	Low risk	Comment: No other source of bias.

Varadarajulu 2013.

Methods	Randomised controlled trial
Participants	Country: USA. Number randomised: 40. Post‐randomisation drop‐outs: not stated. Revised sample size: 40. Average age: 50 years. Females: 12 (30%). Symptomatic patients: 40 (100%). Acute pancreatitis: 13 (32.5%). Chronic pancreatitis: 27 (67.5%). Infected pseudocyst: not stated Mean size of pseudocyst in mm: 108 Follow‐up time: minimum 24 months Concomitant interventions: not stated Inclusion criteria 1. Diagnosis of pancreatic pseudocyst based on CT criteria. 2. Pseudocyst measuring ≥ 6 cm in size and located adjacent to the stomach. 3. Documented history of acute or chronic pancreatitis. 4. Persistent pancreatic pain requiring narcotics or analgesics. 5. Symptomatic gastric outlet or bile duct obstruction induced by the pseudocyst. Exclusion criteria 1. Age < 18 or > 80 years. 2. Contraindications to surgery: ASA class IV, severe portal hypertension. 3. Contraindication to endoscopic drainage: gastrectomy with Billroth II reconstruction, gastric bypass surgery, prior surgery for pancreas‐related complications. 4. Pregnancy. 5. Associated pancreatic necrosis on CT. 6. Pseudocyst not adjacent to the stomach. 7. Multiloculated pseudocyst or multiple pseudocysts.
Interventions	Participants were randomly assigned to two groups. Group 1: Endoscopic EUS‐guided drainage (N = 20). Group 2: Open surgical drainage (N = 20).
Outcomes	The outcomes reported were short‐term mortality, adverse events, length of hospital stay, and requirement for additional procedures.
Notes	Authors provided information on source of funding and length of hospital stay. Source of funding: no funding (author reply).
Risk of bias
Bias	Authors' judgement	Support for judgement
Random sequence generation (selection bias)	Low risk	Quote: "Computer‐generated randomization assignments were provided by the statistician using a block randomization method".
Allocation concealment (selection bias)	Low risk	Quote: "The randomization assignments were placed in sequentially numbered, sealed, opaque envelopes and were opened by one of the study investigators to determine treatment allocation".
Blinding of participants and personnel (performance bias) All outcomes	High risk	Quote: "We conducted a single‐center, open‐label, randomized trial to compare endoscopic and surgical drainage….".
Blinding of outcome assessment (detection bias) All outcomes	High risk	Quote: "We conducted a single‐center, open‐label, randomized trial to compare endoscopic and surgical drainage….".
Incomplete outcome data (attrition bias) All outcomes	Low risk	Comment: There were no post‐randomisation drop‐outs.
Selective reporting (reporting bias)	Low risk	Comment: All important outcomes were reported.
Other bias	Low risk	Comment: No other source of bias.

Yuan 2015.

Methods	Randomised controlled trial
Participants	Country: China. Number randomised: 47. Post‐randomisation drop‐outs: not stated. Revised sample size: 47. Average age: 48 years. Females: 18 (38.3%). Symptomatic patients: not stated Acute pancreatitis: not stated Chronic pancreatitis: not stated Infected pseudocyst: not stated Mean size of pseudocyst in mm: 155 Follow‐up time: minimum 24 months Concomitant interventions: not stated Inclusion criteria 1. Ages 16 to 70 years. 2. Clinical presentation with abdominal distension with or without upper gastrointestinal obstruction. 3. Radiological findings suggestive of a pancreatic pseudocyst > 10 cm. Exclusion criteria 1. Cysts without adherence to the gastric wall. 2. Distance between pseudocyst and gastric wall > 1 cm. 3. Pseudocyst communication with the main pancreatic duct. 4. Pregnancy. 5. Pancreatic tumours. 6. Risk for anaesthesia and surgery. 7. Contraindications to magnetic resonance cholangiopancreatography and endoscopic retrograde cholangiopancreatography. 8. Liver cirrhosis. 9. Previous history of abdominal surgery (e.g., gastrectomy). 10. Inability to give informed consent.
Interventions	Participants were randomly assigned to two groups. Group 1: Endoscopic EUS‐guided drainage (N = 23). Group 2: Endoscopic EUS‐guided drainage with nasocystic drainage (N = 24).
Outcomes	The outcomes reported were short‐term mortality, recurrence, and length of hospital stay.
Notes	Source of funding: not stated.
Risk of bias
Bias	Authors' judgement	Support for judgement
Random sequence generation (selection bias)	Unclear risk	Comment: This information was not available.
Allocation concealment (selection bias)	Low risk	Quote: "Patients were randomized using sealed envelopes to undergo single‐step or 2‐step treatment".
Blinding of participants and personnel (performance bias) All outcomes	Unclear risk	This information was not available.
Blinding of outcome assessment (detection bias) All outcomes	Unclear risk	Comment: This information was not available.
Incomplete outcome data (attrition bias) All outcomes	Unclear risk	Comment: This information was not available.
Selective reporting (reporting bias)	High risk	Comment: Morbidity was not reported adequately.
Other bias	Low risk	Comment: No other source of bias.

Characteristics of excluded studies [ordered by study ID]

Study	Reason for exclusion
Sauer 2010	Comment on an included study (Varadarajulu 2008)

Characteristics of ongoing studies [ordered by study ID]

NCT02041793.

Trial name or title	A Prospective Randomized Controlled Trial Comparing Laparoscopic Versus Endoscopic Drainage for Pseudocyst of the Pancreas
Methods	Randomised controlled trial
Participants	Country: India Estimated enrolment:60 Inclusion criteria Symptomatic patients with pseudocyst of size more than 6 cm, more than 6‐8 weeks duration after an attack of acute pancreatitis. Exclusion criteria Patients with chronic pancreatitis associated pseudocyst. Patients who have undergone any form of intervention previously Patients with significant co‐morbidities Patients unfit for general anaesthesia Bleeding disorders Patients refusing consent Patients having significant necrotic debris not considered fit for endoscopic drainage. The presence of necrotic debris will be assessed by ultrasound of the abdomen and if required magnetic resonance imaging. The volume of the cyst and that of necrotic debris will be calculated and significant debris will be defined as >30% of debris volume/volume Presence of a pseudoaneurysm
Interventions	Participants randomly assigned to two groups. Group 1: Laparoscopic cystogastrostomy Group 2: Endoscopic cystogastrostomy
Outcomes	Primary outcome Resolution of pseudocyst. Secondary outcomes Adverse events (bleeding, sepsis, chest complications and other important events in the post procedure period requiring prolonged stay and/or repeat procedure) Cost per patient. Recurrence rate of pseudocyst.
Starting date	August 2011
Contact information	Pramod K Garg, MD (pgarg10@hotmail.com)
Notes

Differences between protocol and review

1. We included endoscopic‐guided drainage (EUS‐guided drainage) with nasocystic drainage as an additional intervention. Generally, a nasocystic catheter is used during EUS‐guided drainage to irrigate the cyst, if there is a suspicion of presence of debris. The nasocystic catheter is then generally removed, only retaining the stent between the stomach or duodenum and the pseudocyst. Yuan 2015 used routine nasocystic drainage. This was considered to be a significant variation from standard EUS‐guided drainage, so, it was included as an intervention.

2. While network meta‐analysis has its advantages in combining direct and indirect evidence (resulting in more precise evidence) and Bayesian network meta‐analysis allows the calculation of a probability of the best treatments, these advantages were limited in this review because of the sparse data, with zero event trials and lack of direct and indirect evidence for any comparisons. So, we used Frequentist methods, which allowed us to present information in the standard Cochrane format for direct comparisons; we also presented indirect comparisons when able.

3. We had planned to use conservative treatment as the reference group. However, none of the trials included conservative treatment as one of the arms. We plan to use EUS‐guided drainage as the reference group in future updates, since this was the intervention that was included in all the trials.

Contributions of authors

Conceiving the review: KG

Designing the review: KG

Co‐ordinating the review: KG

Designing search strategies: KG

Study selection: KG, EP

Data extraction: KG, EP

Writing the review: KG

Providing statistical advice on the review: NH

Providing general advice on the review: BRD, SP

Securing funding for the review: KG

Performing previous work that was the foundation of the current study: KG

Sources of support

Internal sources

• University College London, UK.

  Salary, equipment, and other resources to complete this review.

External sources

• National Institute for Health Research, UK.

  This project was supported by the National Institute for Health Research, via Cochrane Infrastructure, Cochrane Programme Grant or Cochrane Incentive funding to the Cochrane Hepato‐Biliary and Upper Gastrointestinal and Pancreatic Diseases Groups. The views and opinions expressed therein are those of the authors and do not necessarily reflect those of the Systematic Reviews Programme, NIHR, NHS or the Department of Health. The funding covered salary, equipment, and other resources to complete this review. The review was also supported by the Complex Reviews Support Unit, also funded by the National Institute for Health Research (project number 14/178/29).

Declarations of interest

This report is independent research funded by the National Institute for Health Research (NIHR Cochrane Programme Grants, 13/89/03 ‐ Evidence‐based diagnosis and management of upper digestive, hepato‐biliary, and pancreatic disorders). The views expressed in this publication are those of the authors and not necessarily those of the NHS, the National Institute for Health Research or the Department of Health.

Edited (no change to conclusions)