Three-Color Single-Molecule FRET and Fluorescence Lifetime Analysis of Fast Protein Folding

Abstract

We describe the theory, experiment, and analysis of three-color Förster resonance energy transfer (FRET) spectroscopy for probing conformational dynamics of a fast-folding protein, α₃D. In three-color FRET, site-specific labeling of fluorophores is required to avoid ambiguity resulting from various species with different combinations of labeling positions. To this end, we first attached two dyes to a cysteine residue and an unnatural amino acid, and then appended a cysteine residue to the C-terminus of the protein by the sortase-mediated ligation for attaching the third dye. To determine all three FRET efficiencies, we used alternating excitation of the donor and acceptor 1 with two picosecond-pulsed lasers. Since the folded and unfolded states are not distinguishable in binned fluorescence trajectories due to fast folding on a millisecond time scale, we used a maximum likelihood method that analyzes photon trajectories without binning the data. The extracted kinetic parameters agree very well with the previously measured parameters for the same protein with two-color FRET, suggesting the addition of the third fluorophore does not affect the folding dynamics of the protein. From the extracted fractions of acceptor photon counts, the FRET efficiencies for all three dye pairs were calculated after various corrections. They were compared with the FRET efficiencies obtained from the global analysis of two-color segments collected in the same experiment. The FRET efficiencies of the folded state from the three-color segments agree with those from the two-color segments, whereas the three-color and two-color FRET efficiencies of the unfolded state are different. This happens because fluctuations of all three inter-dye distances contribute to the FRET efficiency measured in three-color FRET. We show that this difference can be accounted for by using the Gaussian chain model for the unfolded state with the parameters obtained from the analysis of two-color segments. This result shows that three-color FRET provides additional information on the flexibility of molecules that cannot be obtained from a combination of two-color FRET experiments with three dye pairs. Using the delay times of photons from the laser pulse, fluorescence lifetimes were determined using the maximum likelihood analysis. The correlation between FRET efficiencies and lifetimes of the donor, acceptor 1, and acceptor 2 was visualized in two-dimensional FRET efficiency-lifetime histograms. These histograms can be used to demonstrate the presence of conformational dynamics in a protein.

Graphical Abstract

Introduction

Single-molecule Förster resonance energy transfer (FRET) is a molecular measure that is sensitive to distance changes on a nanometer scale. For typical donor and acceptor fluorophore pairs with Förster radii of 5 – 6 nm such as Alexa 488/Alexa 594 and Cy3/Cy5, the measurable distance ranges from 2 to 10 nm. Therefore, it has been widely used for investigations of conformational changes of biomacromolecules such as proteins and nucleic acids and their interactions.^1–9

In two-color FRET, the measured quantity is the transfer efficiency between a single donor and acceptor pair. By adding one extra fluorophore, two additional distances can be measured, from which much more detailed information on molecular structures and dynamics can be obtained.^10,11 Measurement of three distances can provide constraints on overall molecular dimension and conformations and detection of global and correlated motions between different regions of a molecule or molecular assembly. For example, three (and four)-color single-molecule FRET has been used to monitor conformational changes and molecular interactions simultaneously.^12–21 In this case, two fluorophores are attached to one molecule for monitoring distance changes (i.e., conformational changes) and the third one is attached to the other molecule for the detection of interactions between the two molecules. In another example, all three dyes can be attached to the same molecule to monitor conformational changes during molecular processes such as folding of nucleic acids or proteins.^22–25

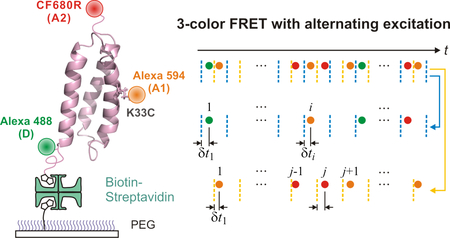
In multi-color FRET studies so far, the timescale of measurement has been slow (tens of milliseconds and longer) primarily due to the complexity of the experiment and relatively low photostability of the fluorophores with absorption and emission at a long wavelength that are used for the third or fourth dye. However, there are many molecular processes on a timescale of millisecond and faster. In this paper, we describe our development of fast three-color single-molecule FRET in combination with fluorescence lifetime analysis to monitor conformational changes during folding of a designed protein, α₃D (Figure 1).^26–28 The folding time of α₃D is ~ 2 ms at the denaturation mid-point.²⁸ To measure the fast folding kinetics, three-color FRET experiments were performed at an average photon count rate of ~ 50 ms⁻¹. We describe detailed experimental and analysis procedures including the preparation of protein constructs, dye labeling, and single-molecule experimental methods. We also describe the theory and analysis of three-color FRET and fluorescence lifetimes for the situations of fixed and fluctuating distances that correspond to the folded and unfolded states of the protein, respectively.

Figure 1.

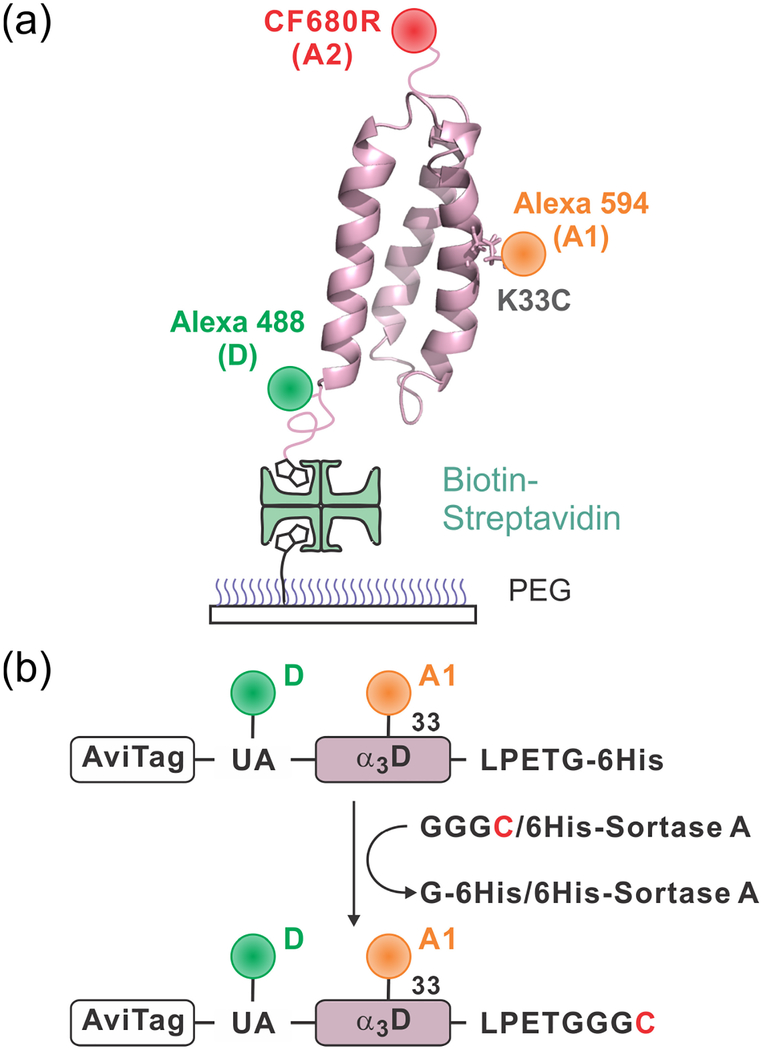
Immobilization of dye-labeled α₃D. (a) The donor (D), Alexa 488, is attached to the N-terminal unnatural amino acid (4-acetylphenylalanine), acceptor 1 (A1), Alexa 594, is attached to cysteine in the middle of helix 2 (residue 33), and acceptor 2 (A2) is attached to the C-terminal cysteine residue. Molecules are immobilized on a polyethylene glycol (PEG)-coated glass surface via a biotin-NeutrAvidin linkage. (b) After labeling D and A1 site-specifically, a cysteine residue is appended at the C-terminus of the protein using the sortase-mediated ligation. Then, A2 is attached to the C-terminal cysteine residue.

In three-color FRET experiments, it is important to attach three dyes site-specifically to avoid complications resulting from different combinations of fluorophore locations. However, for proteins, site-specific labeling of three dyes has been challenging. Various methods have been developed for site-specific labeling of two fluorophores. The first fluorophore is usually attached using the reaction between cysteine and a maleimide group. The second fluorophore can be attached using unnatural amino acids,^29,30 split intein-mediated ligation,³¹ and enzymatic reactions.^32,33 Site-specific labeling of three fluorophores can be achieved by a combination of these techniques. Recently, Lee et al. have demonstrated site-specific labeling of three dyes using chemical ligation.³⁴ We took a different approach to this problem. We used cysteine and unnatural amino acid labeling for two dyes. After labeling the two dyes, the third dye was attached to a cysteine residue that was appended to the C-terminus of the protein by the sortase-mediated ligation (Figure 1b).³³

It is not possible to determine all three FRET efficiencies by single excitation of the donor in three-color FRET. Therefore, alternating excitation (pulse-interleaved excitation)³⁵ was performed using two picosecond pulsed lasers. To improve the time resolution for the measurement of fast folding kinetics, we analyzed photon trajectories without binning using the maximum likelihood method.³⁶ The extracted parameters, the fractions of photon counts, are not directly related to the distances between dyes. Therefore, one of the goals in this work is to determine the two-color FRET efficiencies from the three-color measurement. The two-color FRET efficiency is the transfer efficiency when only two dyes are active. The theory of three-color FRET that we describe in this paper shows that accurate FRET efficiencies for the folded state can be determined after corrections of various factors. For a molecule in which all three distances are rapidly fluctuating such as the unfolded state of a protein, however, the corrected FRET efficiencies in three-color measurements are different from the corresponding two-color FRET efficiencies. To account for this difference, we compare the three-color FRET efficiencies from experimental measurements and those calculated from the two-color FRET efficiencies and the Gaussian chain model that is used to describe the conformational flexibility of unfolded polypeptide chains. By using pulsed lasers, fluorescence lifetimes can also be determined from the measurement of the mean delay time of photons from laser excitation.³⁷ This lifetime information is used to describe the behavior of the unfolded state of the protein by the two-dimensional (2D) FRET efficiency-lifetime analysis.

Materials, Methods, and Theory

Materials.

A DNA insert encoding the sequence: MGMSGLNDIFEAQKIEWHESSGLVPRGSH^(UA)M¹GSWAEFKQRLAAIKTRLQALGGSEAELAAFEC³³EIAAFESELQAYKGKGNPEVEALRKEAAAIRDELQAYRHN⁷³GSLPETGGGSSHHHHHH was synthesized and cloned in PJ414 vector (ATUM, Newark, CA) flanked by Nde1 and BamH1 restriction sites at the 5’ and 3’ end of the insert, respectively. The full-length protein Avi-α₃D-6His encompasses the biotin acceptor peptide termed Avi (underlined) and the de novo designed α₃D (residues 1–73, PDB code 2A3D)²⁶ with an unnatural amino acid (UA, 4-acetylphenylalanine) flanking the N terminus, an internal Cys (residue 33) and a C-terminal LPETG sequence (bolded), to facilitate sortase-mediated ligation, preceding a 6-His tag. The resulting construct was verified by DNA sequencing, as well as electrospray ionization mass spectrometry (ESI-MS) following its expression and purification.

The expression construct Avi-α₃D-6His, a plasmid with an isopropylthiogalactoside (IPTG) inducible birA gene to over-express the biotin ligase (Avidity LLC), and the pEVOL plasmid²⁹ for the incorporation of the UA were co-transformed into E.coli BL-21 (DE3; 200131, Agilent). Cells were grown in Luria-Bertani medium, and expression was induced at an absorbance of 0.7 monitored at 600 nm with a final concentration of 1 mM IPTG for a period of 3–4 h. A final concentration of 50 μM d-biotin (B4501, Sigma-Aldrich) was added to the medium ~ 30 min before induction. Typically, cells harvested from a 500 mL culture were lysed by uniform suspension in 20 mL of bacterial protein extraction reagent (B-PER, Pierce) and sonication. The lysate was centrifuged at 20,000 g for 30 min at 4°C. The supernatant was subjected to affinity chromatography using streptavidin Mutein matrix (Roche Diagnostics GmbH, Mannheim, Germany). The column was equilibrated and washed extensively, after passing the lysate, with 1X PBS (1.7 mM KH₂PO₄, 5 mM Na₂HPO₄, 150 mM NaCl, pH 7.4) and the biotinylated Avi-α₃D-6His was eluted in 1X PBS containing 2 mM d-Biotin. The eluted protein was adjusted to a final concentration of 1 mM DTT, concentrated using Amicon Ultra 10K centrifugal filter (Millipore Corp, Bedford, MA) to ~1.5 mL and loaded onto a Superdex-75 column (1.6 cm × 60 cm; GE HealthCare, Piscataway, NJ) equilibrated in 25 mM Tris-HCl, pH 7.5 and 1 mM DTT at a flow-rate of 1.5 mL/min at room temperature. Peak fractions were analyzed by SDS-PAGE, combined and subjected to reverse-phase HPLC on POROS 20 R2 resin (ThermoFisher Scientific) and eluted using a linear gradient from 99.95% water (v/v) and 0.05% TFA to 60% acetonitrile (v/v), 0.05% TFA (v/v) and 39.95% water (v/v). Aliquots of the peak fraction were lyophilized and stored at −70°C. Biotin ligation to the biotin acceptor peptide was confirmed by ESI-MS.

A fraction (~0.5 mg) of Avi-α₃D-6His was labeled with 5-fold molar excess of Alexa Fluor 488 hydroxylamine (A30629, ThermoFisher Scientific) for ~16 hours at 37 °C in buffer containing 0.1 M sodium acetate, pH 4, and 2 M guanidine hydrochloride. The reaction mixture was fractionated on a Superdex-peptide column (1 × 30 cm) equilibrated in 0.5X PBS. Peak fractions were combined, diluted 5-fold in 25 mM Tris-HCl, pH 8, and subjected to anion-exchange chromatography (Mono-Q, GE HealthCare) to separate the donor-labeled Avi-α₃D-6His (at the 4-acetyl Phe site) from the unreacted protein fraction. The donor-labeled fraction was concentrated, adjusted to a final concentration of 1.5 mM TCEP (Tris(2-carboxy-ethyl)phosphine hydrochloride, Sigma-Aldrich) and 2 M guanidine hydrochloride, and incubated for 2 hours at room temperature. The protein was then reacted with 5-fold molar excess of Alexa Fluor 594 maleimide (A10256, ThermoFisher Scientific) and loaded again on to a Superdex-peptide column equilibrated in 0.5X PBS. Peak fractions were combined and following dialysis against 20 mM Tris-HCl, pH 7.5, 150 mM NaCl and 10 mM CaCl₂ overnight was concentrated.

The donor and one acceptor labeled Avi-α₃D-6His (50 μM) was mixed with 20-fold molar excess of GGGC (G3C) peptide and a final concentration of 10 μM sortase A in a final reaction volume of 110 μL. The reaction was carried out for 20 h at room temperature. Cleavage between Thr and Gly in the LPETG motif to release the 6His-tag, followed by ligation of G3C to Avi-α₃D bearing the LPET C-terminal end, mediated by sortase A, permits the selective elution of Avi-α₃D-G3C final product in the flow-through and its separation from uncleaved Avi-α₃D-6His and His tagged sortase by Ni-NTA affinity chromatography. The flow-through was concentrated and fractionated on Superdex-peptide column to remove the excess unligated G3C peptide from Avi-α₃D-G3C. Peak fractions were pooled, concentrated and labeled with a second acceptor CF680R dye (catalog number 92032, Biotium) to the newly created C-terminal Cys similar to that described for labeling with Alexa Fluor 594 using maleimide chemistry and purified again by size-exclusion chromatography on Superdex-peptide in 0.5X PBS. Peak fractions were combined and stored in aliquots at −20 °C.

Sortase (plasmid pHTT27)³⁸ bearing a 6-His tag was expressed and purified using a combination of Ni-NTA affinity followed by size-exclusion chromatography steps in 50 mM Tris-HCl, pH 7.2, 150 mM NaCl and 10% glycerol. Purified sortase stock solution (120 μM) was stored in aliquots at −70 °C.

Single-molecule spectroscopy.

Single-molecule FRET experiments were carried out using a confocal microscope system (MicroTime 200, PicoQuant) with an oil-immersion objective (UPLSAPO, NA 1.4, × 100, Olympus), a beamsplitter (z488/594rpc, Chroma Technology), and a 75 μm pinhole. Alexa 488 and Alexa 594 were alternately excited at 40 MHz by a 485 nm diode laser (LDH-D-C-485, PicoQuant) at 3.4 μW and a 595 nm diode laser (LDH-D-TA-595, PicoQuant) at 1.1 μW, respectively. Fluorescence signal from three dyes was split into three photon counting avalanche photodiodes (SPCM-AQR-16, PerkinElmer Optoelectronics) using two dichroic beamsplitters (585DCXR and 670DCXR, Chroma Technology) and through bandpass filters (ET525/50m for Alexa 488, ET645/75m for Alexa 594, and ET705/72m for CF680R, Chroma Technology).

Biotinylated α₃D molecules were immobilized on a biotin-embedded, PEG-coated glass coverslip (Bio_01; Microsurfaces Inc.) via biotin (surface)-NeutrAvidin (Thermo Scientific)-biotin (protein) linkage. Molecules immobilized on the surface were identified by raster scanning with donor excitation by the 485 nm laser. To minimize photoblinking and photobleaching of dyes, 100 mM β-mercaptoethanol (Sigma-Aldrich), 10 mM Cysteamine (Sigma-Aldrich),³⁹ 2 mM cyclooctatetraene (COT, Sigma-Aldrich), 2 mM 4-nitrobenzyl alcohol (NBA, Sigma-Aldrich), and 2 mM Trolox (Sigma-Aldrich)^40,41 were added into 50 mM HEPES, pH 7.4 (adjusted with NaOH) buffer with various GdmCl (Invitrogen) concentrations. All experiments were performed at room temperature (23°C). Additional details of single-molecule experiments have been described elsewhere.^21,42,43

Theory of three-color FRET and fluorescence lifetimes.

Below we describe the relationships between FRET efficiencies, lifetimes, and the quantities that are measured in the experiment (i.e., the count rates and delay times of the donor (D), acceptor 1 (A1), and acceptor 2 (A2) photons). We consider two cases: fixed inter-dye distances (e.g., in the folded state) and fluctuating distances (e.g., in the unfolded state).

A. Photon count rates and FRET efficiencies: Non-fluctuating transfer rates.

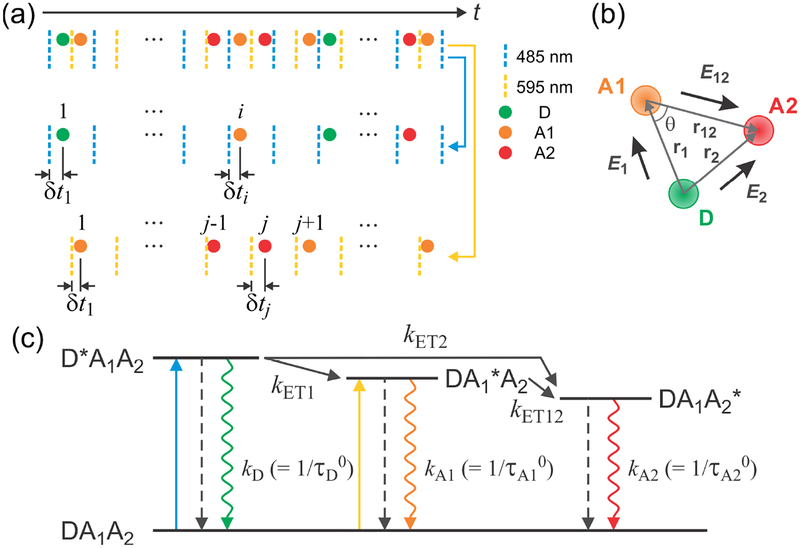
We assume that the photophysics of three dyes is described by the scheme shown in Figure 2a. In this scheme, k_ET1 = k_D (R₁/r₁)⁶, k_ET2 = k_D (R₂/r₂)⁶, and k_ET12 = k_A1 (R₁₂/r₁₂)⁶ are the rate constants of the energy transfer from D to A1, D to A2, and A1 to A2, respectively, and R₁, R₂, and R₁₂ are the corresponding Förster radii. The energy transfer rate constants depend on the distances r₁ (between D and A1), r₂ (between D and A2), and r₁₂ (between A1 and A2) (see Figure 2b). In this section, we assume that all these distances are fixed.

Figure 2.

Three-color FRET using alternating excitation. (a) Photon trajectories of three fluorophores detected after alternating laser excitation of the donor (D) (485 nm, blue dashed line) and acceptor 1 (A1) (595 nm, yellow dashed line) (40 MHz repetition rate). For each photon, the absolute arrival time (t) and the relative delay time (δt) between the laser pulse and the photon arrival is recorded. Photons detected after D excitation (index i) and A1 excitation (index j) can be separated (second and third rows) using ~ 25 ns difference in their delay times. (b) Definition of the FRET efficiencies between dye pairs. E₁ is the energy transfer efficiency from D to A1 in the absence of acceptor 2 (A2), E₂ is the transfer efficiency from D to A2 in the absence of A1, and E₁₂ is the transfer efficiency from A1 to A2. θ is the angle between two distance vectors r₁ and r₁₂. r₂ = r₁ + r₁₂. (c) Excited state dynamics in three-color FRET. After donor excitation (DA₁A₂ → D*A₁A₂), the donor decays to the ground state radiatively (green rippled arrow) or non-radiatively (dashed arrow), or the energy is transferred to either A1 (DA₁*A₂) or A2 (DA₁A₂*), with the energy transfer rates of k_ET1 and k_ET2. A1 excited state decays to the ground state or the energy is further transferred to A2 with the rate of k_ET12. After A1 excitation, A1 decays to the ground state or the energy is transferred to A2. k_D, k_A1, and k_A2 are the sums of the radiative and non-radiative relaxation rates of the excited state of D, A1 and A2, respectively, which are equal to the inverse of the excited state lifetimes in the absence of the energy transfer, ${\tau }_{\text{D}}^0$, ${\tau }_{\text{A}1}^0$, and ${\tau }_{\text{A}2}^0$, respectively.

Consider the count rates (i.e., the numbers of photon counts per unit time) of the donor, n_D, acceptor 1, n_A1, and acceptor 2, n_A2, photons, which are detected after donor excitation. These count rates can be expressed in terms of the rate constants¹⁹ (see Figure 2c)

$$\begin{gathered} n_{\text{D}}={\eta }_{\text{D}}{\varphi }_{\text{D}}{k}_{\text{D}}^{\text{ex}}\frac{k_{\text{D}}}{k_{\text{D}}+k_{\text{ET}1}+k_{\text{ET}2}} \\ {n}_{\text{A}1}={\eta }_{\text{A}1}{\varphi }_{\text{A}1}{k}_{\text{D}}^{\text{ex}}\frac{k_{\text{ET}1}{k}_{\text{A}1}}{\left(k_{\text{D}}+k_{\text{ET}1}+k_{\text{ET}2}\right)\left(k_{\text{A}1}+k_{\text{ET}12}\right)} \\ {n}_{\text{A}2}={\eta }_{\text{A}2}{\varphi }_{\text{A}2}{k}_{\text{D}}^{\text{ex}}\left(\frac{k_{\text{ET}2}}{k_{\text{D}}+k_{\text{ET}1}+k_{\text{ET}2}}+\frac{k_{\text{ET}1}}{k_{\text{D}}+k_{\text{ET}1}+k_{\text{ET}2}}\frac{k_{\text{ET}12}}{k_{\text{A}1}+k_{\text{ET}12}}\right), \end{gathered}$$ (1)

where $k_{\text{D}}^{\text{ex}}$ is the donor excitation rate constant, η_I and ϕ_I are the detection efficiency and quantum yield of fluorophore I (= D, A1, and A2), k_D and k_A1 are the sums of the rates of the non-radiative and radiative decays of the donor and acceptor 1, respectively, in the absence of the energy transfer. For example, the count rate of A1 photons is the product of the donor excitation rate ($k_{\text{D}}^{\text{ex}}$) and the probabilities that the energy is transferred from the donor to A1 excited state (k_ET1/(k_D + k_ET1 + k_ET2)), A1 decays to its ground state (k_A1/(k_A1 + k_ET12)), A1 does so by emitting a photon (ϕ_A1), and the emitted photon is detected (η_A1).

The count rates of A1 ($n_{\text{A1}}^{\text{Aex}}$) and A2 ($n_{\text{A2}}^{\text{Aex}}$) photons that are detected after A1 excitation (indicated by the superscript Aex) are

$$\begin{gathered} n_{\text{A1}}^{\text{Aex}}={\eta }_{\text{A1}}{\varphi }_{\text{A1}}{k}_{\text{A1}}^{\text{ex}}\frac{k_{\text{A1}}}{k_{\text{A1}}+k_{\text{ET12}}} \\ {n}_{\text{A2}}^{\text{Aex}}={\eta }_{\text{A2}}{\varphi }_{\text{A2}}{k}_{\text{A1}}^{\text{ex}}\frac{k_{\text{ET12}}}{k_{\text{A1}}+k_{\text{ET12}}}. \end{gathered}$$ (2)

The photon count rates in eqs 1 and 2 do not account for background noise and donor leak, so they should be corrected for these effects before using in the theory.

The photon count rates are related to the efficiency of energy transfer, which is the probability that the excited donor state transfers its energy to the acceptor rather than decaying to its ground state. We define several FRET efficiencies: 1) E₁ for the transfer from D to A1 in the absence of A2; 2) E₂ for the transfer from D to A2 in the absence of A1; 3) E₁₂ for the transfer from A1 to A2 after A1 excitation; 4) E₁₊₂ for the transfer from D to both A1 and A2. These FRET efficiencies can be expressed in terms of the rate constants (see Figure 2c):

$$\begin{gathered} E_1(r_1)=\frac{k_{\text{ET}1}}{k_{\text{D}}+k_{\text{ET}1}}=\frac{1}{1+{\left(r_1/R_1\right)}^6} \\ {E}_2(r_2)=\frac{k_{\text{ET}2}}{k_{\text{D}}+k_{\text{ET}2}}=\frac{1}{1+{\left(r_2/R_2\right)}^6} \\ {E}_{12}(r_{12})=\frac{k_{\text{ET}12}}{k_{\text{A}1}+k_{\text{ET}12}}=\frac{1}{1+{\left(r_{12}/R_{12}\right)}^6} \\ {E}_{1+2}(r_1,r_2)=\frac{k_{\text{ET}1}+k_{\text{ET}2}}{k_{\text{D}}+k_{\text{ET}1}+k_{\text{ET}2}}={\left(1+\frac{{\left(r_1{r}_2\right)}^6}{{\left(r_1{R}_2\right)}^6+{\left(R_1{r}_2\right)}^6}\right)}^{-1}. \end{gathered}$$ (3)

Here E₁, E₂, and E₁₂ are defined for the energy transfer in the absence of one of the three dyes, and therefore, are the same as those in two-color FRET. E₁₊₂ is the FRET efficiency in the presence of all three dyes.

The FRET efficiencies in eq 3 are related to the photon count rates in eq 1 as²¹

$$\begin{gathered} E_1=\frac{n_{\text{A1}}}{n_{\text{A1}}+{\gamma }_1{n}_{\text{D}}(1-E_{12})} \\ {E}_2=\frac{n_{\text{A2}}-\alpha n_{\text{A1}}}{n_{\text{A2}}-\alpha n_{\text{A1}}+{\gamma }_2{n}_{\text{D}}} \\ {E}_{1+2}=\frac{n_{\text{A2}}+{\gamma }_{12}{n}_{\text{A1}}}{n_{\text{A2}}+{\gamma }_{12}{n}_{\text{A1}}+{\gamma }_2{n}_{\text{D}}}, \end{gathered}$$ (4)

where γ_i = ϕ_Aiη_Ai/ϕ_Dη_D, i = 1, 2, γ₁₂ = ϕ_A2η_A2/ϕ_A1η_A1, α = γ₁₂E₁₂/(1 – E₁₂), and E₁₂ is found from the count rates after A1 excitation:

$$\begin{gathered} E_{12}=\frac{n_{\text{A2}}^{\text{Aex}}}{n_{\text{A2}}^{\text{Aex}}+{\gamma }_{12}{n}_{\text{A1}}^{\text{Aex}}} \\ \alpha =\frac{n_{\text{A2}}^{\text{Aex}}}{n_{\text{A1}}^{\text{Aex}}}, \end{gathered}$$ (5)

It should be noted that only FRET efficiencies E₁, E₂, and E₁₂ are independent, and E₁₊₂ is related to E₁ and E₂, as follows from eq 4:

$$E_{1+2}=\frac{E_1+E_2-2E_1{E}_2}{1-E_1{E}_2}.$$ (6)

This relation also holds when the inter-dye distances fluctuate.

Thus, when all distances are fixed, one can use the relations in eqs 4 and 5 to determine the FRET efficiencies from the measured photon count rates (numbers of photons per unit time) in the three-color experiment, which are equal to the measurements from individual two-color experiments with the corresponding dye pairs (two-color FRET efficiencies). In the case of fluctuating inter-dye distances, these equations are used to determine the measured FRET efficiencies, which in general differ from those in two-color FRET.

In addition to the above FRET efficiencies, we consider fractions of acceptor photon count rates (denoted by ε’s), which are used in the likelihood analysis:

$$\begin{gathered} {\epsilon }_1=\frac{n_{\text{A}1}}{n_{\text{A}1}+n_{\text{A}2}+n_{\text{D}}} \\ {\epsilon }_2=\frac{n_{\text{A}2}}{n_{\text{A}1}+n_{\text{A}2}+n_{\text{D}}} \\ {\epsilon }_{12}=\frac{n_{\text{A}2}^{\text{Aex}}}{n_{\text{A}1}^{\text{Aex}}+n_{\text{A}2}^{\text{Aex}}} \\ {\epsilon }_{1+2}=\frac{n_{\text{A}1}+n_{\text{A}2}}{n_{\text{A}1}+n_{\text{A}2}+n_{\text{D}}}={\epsilon }_1+{\epsilon }_2. \end{gathered}$$ (7)

These fractions are the probabilities to observe acceptor photons in three-color (ε₁, ε₂, and ε₁₊₂) and two-color (ε₁₂) FRET. When all γ’s are equal to 1, ε₁₂ = E₁₂ and ε₁₊₂ = E₁₊₂, whereas ε_i becomes E_i (i = 1, 2) only in the absence of a third dye (see eqs 4, 5, and 7). When all three dyes are present, ε₁ and ε₂ may differ considerably from E₁ and E₂.

The FRET efficiencies in eq 4 are related to the fractions in eq 7. For example, $E_{12}={\left(1+{\gamma }_{12}\left({\epsilon }_{12}^{-1}-1\right)\right)}^{-1}$. Similar expressions relate E₁ and E₂ to ε₁, ε₂, and ε₁₂. In the likelihood analyses, ε₁, ε₂, and ε₁₂ are determined and then used to find the FRET efficiencies E₁, E₂, and E₁₂.

B. FRET efficiencies: Fluctuating transfer rates.

When the inter-dye distances fluctuate, the measured FRET efficiencies are determined using eqs 4 and 5 with the count rates replaced by the mean count rates, 〈n_D〉, 〈n_A1〉, 〈n_A2〉, $\langle n_{\text{A1}}^{\text{Aex}}\rangle$, and $\langle n_{\text{A2}}^{\text{Aex}}\rangle$ determined in the experiment. Here we assume that the distance fluctuations are slow compared to the fluorophore lifetimes, so the averaging in 〈…〉 is equal to the averaging with respect to the steady-state distance distribution. The details of the averaging for the Gaussian chain model are given in section C. Consider first the case of A1 excitation, which is determined in a three-color experiment, but corresponds to two-color FRET. We will use superscript “m” to distinguish the measured (and corrected in the experiment) FRET efficiencies from the theoretical ones defined in eq 3. The measured FRET efficiency $E_{12}^{\text{m}}$ and the factor α^m are determined using the mean photon count rates $\langle n_{\text{A1}}^{\text{Aex}}\rangle$ and $\langle n_{\text{A2}}^{\text{Aex}}\rangle$ instead of $n_{\text{A1}}^{\text{Aex}}$ and $n_{\text{A2}}^{\text{Aex}}$ in eq 5. To proceed further, we express the photon count rates in eq 2 in terms of the FRET efficiency E₁₂ in eq 3, as $n_{\text{A1}}^{\text{Aex}}(r_{12})=c^{\text{Aex}}(1-E_{12})$ and $n_{\text{A2}}^{\text{Aex}}(r_{12})=c^{\text{Aex}}{\gamma }_{12}{E}_{12}$. Here $c^{\text{Aex}}={\eta }_{\text{A}1}{\varphi }_{\text{A}1}{k}_{\text{A1}}^{\text{ex}}$ is a constant, whereas E₁₂ depends on the distance r₁₂ between A1 and A2 and, therefore, fluctuates. Using these in eq 5 (with the mean count rates), we find

$$\begin{gathered} E_{12}^{\text{m}}=\langle E_{12}\rangle \\ {\alpha }^{\text{m}}={\gamma }_{12}\frac{\langle E_{12}\rangle }{1-\langle E_{12}\rangle }, \end{gathered}$$ (8)

Thus, $E_{12}^{\text{m}}$ obtained from the measurements is equal to the FRET efficiency E₁₂ = (1+(r₁₂/R₁₂)⁶)⁻¹ averaged over the distribution of r₁₂.

Similar reasoning can be applied to the FRET efficiency from D to A1 and A2. Using eqs 1, 3, and 4 (with n_D → 〈n_D〉, n_A1 → 〈n_A1〉, and n_A2 → 〈n_A2〉), we can get

$$E_{1+2}^{\text{m}}=\langle E_{1+2}\rangle .$$ (9)

Here the averaging is performed with respect to the distributions of r₁ and r₂.

The relationships for the rest of FRET efficiencies are more complex. The measured FRET efficiencies are found using eq 4 with the mean count rates and α^m and $E_{12}^{\text{m}}$ determined separately from the photons after A1 excitation (see eq 8). To find the mean count rates, let us represent the count rates in eq 1 in terms of the distance-dependent FRET efficiencies defined in eq 3:

$$\begin{gathered} n_{\text{D}}(r_1,r_2)=c^{\text{Dex}}(1-E_{1+2}) \\ {n}_{\text{A1}}(r_1,r_2,r_{12})={\gamma }_1{c}^{\text{Dex}}(1-E_{1+2})(1-E_{12})\frac{R_1^6}{r_1^6} \\ {n}_{\text{A2}}(r_1,r_2,r_{12})={\gamma }_2{c}^{\text{Dex}}(1-E_{1+2})\left(E_{12}\frac{R_1^6}{r_1^6}+\frac{R_2^6}{r_2^6}\right), \end{gathered}$$ (10)

where $c^{\text{Dex}}={\eta }_{\text{D}}{\varphi }_{\text{D}}{k}_{\text{D}}^{\text{ex}}$ is a constant. Here we used the rate constants k_ET1 = k_D(R₁/r₁)⁶ and k_ET2 = k_D(R₂/r₂)⁶. Averaging these count rates and using them in eq 4, we find the FRET efficiencies measured in three-color FRET:

$$\begin{gathered} E_1^{\text{m}}=\frac{\langle u_{12}{u}_{1+2}{(R_1/r_1)}^6\rangle }{1+\langle u_{12}{u}_{1+2}{(R_1/r_1)}^6\rangle } \\ {E}_2^{\text{m}}=\frac{\langle (1-u_{12})u_{1+2}{(R_1/r_1)}^6+u_{1+2}{(R_2/r_2)}^6\rangle }{1+\langle (1-u_{12})u_{1+2}{(R_1/r_1)}^6+u_{1+2}{(R_2/r_2)}^6\rangle } \\ {u}_{12}(r_{12})=\frac{1-E_{12}}{1-\langle E_{12}\rangle } \\ {u}_{1+2}(r_1,r_2)=\frac{1-E_{1+2}}{1-\langle E_{1+2}\rangle }. \end{gathered}$$ (11)

One can verify that, in the absence of fluctuations, u₁₂ = u₁₊₂ = 1, so that the measured FRET efficiencies $E_1^{\text{m}}$ and $E_2^{\text{m}}$ in eq 11 coincide with the FRET efficiencies E₁ and E₂ in eq 3. In general, fluctuations of all distances contribute to the FRET efficiencies measured in three-color FRET.

To summarize, in two-color FRET, the measured FRET efficiency is equal to the FRET efficiency averaged over the distance fluctuation (i.e. conformation-averaged FRET efficiency) as shown in Eq. 8. On the other hand, the FRET efficiencies from D to A1 and from D to A2 determined from three-color photon trajectories differ from those determined from the two-color trajectories. When the distances do not fluctuate (as in the folded state), the effect of the third dye can be taken into account by using the data from A1 excitation, so the two-color and three-color FRET efficiencies coincide. When the inter-dye distances change, this is no longer the case.

C. Gaussian chain model.

To describe the relations between the measured two-color and three-color FRET efficiencies of unfolded proteins, in which distances are fluctuating, one needs to adopt a model of distance fluctuations. In our construct, A1 is in the middle of the protein whereas D and A2 are at the two ends (Figure 1). We assume that the two vectors, r₁ connecting D and A1 and r₁₂ connecting A1 and A2 (Figure 2b), are independent of each other and have a Gaussian distribution:

$$p_i(r_i)={\left(2\pi \langle r_i{}^2\rangle /3\right)}^{-3/2}\text{exp}\left(-\frac{3r_i{}^2}{2\langle r_i{}^2\rangle }\right).$$ (12)

This function is normalized as $\int p_i(r_i)d{r}_i={\int }_0^{\infty }{p}_i(r_i)4\pi r_i^{2}d{r}_i=1$. When r₁ and r₁₂ are arbitrary, the distribution of r₂ = r₁ + r₁₂ is also Gaussian with the probability density $p_2(r_2)=\int p_1(r_1)p_{12}(r_2-r_1)d{r}_1$ given by eq 12 (i = 2) with $\langle r_2^2\rangle =\langle r_1^2\rangle +\langle r_{12}^2\rangle$.

The FRET efficiency E₁₂ depends only on the inter-dye distance r₁₂; therefore, the mean FRET efficiency in eq 8 is as in two-color FRET

$$\langle E_{12}\rangle ={\int }_0^{\infty }\frac{p_{12}(r_{12})4\pi r_{12}^2}{1+r_{12}^6/R_{12}^6}d{r}_{12}.$$ (13)

To find $E_1^{\text{m}}$ and $E_2^m$, one needs to average functions in eq 11 that depend on the inter-dye distances r₁ = |r₁|, r₁₂ = |r₁₂|, and r₂ = |r₁ + r₁₂|. The averaging of any function f(r₁, r₂, r₁₂) that depends on all three distances is performed as follows:

$$\begin{gathered} \langle f\rangle =\int f(r_1,r_2,r_{12})p_1(r_1)p_{12}(r_{12})d{r}_{1}d{r}_{12} \\ =8{\pi }^2{\int }_0^{\infty }d{r}_1{\int }_0^{\infty }d{r}_{12}{\int }_0^{\pi }d\theta f(r_1,r_2,r_{12})p_1(r_1)p_{12}(r_{12})r_1^2{r}_{12}^2\text{sin}\theta , \end{gathered}$$ (14)

Note that f(r₁, r₂, r₁₂) in the integral depends on the angle θ between r₁ and r₁₂ since r₂ = $\sqrt{r_1{}^2+r_{12}{}^2-2r_1{r}_{12}\text{cos}\theta }$ (see Figure 2b).

Finally, the FRET efficiency E₁₊₂ in eq 9 depends on two distances, r₁ and r₂. In this case the averaging is as follows:

$$\begin{gathered} \langle E_{1+2}\rangle =\int E_{1+2}(r_1,r_2)p_1(r_1)p_{12}(r_2-r_1)d{r}_{1}d{r}_2 \\ =\frac{8{\pi }^2\langle r_{12}^2\rangle }{3}\underset{0}{\overset{\infty }{\int }}d{r}_1\underset{0}{\overset{\infty }{\int }}d{r}_2{E}_{1+2}(r_1,r_2)r_1{r}_2{p}_1(r_1)\left[p_{12}(r_1-r_2)-p_{12}(r_1+r_2)\right], \end{gathered}$$ (15)

The Förster radii, R₁ = 5.4 nm, R₂ = 4.3 nm and R₁₂ = 7.0 nm are used in the calculation, which were obtained from the spectral overlap between measured dye spectra. The parameters of the Gaussian model, $\langle r_i^2\rangle$, were obtained by fitting the two-color FRET efficiencies to $\int {\left(1+{\left(r_i/R_i\right)}^6\right)}^{-1}{p}_i(r_i)4\pi r_i^{2}d{r}_i$. The two-color FRET efficiencies were obtained from the two-color segments with one inactive acceptor (i = 1) and from the photons after A1 excitation (i = 12).

D. Fluorescence lifetimes.

The measured delay times are the time intervals between the laser pulse and the detection of photons. We first consider the case when all energy transfer rates are fixed. The mean delay times of acceptor 1, ${\tau }_{\text{A1}}^{\text{Aex}}$, and acceptor 2, ${\tau }_{\text{A2}}^{\text{Aex}}$, photons after A1 excitation are the same as in two-color FRET (see Figure 2c):

$$\begin{gathered} {\tau }_{\text{A1}}^{\text{Aex}}={\left(k_{\text{A1}}+k_{\text{ET12}}\right)}^{-1} \\ {\tau }_{\text{A2}}^{\text{Aex}}={\left(k_{\text{A1}}+k_{\text{ET12}}\right)}^{-1}+k_{\text{A2}}{}^{-1}={\tau }_{\text{A1}}^{\text{Aex}}+{\tau }_{\text{A2}}^{\text{0}} \end{gathered}$$ (16)

where ${\tau }_{\text{A2}}^{\text{0}}=1/k_{\text{A2}}$ is the lifetime of the excited state of acceptor 2. The mean delay times of the donor, τ_D, and acceptor 1, τ_A1, photons after donor excitation are:

$$\begin{gathered} {\tau }_{\text{D}}={\left(k_{\text{D}}+k_{\text{ET1}}+k_{\text{ET2}}\right)}^{-1} \\ {\tau }_{\text{A1}}={\left(k_{\text{D}}+k_{\text{ET1}}+k_{\text{ET2}}\right)}^{-1}+{\left(k_{\text{A1}}+k_{\text{ET12}}\right)}^{-1}={\tau }_{\text{D}}+{\tau }_{\text{A1}}^{\text{Aex}} \end{gathered}$$ (17)

Finally, consider the mean delay time of A2 photons after donor excitation. This delay time is less obvious since the excitation can be transferred through two channels, i.e., D*A1A2 → DA1A2* and D*A1A2 → DA1*A2 → DA1A2*. The distribution of the delay times can be formally found by considering the evolution of the populations of the states p_D*A1A2, p_DA1*A2, and p_DA1A2*. These populations satisfy the following equations (see the scheme in Figure 2c):

$$\begin{gathered} \frac{d{p}_{\text{D*A1A2}}}{dt}=-(k_{\text{D}}+k_{\text{ET1}}+k_{\text{ET2}})p_{\text{D*A1A2}} \\ \frac{d{p}_{\text{DA1*A2}}}{dt}=k_{\text{ET1}}{p}_{\text{D*A1A2}}-(k_{\text{A1}}+k_{\text{ET12}})p_{\text{DA1*A2}} \\ \frac{d{p}_{\text{DA1A2*}}}{dt}=k_{\text{ET2}}{p}_{\text{D*A1A2}}+k_{\text{ET12}}{p}_{\text{DA1*A2}}-k_{\text{A2}}{p}_{\text{DA1A2*}}. \end{gathered}$$ (18)

Initially, the donor is excited, so that p_D*A1A2(0) = 1 and p_DA1*A2(0) = p_DA1A2*(0) = 0. The delay time distributions of the A2 photons after donor excitation is $P_{\text{A2}}(\tau )=p_{\text{DA1A2*}}(\tau )/{\int }_0^{\infty }{p}_{\text{DA1A2*}}(t)dt$. It follows from the solution of eq 18 that P_A2(τ) is a sum of three exponentials.

The mean delay time of A2 photons after donor excitation, ${\tau }_{\text{A2}}={\int }_0^{\infty }\tau P_{\text{A2}}(\tau )d\tau$, is found by solving eq 18:

$${\tau }_{\text{A2}}={(k_{\text{D}}+k_{\text{ET1}}+k_{\text{ET2}})}^{-1}+k_{\text{A2}}{}^{-1}+{(k_{\text{A1}}+k_{\text{ET12}})}^{-1}\frac{k_{\text{ET1}}{k}_{\text{ET12}}}{k_{\text{ET1}}{k}_{\text{ET12}}+k_{\text{ET2}}(k_{\text{A1}}+k_{\text{ET12}})}.$$ (19)

This delay time can be considered as a weighted sum of the mean delay times corresponding to the pathways D*A1A2 → DA1A2* and D*A1A2 → DA1*A2 → DA1A2*. The first pathway results in the mean delay time ${\tau }_{\text{D}}+{\tau }_{\text{A2}}^0$, and the second pathway results in ${\tau }_{\text{D}}+{\tau }_{\text{A2}}^0+{\tau }_{\text{A1}}^{\text{Aex}}$, i.e.,

$$\begin{gathered} {\tau }_{\text{A2}}=({\tau }_{\text{D}}+{\tau }_{\text{A2}}^0)(1-w)+({\tau }_{\text{D}}+{\tau }_{\text{A2}}^0+{\tau }_{\text{A1}}^{\text{Aex}})w \\ w=\frac{k_{\text{ET1}}{k}_{\text{ET12}}}{k_{\text{ET1}}{k}_{\text{ET12}}+k_{\text{ET2}}(k_{\text{A1}}+k_{\text{ET12}})}, \end{gathered}$$ (20)

where w is a statistical weight factor corresponding to the pathway D*A1A2 → DA1*A2 → DA1A2*.

The mean delay times of photons after donor excitation in eqs 17 and 19 can be expressed in terms of the FRET efficiencies in eq 3:

$$\begin{gathered} {\tau }_{\text{D}}={\tau }_{\text{D}}^0(1-E_{1+2}) \\ {\tau }_{\text{A1}}={\tau }_{\text{D}}^0(1-E_{1+2})+{\tau }_{\text{A}1}^0(1-E_{12}) \\ {\tau }_{\text{A2}}={\tau }_{\text{D}}^0(1-E_{1+2})+w{\tau }_{\text{A}1}^0(1-E_{12})+{\tau }_{\text{A}2}^0 \\ w=\frac{k_{\text{ET1}}{E}_{\text{12}}}{k_{\text{ET1}}{E}_{\text{12}}+k_{\text{ET2}}}. \end{gathered}$$ (21)

Similar relationships for the photons after A1 excitation (indicated by the superscript “Aex”) reproduce the results for the lifetimes in two-color FRET:

$$\begin{gathered} {\tau }_{\text{A1}}^{\text{Aex}}={\tau }_{\text{A1}}^0(1-E_{12}) \\ {\tau }_{\text{A2}}^{\text{Aex}}={\tau }_{\text{A1}}^0(1-E_{12})+{\tau }_{\text{A2}}^0. \end{gathered}$$ (22)

The relations in eq 22 are used in two-color FRET as an alternative to determine FRET efficiency from the donor or acceptor delay times.⁴⁴ In three-color FRET, the mean donor delay time, τ_D, is simply related to the FRET efficiency E₁₊₂ to both A1 and A2. The same FRET efficiency E₁₊₂ can be obtained from τ_A1 only if E₁₂ is known (eq 21).

Now consider fluctuating energy transfer rates. When these fluctuations are slow compared to the excited state lifetime, the measured mean delay time is⁴⁵ ${\tau }_i^m=\langle n_I{\tau }_I\rangle /\langle n_I\rangle$, I = D, A1, and A2, where 〈…〉 means the averaging with respect to a steady-state distance distribution. In the case of photons after A1 excitation, the measured mean delay times of A1, ${\tau }_{\text{A1}}^{\text{Aex}}$, and A2, ${\tau }_{\text{A2}}^{\text{Aex}}$, are

$$\begin{gathered} {\tau }_{\text{A1}}^{\text{mAex}}/{\tau }_{\text{A1}}^{\text{0}}=1-\langle E_{12}\rangle +\frac{{\sigma }_{12}^2}{1-\langle E_{12}\rangle } \\ ({\tau }_{\text{A2}}^{\text{mAex}}-{\tau }_{\text{A2}}^{\text{0}})/{\tau }_{\text{A1}}^{\text{0}}=1-\langle E_{12}\rangle -\frac{{\sigma }_{12}^2}{\langle E_{12}\rangle }, \end{gathered}$$ (23)

where ${\sigma }_{12}^2=\langle E_{12}^2\rangle -{\langle E_{12}^{}\rangle }^2$ is the variance of the FRET efficiency due to fluctuations of the distance between A1 and A2. These relations can be derived by presenting $n_{\text{A1}}^{\text{Aex}}(r_{12})=c_{}^{\text{Aex}}(1-E_{12})$ and $n_{\text{A2}}^{\text{Aex}}(r_{12})=c_{}^{\text{Aex}}{\gamma }_{12}{E}_{12}$ (see eqs 2 and 3), where $c^{Aex}={\eta }_{\text{A}1}{\varphi }_{\text{A}1}{k}_{\text{A1}}^{\text{ex}}$ is a constant, and using eq 22. For example, the mean delay time of A1 photons, ${\tau }_{\text{A1}}^{\text{mAex}}=\langle n_{\text{A1}}^{\text{Aex}}{\tau }_{\text{A1}}^{\text{Aex}}\rangle /\langle n_{\text{A1}}^{\text{Aex}}\rangle$, is equal to ${\tau }_{\text{A1}}^{\text{0}}\langle {(1-E_{12})}^2\rangle /\langle 1-E_{12}\rangle$, which leads to the first equation in eq 23.

The relations in eq 23 reproduce the results for the lifetimes in two-color FRET:^37,45 They are used in two-dimensional (2D) histograms of the normalized lifetime and FRET efficiency. In the absence of r₁₂ fluctuations, ${\sigma }_{12}^2=0$ (e.g., in the folded state), so the peaks of the histogram are located on the diagonal of the 2D histogram. When r₁₂ fluctuates, the lifetimes are shifted above (A1 photons) or below (A2 photons) the diagonal.^37,45

Using the same arguments as in eq 23, the measured lifetime of donor photons after donor excitation in three-color FRET can be related to the FRET efficiency E₁₊₂ and its variance. Specifically, presenting n_D(r₁, r₂) = c^Dex(1 – E₁₊₂), where $c^{\text{Dex}}={\eta }_{\text{D}}{\varphi }_{\text{D}}{k}_{\text{D}}^{\text{ex}}$ is a constant (eqs 1 and 3), and using eq 21, we have:

$${\tau }_{\text{D}}^{\text{m}}/{\tau }_{\text{D}}^0=1-\langle E_{1+2}\rangle +\frac{{\sigma }_{1+2}^2}{1-\langle E_{1+2}\rangle },$$ (24)

where ${\sigma }_{1+2}^2=\langle E_{1+2}^2\rangle -{\langle E_{1+2}^{}\rangle }^2$ is the variance of the FRET efficiency due to fluctuations of both r₁ and r₂, which can be correlated.

The relation in eq 24 is used to plot two-dimensional histograms of measured donor lifetimes and the efficiencies of energy transfer to both acceptor 1 and acceptor 2. Since the relations for A1 and A2 delay times in eq 21 are more complicated, we restrict ourselves by considering only 2D $E_{1+2}-{\tau }_{\text{D}}/{\tau }_{\text{D}}^0$ histogram.

Determination of apparent FRET efficiencies, lifetimes, and folding kinetics using maximum likelihood analysis.

In order to determine all three FRET efficiencies between three dye pairs, it is necessary to determine one FRET efficiency independently by alternating excitation (i.e. excitation of A1). The fractions of acceptor photons determined from the maximum likelihood method are converted to the three measured FRET efficiencies in three-color FRET. As described above, when the distances between dyes are fluctuate (e.g., unfolded state of a protein), the measured FRET efficiencies in three-color experiment are different from the corresponding two-color FRET efficiencies. In the experiment, there are always segments with only two active dyes due to incomplete labeling and photobleaching of one of the three dyes during the measurement. We globally analyze all kinds of segments with different combinations of fluorophores to determine and compare measured two- and three-color FRET efficiencies.

A. Two-state likelihood function.

In typical single molecule FRET experiments, a rate coefficient of a process is determined by identifying transitions in binned FRET efficiency trajectories, constructing a distribution of waiting times (residence times) in a state, and fitting the waiting time distribution to a single-exponential function. The folding kinetics of α₃D cannot be determined in this way because transitions are not clearly resolvable in binned trajectories due to the fast folding kinetics. Therefore, we determined the fractions of acceptor photons ε (often called apparent FRET efficiencies in two-color FRET) and the folding and unfolding rates using the maximum likelihood method³⁶ that analyzes photon trajectories without binning. As described previously,³⁶ the likelihood for the j^th photon trajectory with photon colors and arrival times is given by

$$L_j=1^{\text{T}}\prod _{i=2}^{N_j}\left[F(c_i)\text{exp}\left(K(t_i-t_{i-1})\right)\right]F(c_1)p_{eq},$$ (25)

where N_j is the number of photons in the j^th trajectory, c_i is the color of the i^th photon, F is the photon color matrix that describes the probability of detecting photons of different colors for each state, K is the rate matrix, t_i is the arrival time of the i^th photon and p_eq is a vector that describes equilibrium populations of the states. 1^T is the unit row vector (T means transpose). The parameters were determined by maximizing the likelihood function calculated by the diagonalization of K as described in Ref. 36. Practically, the total log-likelihood function of all trajectories was calculated by summing individual log-likelihood functions as ln L = ∑_j ln L_j.

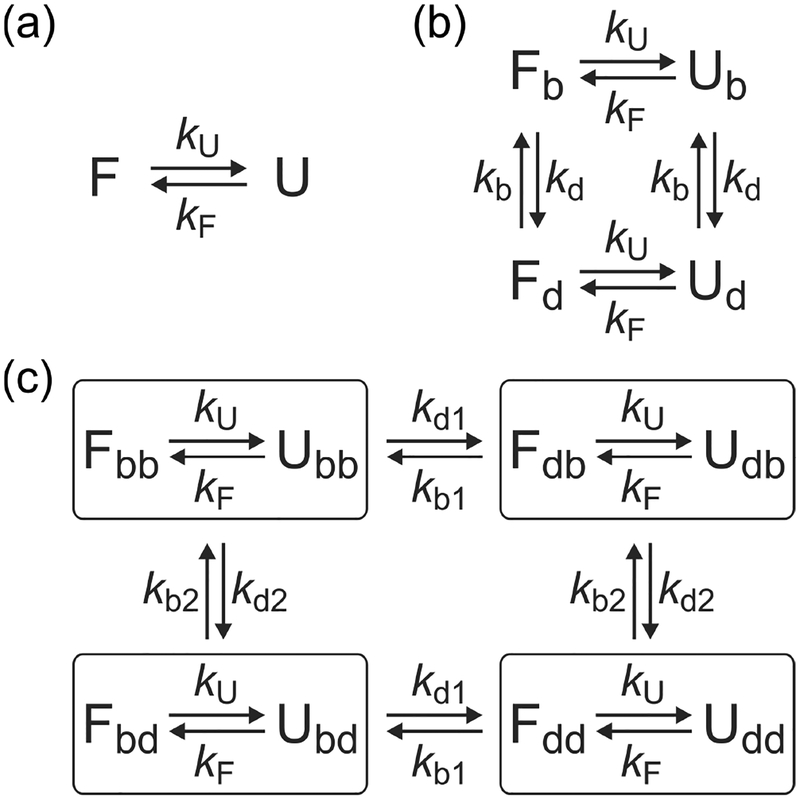
For two-color segments, the color c_i is either donor or acceptor, so that F(acceptor) = E and F(donor) = I – E, where I is the unity matrix and E is a diagonal matrix with the fractions of acceptor photon count rates (probabilities of acceptor photons) of the individual states on the diagonal. For the two-state system in Figure 3a, the matrix E, the rate matrix K, and the vector of the equilibrium populations p_eq are given by

$$\begin{array}{c}E=\left(\begin{array}{cc}{\epsilon }_{\text{F}}& 0\\ 0& {\epsilon }_{\text{U}}\end{array}\right),\\ K=\left(\begin{array}{cc}-k_{\text{U}}& k_{\text{F}}\\ k_{\text{U}}& -k_{\text{F}}\end{array}\right),p_{\text{eq}}=\left(\begin{array}{c}{p}_{\text{F}}\\ 1-p_{\text{F}}\end{array}\right).\end{array}$$ (26)

Figure 3.

Kinetic models used in the maximum likelihood analysis. (a) Two-state model consisting of the folded (F) and unfolded (U) states with folding and unfolding rate coefficients k_F and k_U. (b) Four-state model to account for blinking of acceptor. k_b (k_d) is the rate coefficient from the bright (dark) to the dark (bright) state of the acceptor. (c) Eight-state model including blinking of acceptor 1 and acceptor 2. k_bI (k_dI) is the rate coefficient from the bright (dark) to the dark (bright) state of acceptor I. Note that acceptor blinking occurs between the folded states and between the unfolded states, but not between the folded and unfolded states with different acceptor states similar to the blinking transitions in (b).

Here, ${\epsilon }_{\text{F}}=n_{\text{AF}}/(n_{\text{AF}}+n_{\text{DF}})$ and ${\epsilon }_{\text{U}}=n_{\text{AU}}/(n_{\text{AU}}+n_{\text{DU}})$ are the fractions of acceptor photons in the folded and unfolded state, respectively, k_F and k_U are folding and unfolding rate coefficients, and p_F = k_F/(k_F + k_U) is the equilibrium population of the folded state.

There are two kinds of two-color segments: 1) DA1 segments with active A1 and inactive A2 labels and 2) DA2 segments with active A2 and inactive A1 labels. In the analysis of DA1 segments, the photons detected in A2 channel are mostly due to leakage of A1 fluorescence. Therefore, A1 and A2 photons were combined and considered as A1 photons, so that ε^DA1 = (n_A1 + n_A2)/(n_D + n_A1 + n_A2). Similarly, in the analysis of DA2 segments, D and A1 photons were combined and treated as donor photons, so that ε^DA2 = n_A2/(n_D + n_A1 + n_A2).

In the analysis of three-color segments, there are five kinds of photons: donor (D), acceptor 1 (A1), and acceptor 2 (A2) by donor excitation and acceptor 1 (A1^Aex) and acceptor 2 (A2^Aex) by A1 excitation. Photons by donor and A1 excitation are distinguished by the relative delay times separated by ~25 ns (40 MHz alternating frequency). Donor photons detected after A1 excitation are dark count of the detector and were not included in the analysis. The rate matrix and equilibrium populations are the same as those in eq 26. For the photons detected after donor excitation, F(A1) = E₁, F(A2) = E₂, and F(D) = I – E₁ – E₂, where E₁ and E₂ are diagonal matrices as in eq 26 with the fractions of acceptor photons after donor excitation on the diagonal. Matrix E₁ for A1 photons has diagonal elements ${\epsilon }_{1S}=n_{\text{A1}S}/\left(n_{\text{A1}S}+n_{\text{A2}S}+n_{\text{D}S}\right)$, and matrix E₂ has elements ${\epsilon }_{2S}=n_{\text{A2}S}/\left(n_{\text{A1}S}+n_{\text{A2}S}+n_{\text{D}S}\right)$, S = F, U.

For the photons detected after A1 excitation, the color matrix F is the same as that for two-color segments with donor = A1 and acceptor = A2, F(A2^Aex) = E^Aex, and F(A1^Aex) = I – E^Aex, where E^Aex is a diagonal matrix with elements ${\epsilon }_{12S}=n_{\text{A2}S}^{\text{Aex}}/\left(n_{\text{A1}S}^{\text{Aex}}+n_{\text{A2S}}^{\text{Aex}}\right)$ (S = F, U) on the diagonal.

B. Likelihood function including acceptor blinking.

In the maximum likelihood analysis, the extracted parameters are often affected by photoblinking of the acceptor when the timescale of blinking is not well separated from that of the folding dynamics. We have shown that parameters can be determined more accurately by incorporating acceptor blinking in the kinetic model.⁴⁶

For the analysis of two-color segments, the model consists of four states: folded and unfolded states with bright and dark states of the acceptor (Figure 3b). The matrices of parameters are given by^46,47

$$\begin{array}{l}E=\left(\begin{array}{cccc}{\epsilon }_{\text{F}}& 0& 0& 0\\ 0& {\epsilon }_{\text{U}}& 0& 0\\ 0& 0& {\epsilon }_{\text{d}}& 0\\ 0& 0& 0& {\epsilon }_{\text{d}}\end{array}\right),\\ K=\left(\begin{array}{cccc}-k_{\text{U}}-k_{\text{d}}& k_{\text{F}}& k_{\text{b}}& 0\\ k_{\text{U}}& -k_{\text{F}}-k_{\text{d}}& 0& k_{\text{b}}\\ k_{\text{d}}& 0& -k_{\text{U}}-k_{\text{b}}& k_{\text{F}}\\ 0& k_{\text{d}}& k_{\text{U}}& -k_{\text{F}}-k_{\text{b}}\end{array}\right),p_{eq}=\left(\begin{array}{c}{p}_{\text{F}}{p}_{\text{b}}\\ (1-p_{\text{F}})p_{\text{b}}\\ p_{\text{F}}(1-p_{\text{b}})\\ (1-p_{\text{F}})(1-p_{\text{b}})\end{array}\right),\end{array}$$ (27)

where ε_d is the fraction of acceptor photons (i.e., the probability to detect an acceptor photon) in the acceptor dark state. This fraction is not zero due to the leak of donor photons to the acceptor channel. p_b = k_b/(k_b + k_d) is the equilibrium population of the acceptor bright state. k_b and k_d are the rate coefficients from the dark to the bright states of the acceptor and vice versa. We assumed that k_d is proportional to the photon count rate, whereas k_b is independent of the photon count rate because k_d increases linearly with the time spent in the excited state. Therefore, k_d = k_d⁰(n/n₀), where n is the average photon count rate of each photon trajectory and k_d⁰ is the rate coefficient at the reference photon count rate (n₀ = 100 ms⁻¹).

The model for the analysis of three-color segments consists of eight states because there are two states (folded and unfolded) for α₃D and two states (bright and dark) for both acceptors (Figure 3c). The matrices of parameters are

$$\begin{gathered} E_1=Diag(\{{\epsilon }_{1Sjk}\}) \\ {E}_2=Diag(\{{\epsilon }_{2Sjk}\}) \\ {E}_{12}=Diag(\{{\epsilon }_{12Sjk}\}) \\ {p}_{eq}={\left(\left\{p_{Sjk}\right\}\right)}^{\text{T}},S=\text{F},\text{U},j,k=\text{b},\text{d}. \end{gathered}$$ (28)

Here, ε_ISjk is the fraction of acceptor I (= 1, 2) photons in state S (= F and U) with A1 state j (= b (bright) and d (dark)) and A2 state k (= b and d) by donor excitation. Diag(…) means a diagonal matrix with the diagonal elements in the parenthesis. p_Sjk (= p_Sp_jp_k) is the equilibrium population of state S with A1 state j and A2 state k. For example, the population of the folded state with both acceptors are in the bright state is p_Fbb = p_Fp_b1p_b2. The rate matrix K can be constructed using the kinetic scheme in Figure 3c.

C. Parameter optimization.

As mentioned above, we globally analyzed three-color segments (DA1A2) and two kinds of two-color segments (DA1 and DA2) by maximizing the log of total likelihood, which is the sum of three log-likelihoods, ln L = ln L^(DA1A2) + ln L^(DA1) + ln L^(DA2).

For the two-state model, there are 12 fitting parameters: ${\epsilon }_{\text{F}}^{\text{DA1}}$, ${\epsilon }_{\text{U}}^{\text{DA1}}$, ${\epsilon }_{\text{F}}^{\text{DA2}}$, and ${\epsilon }_{\text{U}}^{\text{DA2}}$ for two-color DA1 and DA2 segments, ε_1F, ε_1U, ε_2F, ε_2U, ε_12F, and ε_12U for three-color segments, and k (= k_F + k_U) and p_F, for all three kinds of segments.

For the model including acceptor blinking, the number of independent parameters can be reduced by using the relationship listed in Table 1. The fraction of acceptor ε values in the dark states of A1 and/or A2 can be replaced by two-color parameters and pre-determined parameters (see Table S1 for the values of the pre-determined parameters). Note that the count rates in these procedures are uncorrected count rates that include background. Overall, there are 16 fitting parameters for the eight-state model that includes blinking of acceptors. In addition to 12 parameters that are the same as in the model without blinking, there are four parameters describing A1 and A2 blinking: the rates of the transition from the dark to bright states of the acceptors and populations of the acceptor bright states, k_b1, k_b2, p_b1, and p_b2.

Table 1.

Relationship between three-color parameters in the presence of acceptor blinking and two-color or pre-determined parameters.

Excitation	Acceptor dark state	3-color Parameter	2-color parametera		Pre-determined parameterb
			DA1	DA2
Donor	A2 dark	ε1Sbd	${\epsilon }_S^{\text{DA1}}\left(1-{\epsilon }_{\text{d}12}\right)$
		ε2Sbd	${\epsilon }_S^{\text{DA1}}{\epsilon }_{\text{d}12}$
	A1 dark	ε1Sdb		$\left(1-{\epsilon }_S^{\text{DA2}}\right){\epsilon }_{\text{d}1}$
		ε2Sdb		${\epsilon }_S^{\text{DA2}}$
	A1, A2 dark	ε1Sdd			εd1
		ε2Sdd			εd2
A1	A1 dark	ε12Sbd			εd12
	A2 dark	ε12Sdb			ε12db
	A1, A2 dark	ε12Sdd			ε12dd

^a${\epsilon }_S^{\text{DA1}}=\left(n_{\text{A}1}+n_{\text{A}2}\right)/\left(n_{\text{D}}+n_{\text{A}1}+n_{\text{A}2}\right)$ and ${\epsilon }_S^{\text{DA2}}={\eta }_{\text{A}2}/\left(n_{\text{D}}+n_{\text{A}1}+n_{\text{A}2}\right)$ (see eq 26).

^bε_d1 (ε_d2) is the fraction of photons detected in A1 (A2) channel after donor excitation when A1 and A2 are in the dark state, which are pre-determined from the donor-only segments. ${\epsilon }_{\text{d}1}=n_{\text{A1}}^0/(n_{\text{D}}^0+n_{\text{A1}}^0+n_{\text{A2}}^0)$ and ${\epsilon }_{\text{d}2}=n_{\text{A2}}^0/(n_{\text{D}}^0+n_{\text{A1}}^{\text{0}}+n_{\text{A2}}^0)$, where $n_{\text{D}}^0,n_{\text{A1}}^{\text{0}},\text{ and }{n}_{\text{A2}}^0$ are the count rates in D, A1 and A2 channels, respectively, of the donor-only segment. Note that ε_d1, ε_d2, and ε_d12 are not corrected for background photons, and therefore, are different from the leak values l₁, l₂, and l₁₂ in eq 31. ε_d12 is the fraction of A2 photons detected after A1 excitation when A2 is in the dark state, which is pre-determined from DA1 segments by A1 excitation. ${\epsilon }_{12\text{db}}=n_{\text{A2}}^{\text{Aex}0}/(n_{\text{A1}}^{\text{Aex}0}+n_{\text{A2}}^{\text{Aex}0}),$ where $n_{\text{A1}}^{\text{Aex0}}\text{ and }{n}_{\text{A2}}^{\text{Aex0}}$ are the count rates in A1 and A2 channels, respectively, of the A2 only segments by the A1 excitation laser. ε_12dd is determined by background photons in both A1 and A2 channels.

FRET efficiency corrections.

To obtain accurate FRET efficiencies, the fractions of acceptor photons determined from the maximum likelihood analysis were corrected for background, leak into other channels, direct excitation of acceptor, and the ratio of the detection efficiencies and quantum yields of the dyes (γ-factor).^21,48 Due to the fast folding kinetics, it is not possible to correct the FRET efficiencies of individual states as in the case of a slow process.²¹ Therefore, we corrected average values of fraction of acceptor photons using the average values of background, leak, direct acceptor excitation and γ-factor. We describe the correction procedures briefly here and the details can be found in Supporting Information (SI).

A. Corrections for background and donor leak.

The FRET efficiencies in the analysis of two-color segments and the fraction of acceptor photons in the analysis of three-color segments can be corrected for background photons as⁴⁸

$${\epsilon }^c=\frac{\epsilon n-b_{\text{A}}}{n-b_{\text{A}}-b_{\text{D}}}(2\text{ color).}$$ (29a)

$${\epsilon }_1^c=\frac{{\epsilon }_{1}n-b_{\text{A}1}}{n-b_{\text{D}}-b_{\text{A}1}-b_{\text{A}2}},{\epsilon }_2^c=\frac{{\epsilon }_{2}n-b_{\text{A}2}}{n-b_{\text{D}}-b_{\text{A}1}-b_{\text{A}2}},\text{ (}3\text{ color).}$$ (29b)

Here, ε’s are the uncorrected values obtained from the maximum likelihood analysis above, n is the average total photon count rate including background photons, and b_D, b_A1, and b_A2 are the average background count rates in D, A1, and A2 channels, respectively. Average background count rates were obtained from the segments after all dyes are photobleached.

For two-color segments, one can correct the donor leak as

$${\epsilon }^{\text{c}}=\frac{\epsilon -l}{1-l},$$ (30)

where ε is the value corrected for background photons in eq 29 and $l\left(=n_{\text{A}}^0/\left(n_{\text{A}}^0+n_{\text{D}}^0\right)\right)$ is the average value of the leak of donor photons into the acceptor channel, which can be determined using $n_{\text{A}}^0$ and $n_{\text{D}}^0$, the background-corrected mean photon count rates in the acceptor and donor channels of donor-only segments.

For three-color segments, the average leak of the donor photons into two acceptor channels and the leak of A1 into A2 channel are

$$\begin{gathered} l_1=n_{\text{A1}}^0/(n_{\text{A2}}^0+n_{\text{A}1}^0+n_{\text{D}}^0) \\ {l}_2=n_{\text{A2}}^0/(n_{\text{A2}}^0+n_{\text{A1}}^0+n_{\text{D}}^0) \\ {l}_{12}=n_{\text{A2}}^{\text{Aex}0}/(n_{\text{A2}}^{\text{Aex}0}+n_{\text{A1}}^{\text{Aex}0}). \end{gathered}$$ (31)

Here, $n_{\text{A2}}^{\text{0}}$, $n_{\text{A1}}^{\text{0}}$, and $n_{\text{D}}^0$ are the background-corrected mean photon count rates in A2, A1, and D channels of donor-only (for l₁ and l₂) segments. $n_{\text{A2}}^{\text{Aex0}}$ and $n_{\text{A1}}^{\text{Aex0}}$ are the background-corrected mean photon count rates in A2 and A1 channels of DA1 segments by A1 excitation. Similar to the correction of the two-color segments, ε₁ and ε₂ can be corrected as

$$\begin{gathered} {\epsilon }_1^{\text{c}}=\frac{{\epsilon }_1(1-l_2)-(1-{\epsilon }_2)l_1}{(1-l_1-l_2)(1-l_{12})} \\ {\epsilon }_2^{\text{c}}=\frac{{\epsilon }_1(l_2-l_{12})+{\epsilon }_2(1-l_1-l_{12})+(l_1+l_2)l_{12}-l_2}{(1-l_1-l_2)(1-l_{12})}. \end{gathered}$$ (32)

ε₁₂ by A1 excitation can be corrected using eq 30.

In the three-color experiment, l₁ = 0.067, l₂ = 0.021, and l₁₂ = 0.25. In two color measurements, l = l₁ + l₂ for DA1 analysis and l = l₂ for DA2 analysis.

B. Corrections for γ-factor and direct acceptor excitation and determination of measured FRET efficiencies.

In the analysis of two-color segments, γ is the ratio of the detection efficiencies (η) and quantum yields (ϕ) of the acceptor and donor, γ = (η_Aϕ_A)/(η_Dϕ_D). The measured FRET efficiency is obtained after corrections of the fraction ε for direct acceptor excitation and γ-factor as (see SI)

$$E^{\text{m}}=\frac{\epsilon (1-f_{\text{A}}^{\text{dir}})}{\epsilon (1-f_{\text{A}}^{\text{dir}})+\gamma (1-\epsilon )},$$ (33)

where ε is the background and donor-leak corrected value in eq 30 and $f_{\text{A}}^{\text{dir}}=n_{\text{A}}^{\text{dir}}/n_{\text{A}}$ is the ratio of the acceptor count rates by direct acceptor excitation and donor excitation.

In the three-color experiment, there are two independent γ-factors defined as γ₁ = (η_A1ϕ_A1)/(η_Dϕ_D) and γ₁₂ = (η_A2ϕ_A2)/(η_A1ϕ_A2). γ₂ = γ₁γ₁₂. The measured FRET efficiency $E_{12}^{\text{m}}$ can be determined using eq 33. One can find other measured FRET efficiencies, $E_1^{\text{m}}$, $E_2^{\text{m}}$, and $E_{1+2}^{\text{m}}$, from the ε’s obtained in the three-color maximum likelihood analysis as (see SI for the details)

$$\begin{gathered} E_{12}^{\text{m}}=\frac{{\epsilon }_{12}(1-f_{\text{A12}}^{\text{dir}})}{{\epsilon }_{12}(1-f_{\text{A12}}^{\text{dir}})+{\gamma }_{12}(1-{\epsilon }_{12})} \\ {E}_1^{\text{m}}=\frac{{\epsilon }_1[1-f_{\text{A1}}^{\text{dir}}(1-{\epsilon }_{12})]}{{\epsilon }_1[1-f_{\text{A1}}^{\text{dir}}(1-{\epsilon }_{12})]+{\gamma }_1(1-E_{12}^{\text{m}})(1-{\epsilon }_1-{\epsilon }_2)} \\ {E}_2^{\text{m}}=\frac{{\epsilon }_2(1-f_{\text{A2}}^{\text{dir}})-{\epsilon }_1{f}_{\text{A1}}^{\text{dir}}{\epsilon }_{12}-{\gamma }_{12}{\epsilon }_1{E}_{12}^{\text{m}}/(1-E_{12}^{\text{m}})[1-f_{\text{A1}}^{\text{dir}}(1-{\epsilon }_{12})]}{{\epsilon }_1(1-f_{\text{A2}}^{\text{dir}})-{\epsilon }_1{f}_{\text{A1}}^{\text{dir}}{\epsilon }_{12}-{\gamma }_{12}{\epsilon }_1{E}_{12}^{\text{m}}/(1-E_{12}^{\text{m}})[1-f_{\text{A1}}^{\text{dir}}(1-{\epsilon }_{12})]+{\gamma }_2(1-{\epsilon }_1-{\epsilon }_2)} \\ {E}_{1+2}^{\text{m}}=\frac{{\epsilon }_1[{\gamma }_{12}-f_{\text{A1}}^{\text{dir}}({\gamma }_{12}+(1-{\gamma }_{12}){\epsilon }_{12})]+{\epsilon }_2(1-f_{\text{A2}}^{\text{dir}})}{{\gamma }_2+{\epsilon }_1[{\gamma }_{12}-{\gamma }_2-f_{\text{A1}}^{\text{dir}}({\gamma }_{12}+(1-{\gamma }_{12}){\epsilon }_{12})]+{\epsilon }_2(1-{\gamma }_2-f_{\text{A2}}^{\text{dir}})}, \end{gathered}$$ (34)

where the ε’s are the background and donor-leak corrected values, $f_{\text{A1}}^{\text{dir}}(=n_{\text{A1}}^{\text{dir}}/n_{\text{A1}})$ and $f_{\text{A2}}^{\text{dir}}(=n_{\text{A2}}^{\text{dir}}/n_{\text{A2}})$ are the ratios of the A1 and A2 count rates by direct A1 and A2 excitation and donor excitation, respectively, and $f_{\text{A12}}^{\text{dir}}(=n_{\text{A2}}^{\text{dir,Aex}}/n_{\text{A2}}^{\text{Aex}})$ is the ratio of A2 count rates by direct A2 excitation and A1 excitation.

Determination and correction of lifetimes.

To obtain the lifetime information of fluorophores, we used a likelihood function that includes the delay times of photons:³⁷

$$L_j=1^{\text{T}}\prod _{i=2}^{N_j}\left[F(c_i)P(c_i,\delta t_i)\text{exp}\left(K(t_i-t_{i-1})\right)\right]F(c_1)P(c_1,\delta t_1)p_{eq},$$ (35)

where the matrix P(c, δt) is a diagonal matrix with the elements P_cS(δt) (S = F, U) depending on the color (c) of a photon. P_cS(δt) is the normalized delay time (δt) distribution of photons when a molecule is in state S. Although all parameters including the lifetimes can be simultaneously determined, for the simplicity of the method, the FRET efficiencies and kinetic parameters were determined first using the likelihood function in eq 25, and then the donor lifetimes by D excitation and A1 lifetimes by A1 excitation were determined by fixing other parameters. Then, A2 lifetimes by A1 excitation were subsequently determined by fixing the parameters determined in the previous step.³⁷

A. Delay time distributions for two-state model.

The matrices of the delay time distributions for the two-color analysis (DA1 and DA2 segments, and A1 excitation for three-color segments) are

$$P(acceptor,\delta t)=\left(\begin{array}{cc}{P}_{\text{AF}}(\delta t)& 0\\ 0& P_{\text{AU}}(\delta t)\end{array}\right),P(donor,\delta t)=\left(\begin{array}{cc}{P}_{\text{DF}}(\delta t)& 0\\ 0& P_{\text{DU}}(\delta t)\end{array}\right).$$ (36)

For the simplicity of the analysis, the donor delay time distributions, P_DF, and P_DU, were approximated to be single-exponential. Note that the distribution in the unfolded state, P_DU, is actually multi-exponential because of conformational fluctuations, which are slower than the donor fluorescence lifetime.³⁷ By using a single-exponential distribution we are going to get the donor fluorescence lifetime averaged with respect to the inter-dye distance distribution. The acceptor delay time distributions, P_AF, P_AU, are approximated as bi-exponential³⁷ (S = F, U)

$$\begin{gathered} P_{\text{D}S}(\delta t)={\tau }_{\text{D}S}^{-1}{e}^{-\delta t/{\tau }_{\text{D}S}}, \\ {P}_{\text{A}S}(\delta t)=\frac{e^{-\delta t/{\tau }_{\text{A}}^0}-e^{-\delta t/{\tau }_{\text{D}S}^{\text{A}}}}{{\tau }_{\text{A}}^0-{\tau }_{\text{D}S}^{\text{A}}}, \end{gathered}$$ (37)

where ${\tau }_{\text{A}}^0$ is the lifetime of the acceptor excited state. The same ${\tau }_{\text{A}}^0$ value was used for the folded and unfolded states for the simplicity of the analysis. τ_DS (S = F, U) is the lifetime of the donor excited state on the condition that the state decays to the ground state by emitting a donor photon and ${\tau }_{\text{D}S}^{\text{A}}\left(={\tau }_{\text{AS}}-{\tau }_{\text{A}}^0\right)$ is the lifetime of the donor excited state on the condition that the state decays to the acceptor excited state.³⁷ In general, these two conditional lifetimes are different although they coincide in the absence of distance fluctuations. The mean value of the donor and acceptor delay time distribution in eq 37 is τ_DS and ${\tau }_{\text{A}}^0+{\tau }_{\text{D}S}^{\text{A}}$, respectively. The acceptor and donor delay time distributions in eq 37 are affected by the instrument response function (IRF) and background noise. The actual distributions for the maximum likelihood analysis are given in eq S14 (see SI).

The likelihood functions with the distributions in eq 37 are optimized with respect to τ_DF and τ_DU (donor delay times) and ${\tau }_{\text{DF}}^{\text{A}}$ and ${\tau }_{\text{DU}}^{\text{A}}$ (acceptor delay times). The obtained parameters are the lifetimes in the folded and unfolded states averaged with respect to distance fluctuations.

In the analysis of the three-color segments, the delay time distributions of photons detected in D and A1 channels after donor excitation and those detected in A1 and A2 channels after A1 excitation are obtained similarly (S = F, U),

$$\begin{gathered} P_{\text{D}S}(\delta t)={\tau }_{\text{D}S}^{-1}{e}^{-\delta t/{\tau }_{\text{D}S}}, \\ {P}_{\text{A1}S}(\delta t)=\frac{e^{-\delta t/{\tau }_{\text{A1}S}^{\text{Aex}}}-e^{-\delta t/{\tau }_{\text{D}S}^{\text{A1}}}}{{\tau }_{\text{A1}S}^{\text{Aex}}-{\tau }_{\text{D}S}^{\text{A1}}}, \end{gathered}$$ (38a)

$$\begin{gathered} P_{\text{A1}S}^{\text{Aex}}(\delta t)={\tau }_{\text{A1}S}^{\text{Aex}}{}^{-1}{e}^{-\delta t/{\tau }_{\text{A1}S}^{\text{Aex}}}, \\ {P}_{\text{A2}S}^{\text{Aex}}(\delta t)=\frac{e^{-\delta t/{\tau }_{\text{A2}}^0}-e^{-\delta t/{\tau }_{\text{A1}S}^{\text{A2,Aex}}}}{{\tau }_{\text{A2}}^0-{\tau }_{\text{A1}S}^{\text{A2,Aex}}}, \end{gathered}$$ (38b)

where ${\tau }_{\text{A2}}^0$ is the lifetime of A2 excited state, ${\tau }_{\text{A1F(U)}}^{\text{Aex}}$ is the mean lifetimes of A1 excited state in the presence of A2, and ${\tau }_{\text{A1F(U)}}^{\text{A2,Aex}}$ (=${\tau }_{\text{A2F(U)}}^{\text{Aex}}$ – ${\tau }_{\text{A2}}^0$, eq 22) is the lifetimes of A1 excited state on the condition that the state decays to A2 excited state.

B. Delay time distributions with acceptor blinking.

For the two-color analysis including the analysis of A1 excitation data of three color segments, the matrices of the delay time distributions are the diagonal matrices

$$\begin{gathered} P\left(acceptor,\delta t\right)=Diag\left[P_{\text{AF}}\left(\delta t\right),P_{\text{AU}}\left(\delta t\right),P_{\text{Ad}}\left(\delta t\right),P_{\text{Ad}}\left(\delta t\right)\right] \\ P\left(donor,\delta t\right)=Diag\left[P_{\text{DF}}\left(\delta t\right),P_{\text{DU}}\left(\delta t\right),P_{\text{Dd}}\left(\delta t\right),P_{\text{Dd}}\left(\delta t\right)\right]. \end{gathered}$$ (39)

The distributions in the bright state, P_DF, P_DU, P_AF, P_AU, are given by eq 38. P_Ad(δt) and P_Dd(δt) are the delay time distributions in the acceptor (due to the leak of donor photons) and donor channels, respectively, when the acceptor is in the dark state. These distributions are the same as the donor delay time distribution for the molecule with an inactive acceptor:

$$P_{\text{Dd}}(\delta t)=P_{\text{Ad}}(\delta t)={({\tau }_{\text{D}}^0)}^{-1}{e}^{-\delta t/{\tau }_{\text{D}}^0}.$$ (40)

The matrices of the delay time distributions for the analysis of three-color segments by donor excitation are

$$\begin{gathered} P\left(I,\delta t\right)=Diag\left[\left\{P_{ISjk}\left(\delta t\right)\right\}\right], \\ I=\text{D},\text{A}1,\text{A}{1}^{\text{Aex}},\text{A}{2}^{\text{Aex}},S=\text{F},\text{U},\text{\hspace{0.17em}and\hspace{0.17em}}j,k=\text{b},\text{d}. \end{gathered}$$ (41)

Here, P_DSbb(δt) and P_A1Sbb(δt) (S = F, U) are the A1 and D delay time distributions by donor excitation when both acceptors are in the bright state, which are given in eq 38a. The delay time distributions after A1 excitation, $P_{\text{A1}S\text{bb}}^{\text{Aex}}(\delta t)$ and $P_{\text{A2}S\text{bb}}^{\text{Aex}}(\delta t)$, are given in eq 38b. When A1 is in the dark state, $P_{\text{D}S\text{db}}\left(\delta t\right)=P_{\text{A}1S\text{db}}\left(\delta t\right)={\tau }_{\text{D}S}{}^{-1}{e}^{-\delta t/{\tau }_{\text{D}S}}$, $P_{\text{A1}S\text{db}}^{\text{Aex}}(\delta t)=P_{\text{A1bkg}}^{\text{Aex}}(\delta t)$, and $P_{\text{A2}S\text{db}}^{\text{Aex}}(\delta t)={\tau }_{\text{A}2}^0{}^{-1}{e}^{-\delta t/{\tau }_{\text{A}2}^0}$. $P_{\text{A1bkg}}^{\text{Aex}}(\delta t)$ is the delay time distribution of the background photons in A1 channel by A1 excitation, which can be pre-determined from DA2 segments. $P_{\text{A2}S\text{db}}^{\text{Aex}}(\delta t)$ results from the direct excitation of A2 by the A1 excitation laser. When A2 is in the dark state, P_DSbd(δt) and P_A1Sbd(δt) are given in eq 41b with a substitution of ${\tau }_{\text{A1}}^0$ for ${\tau }_{\text{A1F(U)}}^{\text{Aex}}$. $P_{\text{A1}S\text{bd}}^{\text{Aex}}(\delta t)=P_{\text{A2}S\text{bd}}^{\text{Aex}}(\delta t)={\tau }_{\text{A}1}^0{}^{-1}{e}^{-\delta t/{\tau }_{\text{A}1}^0}$. When both acceptors are in the dark state, P_DSdd(δt) and P_A1Sdd(δt) are the same and given in eq 40. $P_{\text{A1}S\text{dd}}^{\text{Aex}}(\delta t)$ and $P_{\text{A2}S\text{dd}}^{\text{Aex}}(\delta t)$ are the distributions of background photons in A1 and A2 channels.

C. Lifetime corrections for background, donor leak, and direct acceptor excitation.

The measured mean delay time of the donor in D excitation (eq 24) and that of A1 in A1 excitation (eq 23) requires corrections for only background photons. Since the delay time distributions for the maximum likelihood analysis include the IRF and background photons, the extracted D and A1 delay times are used as the measured delay times in eqs 23 and 24. On the other hand, A2 delay time in A1 excitation needs further corrections for A1 leak (eq S21) and direct A2 excitation (eq S24). The details of the correction procedures are described in SI.

Identifying transition points in photon trajectories using the Viterbi algorithm.

Due to the fast folding kinetics, it is not possible to find transitions between the folded and unfolded states in binned trajectories. However, transition points can be identified at the single photon level using the Viterbi algorithm^49,50 adapted to photon trajectories with the maximum likelihood parameters as feeding parameters. For the two-color analysis, the detailed procedure has been described in Ref. 28. For the three-color segments, the same analysis procedure can be used with only an increased number of color matrices. There are five types of photons: D, A1, and A2 by donor excitation and A1 and A2 by A1 excitation.

Results and Discussion

FRET efficiency histograms in three-color FRET.

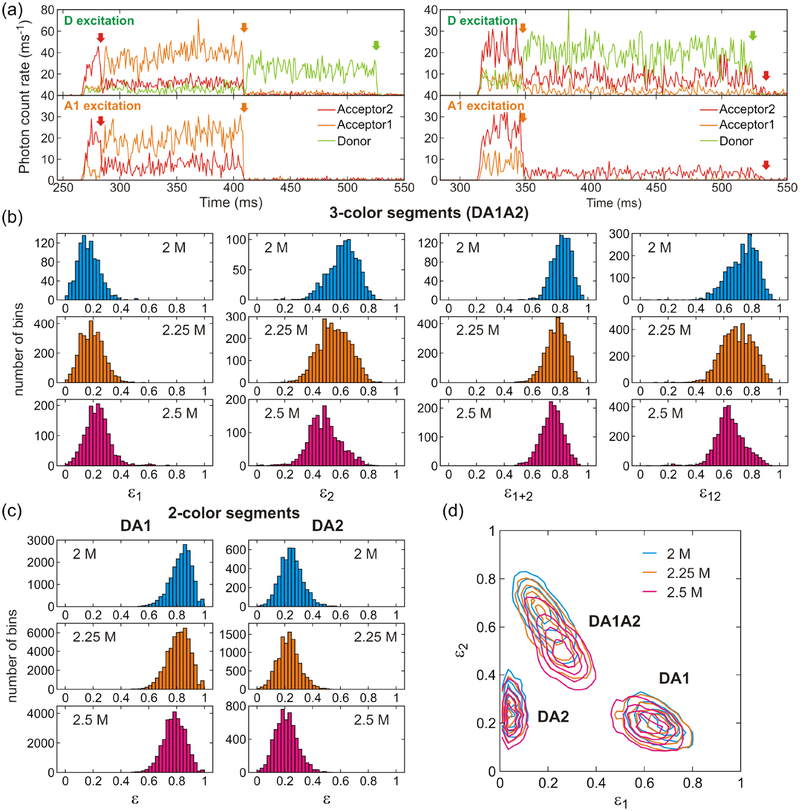
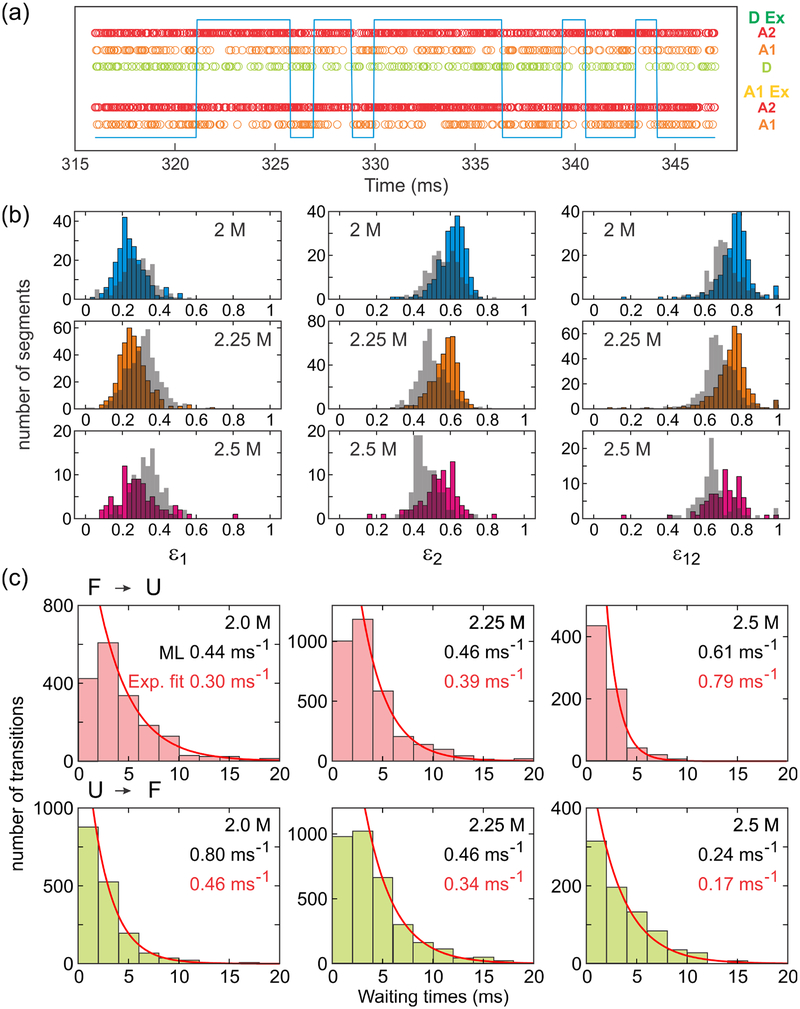
As shown in Figure 1, the donor (D) and acceptor 2 (A2) are attached to the N- and C-termini of the protein, respectively, and acceptor 1 (A1) is attached to residue 33 in the middle of helix 2. Since the distances between dyes are relatively short in the folded state, the FRET efficiencies are expected to be higher in the folded state than in the unfolded state. The transitions between folded and unfolded states are not clearly identifiable in the binned trajectories in Figure 4a because of the fast kinetics (~ 1 ms⁻¹),²⁸ which is comparable to the bin time of 1 ms. In addition, the FRET efficiency difference between the folded and unfolded states is small (see extracted FRET efficiencies in Table 2). As a consequence, the histograms of the fractions of acceptor photons in a bin show a single peak with a gradual shift as the GdmCl concentration increases (Figure 4b and 4c). The separation in the sequence between A1 (residue 33) and A2 (C-terminus) is larger than that between D (N- terminus) and A1. Therefore, only ε₂ (the fraction of A2 fluorescence after D excitation) and ε₁₂ (the fraction of A2 fluorescence after A1 excitation) histograms of the three-color segments show relatively broad distributions at the denaturation mid-point of 2.25 M GdmCl, because the difference between the folded and unfolded state FRET efficiency values is large. The distributions of ε₂ and ε₁₂ are also asymmetric at 2 M and 2.5 M GdmCl (Figure 4b), where more folded and unfolded molecules exist, respectively. As the GdmCl concentration is increased, the population of the unfolded state increases and the unfolded chain expands. Therefore, all FRET efficiency distributions shift to the lower side with increasing GdmCl concentration except ε₁, which is the fraction of A1 photons after D excitation for the three-color segment. Although there is more energy transfer from D to A1 in the folded state than in the unfolded state, the transfer efficiency from A1 to A2 is also higher, which can make ε₁ actually lower in the folded state.

Figure 4.

Fluorescence trajectories and FRET efficiency histograms in three-color FRET at different GdmCl concentrations. (a) Binned (1 ms bin time) fluorescence trajectories of two molecules (left and right) obtained by donor excitation (upper) and A1 excitation (lower). Donor, A1, and A2 trajectories are colored in light green, orange, and red, respectively. Photobleaching steps are indicated by arrows with the corresponding colors. The residual A2 signal after D (A1) photobleaching by D (A1) excitation trajectory on the right side is direct excitation of A2 by the D (A1) excitation laser. (b) Histograms of uncorrected fractions of acceptor photons ε (eq 7) obtained from the segments in which all three dyes are active. Segments with an average total photon count rate higher than 50 ms⁻¹ were included. ε₁ is the fraction of A1 photons (i.e., the number of A1 photons divided by the total number of photons in the bin), ε₂ is the fraction of A2 photons, and ε₁₊₂ = ε₁ + ε₂. These values were calculated from photons emitted after D excitation and collected in 1 ms bins. ε₁₂ was calculated from photons emitted after A1 excitation. (c) FRET efficiency histograms constructed from two-color segments: donor and acceptor 1 (DA1, left) and donor and acceptor 2 (DA2, right). (d) 2D plots of ε₁ and ε₂ for the different types of segments. 2D contours were smoothed as described in Ref. 51.

Table 2.

Folding kinetics parameters.^a

		8-state			2-state
[GdmCl]	2 M	2.25 M	2.5 M	2 M	2.25 M	2.5 M
ε1F	0.16	0.16	0.16	0.16	0.16	0.16
ε1U	0.26	0.28	0.28	0.26	0.28	0.28
ε2F	0.71	0.69	0.70	0.71	0.69	0.69
ε2U	0.55	0.49	0.48	0.54	0.49	0.47
ε12F	0.84	0.83	0.82	0.84	0.83	0.82
ε12F	0.65	0.64	0.64	0.65	0.64	0.63
${\epsilon }_{\text{F}}^{\text{DA1}}$	0.90	0.90	0.89	0.90	0.90	0.89
${\epsilon }_{\text{U}}^{\text{DA1}}$	0.79	0.78	0.77	0.78	0.78	0.77
${\epsilon }_{\text{F}}^{\text{DA2}}$	0.30	0.30	0.32	0.30	0.30	0.32
${\epsilon }_{\text{U}}^{\text{DA2}}$	0.22	0.21	0.20	0.21	0.21	0.20
k	1.24 (±0.06)	0.91 (±0.03)	0.85 (±0.04)	1.32 (±0.06)	0.97 (±0.03)	0.92 (±0.05)
pF	0.65 (±0.01)	0.50 (±0.01)	0.29 (±0.01)	0.65 (±0.01)	0.51 (±0.01)	0.30 (±0.01)
kb1	5.97 (±1.05)	4.71 (±0.45)	5.35 (±0.71)
pb1b	0.99	0.99	0.99
kb2	1.99 (±0.90)	1.59 (±0.39)	1.36 (±0.38)
pb2b	0.99	0.99	0.98

^aErrors are standard deviations calculated from the curvature at the maximum of the likelihood function.

^bp_b1 and p_b2 correspond to the values at the reference photon count rate of 100 ms⁻¹.

Figure 4d shows gradual changes of the FRET efficiency distributions as α₃D unfolds in a two-dimensional (2D) plot. Compared to the very small differences in the distributions from the two color segments (DA1: donor and acceptor1; DA2: donor and acceptor 2), the distribution from the three-color segments (DA1A2) shows a larger shift because ε₁ increases while ε₂ decreases and the distribution is elongated along the diagonal. This suggests that a 2D plot of three-color FRET can offer a better resolution for distinguishing different states or species.

Extracting FRET efficiency and kinetic parameters using maximum likelihood method.

As the FRET efficiency histograms are almost featureless and only show small shift as the protein unfolds, we extracted FRET efficiency and kinetic parameters using the maximum likelihood method. As explained in Methods, the FRET efficiencies obtained from the two-color analysis and three-color analysis are expected to be the same for the folded state, but different for the unfolded state. Therefore, we determined two-color and three-color FRET efficiencies with global kinetic parameters and compared these FRET efficiencies.

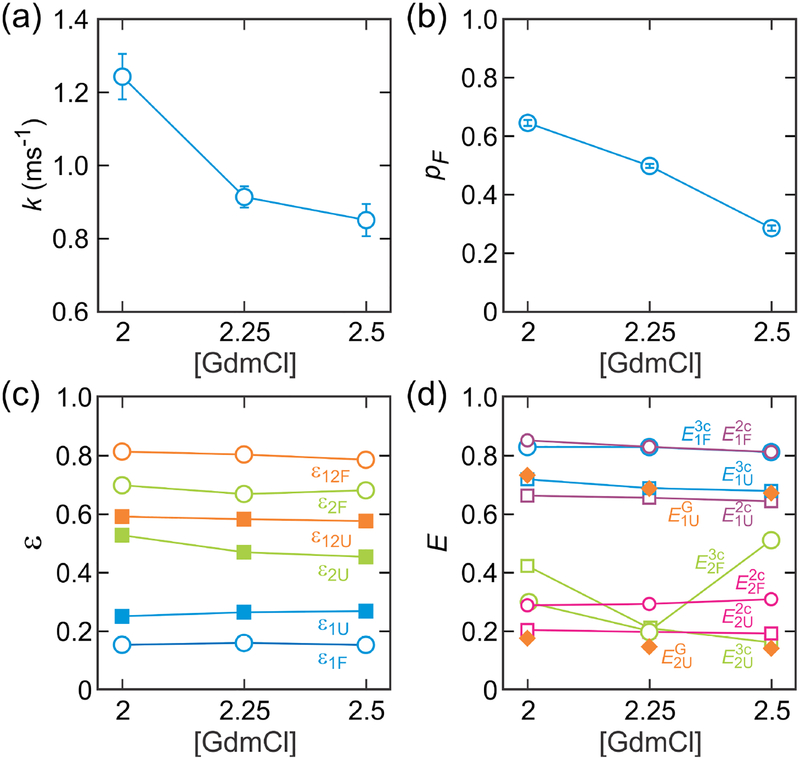
The extracted relaxation rate ranges from 0.9 to 1.2 ms⁻¹ and the folded population ranges from 0.65 to 0.29 at 2 M – 2.5 M GdmCl (Figure 5a and 5b and Table 2). These parameters agree very well with those determined in the previous work with two-color FRET and different fluorophore positions,²⁸ suggesting the addition of the third fluorophore does not perturb the folding dynamics. We analyzed the data using two-state model without blinking and eight-state model including acceptor blinking (Figure 3). The results are compared in Table 2. The very high population of the acceptor bright state (> 0.99 for given photon count rates) at all GdmCl concentrations suggests the combination of the chemicals (see Methods) successfully suppress acceptor blinking. However, the rates obtained from the two-state model are slightly higher (6 – 8 %) than those from the eight-state model (Table 2). This is consistent with previous experimental and simulation results.^46,47, which showed that the effect of blinking is amplified in the case of fast transitions between states. Therefore, we will use the eight-state model parameters for the FRET efficiency corrections below.

Figure 5.

Determination of the FRET efficiencies and kinetic parameters using the maximum likelihood method with the eight-state model, which includes blinking states of the two acceptors. (a) Relaxation rate k (= k_F + k_U). (b) Fraction of the folded state p_F. Errors in (a) and (b) are standard deviations determined from the curvature at the maximum of the likelihood function. (c) Fractions of the acceptor count rates for the folded (open circle) and unfolded (filled square) states determined from the three-color segments. (d) Comparison of the measured two-color FRET efficiencies (eq 33) determined from DA1 segments ($E_{1\text{F}}^{2\text{c}}$, purple circle; $E_{1\text{U}}^{2\text{c}}$, purple square) and DA2 segments ($E_{2\text{F}}^{2\text{c}}$, magenta circle; $E_{2\text{U}}^{2\text{c}}$, magenta square), measured three-color FRET efficiencies (eq 34) ($E_{1\text{F}}^{3\text{c}}$, blue circle; $E_{1\text{U}}^{3\text{c}}$, blue square; $E_{2\text{F}}^{3\text{c}}$, green circle; $E_{2\text{U}}^{3\text{c}}$, green square), and calculated three-color FRET efficiencies for the unfolded state using the Gaussian chain model ($E_{1\text{U}}^{\text{G}}$ and $E_{2\text{U}}^{\text{G}}$, orange filled diamond). FRET efficiencies were corrected for background, donor leak, direct acceptor excitation, and γ-factors.

The extracted FRET efficiency parameters are shown in Figure 5c and 5d and listed in Tables 2 and 3. The parameters ε₁, and ε₂ determined in the maximum likelihood method are not really energy transfer efficiencies, but fractions of A1 and A2 photons by donor excitation in the three-color measurement. To obtain structural information of the protein, one should convert these parameters into the FRET efficiencies, E₁ and E₂, which are related to the distances between dyes. Therefore, we calculated the FRET efficiencies (measured FRET efficiencies, eq 34), $E_1^{\text{3c}}$ and $E_2^{\text{3c}}$ from ε₁ and ε₂ of the three-color segments. Here, the superscripts “3c” and “2c” are used to distinguish the FRET efficiencies obtained from the three-color and two-color segments. For the folded state, $E_{1\text{F}}^{\text{3c}}$ is similar to $E_{1\text{F}}^{\text{2c}}$ determined from the two-color segments (eq 33) (Figure 5d and Table 3). The relatively small fluctuation of the FRET efficiency resulting from the flexible parts of the folded protein, short linkers to which the fluorophores are attached and several disordered residues at the C-terminus for the sortase-mediated ligation do not seem to affect the average FRET efficiency of the folded state. However, for the unfolded state with larger distance fluctuations, $E_{1\text{U}}^{\text{3c}}$ is higher than $E_{1\text{U}}^{\text{2c}}$ for all GdmCl concentrations by 0.04 – 0.06 (Table 3). This is consistent with the theory above. It follows from eq 11 that, when the inter-dye distances fluctuate, the FRET efficiency measured in two-color and three-color experiments are not the same.

Table 3.

Comparison of measured FRET efficiencies.^a

	[GdmCl]
	2 M	2.25 M	2.5 M
$E_{1\text{F}}^{\text{2c}}$	0.83	0.83	0.81
$E_{1\text{F}}^{\text{3c}}$	0.85 (±0.01)	0.83 (±0.01)	0.81 (±0.01)
$E_{1\text{U}}^{\text{2c}}$	0.66	0.65	0.64
$E_{1\text{U}}^{\text{3c}}$	0.72 (±0.01)	0.69 (±0.01)	0.68 (±0.01)
$E_{1\text{U}}^{\text{G}}$	0.73	0.69	0.67
$E_{\text{2F}}^{\text{2c}}$	0.29	0.29	0.31
$E_{\text{2F}}^{\text{3c}}$	0.30 (±0.09)	0.20 (±0.09)	0.51 (±0.06)
$E_{\text{2U}}^{\text{2c}}$	0.20	0.20	0.19
$E_{\text{2U}}^{\text{3c}}$	0.42 (±0.02)	0.21 (±0.03)	0.16 (±0.03)
$E_{\text{2U}}^{\text{G}}$	0.17	0.15	0.14

^aErrors for the three-color FRET efficiencies are obtained from the propagation of the errors (standard deviations) calculated from the curvature at the maximum of the likelihood function.

To account for these differences, we employed the Gaussian chain model for the unfolded protein. This model, eq 12, involves only mean-squared distance $\langle r_i^2\rangle$ as a parameter. $\langle r_1^2\rangle$ and $\langle r_{12}^2\rangle$ were determined using $E_{1\text{U}}^{\text{2c}}$ from the two-color segments and $E_{12\text{U}}^{\text{3c}}$ from the three-color segments. Then the three-color FRET efficiencies, $E_{1\text{U}}^{\text{G}}$ and $E_{2\text{U}}^{\text{G}}$ were calculated using eqs 11–15 (the superscript “G” referrers to the Gaussian chain model).

The calculated $E_{1\text{U}}^{\text{G}}$ values are in excellent agreement with those determined from the experimental $E_{1\text{U}}^{\text{3c}}$ values (Figure 5d and Table 3). Compared to $E_1^{\text{3c}}$, however, $E_2^{3\text{c}}$ values are not so accurate. Some three-color values agree very well with the two-color FRET efficiency values or those calculated from the Gaussian chain model, but other values deviate by a large amount (e.g., $E_{2\text{F}}^{\text{3c}}$ at 2.5 M and $E_{2\text{U}}^{\text{3c}}$ at 2 M). This inaccuracy results from the high E₁ values and the very low E₂ values for both folded and unfolded states. In this case, both the denominator and numerator are very small in the calculation of $E_2^{\text{3c}}$ in eqs 4 or 34. Therefore, small errors in the pre-determined parameters such as $E_{12}^{\text{3c}}$ and γ-factors can make a large fluctuation in the determination of $E_2^{\text{3c}}$. More accurate determination of $E_2^{\text{3c}}$ may require measurement at a much higher photon count rate.

Identifying transitions at the single photon level.

As shown in Figure 4a, states cannot be separated in a binned trajectory due to the fast kinetics compared to the bin time (1 ms) and a relatively small FRET efficiency difference between the folded and unfolded states. Using the Viterbi algorithm^49,50 adapted to photon trajectories and the maximum likelihood parameters, transitions between the folded and unfolded states can be identified at the single photon level. Then, various parameters can be obtained from the separated folded and unfolded photon trajectory segments, which can be compared with the maximum likelihood parameters to validate the consistency of the analysis.

Figure 6a shows an example photon trajectory with folding and unfolding transitions. After separating photon trajectories into two states, the histogram of ε (fraction of acceptor photons) of each state can be constructed. Figure 6b shows that the distributions of the folded and unfolded states still fairly overlap in the individual ε histograms (ε₁, ε₂, and ε₁₂), indicating that combining all three ε’s in the analysis results in a better resolution for state separation. In addition, the waiting time distribution of each state can be obtained (Figure 6c). The rate coefficients determined from exponential fitting are similar to those from the maximum likelihood analysis as expected.

Figure 6.

Identification of transitions at a single photon level. (a) Separation of folded and unfolded states, indicated by high and low levels of the blue line, respectively, in a photon trajectory using the Viterbi algorithm. In the folded state, a small number of D and A1 photons are detected due to the high energy transfers to A2. (b) Acceptor fraction ε histograms of folded (colored bars) and unfolded (grey bars) states constructed from photon trajectory segments separated by the Viterbi algorithm. FRET efficiencies were calculated for the segments containing more than 100 photons and with the mean photon count rate greater than 20 ms⁻¹. (c) Waiting time distributions in the folded (upper) and unfolded (lower) states. Exponential fitting (the first bar is excluded) results in the unfolding and folding rates, respectively. The fitted values (red) are similar to the value obtained from the maximum likelihood method (black).

Lifetime determination and 2D FRET efficiency-lifetime histogram.

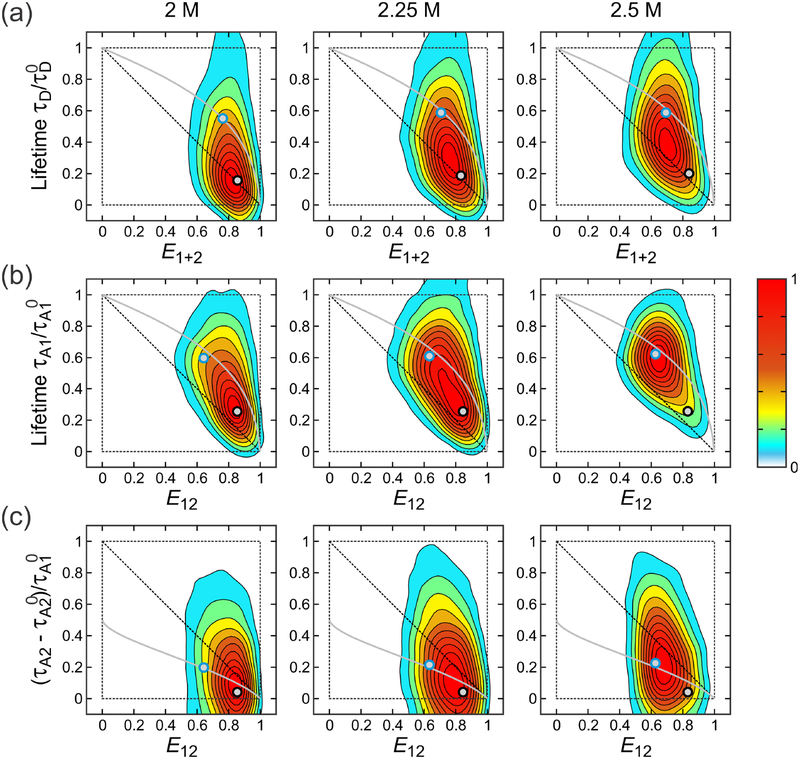
Since picosecond-pulsed lasers are used for alternating laser excitation, the lifetimes of fluorophores can also be determined from the mean delay times. 2D FRET efficiency-lifetime histograms in Figure 7 visualize the correlations between photon delay times and FRET efficiencies:^{21,37,45,52–57} between the donor delay time and E₁₊₂ by D excitation (Figure 7a) and between A1 (Figure 7b) or A2 (Figure 7c) delay times and E₁₂ by A1 excitation. For these three cases, the shift of the peak of the distribution from the diagonal indicates to the presence of the inter-dye distance fluctuations. The variance of the underlying FRET efficiency distribution can be obtained using eqs 23 and 24 with the corrected FRET efficiency and lifetime values. (Note that σ² in eqs 23 and 24 is not the variance of the peak in the FRET efficiency histogram.) When the protein is folded, the variance of the FRET efficiency due to distance fluctuations is very small and the 2D distribution is expected to appear along the diagonal. For the unfolded state with large distance fluctuations the distributions are shifted upward (Figure 7a and b) or downward (Figure 7c) from the diagonal (see eqs 23 and 24). The overlaid lines in Figure 7 are the dependence of the normalized lifetime on the mean FRET efficiency in two-color FRET that is expected if unfolded protein behaviors follow those of a given polymer model. The Gaussian (gray) lines in Figure 7b and 7c are obtained as parametric plots of eq 23 by varying the parameter $\langle r_{12}^2\rangle$ of the Gaussian model. At 2 M GdmCl, the peak of the distributions is close to the diagonal line because the folded fraction is high. On the other hand, the distributions obtained at 2.5 M GdmCl are closer to the lines of the unfolded polymer models because unfolded population is higher. At the denaturation mid-point 2.25 M GdmCl, the distributions are located in the middle of the diagonal and unfolded state lines.

Figure 7.

2D FRET efficiency-lifetime histograms. 2D histograms were constructed for (a) E₁₊₂ and donor delay times (D excitation), (b) E₁₂ and A1 delay time (A1 excitation), and (c) E₁₂ and A2 delay time (A1 excitation). ${\tau }_{\text{A}2}-{\tau }_{\text{A}2}^0={\tau }_{\text{A}1}^{\text{A}2}$ is the A1 lifetime on the condition that the A1 excited state decays to A2 excited state (see eq 38). FRET efficiencies and mean delay times were calculated for each of 1 ms bins and 2D contours were smoothed as described in Ref. 51. Gray lines are the dependence of the lifetimes on E calculated for the unfolded state using the Gaussian chain model. FRET efficiencies were corrected for background, donor leak, direct acceptor excitation, and γ-factors and mean delay times were corrected for background. A2 delay times in (c) were further corrected for the leak of A1 fluorescence and direct A2 excitation. Black and blue circles filled in grey show the FRET efficiencies and lifetimes of the folded and unfolded states, respectively, obtained from the maximum likelihood analysis (see Table 3 and 4, and Figure 8). The variances of the FRET efficiency distribution of the unfolded state calculated using these values are (a) ${\sigma }_{1+2}^2$ = 0.074, 0.086, 0.086, (b) ${\sigma }_{12}^2$ = 0.085, 0.089, 0.092, (c) ${\sigma }_{12}^2$ = 0.104, 0.097, 0.094.

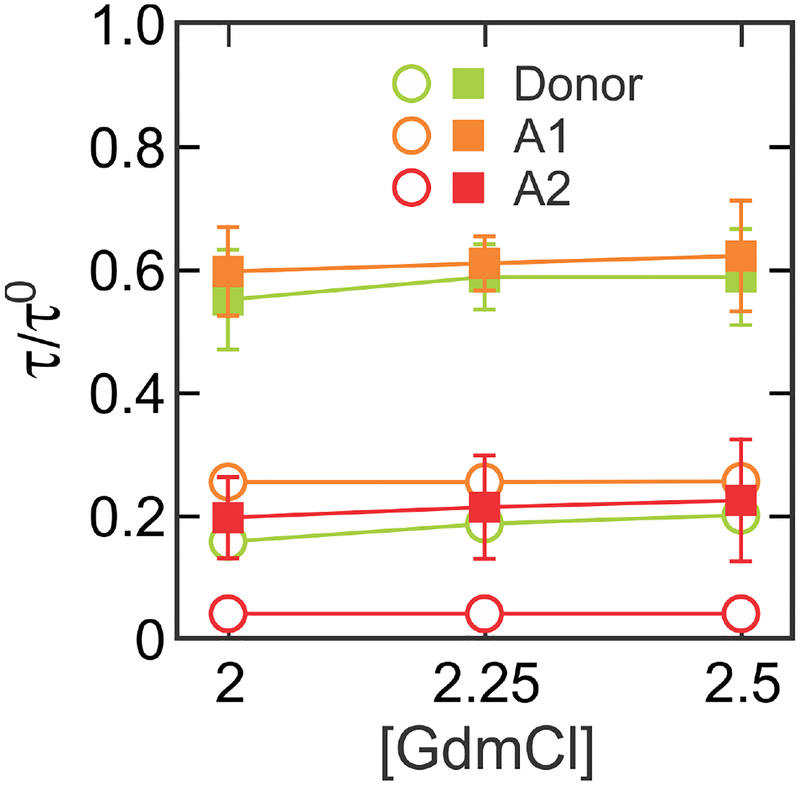
For more accurate comparison, we determined the mean delay times (lifetimes) of fluorophores in the folded and unfolded states of the protein using the likelihood function in eq 35. The determined lifetime values are summarized in Figure 8 and Table 4. These values are also plotted in Figure 7 (black and blue circles). The unfolded state values are located very close to the line from the Gaussian chain model. This result together with the agreement between the measured and calculated $E_{1\text{U}}^{\text{3c}}$ values (Figure 5d and Table 3) indicate that the unfolded state is described very well by the Gaussian chain model.^{1,2,21,54–56,58–60}

Figure 8.

Determination of mean delay times (lifetimes) of photon arrivals from the laser pulse using the maximum likelihood method with the eight-state model. Donor (green) and A1 (orange) delay times were corrected for background and A2 (red) delay times were corrected for background, donor leak, and direct acceptor excitation. Error bars are standard deviations calculated from the curvature at the maximum of the likelihood function and plotted only for the unfolded state (filled square) because errors are much smaller than the size of the symbols for the folded state (open circle). (see Table 4). Relative mean delay times (τ/τ⁰) were calculated as ${\tau }_{\text{DF,U}}^{}/{\tau }_{\text{D}}^0$ (green), ${\tau }_{\text{A1F,U}}^{\text{Aex}}/{\tau }_{\text{A1}}^0$ (orange), and ${\tau }_{\text{A1F,U}}^{\text{A2,Aex}}/{\tau }_{\text{A1}}^0$ (red).

Table 4.

Lifetime parameters.^a

		8-state			2-state
[GdmCl]	2 M	2.25 M	2.5 M	2 M	2.25 M	2.5 M
${\tau }_{\text{DF}}^{}/{\tau }_{\text{D}}^0$	0.157 (±0.002)	0.186 (±0.001)	0.200 (±0.002)	0.159 (±0.002)	0.189 (±0.001)	0.201 (±0.002)
${\tau }_{\text{DU}}^{}/{\tau }_{\text{D}}^0$	0.550 (±0.081)	0.587 (±0.053)	0.587 (±0.078)	0.550 (±0.022)	0.576 (±0.014)	0.587 (±0.075)
${\tau }_{\text{A1F}}^{\text{Aex}}/{\tau }_{\text{A1}}^0$	0.254 (±0.002)	0.254 (±0.001)	0.255 (±0.002)	0.251 (±0.002)	0.251 (±0.001)	0.254 (±0.002)
${\tau }_{\text{A1U}}^{\text{Aex}}/{\tau }_{\text{A1}}^0$	0.596 (±0.072)	0.609 (±0.044)	0.621 (±0.090)	0.596 (±0.042)	0.608 (±0.024)	0.621 (±0.080)
${\tau }_{\text{A1F}}^{\text{A2,Aex}}/{\tau }_{\text{A1}}^0$	0.040	0.040	0.040	0.040	0.040	0.040
${\tau }_{\text{A1U}}^{\text{A2,Aex}}/{\tau }_{\text{A1}}^0$	0.196 (±0.066)	0.213 (±0.084)	0.224 (±0.099)	0.201 (±0.056)	0.207 (±0.054)	0.224 (±0.114)

^aErrors are standard deviations calculated from the curvature at the maximum of the likelihood function.

Summary

In this work, we have described the development of the theory and analysis methods for fast three-color FRET and its application to the analysis of fast protein folding dynamics. We first presented site-specific labeling of three fluorophores that is necessary for unambiguous analysis of three-color FRET data. For the analysis of fast two-state folding dynamics, a maximum likelihood method was used to analyze photon trajectories directly without binning. In this analysis, we used a two-state model without considering acceptor blinking and an eight-state model that includes additional photophysical states resulting from blinking of two acceptors. We showed that the usage of an appropriate combination of chemicals can suppress acceptor blinking and results in only slight increase in the rate coefficients (Table 2). In addition to the relaxation rate and folded fraction, the FRET efficiencies can be determined accurately after corrections for background, donor leak into the acceptor channels, direct acceptor excitation, and γ-factors. The corrected three-color FRET efficiencies are very close to the two-color FRET efficiencies for the folded state, in which the distances are virtually fixed (Figure 5 and Table 3). On the other hand, for the unfolded state, in which distances are fluctuating, the two- and three-color FRET efficiencies are different. This result indicates that three-color FRET is not just a combination of two-color FRET measurements with three different pairs of dye positions but provides additional information on conformational flexibility of molecules. We employed the Gaussian chain model, which have been used to describe unfolded polypeptide chain behaviors, to calculate three-color FRET efficiencies, which shows an excellent agreement for the efficiency of transfer from the donor to acceptor 1 ($E_1^{\text{3c}}$) (Figure 5 and Table 3). We also showed that the presence of distance fluctuations (i.e., conformation fluctuations) of the unfolded state can be visualized by 2D FRET efficiency-lifetime histograms. The distribution of the unfolded state is located as expected from the Gaussian chain model.

The development of the theory and experimental methods of fast three-color FRET in this work for the determination (and correction) of the accurate FRET efficiencies and fluorescence lifetimes and their correlations will be very useful for studies in which high time resolution is required such as the visualization of the transition paths^8,9,61 and protein-protein interaction pathways.