Theoretical optimization of high-frequency optogenetic spiking of red-shifted very fast-Chrimson-expressing neurons

Abstract.

A detailed theoretical analysis and optimization of high-fidelity, high-frequency firing of the red-shifted very-fast-Chrimson (vf-Chrimson) expressing neurons is presented. A four-state model for vf-Chrimson photocycle has been formulated and incorporated in Hodgkin–Huxley and Wang–Buzsaki spiking neuron circuit models. The effect of various parameters that include irradiance, pulse width, frequency, expression level, and membrane capacitance has been studied in detail. Theoretical simulations are in excellent agreement with recently reported experimental results. The analysis and optimization bring out additional interesting features. A minimal pulse width of 1.7 ms at $23\mathrm{mW}/{\mathrm{mm}}^2$ induces a peak photocurrent of 1250 pA. Optimal irradiance ($0.1\mathrm{mW}/{\mathrm{mm}}^2$) and pulse width ($50\mu \mathrm{s}$) to trigger action potential have been determined. At frequencies beyond 200 Hz, higher values of expression level and irradiance result in spike failure. Singlet and doublet spiking fidelity can be maintained up to 400 and 150 Hz, respectively. The combination of expression level and membrane capacitance is a crucial factor to achieve high-frequency firing above 500 Hz. Its optimization enables 100% spike probability of up to 1 kHz. The study is useful in designing new high-frequency optogenetic neural spiking experiments with desired spatiotemporal resolution, by providing insights into the temporal spike coding, plasticity, and curing neurodegenerative diseases.

1. Introduction

Optogenetics has revolutionized neuroscience and cell biology by controlling genetically modified cells in culture, tissue, and living animals with light. It provides unprecedented spatial and temporal precision and opportunities for a wide range of biomedical applications.^1–5 It has enabled the examination of the causal roles of specific neural components in normal and dysfunctional behaviors. The past decade has witnessed an explosive development of optogenetic tools, primarily microbial rhodopsin pumps and channels. When expressed transgenically in neurons, they can optically stimulate and inhibit neural signaling by causing depolarization or hyperpolarization of the cell, respectively.

There is, at present, a tremendous research effort directed at new optogenetic tools through discovery and engineering to provide greater control, with improved kinetics, photosensitivity, spectral tuning, and protein stability.^6–9 A major challenge is to overcome the inverse relationship between light sensitivity and kinetics to achieve low power and ultrafast operation for higher spatiotemporal resolution. Fast channels require higher light irradiances, whereas increasing the light sensitivity results in much slower channelrhodopsins (ChRs), eliciting low-temporal precision spiking in response to longer light pulses.¹⁰ This is due to the greater integration of photons on prolonged light stimulation of cells that express optogenetic protein populations with slower off kinetics, at low light powers. Light sensitivity is drastically reduced in a fast ChR due to small ion-translocation, as has been observed experimentally.^6,10 The single-channel conductance and quantum efficiency have also been experimentally observed to be essentially invariant.^6,10 It has been demonstrated that unfavorable low light sensitivity for activation is compensated with high expression levels of the fast Chrimson mutants or by improving the light delivery (number of photons), for several cell types in vitro and in vivo.¹⁰ Hence, the mutual dependence of channel kinetics and light sensitivity requires optimization of the ChR expression and light delivery, in order to successfully perform experiments in the high-frequency range.

Precise spike timing and high-frequency oscillations are associated with neural plasticity, behavior, and pathology that includes mediation of neural coding in auditory system and alteration of functions in Parkinson’s disease.^11–13 Dysfunction in the fast-spiking parvalbumin-positive (${\mathrm{PV}}^{+}$) interneurons may set low thresholds for impairment of fast network oscillations and higher brain functions and may cause cerebral aging as well as various acute and chronic brain diseases, such as stroke, vascular cognitive impairment, epilepsy, Alzheimer’s disease, and schizophrenia.^14–17 High-frequency spiking may also govern whether spikes propagate throughout dendrites and hence affect localized cellular processes.¹⁸

Another important aspect is to minimize the invasiveness of inserting optical fiber into the brain, which displaces brain tissue and can lead to undesirable side effects that include brain lesion, neural morphology changes, glial inflammation, glial motility, and compromise of asepsis.^19,20 Various red-shifted opsins have developed, including VChR1, C1V1, and ReaChR (590 to 630 nm), to enable deep penetration of light with reduced scattering and phototoxicity in tissue, noninvasive use, as well as for independently activating distinct neural populations with blue light.^21–23 A pair of opsins, namely Chrimson (45-nm red-shifted from previous ChRs) and Chronos (blue and green light-sensitive), have been recently discovered through de novo sequencing of opsins from over 100 algal species, offering two-color activation of distinct neural populations without detectable cross talk.²⁴ Red-shifted opsins thus enable simultaneous all-optical manipulation and recording of neural circuit activity with cellular resolution in vivo.²⁵

Recently, genetic mutations in Chrimson have led to a family of variants that show a wide range of closing kinetics, without shifting the absorption spectrum.¹⁰ The mutants, namely fast-Chrimson Y261F/S267M (f-Chrimson) and very-fast-Chrimson K176R/Y261F/S267M (vf-Chrimson), with fast closing kinetics and no blue-shifting of their action spectra, are especially important for optogenetic applications.¹⁰ The vf-Chrimson exhibits ultrafast closing kinetics with ${\tau }_{\text{off}}=2.7\pm 0.3\mathrm{ms}$, which is as fast as that of Chronos (${\tau }_{\text{off}}=3.6\pm 0.2\mathrm{ms}$), the fastest ChR reported to date.²⁴ The f-Chrimson exhibits fast closing kinetics with ${\tau }_{\text{off}}=5.7\pm 0.5\mathrm{ms}$. At a temperature of 34°C, ${\tau }_{\text{off}}$ is $\sim 3.2\pm 0.2\mathrm{ms}$ for f-Chrimson and $1.6\pm 0.1\mathrm{ms}$ for vf-Chrimson, which in principle enables neural photostimulation in an exceptionally high-frequency range, up to $\sim 600\mathrm{Hz}$.¹⁰ Moreover, red-shifted opsins have been used for a wide range of biomedical applications, including generation of behavior responses in mechanosensory neurons; increase in firing rates in primary visual cortex of mice that result in suppressing endogenous gamma; bimodal neural excitation of Caenorhabditis elegans; dual color control using low-noise multishank optoelectrodes; retinal degeneration in mice; restoration of vision in blind mice, macaque, and human retina; and defibrillation therapy for human heart using LED arrays and also for ${\mathrm{Ca}}^{2+}$ imaging.^26–33 Recently, f-Chrimson has been used to develop optical cochlear implants to restore auditory nerve activity in deaf mice.¹⁰

It is extremely important to develop a theoretical understanding of the biophysical mechanism of the photosensitization agents and their behavior in different cells, to design and control optogenetic devices and circuits. Hence, computational modeling is fundamental to understanding the light-induced ionic transport in cell membranes, not only for cell physiology but also to develop new treatments.^34–40 Although the photoresponse of vf-Chrimson and vf-Chrimson-expressing neurons has only been recently experimentally studied,¹⁰ it is also important to undertake a theoretical analysis to understand and optimize the photodynamics of this ultrafast red-shifted opsin.

The objective of this paper is to (i) formulate an accurate model of the photocycle of vf-Chrimson; (ii) develop integrated neuron circuit models to accurately simulate firing in vf-Chrimson-expressing neurons; (iii) study the effect of various parameters that include irradiance, pulse width, pulse frequency, and expression level; (iv) compare theoretical results with recently reported experimental results; and (v) derive optimized conditions for low-power and high-frequency firing of vf-Chrimson-expressing neurons.

2. Theoretical Model

Photoisomerization of retinal moiety around ${\mathrm{C}}_{13}={\mathrm{C}}_{14}$ bond, from all-trans to cis, results in a conformational change in the microbial opsin. This initiates a photocycle with several intermediates.⁴¹ The transitions between these photointermediates are accompanied by a change in ion conductivity across the membrane, thus allowing light to excite or inhibit neuronal activity.^19,42–45

2.1. vf-Chrimson Photocycle Model

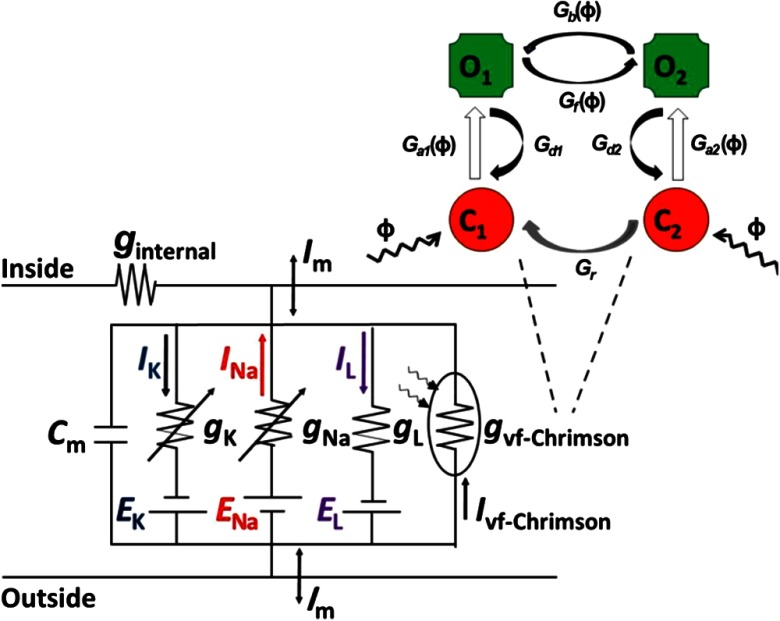
It has been experimentally shown that Chrimson’s primary reaction exhibits a biphasic decay of excited state.⁴¹ This biexponential fit of the decay kinetics of the photocurrent of vf-Chrimson under the long light stimulation suggests a four-state model for its photocycle (Fig. 1).^34,36

Fig. 1.

Equivalent circuit diagram of the vf-Chrimson-expressing neuron.

We consider that the photocycle of vf-Chrimson, a nonspecific ion channel, to have four states, similar to ChR2, i.e., two closed ($C_1$ and $C_2$) and two open conducting states ($O_1$ and $O_2$). Initially, we consider that vf-Chrimson molecule rests in the closed state $C_1$, which can be excited to an open state $O_1$ following the absorption of light. From the excited state $O_1$, vf-Chrimson molecule either decays back to $C_1$ or converts into a different open state $O_2$. In comparison to $O_1$, $O_2$ is less conductive but more stable. The transition from $O_1$ to $O_2$ can be both thermal- and light-induced. The transition between the two open states is reversible. From open state $O_2$, vf-Chrimson either decays to the closed state $C_2$ or converts back to $O_1$ (by thermal or light excitation). From $C_2$, vf-Chrimson can be photoexcited back to $O_2$ or can be slowly converted (thermally) to $C_1$.^34,38 The transition rate from $C_2$ to $C_1$ is much slower than other transitions. To describe the response of vf-Chrimson-expressing neurons to light stimuli, we present a model that combines the kinetic model of the vf-Chrimson photocycle with a single compartment, slow and also a fast-spiking neuron model, respectively (Fig. 1).

The effect of the induced conductance on the neuron is determined with Hodgkin–Huxley (H–H) type elements.⁴⁶ We demonstrate the efficacy of the model by comparing with the experimental results and use the model to investigate different stimulation profiles. We assume that all light-sensitive ion-channel currents ($I_{\mathrm{vf}\text{-}\text{Chrimson}}$) can be expressed in the classic form:

$$I_{\mathrm{vf}-\text{Chrimson}}=g_{\mathrm{vf}-\text{Chrimson}}(V-E),$$ (1)

where $V$ is the membrane voltage, $E$ is the reversal potential, and $g_{\mathrm{vf}-\text{Chrimson}}$ is the channel conductance, which is empirically expressed as $g_{\mathrm{vf}-\text{Chrimson}}=g_0(\lambda )f_{\varphi }(\varphi ,t)$, where $g_0(\lambda )$ accounts for both maximum conductance of a single vf-Chrimson molecule and protein expression level in the cell at a particular wavelength $\lambda$, and $f_{\varphi }(\varphi ,t)$ is a normalized light-dependent function.^10,38

The four-state kinetic model of vf-Chrimson photodynamics involves light-induced and thermal relaxations between open and closed states, as shown in Fig. 1. The transition from $C_1$ to $O_1$ is the fastest (1.7 ms) compared to $O_1$ to $C_1$ (2.7 ms), $O_2$ to $C_2$ (100 ms), and $C_2$ to $C_1$ (25 min), at pH 7.4.^10,41 Considering $C_1$, $O_1$, $O_2$, and $C_2$ to denote the fraction of vf-Chrimson molecules in each of the four states at any given instant of time, the transition rates for the kinetics can be described by the following set of equations:³⁸

$${\dot{C}}_1=G_{d1}{O}_1+G_r{C}_2-G_{a1}(\varphi )C_1,$$ (2)

$${\dot{O}}_1=G_{a1}(\varphi )C_1+G_b(\varphi )O_2-[G_{d1}+G_f(\varphi )]O_1,$$ (3)

$${\dot{O}}_2=G_{a2}(\varphi )C_2+G_f(\varphi )O_1-[G_{d2}+G_b(\varphi )]O_2,$$ (4)

$${\dot{C}}_2=G_{d2}{O}_2-[G_r+G_{a2}(\varphi )]C_2,$$ (5)

where $C_1+O_1+O_2+C_2=1$. $G_{a1}$, $G_{a2}$, $G_{d1}$, $G_{d2}$, $G_f$, $G_b$, and $G_r$ are the rate constants for transitions $C_1\to O_1$, $C_2\to O_2$, $O_1\to C_1$, $O_2\to C_2$, $O_1\to O_2$, $O_2\to O_1$, and $C_2\to C_1$, respectively, as shown in Fig. 1, which are determined from the reported experimental results and defined as, $G_{a1}(\varphi )=k_1{\varphi }^p/({\varphi }^p+{\varphi }_m^p)$, $G_{a2}(\varphi )=k_2{\varphi }^p/({\varphi }^p+{\varphi }_m^p)$, $G_{d1}=1/({\tau }_{\text{close}1})$, $G_{d2}=1/({\tau }_{\text{close}2})$, $G_r=1/({\tau }_r)$, $G_f(\varphi )=G_{f0}+k_f{\varphi }^q/({\varphi }^q+{\varphi }_m^q)$, and $G_b(\varphi )=G_{b0}+k_b{\varphi }^q/({\varphi }^q+{\varphi }_m^q)$. We consider $f_{\varphi }(\varphi )=O_1+\gamma O_2$, where $\gamma =g_{o2}/g_{o1}$ and $g_{o1}$ and $g_{o2}$ are the conductances of open states $O_1$ and $O_2$, respectively. The photon flux per unit area is given as $\varphi =\lambda I/hc$, where $\lambda$ is the wavelength, $I$ is the irradiance, $h$ is the Planck’s constant, and $c$ is the speed of light in vacuum. The other model parameters (${\varphi }_m$, $p$, $q$, $k_1$, $k_2$, $k_b$, and $k_f$) have been obtained by fitting reported experimental results, as shown in Table 1.^10,38,41

Table 1.

Opsin model parameters.^10,38,41

Parameters	Numerical values
$G_{d1}$ (vf-Chrimson) (${\mathrm{ms}}^{-1}$)	0.37
$G_{d1}$ (f-Chrimson) (${\mathrm{ms}}^{-1}$)	0.175
$G_{d1}$ (Chrimson) (${\mathrm{ms}}^{-1}$)	0.041
$G_{d2}$ (${\mathrm{ms}}^{-1}$)	0.01
$G_r$ (${\mathrm{ms}}^{-1}$)	$6.67\times {10}^{-7}$
$g_0$ (nS)	24.96
${\varphi }_m$ ($\mathrm{ph}.{\mathrm{mm}}^{-2}{\sec }^{-1}$)	$1.5\times {10}^{16}$
$k_1$ (${\mathrm{ms}}^{-1}$)	3
$k_2$ (${\mathrm{ms}}^{-1}$)	0.2
$G_{f0}$ (${\mathrm{ms}}^{-1}$)	0.02
$G_{b0}$ (${\mathrm{ms}}^{-1}$)	$3.2\times {10}^{-3}$
$k_f$ (${\mathrm{ms}}^{-1}$)	0.01
$k_b$ (${\mathrm{ms}}^{-1}$)	0.01
$\gamma$	0.05
$p$	1
$q$	1
$V_{\text{rest}}$ (mV)	$-60$
$\lambda$ (nm)	594
$E$ (mV)	0

2.2. vf-Chrimson-Integrated Neuron Circuit Model

The vf-Chrimson-mediated spiking has recently been experimentally reported for two cases: (i) rat hippocampal neurons in the low-frequency range and (ii) neocortical ${\mathrm{PV}}^{+}$ interneurons in the high-frequency range.¹⁰ Even though the complexity of computational models has increased, which reflects the new insights into the diversity of ion channels and their characteristics, the H–H model still captures the dynamic and highly nonlinear process of cellular excitation. Hence, to retain simplicity, the H–H model has been used for low frequency analysis of vf-Chrimson-expressing hippocampal neurons.^10,46 In the case of interneurons, the Wang–Buzsaki (W–B) model has been shown to be applicable for neocortical fast-spiking interneurons and has also been used to simulate optogenetically induced spiking in ChR2/ChETA-expressing interneurons.^47,36 Hence, neural response to optostimulation has been evaluated using two single-compartment neuron models, namely (i) H–H model to mimic the low-frequency hippocampal neuronal spiking, and (ii) W–B model to mimic the fast-spiking response in neocortical ${\mathrm{PV}}^{+}$ interneurons, to provide a theoretical understanding of recently reported experimental results.¹⁰ With fast kinetics of inactivation ($h$) of $I_{Na}$, the activation ($n$) of $I_{\mathrm{K}}$, and relatively high threshold of $I_{\mathrm{K}}$, the interneuron model displays a large range of repetitive spiking frequencies in response to a constant injected current in the W–B neuron model. Neuron models, with the addition of light-dependent vf-Chrimson ion-channel current ($I_{\mathrm{vf}\text{-}\text{Chrimson}}$), can be expressed as a system of differential equations of the form:

$$C_m\dot{V}=I_{\mathrm{DC}}-I_g-I_{\mathrm{vf}-\text{Chrimson}},$$ (6)

where $C_m$ is the membrane capacitance and $I_{\mathrm{DC}}$ is the constant DC bias current that controls the excitability of the neuron. Here, $I_g$ is the sum of the membrane ion-channel currents, $I_{Na}=g_{Na}{m}^{3}h(V-E_{Na})$, $I_K=g_K{n}^4(V-E_K)$, and leakage current $I_L=g_L(V-E_L)$, where, $g_{Na}$, $g_K$, and $g_L$ are the respective conductances. Here, $h$ is the inactivation variable and $n$ and $m$ are the activation variables that obey the first-order kinetics, i.e., $\dot{m}=\phi [{\alpha }_m(1-m)-{\beta }_{m}m]$, $\dot{h}=\phi [{\alpha }_h(1-h)-{\beta }_{h}h]$, and $\dot{n}=\phi [{\alpha }_n(1-n)-{\beta }_{n}n]$, respectively. In the W–B model, ${\mathrm{Na}}^{+}$ current is defined as $I_{Na}=g_{Na}{m}_{\infty }^{3}h(V-E_{Na})$, where $m_{\infty }={\alpha }_m/({\alpha }_m+{\beta }_m)$.⁴⁷ The functional forms of membrane voltage-dependent rate functions are given in Table 2,^36,46,47 and the numerical values of model parameters are given in Table 3.^36,46,47 All simulations have been performed using fourth-order Runge–Kutta method with a time step of 0.01 ms (otherwise mentioned) implemented in MATLAB R2013b by suitably modifying the codes available at ModelDB.

Table 2.

Rate functions.^36,46,47

	W–B model	H–H model
${\alpha }_m$	$\frac{-0.1(V+35)}{\exp [-0.1(V+35)]-1}$	$\frac{-0.1(V+35)}{\exp [-0.1(V+35)]-1}$
${\beta }_m$	$4\exp \left[\frac{-(V+60)}{18}\right]$	$4\exp \left[\frac{-(V+60)}{18}\right]$
${\alpha }_h$	$0.07\exp \left[\frac{-(V+58)}{20}\right]$	$0.07\exp \left[\frac{-(V+60)}{20}\right]$
${\beta }_h$	$\frac{1}{\exp [-0.1(V+28)]+1}$	$\frac{1}{\exp [-0.1(V+30)]+1}$
${\alpha }_n$	$\frac{-0.01(V+34)}{\exp [-0.1(V+34)]-1}$	$\frac{-0.01(V+50)}{\exp [-0.1(V+50)]-1}$
${\beta }_n$	$0.125\exp \left[\frac{-(V+44)}{80}\right]$	$0.125\exp \left[\frac{-(V+60)}{80}\right]$

Table 3.

Neuron model parameters.^36,46,47

Parameters	W–B	H–H
$E_{Na}$ (mV)	55	55
$E_K$ (mV)	$-90$	$-72.14$
$E_L$ (mV)	$-65$	$-70$
$g_{Na}$ ($\mathrm{mS}{\mathrm{cm}}^{-2}$)	35	120
$g_K$ ($\mathrm{mS}{\mathrm{cm}}^{-2}$)	9	36
$g_L$ ($\mathrm{mS}{\mathrm{cm}}^{-2}$)	0.1	0.3
$C_m$ ($\mu \mathrm{F}{\mathrm{cm}}^{-2}$)	1	1
$\phi$	7	1
$I_{\mathrm{DC}}$ ($\mu \mathrm{A}{\mathrm{cm}}^{-2}$)	$-0.51$	0
$V_{\text{rest}}$ (mV)	$-70$	$-70$

3. Results

3.1. vf-Chrimson Photodynamics

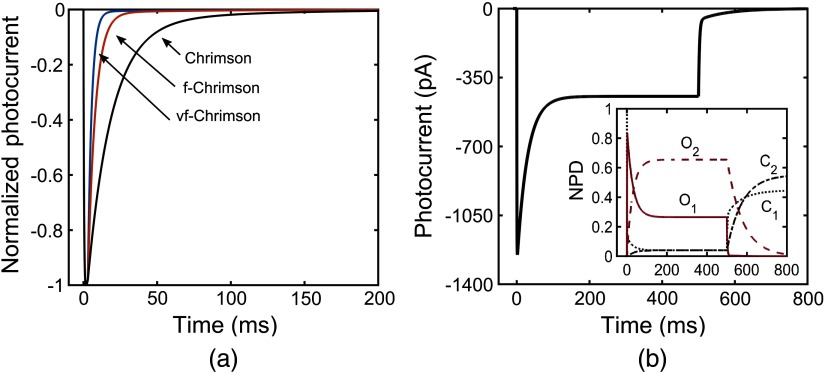
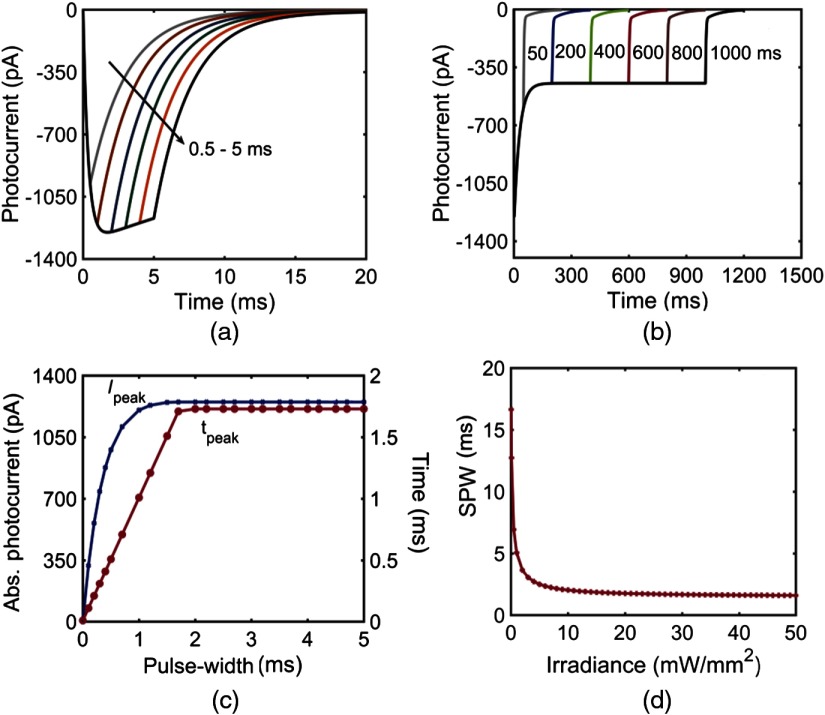
The photoresponse of vf-Chrimson has been studied through numerical simulations using Eqs. (1)–(5), considering the reported experimental parameters in Table 1. Variation of photocurrent with time at different pulse-width excitations, at the same irradiance, is shown in Fig. 2. As shown experimentally, comparison of normalized photocurrents of Chrimson and its mutants shows that vf-Chrimson exhibits shortest photocurrent-off time [Fig. 2(a)]. In general, under long light stimulation, the photocurrent reaches a peak, which decays to a steady-state plateau. The variation of photocurrent of vf-Chrimson with time, under prolonged light stimulation of 500 ms at $I=23\mathrm{mW}/{\mathrm{mm}}^2$ and $\lambda =594\mathrm{nm}$, is shown in Fig. 2(b). Theoretical values of $I_{\text{peak}}$ (1250 pA) and $I_{\text{plateau}}$ (446 pA) match with the reported experimental values of 1250 and 446 pA, respectively.¹⁰ At resting potential of $-60\mathrm{mV}$, the photoexcitation of vf-Chrimson channel allows cations to flow into the cell interior and the negative current is recorded, a process that gets reversed when the potential polarity is reversed. The variation is more clearly understood on studying the population dynamics, as shown in the inset of Fig. 2(b). Absorption of red-shifted photons (594 nm) triggers the vf-Chrimson photocycle. The molecules switch from the closed state ($C_1$) to the first open state ($O_1$), which subsequently decay to $O_2$ state, which is more stable due to its longer lifetime.

Fig. 2.

Optostimulation of photocurrent in vf-Chrimson at different pulse widths and $I=23\mathrm{mW}/{\mathrm{mm}}^2$. (a) Comparison with Chrimson and f-Chrimson at $\lambda =594\mathrm{nm}$ and 3-ms pulse width; (b) at 500-ms pulse width. Inset: corresponding variation of normalized population density with time.

The vf-Chrimson channel opens rapidly after absorption of a photon to generate a large permeability for monovalent and divalent cations.¹⁰ As the turn-on and turn-off times of vf-Chrimson are fast and flux-dependent, the population of states $O_1$ and $O_2$ attain their maximum value during the excitation pulse and the molecules relax to the $C_2$ state, resulting in an increase in its population, which is retained for a longer period of time due to its long lifetime ($\sim 25\min$), before returning back to the initial $C_1$ state.^10,41

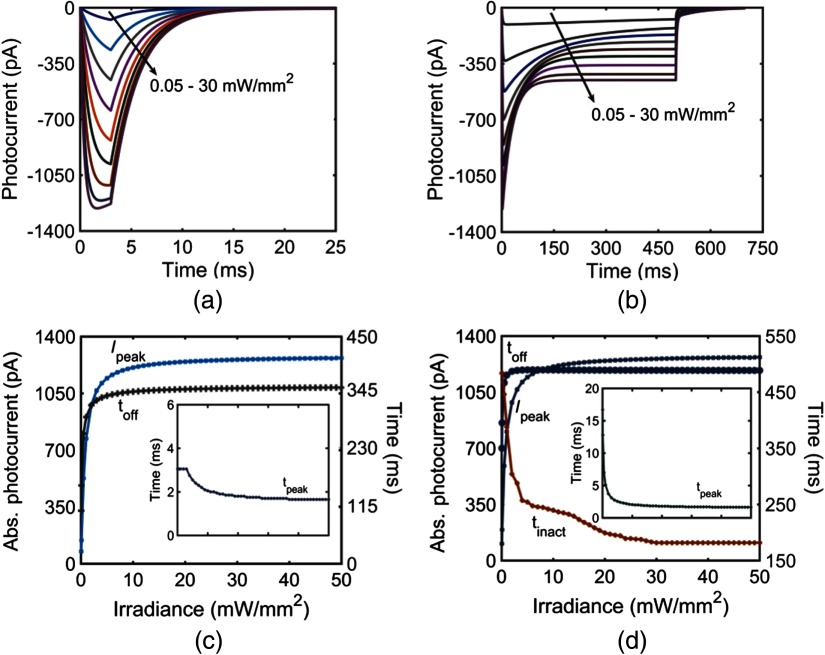
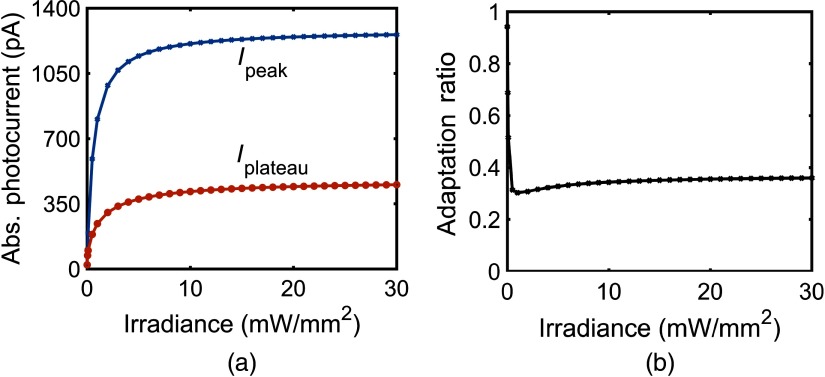
The effect of irradiance on the photocurrent of vf-Chrimson at 594 nm, at pulse widths of 3 and 500 ms is shown in Figs. 3(a) and 3(b), respectively. Here, $I_{\text{peak}}$ increases with an increase in irradiance, as more molecules populate the open $O_1$ and $O_2$ states. For a pulse width of 3 ms, a kink appears above $4\mathrm{mW}/{\mathrm{mm}}^2$, when the time to peak ($t_{\text{peak}}$), which is flux-dependent, is less than the stimulating pulse width. Also, $t_{\text{off}}$, i.e., time taken by the photocurrent to decay from the point where light is turned off to the time it reaches 0.1 pA, increases rapidly with an increase in irradiance of up to $3\mathrm{mW}/{\mathrm{mm}}^2$ and saturates for higher irradiances, as more molecules get transferred to the $O_2$ state, which has a longer turn-off time [Fig. 3(c)]. Here, $t_{\text{peak}}$ remains constant at 3.05 ms for up to $4\mathrm{mW}/{\mathrm{mm}}^2$ and decreases with an increase in irradiance, as $G_{a1}$ is proportional to irradiance. For a longer 500 ms pulse stimulation, $t_{\text{off}}$ increases rapidly below $2\mathrm{mW}/{\mathrm{mm}}^2$ and saturates at higher irradiances [Fig. 3(d)]. The time taken from peak to plateau photocurrent, $t_{\text{inact}}$, decreases with increase in irradiance. In the case of longer pulse irradiance, $t_{\text{peak}}$ does not remain constant even at very low irradiances. It decreases monotonically with an increase in irradiance [inset Fig. 3(d)]. The absolute values of $I_{\text{peak}}$, $I_{\text{plateau}}$, and the adaptation ratio ($I_{\text{plateau}}/I_{\text{peak}}$) depend on the light irradiance and the total number of vf-Chrimson molecules that are illuminated, and their variation is shown in Figs. 4(a) and 4(b). The adaptation ratio decreases from 1 to a minimum value of 0.3 at $1\mathrm{mW}/{\mathrm{mm}}^2$ and saturates to a higher value of 0.35 at higher irradiances ($>10\mathrm{mW}/{\mathrm{mm}}^2$).

Fig. 3.

Effect of irradiance on the photocurrent of vf-Chrimson. (a) At irradiances 0.05, 0.2, 0.4, 0.7, 1.2, 2, 4, 10, and $30\mathrm{mW}/{\mathrm{mm}}^2$, at $\lambda =594\mathrm{nm}$, and 3-ms pulse width; (b) corresponding variation at 500-ms pulse width. (c) Variation in $I_{\text{peak}}$ and $t_{\text{off}}$ with irradiance under 3-ms pulse stimuli. Inset: corresponding $t_{\text{peak}}$ variation with irradiance (on the same scale). (d) Variation of $I_{\text{peak}}$, $t_{\text{off}}$, and $t_{\text{inact}}$ with irradiance at 500-ms pulse stimuli. Inset: corresponding variation of $t_{\text{peak}}$ with irradiance (on the same scale).

Fig. 4.

Effect of irradiance on $I_{\text{peak}}$ and $I_{\text{plateau}}$ of the vf-Chrimson; (a) 500-ms pulse width and (b) corresponding variation of adaptation ratio at $\lambda =594\mathrm{nm}$.

The variation of photocurrent at shorter (0.5 to 5 ms) and longer pulse widths (50 to 1000 ms) is shown in Figs. 5(a) and 5(b), respectively. Here, $I_{\text{plateau}}$ saturates at a pulse width of $\sim 200\mathrm{ms}$ to a value of $-446\mathrm{pA}$, at $23\mathrm{mW}/{\mathrm{mm}}^2$, under prolonged stimulation [Fig. 5(b)]. Under shorter pulse stimulation, $I_{\text{peak}}$ and $t_{\text{peak}}$ increase with an increase in the pulse width and saturate at a pulse width of 1.7 ms [Fig. 5(c)]. Theoretical simulations show that there is a minimum pulse width for any irradiance above which $I_{\text{peak}}$ saturates. It is found that this saturating pulse width (SPW) decreases monotonically and saturates around 2 ms at higher irradiances [Fig. 5(d)].

Fig. 5.

Effect of pulse width on the photocurrent of vf-Chrimson. Variation of photocurrent with time at $I=23\mathrm{mW}/{\mathrm{mm}}^2$, $\lambda =594\mathrm{nm}$, and at (a) shorter pulse widths (0.5, 0.9, 2, 3, 4, and 5 ms). (b) Variation of photocurrent at longer pulse widths (50 to 1000 ms). (c) Corresponding variation of $t_{\text{peak}}$ and $I_{\text{peak}}$ with pulse width. (d) Variation of SPW with irradiance.

A comparison of photocurrent under multiple pulse excitations at varying irradiances and at different pulse widths is shown in Fig. 6. As the opsin is unable to complete its photocycle before the arrival of the next light pulse, the peak photocurrent gradually falls to a lower value for subsequent stimulations. The modulation in photocurrent depends on the irradiance and the pulse width of incident optical excitation. Theoretical simulations show that the ratio $I_{\text{peak}10}/I_{\text{peak}1}$ attains a minimum value of 0.606 at $I=20\mathrm{mW}/{\mathrm{mm}}^2$ and pulse width of 3 ms. However, at lower irradiances and pulse widths, the ratio is $\sim 1$, which is important to achieve higher spiking fidelity.

Fig. 6.

Effect of multiple pulse optostimulation on the vf-Chrimson photocurrent. At indicated irradiances and pulse widths at a photostimulation protocol of 10 stimuli, at 10 Hz, and at $\lambda =594\mathrm{nm}$.

3.2. vf-Chrimson-Expressing Hippocampal Neurons: H–H Model

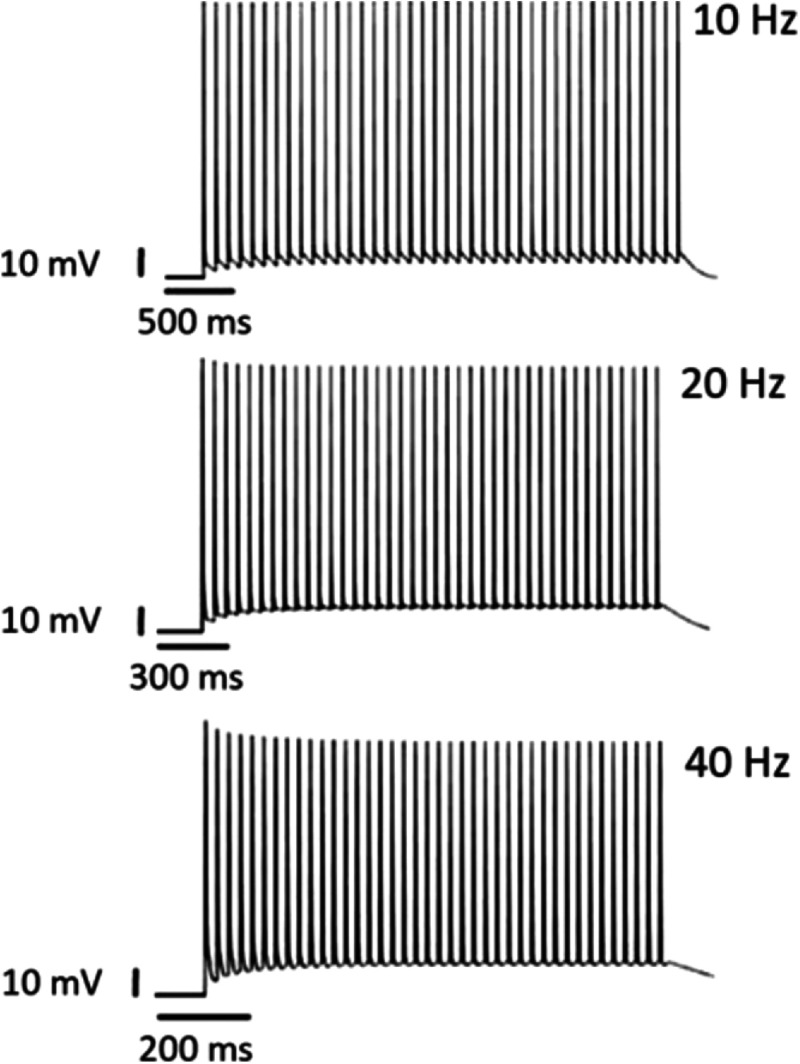
Recent experiments have demonstrated that Chrimson is unable to maintain spiking fidelity in rat hippocampal neurons even up to 20 Hz, although vf-Chrimson-expressed rat hippocampal neurons drive 100% spiking up to 40 Hz.¹⁰ The corresponding theoretical simulations are shown in Fig. 7. At 10, 20, and 40 Hz, the theoretical values of plateau potential are 6.28, 10.28, and 11.94 mV compared to the experimental values of 5.48, 8.06, and 11.61 mV, respectively. Theoretical results are in good agreement with reported experimental results.

Fig. 7.

Light-induced spiking in the vf-Chrimson-expressing neurons. At indicated frequencies and optostimulation protocol of 40 stimuli each of 3-ms pulse width, at $I=23\mathrm{mW}/{\mathrm{mm}}^2$, at $\lambda =594\mathrm{nm}$, and $g_0=10\mathrm{mS}/{\mathrm{cm}}^2$.

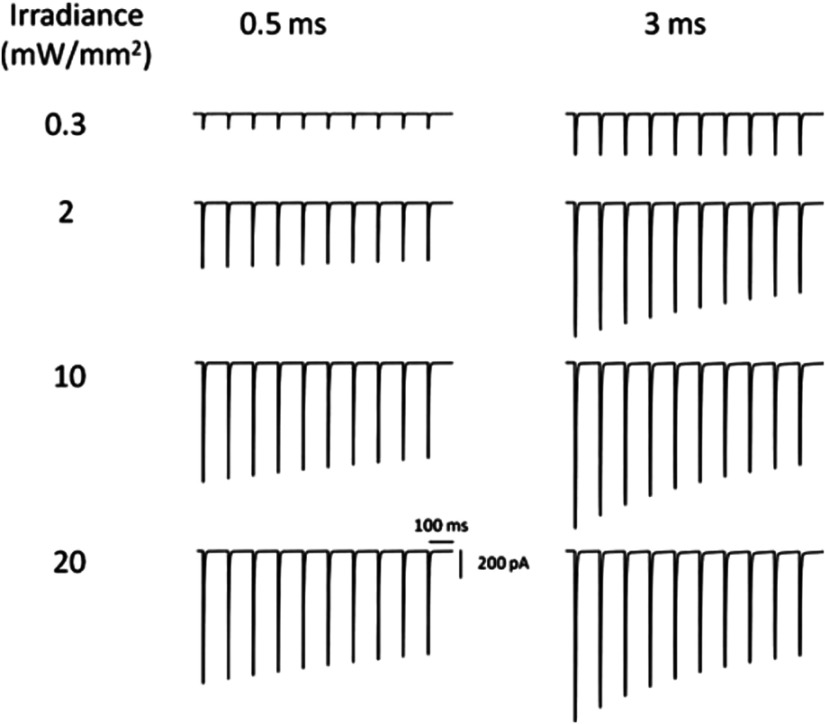
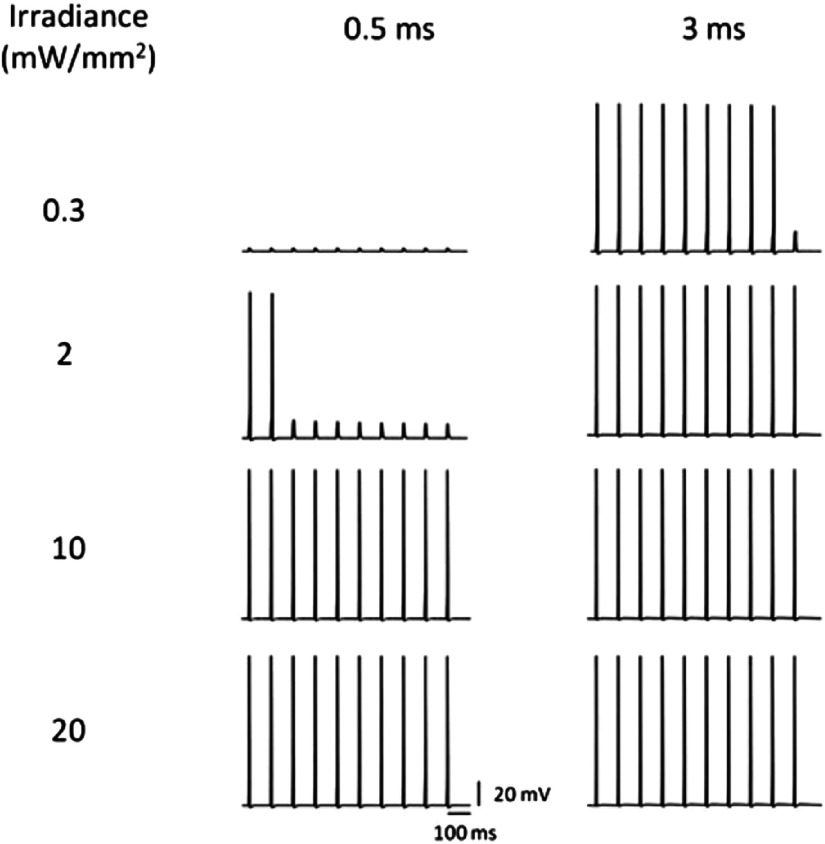
The effect of irradiance and pulse width on the vf-Chrimson-mediated spiking in hippocampal neurons, as shown in Fig. 8, indicates that there is a threshold photocurrent to elicit action potential, achieved either by an increase in irradiance or by stimulation time. Increase in stimulation frequency at lower irradiances results in a spike failure, which can be avoided using higher irradiances (Fig. 9).

Fig. 8.

Comparison of light-induced spiking fidelity in the vf-Chrimson-expressing neurons. At different irradiances and two pulse widths, under optostimulation protocol of 10 stimuli, at 10 Hz, at $\lambda =594\mathrm{nm}$, and $g_0=0.5\mathrm{mS}/{\mathrm{cm}}^2$.

Fig. 9.

Spiking fidelity in the vf-Chrimson-expressing neurons. At different irradiances and frequencies at 10 stimuli each of 3-ms pulse width and $g_0=0.5\mathrm{mS}/{\mathrm{cm}}^2$.

3.3. vf-Chrimson-Expressing Neocortical ${PV}^{+}$ Interneurons: W–B Model

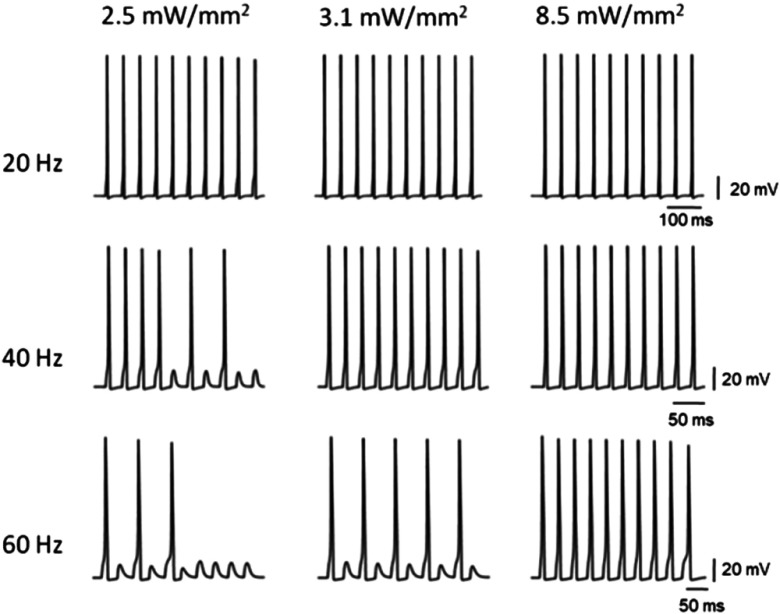
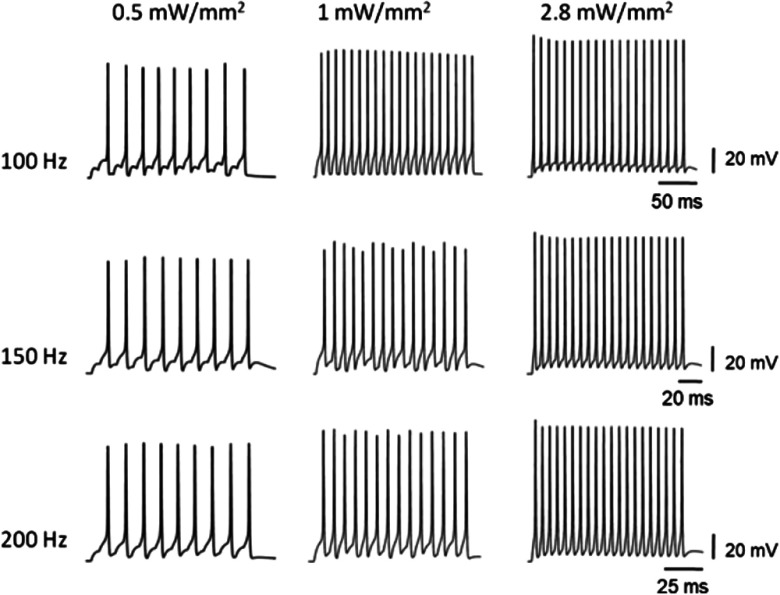
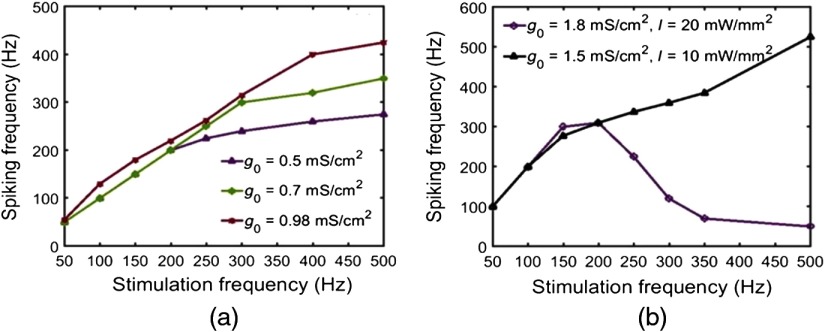
Recent experimental study has shown that vf-Chrimson drives neocortical ${\mathrm{PV}}^{+}$ interneurons with 100% spike probability beyond their intrinsic frequency limit of $301\pm 33\mathrm{Hz}$ but below 400 Hz.¹⁰ Theoretical simulations based on reported experimental photostimulation protocol in which the irradiance and expression levels are different at different frequencies, are shown in Fig. 10(a).¹⁰ The variation of spiking frequency with the stimulation frequency exactly follows the reported experimental variation as shown by Mager et al.¹⁰ in Fig. 3(c). It is important to analyze how far spiking fidelity is maintained with increasing frequency, at a constant irradiance and expression level. Theoretical simulations show that at an optimized value of $I=2.2\mathrm{mW}/{\mathrm{mm}}^2$, $\text{pulse width}=0.5\mathrm{ms}$, and $g_0=0.5\mathrm{mS}/{\mathrm{cm}}^2$, vf-Chrimson is able to maintain 100% spiking fidelity up to 250 Hz [Fig. 10(b)]. At $I=1.2$, 1.4, and $1.7\mathrm{mW}/{\mathrm{mm}}^2$, the frequency limits are 100, 150, 200 Hz, respectively. At irradiances $>2.2\mathrm{mW}/{\mathrm{mm}}^2$, although spiking occurs above 250 Hz, spiking fidelity degrades at lower frequencies.

Fig. 10.

Light-induced spiking in the vf-Chrimson-expressing interneurons at optostimulation protocol of 20 stimuli, each of 0.5 ms pulse widths, at $\lambda =565\mathrm{nm}$, (a) at $I=2.6$, 2.6. 4.9, 4.9, 4.9, 4.9, 4.9, and $8\mathrm{mW}/{\mathrm{mm}}^2$ and $g_0=0.5$, 0.4, 0.34, 0.35, 0.41, 0.42, 0.55, and $0.54\mathrm{mS}/{\mathrm{cm}}^2$, respectively; (b) at $I=2.2\mathrm{mW}/{\mathrm{mm}}^2$ and $g_0=0.5\mathrm{mS}/{\mathrm{cm}}^2$, at indicated frequencies. Upper and lower frequency labels indicate output spiking frequency and input stimulation frequency, respectively.

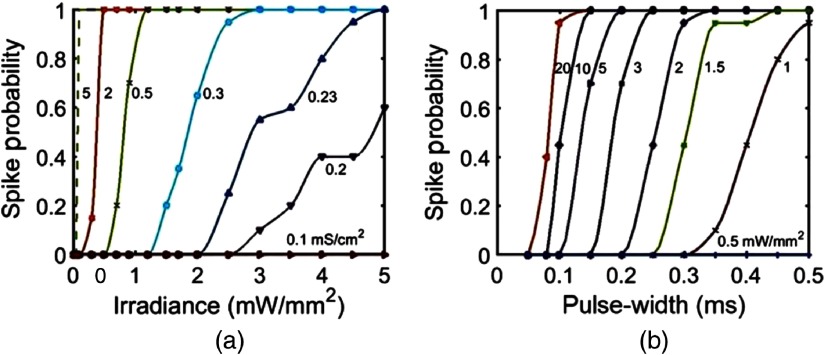
Spiking failure at higher frequencies has also been observed experimentally.¹⁰ An increase in stimulation frequency at lower irradiances results in a spike failure due to the insufficient recovery of photocurrent, which can be overcome by using higher irradiances (Fig. 11). The variation of spike probability with irradiance and pulse width is shown in Fig. 12. Theoretical simulation shows that minimum irradiance of $0.1\mathrm{mW}/{\mathrm{mm}}^2$ is required to evoke single-action potential. The minimal irradiance that is required to achieve 100% spiking (${\mathrm{MIT}}_{100}$) varies from 0.1 to $5\mathrm{mW}/{\mathrm{mm}}^2$ for corresponding expression levels ranging from 5 to $0.23\mathrm{mS}/{\mathrm{cm}}^2$ at 0.5 ms pulse width [Fig. 12(a)]. It is also found that a minimum pulse width of $50\mu \mathrm{s}$ is required to evoke single-action potential. The minimum pulse width required to achieve 100% spiking varies from 0.15 to 0.5 ms at corresponding variation in irradiance from 20 to $1.5\mathrm{mW}/{\mathrm{mm}}^2$ at $g_0=0.5\mathrm{mS}/{\mathrm{cm}}^2$ [Fig. 12(b)].

Fig. 11.

Spiking fidelity in the vf-Chrimson-expressing interneurons. At indicated irradiances and frequencies, at 20 stimuli each of pulse width 0.5 ms and $g_0=0.6\mathrm{mS}/{\mathrm{cm}}^2$.

Fig. 12.

Variation of spike probability in the vf-Chrimson-expressing interneurons under stimulation protocol of $10\mathrm{Hz}$ and 20 stimuli. (a) Irradiance (0 to $5\mathrm{mW}/{\mathrm{mm}}^2$) at different expression levels (0.1 to $5\mathrm{mS}/{\mathrm{cm}}^2$) and pulse width of 0.5 ms. (b) Pulse width (0 to 0.5 ms) at different irradiances (0.5 to $20\mathrm{mW}/{\mathrm{mm}}^2$) and $g_0=0.5\mathrm{mS}/{\mathrm{cm}}^2$.

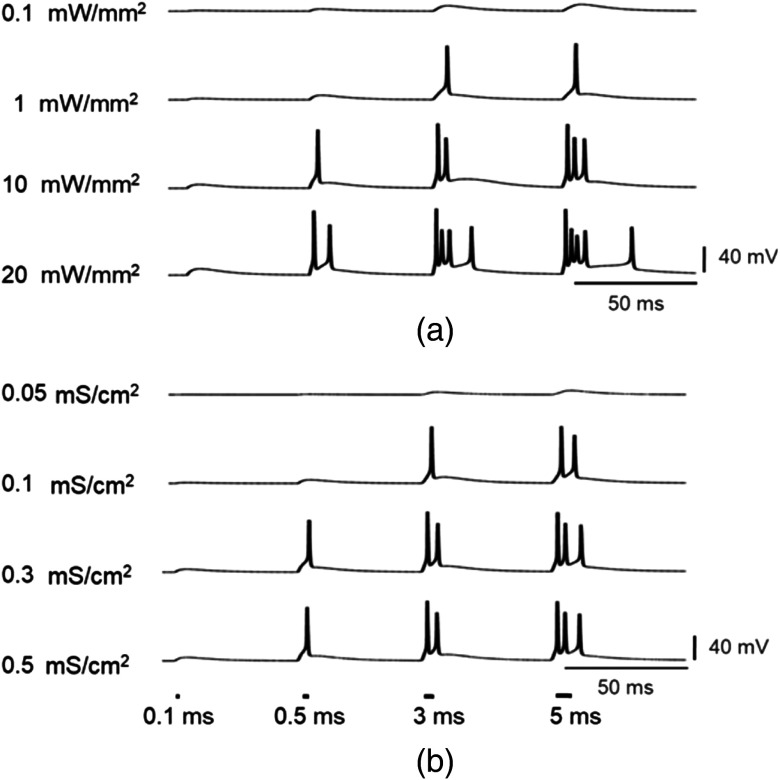
The effect of variation in irradiance and expression level, along with increasing pulse width on spiking fidelity, is shown in Fig. 13. Theoretical simulations show that extra spikes appear in the neural response in some cases and their height, number, regularity, and plateau potential are sensitive to these factors. The increase in pulse width and irradiance leads to an increase in extra spikes [Fig. 13(a)]. The increase in expression level also causes increase in extra spikes at higher pulse widths [Fig. 13(b)]. At higher irradiance, there is a delay after which the final spike appears, due to longer $t_{\text{off}}$, which is less prominent in case of an increase in the expression level considered. The plateau potential also increases with an increase in conductance, pulse width, and irradiance (Fig. 13). Elimination of extra spikes and delay is needed for ultrafast operation, for which it is better to optimize either the expression level or the irradiance. At $I=10\mathrm{mW}/{\mathrm{mm}}^2$, pulse width of 0.5 ms, and $g_0=0.25\mathrm{mS}/{\mathrm{cm}}^2$, there is an elimination of extra spikes and a reduction of plateau potential, which can lead to higher temporal precision [Fig. 13(a)].

Fig. 13.

Effect of irradiance, pulse width, and expression level on the spiking fidelity in vf-Chrimson-expressing interneurons. At $\lambda =565\mathrm{nm}$ and (a) irradiances when $g_0=0.25\mathrm{mS}/{\mathrm{cm}}^2$ and (b) expression level at $I=10\mathrm{mW}/{\mathrm{mm}}^2$.

The effect of stimulation frequency on the spiking frequency of vf-Chrimson-expressing interneurons has been experimentally shown to consist of both singlet and doublets in action potential.¹⁰ Doublets occur at lower frequencies in the spiking pattern with some neurons, which compromise the temporal fidelity of optogenetic control. It has been suggested that this caveat can be minimized by optimizing the expression time and the stimulation light.¹⁰ The occurrence of action potential singlets and doublets at different frequencies has been successfully simulated by the proposed vf-Chrimson-integrated W–B model (Fig 14). Theoretical analysis shows that, other than stimulation time and irradiance, expression level in the cell membrane plays a key role in minimizing the occurrence of extra spikes (Fig. 14).

Fig. 14.

Effect of the stimulation frequency on spiking fidelity in vf-Chrimson-expressing interneurons. (a) Variation of spiking frequency (singlets) of neurons at $I=10\mathrm{mW}/{\mathrm{mm}}^2$, 0.5 ms pulse width, and $G_{d1}=0.625{\mathrm{ms}}^{-1}$. (b) Variation of multispiking frequency (doublets) of neurons at different combinations of expression level and irradiance at 0.5-ms pulse width.

As shown experimentally, the singlet spiking frequency gets plateaued off after a certain stimulation frequency, which varies from cell to cell.¹⁰ The proposed model is also capable of simulating the trend with varying expression level [Fig. 14(a)]. The plateau occurs at higher frequencies for higher $g_0$ values. Variation of doublet spiking with stimulation frequency for two different optimal sets of irradiance and expression level is shown in Fig. 14(b). The doublet spiking frequency is nearly constant around stimulation frequency of 150 to 200 Hz, at $I=20\mathrm{mW}/{\mathrm{mm}}^2$. At $g_0=1.8\mathrm{mS}/{\mathrm{cm}}^2$ and $I=20\mathrm{mW}/{\mathrm{mm}}^2$, the doublet spiking shows a maximum of $\sim 300\mathrm{Hz}$, in the stimulation frequency range of 150 to 200 Hz, after which it decays to below 100 Hz for higher stimulation frequencies, whereas at $g_0=1.5\mathrm{mS}/{\mathrm{cm}}^2$ and $I=10\mathrm{mW}/{\mathrm{mm}}^2$, doublet spiking frequency increases linearly with increase in stimulation frequency [Fig. 14(b)].

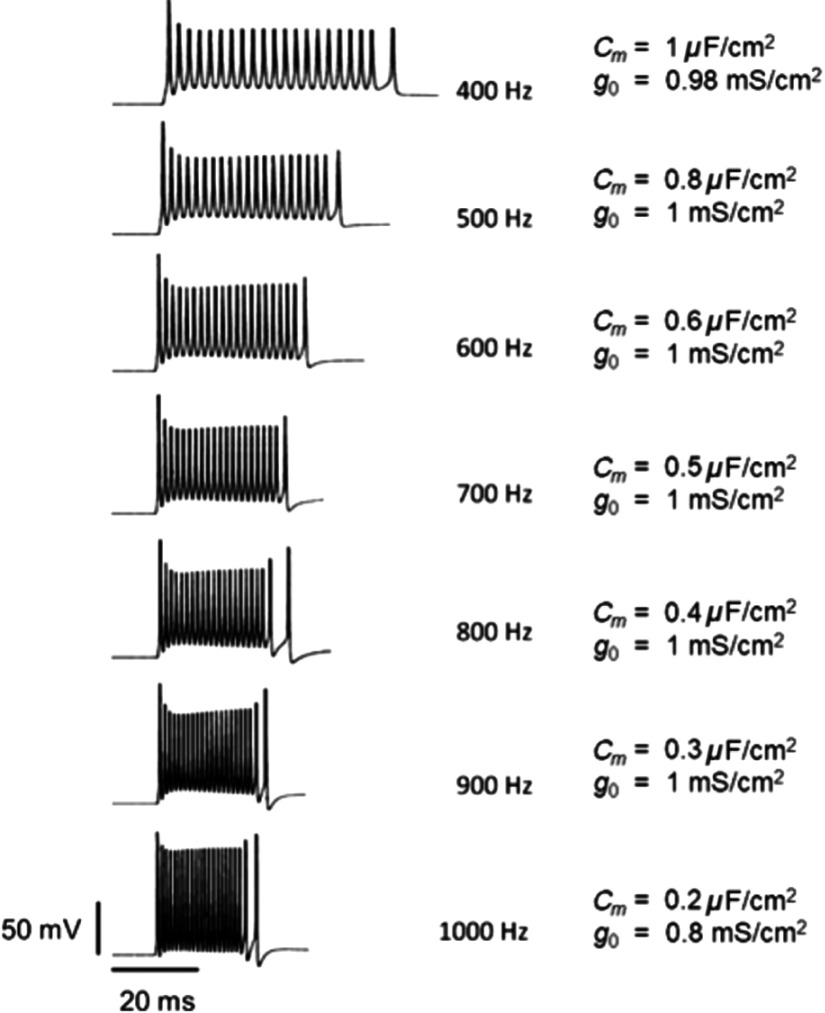
A major challenge is to achieve higher frequency optogenetic control on neuronal signaling. The theoretical study undertaken reveals that optimization of $C_m$ and $g_0$ can lead to much higher-frequency operation with vf-Chrimson. The maximum neural firing frequency at different values of $C_m$ and $g_0$ is shown in Fig. 15. Neuronal firing at as high as 1 kHz can be achieved with $C_m=0.2\mu \mathrm{F}/{\mathrm{cm}}^2$ and $g_0=0.8\mathrm{mS}/{\mathrm{cm}}^2$.

Fig. 15.

Maximum vf-Chrimson-expressing interneuron firing frequency with 100% spiking probability, at $I=10\mathrm{mW}/{\mathrm{mm}}^2$, $G_{d1}=0.625{\mathrm{ms}}^{-1}$ and 0.5-ms pulse width, for optimal combinations of $C_m$ and $g_0$ as indicated.

4. Discussion

The proposed theoretical models accurately simulate reported experimental results and provide important insights. The analysis of the photodynamics of vf-Chrimson reveals that there is a minimal pulse width for which the photocurrent is maximum at a particular irradiance. It decreases rapidly and saturates around 2 ms at higher irradiances (10 to $50\mathrm{mW}/{\mathrm{mm}}^2$) [Fig. 5(d)]. For longer pulse stimulations, the adaptation ratio is minimum at a particular irradiance [Fig. 4(b)], which would result in better spiking fidelity. The ratio $I_{\text{peak}10}/I_{\text{peak}1}$ is $\sim 1$ at lower irradiances and small pulse widths. The vf-Chrimson has recently been discovered, and the experimental data reported in the literature, at present, are inadequate to formulate a six-state model, which would increase the accuracy and the complexity, although the four-state model formulated is capable of accurately explaining the experimental results. Further experiments at short pulse widths are required to be conducted that would reveal the effects of any intermediate state between $C_1$ and $O_1$, if such a state exists in the vf-Chrimson photocycle.

Along with faster on/off kinetics, high-frequency spiking in vf-Chrimson-expressing neurons requires higher irradiance and optimization of pulse width and expression level for high spiking fidelity. Very high-frequency optogenetic firing requires optimization of $C_m$ and expression level. Simulations show that 100% spiking fidelity can be achieved at as high as 1 kHz at relatively low $C_m$ values (Fig. 15). It is well known that the membrane capacitance of a neuron influences the synaptic efficacy and speed of electrical signal propagation. Here, $C_m$ can be changed through various processes that include nonexocytotic processes that can produce changes ranging from 0 to 30 pF, reduction of the surface area of the cell, perfusion of buffered intracellular ${\mathrm{Ca}}^{2+}$ concentrations, variation of myelin and particle uptake, and exposure of cells.^37,48 However, the ability to alter $C_m$ (and therefore achieve higher firing frequencies) is possible in limited experiment types, and not at all possible in an in vivo (or clinical) setting. This reduces the utility of vf-Chrimson in vivo or clinical settings when trying to achieve extremely high firing frequency control of neurons.

In comparison to previously reported fast variants, such as ChETA and Chronos, red-shifted absorption of vf-Chrimson reduces the risk of thermal damage while providing better depth penetration due to negligible heating caused by red light.^19,20 The present theoretical optimization shows that spiking in vf-Chrimson-expressing interneurons can be evoked at low irradiances ($0.1\mathrm{mW}/{\mathrm{mm}}^2$) or pulse widths ($50\mu \mathrm{s}$), thereby minimizing and avoiding unwanted heating effects (Fig. 12). Mager et al.¹⁰ have experimentally shown the dependence of spike probability on light pulse intensity at $2.6\mathrm{mW}/{\mathrm{mm}}^2$ with 0.5 ms pulse for neocortical ${\mathrm{PV}}^{+}$ interneurons and 0.09 to $3.18\mathrm{mW}/{\mathrm{mm}}^2$ for hippocampal cells [Fig. 2(g) in Ref. 10]. The likely cause of the large variability of the dependence of the spike probability on the light intensity observed experimentally has been attributed to the expression differences and the variability of membrane resistance, capacitance, and spiking threshold of the investigated hippocampal neurons.¹⁰

Recently, Chrimson and its variants have been used for dual-color optogenetic control of neural populations.^24,49 The vf-Chrimson would be potentially useful for faster control as well as for lower cross talk. Various red-shifted excitatory opsins have also been used with blue light-sensitive genetically encoded ${\mathrm{Ca}}^{2+}$ indicator fluorescence readouts to simultaneously manipulate and record from neurons in the same animal.^33,50 Using vf-Chrimson in such applications can reduce unwanted cross stimulation and enable higher-frequency all-optical experiments. The vf-Chrimson opens up promising new possibilities to provide high-fidelity, high-frequency operation with high-spatiotemporal resolution in a wide range of biomedical applications in which red-shifted opsins have been used.^26–33 The proposed model of vf-Chrimson can also be integrated with circuit models of other types of cells to check their response in a quick way.

High frequency, temporally precise, and minimally invasive stimulation of selectively defined neural population in the brain is a major goal for existing neuromodulation interventions.^2,51 The present study is very important for various phenomena that are associated with high-frequency neural network events, such as temporal spike coding, neural plasticity, recovery of behavior, pathology, spike-timing-dependent plasticity associated with learning and memory, activity restoration of auditory nerve activity and in cortical areas, Parkinson’s disease, and psychiatric illness.^52–55 For instance, optogenetic stimulation of spiral ganglion neurons (SGNs) in the ear provides a prospective alternative to the electrical stimulation used in cochlear implants. Recently, efficient virus-mediated expression of targeting-optimized Chronos-ES/TS in the mouse cochlea has been shown to elicit optical auditory brainstem responses with minimal latencies of 1 ms, thresholds of $5\mu \mathrm{J}$, $100\mu \mathrm{s}$ per pulse, and sizable amplitudes even at 1 kHz.⁵⁶ Higher temporal fidelity of optogenetic SGN stimulation might be achieved with vf-Chrimson as well. Recently, near-infrared (NIR) deep-brain stimulation has also been demonstrated using molecularly tailored ${\mathrm{NaYF}}_4:\mathrm{Yb}/\mathrm{Tm}$ upconversion nanoparticle (UCNP)-mediated optogenetics, thus opening up exciting prospects for less-invasive manipulation of optical neuronal activity with the potential for remote therapy.⁵⁷ In another recent study, ${\mathrm{Yb}}^{3+}/{\mathrm{Er}}^{3+}/{\mathrm{Ca}}^{2+}$-based lanthanide-doped UCNP has been shown to effectively activate Chrimson-expressing, inhibitory GABAergic motor neurons, leading to a reduced action potential firing in the body wall muscle of C. elegans and resulting in locomotion inhibition.⁵⁸ This UCNP provides a useful integrated optogenetic toolset for wide applications, as it exhibits negligible toxicity in neural development, growth, and reproduction, along with the nonactivation of the animal’s temperature response with the NIR energy required to elicit behavioral and physiological responses. Using it with vf-Chrimson may lead to better NIR optogenetic manipulation of motor circuits in various organisms.

Theoretical simulations provide the opportunity to address the fundamental question of how important temporal codes are for information processing and how large number of neurons can be stimulated with minimal invasion. The translation of therapeutic or scientific network stimulation protocols to the three-dimensional light pattern also involves modeling or empirical solutions. The theoretical analysis presented here would also be, in general, useful in designing new high-frequency, high-fidelity neural spiking all-optical optogenetic experiments.

5. Conclusion

Accurate computational modeling of the photocycle of vf-Chrimson and neural firing events in the vf-Chrimson-expressing neurons opens up prospects for not only engineering new opsins with optimized properties but also understanding and performing precision optogenetic experiments with desired spatiotemporal resolution. The model can also be integrated with circuit models of other cell types to explore the applicability of vf-Chrimson-based optogenetics.

Biographies

Neha Gupta is a PhD scholar at the Department of Physics and Computer Science, Dayalbagh Educational Institute, India. She received her MSc degree in physics from Kumaun University, India, and her MTech degree in solid state electronics from Indian Institute of Technology Roorkee, India, in 2007 and 2011, respectively. She has taught at Teerthanker Mahaveer University, Moradabad, and in colleges affiliated with Maharishi Dayanand University, Rohtak, and Indraprastha University, Delhi, India. Her research interests are focused on computational modeling of optogenetic neuronal switching.

Himanshu Bansal is a PhD scholar at the Department of Physics and Computer Science, Dayalbagh Educational Institute, India. He received his MSc degree in physics from DEI, Agra and his BSc degree from Dr. B.R. Ambedkar University, Agra, India, in 2017 and 2015, respectively. He is a recipient of the DST Inspire Fellowship and his research interests are in computational optogenetics, neuromorphic computing, and photodynamic therapy.

Sukhdev Roy is a professor at the Department of Physics and Computer Science, Dayalbagh Educational Institute, India. He received his PhD from Indian Institute of Technology Delhi in 1993 and has been a visiting scientist at Harvard. He is a fellow of the National Academy of Sciences, India, and the Indian National Academy of Engineering, and is an associate editor of IEEE Access. His research interests are in nanobiophotonics, all-optical ultrafast information processing, quantum and neuromorphic photonics, and computational optogenetics.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.