Evaluating physiological signal salience for estimating metabolic energy cost from wearable sensors

Abstract

Body-in-the-loop optimization algorithms have the capability to automatically tune the parameters of robotic prostheses and exoskeletons to minimize the metabolic energy expenditure of the user. However, current body-in-the-loop algorithms rely on indirect calorimetry to obtain measurements of energy cost, which are noisy, sparsely sampled, time-delayed, and require wearing a respiratory mask. To improve these algorithms, the goal of this work is to predict a user’s steady-state energy cost quickly and accurately using physiological signals obtained from portable, wearable sensors. In this paper, we quantified physiological signal salience to discover which signals, or groups of signals, have the best predictive capability when estimating metabolic energy cost. We collected data from 10 healthy individuals performing 6 activities (walking, incline walking, backward walking, running, cycling, and stair climbing) at various speeds or intensities. Subjects wore a suite of physiological sensors that measured breath frequency and volume, limb accelerations, lower limb EMG, heart rate, electrodermal activity, skin temperature, and oxygen saturation; indirect calorimetry was used to establish the ‘ground truth’ energy cost for each activity. Evaluating Pearson’s correlation coefficients and single and multiple linear regression models with cross validation (leave-one-subject-out and leave-one-task-out), we found that 1) filtering the accelerations and EMG signals improved their predictive power, 2) global signals (e.g., heart rate, electrodermal activity) were more sensitive to unknown subjects than tasks, while local signals (e.g., accelerations) were more sensitive to unknown tasks than subjects, and 3) good predictive performance was obtained combining a small number of signals (4–5) from multiple sensor modalities.

NEW & NOTEWORTHY In this paper, we systematically compare a large set of physiological signals collected from portable sensors and determine which sensor signals contain the most salient information for predicting steady-state metabolic energy cost, robust to unknown subjects or tasks. This information, together with the comprehensive data set that is published in conjunction with this paper, will enable researchers and clinicians across many fields to develop novel algorithms to predict energy cost from wearable sensors.

INTRODUCTION

Wearable assistive robotic devices, such as powered prostheses or exoskeletons, have the potential to aid and restore mobility in users who suffer from conditions such as stroke, spinal cord injury, or amputation. They can also augment performance in able-bodied individuals. Some of these devices are specifically developed to reduce the energy cost of ambulation tasks such as walking, running, or climbing stairs (e.g., see Refs. 5, 6, 20, 33, and 39). From a human augmentation perspective, the less energy a person uses, the longer they can perform a particular activity. This reduction in energy cost also has clinical relevance, as individuals with movement disabilities often have a higher energetic cost of transport than able-bodied individuals, which further limits their activity level (32, 54).

The assistive devices employed for this purpose often have a large number of tunable controller settings that dictate their behavior and their interaction with the user. Such settings might include stiffness, actuation power, or actuation timing. In the clinic, these settings are tuned heuristically, often relying on visual inspection by a trained clinician and verbal feedback from the patient. This approach is time consuming and subjective, two issues that are amplified for research prototypes that often have an even higher number of settings and tunable controller parameters. Identifying the best parameters for each individual is a challenge. As one proposed solution, “body-in-the-loop” optimization algorithms have been successfully employed as a method to quickly tune assistive device parameters on a subject-specific basis and in real time (17, 21, 31, 59, 29). Body-in-the-loop optimization is the process of iteratively and automatically tuning parameters of assistive robotic devices to minimize a physiological cost function while an individual is using the device. Although the aforementioned studies have differed in their optimization algorithms, assistive device hardware, and tuning parameters of interest, all of them have used metabolic energy cost (i.e., how much energy the body requires on a cellular level) as the physiological objective to minimize.

The automatic evaluation of energetic cost that is required for this method is currently one of the rate-limiting factors in the translation of these algorithms to real-world assistive devices. The state-of-the-art experimental measurement system for energy cost is indirect calorimetry, a method that estimates energetic cost using measurements of oxygen consumption and carbon dioxide production (12). Commercially available indirect calorimetry systems comprise a flowmeter embedded in a rubber mask that covers the nose and mouth of the user, and one or more processing units and battery packs are typically secured to the user’s body with a harness. Although these systems are widely used, they are ill-suited for continuous use or long-term data collections because of the obtrustiveness of the mask and processing units. In addition to the bulky equipment, the data obtained from indirect calorimetry are extremely noisy, sparsely sampled, and dynamically delayed. As such, to obtain an accurate estimate of energy cost for a given activity, it is common practice to have individuals walk for 2–3 min to reach a steady-state oxygen consumption level (36, 48). Once steady state has been reached, another 2–3 min of breath data are recorded and subsequently averaged into one estimate of energy cost for that activity. To mitigate some of these challenges, all body-in-the-loop optimization studies to date have leveraged the work of Selinger and Donelan (48), modeling and inverting the kinetics of the respiratory response as a first-order linear system. Although this approach enables researchers to use non steady-state breaths to estimate energy cost, current body-in-the-loop optimization protocols still require 2–4 min to estimate the energy cost at a particular parameter setting (17, 21, 29, 31, 59). These challenges prevent body-in-the-loop optimization algorithms from being used outside the laboratory during clinical fitting sessions and/or integrated into devices that individuals wear in their daily lives.

To realize the full potential of body-in-the-loop optimization algorithms, our estimates of energy cost need to be accurate, fast, comfortable (i.e., no mask), and portable; current indirect calorimetry equipment cannot provide these properties. As such, the long-term goal of our work is to predict energy cost quickly and accurately using physiological signals from portable, wearable sensors, which can then be integrated into an online optimization of assistive device parameters. In this paper, we aim to quantify individual signal salience (i.e., predictive capability) and discover which signals, or groups of signals, have the best predictive power for our application of body-in-the-loop optimization. In particular, we are interested in how well signals or groups of signals can predict steady-state energetic cost (i.e., the amount of energy required to perform a particular activity) as well as generalize across different subjects and tasks.

This approach is enabled by recent developments in wearable sensor technology that have resulted in devices that are capable of providing quick and accurate estimates of physiological quantities (e.g., heart rate, skin temperature) and information about movement (e.g., acceleration). All these quantities relate to how much energy a person is expending. Several previous studies have utilized various types of sensors, signal preprocessing techniques (i.e., filtering and feature extraction), and final predictive algorithms to estimate energy cost during a variety of activities. Commercial accelerometers placed on the chest, hip, feet, and/or wrists are historically the most common sensor used to predict energy cost due to their simplicity and the inherent relationship between movement and energy expenditure (e.g., see Refs. 15, 18, 22, 45, 50, 51, and 52). Heart rate is another common physiological signal used to estimate energy cost, and a linear relationship between heart rate and energy expenditure during submaximal physical activity has been established (28, 37, 41). However, given that heart rate is tightly controlled by the nervous system, changes in heart rate can also be attributed to changes in emotional arousal and may require individual calibration (2, 10, 28, 34). Some of these factors have been mitigated by combining heart rate monitors with accelerometers (10, 11, 19) or biological parameters (e.g., sex, age, weight) (28) in predictive algorithms. Some more recent studies have incorporated autonomic nervous system signals, such as skin temperature, humidity, and electrodermal activity into their estimates of energy cost (2, 3, 57). Electrodermal activity (also called galvanic skin response) is a measure of skin conductance, which changes when an individual begins to sweat. Although electrodermal activity has primarily been used as an indicator of emotional arousal or stress, changes in this signal have also been linked to changes in physical workload (e.g., see Ref. 40). Skin temperature also has been widely used as a measurement tool for cognitive workload; decreasing skin temperature is associated with increased mental workload (40), but its relationship with metabolic work rate has not yet been well defined. Finally, muscle activity [i.e., electromyography (EMG)] and joint kinematics have been used to predict energy cost both in simulation (49) and experimentally (9, 23, 58). Most often, EMG signals are processed in the time domain by calculating a linear envelope or mean activation to correlate with energetic cost (23), but frequency domain-processing methods have also been utilized to resolve EMG signals into intensities to estimate energy cost during cycling (9, 58).

Many studies have concluded that predicting energy cost using a combination of sensors improves estimates of energy cost across participants and across physical activities (e.g., see Refs. 3, 11, 10, 19, 25, and 45). Recent work has thus utilized multi-sensor arrays embedded in textile clothing, such as EMG shorts (53) and the Hexoskin smart shirt (containing a waist-mounted accelerometer, heart rate monitor, and respiratory bands to measure breath frequency and minute ventilation) (8). These systems enable high-fidelity measurement of physiological signals outside the laboratory setting. For example, the Hexoskin smart shirt uses two strain gauge bands positioned around the chest and abdomen to measure breathing frequency and minute ventilation; the physiological signals obtained using the Hexoskin smart shirt have been experimentally validated (e.g., see Ref. 56). With these combinations of sensors, the most common predictive algorithm is multiple linear regression, which has been successful in predicting energy cost across multiple users and tasks. However, linear regression algorithms can produce large task-specific or subject-specific errors, so more sophisticated machine learning algorithms such as neural networks (7, 37, 45) and random forests (8, 18) have also been explored.

Most studies to date have investigated the predictive capability of only a small subset of sensors, which makes it challenging to compare which signals or groups of signals contain the most salient information for predicting energy cost across a variety of tasks and subjects. To design the best predictive algorithms for energetic cost, there is a need to understand the potential that individual signals and groups of signals hold for predicting energy cost. Altini et al. (3) compared the predictive power of a relatively large set of signals (2 accelerometers, heart rate, electrodermal activity, skin humidity, and respiration rate) across a range of physical activities but evaluated only the performance of two groups of signals. Preliminary studies performed by our group investigated the predictive power of a large group of signals (including EMG, accelerometers, electrodermal activity, skin temperature, oxygen saturation, heart rate, and respiratory rate) during a small subset of activities (24,26) as well as the predictive power of different combinations of these signals (25). The goal of the present work is to expand on previous methods and quantify individual signal salience for estimating energetic cost as well as characterize the ability of these signals to generalize to unknown subjects and unknown tasks. In this study, we focused on using simple signal processing techniques and prediction algorithms to stay as close as possible to the original sensor signals. This study is an important step toward the goal of improving the clinical viability and translation of body-in-the-loop optimization algorithms. Furthermore, the data set made available in conjunction with this article (27) will enable researchers and clinicians across many fields to develop novel algorithms to predict energy cost from wearable sensors for a variety of applications.

METHODS

Experimental data collection.

Ten healthy subjects (8 male, 2 female, age (mean ± SD): 27.4 ± 4.5 yr, height: 1.76 ± 0.09 m, weight: 69.1 ± 9.9 kg) participated in this experiment, after giving informed consent to protocol approved by the University of Michigan Institutional Review Board. Each subject completed two experimental sessions in which they performed a variety of physical activities at various speeds and/or intensities (Table 1). The first experimental session consisted of sitting, standing, level walking, incline walking, and backward walking on a treadmill (Bertec Corp., Columbus, OH); the second session consisted of sitting, standing, running on a treadmill, cycling on a stationary bike (Matrix Fitness, Cottage Grove, WI), and stair-climbing on a stairmill (Matrix Fitness, Cottage Grove, WI). For each activity, subjects stood quietly for 6 min, performed each speed/resistance condition for 6 min in a random order, and then sat quietly for 6 min. All changes between speeds or intensities were performed as instantaneous step changes. Subjects rested for ~10 min between activities.

Table 1.

Experimental activities

Task	Intensity
Level walking
0.6 m/s
0.9 m/s
1.2 m/s
Incline walking
0.6 m/s	4°
1.2 m/s	4°
0.6 m/s	9°
1.2 m/s	9°
Backward walking
0.4 m/s
0.7 m/s
Running
1.8 m/s
2.2 m/s
2.7 m/s
Cycling
70 rpm	Resistance 1
70 rpm	Resistance 3
70 rpm	Resistance 5
100 rpm	Resistance 1
Stair climbing
60 Watts
75 Watts
90 Watts

During data collection, subjects wore a variety of sensors that detailed below and in Fig. 1. Oxygen consumption (V̇o₂), carbon dioxide production (V̇co₂), breath frequency, and minute ventilation were recorded breath-by-breath using a portable respirometer (Oxycon Mobile; CareFusion, San Diego, CA). Breath frequency was defined as the number of breaths per minute (units: min), and minute ventilation was defined as liters of expired air per minute (units: l/min). Heart rate (HR) was measured using a wireless heart rate monitor strapped around the chest (Polar Electro, Bethpage, NY). Blood oxygen saturation ($\text{S}{\text{p}}_{{\text{O}}_2}$), defined as the percentage of oxygenated hemoglobin, was measured using a pulse oximeter (Oxycon Mobile) secured to the subject’s left earlobe. The heart rate monitor and pulse oximeter were synchronized with the respirometer, so HR and $\text{S}{\text{p}}_{{\text{O}}_2}$ were recorded breath by breath. Subjects wore four commercial tri-axial accelerometers (Opal; APDM, Portland, OR) affixed to the left and right lateral ankle, the left hip, and the center of the chest using elastic velcro straps; these accelerometers measured accelerations in the x-, y-, and z-axes at 128 Hz. Subjects also wore two bilateral wristbands (E4; Empatica, Milan, Italy) containing tri-axial accelerometers that recorded x-, y-, and z-accelerations of the left and right wrist at 32 Hz. The Empatica wristbands also recorded electrodermal activity (EDA) and skin temperature at 4 Hz. Surface EMG electrodes (Biometrics, Ladysmith, VA) recorded muscle activity from eight bilateral lower limb muscles: gluteus maximus (GMAX), biceps femoris (BF), semitendinosis (ST), rectus femoris (RF), vastus lateralis (VL), medial gastrocnemius (MGAS), soleus (SOL), and tibialis anterior (TA). EMG data were collected at 1 kHz. All sensor signals were time-synchronized during collection.

Fig. 1.

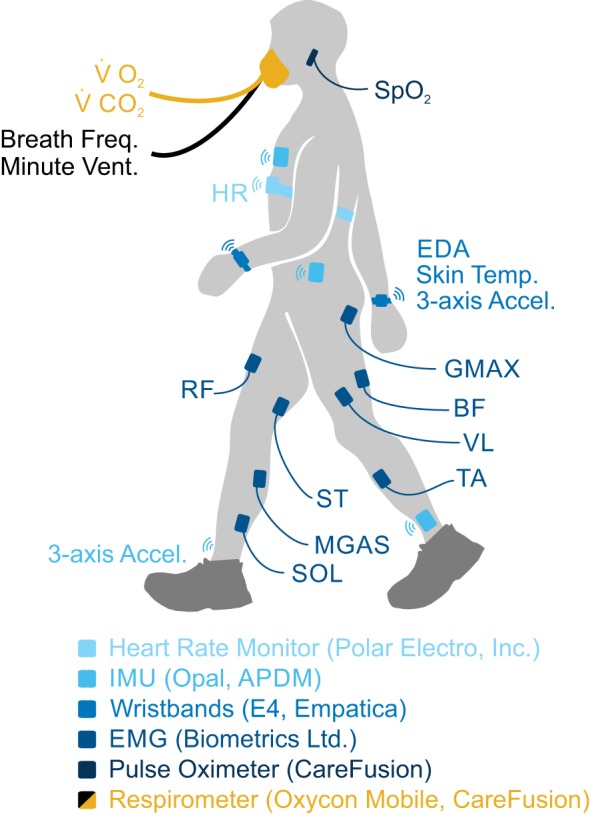
Oxygen consumption (V̇o₂), carbon dioxide production (V̇co₂), breath frequency, and minute ventilation were measured breath-by-breath using a portable respirometer. Heart rate (HR) was measured using a wireless heart rate monitor strapped around the chest. Surface electromyography (EMG) electrodes recorded bilateral muscle activity from 8 lower limb muscles: gluteus maximus (GMAX), biceps femoris (BF), semitendinosis (ST), rectus femoris (RF), vastus lateralis (VL), medial gastrocnemius (MGAS), soleus (SOL), and tibialis anterior (TA). Electrodermal activity (EDA), skin temperature, and accelerations of the wrist were recorded using bilateral wrist sensors. Inertial measurement units (IMUs) placed on the chest, left hip, and ankles measured 3-axis limb accelerations. Blood oxygen saturation ($\text{S}{\text{p}}_{{\text{O}}_2}$) was measured by a pulse oximeter secured to the subject’s left earlobe.

Missing data.

Due to equipment malfunction, we were not able to collect complete data sets from all subjects. Subject 1 did not complete the stair-climbing activity. The right wristband worn by subject 6 did not record data during session 2, so their right wrist accelerometry, electrodermal activity, and skin temperature for running, cycling, and stair climbing tasks were excluded from analysis. In addition, the following signals were excluded from analysis for the given task due to electrode disconnection: subject 5’s left gluteus maximus (walking), subject 3’s right gluteus maximus (cycling), and subject 3’s left semitendinosis (walking).

Ground truth energy cost.

We calculated whole body metabolic energy cost from unfiltered V̇o₂ and V̇co₂ using the Brockway equation (12) and normalized the data to subject body mass. We assumed that energetic cost was constant for a given 6-min condition, and this value was obtained by averaging the final 3 min of steady-state energetic cost measurements for that condition. Henceforth, this value is referred to as the “ground truth” energy cost for each condition. When the conditions were concatenated in time, the ground truth energy cost formed a stair-step function with steps that are 6 min long. These data served as our target data (i.e., the energy cost we aimed to predict). For each activity, the ground truth energy cost from the standing bout at the beginning of the trial was subtracted off to yield net energetic cost.

For this experiment, we used a portable metabolic system (Oxycon Mobile) to establish our ground truth energy cost, as opposed to a tethered system (e.g., the Douglas bag method). The manufacturer’s specifications for the Oxycon Mobile system report an accuracy of 0.05 l/min (3%) for measuring both V̇o₂ and V̇co₂; the accuracy for measuring minute ventilation is reported as 0.05 l/min (2%). Some previous studies have also investigated the reliability of portable metabolic systems and found generally good measurement accuracy compared with other established methods (e.g., see Refs. 1 and 44).

Signal processing.

The total acceleration was calculated for each of the six accelerometers as the vector magnitude of the three axes ($\sqrt{x^2+y^2+z^2}$). We generated EMG linear envelopes by band-pass filtering the raw EMG signals between 30 and 350 Hz, full-wave rectifying, and low-pass filtering with a cutoff frequency of 5 Hz. Each subject’s EMG linear envelopes were normalized to peak activation level of each muscle obtained across all activities performed during the same session. We calculated a composite sum of normalized linear envelope EMG signals (M_i) to provide an overall estimate of muscle activity for the left and right legs (8 muscles/leg, where j indicates left or right leg):

$$M_{total(j)}=\sqrt{{\displaystyle \sum _{i=1}^8{M}_i^2}}$$

We calculated a composite sum of normalized linear envelope EMG signals (M_i) to provide an overall estimate of muscle activity for the left and right legs (8 muscles/leg, where j indicates the left or right leg). Minute ventilation, breath frequency, V̇o₂, electrodermal activity, skin temperature, $\text{S}{\text{p}}_{{\text{O}}_2}$, and heart rate were smoothed using a 1-min Gaussian kernel with a cutoff frequency of 0.01 Hz (as in Refs. 8 and 43). Individual EMG linear envelopes, EMG composite sums, and vector magnitude accelerations were filtered using a 1-min Gaussian kernel with a cutoff frequency of 0.1 Hz. EMG and acceleration signals were filtered more aggressively to account for the higher frequency content in these signals due to their fluctuation within the gait cycle.

Data analysis.

We employed two statistical methods to quantify the predictive capability of individual signals or groups of signals: 1) Pearson’s correlation coefficients and 2) linear regression models. We evaluated the linear regression models using leave-one-task-out and leave-one-subject-out cross-validation. We also found the best possible linear regression models from our data set (across all subjects) containing up to eight signals.

Pearson’s correlation coefficients.

The Pearson’s correlation coefficient (–1 < r < 1) is a measure of the linear relationship between two variables, where 1 is perfect positive linear correlation, 0 is no linear correlation, and −1 is perfect negative linear correlation. We pooled data across all activities for one subject and one individual signal and calculated the correlation coefficient between ground truth energy cost and the individual signal. We repeated this analysis for all 10 subjects and calculated the mean and standard error across subjects. We then performed these calculations for all 16 individual signals both before and after filtering.

Although no formal cutoff exists to define “good” correlation, in this study, we define a correlation greater than 0.7 as a strong linear correlation; this value agrees with other studies which have investigated the relationship between physiological signals and energy cost (e.g., see Refs. 3 and 52). We also calculated the correlation of V̇o₂ with ground truth energy cost to serve as a “benchmark” for comparison; because V̇o₂ is included in the calculation of ground truth energy cost, we expect this correlation to be very high. Yet, this correlation will not be perfect because breath-by-breath V̇o₂ is a noisy signal with a dynamic delay, and only the final 3 min of V̇o₂ measurements were included in the calculation of ground truth energy cost.

Linear regression models.

We calculated single and multiple linear regression models of the following form:

$$\widehat{y}=b_0+{\displaystyle \sum _{i=1}^k{b}_i}{x}_i=Xb$$ (1)

where k is the number of signals included in the regression model and m is the number of samples, $\widehat{y}\hspace{0.17em}\in \hspace{0.17em}{ℝ}^m$ is the vector of predicted energy cost, $X=[1x_1\mathrm{...}{x}_k]\hspace{0.17em}\in \hspace{0.17em}{ℝ}^{m\times (k+1)}$, where $x_i\hspace{0.17em}\in \hspace{0.17em}{ℝ}^m$ are the signals included in the regression model, each interpolated and re-sampled at 1Hz, and $1\hspace{0.17em}\in \hspace{0.17em}{ℝ}^m$ is a vector of ones; $b={[b_0{b}_1\mathrm{...}{b}_k]}^T\hspace{0.17em}\in \hspace{0.17em}{ℝ}^{k+1}$ is the vector of signal weights, including an offset term.

We calculated 17 cross-validated single linear regression models with each of a smaller subset of signals, including six vector magnitude accelerations, two EMG composite sums, left/right electrodermal activity, left/right skin temperature, heart rate, oxygen saturation, breath frequency, minute ventilation, and V̇o₂ (to serve as a benchmark for performance). In addition, we trained and evaluated four cross-validated multiple linear regression models (Table 2). For the multiple linear regression analysis, we divided the signals into two broad categories: the global signals, which give information about the state of the body as a whole (e.g., heart rate, electrodermal activity, skin temperature); and the local signals, which give information about one particular limb segment (e.g., accelerations, EMG). The first three multiple linear regression models contained 1) the local signals alone, 2) the global signals alone, and 3) the combination of global and local signals (see Table 2 for a complete list of signals included in each model). For comparison with a commercially available portable sensor system (i.e., the Hexoskin smart shirt; see Ref. 14), the fourth multiple linear regression model contained the group of signals that can be obtained using the Hexoskin smart shirt (i.e., breathing frequency, minute ventilation, heart rate, and waist accelerometry). This fourth group will henceforth be referred to as the “Hexoskin signals.” All cross-validated single and multiple linear regression models were calculated using preprocessed and filtered signals.

Table 2.

Signal groups included in linear regression models

	Vector Magnitude Acceleration	Composite Sum EMG	Electrodermal Activity	Skin Temperature	Breath Frequency	Minute Ventilation	Heart Rate	Oxygen Saturation
Local	*	*
Global			*	*	*	*	*	*
Local + global	*	*	*	*	*	*	*	*
Hexoskin signals	Hip only				*	*	*

EMG, electromyography.

^*Signal is included in the group.

Cross validation.

We utilized two evaluation methods to examine the effect of task and subject specificity on the predictive capability of each signal or group of signals: 1) leave-one-task-out cross validation and 2) leave-one-subject-out cross validation. For each evaluation method, the data were partitioned into two sets, a training set (including training data, $\overline{X}$; and training targets, $\overline{y}$) and a testing set (including test data, $X\prime$; and test targets, $y\prime$), according to Table 3. The cross-validation was repeated until each task or subject had been left out once; therefore, we conducted sixfold leave-one-task-out cross-validation and 10-fold leave-one-subject-out cross validation (Table 3).

Table 3.

Cross validation for linear regression models

Train	Test	Repeat	No. of Folds (F)
Leave-one-task-out
Subject = S	Subject = S	$t\in T$	6
Task = T\{t}	Task = t
Leave-one-subject-out
Subject = S\{s}	Subject = s	$\text{s}\in \text{S}$	10
Task = T	Task = T

S = {1,2...10} is the set of all subjects and T = {1,2,...6} is the set of all tasks. If s = {1} then S\{s} = {2,3,...10}.

For each fold (indexed by f), we used the training data (${\overline{X}}_f$) and training targets (${\overline{y}}_f$) to calculate the regression weights (b_f) using the pseudoinverse,

$$b_f={({\overline{X}}_f^T{\overline{X}}_f)}^{-1}{\overline{X}}_f^T{\overline{y}}_f$$ (2)

We then used the identified signal weights ($b_f$) to predict the energy cost ($\widehat{y}{\prime }_f$) from the test data ($X{\prime }_f$),

$$\widehat{y}{\prime }_f=X{\prime }_f{b}_f$$ (3)

We compared the predicted energy cost ($\widehat{y}{\prime }_f\hspace{0.17em}\in \hspace{0.17em}{ℝ}^m$) with the ground truth energy cost (i.e., the test targets, $y{\prime }_f\hspace{0.17em}\in \hspace{0.17em}{ℝ}^m$) by calculating the root mean squared error (${\text{RMSE}}_f\hspace{0.17em}\in \hspace{0.17em}ℝ$) between the two time series signals,

$${\text{RMSE}}_f=\sqrt{\frac{1}{m}{(y{\prime }_f-\widehat{y}{\prime }_f)}^T(y{\prime }_f-\widehat{y}{\prime }_f)}.$$ (4)

We then computed the mean and standard deviation of the RMSE across all folds.

Best possible models.

Finally, we determined the best possible combinations of signals from our data set. The goal of this analysis was to determine the best combinations of signals to use if an experimenter chose to use only a small number of sensors (<8 here). To achieve this, we pooled data across all subjects and all activities and trained every possible linear regression model using one to eight of the 16 signals mentioned in the previous section. The number of tested models was calculated using the binomial coefficient (_nC_k, or “n choose k”), which calculates the number of ways to choose an unordered set of k elements from a fixed set of n elements,

$${}_n{C}_k=\frac{n!}{k!(n-k)!}.$$ (5)

In this experiment, n = 16 and k = [1, 2,.., 8], so the number of tested models was ₁₆C_k = [16, 120, 560, 1,820, 4,368, 8,008, 11,440, 12,870], k = [1, 2..,8].

For each k, we calculated the RMSE for all models and then sorted the ₁₆C_k models based on their RMSE. We considered the model with the smallest RMSE the best model for a given k.

RESULTS

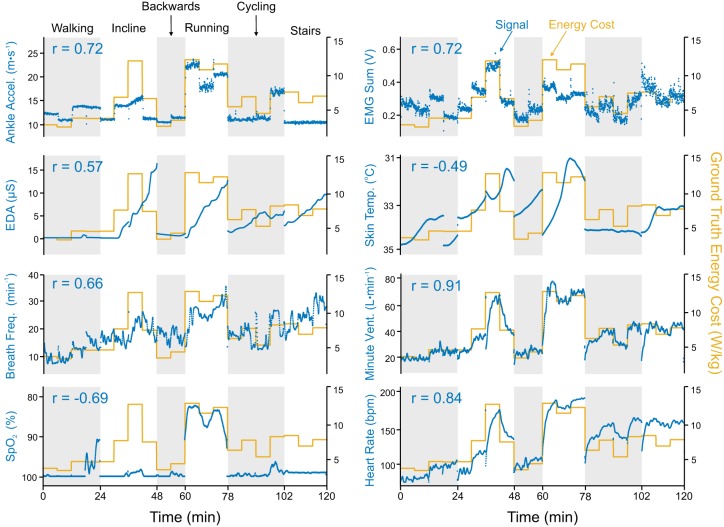
To illustrate the general characteristics of the signals, time series data and correlation coefficients for eight preprocessed and filtered signals are presented for one representative subject, along with ground truth energy cost (Fig. 2). Local signals (i.e., acceleration and EMG) changed nearly instantaneously with a step change in energy cost, whereas global signals (e.g., heart rate, electrodermal activity) demonstrated time-delayed responses to the same step change. Signals that were strongly correlated with ground truth energy cost (e.g., heart rate and minute ventilation) were sensitive to small changes in energy cost. On the contrary, signals such as electrodermal activity, skin temperature, and oxygen saturation ($\text{S}{\text{p}}_{{\text{O}}_2}$) had a coarser relationship with ground truth energy cost and seemed to capture information about general increases or decreases in energy cost while being unable to discern between individual steps.

Fig. 2.

Time series plots for 8 filtered signals from 1 representative subject (subject 4) for all 6 physical activities. Depicted ankle acceleration, electromyography (EMG) sum, electrodermal activity (EDA), and skin temperature are taken from the left side of the body. Left axes measure the physiological signal (blue); right axes measure ground truth energy cost (yellow). Pearson’s correlation coefficient (r) between the signal and ground truth energy cost is written at the top left of each graph. For those signals with negative correlations [blood oxygen saturation ($\text{S}{\text{p}}_{{\text{O}}_2}$) and skin temperature], the left axis is reversed (i.e., smaller values are at the top) to allow for visual overlay.

The diverse set of tasks tested in this experiment resulted in a wide range of intensity levels between tasks. Across subjects, the activity that required the lowest net metabolic energy expenditure was level ground walking at 0.6 m/s; the mean ground truth energy cost for this activity was 3.33 ± 0.48 W/kg (means ± SD). The activity that required the highest net metabolic energy expenditure was running at 2.7 m/s; the mean ground truth energy cost for this activity was 13.33 ± 1.64 W/kg (means ± SD). Therefore, on average, the range of ground truth energy cost experienced by subjects across tasks was 10 W/kg.

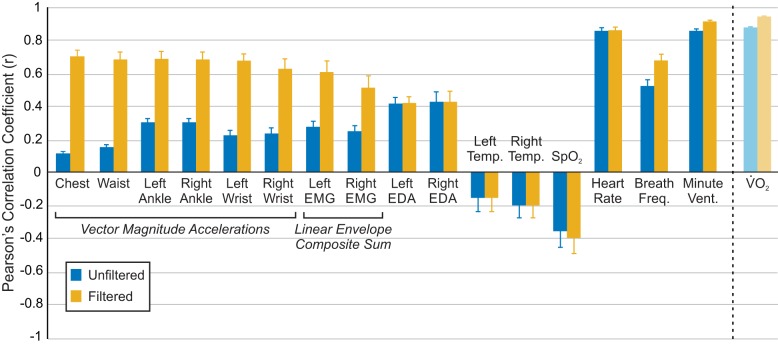
Effect of filtering on correlation with ground truth energy cost.

Filtering dramatically improved the correlation of vector magnitude accelerations and linear envelope EMG signals, which are highly periodic with the gait cycle (Fig. 3). The filtered composite sum EMG signals had higher correlations than individual muscle signals, except for bilateral biceps femoris (Table 4). Filtering only slightly improved the average correlation of electrodermal activity, skin temperature, and heart rate, but it did improve correlation more substantially for breath frequency, minute ventilation, and oxygen saturation (Fig. 3). Unfiltered/filtered V̇o₂, to which we compared the correlations of other signals, had higher mean correlations than any of the other individual unfiltered/filtered signals tested. As aforementioned, we expected the correlation between ground truth energy cost and V̇o₂ to be very high. Therefore, we use this correlation as a ‘benchmark” with which to compare the correlation of other signals.

Fig. 3.

Pearson’s correlation coefficients between unfiltered/filtered signals and ground truth energy cost. Correlations are calculated for individual subjects, with data pooled across all activities. Correlations are then averaged across subjects (n = 10), and error bars represent ±1 SE.

Table 4.

Effect of filtering on predictive capability of signals

	Unfiltered		Filtered
	Left	Right	Left	Right
Vector magnitude accelerations
Chest	0.11 ± 0.03		0.70 ± 0.12
Waist	0.15 ± 0.04		0.68 ± 0.13
Ankle	0.30 ± 0.07	0.30 ± 0.07	0.69 ± 0.14	0.68 ± 0.14
Wrist	0.22 ± 0.09	0.23 ± 0.10	0.68 ± 0.13	0.63 ± 0.19
Linear envelope EMG
Gluteus maximus	0.20 ± 0.03	0.10 ± 0.04	0.47 ± 0.07	0.23 ± 0.09
Rectus femoris	0.12 ± 0.03	0.12 ± 0.03	0.33 ± 0.09	0.29 ± 0.06
Vastus lateralis	0.11 ± 0.03	0.12 ± 0.03	0.41 ± 0.11	0.41 ± 0.10
Semitendinosis	0.20 ± 0.03	0.18 ± 0.04	0.55 ± 0.06	0.46 ± 0.09
Biceps femoris	0.25 ± 0.03	0.27 ± 0.02	0.66 ± 0.06	0.67 ± 0.05
Medial gastrocnemius	0.09 ± 0.03	0.12 ± 0.02	0.33 ± 0.09	0.44 ± 0.07
Soleus	0.15 ± 0.02	0.11 ± 0.03	0.47 ± 0.06	0.34 ± 0.08
Tibialis anterior	0.08 ± 0.04	0.06 ± 0.03	0.19 ± 0.10	0.17 ± 0.08
Composite sum	0.27 ± 0.03	0.25 ± 0.03	0.61 ± 0.07	0.51 ± 0.07
Respiratory and physiological signals
V̇o2	0.88 ± 0.01		0.95 ± 0.00
Breath frequency	0.52 ± 0.04		0.68 ± 0.04
Minute ventilation	0.86 ± 0.01		0.91 ± 0.01
$\text{S}{\text{p}}_{{\text{O}}_2}$	−0.36 ± 0.10		−0.39 ± 0.10
Heart rate	0.86 ± 0.02		0.86 ± 0.02
Electrodermal activity	0.42 ± 0.04	0.42 ± 0.06	0.42 ± 0.04	0.43 ± 0.06
Skin temperature	−0.16 ± 0.08	−0.20 ± 0.08	−0.16 ± 0.08	−0.20 ± 0.08

Values are means ± SE. $\text{S}{\text{pO}}_2$, blood oxygen saturation. Pearson’s correlation coefficient was calculated across subjects (n = 10). For signals collected bilaterally, results from left and right sides are presented in left and right columns, respectively.

Effect of task and subject specificity on prediction of ground truth energy cost.

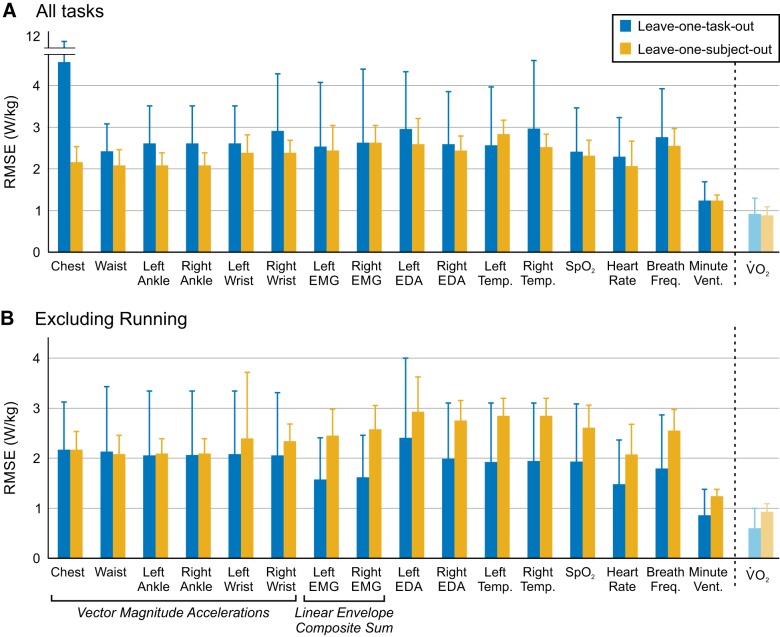
For the 17 cross-validated single linear regression models, which were evaluated using all six tasks, leave-one-task-out cross-validation resulted in higher average root mean squared error (RMSE) than leave-one-subject-out cross validation, and we observed considerable variability between folds (Fig. 4A). For leave-one-task-out cross-validation, the signal with the highest RMSE (i.e., worst performance) was the chest accelerometer (4.56 ± 5.76 W/kg); for leave-one-subject-out cross validation, the signal with the highest RMSE was left electrodermal activity (2.93 ± 0.69 W/kg). Minute ventilation had the lowest RMSE (i.e., best performance) of any signals tested, for both leave-one-task-out (1.22 ± 0.49 W/kg) and leave-one-subject-out (1.24 ± 0.14 W/kg) evaluation methods (Fig. 4A). For comparison, the RMSE of filtered V̇o₂ was 0.88 ± 0.42 W/kg for task-left-out and 0.93 ± 0.16 W/kg for subject-left-out cross-validation (Fig. 4A). We examined the results of each fold of leave-one-task-out cross-validation individually; the mean RMSE (across all signals) was 1.5 to three times higher when running was left out of the cross-validation than any other task (Table 5).

Fig. 4.

Average root mean squared error (RMSE) across folds for each signal using leave-one-task-out (blue) or leave-one-subject-out (yellow) cross-validation. Error bars represent ±1 SD. A: leave-one-task-out cross validation is carried out, including all tasks (6-fold). B: leave-one-task-out cross validation is carried out, excluding running (5-fold). Leave-one-subject-out cross validation (10-fold) is the same in both A and B.

Table 5.

RMSE from individual folds of 6-fold leave-one-task-out cross-validation

Left-Out Task	Walking	Incline	Backward	Running	Cycling	Stairs
RMSE, W/kg	2.24 ± 0.81	2.97 ± 0.75	1.89 ± 0.53	4.45 ± 1.40	1.67 ± 0.94	1.92 ± 0.60

Values are means ± SD. RMSE, root mean squared error.

Given these findings, we also performed a fivefold leave-one-task-out cross-validation, including level walking, incline walking, backward walking, cycling, and stair climbing (i.e., excluding running; Fig. 4B). Across all signals, excluding running from the cross-validation (Fig. 4B) resulted in a 31.1 ± 9.6% reduction in RMSE compared with the sixfold leave-one-task-out cross validation (Fig. 4A). The signals with the largest differences were chest acceleration and left and right EMG composite sums; the signal with the smallest difference was waist acceleration.

Effect of signal groups on prediction of ground truth energy cost.

Regression groups that included the local signals (local, local + global) performed worse when using leave-one-task-out cross validation than when using leave-one-subject-out cross-validation (Fig. 5); regression groups that included mostly global signals (global, Hexoskin signals) did not exhibit such a discrepancy in performance between evaluation methods. For leave-one-task-out cross validation, both the global (1.23 ± 0.54 W/kg) and Hexoskin signals (1.28 ± 0.56 W/kg) models predicted energy cost almost as well as simply using filtered and scaled V̇o₂ measurements (0.88 ± 0.42 W/kg). For leave-one-subject-out cross-validation, the global (1.25 ± 0.34 W/kg), local + global (1.28 ± 0.34 W/kg), and Hexoskin signals (1.24 ± 0.25 W/kg) groups were within 0.4 W/kg of filtered and scaled V̇o₂ (0.93 ± 0.16 W/kg).

Fig. 5.

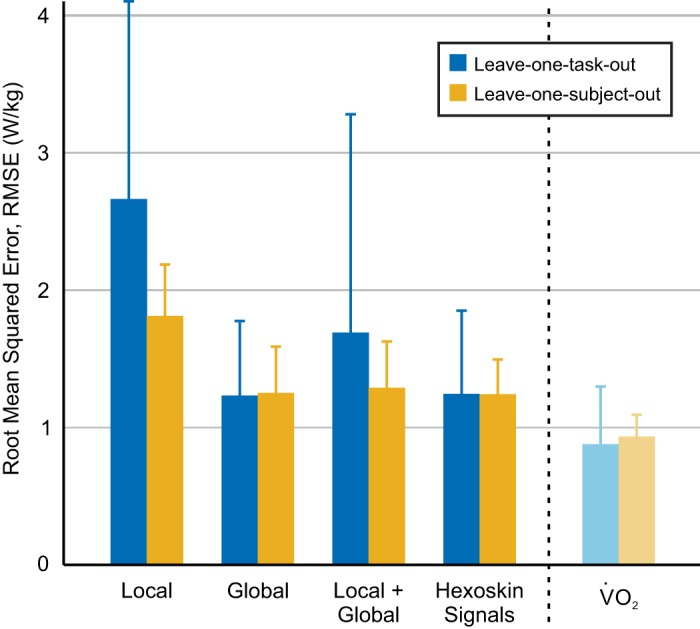
Average root mean squared error (RMSE) for each signal group using leave-one-task-out (blue) or leave-one-subject-out (yellow) cross-validation. Error bars represent ±1 SD. Signals included in each signal group are provided in Table 2. V̇o₂, oxygen consumption.

Effect of using best possible models on prediction of ground truth energy cost.

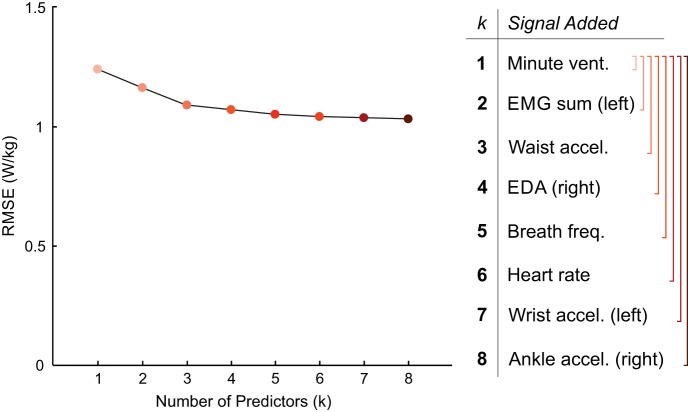
As the number of predictors increased, so did the performance of the regression models, but with diminishing return. The RMSE and signals included in the best-performing regression models (trained and tested on data pooled across all subjects and tasks) with k = [1, 2,... 8] predictors are shown in Fig. 6. This sequence of best predictor combinations exhibited an incremental structure; the best combination of k predictors simply amended the best combination of k – 1 predictors with an additional predictor. For example, for k = 2, we found minute ventilation and EMG composite sum (left) to be the best predictors, and for k = 3, minute ventilation, EMG composite sum (left), and waist acceleration. This structure was not enforced, as we tested every possible combination of predictors independently for each k. In order, the signals found were minute ventilation, EMG composite sum (left), waist acceleration, electrodermal activity (right), breath frequency, heart rate, wrist acceleration (left), and ankle acceleration (right). With the k = 1 predictor, the RMSE was 1.24 W/kg; with the k = 8 predictors, the RMSE improved to 1.03 W/kg.

Fig. 6.

Root mean squared error (RMSE) for the best-performing linear regression models with k = [1,2, . . . 8] predictors. The best model for each k was considered the model with the lowest RMSE out of all possible models containing k predictors. Adding additional signals improves predictive performance, but with diminishing return.

DISCUSSION & CONCLUSION

In this study, we systematically evaluated the predictive capability of multiple physiological signals, alone and in combination with others, to predict metabolic energy cost. We focused on simple signal processing techniques and prediction algorithms to investigate the “baseline” performance for each signal. The study is intended to inform the design and development of algorithms to estimate energy cost from physiological data acquired from wearable sensors to improve the speed, accuracy, and portability of body-in-the-loop optimization algorithms. These findings, as well as the large accompanying data set (27), also have broad applications for any researchers or clinicians interested in predicting energy cost using portable sensors. These applications include but are not limited to the fields of exercise science, athletic training and performance, pediatric medicine, geriatric medicine, personal fitness, and rehabilitation. Using portable sensors to predict energy cost not only eliminates the need to use the bulky and cumbersome respiratory mask but also enables researchers and clinicians to obtain estimates of energy cost outside the laboratory environment, for long or short periods of time, and from people across ages and ability levels.

We found that various combinations of physiological signals can predict steady-state energy cost quite well, even for unknown subjects and unknown activities. To illustrate this point, the overall predictive error obtained using the global or Hexoskin signals groups represented only ∼1.25% of the total range of energy cost experienced across the tasks (which was ∼10 W/kg), and the error obtained using V̇o₂ as a predictor was ∼0.9%. Therefore, the error obtained using the global and Hexoskin signal groups comprised only a small fraction of the natural variation in energy cost across tasks and was very close to the predictive power of V̇o₂ itself. It is very difficult to compare predictive performance across studies due to the large number of confounding variables (e.g., subjects, tasks, sensors, algorithms, units of metabolic power used), but our predictive performance falls into the range of previously reported performance using linear regression algorithms across a variety of tasks. For example, Altini et al. (3) reported an RMSE of 1.59 kcal/min (∼1.5 W/kg for a 70-kg subject) across a set of tasks similar to those tested in our study. These findings demonstrated that, without any advanced signal processing methods or machine learning algorithms, it was possible to predict energy cost using portable, wearable sensors without the use of the cumbersome respiratory mask.

To not bias our findings, we stayed as close as possible to the original sensor signals. Still, some basic data processing was required to improve the predictive capability of certain types of sensors. Filtering, for example, dramatically improved the correlations of ground truth energy cost with the accelerometers and the linear envelope EMG signals (Fig. 3). These filters effectively removed any periodic fluctuations associated with a gait cycle or other repetitive pattern and generated a broader estimate of motion intensity. For signals that did not show such periodic fluctuations, including heart rate, electrodermal activity, or skin temperature, filtering did not improve the correlation. Yet in a real-time application it may still be beneficial to filter these noisy physiological signals to yield smoother estimates.

We also found a benefit to calculating the total EMG activity for one leg (i.e., composite sum), as opposed to using individual muscle signals to predict energy cost (Table 4). Intuitively, different tasks require different muscle activation patterns, and therefore, it is unlikely that one individual muscle would be able to capture the energetic requirements accurately across multiple tasks. Moreover, the composite sum EMG signals are more robust for real-time applications. EMG from individual muscles is highly sensitive to sensor placement and can be affected by donning/doffing the sensors, sweat, and general sensor placement shifts. This effect was observed in this data set, considering the difference in mean correlations between filtered left and right gluteus maximus activity and ground truth energy cost (r = 0.47 and r = 0.23, respectively) (Table 4). Because the tasks tested in this experiment were all symmetrical tasks, these discrepancies were most likely due to differences in sensor placement between the left and right sides.

After filtering, the signals that correlated best with ground truth energy cost were minute ventilation, heart rate, and the accelerometers; the signal that was least correlated with ground truth energy cost was skin temperature. These results agree with a number of previous studies that have demonstrated good predictive ability with accelerations and heart rate (e.g., see Ref. 45).

In terms of signal salience for body-in-the-loop optimization algorithms, these correlations can serve only as a starting point. They were calculated on a subject-specific basis, including data from all tasks; that is, they can explain how well a certain signal can predict the energy cost of a known subject doing a known task. Wearing adaptive assistive robotic devices such as prostheses and exoskeletons, however, might very well constitute an unknown task and might lead to changes in an individual subject’s physiology. This is particularly likely for body-in-the-loop optimization algorithms, which have the declared goal of continuously adapting and optimizing the behavior of assistive robotic devices. This adaptation leads to an ever changing “task” for the user that will, in turn, influence the user’s biomechanics (e.g., gait kinematics, muscle activity) (13, 38). Because the device is designed to assist with the motion, the changes in the task might be quite subtle. An exoskeleton, for example, might adapt to provide more torque during an activity without changing the kinematics of the motion. The user would adapt (30, 47), for example, by reducing muscle activation. Yet from an outside perspective, it will appear as if the task remained the same, whereas the physiological response of the subject has changed. Thus, for body-in-the-loop optimization algorithms to be successful, we need to incorporate signals that are robust to potentially unknown tasks and to unknown subjects. To identify these signals, we tested a broad range of different activities and conducted leave-one-task/subject-out cross-validations to explicitly test the predictive capability of the different signals for unknown tasks and subjects.

When all six activities were included in the analysis, every signal tested in this experiment had higher root mean squared error (RMSE) when evaluated with leave-one-task-out cross-validation than with leave-one-subject-out cross validation (Fig. 4A). Broadly, this implied that all the signals evaluated in this study were more sensitive to unknown tasks than unknown subjects. The standard deviation between folds of the cross-validation was very high, particularly for leave-one-task-out cross validation. Examining these results on a fold-by-fold-basis, we noticed that when the regression model was trained on walking, incline walking, backward walking, cycling, and stair-climbing data and tested on running data, the resultant RMSE was 1.5 to three times higher than any other fold (Table 5). This indicated that the signal data collected during running were drastically different from the signal data collected during the other tasks. Because the running task dominated the error of the leave-one-task-out evaluation, we believed it was masking some of the trends, particularly between different types of sensors.

As such, we performed a secondary analysis in which all running data were removed from the data set (Fig. 4B), and we performed a fivefold leave-one-task-out cross-validation with the remaining tasks. In this evaluation, we saw a dramatic reduction in RMSE compared with the sixfold leave-one-task-out cross validation. Moreover, valuable insights emerged regarding how different types of signals were affected by unknown tasks and unknown subjects. As a broad signal class, the accelerometers were most affected by unknown tasks, with high variability between folds of the validation. We believe this is likely because the accelerometers provide information about the kinematics and the motion pattern of an activity, and therefore, they may be more sensitive to new patterns of activity. On the contrary, EMG and the global signals were more sensitive to an unknown subject than an unknown task. For EMG, this is potentially a result of differences in electrode placement between subjects. For the global sensors, this might be a result of the fact that they measure quantities related to the user’s physiological responses, and they may be affected by subject-specific factors like cardiovascular health (55) or individual differences in sweat and body temperature responses (42, 46). To mitigate some of these factors, previous studies have proposed the personalization of energy expenditure estimates using normalization factors for physiological quantities, such as heart rate or electrodermal activity (2, 4), which could be useful for our future implementations. For our study, we defined EMG activity as local signal, since it provides information about a specific muscle. However, shown in Fig. 4B, the composite sums of EMG signals are more robust to an unknown task than an unknown subject. Despite the fact that EMG activity is related to the kinematics of a task, individual subject differences may play a larger role in the generalizability of EMG signals for predicting energy cost. The difference in performance between the leave-one-task-out cross validations when the running task was included/excluded also highlights that a single algorithm may not be able to appropriately capture the energy cost requirements across all tasks. In this case, more sophisticated task classification algorithms may be necessary to appropriately identify the task and apply the correct prediction algorithm based on that task, a method which has been proposed by previous groups (e.g., see Ref. 4).

In general, combining the signals into groups improved their predictive capability. As with the individual sensors, the groups that contained local signals (local, local + global) performed worse than an unknown subject when predicting an unknown task. The global and Hexoskin signals groups were the best performing groups for both leave-one-subject-out and leave-one-task-out cross validations, and both were able to predict energy cost almost as well as V̇o₂ (within 0.4 W/kg). Although both groups performed similarly, the Hexoskin group (including the waist accelerometer, heart rate, breath frequency, and minute ventilation) may be a more robust predictor of energy expenditure when the user is wearing an assistive device because it combines information from both local and global sensors. The waist accelerometer has the potential to be a good predictor of energy expenditure across multiple tasks because it is located close to the body’s center of mass (COM), and therefore, it is correlated with whole body energetic cost during ambulatory activities (4, 15, 16). Other accelerometers on the ankles and wrists may be more affected by specific kinematic patterns and less robust to unknown tasks, which could explain the larger error in the local + global group.

According to the results of this study, with only one signal (minute ventilation), we could achieve an RMSE of 1.24 W/kg. Adding additional predictors improved performance (up to RMSE = 1.03 W/kg for k = 8), but with diminishing return. These errors correspond to ∼1–1.2% of the total range of energy cost measured in this experiment (10 W/kg); this error is quite small compared with the possible range of energy cost experienced during different activities. In particular, the signals able to be collected by the Hexoskin smart shirt were among the six best predictors of energy cost, which suggested that even with very simple signal processing and regression algorithms, a fully portable device could be used to accurately predict energy cost across a wide variety of tasks. Success using the Hexoskin smart shirt and a random forest regression algorithm to predict oxygen uptake kinetics has recently been demonstrated by Beltrame et al. (8) during activities of daily living and a pseudorandom walking sequence. In our study, the Hexoskin signals showed similar performance when predicting steady-state energy cost. Analysis of the best-performing models demonstrated that adding more predictors improves performance up to a point, but with the right choice of signals, good predictive performance can be achieved using fewer sensors. It would be up to an individual experimenter to decide the acceptable tradeoff between regression performance and number and/or simplicity of sensors.

In this context, it is important to note that the differences between the top-performing models that we identified were rather small. In particular, swapping out one signal for a related one (such as swapping left and right wrist accelerations or left and right EMG) resulted in similar performance. For example, using the right EMG instead of the left EMG increased the RSME only by 0.07 W/kg (<1% of the total range of metabolic cost) for k = 2. At the same time, it is interesting to note that none of the best-performing models included bilateral signals (i.e., both left EMG and right EMG). These analyses suggested that a more robust prediction can be made by combining information from multiple sensor modalities (e.g., combine EMG and electrodermal activity), not simply adding additional examples of the same highly correlated signals (e.g., left EMG and right EMG). Along the same lines, we observed a mix of local and global sensors when we determined the best possible combinations of k signals. Furthermore, the order of signals added to the best combinations (with increasing k) was determined neither by the signals individual Pearson’s correlation coefficients nor by their indiviudal RMSE values. This further highlights that it pays to have different types of sensor modalities when combining multiple signals rather than just use the strongest individual sensors.

The goal of this study was to systematically evaluate the predictive power of physiological signals and groups of signals to draw conclusions about which types of signals are useful for our application of body-in-the-loop optimization. To keep our results general, we did so for multiple subjects and by using a very broad range of activities. Yet our choice of activities is not without drawbacks; we chose a broad set of activities with very different kinematics and dynamics, some of which were novel for subjects (e.g., backward walking). Subjects’ habituation to these activities may have changed their kinematics, kinetics, and energy consumption, and the current analysis did not account for these changes. Our current study is also limited by its small sample size and homogeneous, able-bodied subject population. One could argue that an algorithm specifically designed to estimate the cost of using a particular assistive device should be more hand-tailored to that specific device and based on data that are specific to this device. That is, subsequent studies should investigate how well the predictive algorithms can work with data from individuals using assistive devices. However, such an approach might overly restrict the available data and consequently bias the estimation process. This would limit the applicability of body-in-the-loop optimization algorithms, which should ideally be unbiased in their search for the optimal device setting.

It is important to note that our study was not an attempt to find the best possible way to predict steady-state metabolic effort, and the models discussed in this study are not intended to be complete predictive models. In reality, many of the signals discussed could be cross-correlated, and more rigorous statistical methodology would be required to build an optimal model with the fewest number of predictors. For the current study, we prioritized simplicity over optimal algorithmic performance, and we used linear regression as a common algorithm to compare the predictive power across signals. In the future, other machine learning algorithms (such as random forest or neural networks) that may produce higher prediction accuracy and be more robust to unknown subjects and tasks should be explored. Additionally, more advanced feature extraction and signal-processing techniques (e.g., different filters or normalization) may improve predictive capability of various signals. To facilitate the collaborative development of such advanced techniques and algorithms, we decided to publish our complete data set together with this paper (27). Our hope is that it can be used to compare different approaches that predict energy cost from portable sensors for a wide variety of applications. Although the sensors we used in this study were not fully portable (e.g., EMG, minute ventilation/breath frequency), fully portable versions of these sensors are commercially available, such as the BioStampRC (35) and the Hexoskin smart shirt (8, 14, 56). Future work should involve testing these algorithms in real time using fully portable sensors.

From our analyses of a broad set of physiological signals, we concluded that 1) filtering the accelerations and EMG linear envelopes to remove the periodicity from the gait cycle improved their ability to predict ground truth energy cost; 2) when the physical activities were diverse (i.e., including running), all the signals were more sensitive to unknown tasks than unknown subjects; 3) when the tasks were more similar (i.e., excluding running), physiological signals (e.g., heart rate or electrodermal activity) were more sensitive to unknown subjects than unknown tasks; 4) groups of signals could improve predictive capability over individual signals, but the errors were similarly affected by task and subject specificity; and 5) good predictive performance could be achieved using a small number of sensors. Given these conclusions, for body-in-the-loop optimization and other applications that require predicting energy cost from portable sensors, we recommend combining accelerometers (ideally located close to the center of mass) with heart rate, breath frequency, and/or minute ventilation to provide the most robust prediction of energy expenditure.

GRANTS

This material is based on work supported by National Institute of Child Health and Human Development Grant 1R03-HD-092639 and “Evaluating and Improving Assistive Robotic Devices Continuously and in Real-time” and the National Science Foundation Grant Nos. 1536188 and 1256260.

DISCLAIMERS

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

K.A.I., D.P.F., and C.D.R. conceived and designed research; K.A.I. performed experiments; K.A.I. analyzed data; K.A.I. and C.D.R. interpreted results of experiments; K.A.I. prepared figures; K.A.I. drafted manuscript; K.A.I., D.P.F., and C.D.R. edited and revised manuscript; K.A.I., D.P.F., and C.D.R. approved final version of manuscript.

ENDNOTE

At the request of the authors, readers are alerted to the fact that additional materials related to this article may be found on FigShare, which at the time of publication they indicated is https://doi.org/10.6084/m9.figshare.7473191 (27). These materials are not part of this article and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.