New determination of the ²²⁹Th half-life

Abstract

A new determination of the ²²⁹Th half-life was made based on measurements of the ²²⁹Th massic activity of a high-purity solution for which the ²²⁹Th molality had previously been measured. The ²²⁹Th massic activity was measured by direct comparison with SRM 4328C using 4παβ liquid scintillation counting, NaI counting, and standard addition liquid scintillation counting. The massic activity was confirmed by isotope dilution alpha spectrometry measurements. The calculated ²²⁹Th half-life is (7825 ± 87) years (k = 2), which is shorter than the three most recent half-life determinations but is consistent with these values within uncertainties.

Introduction

²²⁹Th is a relatively long-lived nuclide in the ²³⁷Np decay series that occurs, primarily, as a daughter product of ²³³U [1]. The nuclide decays by a emission to ²²⁵Ra which, in turn, decays to ²²⁵Ac and then, through a series of short-lived nuclides, to ²⁰⁹Bi (Fig. 1). The ²²⁹Th nuclide does not occur in nature, making it useful to the environmental and geological sciences where it is used as a yield tracer for thorium α spectrometry [2] and as an isotope dilution mass spectrometry (IDMS) spike for thorium amount measurements [3]. In addition, ²²⁹Th is a source of high-purity ²²⁵Ac for research in nuclear medicine [4] and is being evaluated for use as a high accuracy nuclear clock [5]. The nuclide is particularly important for nuclear forensics where it is used as an IDMS spike for ²³⁰Th “dating” of uranium materials associated with the nuclear fuel cycle, e.g. [6, 7].

Fig. 1.

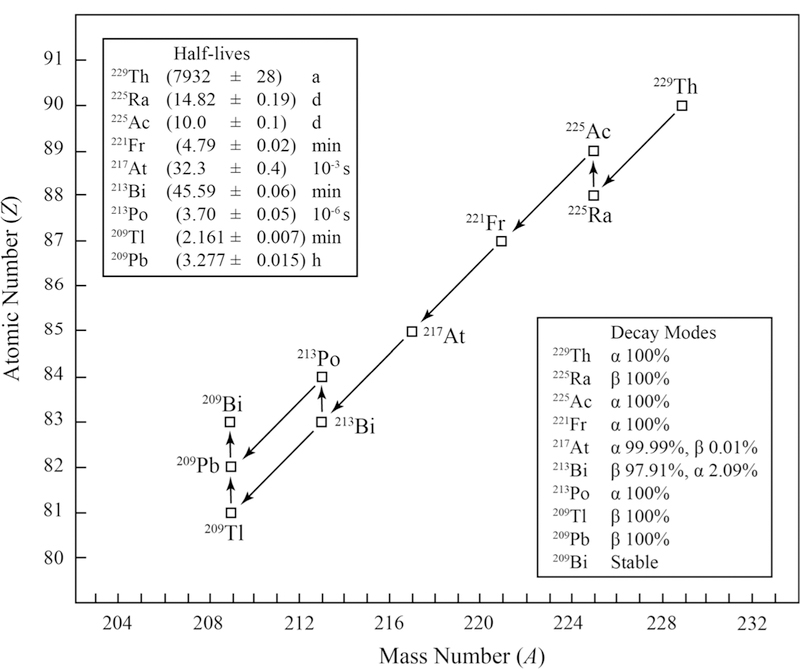
Simplified decay scheme for ²²⁹Th. The uncertainties for the half-lives are standard uncertainties. Half-life and decay mode data for ²²⁹Th are from [8]. Half-life and decay mode data for all other isotopes are from [9]

Due to ongoing interest in ²²⁹Th, the National Institute of Standards and Technology (NIST) has produced four issues of Standard Reference Material (SRM) certified for ²²⁹Th massic activity (Bq g⁻¹). These standards are SRM 4328 issued in 1984, SRM 4328A issued in 1995, SRM 4328B issued in 1996, and SRM 4328C issued in 2008 [10–13]. Fitzgerald et al. [14] describe the massic activity calibration for the ²²⁹Th Master (M) solution used to prepare SRM 4328C. To produce the stock solution for the SRM, an aliquot of the M solution was quantitively diluted by a factor (D_S) of 308.85 ± 0.09. The ²²⁹Th massic activity of the M solution was then measured by live-timed 4παβ-γ anticoincidence counting (LTAC). The massic activity of the SRM solution was calculated using the measured massic activity of the M solution and the gravimetrically determined dilution factor. Relative liquid scintillation (LS) counting of the M and SRM 4328C solutions was used to verify the gravimetric dilution factor for the SRM and the calculated activity value for the SRM was also confirmed by four additional radioactivity measurement methods, including LS counting with ³H CIEMAT/NIST efficiency tracing,¹ triple-to-double coincidence counting (LS TDCR), 2πα proportional counting, and α spectrometry.

In a separate project, two ampoules of the ²²⁹Th M solution were combined and diluted by a factor (D_X) of approximately 56.0² to produce a new reference material that was characterized for ²²⁹Th molality (²²⁹Th mol g⁻¹) and Th isotopic composition [15]. The molality of the new ²²⁹Th reference material (referred to here as ²²⁹Th RM) was measured in two characterization campaigns by IDMS using ²³²Th from a high purity metal as a spike and verified using the SRM 4342A ²³⁰Th massic activity standard as an independent IDMS spike. The resulting ²²⁹Th molality value for the ²²⁹Th RM solution is (0.11498 ± 0.00008) nmol g⁻¹ for a reference date of 15 September 2012.

Considering the variety of uses for ²²⁹Th, an accurate half-life value for the nuclide is important for decay corrections, converting from activity to amount, and estimating the production rate of decay-chain nuclides. To date, four half-life measurements have been published for ²²⁹Th, with the three most recent determinations being relatively consistent. Hagemann et al. [1] published an initial ²²⁹Th half-life of (7340 ± 160)³ years as part of a study of the ²³³U decay chain. This value is significantly shorter than subsequent measurements (≈ 7%) with the discrepancy attributed to a combination of factors including a biased ²³³U half-life value used to calculate the quantity of ²²⁹ Th in the analysis samples, a possible underestimate of ²²⁸Th contributions to ²²⁹Th activity measurements, or ²³³U interference in ²²⁹Th activity measurements [16–18]. Goldstein et al. [16] performed a study to refine the ²²⁹Th half-life value by measuring the molality of ²²⁹Th in a solution with a well-characterized massic activity, SRM 4328. The resulting measurement indicated a half-life of (7880 ± 120) years (k = 2). More recently, Kikunaga et al. [17] calculated a half-life of (7932 ± 55) years (k = 2) based on measured A(²³³U)/A(²³²U) and A(²²⁹Th)/A(²²⁸Th) activity ratios. Finally, Varga et al. [18] measured the molality of the SRM 4328C massic activity standard by IDMS using two different Th spikes. One spike was a commercially prepared natural Th solution [Method A: (7889 ± 32) years] and the second spike was a high purity U material with a calculated quantity of ingrown ²³⁰Th [Method B: (7952 ± 36) years]. The half-lives calculated for each set of IDMS measurements were combined for a reported half-life value of (7917 ± 48) years (k = 2). It was noted in [15], however, that the estimated massic activity and the measured molality of the ²²⁹Th RM indicated a half-life value that was not consistent with the two most recent half-life determinations published for the nuclide.

The following study was performed to investigate the apparent discrepancy between recently published ²²⁹Th half-lives and a half-life based on the estimated massic activity of the newly calibrated ²²⁹Th RM. The massic activity of the ²²⁹Th RM was quantitively determined by direct comparison with the SRM 4328C massic activity standard and was confirmed by isotope dilution alpha spectrometry (IDAS). A new value for the ²²⁹Th half-life is calculated from the measured ²²⁹Th massic activity and the previously measured ²²⁹Th molality.

Experimental

Direct activity comparison

A massic activity value for ²²⁹Th in the ²²⁹Th RM was determined by measuring the ratio of relative activities (i.e. activity per gram solution) for the ²²⁹Th RM solution and the SRM 4328C activity standard. Three counting methods were used to make the relative activity measurements. The first method compared the relative LS counting rates for carefully prepared sources of the two solutions. Then, the relative integral photon emission rates of the LS counting sources were directly compared using a NaI(Tl) well counter. Finally, a standard addition LS counting method was used to determine the activity ratio from a series of mixtures of the two reference materials.

Relative LS counting

The ²²⁹Th decay series consists of a seven-nuclide-long decay chain (Fig. 1) with an LS efficiency of > 6.9 s⁻¹ - Bq⁻¹. To achieve accurate results for the comparative LS counting measurements, it is imperative that the two ²²⁹Th solutions are in identical states of radioactive equilibrium and that the solutions were counted with identical detection efficiency. Nearly identical counting efficiency was achieved by gravimetrically determining the components in the counting source cocktails to assure similar quenching. Identical radioactive equilibrium is also a reasonable assumption when the history and handling of the solutions are considered. Both ²²⁹Th solutions were prepared from quantitative dilutions of aliquots from the same M solution; both solutions were diluted with 1 mol L⁻¹ HNO₃; and no additional separations or processing were performed on either solution prior to sealing in glass ampoules. Ampoules of both reference materials were opened specifically for the activity measurements performed in April 2017, however, the SRM 4328C solution was prepared, dispensed into ampoules, and sealed in October 2007 while the ²²⁹Th RM was prepared and sealed in March 2012. Although it is not possible to categorically rule out chemical fractionation of the sealed M solution aliquots over the 4.5-year period between preparation of the ²²⁹Th solutions (e.g., preferential adsorption or precipitation of an element in the ²²⁹Th decay chain), there is no a priori reason to suspect a difference in the radioactive equilibrium of the two solutions.

Counting sources for high precision LS were prepared from the ²²⁹Th RM and SRM 4328C solutions (Table 1). Two different scintillation fluids were used to create liquid scintillation sources for both ²²⁹Th solutions, Ultima Gold AB⁴ (PerkinElmer, Waltham, MA) and Ecoscint (National Diagnostics, Tampa, FL). Three sources were gravimetrically prepared in 20 mL glass LS vials for each scintillant-²²⁹Th solution combination, resulting in a total of 12 sources. To prepare the sources, aliquots from ampoules of the SRM and ²²⁹Th RM were dispensed using polyethylene aspirating pycnometers with masses measured on an electronic microbalance (AT20, Mettler Toledo, USA). Other cocktail components were weighed with a mechanical analytical balance (Mettler B5, Mettler Toledo, USA). Close matching of the aqueous mass fraction in the sets of cocktails was achieved by the addition of 1 mol L⁻¹ HNO₃ to some of the sources. In addition, each cocktail contained approximately 60 mg of di-(2-ethylhexyl) phosphoric acid (DEHPA or HDEHP), (C₈H₁₇O)₂PO₂H, which is a complexing agent. Matched blank sources of similar composition over the same quench range were also prepared for background subtraction.

Table 1.

²²⁹Th RM and SRM 4328C LS source preparation details and characteristics

LS source series	Mass of scintillant (g)	Mass of 229Th solution aliquot (g)	Mass of blank HNO3 (g)	Total mass cocktail (g)	faq (%)	H#
229Th RM  UGAB	9.850 (3)	0.2039 (9)	0.798 (23)	10.912 (19)	9.18 (19)	89.0 (3)
4328Cs UGAB	9.852 (1)	0.9909 (10)	–	10.906 (11)	9.09 (8)	91.2 (5)
229Th RM  ECOS	8.916 (17)	0.1993 (40)	0.790 (26)	9.969 (42)	9.92 (2)	118.4 (3)
4328Cs ECOS	8.910 (7)	1.0103 (26)	–	9.987 (8)	10.12 (2)	121.1 (3)

Each LS Source Series consisted of 3 separately prepared counting sources. UGAB and ECOS refer to the Ultima Gold AB and Ecoscint scintillation solutions, respectively. The values for the masses (g) and aqueous mass fraction f_aq (in %) are averages for the three sources in the series with the values in parentheses representing the standard deviation of the means. H# is the average quench indicating parameter (as measured in Counter B) which is an additional indicator of the close composition matching between the two ²²⁹Th solutions for each scintillant cocktail

Each source was counted in triplicate on a LS 6500 counter (Beckman Coulter, Fullerton, CA, USA) and on an Accuflex LSC-8000 (Hitachi Aloka Medical Ltd., Tokyo, Japan). Two LS counters were used for this set of experiments to demonstrate that results are independent of the operating characteristics of a particular instrument (detection threshold, photomultiplier efficiency, deadtime, amplification, signal conversion, etc.). Individual LS measurements consisted of integrating the entire LS spectrum, and were of sufficient duration to accumulate over 10⁶ counts (≈ 1 h), such that the relative Poisson counting statistics on each was < 0.1%. In addition to closely matching quenching conditions and cocktail compositions in counting sources, both instruments use quench indicating parameters (QIP) to monitor quenching. The Accuflex LSC-8000 (Counter H) uses the External Standard Channel Ratio (ESCR) quench parameter, which relates quenching to the ratio of two counting windows in the Compton spectrum of ¹³³Ba. The Beckman LS 6500 (Counter B) uses a Horrocks Number (H#) to monitor the quench level, which is based on the downward spectrum shift of the Compton edge of an external ¹³⁷Cs source with increasing quenching in the cocktail.

Relative photon emission

As an independent measurement of the ²²⁹Th RM and SRM 4328C activity ratio, relative photon emission rates were measured on the LS sources described above. Six replicate measurements of each source were made on a NaI (Tl) well-type counter (2480 WIZARD2, PerkinElmer, Waltham, MA). The detector crystal is 75 mm in diameter with a height of 80 mm and is shielded with a minimum of 50 mm of lead. A total of 6 trials for each source were measured sequentially, alternating between SRM and ²²⁹Th RM vials and the spectrum for each measurement was accumulated for an interval of 10800 s (live time). Stability between trials was monitored with a 1.97 kBq ¹²⁹I check source (Half-life = 1.6 × 10⁷ years). The region from, nominally, 20 to 2000 keV was integrated to obtain an integral counting rate that was corrected for background. The Poisson counting statistics for any single measurement were approximately 0.13%.

Results for LS and photon emission counting rates

The measurement results are provided in terms of grandmeans⁵ and great-grand-means of the massic count ratios (Table 2). The measured count rates from the LS and NaI(Tl) experiments are proportional to the massic activity of the respective solutions. If the ²²⁹Th decay chain equilibrium is the same for both solutions, then the ratio of the massic count rates is equivalent to the ²²⁹Th relative activity ratio (A_X/A_S) which, in turn is equivalent of the ratio of M solution dilution factors (D_S/D_X) for the two reference materials. The uncertainty values for the grandmean massic count ratios in Table 2 are computed precision estimators, equivalent to standard deviations of the mean (S_¯x), that consider both the within-source and between-source components of variance. The within-source component is a “typical” (i.e., average) value for the standard deviation of the replicate measurements and the between-source component is the standard deviation of the mean values. The two variance components are combined in quadrature to calculate the standard deviation of the mean for each counter-scintillant combination. Separate great grand-means are calculated for the LS and Na(Tl) measurements with a relative precision estimator calculated as described above.

Table 2.

Count ratios of ²²⁹Th RM—SRM 4328C as measured by LS and NaI(Tl) counters

LS measured count ratios				NaI(Tl) measured count ratios
LS counter	Scintillant	Grand mean massic count ratio	Sx	Scintillant	Grand mean massic count ratio	Sx
B	UGAB	5.5186	0.0121	UGAB	5.5148	0.0143
B	ECOS	5.5199	0.0155
H	UGAB	5.5216	0.0088	ECOS	5.5303	0.0166
H	ECOS	5.5301	0.0166
Great grand mean		5.5226	0.0109		5.5226	0.0170

Counters H and B are as described in the text. UGAB and ECOS are as previously defined. S_¯x is a relative precision estimator equivalent to the standard deviation of the mean

Activity ratio by LS standard addition

A LS standard addition experiment was performed using a series of counting sources prepared as scintillation cocktails that contain mixtures of SRM 4328C and the ²²⁹Th RM in varying proportions (Table 3). A total of five standard addition LS sources were prepared using the Ecosint scintillation solution. Aliquots of both SRM 4328C and the ²²⁹Th RM were added to each source but source preparation was, otherwise, as previously described. The LS counting rate (R_c) for the mixtures of the SRM 4328C, with massic activity (A_S), and the ²²⁹Th RM, with massic activity (A_X), can be given by

$$R_{\text{c}}=\epsilon \left(m_{\text{S}}{A}_{\text{S}}+m_{\text{X}}{A}_{\text{X}}\right)$$ (1)

where ms and mx are the respective aliquot masses of the two solutions in the cocktail and where ε is the overall ²²⁹Th decay chain detection efficiency for the mixture in matched cocktails. Simple rearrangement, by normalization of each term in Eq. (1) by m_S, yields a linear function

$$\frac{R_{\text{c}}}{m_{\text{S}}}=\epsilon A_{\text{S}}+\epsilon A_{\text{X}}\left(m_{\text{X}}/m_{\text{S}}\right)$$ (2)

with intercept ε A_S and slope ε A_X . From a series of matched counting sources with rates R_c for varying m_S and m_X, a linear fit of R_c/m_S as a function of m_X/m_S will determine slope and intercept parameters whose ratio gives A_X/A_S. Additionally, the linear equation, in two independent variables of Eq. (1), can be fit by multiple regression to yield ε A_S and ε A_X directly. The two calculational approaches give identical results, though extraction of the covariance between ε A_S and ε A_X from the covariance matrix is easier with multiple regression.

Table 3.

Standard addition source preparation details and characteristics

Source ID	Mass of scintillant (g)	Mass of 229Th RM aliquot (g)	Mass of SRM 4328C aliquot (g)	Mass of blank HNO3 (g)	Total mass cocktail (g)	faq (%)	H#2
SA1	13.5365	0.076775	1.697757	0	15.3669	11.54	123.5 (5)
SA2	13.5657	0.201698	1.304430	0.2647	15.3962	11.50	123.2 (4)
SA3	13.5808	0.348458	0.995254	0.4289	15.416	11.50	123.6 (4)
SA4	13.5832	0.476746	0.600704	0.6948	15.4124	11.50	122.9 (4)
SA5	13.5711	0.632714	0.327851	0.8073	15.4002	11.48	123.1 (3)

Mass values have a standard uncertainty of < 0.01%. H# is a quench indicating parameter (as measured in Counter B for n = 10 replications) which is an additional indicator of the close composition matching. The values in parentheses represent the numerical values of the standard deviation of the mean for the quoted H#

Ten (10) replicate measurements of the five sources were made in both Counter B and Counter H. The counting rates for the sources integrated over the entire LS spectrum ranged from about 520 s⁻¹ to 950 s⁻¹. So, a duration of 3600 s was used for the measurements in order to accumulate approximately 1.9 10⁶ to 3.4 10⁶ integral counts in each spectrum (corresponding to relative Poisson counting statistics of about 0.07 to 0.05% for each of the 10 measurements).

Results for LS standard addition measurement

The standard deviation of the mean for the average of the 10 replicate measurements of a source on Counter B ranged from 0.25 to 0.37%, and from 0.060 to 0.083% on Counter H. Multiple regressions of the Counter B and Counter H data sets for the R_c (m_X, m_S) two-independent-variable function of Eq. (3) were performed with the LAB Fit code [19]. Table 4 summarizes the results of these regressions. The ratio A_X/A_S was obtained from the fitted parameters ε A_X and ε A_S and its relative standard deviation was computed from

$$S={\left[{\left(\frac{S_{\text{X}}}{A_{\text{X}}}\right)}^2+{\left(\frac{S_{\text{S}}}{A_{\text{S}}}\right)}^2-2\frac{S_{\text{XS}}}{A_{\text{X}}{A}_{\text{S}}}\right]}^{1/2}$$ (3)

where S_X and S_S are the standard deviations on A_X and A_S, respectively, and where S_XS is the covariance between A_X and A_S (refer to Table 4). The reduced χ² values for the two regressions for ν = 3 degrees of freedom were 3.1 and 0.61, with corresponding percentile points of p = 0.024 and p = 0.61 for Counters B and H data, respectively.

Table 4.

Standard addition activity ratio measurement results

Quantities	Counter B	Counter H
$\epsilon A_X$	1347.9	1369.4
$\epsilon A_S$	245.57	249.98
$S_{\text{X}}^2$	0.08892	0.6583
$S_S^2$	0.008953	0.03474
$S_{\text{XS}}$	− 0.01646	− 0.07668
$A_X/A_S$	5.4888	5.4780
S	0.0030	0.0067
Grand mean	Massic activity ratio 5.4834	SD 0.0087

The fitted parameters $\epsilon A_{\text{X}}$ and $\epsilon A_S$ are for the ²²⁹Th RM and SRM 4328C solutions, respectively, with corresponding variances $S_{\text{X}}^2$ and $S_{\text{S}}^2$ and covariance $S_{\text{XS}}$. The estimator S is the propagated standard deviation of the $A_{\text{X}}/A_{\text{S}}$ massic activity ratio

Isotope dilution alpha spectrometry

The massic activity of the ²²⁹Th RM was measured on five subsamples that were prepared for IDAS from a single unit of the reference material. This measurement method is independent of the three activity ratio methods and is not reliant upon comparison with SRM 4328C. The IDAS analysis is a nuclide-specific measurement of ²²⁹Th activity so any perturbation of the radioactive equilibrium of the decay chain for the isotope will not bias the measurement results. Accordingly, the analyses represent a robust verification of massic activity calculated from the previously described relative activity measurements.

The IDAS analysis samples were prepared by transferring aliquots of the SRM 4342A ²³⁰Th activity standard to 5 separate beakers as an isotope dilution spike, followed by aliquots of the ²²⁹Th RM (Table 5). The masses of the SRM 4342A and ²²⁹Th RM aliquots were measured by difference on XP 205 balance (Mettler, Toledo USA). Approximately 2 mL of 0.4 mol L⁻¹ NaHSO₄ (Fisher Scientific, Hampton, NH) and 2 mL 2 mol L⁻¹ HNO₃ were also added to sample beakers which were then refluxed on a hotplate for roughly 1 h. Additional 2 mol L⁻¹ HNO₃ was added to each beaker, as necessary, to yield 10 mL of solution in preparation for ion exchange separation using UTEVA resin (Eichrom Technologies, Chicago, USA). Prior to loading, approximately 1 mg of Zr in a 4 mol L⁻¹ nitrate solution (SPEX Industries, Metuchen, NJ) was added to each sample to assist in the recovery of Th from the UTEVA columns. The Th was eluted from the columns into a beaker using 20 mL of 6 mol L⁻¹ HCl. Approximately 1 mL concentrated H₂SO₄ was added to the samples to break down any organic compounds that may have washed through the UTEVA column during elution and the solution was heated until the sulfuric acid was completely fumed off. Once dry, the samples were cooled and then re-dissolved in 10 mL of 2 mol L⁻¹ HNO₃. Preparation of the samples for counting on the alpha spectrometer entailed co-precipitation of the Th with ≈ 50 µg of NdF₃, (Lindsay Rare Earth Chemicals, West Chicago, IL) in 1 mol L⁻¹ HCL and collection of the sample on a 0.1 µm Metricel filter (Pall Corp. Baltimore, USA). The α-decays from ²³⁰Th and ²²⁹Th were counted for approximately 10⁶ s on an Ortec Octete alpha spectrometer (Ortec, Oak Ridge, USA) with silicon detectors. The measured α activities for ²³⁰Th and ²²⁹Th were corrected for peak tailing, background, and decay probability. The ratio of the corrected activities in conjunction with the known aliquot weights were then used to calculate the ²²⁹Th massic activity using a standard isotope dilution algorithm.

Table 5.

²²⁹Th IDAS sample data. Mass values have a relative standard uncertainty of 0.3%

Source ID	229Th Aliquot (g)	4342A aliquot (g)	229Th corrected counts	230Th corrected counts	Massic activity (Bq g−1)
1A	0.04681	0.23224	201134	208015	195.7 (0.9)
2A	0.03359	0.23442	146521	214837	194.2 (1.0)
3A	0.04935	0.22853	193851	187416	195.5 (0.9)
4A	0.03323	0.21738	121015	160688	201.0 (1.0)
5A	0.03362	0.23496	138180	203920	193.2 (1.0)

The values in parentheses are combined standard uncertainties estimated for the individual massic activity measurements

Results from IDAS

The combined IDAS measurement data indicate a ²²⁹Th massic activity of (195.9 ± 3.2) Bq g⁻¹ (k = 2) for a measurement date of March 5, 2012. The uncertainty of the measured value is dominated by the variability of the replicate massic activity measurements (Table 6) with the uncertainty for solution masses, the SRM 4342A tracer, and peak tail corrections representing minor contributions. Uncertainty contributions from Th blank and α branching ratios were insignificant.

Table 6.

Uncertainty Budget for ²²⁹Th massic activity by IDAS

Component	Comment		Type	ui%
Massic activity	Standard uncertainty of replicate IDAS measurements of 229Th massic activity		A	0.69
Weighing	Estimated relative uncertainty for potential bias in mass of IDAS solution aliquots		B	0.30
Peak tail	Estimated uncertainty of 229Th peak tail correction applied to the α count data		B	0.21
230Th spike	Combined standard uncertainty of the massic activity for SRM 4342A		B	0.20
Background	Estimated uncertainty of 229Th and 230Th background corrections		B	0.04
Relative combined standard uncertainty (uc)			0.81%
229Th massic activity (Bq g−1)		Expanded uncertainty (Bq g−1)
195.9		3.2 (Relative: 1.6%)

The uncertainty estimate for the massic activity was calculated in accordance with Taylor and Kuyatt, [20] and GUM protocols [21] using the GUM Workbench software [22]. u_i% represents the relative standard uncertainty for the listed components. The expanded uncertainty (U = k × u_c) for the massic activity value is the product of the combined standard uncertainty (u_c) and a coverage factor (k), with k = 2 to achieve an approximately 95% level of confidence

Discussion

The physical and analytical linkages between the M solution, SRM 4328C, and the ²²⁹Th RM allow for the measurement of the ²²⁹Th RM massic activity through a direct comparison to SRM 4328C (Fig. 2). The three counting methods used to measure the activity ratios of the ²²⁹Th RM and SRM 4328C should yield the same values, within uncertainties. Results from the LS and NaI(Tl) relative counting methods are consistent among all three counters and both scintillation cocktails used to prepare the sources (Table 2). The LS standard additions results are also consistent for both LS counters (Table 4) but the relative difference between the standard addition and the relative counting methods (δ) is 0.7%, while the relative standard deviation for the results of the two standard addition measurements are both approximately 0.16%. No clear explanation for the apparent discrepancy between the A_X/A_S ratio for the methods has been identified. The composition matching of the five standard addition sources dictated nearly identical detection efficiencies across the series. Secondly, the quality of the fits, as reflected in the adjusted R², reduced χ², and F-values (for ANOVA ratio of variances), suggests that there should have been better agreement. The 95.4% coverage factor on the standard deviation S_X and S_S for A_X and A_S is k = 3.31, such that the expanded relative uncertainties kS on A_X/A_S of 0.18 and 0.40% are roughly a factor of 2 to 3 smaller than the δ from the A_X/A_S ratio. In the absence of identifiable analytical problems for the three activity ratio measurement methods, the overall mean values for each method were averaged to yield a combined activity ratio (A_X/A_S)_c of 5.510 with a standard uncertainty of 0.026. This standard uncertainty is calculated by adding, in quadrature, two variance components. These components are the within-method variability, represented by the typical standard deviation of the mean for the great-grand-means multiplied by the Student’s T distribution for 2 degrees of freedom (n = 3 measurement methods), and the between-method variability represented by the standard deviation of the 3 activity ratio values.

Fig. 2.

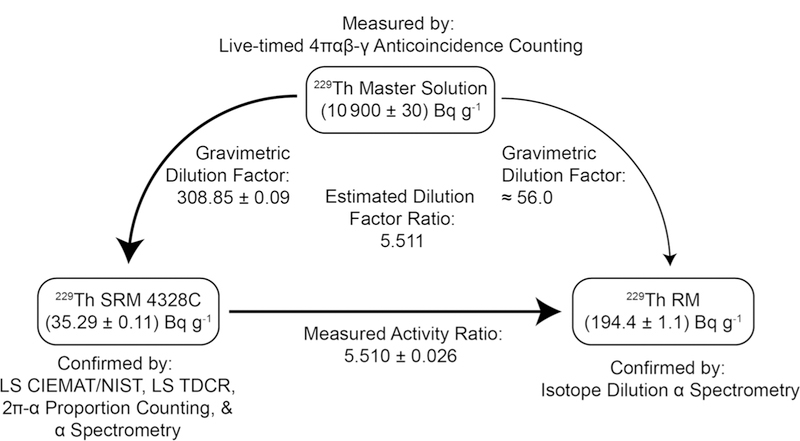
Schematic of material and analytical linkages between the M solution, SRM 4328C, and the ²²⁹Th RM. Bold arrows indicate the activity measurement linkages. The lighter arrow indicates direct production of the ²²⁹Th RM from the M solution. Activity values shown in the figure are for the December 31, 2007 reference date of the massic activity value of the M solution. All uncertainties are combined standard uncertainties

As previously described, the ratio of dilution factors (D_S/D_X) for the two reference materials should be identical to the ²²⁹Th activity ratio, representing an independent confirmation of the measured ratio. Although the dilution factor for the ²²⁹Th RM is an approximation, a calculated D_S/D_X of 5.511 is essentially indistinguishable from the measured activity ratio value indicating the measured ratio is consistent with the values expected based on preparation of the reference material from the M solution.

The massic activity of the ²²⁹Th RM solution (A_X) can be calculated (Eq. 4) from the combined activity ratio (A_X/A_S)_c, as described above, and the measured activity of the M solution (A_m) and the dilution factor for production of SRM 4328C stock solution (D_S), as reported in [14].

$$A_{\text{X}}=\frac{A_m{\left(A_{\text{X}}/A_{\text{S}}\right)}_{\text{c}}}{D_{\text{S}}}$$ (4)

The resulting massic activity value for the ²²⁹Th RM is (194.4 ± 1.1) Bq g⁻¹. For comparison, the ²²⁹Th massic activity measured by IDAS, corrected to the reference date for SRM 4328C (December 31, 2007), is 196.0 Bq g⁻¹ with an expanded uncertainty of 3.2 Bq g⁻¹ (k = 2). The relative difference between the activity measurements is 0.8% which is well within the 1.6% relative uncertainty of the IDAS measurement (Fig. 3).

Fig. 3.

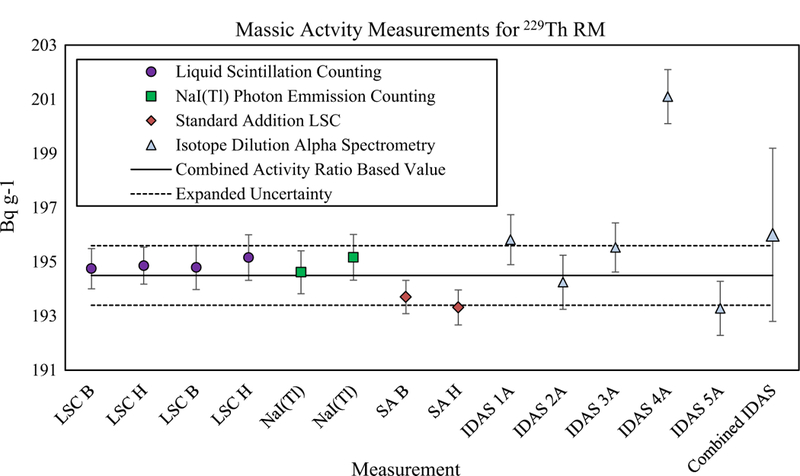
Massic activity values calculated from measured ²²⁹Th RM—SRM 4328C activity ratios and direct measurements by IDAS. Error bars for data points are combined standard uncertainties with the exception of the “Combined IDAS” values which is shown with an expanded uncertainty (k = 2). Note that only the LSC, Standard Addition LSC, and NaI(Tl) data were used to determine the “Combined Activity Ratio Based Value” and “Expanded Uncertainty” interval shown in the figure. All data are presented for a reference date of 31 December 2007

The massic activity from Eq. 4 (A_X) and the ²²⁹Th molality (b_X) of (0.11498 ± 0.00008) nmol g⁻¹, as measured for the ²²⁹Th RM in [15], can then be used to calculate a decay constant (λ) for ²²⁹Th but a decay correction for the (4.7 ± 0.25) year interval between the reference dates for the massic activity and the molality measurements (t) must also be incorporated into the calculation (Eq. 5).

$$\lambda e^{\lambda t}=\frac{A_{\text{X}}}{b_{\text{X}}L}$$ (5)

where L is the Avogadro’s Constant. This function is solved for the decay constant by numerical iteration, which converges rapidly because of the small magnitude of the exponential term. A half-life (T) is then calculated from the decay constant (Eq. 6).

$$T=\frac{\ln \left(2\right)}{\lambda }$$ (6)

The best-fit decay constant for the ²²⁹Th data is 8.858 10⁻⁵ a⁻¹ with a combined standard uncertainty of 0.049 10⁻⁵ a⁻¹ which corresponds to a half-life and expanded uncertainty of (7825 ± 87) years (k = 2). The uncertainty for the half-life determination is dominated by components from the M solution activity measurement and the measured activity ratio for the ²²⁹Th RM (see Table 7). The uncertainties for the measured molality of the ²²⁹Th RM solution, the SRM 4328C dilution factor, and the decay interval between the SRM reference date and the ²²⁹Th molality measurements represent minor contributions to the overall uncertainty for the half-life.

Table 7.

Uncertainty budget for ²²⁹Th half-life determination

Component	Comment		Type	ui%2
Activity ratio	Standard uncertainty of combined activity ratio measurements from this study		A	0.48
LTAC 229Th activity	Standard uncertainty of the M solution massic activity		B	0.28
229Th molality	Combined standard uncertainty of the measured 229Th molality		B	0.07
Dilution factor	Standard uncertainty of the dilution factor for production of SRM 4328C from the M solution		B	0.03
Decay interval	Relative uncertainty associated with the interval between the M solution reference date and molality measurements		B	0.00
Relative combined standard uncertainty (uc)			0.56%
229Th half-life (a)		Expanded uncertainty3 (a)
7825		87 (Relative: 1.1%)

The uncertainty estimate for the half-life was calculated in accordance with Taylor and Kuyatt, [20] and GUM protocols [21] using the GUM Workbench software [22]. u_i% represents the relative standard uncertainty for the listed components. The expanded uncertainty (U = k × u_c) for the half-life value is the product of the combined standard uncertainty (u_c) and a coverage factor (k), with k = 2 to achieve an approximately 95% level of confidence

The ²²⁹Th half-life measured in this study is largely consistent with previous determinations (Fig. 4) with the exception of the first published half-life for the nuclide presented in Hagemann et al. [1]. As previously discussed, the value from Hagemann et al. is significantly shorter than subsequent half-life measurement. The present half-life measurement is consistent with the published half-life reported by Goldstein et al. [16] but is only marginally consistent with the values of Varga, et al. [18] and Kiku-naga et al. [17] as indicated by overlapping expanded uncertainty envelopes. Pommé [23] noted that discrepancies between half-life measurements for the same nuclide are common and speculated that a major cause for the apparent differences is underestimated measurement uncertainty. While it is not possible to assess the uncertainty cited by Hagemann et al. [1] and the uncertainty cited by Goldstein et al. appears to be reasonably conservative, we speculate that the uncertainty of the half-lives from Kikunaga et al. and Varga et al. may be underestimated.

Fig. 4.

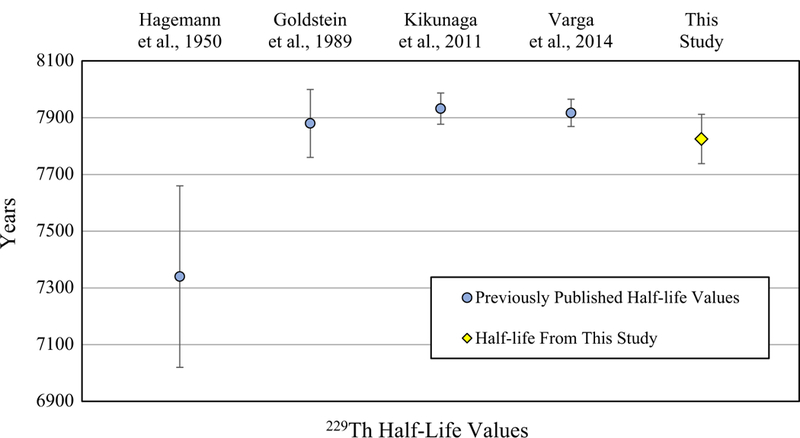
Published half-lives for ²²⁹Th. Error bars for data points are expanded uncertainties (k = 2)

Kikunaga et al. [17] measured the half-life by an indirect method based on known ingrowth periods for Th in a high purity ²³³U material that also contains a small proportion of ²³²U. In their study, the measured α count ratios of A(²³³U)/A(²³²U) and A(²²⁹Th)/A(²²⁸Th) and the half-lives of ²³²U and ²²⁸Th were used to calculate a ²²⁹Th half-life without the necessity of measuring the absolute amount or activity for the nuclide. Accordingly, their calculations are highly sensitive to the ²²⁸Th half-life and the measured ²²⁹Th to ²²⁸Th count ratio, for which they indicate an average uncertainty of 0.2%. The ²²⁸Th half-life appears to be well constrained [9], and Kikunaga, et al. addressed potential sources for significant bias in their data such as corrections for background and interferences in the α spectra. However, the combined alpha spectra for ²²⁹Th and ²²⁸Th are complex and there is potential that their choice of region-of-interest for the nuclides, the magnitude of applied corrections, and/or uncertainties in decay data for the nuclides could result in a bias that is not covered by the 0.15% relative “systematic” uncertainty cited for their measurements.

Varga et al. [18] provided detailed uncertainty budgets for each of the measurement methods used for their half-life determination (Methods A and B). The uncertainties for each method is dominated by the Type B uncertainties for SRM 4328C massic activity. Three replicates of the ²²⁹Th molality measurement were performed for each method but no variability component associated with the replicate IDMS measurements was specified. Varga et al. then combined the two measured half-lives to obtain a weighted mean value of 7917 years with an expanded uncertainty of only 48 years (k = 2), despite a 63-year difference in the half-lives for the two methods. It does not appear that the combined measurement uncertainty incorporated a component for the variability evident between measurement methods and it is unclear whether the type B uncertainty components shared by the methods were appropriately propagated.

Conclusion

A new measured half-life of (7825 ± 87) years (k = 2) is reported for ²²⁹Th. This value is based on the previously determined ²²⁹Th molality of a new thorium IDMS reference material and the detailed characterization of the massic activity value for the reference material, presented here. The measured massic activity is tied directly to the SRM 4328C activity standard through multiple replicate activity ratio measurements using three independent methods and was also independently confirmed by IDAS measurements. This new ²²⁹Th half-life measurement is between 0.7 and 1.4% shorter than other modern half-life determinations but is otherwise consistent with these values (overlapping uncertainties at the 95% level of confidence).