Abstract
We report continuous surface observations of carbon dioxide (CO2) and methane (CH4) from the Los Angeles (LA) Megacity Carbon Project during 2015. We devised a calibration strategy, methods for selection of background air masses, calculation of urban enhancements, and a detailed algorithm for estimating uncertainties in urban-scale CO2 and CH4 measurements. These methods are essential for understanding carbon fluxes from the LA megacity and other complex urban environments globally. We estimate background mole fractions entering LA using observations from four “extra-urban” sites including two “marine” sites located south of LA in La Jolla (LJO) and offshore on San Clemente Island (SCI), one “continental” site located in Victorville (VIC), in the high desert northeast of LA, and one “continental/mid-troposphere” site located on Mount Wilson (MWO) in the San Gabriel Mountains. We find that a local marine background can be established to within ~1 ppm CO2 and ~10 ppb CH4 using these local measurement sites. Overall, atmospheric carbon dioxide and methane levels are highly variable across Los Angeles. “Urban” and “suburban” sites show moderate to large CO2 and CH4 enhancements relative to a marine background estimate. The USC (University of Southern California) site near downtown LA exhibits median hourly enhancements of ~20 ppm CO2 and ~150 ppb CH4 during 2015 as well as ~15 ppm CO2 and ~80 ppb CH4 during mid-afternoon hours (12:00–16:00 LT, local time), which is the typical period of focus for flux inversions. The estimated measurement uncertainty is typically better than 0.1 ppm CO2 and 1 ppb CH4 based on the repeated standard gas measurements from the LA sites during the last 2 years, similar to Andrews et al. (2014). The largest component of the measurement uncertainty is due to the single-point calibration method; however, the uncertainty in the background mole fraction is much larger than the measurement uncertainty. The background uncertainty for the marine background estimate is ~10 and ~15 % of the median mid-afternoon enhancement near downtown LA for CO2 and CH4, respectively. Overall, analytical and background uncertainties are small relative to the local CO2 and CH4 enhancements; however, our results suggest that reducing the uncertainty to less than 5 % of the median mid-afternoon enhancement will require detailed assessment of the impact of meteorology on background conditions.
1. Introduction
Improved understanding of carbon dioxide (CO2) and methane (CH4) emissions from cities has been identified as a priority for both carbon cycle science and to support climate change mitigation efforts (Hutyra et al., 2014; Pacala et al., 2011). More than half of the global population currently resides within cities, with the fraction living in urban areas projected to increase in the future (United Nations, 2014). Currently, more than 70 % of fossil fuel carbon dioxide, and a significant amount of anthropogenic methane, is emitted from cities globally (International Energy Agency, 2008). The combination of carefully designed urban-scale atmospheric CO2 and CH4 monitoring networks, tracer transport modeling, and functionally resolved emissions data sets has the potential to offer significant advances in understanding and managing urban carbon emissions (Duren and Miller, 2012).
Carbon fluxes can be estimated using top-down, bottom-up, or a combination of both methods using measurements in an inverse model framework (Asefi-Najafabady et al., 2014; Gurney et al., 2005; Lauvaux et al., 2016). Top-down and bottom-up approaches are complementary to one another and when combined can be beneficial for informing policy. Top-down approaches typically estimate carbon sources and sinks from measured patterns of variability based on atmospheric observations. By contrast, bottom-up methods require an investigation of activity data and local processes, such as fossil fuel production and consumption data, and/or construction of models that combine fossil fuel usage data with estimates of the carbon content of the fuel type (Asefi-Najafabady et al., 2014; Gurney et al., 2009, 2012). An integrated top-down approach can be very useful, especially given the complex mixtures of anthropogenic and biogenic CO2 and CH4 sources found in urban ecosystems, which may be difficult to quantify using bottom-up methods (Duren and Miller, 2012; Hutyra et al., 2014). Furthermore, combining top-down and bottom-up approaches in an iterative process can lead to a better understanding of gaps in bottom-up emissions models. Top-down measurements are advantageous in that they can be reported with fully traceable and rigorously defined uncertainties. For these reasons, measurement records with both high precision and long-term stability are crucial to the objective evaluation of reported emissions at local, regional, and continental scales (roughly 102 to 106 km2; e.g., Andrews et al., 2014).
In recent years, there has been growing international interest in using top-down atmospheric approaches to quantify urban greenhouse gas (GHG) fluxes (e.g., Duren and Miller, 2012; McKain et al., 2012, 2015). Large, organized urban greenhouse gas monitoring projects have emerged in many cities, including Paris (CO2-Megaparis, http://co2-megaparis.lsce.ipsl.fr; e.g., Bréon et al., 2015; Xueref-Remy et al., 2016), Boston (McKain et al., 2015), Indianapolis (Influx, http://influx.psu.edu; e.g., Turnbull et al., 2015), Salt Lake City (http://lair.utah.edu/page/project/uta/pilot/; e.g., McKain et al., 2012), the San Francisco Bay Area (e.g., Shusterman et al., 2016), and, in this study, the Los Angeles (LA) megacity (https://megacities.jpl.nasa.gov/portal/; see also Feng et al., 2016). To date, most of these research efforts to quantify greenhouse gas emissions in cities have been largely disconnected. The data and methods for greenhouse gas monitoring in urban regions should be fully disclosed and documented with a small degree of latency to make the best use of these atmospheric data for emissions verification and/or for informing policies more generally.
The Megacities Carbon Project was established through a multiagency and multi-institution collaboration to develop and demonstrate policy-relevant carbon monitoring in some of the world’s largest and most complex cities and to help address gaps in our knowledge of greenhouse gas emissions (Duren and Miller, 2012). The Los Angeles test bed project involves both continuous air monitoring and discrete flask sampling of air to monitor greenhouse and trace gas concentrations, together with isotopic ratios of CO2 at multiple surface sites. This study describes the Los Angeles continuous measurement network. The LA project has dramatically expanded the number of greenhouse gas observing sites in the South Coast Air Basin (SCB) since 2013, allowing unprecedented spatiotemporal measurement coverage in this region. In this study, we describe the Los Angeles megacity surface network, sampling strategy, and calibration methods. We also discuss some preliminary results for CO2 and CH4 enhancements in the LA Basin and some detailed metrics for evaluating uncertainties in our observations.
California’s South Coast Air Basin is home to approximately 16.3 million residents and has a geographical area of roughly 17 100 km2 (Fig. 1; CARB, 2014). Observations from the LA network will be useful for future assessment of GHG emissions in the SCB, which encompasses more than 42 % of the CA statewide population. Policies and strategies for mitigation of CO2 and CH4 emissions are currently being implemented in California, with measures being passed at the state and local levels. The California Global Warming Solutions Act of 2006 (AB 32) requires California to reduce its GHG emissions to 1990 levels by 2020, which is a 15 % reduction below emissions expected under a business-as-usual scenario.
Figure 1.
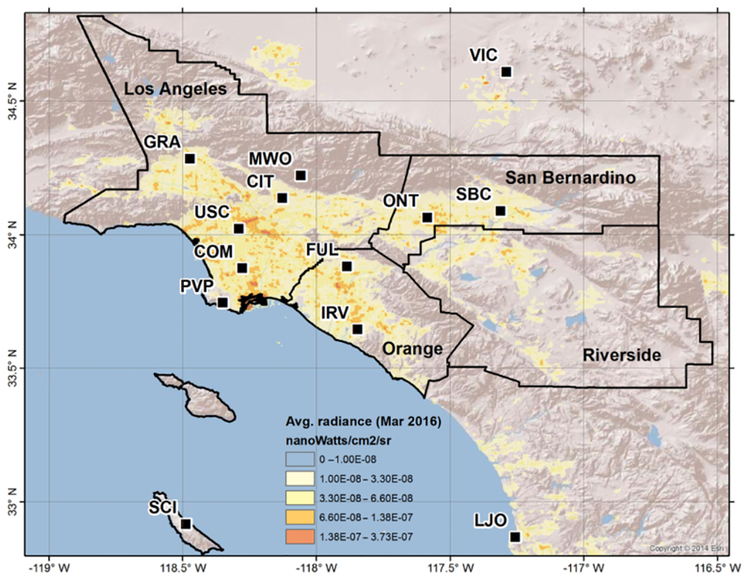
Map of the Los Angeles megacity and locations of the greenhouse gas monitoring network sites. Site locations are shown by the black squares (see Table 1 for details). The South Coast Air Basin (perimeter of the black line) is a geopolitical boundary including non-desert portions of the Los Angeles, Riverside, and San Bernardino counties, as well as all of Orange County (defined by the interior back lines). Background image shows surrounding topography plotted with the average monthly nightlight radiance data from VIIRS during March 2016 (units nW cm−2 sr−1) as a proxy for population density. Continuous measurements from the MWO, SBC, PVP, and CIT sites are not included as part of this study; however, MWO flask data are included as part of the background analysis (Fig. 4).
The SCB presents unique challenges in terms of the complexity of the land surface, meteorology, and spatial–temporal variability of its CO2 and CH4 emissions. The SCB is bordered by the Pacific Ocean to the west and by mountains to the north and east. The mesoscale circulation patterns observed over the LA megacity are challenging to represent in atmospheric transport models (e.g., Angevine et al., 2012; Conil and Hall, 2006; Feng et al., 2016). Complex topography within the basin can allow formation of micrometeorological zones, which may result in concomitant transport complexity. Prior studies suggest a dense measurement network with a high degree of spatial and temporal resolution is required to provide robust, spatially resolved greenhouse gas flux estimates for the Los Angeles megacity (Kort et al., 2013).
Urban and suburban areas in the SCB have high population densities and contain a complex mixture of natural and anthropogenic CO2 and CH4 emissions sources. Urban CO2 emissions can originate from both anthropogenic and biospheric processes. Urban anthropogenic CO2 sources mainly reflect fossil fuel usage – including combustion of gasoline in cars and combustion of natural gas for electricity production for household use and seasonal cooling and heating – while biospheric CO2 fluxes include above- and below-ground respiration and photosynthesis (Djuricin et al., 2010; Hutyra et al., 2014; Newman et al., 2013, 2016). CH4 can be produced via biogenic and thermogenic processes. Biogenic CH4 is produced as a result of microbial decomposition of organic matter under anaerobic conditions (e.g., due to waste disposal in landfills and wastewater treatment plants) and is also produced via enteric fermentation in the gut of livestock and from manure. Thermogenic CH4 is derived from natural geologic processes that produce fossil fuels and therefore is naturally present in fossil fuel deposits, including oil fields and geologic seeps (Etiope and Ciccioli, 2009). Thermogenic CH4 can also be emitted through intentional venting and fugitive leaks in the extraction, storage, refining, transport, and use of natural gas, as well as from the incomplete combustion of fossil fuels.
In the LA Basin, many anthropogenic sources of CO2 and CH4 are co-located with each other and with potential natural sources. LA is a major industrial and shipping hub – with a dense network of roads and freeways for transport, the Port of Los Angeles, and the Los Angeles International Airport – that also has extensive oil drilling infrastructure, with more than 10 local oil refineries and storage facilities. The LA Basin is also known for its naturally occurring geologic seeps, such as the La Brea Tar Pits. In addition to extensive natural gas pipeline networks, LA also has a variety of other CH4 sources, including landfills, wastewater treatment plants, fossil fuel extraction and refining, natural gas storage facilities, compressor stations, vehicle-fueling stations, and dairy agriculture, all of which can result in fugitive emissions (e.g., Hopkins et al., 2016; Peischl et al., 2013; Viatte et al., 2017; Wennberg et al., 2012). The complex mixture of sources and intense human impacts of urbanization further complicate CO2 and CH4 source attribution in the LA Basin.
Several previous efforts have been made to characterize CO2 and CH4 in LA using in situ and remote-sensing observations. Some of the earliest published measurements of CO2 in Los Angeles date back to the 1970s (Newman et al., 2008). Since then, there have been numerous studies investigating atmospheric CO2 and CH4 in the LA Basin using in situ observations, including continuous and flask-based sampling from Mt. Wilson (MWO; Hsu et al., 2010; Wennberg et al., 2012), Pasadena (CIT), and the Palos Verdes Peninsula (PVP; Newman et al., 2008, 2013, 2016), as well as remote-sensing studies, including ground-based and space-based measurements (Kort et al., 2012; Viatte et al., 2017; Wong et al., 2016, 2015; Wunch et al., 2009, 2016). Periodic intensive field campaigns using aircraft have allowed brief “snapshot” assessments (days to weeks in duration) of CO2 and CH4 levels and emissions in LA, including the campaigns ARCTAS-CA in 2008 (Jacob et al., 2010) and CalNex-LA in 2010 (Brioude et al., 2013; Cui et al., 2015; Peischl et al., 2013; Ryerson et al., 2013). Both campaigns were major field studies involving collaboration between the California Air Resources Board and several partner agencies to improve the accuracy of emissions inventories for greenhouse gases and atmospheric pollutants. A smaller, more recent campaign conducted in winter 2015–2016 focused on quantifying methane emissions from the Aliso Canyon natural gas storage facility (Conley et al., 2016).
The local enhancement, or the difference between the observed mole fraction at an urban site relative to an inferred “background” mole fraction (referred to in this study as CO2xs and CH4xs), is of particular interest for urban studies. Prior studies have consistently reported large enhancements of CO2 (e.g., 20 to 100 ppm CO2xs at the surface and 2 to 8 ppm XCO2 enhancement in the column averaged dry-air mole fraction) and CH4 (e.g., 10’s to 1000’s of ppb CH4xs at the surface and 0.2 to 50 ppb XCH4xs), with significant temporal variability of the signals (Kort et al., 2012; Newman et al., 2013, 2016; Viatte et al., 2017; Wecht et al., 2014; Wennberg et al., 2012; Wong et al., 2015; Wunch et al., 2009). For CO2, radiocarbon (14C) isotopic tracer measurements have also been made at a limited number of sites in southern California (Djuricin et al., 2010, 2012; Newman et al., 2013, 2016; Riley et al., 2008). Djuricin et al. (2010) demonstrated that fossil fuel combustion contributed up to 50 to 70 % to CO2 sources during winter, while aboveground biological respiration was found to contribute more CO2 than other sources during spring, when fossil fuel contributions were smaller. Recently, Newman et al. (2016) determined that fossil fuel combustion is the dominant source of CO2 for inland Pasadena using a three-isotope approach, using 14C along with 13C and 18O stable isotopes, similar to Djuricin et al. (2010). In California, gasoline is approximately 10 % ethanol by volume. Ethanol that is derived from biofuel (i.e., from C4 grasses, such as corn) will increase the ratio of atmospheric 13C / 12C when gasoline is combusted, adding complexity to the attribution of fossil CO2 emissions (Djuricin et al., 2010; Newman et al., 2016). For CH4, emissions estimates based on top-down methods indicate that bottom-up methods systematically underestimate CH4 emissions in the LA megacity by roughly 30 to > 100 % (Cui et al., 2015; Jeong et al., 2013; Peischl et al., 2013; Wecht et al., 2014; Wennberg et al., 2012; Wong et al., 2016, 2015; Wunch et al., 2009). Recent evidence from stable isotopes of CH4 and light alkanes (e.g., ethane, propane, and butane) suggests that fossil emissions are the predominant source of CH4 (Hopkins et al., 2016; Peischl et al., 2013; Wennberg et al., 2012; Townsend-Small et al., 2012), particularly leakage from natural gas infrastructure and from local fossil CH4 sources.
In contrast to some of these earlier studies, the monitoring network described here provides near-continuous and systematic monitoring of in situ CO2 and CH4 levels (as well as CO, which is not discussed in this work) at multiple sites in the LA metropolitan area. The LA network allows continuous spatial and temporal measurement coverage at multiple sites, spanning multiple years, which can be used in future top-down atmospheric inversion studies. The first part of this study focuses on the sampling strategy and calibration method (Sect. 2). Next, we estimate hourly average CO2 and CH4 mole fractions (Sect. 3) and discuss observation-based selection criteria for determining the background CO2 and CH4 mole fractions using data from “extra-urban” sites (Sect. 4). One important result from this analysis is the near-equivalence of continental and marine boundary layer (MBL) background estimates for this region. We then use a marine background estimate to calculate urban CO2 and CH4 enhancements from the LA surface network during afternoon hours, which is the typical period of focus for atmospheric flux inversions (Sect. 5). We also present a framework for estimating detailed time-dependent uncertainties in the enhancement based on the combined uncertainty in the air sample data collected from the measurement system and the background estimate (Sect. 6). We compare data collected from analyzers in the field and independent data collected at the National Oceanic and Atmospheric Administration Earth System Research Laboratory (NOAA/ESRL) and Scripps Institution of Oceanography (SIO) laboratories to estimate measurement uncertainties and provide suggestions for future accommodation of additional high mole fraction tanks in our network. In addition to providing a foundation for subsequent flux studies for LA, the sampling strategy, calibration methods, and uncertainty calculations described here are intended to provide a blueprint for other surface observation networks in complex cities around the world.
2. Methods
2.1. Site selection criteria
The Los Angeles network design strategy began with a preliminary analysis based on a network receptor footprint sensitivity analysis for CO2 using the wind fields generated with the Weather Research and Forecasting (WRF) Model to drive the Stochastic Time-Inverted Lagrangian Transport (STILT) model (Kort et al., 2013) and Vulcan fossil fuel CO2 emissions (Gurney et al., 2009, 2012). Kort et al. (2013) found that a minimum of eight optimally located in-city surface observation sites were required for accurate monitoring of fossil fuel CO2 emissions in the LA megacity. Such a network was estimated to distinguish fluxes to within approximately 12 g C m−2 d−1 (roughly 10 % of average peak fossil CO2 flux in the LA domain) on 8-week timescales and 10 km spatial scales. In general, we do not expect the surface sites to be equally sensitive for CO2 and CH4, as the network design was only optimized for detection of fossil fuel CO2 emissions (Kort et al., 2013).
We initially assessed the logistics of deploying instruments at or near each of the locations specified by Kort et al. (2013). Site evaluation and siting criteria involved one or more of the following steps: (1) visual inspection of maps and satellite imagery to investigate whether suitably tall structures were available and to assess potential impacts of terrain and nearby strong greenhouse gas emission sources; (2) on-site surveys;(3) mobile measurement surveys in the region of interest (Hopkins et al., 2016); and/or (4) short-term deployment of a continuous cavity ring-down spectroscopy (CRDS) analyzer on a short tower (approx. 10 m) for roughly 1–2 weeks prior to a more permanent, fixed installation.
Where possible, measurement locations were sought on open-lattice communications towers. These structures were favored as they tend to reduce the influence of perturbed airflow from the supporting structure itself and remote locations minimize the influence of nearby emissions (Prasad et al., 2013). In the SCB, access to tall towers (> 100 m a.g.l., meters above ground level) was limited to the surrounding mountain ranges, which would present unique complexities for modeling and interpretation of the data. Therefore, towers within the basin were limited to shorter cellular tower sites (< 60 m), where available. Although there are a large number of shorter cellular towers in the SCB, these structures were often inaccessible due to permitting or other restrictions. When no tower sites were available in a critical sampling area, we sought secure locations on the rooftops of tall, multistory buildings in the area of interest. The siting criteria and sampling design framework were based on recommendations from Prasad et al. (2013) and McKain et al. (2015). In cases where rooftop sites were evaluated, large eddy simulations were performed to study the impact of recirculation and nearby structures on the flow field around a building rooftop (Prasad et al., 2013).
2.2. Sampling locations
We deployed a total of 12 new analyzers at surface observation sites distributed throughout three counties in the SCB (Fig. 1). The geographic coordinates, inlet heights, site elevation, and analyzer models are summarized in Table 1. The tower sites include Compton (COM), Granada Hills (GRA), Ontario (ONT), Victorville (VIC), and San Clemente Island (SCI). The building/rooftop sites are all located on university campuses in the following cities: Los Angeles (USC, University of Southern California), Pasadena (CIT, California Institute of Technology), Fullerton (FUL, California State University, Fullerton), Irvine (IRV; UCI, University of California, Irvine), and Canoga Park (CNP, Canoga Park High School). The La Jolla site (LJO) is located on Scripps Pier, near a flask sampling location that has been discussed previously in the literature (e.g., Graven et al., 2012). The Palos Verdes Peninsula (PVP) and Pasadena (CIT-1) measurements have been described previously in the literature but are not discussed in this study (Newman et al., 2013, 2016).
Table 1.
Site information for the Los Angeles Megacity Carbon Project surface network. Continuous measurements from the CIT, CNP, MWO, SBC, and PVP sites are not included as part of this study.
| Code | Full site name | Inlet height (ma.g.l.) | Site elevation (ma.s.l.) | Lat (° N) | Long (° W) | Analyzer |
|---|---|---|---|---|---|---|
| VIC | Victorvillea | 100/100/50 | 1370 | 34.61 | 117.29 | Picarro G2301 |
| GRA | Granada Hillsa | 51/51/31 | 391 | 34.28 | 118.47 | Picarro G2401 |
| USC-1 | downtown LA (University of Southern California)b,c | 50 | 55 | 34.02 | 118.29 | Picarro G2301 |
| USC-2 | downtown LA (University of Southern California)b,c | 50 | 55 | 34.02 | 118.29 | Picarro G2401 |
| COM | Comptona | 45/45/25 | 9 | 33.87 | 118.28 | Picarro G2401 |
| FUL | Fullerton (CSU Fullerton)b | 50 | 75 | 33.88 | 117.88 | Picarro G2401 |
| IRV | Irvine (UC Irvine)b | 20 | 10 | 33.64 | 117.84 | Picarro G2301 |
| SCI | San Clemente Islanda | 27 | 489 | 32.92 | 118.49 | Picarro G2401 |
| ONT | Ontarioa | 41/41/25 | 260 | 34.06 | 117.58 | Picarro G2301 |
| CNP | Canoga Park* | 15 | 245 | 34.19 | 118.6 | Picarro G2301 |
| LJO | La Jolla (Scripps Pier)b | 13 | 0 | 32.87 | 117.25 | Picarro G2301 |
| CIT-1 | Pasadena (Caltech, Arms Laboratory)b,d,* | 10 | 230 | 34.14 | 118.13 | |
| CIT-2 | Pasadena (Caltech, Millikan Library)d,* | 48 | 230 | Picarro G2401 | ||
| MWO | Mt. Wilsonb,e,* | 3 | 1670 | 34.22 | 118.06 | |
| PVP | Palos Verdes Peninsulab,* | 3 | 320 | 33.74 | 118.35 | |
| SBC | San Bernardinoa,b,* | 27/58 | 300 | 34.09 | 117.31 | Picarro G2301 |
Tower sites include VIC, GRA, COM, SCI, ONT, and SBC. All other sites have rooftop configurations (USC, FUL, IRV, CIT, and CNP), with air inlets plumbed to the four corners of the building, sampling each corner every 15 min (similar to McKain et al., 2015). For rooftop configurations, “upwind” hourly averages are computed using data from the upwind corner of the building determined based on the corner with the highest wind speed measurement. Rooftop inlet height indicates the total height above the surface (building + mast).
indicates the flask collection site for 14C observations (during current or past studies). CO2 flask observations began near the LJO site in 1979 but are not included as part of this study. The Earth Networks configuration at LJO was implemented in January 2012 with an inlet that is located near Scripps Pier.
USC: at the time of this study, the USC site had two Picarro analyzers installed (model G2301 and G2401), referred to here as USC-1 and USC-2, respectively.
CIT: flask observations at the Caltech Arms Laboratory site (CIT-1) began in 1998. The CIT-1 site has a Picarro G1101-i (isotopic CO2 analyzer) with continuous measurements of 12CO2 and 13CO2 as described previously (Newman et al., 2008, 2013, 2016) and, since roughly 2001, has had an LGR (Los Gatos Research) N2O/CO EP analyzer installed. The Caltech Millikan Library site (CIT-2) was installed nearby in December 2015 and includes a Picarro G2401 analyzer. The Millikan site has a four-corner rooftop sampling strategy identical to other rooftop sites, while the Caltech Arms Laboratory site is a building site with a different configuration. Results are not included as part of this study.
MWO: flask data have been collected by NOAA/ESRL since 2010 and are included as part of the background analysis in this study. At the time of this study, there were three continuous analyzers installed at the California Laboratory for Atmospheric Remote Sensing (CLARS) facility near MWO, which are managed by the Air Resources Board: Picarro G2201-i analyzer measuring CH4/13CH4/CO2, Picarro G5310 measuring N2O/CO/CO2, and an LGR model 913–0015 measuring N2O/CO.
Continuous measurements from the CIT, CNP, MWO, SBC, and PVP sites are not included as part of this study. Some data from the CIT-1, PVP, MWO, and SBC sites have been described previously (e.g., Hsu et al., 2010; Jeong et al., 2013; Newman et al., 2013). At the time of this study, the PVP site also had a continuous CO2 analyzer installed (PP Systems CIRAS-SC) and the SBC site also had an LGR N2O/CO EP analyzer.
The measurement methods discussed in this study only apply to the following new observation sites: COM, GRA, ONT, VIC, SCI, LJO, USC-1, USC-2, CIT-2, FUL, IRV, and CNP. All are equipped with similar instrumentation and use an internally consistent sampling protocol and calibration strategy (see Sect. 2.3–2.4). The LJO, SCI, VIC, and MWO sites are located outside the SCB boundary and are considered here as extra-urban sites, which can be used to estimate background or boundary condition for the SCB (Fig. 1). We use an observation-based method to select background mole fractions from extra-urban sites, in part due to their remote locations (see Sects. 3 and 4 for further discussion).
2.3. Instrumentation
The Los Angeles megacity greenhouse gas monitoring network utilizes wavelength-scanned cavity ring-down spectroscopy instruments (Picarro Inc., series G2301 and G2401; Rella et al., 2013; Welp et al., 2013). All the CRDS instruments measure CO2, CH4, and water vapor, while sites with Picarro G2401 instruments also measure CO (Table 1). There are three standard configurations for the sites discussed in this study: (1) towers with a single inlet height, (2) towers with multiple inlet heights, and (3) rooftop sites, which follow a four-corner sampling strategy. Table 1 also indicates the site type, number of air inlets, and approximate heights for the air inlets. Air inlet heights vary from 13 to 100 m a.g.l. for tower sites and from 20 to 55 m a.g.l. for the rooftop sites. Many of the measurement sites discussed in this study were installed, maintained, and/or operated by Earth Networks (EN, Germantown, MD, https://www.earthnetworks.com/).
The gas-handling configuration for the EN greenhouse gas monitoring stations is shown in the Supplement (Fig. S1, adapted from Welp et al., 2013). The Earth Networks sample module houses a Valco eight-port low-pressure, dead-end flow path selector with standard bore size of 0.75 mm (VICI, Valco Instruments Co. Inc., http://vici.com/vval/sd.php) housed inside a heated box maintained at 38 °C. The selector valve determines the sample type entering the CRDS cell (either outside air or standard/calibration gases).
All tower and rooftop sites are equipped with EN meteorological stations (WeatherBug, http://download.aws.com/manuals/RedBugBoxInstall.pdf), which measure wind speed, wind direction, ambient pressure, ambient temperature, humidity, dew point temperature, and incident solar radiation. Rain gauges are installed below the gas inlets. For tower sites, the wind measurements are located near the uppermost air inlet for the in situ greenhouse gas analyzers. For rooftops, the air inlets and wind sensors are installed on the four corners of the building, with masts typically positioned roughly 3 to 5 m above the roofline and roughly 90° from the walls or edge of the building’s rooftop. Co-located meteorological measurements will allow better determination of the sensitivity of rooftop sites to local and regional emissions(i.e., when the winds are stronger or more consistent) relative to potential emissions from the building itself (i.e., when the winds are calm).
The EN sample modules used in the LA surface network include a Nafion dryer housed in a thermostatic box (see Fig. S1 and description by Welp et al., 2013). The drying system consists of a 183 cm (72 in)-long Nafion membrane dryer (PermaPure, Inc., model MD-050–72S-1). An MKS640 pressure controller maintains a constant pressure to the Nafion dryer during routine sampling of ambient air and calibration gases (set point roughly 800 mbar, 600 Torr). Both sample air and reference gases pass through a Nafion dryer before entering the CRDS cavity (Fig. S1). The water vapor concentrations in the sample and standard gases are roughly 0.1 ± 0.01 % H2O after passing through the Nafion dryer. The analyzer pump redirects roughly 30 % of the dry gas exiting the Nafion dryer to the outer shell side of the dryer. Welp et al. (2013) provide further discussion on the design, testing, and implementation of this drying inlet system. Both the sample air and reference gases are delivered to the Nafion dryer at the same pressure in order to reduce the drying bias due to permeation through the Nafion dryer during routine operation, based on recommendations from Welp et al. (2013). The CRDS water vapor correction and uncertainty due to the treatment of water vapor are described in more detail in Sect. 6 and the Supplement.
Before each analyzer was deployed, the Picarro factory default orifice (O’Keefe A-18-NY) was replaced with a smaller one (O’Keefe A-9-NY) to reduce the flow to about 70 sccm (cm3 min−1 at STP). A second critical orifice (O’Keefe A-6-NY) was installed downstream of the Nafion dryer to reduce the counterflow rate to about 30 sccm, and filters were added upstream of the critical orifice to prevent particles from disrupting the flow. A separate small pump (ALITA AL-6SA air pump) module is installed for each air inlet and delivers a constant stream of sample air at 10 standard liters per minute (sL min−1) to the EN sample module. The air inlets consist of9.525 mm (3/8 in) Synflex tubing and an air intake filter consisting of either a stainless steel (SS) or titanium wire mesh screen (100 Mesh SS or Monel mesh).
The CRDS analyzers communicate data directly with a Linux minicomputer on-site that receives the data stream through a TCP connection. The site computer runs software (GCWerks, http://www.gcwerks.com) which controls the port sampling sequence in the EN sample module. The software acquires all the high-frequency data points from the CRDS (i.e., roughly 2.5 s time interval), EN sample module, and weather stations at each site, and records extensive engineering data. GCWerks also sends out preprogrammed email alarms so that instrument issues can be diagnosed remotely. All high-resolution data (Level 0 data) are retained. The GCWerks software then applies some basic automated quality control flags and filters to the Level 0 data (the uncorrected, roughly 2.5 s resolution CRDS reading) and also rejects some data points to create higher-level data products (see Supplement and Table S1).
2.4. Calibration gases and sampling
Each measurement site is equipped with two natural air standard gas tanks. In the field, Parker Veriflo regulators (part no. 45100653, model 95930S4PV3304) are used to deliver gas from the calibration tanks and are connected to the Earth Networks sample module via 0.16 cm OD (1/16 in) SS tubing. Field standards are prepared by the National Oceanic and Atmospheric Administration Earth System Research Laboratory and/or Scripps Institution of Oceanography laboratory and are calibrated relative to the World Meteorological Organization (WMO) scales before and after deployment in the field. The NOAA/ESRL ambient-level standards are natural air tanks filled at Niwot Ridge, Colorado, and calibrated against standards on the WMO scales maintained by NOAA/ESRL (X2007 for CO2, X2004A for CH4, http://www.esrl.noaa.gov/gmd/ccl/; Dlugokencky, 2005; Zhao and Tans, 2006). All ambient-level tanks have mole fractions close to clean-air ambient conditions (roughly 400 ppm CO2 and 1850 ppb CH4). Our calibration strategy ensures compatibility within the LA surface network and with other global atmospheric observations tied to the WMO scales.
In addition to the ambient-level calibration and target tanks, the VIC and LJO sites had high mole fraction standard tanks installed at the time of this study. These high mole fraction tanks were prepared by NOAA/ESRL, and calibration assignments were provided prior to deployment (roughly 500 ppm CO2 and 2600 ppb CH4). The NOAA/ESRL high mole fraction tanks are prepared by adding a 10 % CO2-in-air mixture to natural air during the pressurization of the cylinder at Niwot Ridge, Colorado (and a similar procedure is used for CH4). The cylinder is then moved to the NOAA calibration laboratory in Boulder, CO, where it is calibrated relative to NOAA/WMO secondary standards. For all standard tanks, we retrieve the most recent tank assignments from the NOAA Central Calibration Laboratory (http://www.esrl.noaa.gov/gmd/ccl/refgas.html). The SIO standards are filled using a similar procedure, except tanks are filled with natural coastal air from Scripps Pier in La Jolla, California, and the tanks are also calibrated against standards on the same WMO scales. All mole fractions are reported in units of μmol gas per mol dry air (ppm) or nmol gas per mol dry air (ppb).
The current calibration strategy for the LA surface network relies on a single-point calibration, which is tied to the NOAA/WMO scale. One of the ambient-level tanks is assigned as the calibration standard, and the other tank is a target standard, which is treated as an unknown sample. This calibration method assumes a linear response in the analyzer. This calibration framework has been used extensively for calibration of gas chromatography (GC–MS) instruments in remote monitoring networks, such as the Advanced Global Atmospheric Gases Experiment (ALE/GAGE/AGAGE network, see for example Prinn et al., 2001). The details of the calibration gas composition will be discussed in a separate publication.
The CRDS analyzer samples each standard tank approximately every 22 h (i.e., approximately daily). The target tank measurement is staggered roughly 8–12 h after the calibration gas (as well as the high mole fraction tank, where applicable). All tanks are sampled for 20 min. The first 10 min of each tank run are rejected, and only data from the last 10 min are used in the calibration of CO2 and CH4 mole fractions to account for the stabilization of air in the CRDS after the inlet is switched (Welp et al., 2013). Variations in the measured target values and deviations from the assigned values are used to track the performance of the analyzer over time and determine uncertainties for the air data (Sect. 6.1).
The instrument sensitivity (S) is calculated for each standard tank (the calibration tank, the target tank, and the high mole fraction tank) and is determined as the ratio between the uncorrected CRDS reading and the tank’s assigned value on the WMO scales :
| (1) |
where is the uncorrected CRDS reading (the dry mole fraction of the species of interest, in units ppm or ppb for CO2 and CH4, respectively) of the calibration standard. The sensitivity of the calibration tank is used to correct the air sample data, as described below. Sensitivities for the target tank (and high-concentration tank, where available) are also tracked over time; however, these tanks are not used in the calibration of the air data.
The CRDS analyzer provides a nominal mole fraction value, which we take as an uncalibrated measurement. We then calibrate the uncorrected dry-air sample mole fraction readings from the CRDS analyzer using the single-point drift-correction method:
| (2) |
where Xcorr is the calibrated data, is the dry mole fraction measurement of the calibration tank, and is the assigned value of the calibration standard on the WMO scales (which is constant in time). For each instrument, we interpolate the daily runs of the field calibration gas standard in time to provide a time stamp for at the time of the air sample measurement. The units of Xcorr are in ppm CO2 or ppb CH4.
The sensitivity (S) of the high mole fraction tank is also tracked over time, providing a check on the analyzer stability at higher mole fractions. For the purposes of this study, we treat the high mole fraction tanks as unknown target tanks and use them to estimate the uncertainty associated with our single-point calibration strategy by calculating the residual of repeated measurement of the high mole fraction tank from its assigned value. In Sect. 6.1 we discuss the individual components of uncertainty in the air measurements, including the extrapolation uncertainty, which is the uncertainty due to our assumption that S is not dependent on the mole fraction (see Sect. 6.1.1). In the Supplement, we discuss an “alternate calibration method” using limited measurements of a high mole fraction tank installed at the LJO and VIC sites in 2016 (see also Figs. S2 and S3).
3. Results
3.1. CO2 and CH4 observations
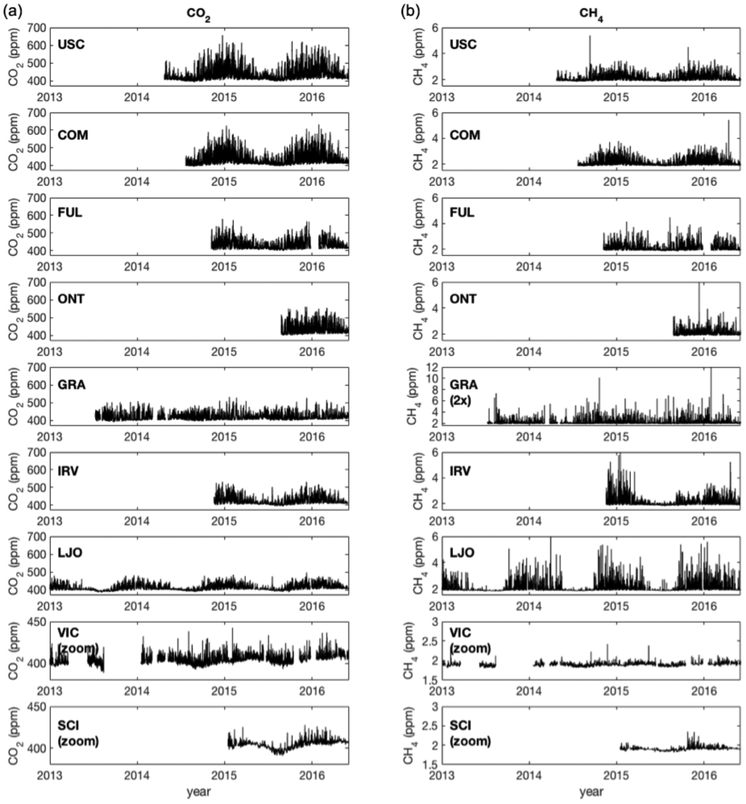
Figure 2 shows the 1 h average observations collected from nine sites in the Los Angeles surface network between 1 January 2013 and 1 June 2016. Tables 2 and 3 show the statistics on the CO2 and CH4 mole fractions collected during 2015 based on 1 h observations collected during all hours and mid-afternoon hours (i.e., hourly observations collected between 12:00 and 16:00 LT (local time), or UTC – 8, with no local adjustment for daylight savings time). Generally, each site exhibits the expected seasonal cycle for CO2 and CH4, with wintertime maxima and summertime minima. The downtown LA (USC), Compton, and Fullerton sites exhibit the highest average mid-afternoon CO2 mole fractions during 2015 (Table 2). The annual average CO2 mole fraction was 421.6 ppm (USC), 418.6 ppm (FUL), and 418.0 ppm (COM) based on 1 h average data collected during mid-afternoon hours in 2015 (Table 2). For CH4, the annual average mole fraction was 2009.9 ppb (USC), 1985.6 ppb (GRA), 1978.2 ppb (FUL), and 1977.2 ppb CH4 (COM), based on data collected during mid-afternoon hours in 2015 (Table 3). While USC exhibits the highest CO2 and CH4 mole fractions on average, CH4 exhibits a somewhat different spatial pattern relative to CO2, with the GRA site showing the second largest CH4 mid-afternoon enhancements.
Figure 2.
Time series plots showing the calibrated 1 h average dry-air mole fractions for CO2 (a) and CH4 (b) in units parts per million (ppm) from nine CRDS analyzers in the LA megacity network. Atmospheric CO2 and CH4 observations were corrected using the single-point calibration method. Site codes (from top): University of Southern California/downtown LA (USC), Compton (COM), California State University, Fullerton (FUL), Ontario (ONT), Granada Hills (GRA), University of California, Irvine (IRV), La Jolla (LJO), Victorville (VIC), and San Clemente Island (SCI). Data are shown for observations collected between January 2013 and June 2016. The length of each record reflects the commissioning date of each site. Data gaps in these records indicate periods when the instruments were nonoperational or data quality was determined to be poor and was flagged (see Supplement). Note that the y-axis scale is different for the VIC and SCI (CO2 and CH4) and GRA (CH4 only) sites.
Table 2.
Statistics for CO2 observations from the nine sites shown in Fig. 2. Annual average; SD; 16th, 50th (median), and 84th percentiles; minimum and maximum; and RMS values were computed based on the hourly average observations collected during calendar year 2015, with results shown for observations collected during “All hours” and during “Mid-afternoon” hours only (12:00–16:00 LT).
| CO2 (ppm) | VIC | GRA | ONT* | USC | FUL | COM | IRV | SCI | LJO | |
|---|---|---|---|---|---|---|---|---|---|---|
| All hours | mean | 404.7 | 421.4 | 434.0 | 434.8 | 429.0 | 430.5 | 419.4 | 402.4 | 412.9 |
| 1σ SD | 3.7 | 17.0 | 25.2 | 31.2 | 23.3 | 30.3 | 19.3 | 4.3 | 14.9 | |
| min | 393.5 | 399.0 | 400.0 | 397.5 | 398.1 | 395.9 | 392.6 | 390.7 | 388.8 | |
| 16th | 401.3 | 407.5 | 410.9 | 410.0 | 409.4 | 407.4 | 403.9 | 397.9 | 400.4 | |
| median | 404.4 | 416.3 | 428.1 | 424.4 | 421.3 | 419.5 | 413.0 | 403.1 | 407.3 | |
| 84th | 407.8 | 435.8 | 457.1 | 460.7 | 451.2 | 457.4 | 436.9 | 406.1 | 428.8 | |
| max | 442.6 | 532.6 | 561.1 | 621.8 | 572.9 | 625.8 | 531.9 | 427.7 | 498.2 | |
| RMS | 0.8 | 3.9 | 3.4 | 7.0 | 5.1 | 6.9 | 4.2 | 1.0 | 3.4 | |
| Mid-afternoon | mean | 404.4 | 414.6 | 415.4 | 421.6 | 418.6 | 418.0 | 412.0 | 402.4 | 407.9 |
| 1σ SD | 3.6 | 12.8 | 11.8 | 17.5 | 14.9 | 16.9 | 13.5 | 4.4 | 10.6 | |
| min | 395.9 | 399.2 | 400.0 | 397.5 | 398.7 | 396.9 | 392.6 | 391.2 | 392.5 | |
| 16th | 401.2 | 404.9 | 406.2 | 408.2 | 407.2 | 406.0 | 401.4 | 397.9 | 398.5 | |
| median | 404.0 | 411.2 | 412.3 | 416.5 | 414.4 | 412.9 | 408.2 | 403.1 | 405.1 | |
| 84th | 407.3 | 423.5 | 423.3 | 435.0 | 430.0 | 429.3 | 422.7 | 406.1 | 417.9 | |
| max | 442.6 | 521.6 | 487.8 | 530.0 | 498.8 | 558.1 | 494.9 | 425.2 | 468.1 | |
| RMS | 0.8 | 2.9 | 1.6 | 3.9 | 3.3 | 3.9 | 2.9 | 1.0 | 2.4 |
Statistics for the ONT site are based on measurements from September to December 2015 only.
Table 3.
Same as Table 2, but for CH4 observations.
| CH4 (ppb) | VIC | GRA | ONT* | USC | FUL | COM | IRV | SCI | LJO | |
|---|---|---|---|---|---|---|---|---|---|---|
| All hours | mean | 1901.7 | 2103.9 | 2126.1 | 2126.5 | 2079.3 | 2090.7 | 2045.7 | 1901.4 | 2009.5 |
| 1σ SD | 34.2 | 331.3 | 231.5 | 227.9 | 218.0 | 240.8 | 246.7 | 39.9 | 247.0 | |
| min | 1824.9 | 1828.8 | 1860.3 | 1864.9 | 1849.9 | 1848.6 | 1845.6 | 1823.3 | 1838.2 | |
| 16th | 1869.4 | 1927.3 | 1956.6 | 1946.2 | 1923.7 | 1914.9 | 1902.5 | 1866.4 | 1883.7 | |
| median | 1898.5 | 2003.6 | 2073.6 | 2047.2 | 1998.1 | 1998.4 | 1966.7 | 1897.6 | 1925.2 | |
| 84th | 1933.4 | 2228.1 | 2287.1 | 2321.3 | 2245.8 | 2296.3 | 2183.5 | 1928.9 | 2108.6 | |
| max | 2383.1 | 6946.1 | 8675.7 | 4511.1 | 4474.8 | 3788.6 | 8432.4 | 2348.3 | 5439.1 | |
| RMS | 7.2 | 76.0 | 31.4 | 51.1 | 47.5 | 55.1 | 53.5 | 8.9 | 55.7 | |
| Mid-afternoon | mean | 1898.6 | 1985.6 | 1990.7 | 2009.9 | 1978.2 | 1977.2 | 1962.6 | 1900.9 | 1935.3 |
| 1σ SD | 32.9 | 130.5 | 93.3 | 116.4 | 100.2 | 109.8 | 101.5 | 37.9 | 77.5 | |
| min | 1832.7 | 1828.8 | 1862.5 | 1864.9 | 1849.7 | 1848.9 | 1845.6 | 1824.7 | 1838.3 | |
| 16th | 1866.5 | 1902.9 | 1924.7 | 1923.6 | 1907.5 | 1901.6 | 1889.7 | 1866.4 | 1877.3 | |
| median | 1896.7 | 1949.8 | 1969.3 | 1973.0 | 1947.6 | 1943.7 | 1929.2 | 1897.3 | 1911.3 | |
| 84th | 1928.6 | 2056.3 | 2042.2 | 2095.7 | 2041.2 | 2050.3 | 2036.4 | 1927.9 | 1997.6 | |
| max | 2105.3 | 3567.8 | 2634.0 | 2677.9 | 2710.1 | 3109.6 | 2960.0 | 2231.4 | 2758.3 | |
| RMS | 7.0 | 29.9 | 12.7 | 26.2 | 22.0 | 25.2 | 22.1 | 8.4 | 17.5 |
Statistics for the ONT site are based on measurements from September to December 2015 only.
Victorville and San Clemente Island show less variability in CO2 and CH4 mole fractions compared to the other sites within the SCB (Fig. 2). During 2015, CO2 mole fractions at SCI ranged from 391.2 to 425.2 ppm CO2, with an average mole fraction of 402.4 ppm CO2 during mid-afternoon hours. Similarly, CH4 mole fractions ranged from 1824.7 to 2231.4 ppb CH4, with an average of 1900.9 ppb CH4 during mid-afternoon hours. At VIC, CO2 mole fractions ranged from 395.9 to 442.6 ppm CO2, with an average of 404.4 ppm CO2, while CH4 mole fractions ranged from 1832.7 to 2105.3 ppb CH4, with an average of 1898.6 ppb CH4 during mid-afternoon hours. We find that SCI and VIC are the cleanest sites due to their small annual average variability. A third “extra-domain” site is located outside the SCB boundary, at La Jolla. On average, LJO exhibits more variability and higher CO2 and CH4 mole fractions compared to the SCI and VIC sites.
Feng et al. (2016) used a forward modeling framework to explore variability in modeled CO2 mole fractions during the CalNex period (May–June 2010). Their results, based on modeled pseudo-CO2 data, are generally in agreement with the observations from the SCI and VIC sites. Feng et al. (2016) also showed that the IRV site was relatively clean with respect the modeled pseudo-CO2 data. As shown in Fig. 2, during spring and summer months, sites such as IRV and LJO typically show less trace gas variability relative to winter months due to more persistent onshore flow. However, during the rest of the year, the IRV site shows CO2 and CH4 mole fractions in the same range as other suburban sites, such as GRA and FUL (Fig. 2, Tables 2 and 3). The LJO site is outside the innermost model domain used Feng et al. (2016) and was not discussed as part of that study. Future work should focus on comparing modeled and observed CO2 and CH4 mole fractions during different meteorological conditions, but using periods with overlapping model and measurement results from the same time period.
Tables 2 and 3 also show the median and interquartile ranges for the CO2 and CH4 observations. At most sites, the data distributions are skewed and have long tails, where a relatively small fraction of observations exhibit significantly elevated CO2 and/or CH4 mole fractions (see also Sect. 5, where we discuss the long-tail distribution with regards to the enhancement above background). Generally, high-concentration spikes can occur at night and in the early morning, when the atmosphere is more stable and when the site is more sensitive to nearby sources. One example is the suburban GRA site, which shows many high-concentration CH4 spikes since data collection began in 2013 (Fig. 2, right panels, note scale difference on the y axis). Many of the CH4 spikes throughout the GRA record occur at night, suggesting contributions from a nearby source. Shallower planetary boundary layer (PBL) heights at night will lead to higher trace gas enhancements and higher sensitivity to local surface emissions (e.g., Djuricin et al., 2010; Turnbull et al., 2015).
In addition to emissions, it has been demonstrated previously that meteorology plays an important role in controlling the variability of trace gas observations within the planetary boundary layer (e.g., Feng et al., 2016; Newman et al., 2013; Xueref-Remy et al., 2016). Diurnal variations in trace gases are driven in part by changes in the height of the PBL. A stable PBL prevents surface emissions from mixing with the atmosphere above. Given a constant flux, and assuming that transport in and out of the boundary layer remains approximately constant, the trace gas mole fraction observed within the PBL will increase or decrease as the PBL height falls or rises, respectively. Newman et al. (2013) demonstrated this for CO2 using observations from Pasadena, CA (the Caltech Arms Laboratory site, CIT-1, in Table 1). The LA surface observations from mid-afternoon hours show less variance in the within-hour CO2 and CH4 values and a smaller interquartile range relative to all hours (Table 2). The reduced variability in the CO2 and CH4 observations during mid-afternoon hours is in part due to the larger height of the PBL during the mid–late afternoon.
Rahn and Mitchell (2016) evaluated Aircraft Meteorological Data Relay (AMDAR) automated weather reports from three major international airports in southern California (LA, Ontario, and San Diego) between 2001 and 2014. Overall, they found that PBL depth observations from LA (in the western LA Basin) showed the least variability (smallest interquartile range) during the hours just before sunset (~21:00 to 03:00 UTC), indicating a fairly regular range of the boundary layer height at this time (Rahn and Mitchell, 2016). CO2 and CH4 observations are also more likely to be sensitive to local sources when the PBL is shallow and the atmosphere is less well mixed (and at low wind speeds). The PBL height may also vary with season. Southern California is characterized by a well-defined boundary layer during the spring and summer months due to strong temperature inversions associated with large-scale subsidence. During the autumn and winter, the large-scale subsidence is less prominent and the presence of a weak temperature inversion (or one that extends down to near the surface) makes it more difficult to identify a boundary layer (Rahn and Mitchell, 2016). As part of future work, we plan to evaluate the diurnal and seasonal variability in the CO2 and CH4 signals with PBL depth measurements from a Sigma Space Mini Micropulse Lidar (MiniMPL) instrument located in Pasadena near the CIT measurement sites (Ware et al., 2016).
Wind speed is also an important factor controlling variability in observed trace gas mole fractions, as has been demonstrated previously for CO2 (e.g., Newman et al., 2013; Xueref-Remy et al., 2016). This is also related to the measurement footprint, as discussed earlier. For example, at low wind speeds, observations within the PBL are more likely to reflect sources and sinks in close proximity to the site (with distances of roughly 10 km or less), while at higher wind speeds the observation site will become more sensitive to transported emissions from more distant sources (d ~ 10 to 100 km), while the influences from nearby sources will appear more diluted. We do not go into further detail on the impacts of meteorology on the CO2 and CH4 signals as part of this analysis. Future work will explore the impacts of meteorology and PBL height on the CO2 and CH4 (and CO) signals observed by the network using footprint analysis and weather reanalysis products.
There are three potential signals of interest for urban and regional greenhouse gas studies. All may be potentially relevant for utilizing greenhouse gas measurements in local or regional inverse modeling studies: (1) diurnal changes in the measured mole fraction at one location over a 24 h period;(2) gradients in the measured mole fraction between locations; and (3) the local enhancement, which is the difference between an observed mole fraction at one location and a defined background mole fraction and is referred to here as CO2xs and CH4xs (see below). In the remainder of this paper, we focus on the third type of signal discussed above, the enhancement above background.
3.2. Calculating CO2 and CH4 enhancements
The enhancement relative to the background mole fraction can be useful for evaluating local additions of CO2 and CH4 from urban regions. We define the enhancement or excess signal (XXS) as follows:
| (3) |
where XOBS is the calibrated CO2 or CH4 mole fraction at the site of interest, and XBG is the background mole fraction(i.e., the mole fraction from an air mass entering the domain or region of interest), all with units of ppm CO2 or ppb CH4.
4. Estimating background mole fractions
A critical goal for the LA Megacity Carbon Project is to identify an optimized background measurement location (or locations). Prior studies in the LA region have used either a coastal marine boundary layer background derived from observations from La Jolla, CA (32.87° N, 117.25° W; 0 m a.s.l.; Graven et al., 2012), the Palos Verdes Peninsula(33.74° N, 118.35° W; 116 m a.s.l.; Newman et al., 2013, 2016), or a continental, free-troposphere background based on nighttime flask measurements from the mountaintop site at Mt. Wilson, CA, in the San Gabriel Mountains bordering the northern edge of the LA Basin (MWO, 34.22° N, 118.06° W; 1670 m a.s.l.; Fig. 1). Prior studies attempting to constrain CH4 emissions in California have also estimated background mole fractions along their model domain boundary using particle trajectory endpoints from WRF–STILT footprint simulations as a lookup for a latitudinally averaged, 3-D marine boundary layer “curtain” product (Jeong et al., 2012, 2013; Zhao et al., 2009).
Determining the appropriate background for a study region depends in part on the application. For example, in forward and inverse modeling studies, the location and scale of the domain of interest will determine the background requirements. A model that is used to estimate the enhancement due to local emissions should account for influences from sources both within and outside the domain of interest as well as recirculation effects (i.e., when air exits the domain and returns a short while later). There is obviously no single background that is representative for all cases. There may also be cases when a single background site is not appropriate for estimating enhancements throughout the basin. Out-of-domain sites may help resolve within-domain emissions under some conditions; however, the appropriate background site will also depend on the prevailing meteorological conditions. For Los Angeles, if the prevailing wind is offshore, then a continental background may be most appropriate, whereas, if the wind is onshore from the western coastal boundary, then a marine background may be most appropriate. Out-of-domain influences can also lead to spatial gradients that are independent of within-domain emissions and will be more difficult to discern or characterize. In such cases, within domain sites may occasionally be useful for characterizing background conditions.
In this study, the domain of interest is defined by the South Coast Air Basin boundary (Fig. 1). The sites most suitable for characterizing background (or upwind) conditions are SCI, LJO, VIC, and MWO, which are all located outside of this SCB domain. LJO is a coastal, suburban site in La Jolla, CA (as described above); SCI is an offshore island site located on San Clemente Island, CA, just southwest of LA (32.92° N, 118.49° W; 480 m a.s.l.). VIC is a rural, desert site located outside the city of Victorville, CA (34.61° N, 117.29° W; 1370 m a.s.l.); and MWO is a mountaintop site, as described above. LJO and SCI are potentially useful for characterizing the Pacific marine boundary layer background values, VIC for characterizing a continental background, and MWO for characterizing a continental, mid-tropospheric background. At best, background conditions may only be observed intermittently from any of these sites because each site can also be influenced by local and within-domain emissions under certain meteorological conditions. In Sect. 4.1, we use an observation-based method to select background observations at the LJO, SCI, VIC, and MWO sites, and in Sect. 4.2 we compare these estimates. In Sect. 4.3, we discuss some air mass back trajectories and the implications for background estimates for the LJO, SCI, VIC, and MWO sites.
4.1. Background methods
Estimating greenhouse gas enhancements at the local scale requires measurements that resolve variability in background air masses (e.g., Graven et al., 2012; Turnbull et al., 2015). In the literature, several methods have been demonstrated for identifying background observations, including applying statistical filters to look for periods with stable measurements, filtering for meteorological conditions and/or chemical parameters, or using modeled and/or reanalysis products in combination with observations to estimate gradients (e.g., Alden et al., 2016; Ruckstuhl et al., 2012; Thoning et al., 1989). Methods relying on chemical filtering techniques involve monitoring multiple species to identify pollution events or to inform about the sensitivity of a site to local pollution, while methods relying on meteorological filters assume some prior knowledge about the transport of polluted air masses to the site.
In this study, we used a data selection approach based on simple statistical filtering criteria, where the stability of the observed CO2 and CH4 mole fractions is used as an indicator of background air. Using this approach, we aim to estimate a local continental and marine background that can be used to estimate CO2 and CH4 enhancements in Los Angeles with relatively low latency (i.e., with reduced delays such that near-real-time atmospheric monitoring of the enhancement signal will be possible). Our data selection approach relies on several criteria: (1) a small degree of variability within a 1 h period, (2) small hour-to-hour variability, and (3) persistence of the first two conditions for several hours. Based on these criteria, we exclude observations that are impacted by local emissions or recirculation effects at the continuous observation sites. This data filtering approach does not rely on the availability of any other observations (i.e., winds, boundary layer height, etc.). In this sense, we consider this background selection algorithm to be operational in that it can be used to estimate background mole fractions in real time or near-real time.
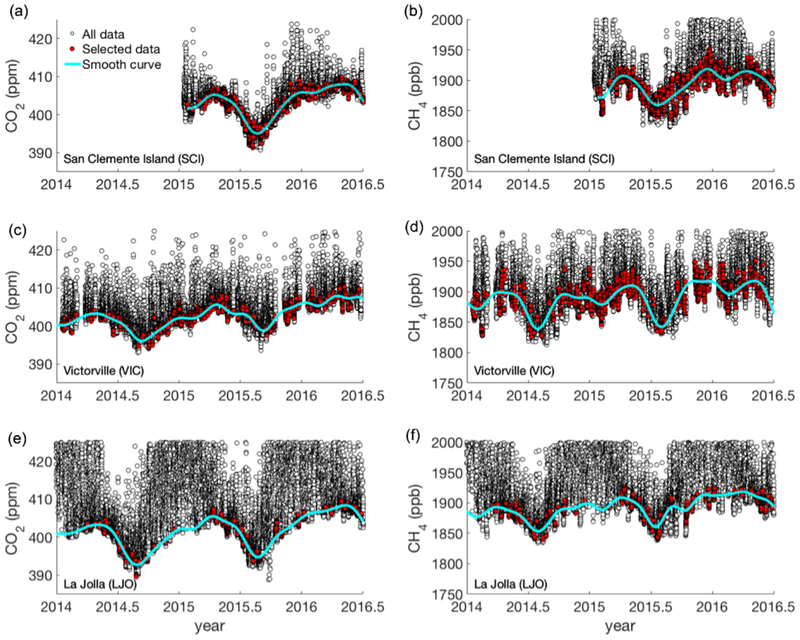
For LJO and SCI “marine” background and VIC “continental” background estimates, the air observations were filtered according to statistical criteria based on the variability in the hourly average data (see Supplement). As shown in Figs. 2 and 3, the CO2 and CH4 observations from SCI exhibit much lower variability compared to VIC and LJO. Figure S4 shows histograms of the hourly standard deviations for the SCI, VIC, and LJO observations. As discussed earlier, the variability in the LJO record is more similar to an urban or suburban site than a background site. This is primarily due to along-shore transport from the north and the proximity to other local sources (including a large landfill immediately to the east). After applying the selection criteria respective to each site, the CCGCRV curve-fitting software was used to estimate a “smooth curve” fit to the selected observations (Thoning et al., 1989; http://www.esrl.noaa.gov/gmd/ccgg/mbl/crvfit/crvfit.html). The curve-fitting parameters are described further in the Supplement. The full time series, selected data, and “smooth curve” results are shown in Fig. 3, and the final smooth curve results for each site are shown in Fig. 4a–b. We discuss the uncertainty in the smooth curve estimates in Sect. 6.2 (see also, Fig. S10).
Figure 3.
Time series of 1 h average observations from the San Clemente Island (SCI; a, b), Victorville (VIC; c, d), and La Jolla (LJO; e, f) sites between January 2014 and June 2016. Hourly average observations of CO2 (a, c, e) and CH4 (b, d, f) were filtered using stability criteria, as described in the text. The CCGCRV curve-fitting algorithm was then used to fit the selected data in an iterative approach by removing CO2 and CH4 outliers > ±2σ (see Supplement for further information on the fitting parameters). The final filtered data set (red points) and smooth curve fits (cyan lines) are also shown. Note: values outside of the range plotted are not shown.
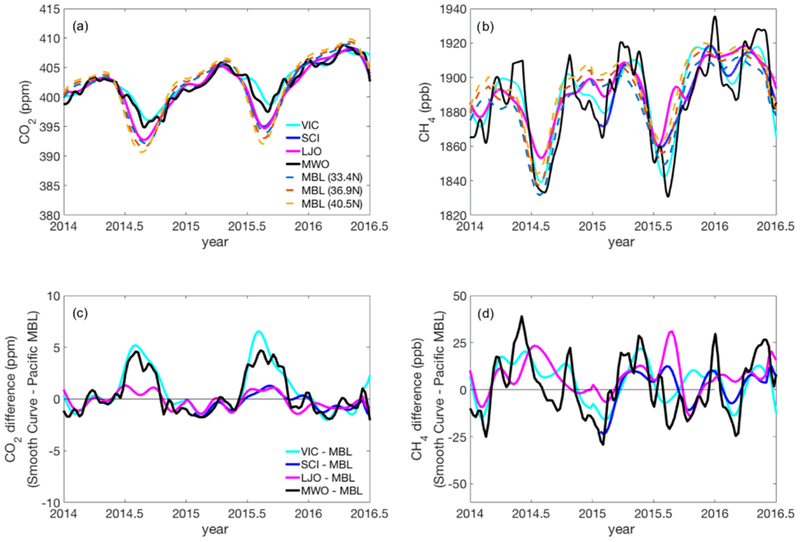
Figure 4.
Comparison of background estimates for Los Angeles for CO2 (a, c) and CH4 (b, d) at various sites from January 2014 to June 2016. (a–b) Smooth curve results for Victorville (VIC; cyan), San Clemente Island (SCI; blue), La Jolla (LJO; magenta), Mt. Wilson (MWO; black), and a 2-D Pacific marine boundary layer curtain estimate (MBL; light blue, red, and yellow dashed lines show results for at 33.4, 36.9, and 40.5° N, respectively). The SCI, VIC, and LJO curves were generated using data selected based on stability criteria. The MWO curve was generated using nighttime flask data collected every 3–4 days. (c–d) Background estimates from each site plotted as a difference from the MBL curtain at 33.4° N.
The MWO “continental” background estimate was developed using nighttime flask data from the Mt. Wilson mountaintop observatory (Fig. 1). At night, the PBL is shallow and the MWO site is more likely to be influenced by air from the free-troposphere. During the daytime, the MWO CO2 and CH4 mole fractions can be influenced by emissions from the basin either due to upslope winds or due to the rising of the PBL above MWO. Calibrated continuous in situ observations from MWO were not available at the time of this study. Instead, we used the MWO nighttime flask record from NOAA/ESRL to produce a smooth curve background estimate using a similar approach to that described above for the SCI, LJO, and VIC sites. Flask samples have been collected at MWO approximately every 3–4 days since 2010. Only flask samples collected between 23:00 and 05:00 LT were used in the smooth curve fit because nighttime samples are more likely to be representative of background conditions. The curve-fitting parameters are described in the Supplement. The final smooth curve results are shown in Fig. 4a–b.
The Pacific MBL reference surface was developed using weekly flask air samples from the NOAA’s Global Greenhouse Gas Reference Network (GGGRN, see http://www.esrl.noaa.gov/gmd/ccgg/mbl/ and Masarie and Tans, 1995; Fig. 4). The MBL reference surface is a data product smoothed in time and over latitude that uses NOAA measurements from samples that are predominantly influenced by well-mixed MBL air (typically remote, marine sea level locations with prevailing onshore winds). The Pacific MBL product provides a 2-D (latitude and time) representation of CO2 and CH4 mole fractions along the Pacific boundary of North America based on the subset of GGGRN MBL sites in the Pacific basin. We compare the results from SCI, LJO, VIC, and MWO to the Pacific MBL reference surface in Fig. 4.
We noted that the method used to estimate background would fail to give a measure of influences from outside the domain under some conditions. Below we compare the background estimates described above (Sect. 4.2) and discuss some meteorological considerations for background estimation (Sect. 4.3).
4.2. Comparison of background estimates
We compared the background estimates derived from the SCI, LJO, VIC, and MWO sites from January 2014 to June 2016 with the 2-D Pacific marine boundary layer reference from 33.4, 36.9, and 40.5° N (Fig. 4a–b). There are small but systematic differences in the background estimates determined for each site. Next, we subtracted each background reference curve and the Pacific MBL background estimate from 33.4° N (Fig. 4c–d). For CO2, the background estimates from SCI and LJO are both more similar to the Pacific MBL estimate from 33.4° N and show a more pronounced CO2 minima in the summer compared to the MWO and VIC background estimates. The average absolute difference between the Pacific MBL estimate at 33.4° N and each background estimate from SCI, LJO, VIC, and MWO for the period shown in Fig. 4 is 0.8, 0.7, 1.7 and 1.5 ppm CO2, and 8.0, 8.9, 10.1, and 13.7 ppb CH4, respectively. For CH4 the background curve from SCI is most similar to the Pacific MBL estimate. The average absolute differences between the background estimates from SCI and LJO and the Pacific MBL estimate from 33.4° N are < 1 ppm CO2 and < 10 ppb CH4, suggesting that both sites are useful for deriving marine background estimates for CO2 and CH4 when the appropriate filtering criteria are used. The cause of the larger differences between the continental (i.e., VIC and MWO) and marine (i.e., SCI, LJO, and Pacific MBL) background estimates is not clear. Future modeling studies could investigate whether a time-dependent background selection method – e.g., based on meteorological information and the origin of the incoming air mass – can be used to determine the appropriate background site under some of the more common meteorological regimes in the SCB. In Sect. 4.3 we discuss some additional considerations regarding atmospheric transport. In Sect. 5 we estimate CO2 and CH4 enhancements using the SCI background estimate, and in Sect. 6.2 we assess the uncertainty in the SCI background estimates relative to the enhancements near downtown LA.
4.3. Back-trajectory analysis
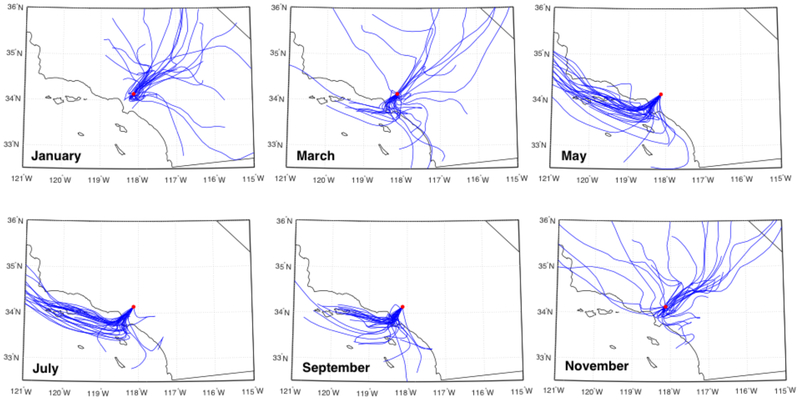
Our approach for estimating background mole fractions thus far has ignored variations in atmospheric transport. In reality, winds transport air masses in and through the SCB on various timescales. Therefore, the optimal background site for selecting observations could vary diurnally, weekly, monthly, and/or seasonally. Wind back trajectories can be useful for selecting a primary background site, based on the prevailing winds. We performed a simple back trajectory analysis and discuss below some preliminary conclusions based on that analysis. Results in Fig. 5 are shown for 14:00 LT; however, in general, the back trajectories computed for 12:00 and 16:00 LT show similar results.
Figure 5.
HYSPLIT back trajectories estimated for the previous 24 h, ending in Pasadena, CA (red circle, at the CIT measurement site), at 14:00 LT. Results are shown for January, March, May, July, September, and November 2015 (from top left to bottom right) using NAM12 hourly winds.
We computed 24 h back trajectories for winds arriving at the CIT site in Pasadena at 14:00 LT using the NOAA’s HYSPLIT model (Fig. 5; Stein et al., 2015; Rolph, 2016). During the warmer months (spring and summer, or roughly May through September), winds enter the basin almost exclusively onshore, originating over the ocean. These air masses generally travel south along the coast before being directed inland. Conversely, during the cooler months (fall and winter months, roughly November to March), there is much more variety in the provenance of the air masses (Fig. 5). During November to March, a significant fraction of days have offshore winds (i.e., from the north to northeast, and originating from the Mojave desert region over the mountains), which could indicate Santa Ana conditions, a typical mode of variability in the Los Angeles climatology (e.g., Conil and Hall, 2006). During offshore wind conditions, coastal sites such as La Jolla or San Clemente Island may not be relevant choices for selecting background observations as these sites may be subject to outflow and recirculation of an air mass from over land. Coastal (“Catalina”) eddies are also a common occurrence along the CA bight, which is the mostly convex part of the southern California coastline (Figs. 1 and 5). Conditions that favor coastal eddies are most common between April and September, though they can develop at almost any time of the year (Rahn and Mitchell, 2016). During such conditions, a site northwest of the Los Angeles Basin may be a more relevant choice for background. However, as shown in Sect. 4.2, the MBL background derived using the SCI and LJO sites was very similar to the Pacific MBL reference curves between ~33 and 40° N.
At least some of the differences in our background estimates from the LA sites can be explained by differences in the prevailing meteorological conditions and a lag in the transport of air masses between the sites. The VIC and MWO sites show larger differences from the marine background estimates during summer months for both CO2 and CH4. During summer months, the marine CO2 background estimates (from SCI, LJO, and the MBL estimates) all show a more pronounced CO2 minima in the summer compared to the MWO and VIC background estimates. This is consistent with the back-trajectory analysis in Fig. 5, which shows that onshore flow conditions are more persistent from May to September. Overall, the CO2 background estimates from VIC and MWO are most similar to one another. The total inlet elevation at VIC (1370 m a.s.l. + 100 m a.g.l. inlet height) is only about 200 m lower than at MWO (1670 m a.s.l.), suggesting these two sites may be sensitive to similar air masses under some meteorological conditions. Overall, the VIC and MWO sites may not be relevant choices for background during summer, when onshore flow patterns dominate. Conversely, SCI and LJO may not be relevant choices for background when flow is from the continent. In future studies, background data could also be selected based on the prevailing flow patterns in the region of interest (e.g., McKain et al., 2015).
Our back-trajectory analysis does not have the temporal resolution necessary to evaluate diurnal land–sea breezes. The spatial resolution of the NAM12 meteorological data used by HYSPLIT is 12 km. From this analysis, we can certainly see seasonal variations of the wind direction and the incoming air masses for the LA Basin. We do not compare the day–night differences in meteorology, such as land–sea breezes, in our analysis, though we note that these circulation patterns could be important for understanding the greenhouse gas variability (especially at coastal sites such as SCI, LJO, and possibly IRV). Such analysis would require a higher resolution model, such as the 1.3 km resolution WRF-Chem model discussed by Feng et al. (2016), which is beyond the scope of this study. Feng et al. (2016) found that sea breezes prevailed over the LA megacity at ~14:00 LT during the May–June 2010 (CalNex) study. Furthermore, the modeled topography of the Palos Verdes Peninsula was found to divide the sea breeze into west and southwest onshore flows that later converged in the Central Basin. In general, transport models do not do well overnight (Feng et al., 2016), which makes evaluation of diurnal variations challenging using modeled CO2 or CH4 output. Future modeling studies that overlap with the CO2 and CH4 measurement records will be needed to evaluate the impact of land–sea breezes on CO2 and CH4 observations from coastal sites and could also improve our understanding of the impacts of winds induced by topography on the greenhouse gas observations.
Feng et al. (2016) used results from a forward model simulation to explore correlations in pseudo-CO2 data in the SCB. They showed that CO2 is trapped and accumulates due to the mountain barrier, leading to CO2 enhancements at in-basin sites relative to the desert site at VIC. Feng et al. (2016) also found that while the modeled CO2 levels at the VIC desert site were mainly anticorrelated with the LA Basin sites, CO2 that accumulated in the basin could occasionally be pushed over the mountains and into the desert due to episodic strong sea breezes and onshore flow conditions. This supports our conclusions that VIC and MWO (nighttime) observations may not always provide representative background mole fractions, particularly during summer months when onshore flow conditions prevail.
It is important to note that our approach for evaluating background mole fractions from MWO relied on nighttime flask observations only, which were collected between 23:00 and 05:00 LT. Feng et al. (2016) refer to MWO as a “western basin” site, exhibiting spatial CO2 correlations similar to the GRA, CIT, USC, and COM sites. Feng et al. (2016) do not discuss day–night differences in the sensitivity of the MWO site. At night, when the PBL is shallower, there is a reduced likelihood for air from the SCB to be transported to the MWO site. In the future, continuous observations from MWO should be analyzed in conjunction with the nighttime flask record to evaluate diurnal variability in CO2 and CH4. While the simulations discussed by Feng et al. (2016) only cover a brief period during spring and summer 2010, future modeling studies over longer periods (e.g., 1 year) could improve our understanding of variations in the mesoscale circulation in the LA megacity and the impacts on the observed CO2 and CH4 mole fractions. The variety and complexity of meteorology in the South Coast Air Basin suggests that a more sophisticated background selection algorithm is needed to determine the site that is “upwind” during different prevailing wind conditions. Future model analyses could also help determine when our observation sites are most relevant for estimating background.
Overall, the LJO and SCI background estimates establish a marine sector background to within roughly 1 ppm CO2 and 10 ppb CH4 (excluding the period during summer 2015 discussed above). SCI is the most representative of local marine background conditions for both CO2 and CH4 throughout the year. The LJO background curve also helps confirm that the background estimate from SCI is reasonable. Therefore, we use SCI as the background reference site to calculate CO2 and CH4 enhancements for the LA surface sites (see Sect. 5).
5. CO2 and CH4 enhancements
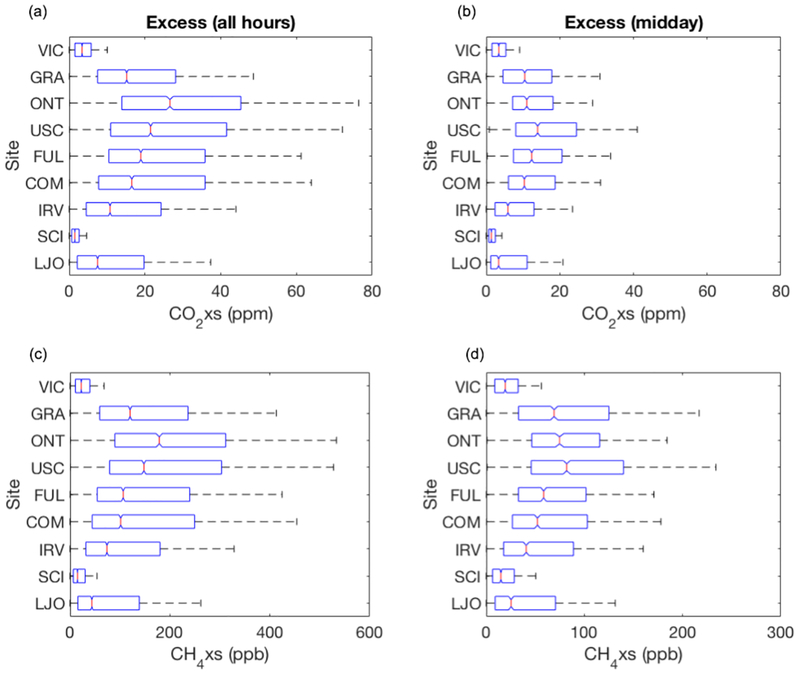
We calculated the average enhancement at each site using the SCI marine background reference. Moderate to large CO2 and CH4 enhancements (CO2xs and CH4xs) are observed above the background mole fractions. Tables 4 and 5 show statistics regarding the enhancement at each site estimated for all hours and mid-afternoon hours (12:00–16:00 LT, not including adjustment for daylight savings time) during 2015. Figure 6 shows the annual average CO2xs and CH4xs values at nine sites for observations collected during all hours and mid-afternoon hours during 2015, with sites arranged by latitude. Overall, the results show that the CO2 and CH4 enhancements in LA are characterized by a large degree of spatial and temporal variability (Fig. 6). During mid-afternoon hours – the period of the day that is most relevant for flux inversions – the median enhancement in 2015 was 13.9, 12.310.3, 10.4, and 5.9 ppm CO2xs and 82, 58.3, 52, 69, and40.6 ppb CH4xs at the USC, FUL, COM, GRA, and IRV sites, respectively (Tables 4 and 5). During 2015, largest mid-afternoon median CO2 values were observed at the USC and FUL sites and the largest CH4 enhancements were observed at the USC and GRA sites. We do not discuss the results from the Ontario site in detail because measurements were only available from September to December 2015 and therefore are not representative of the annual average.
Table 4.
Statistics for the CO2xs observations from eight of the sites shown in Fig. 2. Mean; SD; 16th, 50th (median), and 84th percentiles; minimum and maximum; and RMS values were computed based on the hourly average enhancements calculated during calendar year 2015. Results are shown for observations collected during “All hours” and “Mid-afternoon” hours only (12:00–16:00 LT). For USC, results are shown for the G2401 analyzer only. ONT results are not shown because measurements were only available from September to December 2015.
| CO2xs | VIC | GRA | USC | FUL | COM | IRV | SCI | LJO | |
|---|---|---|---|---|---|---|---|---|---|
| All hours | mean | 4.2 | 19.9 | 30.8 | 26.3 | 26.7 | 17.1 | 2.0 | 12.7 |
| 1σ SD | 3.5 | 16.8 | 28.6 | 22.0 | 27.5 | 17.5 | 2.2 | 13.5 | |
| min | 0 | 0 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | |
| 16th | 1.0 | 5.1 | 8.1 | 7.9 | 5.8 | 2.9 | 0.4 | 1.3 | |
| median | 3.4 | 15.2 | 21.5 | 18.9 | 16.5 | 10.8 | 1.5 | 7.5 | |
| 84th | 7.3 | 35.1 | 53.8 | 46.9 | 49.9 | 32.5 | 3.3 | 26.4 | |
| max | 41.0 | 126.5 | 222.6 | 171.2 | 203.4 | 126.8 | 23.0 | 93.0 | |
| RMS | 1.0 | 5.4 | 9.0 | 6.8 | 8.8 | 5.3 | 0.6 | 3.9 | |
| Mid-afternoon | mean | 3.9 | 12.8 | 18.8 | 16.4 | 15.2 | 10.1 | 1.9 | 7.6 |
| 1σ SD | 3.2 | 11.1 | 15.9 | 13.8 | 15.2 | 11.8 | 2.0 | 9.5 | |
| min | 0 | 0 | 0.8 | 0.3 | 0.1 | 0 | 0 | 0 | |
| 16th | 1.0 | 2.8 | 6.1 | 5.7 | 4.9 | 1.5 | 0.5 | 0.7 | |
| median | 3.4 | 10.4 | 13.9 | 12.3 | 10.3 | 5.9 | 1.4 | 3.4 | |
| 84th | 6.6 | 22.3 | 31.3 | 25.9 | 24.1 | 18.9 | 3.1 | 16.6 | |
| max | 41.0 | 99.1 | 124.8 | 94.4 | 152.9 | 93.2 | 21.3 | 66.4 | |
| RMS | 0.9 | 3.5 | 5.0 | 4.3 | 4.9 | 3.5 | 0.5 | 2.7 |
Table 5.
Same as Table 4, but for CH4xs observations.
| CH4xs | VIC | GRA | USC | FUL | COM | IRV | SCI | LJO | |
|---|---|---|---|---|---|---|---|---|---|
| All hours | mean | 29.8 | 217.0 | 224.0 | 183.5 | 188.9 | 144.0 | 25.3 | 129.9 |
| 1σ SD | 26.0 | 335.1 | 212.8 | 209.2 | 219.9 | 195.9 | 32.1 | 250.5 | |
| min | 0 | 0 | 0.8 | 0.1 | 0 | 0.1 | 0 | 0 | |
| 16th | 6.6 | 39.8 | 59.6 | 40.6 | 30.3 | 21.4 | 4.3 | 9.1 | |
| median | 22.5 | 120.1 | 147.9 | 106.4 | 101.4 | 73.9 | 14.9 | 43.7 | |
| 84th | 50.3 | 328.3 | 403.8 | 331.8 | 372.4 | 268.5 | 43.6 | 216.8 | |
| max | 484.9 | 5085.0 | 2615.0 | 2611.4 | 1614.0 | 2821.3 | 453.3 | 3520.4 | |
| RMS | 6.8 | 63.5 | 61.4 | 48.6 | 52.9 | 38.6 | 6.0 | 34.3 | |
| Mid-afternoon | mean | 24.6 | 99.2 | 113.8 | 85.6 | 84.4 | 72.2 | 23.6 | 53.6 |
| 1σ SD | 23.2 | 119.4 | 105.8 | 88.9 | 98.0 | 92.2 | 29.2 | 68.4 | |
| min | 0.2 | 0 | 0.8 | 0.1 | 0.3 | 0.2 | 0 | 0 | |
| 16th | 5.2 | 20.3 | 35.1 | 24.4 | 18.3 | 11.0 | 3.7 | 6.1 | |
| median | 19.3 | 69.0 | 82.0 | 58.3 | 52.0 | 40.6 | 14.9 | 25.3 | |
| 84th | 43.0 | 162.3 | 187.7 | 139.0 | 140.3 | 125.9 | 40.5 | 114.1 | |
| max | 187.2 | 1666.3 | 785.9 | 813.3 | 857.5 | 1063.8 | 313.7 | 508.7 | |
| RMS | 5.4 | 37.1 | 33.4 | 27.2 | 31.0 | 27.4 | 7.6 | 19.7 |
Figure 6.
Boxplot of enhancements (CO2xs and CH4xs) in the LA megacity observed during 2015 relative to the San Clemente Island background estimate. Results are shown for CO2xs (a, b) and CH4xs (c, d) and for all hours (a, c) and mid-afternoon hours (12:00–16:00 LT, b, d). The sites are arranged by latitude from north to south (top to bottom): Victorville (VIC), Granada Hills (GRA), Ontario (ONT), downtown LA (USC), California State University, Fullerton (FUL), Compton (COM), University of California, Irvine (IRV), San Clemente Island (SCI), and La Jolla (LJO). Boxes outline the 25th and 75th percentiles of the sample data, respectively, and red horizontal lines show the median values at each site. Values outside the 25th and 75th percentiles are not shown here but are plotted in Fig. S11. (Note: only positive enhancements are shown. Results for the ONT site are for September to December 2015, while all other results are annual averages. Results from the USC site are shown for the G2401 analyzer only).
In general, the CO2 and CH4 enhancements are larger in winter relative to spring and summer months. Anthropogenic (fossil) CO2 sources dominate in winter months due to increased emissions from the residential and electric production sectors (Wong et al., 2015). Increased summertime insolation is expected to produce a deeper afternoon mixed layer depth in summer relative to winter, which in turn would result in larger trace gas enhancements within the PBL during winter relative to summer. As discussed earlier, Ware et al. (2016) used backscatter data from a MiniMPL instrument located in Pasadena, CA, to estimate mixing heights over 2 years from 2012 to 2014. They found that the mean afternoon maximum mixing depth was 770 m a.g.l. in summer (June and August) and 670 m a.g.l. in winter (December–February). However, seasonal differences in mixing depth should also be considered in the context of the daily and weekly variability. Ware et al. (2016) show that the maximum depth of the afternoon mixing layer may differ by a factor of 2 from day to day. Additionally, Ware et al. (2016) show that the within-season SD for the afternoon maximum mixing height is about 220 m, or approximately 30 % of the mean afternoon maximum mixing depth in either summer or winter (which is larger than the observed average seasonal differences in mixing height). Overall, the large variability in mixing layer depth over different timescales suggests that the meteorological impacts on trace gas concentrations in the PBL can also be quite variable.
On average, the more urbanized areas, such as the USC site near downtown LA, exhibit larger median CO2xs values during 2015 (Fig. 6 and Table 4). CH4 shows a slightly different spatial distribution in the median enhancement relative to CO2, with the second largest CH4 enhancements observed at the GRA site (Fig. 6), which is a suburban site located in the San Fernando Valley. CO2xs and CH4xs exhibit long-tail distributions, which is a reason why we report the median and interquartile range in Tables 4 and 5 in addition to the other statistics. As mentioned earlier, relatively large CH4 excursions, on the order of 4 ppm above background or more, are observed throughout the GRA time series (Fig. 2). The GRA site also exhibits a long-tail distribution with respect to the CH4 enhancements, which is more pronounced compared to the other sites, even during mid-afternoon hours (see Supplement, Fig. S11, which shows data outside the interquartile range). Many of the larger enhancements occur during nighttime–early morning hours. The smaller enhancements during mid-afternoon hours relative to night suggest that GRA may be sensitive to a local CH4 source at night, when the PBL becomes shallower and could be more stratified.
The long-tail distribution for CH4 in Los Angeles and the prevalence of fugitive CH4 emissions across the LA urban landscape was previously demonstrated by Hopkins et al. (2016), using extensive mobile surveys. Hopkins et al. (2016) identified 75 % of methane hotspots to be of fossil origin, while 20 % were biogenic, and 5 % of indeterminate source using the ratio of ethane to methane (C2H6 / CH4). They also found that fossil fuel sources accounted for 58 to 65 % of methane emissions and suggested that there are widely distributed methane sources, primarily of fossil origin, that are not included in bottom-up inventories. In future work, detailed analysis of winds, measurement footprints, and tracer–tracer analyses will be used to evaluate the origin of the anomalous CH4 enhancements.
6. Uncertainty in the CO2 and CH4 enhancements (Uexcess)
Both measurement uncertainty and imperfect knowledge of the composition of background air limit the precision of observation-based estimates of local- or regional-scale greenhouse gas enhancements (e.g., Graven et al., 2012; Turnbull et al., 2009, 2015). We estimate the uncertainty in the enhancement as follows:
| (4) |
where Uexcess is the total uncertainty in the enhancement of CO2 or CH4 and is defined as the quadrature sum of the uncertainty in the air measurement (Uair) and the uncertainty in the background mole fraction (UBG). We note that UBG is not statistically independent of Uair because UBG is derived from measured values. In the remainder of this study, we explore the measurement uncertainty in our approach and calibration strategy (Uair) using data from the LJO site (Sect. 6.1) and the uncertainty in the background mole fraction using the marine reference background from SCI (Sect. 6.2).
6.1. Measurement uncertainty analysis (Uair)
We model the uncertainty in the air measurements following the general methods outlined in Andrews et al. (2014), using the quadrature sum of multiple uncertainty components:
| (5) |
where
| (6) |
or
| (7) |
(whichever is greater).
Equation (5) describes Uair, the total uncertainty in the reported air mole fractions, and its individual components, which have units in mole fraction CO2 or CH4 (ppm or ppb). In Eq. (5), Uextrap is the extrapolation uncertainty, or the uncertainty introduced because the measured mole fraction of the air sample differs from the value of the calibration standard (Sect. 6.1.1), and Uh2o is uncertainty from the treatment of water vapor (Sect. 6.1.2). In Eqs. (6)–(7), UM is the greater of two terms, defined by either UTGT, the uncertainty determined by the target tank measurements, or the quadrature sum of several terms: Up is the analyzer precision (Sect. 6.1.4), Ub is the analyzer calibration baseline uncertainty (Sect. 6.1.5), and Uscale is the scale reproducibility (Sect. 6.1.6). In Eq. (6), UTGT is equivalent to a root mean square error (RMSE), and is estimated using the corrected target tank residual over 10 days, similar to Andrews et al. (2014) (Sect. 6.1.3).
Overall, Eqs. (5) to (7) describe a generic algorithm that can be applied to other analyzers as well as to CO measurements. Time-dependent monitoring of Ub, Up, and UTGT is useful when tracking analyzer performance. Although the overall measurement uncertainty is typically small, an increase in any of these values (Ub, Up, or UTGT) may indicate problems with a specific analyzer. Thus, this system could be used to generate alerts for the data user to identify periods when an analyzer is performing poorly or to indicate periods when the measurements may not be useful for atmospheric inverse modeling studies.
6.1.1. Extrapolation uncertainty (Uextrap)
We corrected the air measurements in Fig. 2 using a single-point calibration method. As a result, any air measurement that is different from the value of the calibration standard is subject to an extrapolation uncertainty, Uextrap, which is the uncertainty introduced because the measured mole fraction of the air sample differs from (and in many cases is larger than) the value of the calibration standard (around 400 ppm CO2 and 1850 ppb CH4). We estimate Uextrap as follows:
| (8) |
where ε (described below) has units of ppm ppm−1 or ppb ppb−1 and is multiplied by the absolute value of the difference between the sampled air concentration and the assigned calibration tank value . We estimate this uncertainty as a linear function of based on calibration analysis of multiple similar model CDRS units in the laboratory that show a linear relationship in the error (discussed further below and shown in Figs. S5 and S6).
Our approach relies on independent estimates of ε, the slope parameter, to determine the magnitude of the systematic and random components of the error in our calibration method. Ideally, initial estimates of ε would be determined empirically by testing each analyzer in a laboratory prior to deployment in the field to provide estimates of the magnitude of the extrapolation uncertainty (e.g., Andrews et al., 2014; Richardson et al., 2012). At the time of this study, it was not possible to test many of the CRDS analyzers in a laboratory prior to deployment in the field because high mole fraction standards spanning the range of CO2 and CH4 measurements expected in LA were not available.
Since a suite of calibration standards was not available at the time of this study, we determined “ using the average “correction” slope determined from analysis of a series of standard tanks at different mole fraction tanks on a suite of CRDS analyzers. Within the LA network, only the LJO and VIC analyzers had field calibration data from high mole fraction tanks available at the time of this study. We used the limited measurements of these high mole fraction tanks (approximately 500 ppm CO2 and 2600 ppb CH4) to compute an average ε over the period when the tank was available. We also investigated laboratory calibration data from the seven additional Picarro CRDS model G2401 and G2401-m analyzers, as described below. These analyzers are not part of the network but are similar to the CRDS analyzers used in the field in the LA network.
Calibration analyses for the seven independent analyzers were performed at NOAA/ESRL during 2014 to 2015 with between three and seven reference tanks calibrated on the WMO scales for each gas (up to approximately 470 ppm CO2 and 3060 ppb CH4). A single standard tank (the tank with a CO2 value closest to 400 ppm) was set as the calibration standard and was used to correct the CRDS reading for the other standard gases using Eq. (2). Next, we plotted the residual of the corrected mole fraction for each tank measurement and its assigned value (Xcorr − Xassign) as a function of the difference in the assigned mole fraction between a given tank and the calibration tank . The slope of this relationship is equivalent to ε for a given analyzer. Estimates of the correction factor, ε, and regression statistics for these seven analyzers are summarized in Tables S2 and S3, and the data are shown in Figs. S5 and S6 (see Supplement).
The values of the slope correction (ε) are 0.0027 and 0.0018 ppm ppm−1 for CO2 and 0.0012 and0.0060 ppb ppb−1 for CH4, for the LJO and VIC analyzers, respectively. These results are compared with the other analyzers in Table S2. For CH4, all analyzers show a clear linear relationship between the error and the mole fraction of the tank, and there is very little difference in the slope between different analyzer units (see Supplement, Fig. S6). Interestingly, for CO2, we find that the two older analyzers (CFKBDS-2007 and CFKBDS-2008) have larger slopes, while the majority of the analyzers have very little dependence on the mole fraction and have errors close to zero (see Fig. S5). The results in Table S2 are used to estimate the magnitude of the error in the corrected air sample mole fractions caused by assuming a constant analyzer sensitivity, or slope correction. The average value of ε from all nine analyzers was used in Eq. (8) to estimate the uncertainty in this correction (Uextrap). The slope from these calibration experiments (ε) gives an estimate of the error in the single-point calibration and how it increases when the measurement is farther from the value of the single calibration point. Overall, Uextrap is proportional to the fractional difference between the mole fraction of the air sample and that of the ambient-level calibration tank. The average and standard deviation of ε also provide estimates of the systematic and random components of the error in the single-point calibration method (Table S3).
We also estimated the error associated with the single-point calibration strategy using Eq. (8) and various estimates of ε for three cases: (1) the average and standard deviation of ε from all nine analyzers, (2) the average ε from seven analyzers (excluding LJO and VIC), and (3) an instrument-specific estimate of ε from the LJO site (Tables S2 and S3). Next, we estimated the error, assuming an hourly average air measurement of 500 ppm CO2 and 6000 ppb CH4(i.e., roughly 100 ppm CO2 and 4000 ppb CH4 enhancement above the near-ambient calibration standard). Finally, we corrected air data from the LJO and VIC sites using an “alternate calibration method”, during times when a limited number of measurements of a high mole fraction CO2 and/or CH4 standard were available for analysis (see Supplement, Figs. S2 and S3). Overall, the difference between the single-point (default) calibration method and the “alternate calibration method” are < 0.2 ppm CO2 and < 5 ppb CH4 for the majority of air measurements. We also estimated the maximum correction using both approaches (the “alternate calibration method” and a correction and error based on Uextrap), and the results are summarized in Table S3.
While the initial results are very promising, and the corrections tend to be small, there is a large degree of variability in the estimates of ε for individual analyzers. The value of ε can be different for different analyzers and can also change over time for a single analyzer (Tables S2 and S3 and Figs. S5 and S6). Based on the experiments discussed here, our current calibration strategy could be modified to correct the concentration data using the mean value of ε found from all the analyzers and estimating an uncertainty in that correction. However, our approach for estimating ε is based on a relatively small statistical sample of analyzers. Furthermore, the two estimates we do have from the LJO and VIC field sites only rely on one additional calibration point other than the calibration tank, making it difficult to estimate a robust fit for these analyzers. An estimate of ε for each analyzer in the field (or from a larger statistical sample of analyzers) is needed to provide a robust estimate of the mean ε to correct the air sample data. Values of ε could also be estimated for the analyzers deployed in the field, for example, by deploying a suite of calibration standards with varying concentrations of CO2 and CH4 (e.g., a round robin). We have chosen not to correct the data and keep it tied to the single-point calibration until more experimental evidence can be obtained. In the future, the surface network will move to a two-point calibration strategy. This will rely on the availability of high mole fraction tanks for deployment in the field and a calibration uncertainty that is lower than our current estimates for Uextrap.
6.1.2. Uncertainty associated with water vapor (Uh2o)
The presence of water vapor in the sample air contributes to the uncertainty in the CRDS measurements. Below we describe three potential sources of uncertainty in the measurements due to water vapor: (1) the coefficients used to determine the water vapor correction, which can vary from instrument to instrument; (2) bias due to imperfect drying; and (3) random noise in the H2O measurement reported by the CRDS analyzer, which ultimately gets incorporated into the water vapor correction (Rella et al., 2013).
The Picarro CRDS analyzers use a factory default water vapor correction model that relies on the parameters derived by Chen et al. (2010):
| (9) |
| (10) |
where Hrep is the water vapor mole fraction reported by the analyzer, (CO2)wet and (CH4)wet are the uncorrected CRDS, wet-gas mole fractions reported by the analyzer, and (CO2)dry and (CH4)dry are the dry-gas mole fractions, while a, b, c, and d are experimentally determined parameters (where a = −0.012000, b = −0.0002674, c = −0.00982, and d = −0.000239). This correction is currently being applied to the analyzers in the LA network. Users are free to design and perform their own experiments and derive parameters specific to each instrument (Nara et al., 2012; Rella et al., 2013; Welp et al., 2013). However, while an instrument-specific correction of water vapor could potentially lead to reduced uncertainty, prior laboratory studies have also found that the benefits of applying an instrument-specific correction are small at low water vapor levels (Nara et al., 2012; Rella et al., 2013).
The Nafion drying system described in Sect. 2.3 and by Welp et al. (2013) allows us to stabilize the water vapor concentrations in the sample gas stream (Hrep in Eqs. 9–10) to 0.1 ± 0.01 %. With this drying system, the uncertainty in the water vapor correction drops to 0.015 ppm for CO2 and 0.21 ppb for CH4 when using the factory parameters described above (Rella et al., 2013; Welp et al., 2013).
The use of a Nafion dryer could also potentially introduce a bias due to imperfect drying. A slight permeation of CO2 and CH4 can occur across the membrane, especially when the Nafion membrane is wet (e.g., Ma and Skou, 2007; Welp et al., 2013). In our measurement setup, running the dry standard gases through the Nafion dryer significantly reduces this bias effect. The water vapor concentration from the dry standard gas runs is similar to that of the preceding air measurements. We find that the water vapor mole fraction in the air measurements after a standard tank run drops by 0.01 % (from 0.10 to 0.09 %). A similar effect has been described by Rella et al. (2013). We estimate the Nafion dryer bias in our system based on this 0.01 % variability in water vapor to be −0.011 ppm for CO2 and 0.00028 ppb for CH4 based on laboratory experiments performed at the SIO laboratories with the same Nafion drying system used in the field. Details about the laboratory experiments are available in the Supplement (Fig. S7).
A final source of uncertainty regarding the water vapor correction comes from the variability of the water vapor measurement on the CRDS analyzers. We estimate this to be0.014 ppm for CO2 and 0.069 ppb for CH4 at the water vapor concentrations of our measurements (Rella et al., 2013; Welp et al., 2013).
The total uncertainty due to water vapor (Uh2o) is the quadrature sum of the water vapor correction uncertainty, the Nafion-dryer-induced bias due to changes in water vapor, and the variability (noise) of the water vapor measurements. Therefore, we estimate that Uh2o is 0.0233 ppm for CO2 and0.221 ppb for CH4 across the network, and it is assumed to be constant at all times.
6.1.3. Uncertainty derived from target tank measurements (UTGT)
We define UTGT in Eq. (6), where the target tank is treated as an unknown and the measured value is compared to the tank assignment to calculate the root mean square error:
| (11) |
where is the corrected target tank measurement and is the assigned value of the target tank by the calibration laboratory (NOAA/ESRL or SIO). The assigned values are constant over the lifetime of the cylinder and are determined based on laboratory measurements traceable to the WMO scales. Errors in the tank assignments are typically small and would result in a bias in the measurement rather than a random error (see Sect. 6.1.6). To calculate , the uncorrected CRDS target tank concentration readings are treated as an unknown sample and are corrected using Eq. (2). For each target tank measurement, UTGT is calculated as the RMSE (Eq. 11) over 11 target measurements centered on the measurement time (this is usually a 10-day period). Then, this time-dependent UTGT is interpolated in time onto all the air measurements. Overall, UTGT includes errors in the assigned value of the calibration tank and the target tank, and also encompasses other errors (e.g., the instrument precision and the calibration standard baseline uncertainty), as well as additional and possibly unknown errors due to delivery of air to the analyzer downstream of the Valco valve. Drift in either the calibration or target cylinders will also manifest as an increasing UTGT. In this way, UTGT is useful as a diagnostic of instrument performance.
6.1.4. Analyzer precision (Up)
The analyzer precision (Up) is defined as the standard deviation of the 10 min daily calibration standard tank measurement:
| (12) |
where σcal is the standard deviation of the uncorrected CRDS, dry mole fraction measurements for the calibration tank at roughly 2.5 s resolution. Our definition of Up is different from that described by Andrews et al. (2014), where the analyzer precision was defined as the standard error of the calibration measurements. To use the standard error, we must assume statistical independence of the measurements and estimate a maximum value for N, which is the number of samples in the average that reduce the uncertainty.
We performed an Allan deviation analysis to estimate the stability of the Picarro CRDS analyzer due to noise processes. The Allan deviation is the square root of the Allan variance (Allan, 1966, 1987) and was plotted as a function of averaging time for calibration runs at the LJO site during January 2016 (Fig. S8). During this month, the calibration tank was run 28 times through the CRDS analyzer for 30 min each time (10 min longer than the normal calibration run period, for quality check purposes). We omitted the first 10 min of data and performed the Allan deviation analysis on the next 20 min of data for each of the 28 calibration runs. We found that the instrument variability does not decrease with averaging as would be expected (with a slope of −1/2) for a white noise profile, indicating a correlation in the noise at various longer timescales. In other words, the deviation (noise) does not decrease as the inverse square root of the averaging time , as it would for white noise. Filges et al. (2015) found a comparable result using similar CRDS units. Figure S8 shows the Allan deviation analysis for a subset of six (for figure clarity) of the LJO calibration runs over the course of the month, which also indicates that the characteristics of the noise in the analyzer may vary. The deviation does decrease with averaging time, but not in a consistent manner. Therefore, we have chosen not to compute the standard error in the mean by dividing the standard deviation by the square root of the number of measurements, because the characteristics of the noise in the analyzer vary with time and the data does not fit the criterion of the measurements being truly independent. We therefore quantify the precision of the analyzers as the 2.5 s standard deviation independent of averaging time, recognizing that it is likely an overestimate of the analyzer precision. This uncertainty for CO2 and CH4 is small compared to other sources, so we chose to retain it, and in the future (or for other species, such as CO) the precision could be modeled in a more robust manner.
6.1.5. Calibration baseline uncertainty (Ub)
To estimate the calibration baseline uncertainty (Ub) we follow a process similar to that described by Andrews et al. (2014). First, we calculate three different possible time series of the calibration tank measurement (X′) to estimate S (in this case, the instrument sensitivity measured for the calibration tank). The first is an interpolation onto air data using every calibration run. The second and third time series use alternate sampling of the calibration tank time series (i.e., by either odd or even sampling of every other daily calibration run) to interpolate X′ onto the time series of the air sample data (Fig. S9). Next, we calculate the dry-air mole fraction corrected at each point using each of these three different time series. The maximum uncertainty, , is estimated as the standard deviation of the three corrected mole fractions (black solid line, Fig. S9). The actual baseline uncertainty, Ub, is equal to this maximum value at the halfway point in time between subsequent calibration runs, and goes to zero at the time of a calibration run, since at that time the calibration value is known exactly. Thus, Ub is equal to weighted by the time difference between an air sample measurement and the adjacent calibration run (dashed line, Fig. S9).
6.1.6. Uncertainty in calibration tank assignments (Uscale)
Absolute scale accuracy includes uncertainties in the values assigned to the primary calibration standards as well as scale propagation errors (Andrews et al., 2014). Here we report an expanded uncertainty (95 % CL, approximately 2σ): 0.20 at 400 ppm CO2 (WMO X2007 scale) and 3.5 at 1850 ppb CH4 (WMO X2004A scale), where the total uncertainty is a relatively small function of the measured mole fraction. However, in our case, all measurements are calibrated relative to the same (WMO) scales, so scale reproducibility is the relevant metric for assessing measurement compatibility over time and between sites. Similar to Andrews et al. (2014), the reported scale reproducibility is 0.06 ppm for CO2 and 1.0 ppb for CH4 (2σ) (B. Hall, personal communication, 2016). We use the 1σ scale reproducibility (Uscale) in the calculation of Uair (0.03 ppm CO2 and 0.31 ppb CH4).
Cylinder drift has not been discussed and could also impact the measurement uncertainty. Andrews et al. (2014) report a mean difference between pre- and post-deployment tank calibrations of CO2 and CH4 for tanks prepared by the NOAA/ESRL laboratories. CO2 has rarely been observed to drift in cylinders. Andrews et al. (2014) report a mean difference between pre- and post-deployment tank calibrations of 0.02 ± 0.05 ppm CO2 (post-minus pre-deployment from 177 tanks analyzed over approximately 10 years). CH4 standards are generally very stable, and field calibration residuals reported for CH4 have not indicated any drift in the tanks (for CH4 absolute stability is reported as 0 ± 0.1 ppb year−1; Dlugokencky, 2005; Dlugokencky et al., 1994; Andrews et al., 2014). At the time of this study, none of our field calibration cylinders for the LA surface network had final calibrations; however, routine field measurements of standard tanks to date do not indicate significant drift in either gas.
6.2. Uncertainty in the background estimates
We define the time-varying uncertainty in the background estimate as follows:
| (13) |
where is the absolute value of the monthly average residual of the selected background observations (red points, Fig. 3) from the smooth curve result. Due to the method used to filter the observations, there are some gaps in the background observations. The background reference curves interpolate over observation gaps; however, the portions of the curve that are not constrained by observations are more uncertain relative to other periods. For data gaps longer than 1 month, it is not possible to estimate . Since there are no observations to constrain the curve, we assign an interpolation uncertainty based on the maximum annual average residual. In other words, if there are long observation gaps, the interpolation uncertainty will default to the maximum residual based on periods when observations were available. The time-varying uncertainty estimates for the SCI, VIC, and LJO reference curves are shown in Fig. S10. During 2015, the annual average uncertainty in the SCI smooth curve estimate is 1.4 ppm CO2 and 11.9 ppb CH4. This amounts to roughly 10 and 15 % of the median mid-afternoon enhancement near downtown LA (i.e., at the USC site) for CO2 and CH4, respectively.
6.3. Comparison of uncertainty estimates
Figure 7 shows the time-dependent measurement uncertainty estimates for the LJO site, and Table 6 gives the average values for each uncertainty term during 2015. We assigned fixed values for Uscale (0.03 ppm CO2 and 0.31 ppb CH4) and Uh2o(0.0233 ppm CO2, 0.221 ppb CH4). Overall, Uh2o and Uscale are small components of Uair, which is the overall measurement uncertainty. We do not have time-dependent estimates of all the uncertainty terms used in calculating Uair for every analyzer.
Figure 7.
Time series of uncertainties in the La Jolla (LJO) air observations. Up is the analyzer precision, UTGT is the uncertainty derived from the target tank measurements, Ub is the calibration baseline uncertainty, and Uextrap (abbreviated Uex in this figure) is the extrapolation uncertainty, or the uncertainty due to the single-point calibration strategy. Uextrap was estimated using a mean ε for nine analyzers (see text and Supplemental materials). The total analytical uncertainty in the air measurements (Uair) is calculated as described by Eqs. (5)–(7).
Table 6.
Summary of the average uncertainty estimates for the LJO analyzer during 2015. Each component of the total measurement uncertainty is listed, where is the total mean annual uncertainty in the air measurements collected during 2015 and calculated as described by Eqs. (5)–(7), is the average annual uncertainty in the enhancement, Uh2o is the uncertainty due to the treatment of water vapor, is the mean uncertainty derived from the target tank measurements, is the mean analyzer precision, is the mean calibration baseline uncertainty, and is the extrapolation uncertainty, or the uncertainty due to the single-point calibration strategy, which was estimated using a mean ε for nine analyzers (see text and Supplement).
| Uncertainty estimates | CO2 (ppm) | CH4(ppb) |
|---|---|---|
| Uh2o | 0.0233 | 0.221 |
| Uscale | 0.03 | 0.31 |
| 0.0166 | 0.2126 | |
| 0.0242 | 0.2205 | |
| 0.0028 | 0.0444 | |
| 0.0477 | 0.4618 | |
| 0.0699 | 0.7224 | |
| 1.36 | 11.89 |
Under normal operating conditions, the calibration baseline uncertainty (Ub) and the analyzer precision (Up) are also negligible. The average Ub is 0.0042 ppm and 0.054 ppb for CO2 and CH4, respectively, with no significant outliers (based on the average for 11 analyzers deployed in the field). Similarly, Up is a very small component of the overall uncertainty. Similarly, the values for analyzer precision across the network are similar to those derived from the LJO analyzer under normal operating conditions (roughly 0.024 ppm CO2, 0.22 ppb CH4 for the 20 min average air observations, and0.011 ppm CO2 and 0.12 ppb CH4 for the 1 min average air observations). Both Ub and Up can become non-negligible components of the uncertainty if there are problems with either the CRDS analyzer or the delivery of calibration gas to the analyzer. For example, the standard deviation of some calibration runs may be higher than the values reported for the LJO analyzer suggest, either because of analyzer noise increasing due to hardware or software problems, analyzer drift during a calibration run, or because a limited number of calibration measurements were available to calculate an average due to analyzer problems. Therefore, the values derived from the LJO analysis represent the minimum quantities we expect for Up, which is representative of the precision from a well-performing analyzer.
Overall, Uextrap provides an estimate of the uncertainty due to the single-point calibration method, which is the largest component of uncertainty in the air measurements (Fig. 7 and Table S3). We find that Uextrap is linearly dependent on the difference between the mole fraction of the air sample and that of the ambient-level calibration tank, at least over the range of mole fractions tested (see Supplement, Figs. S5 and S6). As described earlier, we do not have instrument-specific estimates of ε for every analyzer to use in estimating Uextrap. Therefore, we assumed constant values for ε based on the average of the nine analyzers shown in Table S2. During 2015, the average Uextrap value estimated for the LJO analyzer is0.047 ppm CO2 and 0.46 ppb CH4. The magnitude of Uextrap is larger for air data with higher mole fractions and scales as a percentage of the difference in the mole fraction of the air sample above the assigned value of the calibration tank. On average, the uncertainty due to Uextrap results in an uncertainty in the enhancement on the order of 0.0025 ppm ppm−1(0.25 %, or 0.25 ppm for a 100 ppm enhancement) for CO2 and 0.003 ppb ppb−1 (0.3 %, or 0.30 ppb for a 100 ppb enhancement) for CH4. Based on analysis of the LJO data during 2015, the average value of Uair is 0.070 ppm CO2 and0.72 ppb CH4 (Table 6). Overall, these experiments show that the single-point calibration introduces rather small errors in the final mole fraction assignments for CO2 or CH4 and especially relative to the enhancement above background (Fig. 7 and Tables 4–5).
We used Eq. (4) to estimate the uncertainty in the enhancement signal using the estimates of Uair and UBG for the LJO analyzer and the SCI background estimate, respectively. Since Uair and UBG are both time varying, the uncertainty in the enhancement is also time dependent. On average, uncertainty in the enhancement is roughly 1.1 ppm and 11.7 ppb, for CO2 and CH4, respectively, for the LJO air data. Overall, the uncertainty due to the assumptions about the background condition is the largest component of the error in the enhancement. However, on an annual average basis, the total uncertainty is generally less than roughly 10 and 15 % of the median mid-afternoon enhancement in downtown LA for CO2 and CH4, respectively.
7. Summary and conclusions
Concerns about rising greenhouse gas levels have motivated many nations to begin monitoring or mitigating emissions, motivating the need for robust, consistent, traceable greenhouse gas observation methods in complex urban domains. Observations from organized urban greenhouse gas monitoring networks such as the LA surface network are emerging elsewhere (e.g., Shusterman et al., 2016; Turnbull et al., 2015; Xueref-Remy et al., 2016). To date, most of these research efforts have been largely disconnected. More information flow between existing urban observational networks and the science and applications communities is needed to understand greenhouse gas emissions from cities. Data and methods for greenhouse gas monitoring in urban regions should be fully disclosed and documented with a small degree of latency to make the best use of these atmospheric data for emissions verification and/or for informing policies more generally.
In this study, we describe the instrumentation and calibration methods used for the Los Angeles megacity surface network. The measurement and sample module systems described here provide robust, near-continuous, and unattended measurement of CO2 and CH4 at urban and suburban monitoring stations in the South Coast Air Basin. A total of 12 analyzers have been deployed thus far and most have been operational for more than 2 years. We reported the sampling configuration, algorithms to compute calibrated CO2 and CH4 mole fractions, and methods for estimating the local enhancement above background and uncertainties.
We presented an observation-based method for estimating background mole fractions using measurements from four remote extra-domain sites. Our approach to background determination is useful for exploring variability in the enhancement signals. Relative to the enhancements observed at most sites, there is near-equivalence of continental and marine background estimates, except during summer months, when continental sites may not be relevant for estimating background due to prevailing onshore flow conditions in the LA Basin. One strength of our observation-based strategy for background determination is the relatively short latency with which background observations can be evaluated (hours to days). This will be important as greenhouse gas research networks such as the LA network transition from research networks into monitoring networks and will allow near-real-time estimation of local greenhouse gas enhancements. The stability criteria discussed here could also be used to identify periods that are optimal for flux inversion. For example, it may not be useful to select background observations when influences from outside the domain cause large gradients or fluctuations within the domain. Similarly, periods that are impacted by recirculation effects are not ideal for identifying background and thus are also not useful for estimating fluxes, and the measurement stability criteria may also be useful for identifying such periods.
We calculated CO2 and CH4 enhancements in the LA megacity during 2015 using a marine background estimate. An urban site near downtown LA has a median enhancement of roughly 20 ppm CO2 and 150 ppb CH4 during all hours and roughly 15 ppm CO2 and 80 ppb CH4 during mid-afternoon hours (12:00–16:00 LT, local time), which is the typical period of focus for flux inversions. “Suburban” sites show moderate, but slightly smaller, enhancements, with median values of 5 to 10 ppm CO2 and 30 to 70 ppb CH4 during mid-afternoon hours. Overall, the largest CO2 and CH4 enhancements were observed at the USC site near downtown Los Angeles.
We also described the components of the analytical uncertainty that we believe to be most important for urban studies. The uncertainty in the enhancement was estimated using both the uncertainty in the air sample data collected from the measurement system and the uncertainty in the background mole fraction. The algorithm discussed here can also help determine periods when uncertainties in the observations are small and are therefore most useful for atmospheric inversion studies. The acceptable threshold for the measurement uncertainty depends in part on the question of interest and on how large the signal is relative to a local background.
Our analysis shows that the uncertainty in the single-point calibration method (Uextrap) is the largest component of the measurement uncertainty. Overall, Uextrap, the uncertainty in the single-point calibration strategy, scales as a function of the enhancement in the air data (roughly 0.3 % of the enhancement for both CO2 and CH4). Based on our error analysis, Uextrap depends on the response, or sensitivity, of the individual analyzer, which is time varying. Our assessment of Uextrap could be further improved with more estimates of the correction factor (ε) from a larger statistical sample of analyzers. Currently, our ability to fully evaluate the magnitude of the correction to the air data is limited by the availability of high-concentration standards in the field. In the near future, the LA measurement network will begin using analyzer-specific estimates of the correction factor based on periodic measurements with high mole fraction tanks, which will allow correction of the random and systematic components of the uncertainty associated with the single-point calibration strategy.
While measurement uncertainty is important for estimating gradients between sites, accurate background determination and uncertainties in atmospheric transport will likely be more important for estimating urban enhancements and using observations in flux inversions. Overall, the uncertainty associated with background is larger than the analytical uncertainty. We find that a local marine background can be established to within ~1 ppm CO2 and ~10 ppb CH4 using local measurement sites. Overall, the background uncertainty is ~10 and ~15 % of the mid-afternoon enhancement near downtown LA for CO2 and CH4, respectively, based on the marine background estimate from SCI. However, both the analytical and background uncertainty are likely to be much smaller than the uncertainty due to atmospheric transport, which is a topic that we have only discussed briefly to provide context for the observations presented in this study. Our results suggest that reducing the uncertainty to less than 5 % of the enhancement will require detailed assessment of the impact of meteorology on background conditions over a range of conditions. Future modeling efforts for the LA Megacity Carbon Project may require equivalent attention to meteorological validation, as has been demonstrated here for the greenhouse gas observations, due to uncertainties in atmospheric transport.
Top-down flux inversions relying on in situ greenhouse gas observations require accurate determination of urban enhancements relative to a local background. We calculated an expected atmospheric signal of Los Angeles carbon emissions assuming emissions are distributed evenly over the roughly 17 100 km2 area of the South Coast Air Basin, an average wind speed of 2 m s−1 (based on an annual average wind speed observed at the USC observation site, equivalent to a transit time of ~18 h), an average mixed layer depth of 1 km (Rahn and Mitchell, 2016; Ware et al., 2016), and estimated emissions (Pacala et al., 2011). Estimated annual emissions of 144 Tg CO2 year−1 would raise CO2 mole fractions by roughly 10 ppm (based on Hestia-LA 2012, see for example Gurney et al., 2012, 2015). Assuming0.4 Tg CH4 year−1 annual emissions in the SCB based on a top-down study, CH4 mole fractions would be enhanced by roughly 75 ppb (Wong et al., 2015). This is consistent with the mid-afternoon enhancements observed over downtown LA during 2015 (Fig. 6 and Tables 4–5) and those reported in prior studies (Newman et al., 2013, 2016; Wong et al., 2015).
In the future, urban greenhouse gas monitoring networks such as the LA surface network could also be used to understand episodic sources or disturbance events such as fires, gas leaks, which are difficult to capture with bottom-up approaches. This will also require background estimation in near-real time. Co-monitoring of tracers (e.g., CO2 and CO enhancements, calibrated with 14C measurements) is also planned as part of future work and will allow continuous or near-continuous estimation of fossil carbon signals in Los Angeles (Miller et al., 2015). Establishing greenhouse gas enhancements and emissions trends over a period of several years could help assist in determining the effectiveness of local control measures and mitigation strategies. As part of future work, forward and inverse modeling studies and tracer–tracer analyses should be used in conjunction with the calibrated CO2 and CH4 observations from the LA surface network to estimate fluxes, determine spatial and temporal emissions trends, and attribute those fluxes to specific sectors and/or sources.
Supplementary Material
Acknowledgements.
The authors thank three anonymous reviewers for helpful comments that improved this paper. The authors are thankful for helpful discussions on the uncertainty analysis and comments on the manuscript from A. Pintar, A. Possolo,S. Ghosh, K. Mueller, and J. Whetstone. We are also thankful for valuable advice from A. Andrews on the background selection method and uncertainty analysis based on experience with the NOAA tall tower network and for comments that significantly improved the manuscript. We also thank E. Dlugokencky andA. Andrews for providing the Pacific marine boundary layer reference, which is constructed using measurements from the NOAA Global Greenhouse Gas Reference Network. We thankC. Sweeney and T. Newberger at NOAA/ESRL for calibration data on the series of Picarro G2401 analyzers presented in this study and B. Hall for providing calibration gases and for advice regarding the uncertainty in the NOAA/WMO scales. We also thank A. Cox, W. Paplawsky, and T. Lueker at the SIO calibration laboratories for support regarding site operations and calibration tanks. Earth Networks provided invaluable support for installation of sample modules and calibration gases at many of the sites. We would like to thank several Earth Networks staff, includingB. Angel and C. Fain, for keeping sites maintained and online and for regular status updates throughout the course of this study,D. Bixler and B. Biggs for network support, and J. Aman for regular quality control checks. A portion of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Additional support was provided by the NIST Greenhouse Gas and Climate Science Measurements Program and the NOAA Atmospheric Chemistry, Carbon Cycle, and Climate Program. Francesca Hopkins’ research was supported by an appointment to the NASA Postdoctoral Program at the Jet Propulsion Laboratory, California Institute of Technology, administered by Universities Space Research Association under contract with NASA. Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
Footnotes
Data availability. The data are located on a portal at the following address: https://megacities.jpl.nasa.gov/.
The Supplement related to this article is available online at https://doi.org/10.5194/acp-17-8313-2017-supplement.
Competing interests. The authors declare that they have no conflict of interest.
References
- Alden CB, Miller JB, Gatti LV, Gloor MM, Guan K, Michalak AM, van der Laan-Luijkx IT, Touma D, Andrews A, Basso LS, Correia CSC, Domingues LG, Joiner J, Krol MC, Lyapustin AI, Peters W, Shiga YP, Thoning K, van der Velde IR, van Leeuwen TT, Yadav V, and Diffenbaugh NS: Regional atmospheric CO2 inversion reveals seasonal and geographic differences in Amazon net biome exchange, Glob. Change Biol, 22, 3427–3443, 10.1111/gcb.13305, 2016. [DOI] [PubMed] [Google Scholar]
- Allan DW: Statistics of Atomic Frequency Standards, Proc. IEEE, 54, 221–230, 10.1109/PROC.1966.4634, 1966. [DOI] [Google Scholar]
- Allan DW: Time and frequency (time-domain) characterization estimation and prediction of precision clocks and oscillators, IEEE Trans. Ultrason. Ferr, 34, 647–654, 1987. [DOI] [PubMed] [Google Scholar]
- Andrews AE, Kofler JD, Trudeau ME, Williams JC, Neff DH, Masarie KA, Chao DY, Kitzis DR, Novelli PC, Zhao CL, Dlugokencky EJ, Lang PM, Crotwell MJ, Fischer ML, Parker MJ, Lee JT, Baumann DD, Desai AR, Stanier CO, De Wekker SFJ, Wolfe DE, Munger JW, and Tans PP: CO2, CO, and CH4 measurements from tall towers in the NOAA Earth System Research Laboratory’s Global Greenhouse Gas Reference Network: instrumentation, uncertainty analysis, and recommendations for future high-accuracy greenhouse gas monitoring efforts, Atmos. Meas. Tech, 7, 647–687, 10.5194/amt-7-647-2014, 2014. [DOI] [Google Scholar]
- Angevine WM, Eddington L, Durkee K, Fairall C, Bianco L, and Brioude J: Meteorological model evaluation for CalNex 2010, Mon. Weather Rev, 140, 3885–3906, 10.1175/MWR-D-12-00042.1, 2012. [DOI] [Google Scholar]
- Asefi-Najafabady S, Rayner PJ, Gurney KR, McRobert A, Song Y, Coltin K, Huang J, Elvidge C, and Baugh K: A multiyear, global gridded fossil fuel CO2 emission data product: Evaluation and analysis of results, J. Geophys. Res.-Atmos, 119, 10213–10231, 10.1002/2013JD021296, 2014. [DOI] [Google Scholar]
- Bréon FM, Broquet G, Puygrenier V, Chevallier F, Xueref-Remy I, Ramonet M, Dieudonné E, Lopez M, Schmidt M, Perrussel O, and Ciais P: An attempt at estimating Paris area CO2 emissions from atmospheric concentration measurements, Atmos. Chem. Phys, 15, 1707–1724, 10.5194/acp-15-1707-2015, 2015. [DOI] [Google Scholar]
- Brioude J, Angevine WM, Ahmadov R, Kim S-W, Evan S, McKeen SA, Hsie E-Y, Frost GJ, Neuman JA, Pol-lack IB, Peischl J, Ryerson TB, Holloway J, Brown SS, Nowak JB, Roberts JM, Wofsy SC, Santoni GW, Oda T, and Trainer M: Top-down estimate of surface flux in the Los Angeles Basin using a mesoscale inverse modeling technique: assessing anthropogenic emissions of CO, NOx and CO2 and their impacts, Atmos. Chem. Phys, 13, 3661–3677, 10.5194/acp-13-3661-2013, 2013. [DOI] [Google Scholar]
- CARB: California’s 2000–2012 Greenhouse Gas Emissions Inventory Technical Support Document, 2014.
- Chen H, Winderlich J, Gerbig C, Hoefer A, Rella CW, Crosson ER, Van Pelt AD, Steinbach J, Kolle O, Beck V, Daube BC, Gottlieb EW, Chow VY, Santoni GW, and Wofsy SC: High-accuracy continuous airborne measurements of greenhouse gases (CO2 and CH4) using the cavity ring-down spectroscopy (CRDS) technique, Atmos. Meas. Tech, 3, 375–386, 10.5194/amt-3-375-2010, 2010. [DOI] [Google Scholar]
- Conil S and Hall A: Local Modes of Atmospheric Variability: A Case Study of Southern California, J. Climate, 19, 4308–4325, 2006. [Google Scholar]
- Conley S, Franco G, Faloona I, Blake DR, Peischl J, and Ryerson TB: Methane emissions from the 2015 Aliso Canyon blowout in Los Angeles, CA, Science, 351, 1317–1320, 10.1126/science.aaf2348, 2016. [DOI] [PubMed] [Google Scholar]
- Cui YY, Brioude J, McKeen SA, Angevine WM, Kim S-W, Frost GJ, Ahmadov R, Peischl J, Bousserez N, Liu Z, Ryerson TB, Wofsy SC, Santoni GW, Kort EA, Fischer ML, and Trainer M: Top-down estimate of methane emissions in California using a mesoscale inverse modeling technique: The South Coast Air Basin, J. Geophys. Res.-Atmos, 120, 6698–6711, 10.1002/2014JD023002, 2015. [DOI] [Google Scholar]
- Djuricin S, Pataki DE, and Xu X: A comparison of tracer methods for quantifying CO2 sources in an urban region, J. Geophys. Res, 115, D11303, 10.1029/2009JD012236, 2010. [DOI] [Google Scholar]
- Djuricin S, Xu X, and Pataki DE: The radiocarbon composition of tree rings as a tracer of local fossil fuel emissions in the Los Angeles basin: 1980–2008, J. Geophys. Res.-Atmos, 117, 1–15, 10.1029/2011JD017284, 2012. [DOI] [Google Scholar]
- Dlugokencky EJ: Conversion of NOAA atmospheric dry air CH4 mole fractions to a gravimetrically prepared standard scale, J. Geophys. Res, 110, D18306, 10.1029/2005JD006035, 2005. [DOI] [Google Scholar]
- Dlugokencky EJ, Steele LP, Lang PM, and Masarie KA: The growth rate and distribution of atmospheric methane, J. Geophys. Res, 99, 17021–17043, 10.1029/94JD01245, 1994. [DOI] [Google Scholar]
- Duren RM and Miller CE: Measuring the carbon emissions of megacities, Nature Climate Change, 2, 560–562, 10.1038/nclimate1629, 2012. [DOI] [Google Scholar]
- Etiope G and Ciccioli P: Earth’s degassing: A missing ethane and propane source, Science, 323, 478, 10.1126/science.1165904, 2009. [DOI] [PubMed] [Google Scholar]
- Feng S, Lauvaux T, Newman S, Rao P, Ahmadov R, Deng A, Díaz-Isaac LI, Duren RM, Fischer ML, Gerbig C, Gurney KR, Huang J, Jeong S, Li Z, Miller CE, O’Keeffe D, Patarasuk R, Sander SP, Song Y, Wong KW, and Yung YL: Los Angeles megacity: a high-resolution land–atmosphere modelling system for urban CO2 emissions, Atmos. Chem. Phys, 16, 9019–9045, 10.5194/acp-16-9019-2016, 2016. [DOI] [Google Scholar]
- Filges A, Gerbig C, Chen H, Franke H, Klaus C, and Jordan A: The IAGOS-core greenhouse gas package: a measurement system for continuous airborne observations of CO2, CH4, H2O and CO, Tellus B, 67, 27989, 10.3402/tellusb.v67.27989, 2015. [DOI] [Google Scholar]
- Graven HD, Guilderson TP, and Keeling RF: Observations of radiocarbon in CO2 at La Jolla, California, USA 1992–2007: Analysis of the long-term trend, J. Geophys. Res, 117, D02302, 10.1029/2011JD016533, 2012. [DOI] [Google Scholar]
- Gurney KR, Chen YH, Maki T, Kawa SR, Andrews A, and Zhu Z: Sensitivity of atmospheric CO2 inversions to seasonal and interannual variations in fossil fuel emissions, J. Geophys. Res.-Atmos, 110, 1–13, 10.1029/2004JD005373, 2005. [DOI] [Google Scholar]
- Gurney KR, Mendoza DL, Zhou Y, Fischer ML, Miller CC, Geethakumar S, and de la Rue du Can S: High Resolution Fossil Fuel Combustion CO2 Emission Fluxes for the United States, Environ. Sci. Technol, 43, 5535–5541, 10.1021/es900806c, 2009. [DOI] [PubMed] [Google Scholar]
- Gurney KR, Razlivanov I, Song Y, Zhou Y, Benes B, and Abdul-Massih M: Quantification of Fossil Fuel CO2 Emissions on the Building/Street Scale for a Large U.S. City, Environ. Sci. Technol, 46, 12194–12202, 10.1021/es3011282, 2012. [DOI] [PubMed] [Google Scholar]
- Gurney KR, Romero-Lankao P, Seto KC, Hutyra LR, Duren RM, Kennedy C, Grimm NB, Ehleringer JR, Marcotullio P, Hughes S, Pincetl S, Chester MV, Runfola DM, Feddema JJ, and Sperling J: Track urban emissions on a human scale, Nature, 525, 179–181, 10.1038/525179a, 2015. [DOI] [PubMed] [Google Scholar]
- Hopkins FM, Kort EA, Bush SE, Ehleringer JR, Lai C-T, Blake DR, and Randerson JT: Spatial patterns and source attribution of urban methane in the Los Angeles Basin, J. Geophys. Res.-Atmos, 121, 2490–2507, 10.1002/2015JD024429, 2016. [DOI] [Google Scholar]
- Hsu Y-K, VanCuren T, Park S, Jakober C, Herner J, FitzGibbon M, Blake DR, and Parrish DD: Methane emissions inventory verification in southern California, Atmos. Environ, 44, 1–7, 10.1016/j.atmosenv.2009.10.002, 2010. [DOI] [Google Scholar]
- Hutyra LR, Duren R, Gurney KR, Grimm N, Kort EA, Larson E, and Shrestha G: Urbanization and the carbon cycle: Current capabilities and research outlook from the natural sciences perspective, Earth’s Futur, 2, 473–495, 10.1002/2014EF000255, 2014. [DOI] [Google Scholar]
- International Energy Agency: IEA World Energy Outlook 2008, chap. 8, 179–193, 2008. [Google Scholar]
- Jacob DJ, Crawford JH, Maring H, Clarke AD, Dibb JE, Emmons LK, Ferrare RA, Hostetler CA, Russell PB, Singh HB, Thompson AM, Shaw GE, McCauley E, Pederson JR, and Fisher JA: The Arctic Research of the Composition of the Troposphere from Aircraft and Satellites (ARCTAS) mission: design, execution, and first results, Atmos. Chem. Phys, 10, 5191–5212, 10.5194/acp-10-5191-2010, 2010. [DOI] [Google Scholar]
- Jeong S, Zhao C, Andrews AE, Bianco L, Wilczak JM, and Fischer ML: Seasonal variation of CH4 emissions from central California, J. Geophys. Res, 117, D11306, 10.1029/2011JD016896, 2012. [DOI] [Google Scholar]
- Jeong S, Hsu YK, Andrews AE, Bianco L, Vaca P, Wilczak JM, and Fischer ML: A multitower measurement network estimate of California’s methane emissions, J. Geophys. Res.-Atmos, 118, 11339–11351, 10.1002/jgrd.50854, 2013. [DOI] [Google Scholar]
- Kort EA, Frankenberg C, Miller CE, and Oda T: Space-based observations of megacity carbon dioxide, Geophys. Res. Lett, 39, L17806, 10.1029/2012GL052738, 2012. [DOI] [Google Scholar]
- Kort EA, Angevine WM, Duren R, and Miller CE: Surface observations for monitoring urban fossil fuel CO2 emissions: Minimum site location requirements for the Los Angeles megacity, J. Geophys. Res.-Atmos, 118, 1577–1584, 10.1002/jgrd.50135, 2013. [DOI] [Google Scholar]
- Lauvaux T, Miles NL, Deng A, Richardson SJ, Cambaliza MO, Davis KJ, Gaudet B, Gurney KR, Huang J, O’Keefe D, Song Y, Karion A, Oda T, Patarasuk R, Razlivanov I, Sarmiento D, Shepson P, Sweeney C, Turnbull J, and Wu K: High-resolution atmospheric inversion of urban CO2 emissions during the dormant season of the Indianapolis Flux Experiment (INFLUX), J. Geophys. Res.-Atmos, 121, 5213–5236, 10.1002/2015JD024473, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma S and Skou E: CO2 permeability in Nafion ® EW1100 at elevated temperature, Solid State Ionics, 178, 615–619, 10.1016/j.ssi.2007.01.030, 2007. [DOI] [Google Scholar]
- Masarie KA and Tans PP: Extension and integration of atmospheric carbon dioxide data into a globally consistent measurement record, J. Geophys. Res, 100, 11593–11610, 10.1029/95JD00859, 1995. [DOI] [Google Scholar]
- McKain K, Wofsy SC, Nehrkorn T, Eluszkiewicz J, Ehleringer JR, and Stephens BB: Assessment of ground-based atmospheric observations for verification of greenhouse gas emissions from an urban region, P. Natl. Acad. Sci. USA, 109, 8423–8428, 10.1073/pnas.1116645109, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKain K, Down A, Raciti SM, Budney J, Hutyra LR, Floerchinger C, Herndon SC, Nehrkorn T, Zahniser MS, Jackson RB, Phillips N, and Wofsy SC: Methane emissions from natural gas infrastructure and use in the urban region of Boston, Massachusetts, P. Natl. Acad. Sci. USA, 112, 1941–1946, 10.1073/pnas.1416261112, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JB, Lehman S, Verhulst KR, Miller C, Duren R, Newman S, Higgs J, and Sloop C: Initial Atmospheric Fossil-fuel CO2 Estimates from the Los Angeles Megacity Project, in 43rd Global Monitoring Annual Conference, 2015 Program and Abstracts Booklet, NOAA Earth System Research Laboratory, Global Monitoring Division, 2015. [Google Scholar]
- Nara H, Tanimoto H, Tohjima Y, Mukai H, Nojiri Y, Katsumata K, and Rella CW: Effect of air composition (N2, O2, Ar, and H2O) on CO2 and CH4 measurement by wavelength-scanned cavity ring-down spectroscopy: calibration and measurement strategy, Atmos. Meas. Tech, 5, 2689–2701, 10.5194/amt-5-2689-2012, 2012. [DOI] [Google Scholar]
- Newman S, Xu X, Affek HP, Stolper E, and Epstein S: Changes in mixing ratio and isotopic composition of CO2 in urban air from the Los Angeles basin, California, between 1972 and 2003, J. Geophys. Res, 113, D23304, 10.1029/2008JD009999, 2008. [DOI] [Google Scholar]
- Newman S, Jeong S, Fischer ML, Xu X, Haman CL, Lefer B, Alvarez S, Rappenglueck B, Kort EA, Andrews AE, Peischl J, Gurney KR, Miller CE, and Yung YL: Diurnal tracking of anthropogenic CO2 emissions in the Los Angeles basin megacity during spring 2010, Atmos. Chem. Phys, 13, 4359–4372, 10.5194/acp-13-4359-2013, 2013. [DOI] [Google Scholar]
- Newman S, Xu X, Gurney KR, Hsu YK, Li KF, Jiang X, Keeling R, Feng S, O’Keefe D, Patarasuk R, Wong KW, Rao P, Fischer ML, and Yung YL: Toward consistency between trends in bottom-up CO2 emissions and top-down atmospheric measurements in the Los Angeles megacity, Atmos. Chem. Phys, 16, 3843–3863, 10.5194/acp-16-3843-2016, 2016. [DOI] [Google Scholar]
- Pacala SW, Breidenich C, Brewer PG, Fung I, Gunson M, Heddle G, Law B, Marland G, Paustian K, Prather M, Randerson JT, Tans P, and Wofsy SC: Verifying greenhouse gas emissions: methods to support international climate agreements, available at: http://www.tandfonline.com/doi/full/10.1080/20430779.2011.579358 (last access: 27 September 2014), 2011.
- Peischl J, Ryerson TB, Brioude J, Aikin KC, Andrews AE, Atlas E, Blake D, Daube BC, de Gouw JA, Dlugokencky E, Frost GJ, Gentner DR, Gilman JB, Goldstein AH, Harley RA, Holloway JS, Kofler J, Kuster WC, Lang PM, Novelli PC, Santoni GW, Trainer M, Wofsy SC, and Parrish DD: Quantifying sources of methane using light alkanes in the Los Angeles basin, California, J. Geophys. Res.-Atmos, 118, 4974–4990, 10.1002/jgrd.50413, 2013. [DOI] [Google Scholar]
- Prasad K, Bova A, Whetstone JR, and Novakovskaia E: Greenhouse gas emissions and dispersion-optimum placement of gas inlets on a building rooftop for the measurement of greenhouse gas concentration, in: NIST special Publication; 1158, NIST, 2013. [Google Scholar]
- Prinn RG, Huang J, Weiss RF, Cunnold DM, Fraser PJ, Simmonds PG, McCulloch a, Harth C, Salameh P, O’Doherty S, Wang RH, Porter L, and Miller BR: Evidence for substantial variations of atmospheric hydroxyl radicals in the past two decades, Science, 292, 1882–1888, 10.1126/science.1058673, 2001. [DOI] [PubMed] [Google Scholar]
- Rahn DA and Mitchell CJ: Diurnal Climatology of the Boundary Layer in Southern California Using AMDAR Temperature and Wind Profiles, J. Appl. Meteorol. Clim, 55, 1123–1137, 10.1175/JAMC-D-15-0234.1, 2016. [DOI] [Google Scholar]
- Rella CW, Chen H, Andrews AE, Filges A, Gerbig C, Hatakka J, Karion A, Miles NL, Richardson SJ, Steinbacher M, Sweeney C, Wastine B, and Zellweger C: High accuracy measurements of dry mole fractions of carbon dioxide and methane in humid air, Atmos. Meas. Tech, 6, 837–860, 10.5194/amt-6-837-2013, 2013. [DOI] [Google Scholar]
- Richardson SJ, Miles NL, Davis KJ, Crosson ER, Rella CW, and Andrews AE: Field testing of cavity ring-down spectroscopy analyzers measuring carbon dioxide and water vapor, J. Atmos. Ocean. Tech, 29, 397–406, 10.1175/JTECH-D-11-00063.1, 2012. [DOI] [Google Scholar]
- Riley WJ, Hsueh DY, Randerson JT, Fischer ML, Hatch JG, Pataki DE, Wang W, and Goulden ML: Where do fossil fuel carbon dioxide emissions from California go? An analysis based on radiocarbon observations and an atmospheric transport model, J. Geophys. Res.-Biogeo, 113, 1–16, 10.1029/2007JG000625, 2008. [DOI] [Google Scholar]
- Rolph GD: Real-time Environmental Applications and Display sYstem (READY) Website, available at: http://www.ready.noaa.gov (last access: 17 June 2017), NOAA Air Resources Laboratory, College Park, MD, 2016. [Google Scholar]
- Ruckstuhl AF, Henne S, Reimann S, Steinbacher M, Vollmer MK, O’Doherty S, Buchmann B, and Hueglin C: Robust extraction of baseline signal of atmospheric trace species using local regression, Atmos. Meas. Tech, 5, 2613–2624, 10.5194/amt-5-2613-2012, 2012. [DOI] [Google Scholar]
- Ryerson TB, Andrews AE, Angevine WM, Bates TS, Brock CA, Cairns B, Cohen RC, Cooper OR, De Gouw JA, Fehsenfeld FC, Ferrare RA, Fischer ML, Flagan RC, Goldstein AH, Hair JW, Hardesty RM, Hostetler CA, Jimenez JL, Langford AO, McCauley E, McKeen SA, Molina LT, Nenes A, Oltmans SJ, Parrish DD, Pederson JR, Pierce RB, Prather K, Quinn PK, Seinfeld JH, Senff CJ, Sorooshian A, Stutz J, Surratt JD, Trainer M, Volkamer R, Williams EJ, and Wofsy SC: The 2010 California Research at the Nexus of Air Quality and Climate Change (CalNex) field study, J. Geophys. Res.-Atmos, 118, 5830–5866, 10.1002/jgrd.50331, 2013. [DOI] [Google Scholar]
- Shusterman AA, Teige VE, Turner AJ, Newman C, Kim J, and Cohen RC: The BErkeley Atmospheric CO2 Observation Network: initial evaluation, Atmos. Chem. Phys, 16, 13449–13463, 10.5194/acp-16-13449-2016, 2016. [DOI] [Google Scholar]
- Stein AF, Draxler RR, Rolph GD, Stunder BJB, Cohen MD, and Ngan F: NOAA’s HYSPLIT atmospheric transport and dispersion modeling system, B. Am. Meteorol. Soc, 96, 2059–2077, 10.1175/BAMS-D-14-00110.1, 2015. [DOI] [Google Scholar]
- Thoning KW, Tans PP, and Komhyr WD: Atmospheric carbon dioxide at Mauna Loa Observatory: 2. Analysis of the NOAA GMCC data, 1974–1985, J. Geophys. Res, 94, 8549, 10.1029/JD094iD06p08549, 1989. [DOI] [Google Scholar]
- Townsend-Small A, Tyler SC, Pataki DE, Xu X, and Christensen LE: Isotopic measurements of atmospheric methane in Los Angeles, California, USA: Influence of “fugitive” fossil fuel emissions, J. Geophys. Res.-Atmos, 117, 1–11, 10.1029/2011JD016826, 2012. [DOI] [Google Scholar]
- Turnbull J, Rayner P, Miller J, Naegler T, Ciais P and Cozic A: On the use of 14CO2 as a tracer for fossil fuel CO2?: Quantifying uncertainties using an atmospheric transport model, J. Geophys. Res, 114, D22302, 10.1029/2009JD012308, 2009. [DOI] [Google Scholar]
- Turnbull JC, Sweeney C, Karion A, Newberger T, Lehman SJ, Tans PP, Davis KJ, Lauvaux T, Miles NL, Richardson SJ, Cambaliza MO, Shepson PB, Gurney K, Patarasuk R, and Razlivanov I: Toward quantification and source sector identification of fossil fuel CO2 emissions from an urban area: Results from the INFLUX experiment, J. Geophys. Res.-Atmos, 120, 292–312, 10.1002/2014JD022555, 2015. [DOI] [Google Scholar]
- United Nations: World Urbanization Prospects: The 2014 Revision, Highlights (ST/ESA/SER.A/352), 2014.
- Viatte C, Lauvaux T, Hedelius JK, Parker H, Chen J, Jones T, Franklin JE, Deng AJ, Gaudet B, Verhulst K, Duren R, Wunch D, Roehl C, Dubey MK, Wofsy S, and Wennberg PO: Methane emissions from dairies in the Los Angeles Basin, Atmos. Chem. Phys, 17, 7509–7528, 10.5194/acp-17-7509-2017, 2017. [DOI] [Google Scholar]
- Ware J, Kort EA, Decola P, and Duren R: Aerosol lidar observations of atmospheric mixing in Los Angeles: Climatology and implications for greenhouse gas observations, J. Geophys. Res.-Atmos, 121, 1–17, 10.1002/2016JD024953, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wecht KJ, Jacob DJ, Sulprizio MP, Santoni GW, Wofsy SC, Parker R, Bösch H, and Worden J: Spatially resolving methane emissions in California: constraints from the Cal-Nex aircraft campaign and from present (GOSAT, TES) and future (TROPOMI, geostationary) satellite observations, Atmos. Chem. Phys, 14, 8173–8184, 10.5194/acp-14-8173-2014, 2014. [DOI] [Google Scholar]
- Welp LR, Keeling RF, Weiss RF, Paplawsky W, and Heckman S: Design and performance of a Nafion dryer for continuous operation at CO2 and CH4 air monitoring sites, Atmos. Meas. Tech, 6, 1217–1226, 10.5194/amt-6-1217-2013, 2013. [DOI] [Google Scholar]
- Wennberg PO, Mui W, Wunch D, Kort EA, Blake DR, Atlas EL, Santoni GW, Wofsy SC, Diskin GS, Jeong S, and Fischer ML: On the sources of methane to the Los Angeles atmosphere, Environ. Sci. Technol, 46, 9282–9289, 10.1021/es301138y, 2012. [DOI] [PubMed] [Google Scholar]
- Wong CK, Pongetti TJ, Oda T, Rao P, Gurney KR, Newman S, Duren RM, Miller CE, Yung YL, and Sander SP: Monthly trends of methane emissions in Los Angeles from 2011 to 2015 inferred by CLARS-FTS observations, Atmos. Chem. Phys, 16, 13121–13130, 10.5194/acp-16-13121-2016, 2016. [DOI] [Google Scholar]
- Wong KW, Fu D, Pongetti TJ, Newman S, Kort EA, Duren R, Hsu Y-K, Miller CE, Yung YL, and Sander SP: Mapping CH4c: CO2 ratios in Los Angeles with CLARSFTS from Mount Wilson, California, Atmos. Chem. Phys, 15, 241–252, 10.5194/acp-15-241-2015, 2015. [DOI] [Google Scholar]
- Wunch D, Wennberg PO, Toon GC, Keppel-Aleks G, and Yavin YG: Emissions of greenhouse gases from a North American megacity, Geophys. Res. Lett, 36, L15810, 10.1029/2009GL039825, 2009. [DOI] [Google Scholar]
- Wunch D, Toon GC, Hedelius JK, Vizenor N, Roehl CM, Saad KM, Blavier J-FL, Blake DR, and Wennberg PO: Quantifying the loss of processed natural gas within California’s South Coast Air Basin using long-term measurements of ethane and methane, Atmos. Chem. Phys, 16, 14091–14105, 10.5194/acp-16-14091-2016, 2016. [DOI] [Google Scholar]
- Xueref-Remy I, Dieudonné E, Vuillemin C, Lopez M, Lac C, Schmidt M, Delmotte M, Chevallier F, Ravetta F, Perrussel O, Ciais P, Bréon F-M, Broquet G, Ramonet M, Spain TG, and Ampe C: Diurnal, synoptic and seasonal variability of atmospheric CO2 in the Paris megacity area, Atmos. Chem. Phys. Discuss, 10.5194/acp-2016-218, in review, 2016. [DOI] [Google Scholar]
- Zhao C, Andrews AE, Bianco L, Eluszkiewicz J, Hirsch A, MacDonald C, Nehrkorn T, and Fischer ML: Atmospheric inverse estimates of methane emissions from Central California, J. Geophys. Res.-Atmos, 114, 1–13, 10.1029/2008JD011671, 2009. [DOI] [Google Scholar]
- Zhao CL and Tans PP: Estimating uncertainty of the WMO mole fraction scale for carbon dioxide in air, J. Geophys. Res.-Atmos, 111, 1–10, 10.1029/2005JD006003, 2006. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.