PRIMARY STANDARDIZATION OF THE MASSIC ACTIVITY OF A PROTACTINIUM-233 SOLUTION

Abstract

Protactinium-233 (²³³Pa) is used as a tracer for radiochemical analysis and is of particular interest as an isotope dilution mass spectrometry (IDMS) spike for ²³¹Pa/²³⁵U radio-chronometry. To this end, we present massic activity determinations by two methods for a ²³³Pa solution, which was prepared at Lawrence Livermore National Laboratory (LLNL) and is being characterized at multiple labs as part of a ²³¹Pa reference material production project. One activity determination method was 4πβ-γ anti-coincidence counting in a multi-dimensional extrapolation model, with Monte Carlo corrections. An independent massic activity determination was completed by γ-ray spectrometry using 5 HPGe detectors using 5 γ-ray lines. The anti-coincidence and γ-ray spectrometry results agree and have combined standard uncertainties of about 0.33 % and 1.0 % respectively. In addition, the two methods were combined to derive γ-ray emission probabilities from ²³³Pa decay.

Introduction

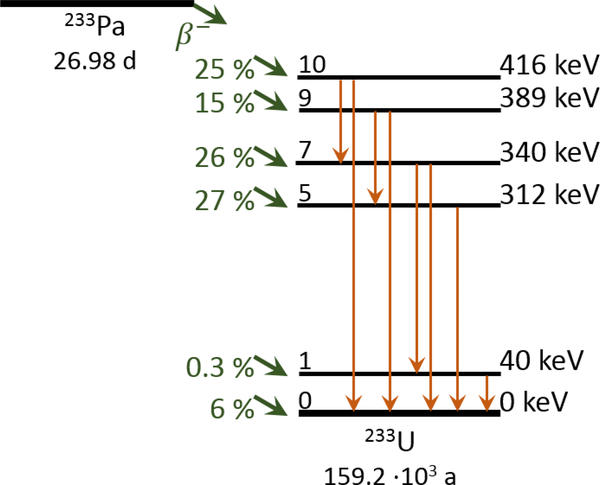
Protactinium-233 (²³³Pa) is an important tracer for radiochemical analysis of ²³¹Pa [1–3]. Whereas ²³¹Pa undergoes alpha decay without significant γ-ray emission, ²³³Pa decays by β-particle emission accompanied by numerous γ-rays (Figure 1); as such the ²³¹Pa γ-ray signal can be used for monitoring Pa separations.

Figure 1.

Simplified ²³³Pa decay scheme, adapted from DDEP [6,7].

In the field of nuclear forensics, there is an outstanding challenge for producing well-characterized ²³³Pa solutions for use as a spike in Isotope Dilution Mass Spectrometry (IDMS) analysis of ²³¹Pa for ²³¹Pa/²³⁵U dating [4,5]. The present work is motivated by a project led by Lawrence Livermore National Laboratory (LLNL) to produce a reference material characterized for amount of ²³¹Pa. This reference material will allow for traceable calibrations of the necessary short-lived ²³³Pa spikes (half-life: 26.98 d ± 0.02 d [6,7]). That project requires a ²³³Pa spike with well characterized concentration (mol/g) for reverse-IDMS measurements. One method for obtaining that concentration is to measure the ²³³Pa massic activity (Bq/g) of the spike solution and then use the half-life to convert to concentration. To that end, LLNL sent aliquots of their spike solution to multiple radionuclide metrology labs for assay. Here, we report the results from the National Institute of Standards and Technology (NIST).

This project presented an opportunity to measure the massic activity by live-timed 4πβ-γ anticoincidence counting (LTAC) of a very pure ²³³Pa solution. Previous standardizations have relied on the equilibrium conditions of ²³³Pa with its parent ²³⁷Np, taking advantage of the relative ease of measuring absolute alpha decay of ²³⁷Np rather than beta decay of ²³³Pa [8–17]. In some of those works, both nuclides were measured in equilibrium using 4παβ-γ coincidence [15,16]. The γ-ray emission probabilities ( ) for ²³³Pa decay have been evaluated [14,7,18]. The P_γ for the 312 keV transition as measured by [17] differs significantly from the evaluated value. A subsequent study [10] agrees with the evaluated value. The P_γ in question has implications for the ²³⁷Np and ²³²Th neutron capture cross sections. The present work provides an independent measurement of the 312-keV P_γ.

Experimental

Source Preparation

The final purification of the ²³³Pa solution occurred at LLNL on 27 June 2017 at 15:50 PDT, which serves as the reference time for the activity measurements reported here. The solution consisted of 2 mol L⁻¹ HNO3 + 0.1 mol L⁻¹ HF. The activity ratio of ²³⁷Np to ²³³Pa at separation was < 1 ⋅ 10⁻⁸ [Williams, R.W.; personal communication 2017]. Approximately 5.3 g of the ²³³Pa solution was shipped to NIST in a Teflon vial.

In July 2017, the LLNL vial was opened at NIST. Approximately 0.04 g to 0.16 g was transferred gravimetrically into each of 8 liquid scintillation (LS) vials containing 4 mL of either “Ultima Gold”¹ (2 vials) or “Ultima Gold AB” scintillants (Perkin Elmer, Waltham, MA, USA). Additional 2 mol L⁻¹ HNO₃ carrier was added to bring the aqueous content of the LS sources up to 2 % for Ultima Gold and 6 % for Ultima Gold AB. The ²³³Pa solution was diluted with carrier by a factor of 1.2960 ± 0.0006 for gravimetrically filling a standard 5 mL NIST ampoule [19] for which our HPGe detectors are calibrated. All of the gravimetric transfers were done by measuring by difference the masses of solution dispensed from an aspirating polyethylene pipette (“pycnometer”) using a 6-digit microbalance.

4πβ-γ anticoincidence measurements

The 4πβ-γ anticoincidence (LTAC) method was used to determine the massic activity of the ²³³Pa solution. The NIST LTAC system and Monte Carlo analysis method have been described previously [20,21]. In brief, the 4πβ detector consists of a liquid scintillation (LS) source coupled to a single photomultiplier tube. The γ-ray (and x-ray) detector is a NaI(Tl) well detector. A digital data acquisition system is used to record the pulse heights and time stamps from both detectors. The data are processed offline by the multiple channel anticoincidence method with shared, controllable extending deadtime [22]. The LS efficiency is varied by changing the lower-level discriminator for the LS amplitude in the software.

Up to 3 NaI(Tl) gates were used in anti-coincidence mode to monitor the LS inefficiency for three different subsets of decays. The output of the data processing was the LS rate (N_LS), and the NaI(Tl) anticoincident-to-total ratios (Y_i) for each of the 3 gates. A linear combination of the Y_i is adopted as the effective LS inefficiency,

$$Y_{\text{eff}}=\sum a_i{Y}_{\text{i}},$$ (1)

where the a_i are weighting factors. Either a linear or quadratic least-squares fit of the LS rate (N_LS) vs. Y_eff is carried out and extrapolated to Y_eff=0, to obtain the nominal source decay rate (N₀). The linear fit equation with free parameters N₀, k, and the a_i is,

$$N_{LS}=N_0\left(1-k{Y}_{\text{eff}}\right).$$ (2)

Due to the complex decay scheme, N₀ from the fit can differ from the true activity. To correct for this, a Monte Carlo simulation, using Geant4 library [23], of the entire experiment was performed with identical extrapolations as for the data. A correction factor, F, was derived by the ratio of N₀ to the “true” activity input to the Monte Carlo.

The final massic activity (A) was determined for each source from N₀, F, and mass, m of the ²³³Pa solution in the source.

$$A_m=\frac{F{N}_0}{m}$$ (3)

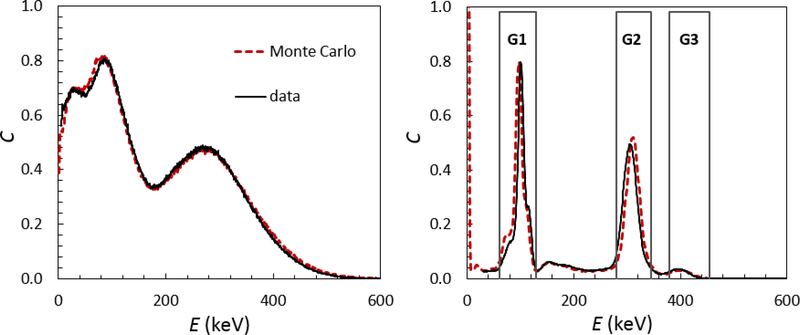
The free parameter in the Monte Carlo simulation is the scintillation efficiency, which was set to 4500 UV photons per MeV of electron energy, which matched the experimental LS spectrum (Figure 2). The three NaI(Tl) gates were set to be sensitive to various decay pathways (Table 1), such that the LS efficiency for each path could be extrapolated to 100 % (Y_i = 0). Since ²³³Pa does have a significant β branch to the ²³³U ground state (β₀), without emission of a photon, the LS efficiency of that branch is not monitored by any of the gates. However, since all the β spectra are of similar shape, (same nucleus, all first-forbidden), one can use a linear combination of Y_i^′s from other transitions to represent the inefficiency for detecting β₀ [22]. However, given the complicated decay scheme, including numerous conversion electrons, achieving a linear extrapolation using the three Y_i values is not necessarily possible. Therefore, the Monte Carlo correction, F, was employed throughout.

Figure 2.

Measured (solid black lines) and simulated (dashed red lines) spectra from LS (left) and NaI(Tl) (right) detectors, where C is counts with arbitrary scaling and E is approximate energy, proportional to pulse height. In the LS spectrum, the three peaks correspond to conversion electrons. In the NaI(Tl) spectrum, the three gates used for LTAC are shown.

Table 1.

Energy gates in the LTAC NaI(Tl) detector. For each gate, we list the photon energy range encompassed by the gate, the major γ-ray and x-ray photons detected in the gate, and correlated LS events, whose efficiency is monitored by the coincident photon events. Subscripts correspond to energy levels shown in Figure 1.

Gate	E (keV)	photons	Correlated LS events
1	60 to 130	γ10,7 γ9,5 XK	β10 → γ7,0 β9 → γ5,0 βi≥5 → CE5,0
2	280 to 345	γ7,0 γ5,0 γ7,1	β7; β10 → CE10,7 β5; β7 → CE7,5 β7 → CE1,0
3	380 to 455	γ10,0 γ9,0	β10 β9

HPGe detector measurements

Gamma-ray spectrometry measurements were carried out to determine the γ-ray emitting impurities in the source and the source activity. Five different HPGe detectors (both n-type and p-type detectors) with well-characterized efficiency curves [24] were used to determine the source activity. A total of ten measurements were performed for the standard 5 mL NIST ampoule using seven different source measurement geometries. For these different measurement geometries, the sources were placed above and on the side of the HPGe detectors at several source-to-detector distances varying between 20 cm and 50 cm. For each measurement, the live time was 1 day. The activity was calculated based on the 300.129 keV, 311.904 keV, 340.476 keV, 398.492 keV and 415.764 keV γ-ray peaks and the 2010 DDEP (Decay Data Evaluation Project) evaluated emission probabilities (P_γ’s) and half-life [6,7]. The full-energy-peak efficiency values for the HPGe detectors were previously determined using standard 5 mL NIST ampoules containing calibrated solutions of radionuclides that cover an energy range from 35 keV to 1.8 MeV and which were placed at the same source-to-detector distances as those used in the present measurements. The efficiency curves were fitted using two different methods (sixth degree polynomial and dual polynomial fit (spline function) with a cross-over point at around 200 keV) in order to assess possible variability in the calculated values for the different γ-ray energies for ²³³Pa.

Results

4πβ-γ anticoincidence measurements

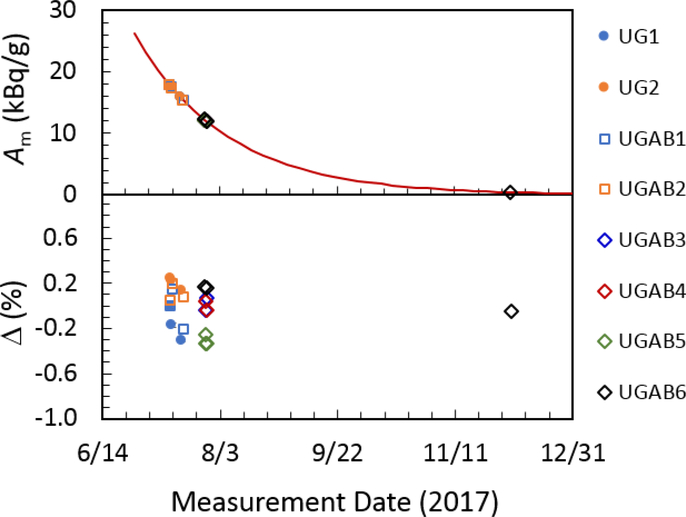
Each of the 8 LS sources was measured either 2 or 3 times between 7 July 2017 and 28 July 2017. No systematic difference was seen between the results for the two LS cocktails, and the source-to-source standard deviation was 0.17 %. There was no statistically-significant trend in activity measurement vs. time for a given source, averaged over all sources. However, for the four sources that were measured over a longer (5 day) period, three of them showed a decreasing trend of intercept value over time. To conservatively account for any LS cocktail instability, the average decrease in intercept value for those 4 sources was included as an uncertainty component in the massic activity determination.

To check for long-lived impurities, one source was measured again on 4 December 2017, after the ²³³Pa had decayed by 6 half-lives. The measured activity differed from the mean of the earlier measurements by (−0.5 ± 1.4) %². This uncertainty would correspond to a limit on long-lived α- or β-emitting impurities of about 0.04 % at the midpoint of the July measurements (2017–07-20 07:00 EST).

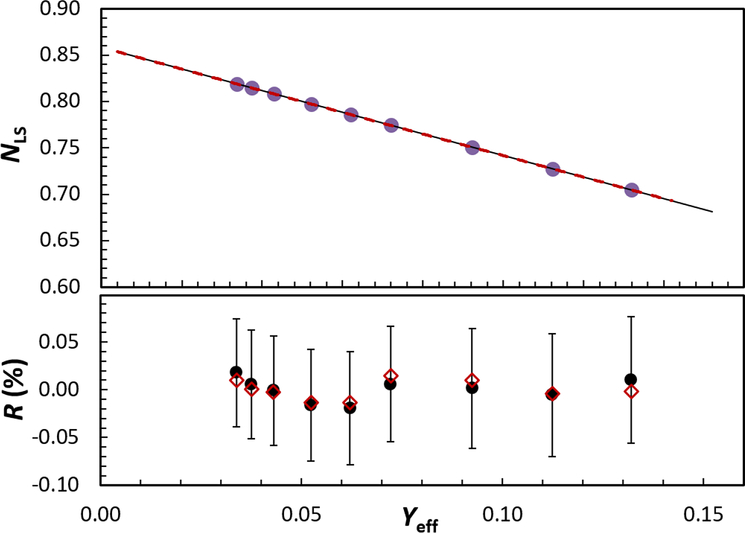
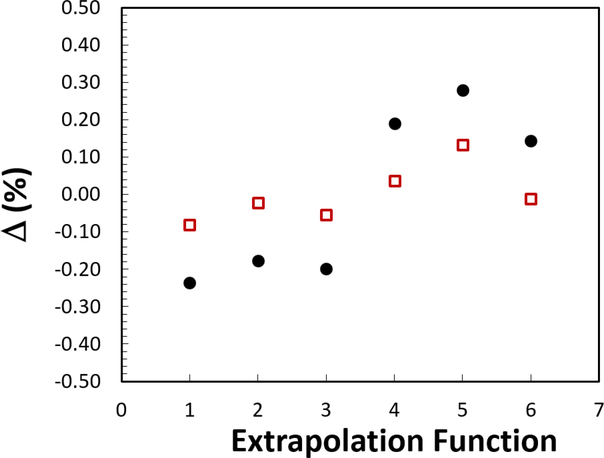
Various efficiency extrapolation functions were used to test the sensitivity of the extrapolation intercept to the functional form (linear or quadratic) and number of γ-ray gates (up to 3) included. Example efficiency extrapolations and fit residuals are shown in Figure 4. The various fits are summarized in Table 2 and the relative results are shown in Figure 5.

Figure 4.

Example efficiency extrapolation from source UGAB1. Linear (solid black line) and quadratic (dashed red line) are indistinguishable by eye. Residuals for linear (black circles) and quadratic (red diamonds) are shown

Table 2.

Summary of extrapolation functions used to analyze the LTAC data. In cases where the a_i were not free, they were fixed by the best fit to the Monte Carlo simulation results.

Function	Energy Range (keV)	Order	Free Parameters
1	14 to 50	Linear	N0, k
2	14 to 50	Linear	a1, a2, a3, N0, k
3	14 to 50	Quadratic	N0, k
4	30 to 100	Linear	N0, k
5	30 to 100	Linear	a1, a2, a3, N0, k
6	30 to 100	Quadratic	N0, k

Figure 5.

Percent difference (Δ) from the average result for 6 different extrapolation functions, without (●) and with (□) Monte Carlo correction factor (F). The corrected values show less model-dependence

The final value for the LTAC ²³³Pa massic activity determination was taken as the mean of methods 1, 2, and 3 in Table 2. Those three values were chosen since they included the highest-efficiency LS data, therefore had the shortest extrapolation in Y_eff. However, the standard deviation of all 6 values were used in the uncertainty analysis. The final LTAC ²³³Pa massic activity at the reference time of 27 June 2017 15:50 PDT was 2.361 ⋅ 10⁴ Bq g⁻¹ with a combined standard uncertainty of 0.33 %. The uncertainty analysis is summarized in Table 3.

Table 3.

Uncertainty evaluation [25,26] for the LTAC determination of the ²³³Pa massic activity.

Uncertainty component	ui (%)	Evaluation
Source stability: Average deviation between measured activity for the same source measured 5 days apart, averaged over 4 sources.	0.15	A
Source-to-source variability: Standard deviation of the distribution (N=5) for the extrapolation intercepts of 5 sources. The value for each source was an average of 2 or 3 measurements.	0.17	A
Least-squares fit: uncertainty on extrapolation value due to the fit	0.07	A
Extrapolation range and function: Standard deviation of the distribution (N = 6) for 6 fits spanning 2 LS efficiency ranges, each with its own Yeff weighting. For each range, three fits were carried out: Linear Yeff, Linear 3gate, Quadratic Yeff. Results were then corrected for bias using Geant4.	0.06	A
Geant4 model uncertainty: Uncertainty on the corrections (−0.09 % to 0.22 %) using Geant4 model due to nuclear data and matching of model to data.	0.17	B
Background: Standard deviation in mean intercept from using various background measurements (7 background measurements made).	0.06	A
Gravimetric links: Estimated uncertainty in the mass of 233Pa solution added to the LS hemispheres based on previous tests.	0.05	B
Live-time: Estimated uncertainty in the live time of the counting system, based on limits of previous systematic tests	0.10	B
Half-life: Uncertainty due to DDEP half-life (26.98 +/− 0.02) d.	0.002	B
Impurities: None seen. From limit on LTAC and HPGe analyses.	0.03	B
Combined standard uncertainty: uc (%)	0.33

HPGe detector impurity measurements

No γ-ray emitting impurities were observed in the source. The estimated limits of detection for the photon-emitting impurities as of August 1, 2017 were: 90 γ s⁻¹ for energies between 15 keV and 35 keV, 20 90 γ s⁻for energies between 40 keV and 55keV, 30 90 γ s⁻for energies between 60 keV and 180 keV, 18 90 γ s⁻for energies between 185 keV and 280 keV, 40 90 γ s⁻for energies between 258 keV and 330 keV, 14 90 γ s⁻for energies between 340 keV and 430 keV, and 4.8 90 γ s⁻for energies between 440 keV and 2000 keV.

HPGe detector activity determination

The peak areas used to determine the ²³³Pa activity were obtained using Genie 2000 (Canberra Industries, Inc., Meriden, CT, USA) (using interactive peak fit without the fit singlet option). Due to the low counting rates, no pile-up corrections were necessary. Decay corrections during the measurement time and to the reference time were performed for all measurements. The dilution mass of solution in the HPGe ampoule and dilution factor were used to calculate a massic activity of the NIST-1 solution. The measured massic activity of ²³³Pa at the reference time was 2.611 ⋅ 10⁴ Bq g⁻¹ with a combined standard uncertainty of 0.93 %. The uncertainty evaluation is summarized in Table 4.

Table 4.

Uncertainty analysis for the ²³³Pa massic activity determined by HPGe γ-ray spectrometry.

Uncertainty component	ui (%)	Evaluation
Peak fitting and counting statistics: Standard deviation of the mean value of the peak areas	0.11	A
Gamma-ray emission probabilities: Standard deviation of the mean value of Pγ(E)	0.73	B
Efficiency: HPGe detector full-energy peak efficiency fit based on measured efficiency curve	0.57	B
Decay correction during measurement: Uncertainty due to the application of a decay correction during the measurement time.	0.0005	B
Decay factor: Uncertainty due to the application of a decay factor correction for the source activity from the reference time to the measurement time.	0.04	B
Combined Standard Uncertainty: uc (%)	0.93

HPGe detector γ-ray emission probability (P_γ) determination

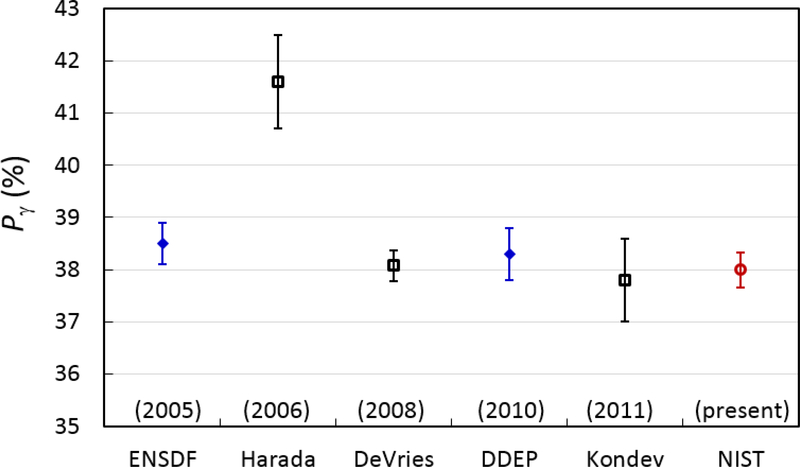
The HPGe measurements of the ²³³Pa source and the LTAC massic activity determination were used to determine the emission probability of five of the main γ-ray lines. For the determination of the P_γ values, the same corrections as for the HPGe activity determination were applied. The activity of the source used for the HPGe measurements was (59.420 ± 0. 196) kBq at the reference time of 20 July 2017, 7:00 AM EST. The P_γ values determined in this work are listed in Table 5 together with the most-recent values from DDEP [7,6]. The result for the 312 keV P_γ is shown in Figure 6, along with recent experimental and evaluation results. The present work is in good agreement with recent evaluations, though disagrees with the anomalously-high P_γ from [17].

Table 5.

Measured P_γ values for five main γ-ray lines of ²³³Pa

Energy (keV)	Pγ (this work)	Pγ (DDEP 2010 [7,6])
300.129	0.0654 ± 0.0006	0.0660 ± 0.0021
311.904	0.3799 ± 0.0033	0.383 ± 0.005
340.476	0.0444 ± 0.0004	0.0447 ± 0.0003
398.492	0.01405 ± 0.00013	0.01408 ± 0.00014
415.764	0.01729 ± 0.00016	0.01747 ± 0.00007

Figure 6.

Recent P_γ results for the 312 keV γ-ray in ²³³Pa decay. Blue diamonds are evaluations, open squares are previous experimental results and the red open circle is the present work. ENDSF refers to [18] and DDEP to [7,6].

Discussion

The LTAC determination of ²³³Pa massic activity using multiple γ-ray gates proved robust against a variety of extrapolation functions. By implementing Monte Carlo correction factors, the variance in extrapolation intercepts among extrapolation functions and efficiency domains was reduced significantly. Furthermore, the lack of radionuclidic impurities detected by both HPGe γ-ray analysis and the consistent LTAC ²³³Pa activity results over 6 half-lives, indicate that the ²³³Pa solution is quite pure, making it an excellent reference material.

By combining the 4πβ-γ anticoincidence result with the evaluated half-life of ²³³Pa (26.98 ± 0.02) d, and Avogadro’s number, we obtain a concentration of the measured ²³³Pa atom mole concentration at the reference date of 1.471 ⋅ 10⁻¹⁰ mol/kg with a combined standard uncertainty of 0.34 %. This can now be used as a reference for isotope dilution mass spectrometry of ²³¹Pa, which was carried out using the solution shortly after separation. The HPGe γ-ray measurement result for the massic activity of ²³¹Pa agrees with the LTAC value, differing by (−0.8 ± 1.1) %, where the uncertainty is the combined standard uncertainty on the difference, ignoring small correlations due to half-life. This excellent agreement confirms the LTAC activity value and is also an indication that the uncertainty on the γ-ray emission probabilities used in the HPGe analysis were reasonable. Conversely, by combining LTAC and HPGe measurements, our derived values for the P_γ values are in good agreement with published values. Our value for the strong 312 keV γ-ray agrees with, and has a smaller uncertainty than, the evaluated value. In essence, that result validates our direct measurement of ²³³Pa by LTAC, compared to earlier indirect values based on ²³⁷Np parent measurements and equilibrium assumptions.

Figure 3.

Decay-corrected LTAC measurement results for 8 LS sources (named in caption). Top: massic activity, A_m. Bottom: decay-corrected A_m plotted as a percent difference (Δ) from the average (excluding the final measurement, used only as an impurity check). Results from linear efficiency extrapolations (Function 1 in Table 2) are shown.