High-throughput first principles search for new ferroelectrics

Abstract

We use a combination of symmetry analysis and high-throughput density functional theory calculations to search for new ferroelectric materials. We use two search strategies to identify candidate materials. In the first strategy, we start with non-polar materials and look for unrecognized energy-lowering polar distortions. In the second strategy, we consider polar materials and look for related higher symmetry structures. In both cases, if we find new structures with the correct symmetries that are also close in energy to experimentally known structures, then the material is likely to be switchable in an external electric field, making it a candidate ferroelectric. We find sixteen candidate materials, with variety of properties that are rare in typical ferroelectrics, including large polarization, hyperferroelectricity, antiferroelectricity, and multiferroism.

I. INTRODUCTION

Ferroelectrics, which are materials that have a ground state polar phase that can be switched to a symmetry-equivalent structure by the application of an external electric field, have been studied and used in applications for many years. Much of the attention on ferroelectrics has focused on prototypical examples from the perovskite oxides, like PbTiO₃ and BiFeO₃. However, in recent years, there has been a renewed theoretical and experimental interest in discovering and understanding the properties of new ferroelectric materials^1–14. These new materials have shown a variety of new or rare behaviors, including hybrid improper ferroelectricity, hyperferro-electricity, topological defects/domain walls, etc. In addition, there is interest in and need for ferroelectrics with improved functionality for various applications, including magnetoelectrics, Pb-free piezoelectrics, room temperature multiferroics, solar energy converters, silicon compatible ferroelectrics, ferroelectric catalysts, etc.^15–20

High-throughput first principles density functional theory (DFT) calculations have been used increasingly in recent years as a tool for materials discovery and screening, and large databases of electronic structure calculations of experimentally known materials exist^21–26. DFT calculations using semilocal functionals are generally reliable tools for computing ground state properties and the energy differences between closely related phases, which is the primary screening tool needed to identify ferroelectrics. The main obstacle to finding new ferroelectric materials computationally is identifying the relevant polar and non-polar structures to consider. Any insulator known experimentally to have both a polar and a nonpolar phase has likely already been recognized as a potential ferroelectric, necessitating a search for new structures of known compounds. For a single family of materials like the perovskites, it may be possible to systematically consider all possible distortions of a certain type, organized by symmetry considerations^27–29. However, searching all insulating compounds for every possible distorted phase is too computationally demanding to attempt systematically, as any polar subgroup of a reference structure is allowed in general.

In this work, we employ two strategies to identify new ferroelectrics, which we apply to a much larger range of materials than related previous searches^{1,10,14,30–37}. In the first strategy, aimed at finding proper ferroelectrics, we start with a list of experimentally known non-polar transition metal oxides, nitrides, and sulfides, and we perform a Γ-point phonon calculation, looking for materials with unstable polar modes. In order to reduce the computational cost of this step, we reuse phonon calculations from our earlier study of transition metal thermoelectricity³⁸, and we supplement this list with additional calculations of materials with small unit cells. After identifying materials with unstable polar distortions, we proceed to look for the ground state structure, including possible non-polar distortions. If the ground state is polar, then the material is a candidate ferroelectric.

In the second strategy, we begin instead with a list of materials already known to be polar but not known to be switchable in an external electric field. We attempt to identify switchable materials by using a symmetry search algorithm³⁹ and adjusting the tolerance factor systematically to allow the algorithm to identify possible higher symmetry structures that are related to the polar ground state. We then calculate the energy of these new structures, and if they are close in energy to the polar structure, the materials are likely to be switchable¹. An advantage to both of our search strategies is that they are not limited to generating previously observed structure types, allowing us to consider new mechanisms for creating polar distortions. Furthermore, all of the materials we consider have been synthesized experimentally in previous works.

In the remainder of this work, we will detail our search strategy, identify candidate ferroelectrics, and discuss some of their interesting properties. We find materials with unusual chemistry for ferroelectrics, as well as potentially useful properties that include strong polarization, magnetism, hyperferroelectricity, and antiferro-electricity. In addition, we rediscover and identify the missing structures of two materials that were previously studied as ferroelectrics but have not been fully characterized. Full structural details our of candidate materials can be found in the supplementary materials.

II. METHODS

A. First Principles Calculations

We perform first principles DFT calculations^40,41 with a plane-wave basis set as implemented in QUANTUM ESPRESSO⁴² and using the GBRV high-throughput ultrasoft pseudopotential library^43,44. We use a plane wave cutoff of 40 Ryd for band structure calculations and 45–50 Ryd for phonon calculations⁴⁵. For Brillouin zone integration, we use a Γ-centered grid with a density of 1500 k-points per atom.

We use the PBEsol exchange-correlation functional⁴⁶, which provides more accurate lattice constants and phonon frequencies than other generalized gradient approximation functionals (except for CuBiW₂O₈, see Sec. III D). We perform phonon calculations using DFT perturbation theory⁴⁷, and polarization calculations with the Berry phase method⁴⁸. We use PYMATGEN³⁹ to manipulate files from the Inorganic Crystal Structure Database (ICSD) to setup the initial structures for relaxation. We relax each structure several times to ensure consistency between the basis set and the final structure, with a force tolerance of 0.001 Ry/Bohr, an energy tolerance of 1 × 10⁻⁴ Ry, and a stress tolerance of 0.5 Kbar. For phonon calculations, we decrease the force tolerance to 5 × 10⁻⁵ Ry/Bohr.

B. Search Strategy

To identify ferroelectrics, we look for materials that are a) insulating, b) have a polar ground state, and c) have a higher symmetry reference structure that is close in energy to the polar structure, which we take as an indication the material is likely to be switchable in an external electric field. Some examples of this energy difference for known ferroelectrics include PbTiO₃ (20 meV/atom), Ca₃Ti₂O₇ (40 meV/atom), ZrO₂ (16 meV/atom)^5,9. Of course, in real ferroelectrics, the switching proceeds via a combination of domain wall nucleation and motion, and does not correspond directly to the first principles energy difference; however, a small energy difference has proven to be a useful indicator of whether a material is likely to be switchable.^{1,2,5,30,32–34,49}

In our first search strategy, we start with materials where a high symmetry non-polar structure is known to exist, and we search for possible energy-lowering polar distortions. Because our calculations are done at zero temperature while most structure determinations are done at room temperature, if an energy-lowering polar distortion is found, and potential competing phases are ruled out, it should be possible to reach the polar phase experimentally by lowering the temperature. A second possibility is that a material with a small polar distortion could have been misidentified as non-polar during an experimental structure deterimination.

At zero temperature, some degrees of freedom of the high symmetry structure are not at local minima, and the structure is only found on average due to thermal fluctuations at higher temperatures. However, analysis of ferroelectrics based on zero temperature distortions of the unstable high symmetry phase is widely used to gain understanding of the possible low symmetry phases, and our main purpose is to identify possible low symmetry phases.^50,51 Full relaxations are necessary to determine the low energy structures.

In this strategy, the initial screening step is to perform a Γ-point phonon calculation, which we did for 267 transition metal oxides, nitrides, and sulfides. A Γ-point phonon calculation is sufficient to eliminate materials without energy-lowering polar distortions, but further calculations are necessary to find the ground state structure. This screening step also will generally eliminate improper ferroelectrics. We identified 90 compounds with unstable modes at Γ, although some of these distortions were non-polar. After excluding known ferroelectrics and materials with known non-polar distortions, we proceeded to search for the ground state structure.

This search consisted of first calculating the full phonon dispersion of the material, and then freezing in finite amounts of each unstable phonon eigenvector, as well as pairs of eigenvectors, into supercells that correspond to points in the Brillouin zone with unstable modes. For unstable modes away from Γ, this requires increasing the size of the unit cell to accommodate antipolar distortions. We then relax the resulting structures^14,52,53. For systems with many unstable modes, which could have ground states consisting of complicated distortion patterns, we supplemented this searching with a random search strategy⁵³. To perform a random search, we take a supercell, freeze in small random distortions, and relax. For most materials, we found that after a set of ten random relaxations in a given supercell, the same low energy structures repeated several times, and we terminated the search. There is no symmetry constraint on our ground structure search, and we use a symmetry search algorithm³⁹ to determine the final symmetry.

After this search process, if a material has a polar ground state, then the material is a candidate ferroelectric. In addition, if the material has competing polar and antipolar phases, then the material is a candidate antiferroelectric^2,49. In the top rows of table I, we present six candidate ferroelectrics discovered with this strategy.

Table I:

Data on candidate ferroelectrics, found by starting from high symmetry (top) and low symmetry (bottom) structures. The second and third columns are space groups of the high and low symmetry structures, column four is the energy difference in meV/atom, and the last column is the polarization in μC/cm².

Composition	High-sym space grp.	Polar space grp.	ΔE(meV/atom)	Polariz.μC/cm2
SrNb6O16	Amm2	Cm	5.5	7
NaNb6O15F	Amm2	Cm	9.5	6
RbCa2Nb3O10	P4/mmm	Pc	46.6	23
BaBi2Ta2O9	I4/mmm	Cmc21	15.7	37
LiScAs2O7	C2	P1	1.6	7
YSF	P63/mmc	P63mc	11.1	1.2
CuBiW2O8	$P\overline{1}$	P1	P1 0.3	6
PbGa2O4	$P\overline{6}2c$	Ama2	108	23
PbAl2O4	$P\overline{6}2c$	Ama2	75	18
LiV2O5	Pmmn	Pmn21	0.4	9
NaVO2F2	P21/m	P21	0.3	18
SbW2O6	P21/c	P21	4.4	21
V2MoO8	Cmmm	Cmm2	84	108
Zn2BrN	Pnma	Pna21	1.3	1.4
Zn2ClN	Pnma	Pna21	2.4	1.5
AlAgO2	Pnma	Pna21	71	0.2

In our second search strategy, we considered a list about 2750 compounds from the ICSD with small unit cells and polar ground states. For each compound, we used the symmetry detection algorithm of pymatgen³⁹ and varied the tolerance factor from 10⁻⁶ to 3, looking for related structures with higher symmetry that have otherwise reasonable structures (e.g. no atoms on top of each other). For compounds where new structures were found, we then relaxed both the experimentally known polar structure and any new structures. In most cases, the new structures were very high energy. For example, in many structures with covalent bonds, the new structures had broken bonds and were unrealistic. In addition, we found a small number of compounds in the opposite situation, where the polar phase relaxed to a non-polar structure. These materials were either misidentified as polar experimentally, or are not well described by the PBEsol functional.

However, in addition to those cases, we found ten compounds that have a low but non-zero energy difference between their polar and non-polar structures, making them candidate ferroelectrics. In this case, we do not search for possible competing phases unless they are already known to exist experimentally. We list them in the second section of table I, and we discuss a few interesting cases below.

III. RESULTS

First, we note that after doing our analysis, we discovered that BaBi₂Ta₂O₉ and related materials with Sr and Ca have has previously been studied as a ferroelectrics⁵⁴. However, only a pseudotetragonal twinned version of the polar structure of BaBi₂Ta₂O₉ had been determined, ex-plaining why it did not show up in our database search as a polar. This material has a layered structure that consists of perovskite-like BaTaO₃ layers separated by BiO layers, and these layers shift relative to each other in-plane, resulting in a relatively large polarization. Re-identifying a known ferroelectric gives us confidence in the utility of our computational methodology.

Sb₂WO₆ is a second example of a previously known (anti-)ferroelectric/ferroelastic⁵⁵ that our procedure rediscovered. In this case, the polar structure was previously characterized experimentally, and we have provided new information about the non-polar phase.

In the rest of this section we briefly discuss the properties of many of our new candidate ferroelectrics.

A. SrNb₆O₁₆ and NaNb₆O₁₅F

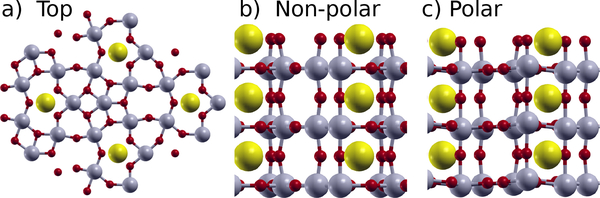
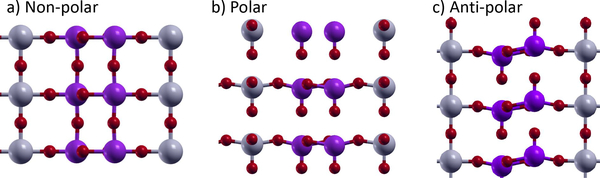
SrNb₆O₁₆⁵⁶, shown in Fig. 1, and the closely related NaNb₆O₁₅F, have a variety of notable properties. We will concentrate on SrNb₆O₁₆, which has a high symmetry structure consisting of layers of Nb₆O₁₀ spaced by SrO₆ layers. The material has a non-reversible in-plane polarization, but the switchable portion of the polarization consists of out-of-plane buckling in the Nb₆O₁₀ layers. Because of the large number of atoms in the unit cell, there are a variety of unstable polar and non-polar bucklings. SrNb₆O₁₆ has anomalously large Born effective charges in the z-direction of 9 to 11 on the Nb atoms and −7 to −9 on the O atoms. In the xy-plane, the effective charges are much lower, and Sr has an effective charge of 2.4. Similar anomalous effective charges are well-known in the perovskite oxides⁵⁰ but are not present in many alternative ferroelectrics^4,6.

FIG. 1:

Atomic positions of SrNb₆O₁₆. a) Top view, b) side view of non-polar structure, and c) side view of polar structure. The Sr are the large yellow atoms, the Nb are the medium gray atoms, and the O are the small red atoms. direction.

Despite these enormous effective charges, SrNb₆O₁₆ is actually a candidate hyperferroelectric⁴, a very rare category of proper ferroelectrics with instabilities of both the longitudinal optic (LO) and transverse optic (TO) modes, as shown in table II. These instabilities correspond to unstable polar modes under both zero electric field (E=0) and zero displacement field (D=0) boundary conditions. The polar distortions of normal ferroelectrics are stable under D=0 boundary conditions.

Table II:

Unstable LO and TO phonon frequencies and mode effective charges in SrNb₆O₁₆ at Γ. The first two columns are the frequency in cm⁻¹ and the mode Born effective charge of the LO modes, the second two columns are the same but for the TO modes. There is one anti-polar mode with zero mode effective charge that is unaffected by electrostatic boundary conditions.

Mode Number	LO Freq. cm−1	LO Mode Z*	TO Freq. cm−1	TO Mode Z*
1	176i	21.8	139i	0.23
2	138i	5.9	128i	0
3	128i	0	85i	1.2
4	44i	10.2	29i	0.32

We were initially very surprised to find a hyperferro-electric with large effective charges, as the energetic cost of producing long range electric fields is proportional to (Z*)²/ϵ, where is the electronic dielectric constant and Z* is the effective charge^4,57. SrNb₆O₁₆ avoids this by having three different unstable polar modes that can mix with each other, producing modes that are still polar, but with much smaller mode effective charges under D = 0 boundary conditions, as detailed in table II. Hopefully, hyperferroelectric oxides similar to SrNb₆O₁₆ are more common than previously thought, especially as hyper-ferroelectrics have potential applications as single layer ferroelectric devices. Further work must be done to understand the D=0 ground state in this material⁵⁸.

B. YSF

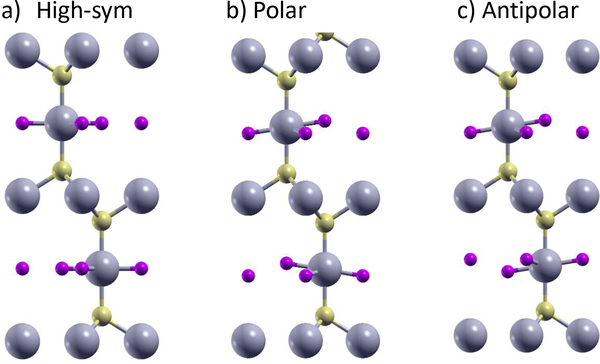
Another compound with interesting behavior is YSF⁵⁹. As shown in Fig. 2, YSF consists of alternating layers of YF₂ and YS₂, and the YF₂ layers display an energy lowering out-of-plane buckling that is locally antipolar. However, due to longer range interactions with the YS₂ layers, this buckling is actually weakly polar^60,61, and the material can become either polar or antipolar depending on how the buckling in adjacent YF₂ layers is aligned. We find that the polar phase of YSF is nominally lower in energy than the antipolar version, but the energy difference is less than 0.1 meV/atom, making YSF a potential antiferroelectric as well. In fact, given the weak coupling between layers, there are likely a high number of layer stackings with nearly degenerate energies, which could then be ordered by an external field.

FIG. 2:

Atomic positions of YSF. a) High symmetry, b) polar, and c) antipolar phases. Y are the large gray atoms, S are the medium yellow atoms, and F are the small purple atoms.

C. LiScAs₂O₇

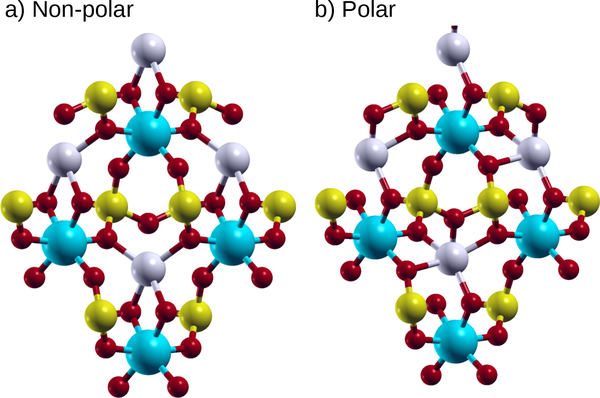
As shown in Fig. 3, the polar distortion of LiScAs₂O₇ consists almost entirely of the Li atom off-centering, likely due to its small size. By moving off-center, the Li atom increases its coordination from four-fold to fivefold, while the four shortest Li-O bonds average 2.12 Å in either structure. This polar distortion pattern of Li moving off-center is similar to LiV₂O₅, as discussed below.

FIG. 3:

Atomic positions of LiScAs₂O₇. a) High symmetry, and b) polar phases. Li are the light gray atoms, As are the medium yellow atoms, Sc are the large cyan atoms, and O are the small red atoms.

D. CuBiW₂O₈

The compound CuBiW₂O₈, as well as the five related materials listed in the ICSD with structure type CuNb(WO₄)₂β, is listed as having no symmetry in the ICSD⁶². However, according to PBEsol calculations, CuBiW₂O₈ and the related CuYW₂O₈ relax to a higher symmetry structure with only inversion symmetry, suggesting that these materials do not have a polar phase. We were surprised to find so many materials possibly misidentified, so we performed LDA⁶³ calculations to verify our result. We instead found that CuBiW₂O₈ (but not CuYW₂O₈) does have polar distortion, with a very small energy difference and polarization, as listed in table I. This functional-dependent behavior is the opposite of the typical behavior of LDA and GGA functionals, where GGA tends to overestimate polar distortions, while LDA underestimates. Further work may be necessary to reveal whether this class of materials is really polar/ferroelectric.

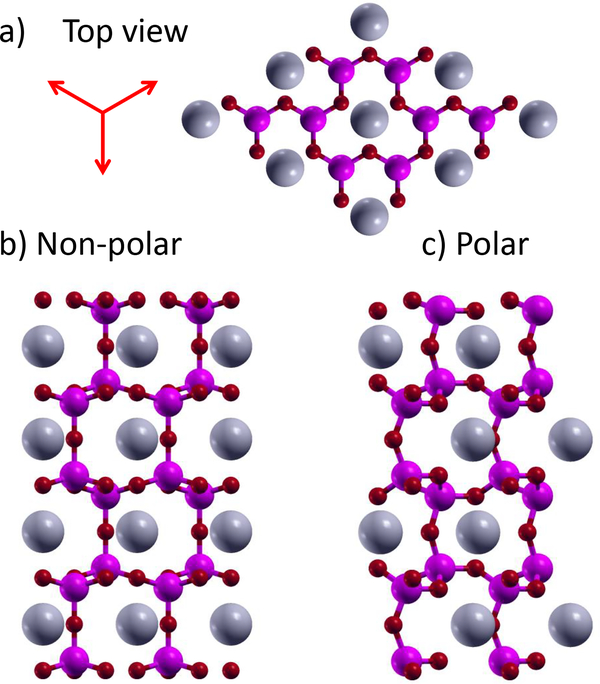
E. PbGa₂O₄ and PbAl₂O₄

The pair of compounds PbGa₂O₄ and PbAl₂O₄ consist of (Al,Ga)O₄ tetrahedra separated by Pb atoms⁶⁴, as shown for PbAl₂O₄ in Fig. 4. Their high symmetry structures have a three-fold rotation axis, and the polarization, which is due to a collective tilting of the tetrahedra, points in one of three equivalent in-plane directions, as shown in Fig. 4a. The structure with 180° reversed polarization does not have the same energy, which can be understood by examining the symmetry invariant free energy of the two-dimensional Γ₅ distortion up to fourth order:

$$F=c_2\left({\Gamma }_{5a}^2+{\Gamma }_{5b}^2\right)+c_3\left({\Gamma }_{5a}^3-3{\Gamma }_{5a}{\Gamma }_{5b}^2\right)+c_4({\Gamma }_{5a}^4+2{\Gamma }_{5a}^2{\Gamma }_{5b}^2+{\Gamma }_{5b}^4).$$ 1

FIG. 4:

Atomic positions of PbAl₂O₄. a-b) Top and side view of non-polar phase. c) Side view of polar phase. Red arrows in a) show three equivalent polarization directions. Large gray atoms are Pb, medium magenta atoms are Al, and small red atoms are O.

In this notation the ground state polar structure corresponds to Γ_5a >0, Γ_5b =0, and the constants c₂ and c₃ are negative, while c₄ is positive. Unlike a typical proper ferroelectric, there is a third-order term, which explains why the structure with reversed polarization is inequivalent.

The reversed polarization direction structure is only 9 meV/atom higher in energy higher than the ground state for PbAl₂O₄. This intermediate structure represents the transition state between two stable polarization directions, which we confirm with nudged elastic band calculations⁶⁵. Therefore, it is possible to switch the polarization of PbGa₂O₄ and PbAl₂O₄ by rotating it 120° while avoiding the higher energy high-symmetry structure, resulting in a barrier that is eight times lower in energy than the naive switching path. In effect, there is very little barrier to rotating the polarization direction any direction in-plane, even though reducing the polarization to zero results in a high energy state. This combination could allow for a high Curie temperature ferro-electric material.

F. V₂MoO₈

The layered structure of V₂MoO₈⁶⁶ is interesting for possible applications because it has an enormous polarization of 108 μC/cm², comparable to the largest polarizations in perovskites⁶⁷. Both the V and the Mo atoms are located in distorted oxygen octahedra, and all three ions displace in the same direction in the polar structure. This combined distortion of ions, all with large nominal charges, is what results in the enormous polarization in this material.

As shown in Fig. 5, this material actually has three low energy structures: the high-symmetry phase, the polar phase, and an antipolar phase^68,69, which is also seen experimentally and which is 48 meV/atom lower in energy than the polar phase. In the anti-polar phase, the V atoms still have large polar distortions, but they distort in opposite directions, and the Mo remains in the center of its octahedron. Because the ground state of V₂MoO₈ is antipolar with a competing polar phase, this material is better characterized as a candidate antiferroelectric. The very large polarization of the polar phase of this material could make V₂MoO₈ useful in applications like antiferroelectric energy storage, where a large polarization jump is desirable.

FIG. 5:

a) High-symmetry, b) polar, and c) antipolar phases of V₂MoO₈. The medium gray and magenta atoms are Mo and V, respectively, and the small red atoms are O.

Also, we note that due to the Mo(+6) and V(+5) ions in the structure, this material has a relatively small band gap of only 0.95 eV according to our calculations. Although quantitatively predicting the band gap of transition metal oxides is difficult, the combination of an oxide with a large polarization and a small gap are potentially useful for solar power applications.

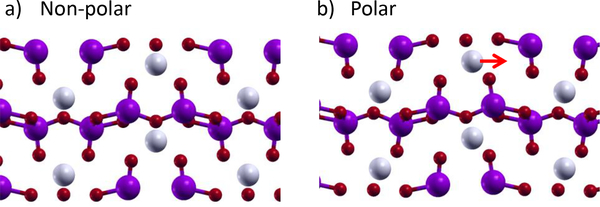
G. LiV₂O₅

LiV₂O₅ consists of layers of V₂O₅ spaced by Li ions, as shown in Fig. 6, and has shown experimental evidence of a phase transition⁷⁰. The ferroelectric polarization is driven by the off-centering of Li atoms. According to PBEsol, the material is non-magnetic; however, we also examined various magnetic orderings using DFT+U^71–73, with a U value of 3 eV on the V d-states. These calculations, which we expect to be more accurate for a material with partially occupied 3d orbitals, shows that LiV₂O₅ is a ferromagnetic insulator with a gap of 0.37 eV in the non-polar phase and 1.00 eV in the polar phase, making LiV₂O₅ a candidate multiferroic. However, the energy difference between the ferromagnetic phase and the lowest energy anti-ferromagnetic phase is only 2.4 meV/V atom, so the magnetic ordering temperature is likely to be low. LiV₂O₅ is also a potential small band gap ferro-electric.

FIG. 6:

a) Non-polar and b) polar phases of LiV₂O₅. The red arrow in b) highlights off-centering of Li. Light gray atoms are Li, magenta atoms are V, and small red atoms are O.

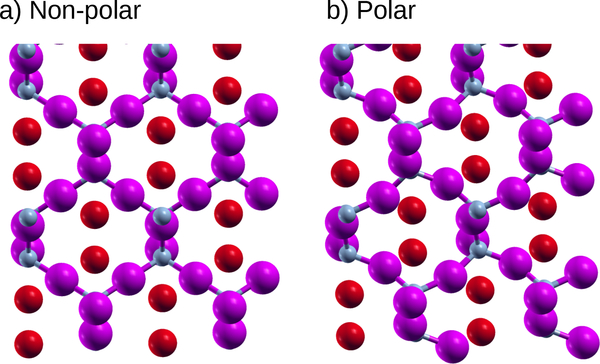
H. Zn₂BrN, Zn₂ClN, and AlAgO₂

Zn₂BrN and Zn₂ClN consist of tetrahedrally coordinated N atoms linked by two-fold coordinated Zn, with Br/Cl serving as spacing atoms, as shown in Fig. 7. AlAgO₂ shares the same structure, but with AlO₄ tetrahedra spaced by Ag atoms. The polar distortion in these materials consists primarily of a locally non-polar rotation of the tetrahedra; however, due to the connectivity of the tetrahedra, this results in a polar distortion. The tetrahedra primarily rotate rigidly, and unlike PbAl₂O₄, which also has rotating tetrahedra, there is no strong off-centering of the atoms in any direction. The result is that even in the case of AlAgO₂, where the energy gain from the distortion is substantial, the net polarization is very small. Increasing the polarization in this class of materials would likely require searching for spacing atoms that would couple more strongly to the weakly polar rotation mode, which is reminiscent of the proposed engineering of some improper ferroelectrics^5,74.

FIG. 7:

a) Non-polar and b) polar phases of Zn₂BrN. Polarization is to the left. Small gray atoms are N, magenta atoms are Zn, and red atoms are Br.

IV. CONCLUSIONS

In conclusion, we have performed a high-throughput first principles search for new ferroelectric compounds. We use two search strategies: 1) starting with known non-polar structures and looking for polar distortions, and 2) starting with known polar structures and looking for related high-symmetry structures. We discover 16 candidate materials with a variety of interesting properties, including very large polarizations, hyperferroelectricity, antiferroelectricity, and multiferroism. In addition, all the candidates are experimentally synthesized oxides, nitrides, or sulphides, making them likely to be stable under practical conditions, and many of the materials consist non-toxic and earth abundant elements.

This search uncovers several related classes of materials with similar mechanisms for their polar distortions. We found two materials where the primary polar distortion is due to Li off-centering (LiScAs₂O₇, LiV₂O₅), five materials with distortions related to shifting tetrahedral networks (Zn₂BrN, Zn₂ClN, AlAgO₂, PbGa₂O₄, PbAl₂O₄), and four materials that consist of buckling in a layered structure (SrNb₆O₁₆, NaNb₆O₁₅F, YSF, V₂MoO₈), as well as a few structures with more complicated distortions. Further work will be necessary to understand the full range of properties of these newly discovered ferro-electrics, including the character of the phase transitions of these unusual ferroelectrics and how they couple to strain and other ways of tuning their properties. Never-theless, we hope that by identifying new classes of materials with energy-lowering polar distortions, we have expanded the universe of materials considered as potential ferrolectrics.

Finally, the high-throughout search techniques used in this work should be applicable to future studies of structural phase transitions.