Matching the LenStar Optical Biometer to A-Scan Ultrasonography for use in Small Animal Eyes with Application to Tree Shrews

Abstract

We describe an analysis strategy to obtain ultrasonography-matched axial dimensions of small animal eyes using the LenStar biometer. The LenStar optical low-coherence reflectometer is an attractive device for animal research due to its high precision, non-invasiveness, and the ability to measure the axial dimensions of cornea, anterior chamber, lens, vitreous chamber, and axial length. However, this optical biometer was designed for clinical applications in human eyes and its internal analysis provides inaccurate values when used on small eyes due to species-dependent differences in refractive indices and relative axial dimensions. The LenStar uses a near infrared light source to measure optical path lengths (OPLs) that are converted by the LenStar’s EyeSuite software into geometrical lengths (GLs) based on the refractive indices and axial dimensions of the human eye. We present a strategy that extracts the OPLs, determines refractive indices specific for the small animal eye of interest and then calculates corrected GLs. The refractive indices are obtained by matching the LenStar values to ultrasonography values to ultrasonography values in the same eyes. As compared to ultrasounography, we found that the internal calculations of the LenStar underestimate the axial dimensions of all ocular compartments of the tree shrew eye: anterior segment depth by 6.17 ± 4.50%, lens thickness by 1.37 ± 3.06%, vitreous chamber depth by 29.23 ± 2.35%, and axial length by 10.62 ± 1.75%. Using tree shrew-specific refractive indices, the axial dimensions closely matched those measured by ultrasonography for each compartment. Our analysis strategy can be easily translated to other species by obtaining a similar paired data set using ultrasonography and LenStar, and applying our step by step procedures.

1. Introduction

In vivo measurements of ocular dimensions are essential for a wide range of research and clinical applications including, but not limited to, cataract and refractive surgeries (Drexler et al., 1998; Norrby, 2008), diagnosis of ocular conditions and progression (Goebel and Kretzchmar-Gross, 2002; Bowd et al., 2001; Pflugfelder et al., 2002), and research on refractive error development (Dirani et al., 2006; VanAlphen, 1961; Grosvenor and Scott, 1993; Zadnik et al., 2003). Since the 1980s A-scan ultrasonography has been the gold standard technique to measure ocular dimensions in humans (Butcher and Obrien, 1991; Raj et al., 1998; Coleman et al., 1977) and animals (Norton and McBrien, 1992; Marsh-Tootle and Norton, 1989; Schaeffel and How-land, 1991; Wallman and Adams, 1987). In animals (chicks, tree shrews, monkeys, guinea pigs), ultrasound has been used to examine the structural changes of eyes that are made myopic or hyperopic as a result of environmental manipulations. It allows in vivo measures of the ocular compartments to show the structural changes that produce refractive changes. This has led to a better understanding of the mechanisms underlying refractive error development. Recently, mice have been frequently used in these studies because they can be genetically manipulated to explore gene-environment interactions. However, ultrasound does not have sufficient resolution for use in mice, where a 1 diopter change would require the detection of 6 microns in axial length change (Schmucker and Schaeffel, 2004). Optical biometers such as the IOLMaster and LenStar have been found to provide higher resolution (0.01–0.02 mm) than ultrasound (0.10 mm) in human and animal eyes (Suheimat et al., 2014; Aleman and Schaeffel, 2018).

In the late 1990’s Carl Zeiss Meditec (Jena, Germany) revolutionized cataract surgery by introducing the IOLMaster partial coherence interferometry biometer. This is a non-contact instrument that measures anterior chamber depth and axial length, providing values used to calculate intraocular lens power. Ten years later, Haag-Streit AG (Koeniz, Switzerland) introduced its near-infrared optical low-coherence reflectometer, the LenStar LS900, as an alternative to the IOLMaster. The LenStar biometer provides measures of corneal thickness, anterior chamber depth, lens thickness, retinal thickness and axial length, providing additional information to cataract and refractive surgeons (Rohrer et al., 2009b). Several studies have evaluated its accuracy and repeatability in comparison to the IOLMaster and other instruments (Rohrer et al., 2009a; Buckhurst et al., 2009; Cruysberg et al., 2010; Chen et al., 2011; Cooke and Cooke, 2016).

The LenStar is a non-contact instrument and can, therefore, be used to make frequent and highly accurate measures of ocular compartments in unanesthetized animals (Ward et al., 2018; Gawne et al., 2017; Jnawali et al., 2018; Aleman and Schaeffel, 2018). To learn if LenStar measures could directly substitute for ultrasound measures, a comparison was carried out in chicks (Penha et al., 2012) and tree shrews (Gann, 2013), as well as humans (Buckhurst et al., 2009; Chen et al., 2011; Gursoy et al., 2011). These studies verified the utility of the LenStar and found a high correlation between the LenStar and ultrasonography measurements for the ocular compartments in chicks and tree shrews. However, the LenStar values differ from those obtained with ultrasound. In particular, the vitreous chamber depth (VCD) obtained from the LenStar is smaller than the value obtained with ultrasound.

The LenStar results can still be valid, despite the above mentioned differences, when comparing relative changes between treated and control eyes (Ward et al., 2016). However, realistic measurements of axial dimensions remain critical for many purposes. For instance, obtaining realistic axial dimensions is critical for optical models that can correct non-linear distortions in optical coherence tomography (Kuo et al., 2013) as well as for predictive biomechanical eye models that simulate physiological and pathological eye conditions (Grytz and El Hamdaoui, 2017; Grytz et al., 2011; Schwaner et al., 2018; Hua et al., 2018).

Because the LenStar is increasingly used to measure axial dimensions in animals with small eyes, we have developed an analysis strategy to obtain axial dimensions from the LenStar biometer that matches the values obtained with from ultrasound. In this study, we used data obtained from the eyes of tree shrews.

Northern tree shrews (Tupaia belangeri) are small (150 – 250 g), semi-arboreal mammals, common to Southeast Asia, that are closely related to primates (Sargis, 2004; Olson et al., 2004). They have a cone-dominated retina and excellent acuity for their size. In our laboratories, they have been used for many years as an animal model of refractive development (Sherman et al., 1977; Marsh-Tootle and Norton, 1989; Norton and McBrien, 1992; Siegwart and Norton, 1999; Grytz and El Hamdaoui, 2017). During the postnatal period their eyes grow from < 7 mm to approximately 8 mm, larger than mice and rats and comparable to guinea pigs. Until the development of the LenStar, ocular component dimensions were measured with A-scan ultrasonography (Marsh-Tootle and Norton, 1989), yielding a large database of measures. The present study was driven, in part, by our interest in learning how to match measures made with the LenStar to the existing A-scan measurements. Specifically, we estimated refractive indices for tree shrew eyes that were then used to convert the raw optical path lengths (OPLs) measured by LenStar into geometrical lengths (GLs) that closely matched the GLs measured with ultrasound in the same eyes. The strategy described here can easily be adapted to use with the eyes of other small animals in which a data set of A-scan ultrasound and LenStar measures are available on the same eyes.

1.1. A-scan Ultrasonography in Animal Research

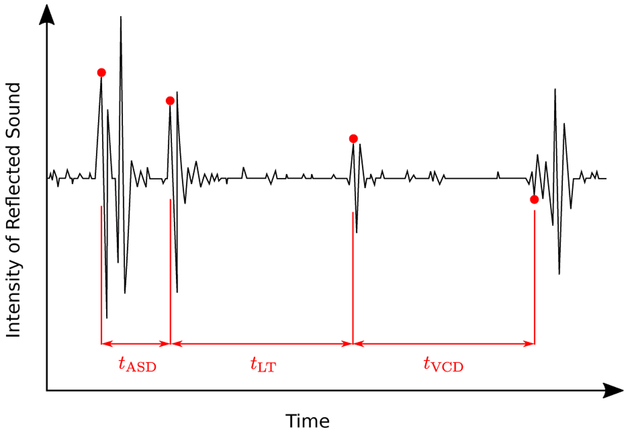
In A-scan ultrasound measures, a pulse of ultra-sound (typically 10 – 25 MHz) is sent into the eye and is reflected every time the wavefront cross the interface between two ocular compartments (see Fig. 1). The time delay for an echo to return to the front of the eye is a function of the distances and the sound velocities of the ocular media that are in between the interface and the front of the eye. At each interface, the generated echoes ring at the frequency of the ultrasound pulse before returning to baseline. Consequently, the echo from the posterior surface of thin ocular compartments is obscured by the waveform of the echo at the anterior surface and the posterior surface cannot accurately be located. This typically is the case in small animal eyes where the cornea is thin compared to human corneas; its posterior surface is not resolved with most ultrasound systems (Fig. 1). Consequently, separate measures of corneal thickness (CT) and anterior chamber depth (ACD) cannot be obtained from ultrasound in these animal eyes. Instead, a value is obtained for the time delay between the front of the cornea and the front of the lens, the anterior segment depth (ASD) combining CT and ACD. Two additional compartments are typically measured with ultrasound and used here: lens thickness (LT) and VCD, where VCD is measured from the back of the lens to the front of the retina.

Figure 1:

A representative ultrasonography trace (waveform not rectified) of a tree shrew eye showing the echoes that are generated at the interfaces between adjacent ocular media. t_ASD, t_LT and t_VCD are the time delays for anterior segment depth (ASD), lens thickness (LT) and vitreous chamber depth (VCD), respectively. Refer to (Norton and McBrien, 1992; Marsh-Tootle and Norton, 1989; Shaikh et al., 1999) for more details regarding ultrasonography in tree shrews.

To convert the time delays between the surfaces of the ocular compartments to distances (geometric length, GL), the time delay of each compartment is multiplied by the sound velocity of the ultrasound pulse in that compartment. This is done internally by commercial ultrasound systems using proprietary sound velocities. For small animal research, separate sound velocity values are usually used for the LT (Wallman and Adams, 1987) and VCD, as summarized in Table 1 for tree shrew eyes. For the ASD (the sum of corneal thickness and anterior chamber depth), a mean sound velocity is calculated, based on the relative dimensions and sound velocities of the cornea and aqueous humor Table 1. Axial length (AL), measured to the front of the retina, is then calculated as the sum of ASD, LT, and VCD.

Table 1:

The sound velocities in mm/μs that were used in tree shrews to convert the time delays between two A-scan ultrasonography peaks (Fig. 1) into geometrical lengths (GLs) (Coleman et al., 1977; McBrien and Norton, 1992; Marsh-Tootle and Norton, 1989). For anterior segment depth (ASD), an average sound velocity was typically used based on an assumed CT:ACD ratio of 1:3.

Medium	Cornea	Aqueous	Lens	Vitreous
Velocity	1.610	1.540	1.7233	1.540

1.2. LenStar in Animal Research

The LenStar is an optical interferometer that uses a broadband near infrared light source (approximately 825 nm with a 25 nm bandwidth) to detect the surfaces of the ocular compartments (Suheimat et al., 2014) measured as OPLs within each ocular compartment. Similar to ultrasonography, the OPLs must be converted to GLs. The LenStar EyeSuite software internally analyzes the acquired OPL data and displays the calculated GLs for CT, ACD, LT, retina thickness (RT) and AL.

The EyeSuite software uses proprietary algorithms and assumptions that are not disclosed by the manufacturer and that were chosen to measure axial dimensions in human eyes and to match the IOLMaster measurements. Suheimat et al. (2014) have provided insights into the functioning of the LenStar, which uses different refractive indices for the ocular media in each compartment to calculate the axial dimensions (GLs). The refractive indices of ocular media are known to differ across species (Sivak and Mandelman, 1982; Remtulla and Hallett, 1985; Marshall et al., 1973; Oswaldo-Cruz et al., 1979; Hughes, 1979; Martin, 1982). This presumably contributes to the significant differences between A-scan ultrasonography and LenStar measurements of the axial compartments reported in chicks by Penha et al. (2012) and in tree shrews by Gann (2013). A value for the VCD is not provided directly by the LenStar; VCD must be obtained by subtracting the dimensions of the cornea, anterior chamber and lens from the axial length. In small eyes, the LenStar VCD can differ substantially from the ultrasound value (Gann, 2013).

1.3. Matching LenStar Output to A-scan Ultrasonography

The issue we address in this paper is how to convert the LenStar internal measurements of small animal eyes so that they match the GL values obtained by ultrasound. Doing this requires (1) exporting OPL values from the LenStar and (2) calculating animal-specific refractive indices for each ocular compartment. These are then used (3) to determine axial dimensions (GLs) that match the values provided by ultrasound. The same approach can be applied to match the LenStar values to measurements made with other reference techniques.

2. Materials and Supplies

The animal experiments in this study were carried out using northern tree shrews (Tupaia belangeri) in accordance with the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research and were approved by the University of Alabama at Birmingham Institutional Animal Care and Use Committee. A total of 184 paired measurements of axial dimensions were performed in 66 tree shrews using both A-scan ultrasonography and a LenStar Biometer LS 900. The animals were mostly juveniles at a variety of ages (measured between 10 and 62 days after eye opening) and, hence, ocular dimensions. There were 40 animals with normal eyes and 26 lens-treated animals that wore a plus-power or minus-power lens or a translucent diffuser on one eye for varying periods of time to produce myopia or hyperopia, thus further extending the range of axial dimensions, especially of the vitreous chamber. Most of the normal animals were measured once; treated animals were measured twice, at the beginning and end of treatment.

3. Detailed Methods

In the following, we use the subscripts “LS” and “US” to distinguish variables that relate to the LenStar and ultrasonography, respectively.

3.1. A-Scan Ultrasonography Measurements

For ultrasound measures, the animals were anesthetized (90 mg/kg Ketamine 10 mg/kg Xylazine, i.m.) and measured using a 15 MHz ultrasound transducer following published procedures (Marsh-Tootle and Norton, 1989; Norton and McBrien, 1992). The ultrasound signal-to-noise ratio was enhanced by averaging eight waveforms. Six of the averaged waveforms were collected per each eye. The ultrasound time delays, t_US, of ASD, LT, and VCD were measured using the waveform analysis package TAMS (Tektronix Inc.). These time delays were converted to GLs using the medium-specific sound velocities v in Table 1

$${\text{GL}}_{\text{US}}=v{t}_{\text{US}}.$$ (1)

If the ultrasound system being used can resolve the corneal posterior surface, one can use the above equation to also calculate the GLs of CT and ACD.

3.2. LenStar Measurements

LenStar measures were taken in awake animals that were gently restrained on a platform that substituted for the LenStar chin rest. In many cases, the LenStar and ultrasound measures were taken on the same day but, in some instances, the ultrasound measures were made up to 3 days before the LenStar measures. We randomly split the dataset of paired LenStar and ultra-sound measurements into two fractions. 75% of the data pairs (138 pairs) were used to fit the exported LenStar OPLs to the measured ultrasonography GLs to establish ultrasonography-matched refractive indices for tree shrews. These refractive indices can then be used in the future to calculate GLs from LenStar OPLs. The fitted model was then validated using the remaining 25% of the dataset (46 pairs) and compared against the results of the internal LenStar analysis and an alternative method used by (Ward et al., 2016).

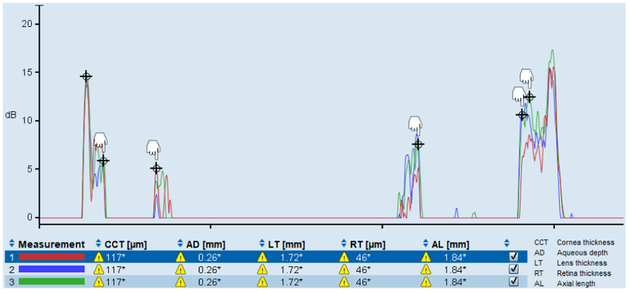
Each LenStar recording takes about 2s, during which the LenStar averages sixteen individual waveforms into one (Penha et al., 2012). We performed three recordings per eye and imaging session, and considered the average result from these three recordings as one measurement. Fig. 2 shows the three recordings of one representative LenStar measurement of a tree shrew eye. In human eyes, the EyeSuite software automatically detects the peaks of the six intraocular interfaces. In small animal eyes, the automatic peak detection fails. However, the international version of the EyeSuite software allows the manual delineation of these peaks by manually setting the six cursors. As shown in the inset of Fig. 2, we set each cursor at what was judged to be the average location of the peaks in the three recordings and considered that as one LenStar measurement. The distance between these peaks represents the OPLs of the following 5 ocular compartments: CT, ACD, LT, VCD, RT. The GLs processed internally by the EyeSuite software are provided in Fig. 2 below the waveforms by the graphical user interface (GUI). Note that the abbreviations for the ocular compartments used in the EyeSuite GUI differ from the abbreviations used here and that the GUI does not provide a GL for the VCD (Fig. 2). However, OPL values for this compartment can be obtained from the LenStar using an export option as explained in the following section.

Figure 2:

Image of the graphical user interface (GUI) of the LenStar “ΈyeSuite” software (version i8.1.1.0) showing three traces from a tree shrew eye. The six peaks indicated by ⊕ represent (left-to-right) the anterior corneal surface, posterior cornea, anterior lens, posterior lens, internal limiting membrane, and retinal pigment epithelium. The EyeSuite aligns each trace so that the anterior corneal peaks all traces match each other. The remaining peaks can be manually delineated by placing the respective cursors (white hands) at the peak of each trace. Parts of the trace can be magnified horizontally to allow an easier placement of the cursors (inset) at the average location of each peak in the three traces. The distance between these peaks represents the optical path lengths (OPLs) of five ocular compartments (left-to-right): corneal thickness (CCT), aqueous chamber depth (AD), lens thickness (LT), vitreous chamber depth, retinal thickness (RT). At the bottom of the GUI, geometric lengths (GLs), converted by the EyeSuite software, are reported for only four compartments and the axial length (AL). No numerical value is provided for the GL of VCD.

3.2.1. Exporting the OPL Values

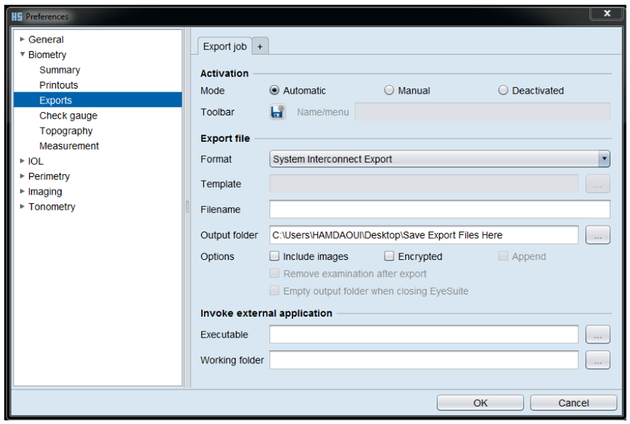
The next step in obtaining the data needed to apply our approach was to generate an export file, which can be obtained by changing the settings of EyeSuite to “System Interconnect Export” as shown in Fig. 3. Note that other export options exist, including a template-based format (“EyeSuite template exporter”), where the output variables can be specified by the user (Suheimat et al., 2014). However, the template-based format has fewer significant digits and will not export the OPL of the VCD if this value is below a certain threshold. In small eyes such as tree shrew, where the OPL value of VCD is below this threshold, this export option cannot be used for determining VCD.

Figure 3:

EyeSuite settings to generate the export file shown in Fig. 4. The export settings can be set by navigating through Tools >Preferences >Biometry >Exports. The activation mode and the export file format should be set to “Automatic” and “System Interconnect Export”, respectively. Then, name the output folder in which the exported files will be stored before clicking the “OK” button.

With the “System Interconnect Export” export setting activated, two export files, one for each eye, are automatically generated and saved in the specified output folder. The names of these files contain information related to the measured subject (subject ID, project name, date and time when measurement was performed among other information) with the extension “.OD” for the right eye and “.OS” for the left eye. The export files contain several useful variables including the OPLs and EyeSuite calculated GLs of all compartments (except the GL of VCD) and the wavelength of the LenStar used to perform the measurements. An example of the export file is shown in Fig. 4; Table 2 summarizes prefixes of variables of interest that can be found in the export file, primarily the values “in air” which are the OPL values.

Figure 4:

The export files structure. Variables of interest are highlighted in bold font and described in Table 2.

Table 2:

Variables and corresponding descriptions that can be found in the export file shown in Fig. 4. All shown variables except MEASNR are given in the unit meter. The wavelength and OPL variables (highlighted in italic font) are required for the here proposed method. The remaining GL variables are only needed for the error estimation presented in Section 3.5.

Prefix	Description
BEAM_WAVELENGTH	Center wavelength λ of your machine
MEASNR	Measurement number (max. 6 from 0 to 5)
CORNEA_THICKNESS	GL of CT internally analyzed by EyeSuite
ACDH_DEPTH	GL of ACD internally analyzed by EyeSuite
LENS_THICKNESS	GL of LT internally analyzed by EyeSuite
EYE_LENGTH	GL of AL calculated by EyeSuite
RETINA_THICKNESS	GL of RT internally analyzed by EyeSuite
CORNEA_IN_AIR	OPL of CT
ACD_IN_AIR	OPL of ACD measured by LenStar
LENS_IN_AIR	OPL of LT
AL_IN_AIR	OPL of AL measured by LenStar
RT_IN_AIR	OPL of RT measured by LenStar
VITREOUS_IN_AIR	OPL of VCD

Algorithm 1.

Iterative algorithm to estimate the aqueous group refractive index n_ACD and the ratio x = GL_ACD/GL_ASD.

1: Set initial guess for xlast

2: while r > tol do

3:  Compute $v_{\text{ASD}}=\frac{v_{\text{CT}}}{1+x\left(v_{\text{CT}}-v_{\text{ACD}}\right)/v_{\text{ACD}}}$

4:  for each paired measurement i do

5:   Compute ${\text{GL}}_{\text{US},\text{ASD}}^{\text{i}}=v_{\text{ASD}}{t}_{\text{ASD}}^i$

6:   Compute ${\text{GL}}_{\text{LS},\text{CT}}^i={\text{OPL}}_{\text{LS},\text{CT}}^i/n_{\text{CT}}$

7:  end for

8:  Compute nACD by minimizing SSRACD (7)

9:  Compute $x=\frac{1}{N_{\text{data}}}\sum _i^{N_{\text{data}}}\left(\frac{{\text{OPL}}_{\text{LS},\text{ACD}}^i}{{\text{GL}}_{\text{US},\text{ASD}}^i{n}_{\text{ACD}}}\right)$

10:  Compute r = |x – xlast|/x

11:  Update xlast = x

12: end while

13: Output: nACD and x

To calculate LenStar GLs that match the ultrasound data, the OPLs of CT, ACD, LT, VCD, RT, and the wavelength need to be extracted from the export files. A simple script can be written in a language of your choice to read the export files and extract the variables. Note that each OPL appears multiple times in each export file, one for each LenStar recording (three in our case). However, when the manual peak delineation method is used to determine an average OPL for all recordings, the exported values are identical in each repetition listed in the export file as described in Fig. 2. Consequently, only the OPLs of the first measurement (MEASNR: 0) need to be extracted from the export file. Note that the export file contains the OPL of the VCD (VITREOUSJN_AIR), which is used here to calculate the GL of the VCD.

3.3. Calculating A-scan Ultrasonography-Matched Re-fractive Indices

In a given medium, OPLs measured by an optical interferometer that uses a broadband light source like the LenStar can be translated into GLs by means of the group refractive index n of the medium

$${\text{GL}}_{\text{LS}}=\frac{{\text{OPL}}_{\text{LS}}}{n}.$$ (2)

The group refractive index n differs across species and between tissues, and also depends on the center wavelength λ. We suggest to estimate n for each ocular compartment by matching the calculation of GL_LS in Eq. (2) to a paired data set of GL_US obtained from A-scan ultra-sonography. This can be achieved by running a simple curve fitting algorithm or linear regression. We used the MATLAB (MathWorks) function fit to minimize the sum of squared residuals (SSR)

$$\text{SSR}=\sum _{i=1}^{N_{\text{data}}}{\left(\frac{{\text{OPL}}_{\text{LS}}^i}{n}-{\text{GL}}_{\text{US}}^i\right)}^2.$$ (3)

In the equation above, ${\text{OPL}}_{\text{LS}}^i$ and ${\text{GL}}_{\text{US}}^i$ represent the OPL and GL obtained from paired measurements of the same eye using the LenStar and A-scan ultrasonography, respectively. N_data represents the number of paired measurements used to fit the refractive index n. We suggest to also use the option Bisquare to reduce the impact of outliers on the fitted model.

We used the above approach to obtain the group refractive index of the lens and vitreous.

3.3.1. Special Case: Anterior Segment

The foregoing procedure provides the GLs of ocular compartments, where paired measurements can be directly obtained from both, ultrasonography and LenStar. If the reference technique does not provide separate GLs for CT and ACD (as is often the case for ultrasound measures), a modified approach is needed to estimate the refractive indices of the cornea and aqueous. Similar to the human cornea, the cornea in most species is composed mainly of collagen type I fibrils with associated proteoglycans and elastin (Maurice, 1957; Meek and Knupp, 2015; Sivak and Mandelman, 1982; White et al., 2017). We thus assumed that the refractive index of the tree shrew cornea can be approximated by the refractive index of the human cornea. To estimate the corneal refractive index, we used the Cauchy model (Cauchy, 1895), which is one of the most common analytical models used to describe the variation of refractive indices of optical media with wavelength λ. Atchison and Smith (2005) found that the Cauchy model provides an excellent fit to human eye data. The original Cauchy model was derived for phase refractive indices, which are applicable to single rays. The group refractive index that is applicable to wave bundles can be obtained by

$$n_g(\lambda )=n_p(\lambda )-\frac{\partial n_p(\lambda )}{\partial \lambda },$$ (4)

where n_g(λ), n_p(λ) are group and phase refractive indices at wavelength λ, respectively. Using Eq. (4), the Cauchy model (Atchison and Smith, 2005, eq. 3a) was modified to represent group refractive indices

$$n_{\text{Cauchy}}(\lambda )=A+\frac{3B}{{\lambda }^2}+\frac{5C}{{\lambda }^4}+\frac{7D}{{\lambda }^6},$$ (5)

where A, B, C, D are media-dependent parameters that can be found in Atchison and Smith (2005, Table 5) for different ocular media. We used Eq. (5) with the human corneal parameters (A = 1.361594, B = 6.009687 · 10³, C = −6.760760 · 10⁸, D = 5.908450 · 10¹³) to estimate the group refractive index of the tree shrew cornea at the wavelength λ of the LenStar.

We used an iterative process to estimate the refractive index of the aqueous. The GL of ASD can be obtained from ultrasonography data by using Eq. (1) and the mean sound velocity of ASD in Eq. (6)

$$v_{\text{ASD}}=\frac{v_{\text{CT}}}{1+x\frac{v_{\text{CT}}-v_{\text{ACD}}}{v_{\text{ACD}}}}\text{with}x\text{=}\frac{{\text{GL}}_{\text{ACD}}}{{\text{GL}}_{\text{ASD}}},$$ (6)

where v_CT and v_ACD are corneal and aqueous velocities from Table 1, respectively. The ratio x is iteratively determined. We used the mean velocity of ASD to compute the GL_US,_ASD from the ultrasonography data according to Eq. (1). The GL_LS,_CT is obtained from the LenStar data by using Eq. (2) and the human corneal refractive index (Eq. (5)). With these values in hand, the refractive index of the aqueous n_ACD can be calculated by minimizing the following SSR

$${\text{SSR}}_{\text{ACD}}=\sum _{i=1}^{N_{\text{data}}}{\left(\frac{{\text{OPL}}_{\text{LS},\text{ACD}}^{\text{i}}}{n_{\text{ACD}}}-{\text{GL}}_{\text{US},\text{ASD}}^i+{\text{GL}}_{\text{LS},\text{CT}}^i\right)}^2.$$ (7)

Once n_ACD has been obtained, the GL of ACD can be calculated from Eq. (2) and the ratio x together with the mean velocity v_ASD can be updated using Eq. (6). This process is repeated until the algorithm converges. The proposed iterative algorithm is summarized in Algorithm 1. At the converged state, the iterative algorithm estimated the ratio between GL_ACD and GL_ASD to x = 0.767 which is close to the histology-based estimation by Marsh-Tootle and Norton (1989) (x = 0.75). The proposed algorithm was implemented in MATLAB. The code used to obtain the A-scan ultrasonography-matched refractive indices together with the data used in this study can be found in the Supplementary Material of this paper.

3.4. Estimated Refractive Indices and Calculating GLs

The central wavelength of our LenStar is λ = 832 nm. For this wavelength, Table 3 summarizes the ultrasonography-matched refractive indices for tree shrews that we obtained by using the approach described in the previous sections. Once the refractive indices were established, GLs were calculated for each compartment and for each animal using Eq. (2).

Table 3:

Comparison of group refractive indices. First row: the estimated A-scan ultrasonography-matched refractive indices for tree shrew eyes at a wavelength of λ = 832 nm. Second row: human group refractive indices obtained from Atchison and Smith (2005) using Cauchy model at a wavelength of λ = 832 nm (the “high” lens values were used). Third row: the effective refractive indices of the LenStar estimated by Suheimat et al. (2014). Note that the refractive index of the vitreous is missing as the LenStar software does not compute this compartment.

	Tree Shrew	Human	LenStar
Cornea	1.3818	1.3818	1.3398
Anterior chamber	1.3896	1.3419	1.3406
Lens	1.3951	1.4124	1.4149
Vitreous	1.3662	1.3415	—

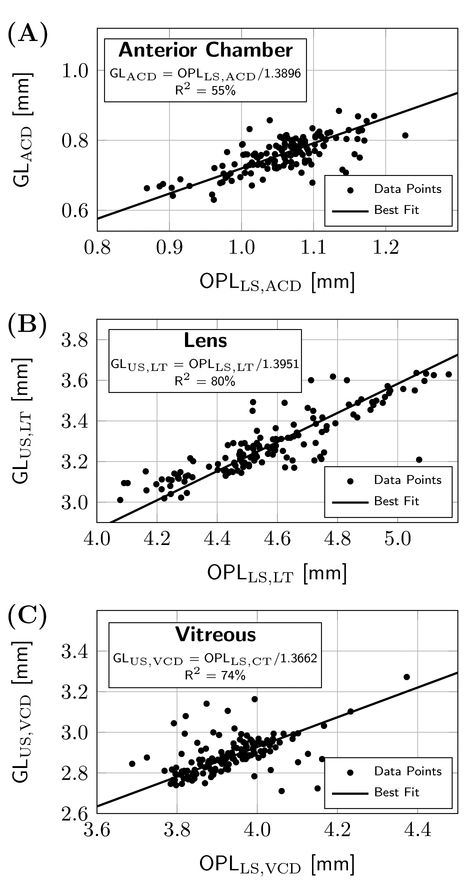
Suheimat et al. (2014) estimated the effective refractive indices of the LenStar, which are also shown in Table 3 together with the Cauchy model values for human eyes. Large differences can be seen between human-and tree shrew-specific refractive indices for the aqueous and vitreous, underlining the importance of using species-dependent refractive indices for optical interferometers such as the LenStar. Fig. 5 illustrates the fitted models for each compartment using the refractive indices we derived for each ocular compartment following the procedures described in Section 3.3. The fitted models (lines in each scatter plot relating OPL to GL) account for most of the variability of the individual measures around the line.

Figure 5:

Scatter plots showing the paired measurements of ultrasound GLs and LenStar OPLs for 75% of the paired dataset, along with the fitted model that uses the derived n values to convert exported LenStar OPLs to GLs that match the paired ultrasound measures for (A) the anterior chamber depth with GL_ACD = GL_US,_ASD - GL_{LS CT}, (B) the lens thickness, and (C) the vitreous chamber depth.

3.5. Validation

In summary, our analysis strategy consists of: manual delineation of the intraocular interfaces using the LenStar GUI (Fig. 2); exporting the OPLs of all compartments (Fig. 4), calculating species-specific refractive indices for each compartment and then translating the OPLs into GLs using the estimated refractive indices (Table 3) andEq. (2). After this was accomplished using 75% of the dataset, we validated the estimated refractive indices using the remaining 25% (46 paired measurements). We compared the following three different strategies for analyzing the LenStar databy calculating the relative errors with respect to the ultrasonography validation data set: (i) the LenStar internal analysis, (ii) the modified LenStar analysis used by Ward et al. (2016) and (iii) the present analysis strategy.

For the LenStar internal analysis (i), the GLs of CT, ACD, LT, and AL (minus RT) were directly obtained from the export file (Fig. 4) and VCD was calculated as VCD = AL - CT - ACD - LT. For the modified LenStar analysis (ii), the retinal coursers (Fig. 2) were used to delineate VCD and its GL was recorded from the EyeSuite GUI while the GLs of CT, ACD, and LT were obtained from the export file.

For methods (ii) and (iii), AL was calculated as AL = CT + ACD + LT + VCD. ASD was computed as ASD=CT+ACD across all methods. The relative error was calculated for each method and for each paired LenStar-ultrasound measurement as

$$error=\left({\text{GL}}_{\text{L}S,\text{i-ii }}-{\text{GL}}_{\text{US}}\right)/{\text{GL}}_{\text{US}},$$ (8)

where GL_US and GL_LS,_i-iii represent the GLs obtained by ultrasonography and the three methods used to analyze the LenStar data, respectively.

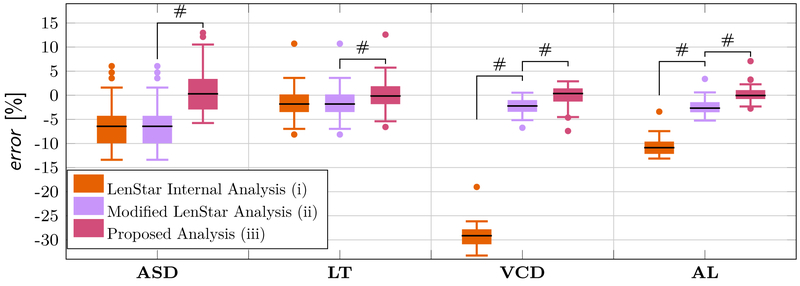
The mean relative errors and standard deviations are shown in Table 4 and the distribution of the relative errors are illustrated using box plots in Fig. 6 for each method and compartment. The LenStar internal analysis (i) underestimated all compartments. The errors were noticeably more pronounced for VCD and AL than for the other compartments. Compared to the LenStar internal analysis, the modified analysis used by Ward et al. (2016) (ii) produced significantly lower errors for both, the VCD and AL. Our proposed method (iii) produced significantly lower errors for all four compartments, closely matching the ultrasound measurements.

Table 4:

The mean relative error ± standard deviation was calculated using Eq. (8) for each compartment and each analysis method.

	LenStar Internal Analysis (i)	Modified LenStar Analysis (ii)	Proposed Analysis (iii)
ASD	−6.17 ± 4.50 %	−6.17 ± 4.50 %	0.70 ± 4.53 %
LT	−1.37 ± 3.06 %	−1.37 ± 3.06 %	0.30 ± 3.12 %
VCD	−29.23 ± 2.35 %	−2.27 ± 1.50 %	0.04 ± 2.41 %
AL	−10.62 ± 1.75 %	−2.41 ± 1.48 %	0.24 ± 1.61 %

Figure 6:

Boxplots showing the relative error between the three LenStar analysis methods and A-scan ultrasonography using the verification data set. A paired t-test was used to test if the difference between methods was significant. # represents a significance level with a p-value < 0.0001.

3.6. Comparison with Tissue Measurements

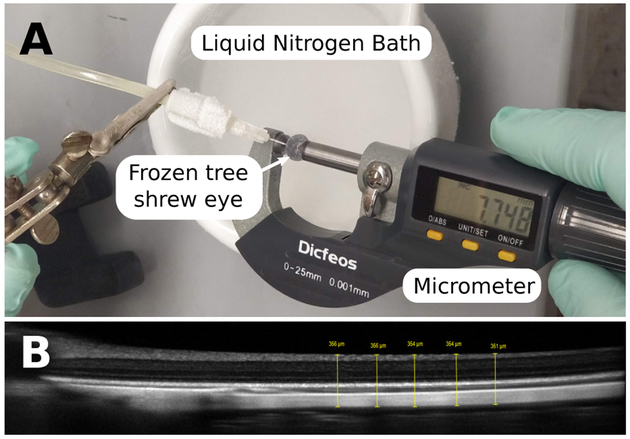
Although our primary goal was to match the LenStar with ultrasound, it also is of interest to learn if the corrected LenStar axial length measures match physical measures of the same eyes. To this end, 5 eyes were enucleated immediately after confirmed euthanasia, cleaned from orbital tissues, cannulated using a 30G needle and pressurized to normal IOP level of 9 mmHg (Samuels et al., 2018) using phosphate buffered saline. IOP was maintained for 15 minutes before each eye was flash frozen by immersing it into liquid nitrogen to minimize the formation of large ice crystals that might cause expansion of the globe. The eye was removed from the liquid nitrogen and the outer axial dimension (from the front of the cornea to the back of the posterior sclera) was measured using a micrometer Fig. 7A. This measurement was repeated ten times, where the eye was placed back into liquid nitrogen between each measurement to keep it frozen. The frozen eye provided enough resistance to quickly take the measurements with a micrometer.

Figure 7:

A: The experimental setup used to measure the outer axial dimension of frozen eyes. The eye was pressurized at 9 mmHg followed by immersing it into a liquid nitrogen bath to flash freeze it. A micrometer was used to measure the outer dimension of the eye from the corneal apex to the back of the posterior sclera. B: A representative OCT image of the posterior pole (the optic nerve head is partially visible at the left hand side) showing the five thickness measurements that were averaged to estimate the distance from the front of the retina to the back of the sclera. OCT images were obtained with the Spectralis (Heidelberg Engineering, Inc., Heidelberg, Germany) using the high resolution and enhanced-depth imaging settings.

On the same day, before the animals were euthanized, in-vivo axial dimensions and optical coherence tomography (OCT) images of the posterior pole were obtained using the LenStar and Spectralis OCT (Heidelberg Engineering, Inc., Heidelberg, Germany), respectively. The OCT images were used to obtain the axial distance between the front of the retina and the back of the sclera at the posterior pole Fig. 7B. The AL of our independent technique was obtained by subtracting the in vivo OCT-based distance (front of retina to back of sclera) from the outer dimension measured in frozen eyes. The LenStar data was analyzed using the three methods described in Section 3.5.

The AL obtained by the LenStar analysis method (iii) differed from the frozen eye measurements by 10 ± 31μm, while methods (i) and (ii) differed by 1205 ± 368μm and 215 ± 21μm, respectively. Although the close match between the proposed method (iii) and the flash-frozen eyes is reassuring, it is unknown if the frozen eyes were exactly the same size as they were before freezing.

4. Potential Pitfalls and Trouble Shooting

Although the LenStar LS900 was designed for clinical applications in humans, it has a great potential for use in animal research. However, the axial dimensions provided by the LenStar internal analysis are smaller than those provided by A-scan ultrasonography in tree shrew eyes as shown in Table 4 and Fig. 6. The pronounced underestimation of AL and VCD that resulted from using the LenStar internal analysis method (i) cannot be explained by species-dependent differences in refractive indices alone. This observation becomes obvious when comparing analyses methods (i) and (ii), where errors in VCD of the modified analysis method (ii) are only caused by differences in the refractive indices used to convert the OPLs to GLs. This observation suggests that the LenStar internal analysis uses an average refractive index to calculate AL based on human eye dimensions and this error propagates into the calculation ofVCD. Consequently, the internal analysis of the LenStar leads to inaccurate results in small animal eyes due to both, species-dependent differences in refractive indices and relative eye dimensions, and should not be used in small animal eyes. In addition to tree shrews, we measured the axial dimensions of 8 mouse eyes using the LenStar. When the internal analysis (method (i)) was used to calculate the VCD in the mouse eye, the result was a negative number in all eight cases (Fig. 8).

Figure 8:

Representative LenStar measurement of a mouse eye showing that the calculation of VCD results in a negative number if the LenStar internal analysis (i) is used for this species: VCD = 1.84–0.117–0.26–1.72–0.046 = −0.303 mm.

The comparison with the frozen eye measurements confirmed that our proposed method provides a significantly more accurate match to ultrasound in tree shrew eyes compared to analysis methods (i) and (ii). Studies that used the analysis method (ii) should remain valid as the difference between method (ii) and our proposed method (iii) can be expressed by a linear relationship. However, this may not be true for analysis method (i), where VCD and AL are calculated based on relative human eye dimensions. It is important to note that freezing the eyes may have altered the eye dimensions due to crystal formation, which causes water to expand during freezing. We tried to minimize this effect by freezing the eye quickly with liquid nitrogen preventing large crystal formation.

In this study, we defined AL as the distance between the front of the cornea and the front of the retina. This decision was motivated by being unable to fully resolve the posterior surface of the retina in the A-scan ultra-sonography echo signal (Fig. 1). The RT can, however, be obtained from the LenStar signal (Fig. 2). If one wishes to measure axial length from the front of the cornea to the front of the sclera, we recommend to include RT, directly obtained as the GL from the LenStar export file, and calculate AL = CT + ACD + LT + VCD + RT. The LenStar uses a refractive index of 1.4 to convert the retinal OPL into GL. This index was easily identified by changing the retinal coursers in the EyeSuite GUI, extracting the OPLs and GLs from the LenStar export file, and fitting a linear function that relates the exported OPLs and GLs of RT.

In applying our method to other LenStar instruments, it is important to note that the center wavelength of the LenStar near-infrared light source differs somewhat from instrument to instrument. Thus, the estimated refractive indices described here are not only species-dependent (tree shrews) but also wavelength-dependent. However, our strategy can be applied to other species and other instruments.

Applying our strategy to other species requires the estimation of the species-dependent group refractive indices that can be used to convert the LenStar raw OPLs into GLs. We recommend to generate a similar paired data set as used here. Note that the the iterative algorithm presented in Algorithm 1 can be avoided if the reference technique being used can determine CT and ACD. In this case, the minimization of Eq. (3) can be applied to obtain the refractive indices of CT and ACD.

If refractive indices have been already established for the intended species at a given center wavelength, we recommend scaling those refractive indices to the wavelength that your LenStar instrument uses. We recommend using the Cauchy model that was derived for group refractive indices in Eq. (5) to scale the refractive indices as follows

$$n(\lambda )=n_{\text{ref}}\frac{n_{\text{Cauchy}}(\lambda )}{n_{\text{Cauchy}}\left({\lambda }_{\text{ref}}\right)}.$$ (9)

In the above equation, λ represents the wavelength of your LenStar while nref represents the known group refractive index that was established at the center wavelength λref. The parameters of the Cauchy model can be obtained for each ocular compartment from Atchison and Smith (2005, Table 5). We recommend to use the “high” values for the lens. Note that the wavelength of the LenStar can change throughout its life cycle, e.g. after a maintenance visit. However, small changes in the center wavelength have a negligible impact and may not require the scaling of established refractive indices. We estimated that a 30nm change in center wavelength would change the refractive indices by about 0.1%.

It is interesting to note that the internal analysis of the LenStar software seems to use wavelength-dependent refractive indices that account for instrument-dependent differences or any changes in the center wavelength. The center wavelength of our LenStar instrument changed by about 3nm after a maintenance visit. We calculated the effective refractive indices used by the LenStar by exporting OPLs and GLs of 10 measurements before and after this change in center wavelength occurred. Our calculations confirmed that the refractive indices used by the LenStar to convert OPLs into GLs changed slightly but consistently after this maintenance visit (e.g. the effective refractive index of the lens used by the LenStar was 1.41902 at 828.58nm and 1.41888 at 831.78 nm). To what extent the weekly calibrations of the LenStar impact its measurements is unclear but our investigations suggest that the internal translation from OPLs into GLs remains unaffected by the weekly calibrations as long as the center wavelength remains unchanged.

We have not explored applying our technique in intermediate sized eyes. Adult tree shrew eyes have an AL of approximately 8 mm, one-third the size of humans. In principle, the procedures we have applied should work in larger animal eyes, such as rabbit, marmoset, and other non-human primate models. Although we measured juvenile tree shrews at a variety of ages, we did not systematically explore if the estimated refractive indices provide valid results in older animals. One can imagine that the refractive index (and sound velocity) of the lens in mature tree shrews (2 to 5 years old) might differ from that in juvenile animals.

Aleman and Schaeffel (2018) reported that the peak related to the anterior surface of the lens was not displayed in the EyeSuite GUI using the software version i8.1.1.0. We used the same software version in this study and rarely found a case where one of the lens peaks was missing in tree shrews. When this occurred, we discarded these measures and made additional ones until the missing peak was visible.

It is unclear why the anterior lens peak was missing in chicks, but the EyeSuite software may suppress signals that do not fit into the expected positions in human eye as speculated by Aleman and Schaeffel (2018). However, all peaks were found in mice.