On the theory of the unsteady-state growth of spherical crystals in metastable liquids

Abstract

Motivated by a large number of applications, we consider the process of non-stationary growth of spherical crystals in a supercooled binary melt. The moving-boundary problem describing the unsteady-state distributions of temperature and impurity concentration around the growing crystal as well as the dynamics of its radius and growth rate is solved by means of the methods of small-parameter expansion and Laplace–Carson integral transform. We show that the growth rate of crystals contains the main contribution (which is proportional to the supercooling degree Δ) and the first correction (which is proportional to Δ²t, where t is time). The second correction is also found. The non-stationary temperature and concentration fields are determined as power functions of Δ and t. We demonstrate that the first corrections to the dynamics of crystal radius R(t) and its growth rate V (t) play an important role. It is shown that R(t) and V (t) can change more than twice in comparison with the previously known steady-state solution with the course of time. Such a behaviour will significantly modify the dynamics of a polydisperse ensemble of crystals evolving in a metastable liquid.

This article is part of the theme issue ‘Heterogeneous materials: metastable and non-ergodic internal structures’.

1. Introduction

It is well known that the processes of nucleation and growth of individual particles determine the dynamics of the evolution of supercooled melts and supersaturated solutions in the intermediate stage of phase transformations (see, among others, [1–5]). The rate of particle growth enters the Fokker–Planck equation to determine the particle-size distribution function, and also to the boundary condition determining the flux of particles overcoming the critical barrier [6–8]. Therefore, accurate determination of the law for the growth rates of individual crystals is an important task, the solution of which completely describes the evolution of the polydisperse ensemble of particles, i.e. determines the particle size distribution function and the dynamics of desupercooling or desupersaturation of the metastable system.

In theoretical studies, the following expression is frequently used for the growth rates V of spherical crystals in supercooled single-component systems:

$$\frac{\mathrm{d}R}{\mathrm{d}t}=V(t)=\frac{{\beta }_{\ast }\mathrm{\Delta }}{1+{\beta }_{\ast }qR},$$ 1.1

where R is the radius of growing crystal, β_* is the kinetic coefficient, Δ = T_p − T_l is the supercooling, T_p is the phase transition temperature, T_l is the mean temperature of a metastable liquid, t is the growth time, q = ρ_sL/λ_l, ρ_s is the density of solid phase, L is the latent heat of phase transition, and λ_l is the thermal conductivity. Formula (1.1) follows from the solution of the quasi-stationary problem of the growth of a spherical crystal in a supercooled liquid [9]

$$\begin{array}{rlr}& {\mathrm{\nabla }}^{2}T=0,& r>R(t),\\ & \frac{\mathrm{d}R}{\mathrm{d}t}=-\frac{{\mathrm{\lambda }}_l}{{\rho }_{s}L}\frac{\mathrm{\partial }T}{\mathrm{\partial }r}={\beta }_{\ast }(T_p-T),& r=R(t)\\ \mathrm{and}& T\to T_l,& \frac{r}{R(t)}\gg 1,\end{array}\}$$ 1.2

where r is the spherical coordinate and T is the temperature field around the growing crystal. Note that an analogous formula for the growth rates of particles in binary systems was obtained in [10] when considering quasi-stationary fields of temperature and impurity concentration.

Generally speaking, the assumption of a stationary temperature field (∇²T = 0, r > R(t)) around the growing crystal is not correct due to the following reason. On the surface of the growing crystal, the latent heat of crystallization is released, which changes the temperature field. In the case of the growth of particles in a supersaturated solution, the interface between the solid and liquid phases displaces the dissolved impurity and increases the impurity concentration C in the near-surface layer adjacent to the growing crystal. Therefore, the concentration field is also incorrectly described by the quasi-stationary diffusion equation (∇²C = 0, r > R(t)).

Below we develop a method for determining the growth rates of spherical crystals in supercooled binary liquids with allowance for the non-stationary temperature and impurity concentration fields. It is also shown that accounting for non-stationary fields T and C, the rate of crystal growth dR/dt = V (t) significantly changes in comparison with the previously known solution obtained under quasi-stationary conditions.

2. Unsteady-state growth of spherical crystals in a metastable binary melt

Let us consider the process of evolution of spherical crystals of radius R(t) in a metastable binary melt. We will assume that the crystals are at large distances from each other so that interactions between them can be neglected. We will also assume that the growing particles are randomly arranged in the volume of the binary system and form a face-centred cubic lattice. Under such assumptions, the evolution of each individual particle can be considered within a single cell (in this case, the entire volume of the system is divided into a set of such cells). We denote by R_e the radius of the equivalent sphere inscribed in such a cell (figure 1). For the sake of simplicity of the solution of the problem, we neglect the critical radius of the growing crystallites.

Figure 1.

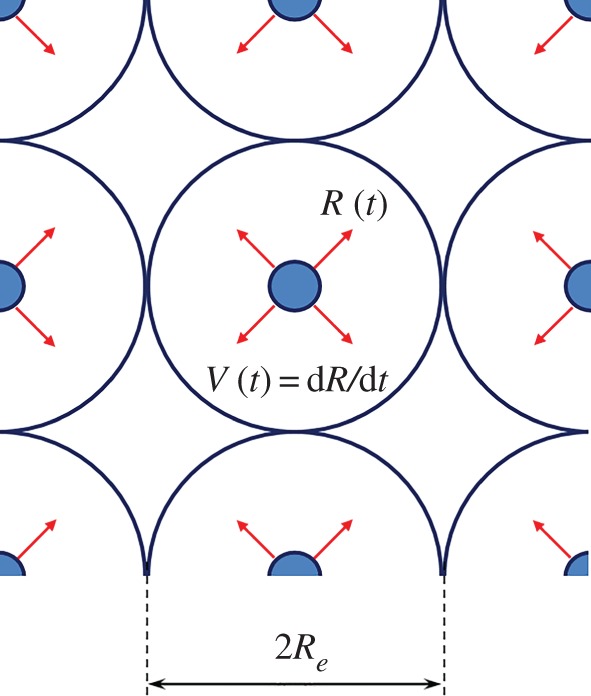
A scheme of evolution of spherical crystals in a metastable melt. The total volume of a metastable system is divided into cells (equivalent spheres) in which individual particles grow.

Let us write down the temperature conductivity and diffusion equations governing the temperature and concentration fields around the evolving crystals within a particular cell. In the spherical coordinate system, these equations take the form

$$\begin{array}{rlr}& \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{r}^2}+\frac{2}{r}\frac{\mathrm{\partial }T}{\mathrm{\partial }r}=\frac{1}{a}\frac{\mathrm{\partial }T}{\mathrm{\partial }t},& R(t)<r<R_e\\ \mathrm{and}& \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{r}^2}+\frac{2}{r}\frac{\mathrm{\partial }C}{\mathrm{\partial }r}=\frac{1}{D}\frac{\mathrm{\partial }C}{\mathrm{\partial }t},& R(t)<r<R_e,\end{array}\}$$ 2.1

where r is the radial coordinate, a is the thermal diffusivity and D is the diffusion coefficient.

Equations (2.1) must be considered under the following boundary conditions at the interphase boundary and away from it on an equivalent sphere

$$\begin{array}{rl}& \frac{\mathrm{d}R}{\mathrm{d}t}=-\frac{{\mathrm{\lambda }}_l}{{\rho }_{s}L}\frac{\mathrm{\partial }T}{\mathrm{\partial }r}={\beta }_{\ast }(T_p-mC-T),r=R(t),\\ & (1-k)C\frac{\mathrm{d}R}{\mathrm{d}t}+D\frac{\mathrm{\partial }C}{\mathrm{\partial }r}=0,r=R(t)\\ \mathrm{and}& \frac{\mathrm{\partial }T}{\mathrm{\partial }r}=0,\frac{\mathrm{\partial }C}{\mathrm{\partial }r}=0,r=R_e,\end{array}\}$$ 2.2

where k and m stand for the equilibrium distribution coefficient and liquidus slope, respectively. Note that the boundary conditions at r = R_e show the absence of heat and mass fluxes on the surface of the equivalent sphere.

For the convenience of mathematical manipulations, we introduce dimensionless variables as follows:

$$\rho =\frac{r}{R_e},\tau =\frac{at}{R_e^2},{\rho }_0(\tau )=\frac{R(t)}{R_e},\mathit{\Lambda }=\frac{{\mathrm{\lambda }}_l}{{\rho }_{s}La}\mathrm{and}{\tilde{\beta }}_{\ast }=\frac{Re{\beta }_{\ast }}{a}.$$ 2.3

The heat and mass transfer equations (2.1) and boundary conditions (2.2) in dimensionless variables (2.3) take the form

$$\begin{array}{rlr}& \frac{{\mathrm{\partial }}^{2}T}{\mathrm{\partial }{\rho }^2}+\frac{2}{\rho }\frac{\mathrm{\partial }T}{\mathrm{\partial }\rho }=\frac{\mathrm{\partial }T}{\mathrm{\partial }\tau },& {\rho }_0(\tau )<\rho <1\\ \mathrm{and}& \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{\rho }^2}+\frac{2}{\rho }\frac{\mathrm{\partial }C}{\mathrm{\partial }\rho }=\gamma \frac{\mathrm{\partial }C}{\mathrm{\partial }\tau },& {\rho }_0(\tau )<\rho <1,\end{array}\}$$ 2.4

$$\begin{array}{rl}& \frac{\mathrm{d}{\rho }_0}{\mathrm{d}\tau }=-\mathit{\Lambda }\frac{\mathrm{\partial }T}{\mathrm{\partial }\rho }={\tilde{\beta }}_{\ast }(T_p-mC-T),\rho ={\rho }_0(\tau ),\\ & (1-k)\gamma C\frac{\mathrm{d}{\rho }_0}{\mathrm{d}\tau }+\frac{\mathrm{\partial }C}{\mathrm{\partial }\rho }=0,\rho ={\rho }_0(\tau )\\ \mathrm{and}& \frac{\mathrm{\partial }T}{\mathrm{\partial }\rho }=0,\frac{\mathrm{\partial }C}{\mathrm{\partial }\rho }=0,\rho =1,\end{array}\}$$ 2.5

where γ = a/D is typically much greater than 1.

The solution of dimensionless equations (2.4) satisfying the boundary conditions (2.5) at ρ = 1 can be presented in the form [11]

$$\begin{array}{rl}& T(\rho ,\tau )=\frac{1}{\rho }\sum _{n=0}^{\mathrm{\infty }}\frac{{(1-\rho )}^{2n}}{(2n)!}(1-\frac{1-\rho }{2n+1})\frac{{\mathrm{d}}^{n}B(\tau )}{\mathrm{d}{\tau }^n}\\ \mathrm{and}& C(\rho ,\tau )=\frac{1}{\rho }\sum _{n=0}^{\mathrm{\infty }}\frac{{(1-\rho )}^{2n}}{(2n)!}(1-\frac{1-\rho }{2n+1}){\gamma }^n\frac{{\mathrm{d}}^{n}A(\tau )}{\mathrm{d}{\tau }^n},\end{array}\}$$ 2.6

where B(τ) = T(1, τ) and A(τ) = C(1, τ).

Substituting now the solutions (2.6) into the boundary conditions (2.5) at ρ = ρ₀(τ), we obtain three equations for finding the functions ρ₀(τ), B(τ) and A(τ)

$$\begin{array}{rl}& {\rho }_0\frac{\mathrm{d}{\rho }_0}{\mathrm{d}\tau }={\rho }_0\beta (\tau )+\sum _{n=1}^{\mathrm{\infty }}\frac{{(1-{\rho }_0)}^{2n}}{(2n)!}(1-\frac{1-{\rho }_0}{2n+1})\frac{{\mathrm{d}}^n\beta (\tau )}{\mathrm{d}{\tau }^n}\\ & -m{\tilde{\beta }}_{\ast }\sum _{n=1}^{\mathrm{\infty }}\frac{{(1-{\rho }_0)}^{2n}}{(2n)!}(1-\frac{1-{\rho }_0}{2n+1}){\gamma }^n\frac{{\mathrm{d}}^{n}A(\tau )}{\mathrm{d}{\tau }^n},\\ & (P{\rho }_0+1)\frac{\mathrm{d}{\rho }_0}{\mathrm{d}\tau }=\beta (\tau )-\sum _{n=1}^{\mathrm{\infty }}\frac{{(1-{\rho }_0)}^{2n-1}}{(2n-1)!}(1-\frac{1-{\rho }_0}{2n})\frac{{\mathrm{d}}^n\beta (\tau )}{\mathrm{d}{\tau }^n}\\ & -m{\tilde{\beta }}_{\ast }\sum _{n=1}^{\mathrm{\infty }}[\frac{{(1-{\rho }_0)}^{2n-1}}{(2n-1)!}(1-\frac{1-{\rho }_0}{2n})\frac{{\mathrm{d}}^{n}A(\tau )}{\mathrm{d}{\tau }^n}\\ & +\frac{{(1-{\rho }_0)}^{2n}}{{\rho }_0(2n)!}(1-\frac{1-{\rho }_0}{2n+1}){\gamma }^n\frac{{\mathrm{d}}^{n}A(\tau )}{\mathrm{d}{\tau }^n}]\\ \mathrm{and}& (k-1)\gamma {\rho }_0^2\frac{\mathrm{d}{\rho }_0}{\mathrm{d}\tau }A(\tau )+[(k-1)\gamma {\rho }_0\frac{\mathrm{d}{\rho }_0}{\mathrm{d}\tau }+1]\\ & \times \sum _{n=1}^{\mathrm{\infty }}\frac{{(1-{\rho }_0)}^{2n}}{(2n)!}(1-\frac{1-{\rho }_0}{2n+1}){\gamma }^n\frac{{\mathrm{d}}^{n}A(\tau )}{\mathrm{d}{\tau }^n}\\ & +{\rho }_0\sum _{n=1}^{\mathrm{\infty }}\frac{{(1-{\rho }_0)}^{2n-1}}{(2n-1)!}(1-\frac{1-{\rho }_0}{2n}){\gamma }^n\frac{{\mathrm{d}}^{n}A(\tau )}{\mathrm{d}{\tau }^n}=0.\end{array}\}$$ 2.7

Here we assume that γ≫1 and

$$\beta (\tau )=[T_p-B(\tau )-mA(\tau )]{\tilde{\beta }}_{\ast },P=\frac{{\tilde{\beta }}_{\ast }}{\mathit{\Lambda }}.$$

An important point is that equations (2.7) obtained for binary melts transform to the corresponding equations derived in [12] for one-component melts if we formally put A = 0.

Taking into account that β(0) = β₀≪1 [9,13], we seek solutions of nonlinear equations (2.7) in the form of series in the small parameter β₀ as

$$\begin{array}{rl}{\rho }_0(\tau )& ={\beta }_0{\phi }_1(\tau )+{\beta }_0^2{\phi }_2(\tau )+{\beta }_0^3{\phi }_3(\tau )+\cdots ,\\ \beta (\tau )& ={\beta }_0{\psi }_1(\tau )+{\beta }_0^2{\psi }_2(\tau )+{\beta }_0^3{\psi }_3(\tau )+\cdots \\ \mathrm{and}A(\tau )& ={\chi }_0(\tau )+{\beta }_0{\chi }_1(\tau )+{\beta }_0^2{\chi }_2(\tau )+\cdots ,\end{array}\}$$ 2.8

where A(0) = C(1, 0) = C₀ = const.

Now substituting the asymptotic expansions (2.8) into expressions (2.7) and equating the contributions at the same powers of small parameter β₀, one can obtain

$$\begin{array}{rl}& {\phi }_1=\tau ,{\psi }_1=1,{\chi }_0=C_0,{\chi }_1=0,{\psi }_2=0,{\chi }_2=0,\\ & {\phi }_2=\mu {\tau }^2,\mu =-\frac{P+m{\tilde{\beta }}_{\ast }(1-k)\gamma C_0}{2}\hspace{0.17em}\\ \mathrm{and}& {\phi }_j(0)=0,{\psi }_j(0)=0,{\chi }_j(0)=0,j\ge 2.\end{array}\}$$ 2.9

To determine the functions φ₃, ψ₃ and χ₃, we have the following system of equations:

$$\begin{array}{rl}& \frac{\mathrm{d}{\phi }_3}{\mathrm{d}\tau }+Q{\tau }^2={\psi }_3-\sum _{n=1}^{\mathrm{\infty }}[\frac{1}{(2n-1)!}-\frac{1}{(2n)!}](\frac{{\mathrm{d}}^n{\psi }_3}{\mathrm{d}{\tau }^n}+m{\tilde{\beta }}_{\ast }\frac{{\mathrm{d}}^n{\chi }_3}{\mathrm{d}{\tau }^n}),\\ & \sum _{n=1}^{\mathrm{\infty }}[\frac{1}{(2n)!}-\frac{1}{(2n+1)!}]\frac{{\mathrm{d}}^n{\psi }_3}{\mathrm{d}{\tau }^n}=-P{\tau }^2\\ \mathrm{and}& \sum _{n=1}^{\mathrm{\infty }}[\frac{1}{(2n)!}-\frac{1}{(2n+1)!}]{\gamma }^n\frac{{\mathrm{d}}^n{\chi }_3}{\mathrm{d}{\tau }^n}=(1-k)\gamma C_0{\tau }^2,\end{array}\}$$ 2.10

where

$$Q=3\mu [P+m{\tilde{\beta }}_{\ast }(1-k)\gamma C_0]-m{\tilde{\beta }}_{\ast }(1-k)\gamma C_0.$$

Equations (2.10) can be solved using the Laplace–Carson integral transform. To apply this method, we note that the following initial conditions follow from equations (2.10):

$$\frac{{\mathrm{d}}^n{\psi }_3}{\mathrm{d}{\tau }^n}=0,\frac{{\mathrm{d}}^n{\chi }_3}{\mathrm{d}{\tau }^n}=0,\tau =0.$$ 2.11

Now taking into account (2.11), we have from (2.10) [14]

$$\begin{array}{rl}& \sum _{n=1}^{\mathrm{\infty }}[\frac{1}{(2n)!}-\frac{1}{(2n+1)!}]s^n{\psi }_3^{\ast }=-\frac{2P}{s^2}\\ \mathrm{and}& \sum _{n=1}^{\mathrm{\infty }}[\frac{1}{(2n)!}-\frac{1}{(2n+1)!}]{\gamma }^n{s}^n{\chi }_3^{\ast }=\frac{2\alpha }{s^2},\end{array}\}$$ 2.12

where * shows the Laplace–Carson transform, s represents the Laplace–Carson variable, and

$$\alpha =(1-k)\gamma C_0.$$

Keeping in mind that [11]

$$\sum _{n=1}^{\mathrm{\infty }}\frac{s^n}{(2n)!}=\cosh \sqrt{s}-1,\sum _{n=1}^{\mathrm{\infty }}\frac{s^n}{(2n+1)!}=\frac{\sinh \sqrt{s}}{\sqrt{s}}-1,$$ 2.13

we get from expressions (2.12)

$$\begin{array}{rl}{\psi }_3^{\ast }(s)& =-\frac{2P}{s^{3/2}(\sqrt{s}\cosh \sqrt{s}-\sinh \sqrt{s})}\\ \mathrm{and}{\chi }_3^{\ast }(s)& =\frac{2\alpha \sqrt{\gamma }}{s^{3/2}(\sqrt{\gamma s}\cosh \sqrt{\gamma s}-\sinh \sqrt{\gamma s})}.\end{array}\}$$ 2.14

To find the inverse Laplace–Carson transform, we present the right-hand sides of expressions (2.14) by means of the following formula:

$$\frac{1}{s^{3/2}(\sqrt{s}\cosh \sqrt{s}-\sinh \sqrt{s})}=\frac{1}{s}{\mathit{\Psi }}_1^{\ast }(s){\mathit{\Psi }}_2^{\ast }(s),$$ 2.15

where

$${\mathit{\Psi }}_1^{\ast }(s)=\frac{1}{s^2},{\mathit{\Psi }}_2^{\ast }(s)=\frac{s^{3/2}}{\sqrt{s}\cosh \sqrt{s}-\sinh \sqrt{s}}.$$ 2.16

Now keeping in mind the inverse transforms [11,14]

$$\begin{array}{rl}& \frac{1}{s^n}\to \frac{{\tau }^n}{n!},{\mathit{\Psi }}_2^{\ast }(s)\to 3+2\sum _{k=1}^{\mathrm{\infty }}\frac{\sqrt{s_k}\exp \left(s_k\tau \right)}{\sinh \sqrt{s_k}}\\ \mathrm{and}& \frac{1}{s}{f}_1^{\ast }(s)f_2^{\ast }(s)\to {\int }_0^{\tau }{f}_1(x)f_2(\tau -x)\hspace{0.17em}\mathrm{d}x,f^{\ast }(as)\to f\left(\frac{\tau }{a}\right),\end{array}$$

where s_k satisfies the following equation:

$$\sqrt{s_k}\cosh \sqrt{s_k}-\sinh \sqrt{s_k}=0,$$

we have ψ₃(τ) and χ₃(τ) from (2.14)–(2.16)

$$\begin{array}{rl}& {\psi }_3(\tau )=-P{\tau }^3+2P\sum _{k=1}^{\mathrm{\infty }}\frac{2\exp (-{\mu }_k^2\tau )+2{\mu }_k^2\tau -{\mu }_k^4{\tau }^2-2}{{\mu }_k^5\sin {\mu }_k}\\ \mathrm{and}& {\chi }_3(\tau )=\alpha {\tau }^3+2\alpha \gamma \sum _{k=1}^{\mathrm{\infty }}\frac{2{\gamma }^2-2{\mu }_k^2\gamma \tau +{\mu }_k^4{\tau }^2-2{\gamma }^2\exp (-{\mu }_k^2\tau /\gamma )}{{\mu }_k^5\sin {\mu }_k},\end{array}\}$$ 2.17

where $\sqrt{s_k}=\mathrm{i}{\mu }_k$, μ_k satisfies the equation μ_kcosμ_k = sinμ_k, and ‘i’ is the imaginary unit. Note that ψ₃(τ) coincides with the solution of thermally controlled crystal growth found in [12] in the case of single-component systems (C₀ = 0).

Now the first equation (2.10) can be easily integrated so that

$${\phi }_3(\tau )=-\frac{Q{\tau }^3}{3}+{\int }_0^{\tau }{\psi }_3\left(\overline{\tau }\right)\hspace{0.17em}\mathrm{d}\overline{\tau }-\sum _{n=1}^{\mathrm{\infty }}[\frac{1}{(2n-1)!}-\frac{1}{(2n)!}](\frac{{\mathrm{d}}^{n-1}{\psi }_3}{\mathrm{d}{\tau }^{n-1}}+m{\tilde{\beta }}_{\ast }\frac{{\mathrm{d}}^{n-1}{\chi }_3}{\mathrm{d}{\tau }^{n-1}}),$$

where ψ₃ is determined by the first expression (2.17).

Now the asymptotic expansions (2.8) can be rewritten in the form

$$\begin{array}{rl}{\rho }_0(\tau )& ={\beta }_0\tau +{\beta }_0^2\mu {\tau }^2+{\beta }_0^3{\phi }_3(\tau )+\cdots \\ \mathrm{and}\beta (\tau )& ={\beta }_0+{\beta }_0^3{\psi }_3(\tau )+\cdots ,A(\tau )=C_0+{\beta }_0^3{\chi }_3(\tau )+\cdots .\end{array}\}$$ 2.18

If we restrict ourselves to the main contribution to the crystal radius and its first correction, one can obtain the following dimensional expressions for R(t) and V (t) from (2.18):

$$\begin{array}{rl}R(t)& ={\beta }_{\ast }\mathrm{\Delta }t-\frac{{\beta }_{\ast }^3{\mathrm{\Delta }}^2{t}^2}{2a\mathit{\Lambda }}(1+\frac{m(1-k)a\mathit{\Lambda }{C}_0}{D})\\ \mathrm{and}V(t)& ={\beta }_{\ast }\mathrm{\Delta }-\frac{{\beta }_{\ast }^3{\mathrm{\Delta }}^{2}t}{a\mathit{\Lambda }}(1+\frac{m(1-k)a\mathit{\Lambda }{C}_0}{D}),\end{array}\}$$ 2.19

where Δ = T_p − T(1, 0) − mC(1, 0) represents the system supercooling. If we formally put C₀ = 0, expressions (2.19) transform to the corresponding solutions for one-component systems [12]. Note that the growth rate V (t) of crystals in binary melts is less than the rate of their growth in single-component systems (m > 0, k < 1). An important feature of expressions (2.19) is the fact that they do not depend on the radius R_e of the equivalent sphere. Considering the intermediate stage of crystal growth in a metastable liquid when all particles do not interact with their neighbouring crystals, we note that T(1, 0) and C(1, 0) correspond to the mean temperature T_l and concentration C_l of a metastable binary system.

3. Discussion and conclusion

Figures 2 and 3 illustrate our asymptotic solution (2.19) for the Ti–Al alloy (its material parameters are given in table 1). Note that the first terms in the right-hand sides of expressions (2.19) represent the analytical solutions in the so-called kinetically controlled growth regime [9,10]. In this case, the crystal radius R(t) and its growth rate V (t) evolve as R(t) = R₀(t) = β_*Δt and V (t) = V₀(t) = β_*Δ.

Figure 2.

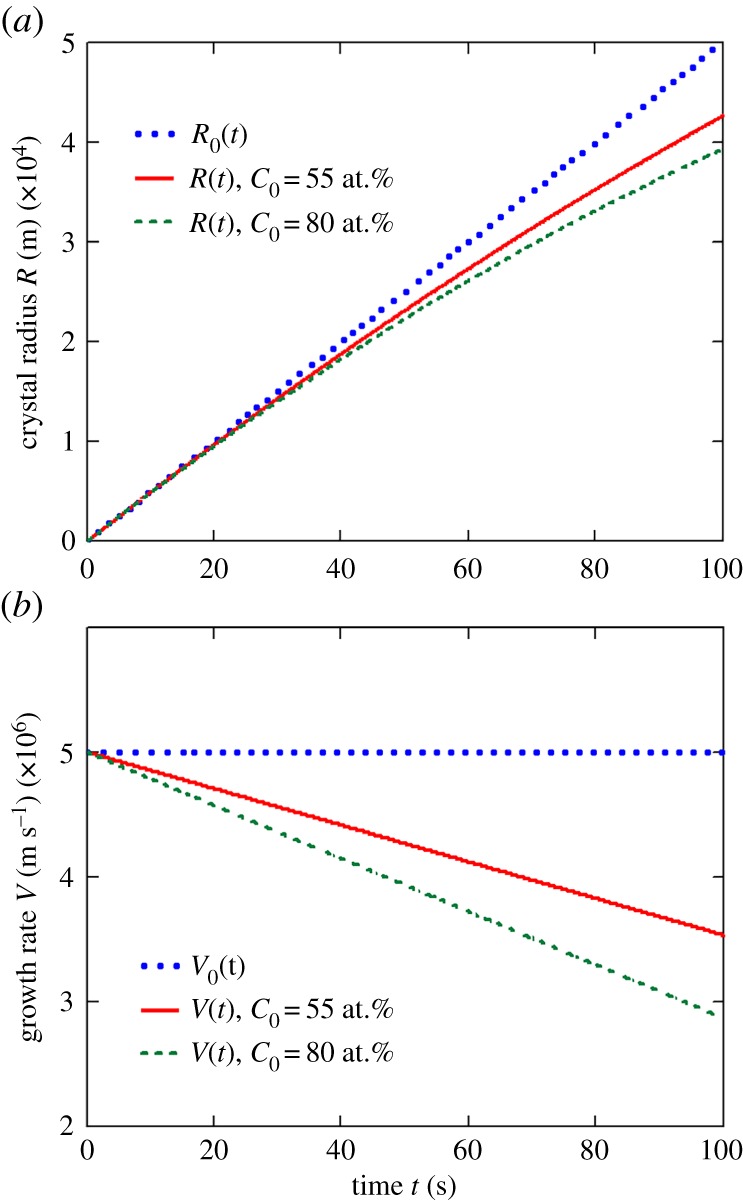
The influence of impurity concentration C₀ on the evolution of crystal radius R(t) (a) and its growth rate V (t) (b), β_* = 0.5 · 10⁻⁷ m K⁻¹ s⁻¹.

Figure 3.

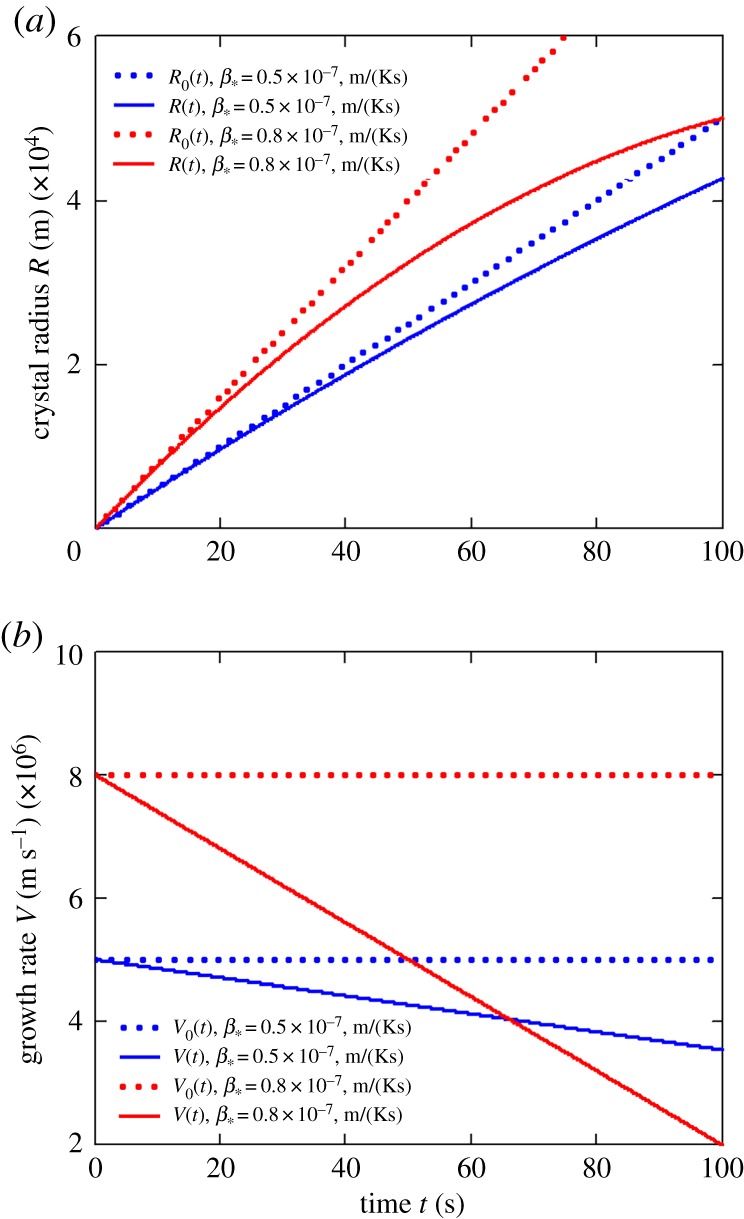
The influence of kinetic coefficient β_* on the evolution of crystal radius R(t) (a) and its growth rate V (t) (b), C₀ = 55 at.%.

Table 1.

Material parameters of Ti–Al alloy [17].

parameter			value
thermal diffusivity	a	m2 s−1	7.5 × 10−6
liquidus slope	m	K/at.%	8.8
partition coefficient	k	—	0.8
diffusion coefficient	D	m2 s−1	8.27 × 10−9
supercooling	Δ	K	100
parameter	Λ	K−1	3.67 × 10−3

First, we note a strong shift of the unsteady-state solutions (2.19) from the previously known steady-state solutions R₀(t) and V₀(t) (compare R(t) and R₀(t) as well as V (t) and V₀(t) in figures 2 and 3). Secondly, as the impurity concentration C₀ increases, this shift increases too (figure 2). Third, an increase in the kinetic coefficient β_* also leads to a shift in the radius and growth rate of the crystals (figure 3). An important point is that the growth rate V₀ does not depend on t at constant supercooling Δ, whereas V (t) from (2.19) is a decreasing function of t (figures 2b and 3b). We note that the growth rate of crystals can change several times in comparison with previously known solution V₀ (figures 2b and 3b). This leads to the conclusion that in the initial stages of crystal growth (when supercooling is almost unchanged), the non-stationary rate of their growth substantially changes the solution of the Fokker–Planck equation for the crystal size distribution function, and also the solution of the heat (mass) balance equation. This question is studied in more detail in papers [15,16] from the present theme issue.

Let us now estimate the typical times when the non-stationary contributions in expressions (2.19) become significant. To do this, let us rewrite the growth rate V (t) as

$$V(t)={\beta }_{\ast }\mathrm{\Delta }(1-\zeta t),\zeta =\frac{{\beta }_{\ast }^2\mathrm{\Delta }}{a\mathit{\Lambda }}(1+\frac{m(1-k)a\mathit{\Lambda }{C}_0}{D}).$$ 3.1

The non-stationary contribution ζ is of the order of 2.9 · 10⁻³ s⁻¹ for the parameter values listed in table 1 and β_* = 0.5 · 10⁻⁷ m s⁻¹ K⁻¹, and C₀ = 55 at%. Now we see that the non-stationary term (proportional to ζ) must be taken into account at times t ≳10² s (this time is counted from the nucleation of a single crystal). However, this estimate must be recalculated, for long times, when supercooling becomes dependent on time.

Let us emphasize in conclusion the key result of the present analysis. Non-stationary contributions entering in the growth rates of spherical particles, their radii, and the distribution of temperature and concentration fields must be taken into account in the theoretical description of the intermediate stage of phase transformation in melts and solutions (the analytical description of crystal growth in dilute solutions is presented in appendix A). For this reason, many theories of growth of crystals or droplike aggregates in supersaturated solutions, supercooled melts, mushy layers, colloids, magnetic fluids and other physical systems (see, among others, [18–27]) should be reconsidered with allowance for the non-stationary contributions to the particle growth rates.

Appendix A. Appendix A. Unsteady-state growth of spherical crystals in a supersaturated solution

If the growth of spherical particles occurs in a supersaturated solution, the moving-boundary problem takes the form

$$\begin{array}{rl}& \frac{{\mathrm{\partial }}^{2}C}{\mathrm{\partial }{r}^2}+\frac{2}{r}\frac{\mathrm{\partial }C}{\mathrm{\partial }r}=\frac{1}{D}\frac{\mathrm{\partial }C}{\mathrm{\partial }t},R(t)<r<R_e,\\ & (1-k)C\frac{\mathrm{d}R}{\mathrm{d}t}+D\frac{\mathrm{\partial }C}{\mathrm{\partial }r}=0,r=R(t),\\ & \frac{\mathrm{d}R}{\mathrm{d}t}={\beta }_{\ast }(C-C_p),r=R(t)\\ \mathrm{and}& \frac{\mathrm{\partial }C}{\mathrm{\partial }r}=0,r=R_e,\end{array}$$

where C_p is the concentration at saturation. Its solution can be found by analogy with the theory presented in §2 (see, for details, [28]).

$$R(t)={\beta }_{\ast }\mathrm{\Delta }t(1-\frac{(k-1)C_p{\beta }_{\ast }^2\mathrm{\Delta }t}{2D})\mathrm{and}V(t)=\frac{\mathrm{d}R}{\mathrm{d}t}={\beta }_{\ast }\mathrm{\Delta }(1-\frac{(k-1)C_p{\beta }_{\ast }^2\mathrm{\Delta }t}{D}).$$

Here Δ designates the supersaturation of the liquid solution.

The last expressions for R(t) and V (t) should be used for a more precise description of nucleation and crystal growth processes in supersaturated solutions. Note that the correction of a higher order of smallness, as well as the impurity concentration around the growing spherical particle, are determined by Alexandrov et al. [28].

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed equally to the present research article.

Competing interests

We declare that we have no competing interests.

Funding

This work was supported by the Russian Science Foundation (grant no. 18-19-00008).