Improvements in CBCT Image Quality Using a Novel Iterative Reconstruction Algorithm: A Clinical Evaluation

Abstract

Purpose

This study aimed to evaluate the clinical utility of a novel iterative cone beam computed tomography (CBCT) reconstruction algorithm for prostate and head and neck (HN) cancer.

Methods and Materials

A total of 10 patients with HN and 10 patients with prostate cancer were analyzed. For each patient, raw CBCT acquisition data were used to reconstruct images with a currently available algorithm (FDK_CBCT) and novel iterative algorithm (Iterative_CBCT). Quantitative contouring variation analysis was performed using structures delineated by several radiation oncologists. For prostate, observers contoured the prostate, proximal 2 cm seminal vesicles, bladder, and rectum. For HN, observers contoured the brain stem, spinal canal, right-left parotid glands, and right-left submandibular glands. Observer contours were combined to form a reference consensus contour using the simultaneous truth and performance level estimation method. All observer contours then were compared with the reference contour to calculate the Dice coefficient, Hausdorff distance, and mean contour distance (prostate contour only). Qualitative image quality analysis was performed using a 5-point scale ranging from 1 (much superior image quality for Iterative_CBCT) to 5 (much inferior image quality for Iterative_CBCT).

Results

The Iterative_CBCT data sets resulted in a prostate contour Dice coefficient improvement of approximately 2.4% (P = .029). The average prostate contour Dice coefficient for the Iterative_CBCT data sets was improved for all patients, with improvements up to approximately 10% for 1 patient. The mean contour distance results indicate an approximate 15% reduction in mean contouring error for all prostate regions. For the parotid contours, Iterative_CBCT data sets resulted in a Hausdorff distance improvement of approximately 2 mm (P < .01) and an approximate 2% improvement in Dice coefficient (P = .03). The Iterative_CBCT data sets were scored as equivalent or of better image quality for 97.3% (prostate) and 90.0% (HN) of the patient data sets.

Conclusions

Observers noted an improvement in image uniformity, noise level, and overall image quality for Iterative_CBCT data sets. In addition, expert observers displayed an improved ability to consistently delineate soft tissue structures, such as the prostate and parotid glands. Thus, the novel iterative reconstruction algorithm analyzed in this study is capable of improving the visualization for prostate and HN cancer image guided radiation therapy.

Introduction

On-board cone beam computed tomography (CBCT) has provided an invaluable tool for targeting of radiation therapy procedures in the last 20 years.¹ The 3-dimensional anatomic information provided by CBCT has allowed for soft tissue visualization for prostate radiation therapy (RT),² direct target visualization in lung stereotactic body RT,3, 4 and even frameless radiosurgery,5, 6 to name a few. However, the cone beam geometry inherent to CBCT imaging results in more scattered radiation at the flat-panel detector, causing degradation in image quality.7, 8

Several modifications of the CBCT setup and acquisition have resulted in improved efficiency and image quality.9, 10 Techniques to account for the effects of scatter have also resulted in improvements in clinical CBCT image quality. These techniques fit into several categories, according to Maslowski et al,¹¹ including modulation of the source x-ray fluence, scatter deconvolution, using knowledge of the object, Monte Carlo modeling, and other empirical approaches. The current CBCT imaging available on Varian TrueBeam linear accelerators (Varian Medical Systems, Palo Alto, CA) uses a kernel-based scatter deconvolution technique12, 13 to account for the influence of scatter, resulting in improved image quality.¹⁴

Recently, a novel scatter estimation algorithm, Acuros CTS, has been developed.11, 15 The Acuros algorithm seeks to deterministically solve the linear Boltzmann transport equation to rapidly and accurately estimate the influence of scatter in x-ray projection images. In short, the Acuros CTS algorithm involves first-pass reconstruction using the current TrueBeam reconstruction method, incorporation of the treatment couch model, creation of a patient-object model in terms of material type and mass density, calculation of primary and scatter images, scatter correction, and second-pass reconstruction.¹⁵ During the scatter correction, the Acuros CTS algorithm discretizes the spatial, energy, and angular domains of the x-ray fluence to deterministically solve the linear Boltzmann transport equation.¹¹ The Acuros CTS algorithm has been validated against the Monte Carlo data for a heterogeneous phantom and realistic pelvis phantom based on CT data.¹¹

In Part II of their manuscript introducing the Acuros CTS algorithm, Wang et al noted the potential for statistical iterative reconstruction to be used as second-pass reconstruction.¹⁵ Statistical iterative reconstruction for computed tomography (CT) offers the potential to reduce imaging dose and improve image quality relative to standard filtered back-projection approaches.16, 17, 18, 19, 20 In particular, statistical iterative reconstruction can recognize and then correct local variations in pixel value that are unlikely to be due to the subject's anatomic features.¹⁶ In other words, iterative reconstruction can help reduce the impact of quantum mottle without increasing the imaging dose or losing image features.

Historically, the output of statistical iterative reconstruction algorithms was promising, but the efficiency of the reconstruction was a barrier to real-time clinical use. Recent advancements have allowed for substantial improvements in reconstruction efficiency by at least an order of magnitude, including the algorithm described by Wang et al that takes into account the Poisson quantum noise distribution while applying edge-preserving image regularization.17, 21

A new CBCT reconstruction algorithm, iterative CBCT, has recently been introduced into the TrueBeam system, and combines the 2 image reconstruction approaches mentioned previously: efficient scatter correction using Acuros CTS and statistical iterative reconstruction for final-pass image reconstruction for on-board CBCT imaging. The use of the new algorithm results in an increase of approximately 10 to-25 seconds in reconstruction time, depending on the reconstruction mode. For pelvis imaging protocols, the new algorithm uses both new components (statistical iterative reconstruction and scatter correction using Acuros CTS), but the algorithm does not employ Acuros CTS for head protocols.

The purpose of this study was to perform a comprehensive clinical evaluation of the iterative CBCT (referred to as Iterative_CBCT) image reconstruction for both the prostate and HN patient data sets. To this end, we performed a quantitative (contouring variation) and qualitative (image quality observer scoring) analysis of the Iterative_CBCT images, comparing the new reconstruction algorithm with the currently available TrueBeam on-board imager reconstruction (referred to as FDK_CBCT).

Methods and Materials

A total of 10 patients with head and neck (HN) cancer and 10 patients with prostate cancer were randomly selected from a 6-month time window in early 2017 for analysis in this institutional review board–approved retrospective study. Patients with truncation of image data in the central portion of the superoinferior field of view were excluded based on the intended use of the Iterative_CBCT reconstruction algorithm. The analysis included 2 image sets for each patient: 1) conventional CBCT image acquired on TrueBeam on-board imager systems, and 2) CBCT reconstructed with a novel iterative method (Iterative_CBCT; Varian Medical Systems, Palo Alto, CA).11, 15

The study is divided into 2 parts: (1) quantitative analysis of the contouring variation for both types of images, and (2) qualitative analysis of the clinical image quality using a 5-point scale. The Iterative_CBCT reconstruction has 5 options for noise suppression: very low, low, medium (default), high, and very high. For our clinic, image sharpness is a priority, so the very low setting was used for image reconstruction.

Contouring variation analysis

Contouring work was performed for both prostate and HN data sets in the ARIA (version 13) Contouring workspace (Varian Medical Systems, Palo Alto, CA). For 9 prostate data sets, 4 to 5 physician observers delineated the following structures on each image set: prostate gland alone, proximal 2 cm seminal vesicles, rectum, and bladder. One patient with prostate cancer from the original group of 10 patients was excluded because of truncation of data in the axial plane; the iterative CBCT algorithm is not recommended for use in instances of patient data truncation. For the contouring analysis, the observers contoured patient data sets for 1 patient at a time and were blinded to the image set reconstruction mode. The image sets were labeled with _A and _B for each patient to represent the FDK and Iterative data sets, and the labels were randomly assigned for each patient.

To guide the observers for prostate contouring, the following guidance was provided: Rectum borders are defined inferiorly as the pubic ramus and ischial tuberosity and superiorly as the flexure of sigmoid colon. For 10 HN data sets, 3 physician observers delineated the following structures on each image set: brain stem, spinal canal, left-right parotid glands, and left-right submandibular glands. For each structure type, a consensus contour was created using the simultaneous truth and performance level estimation (STAPLE) method in the Computational Environment for Radiotherapy Research software package.²² Further details on the STAPLE method were previously published.²³ The statistical analysis of the contouring results was performed using a Student's t test (1 tail, P < .05; significant).

Several metrics were used to evaluate the agreement between observer and consensus contours. The Dice coefficient was used to evaluate the general overlap between the observer and consensus contours²⁴:

$$DC=\frac{2\left|X\cap Y\right|}{\left|X\right|+\left|Y\right|}\text{.}$$

The Hausdorff distance was used to evaluate gross error between the observer and consensus contour. The Hausdorff distance is the maximum distance of a point in 1 contour to the nearest point of the other contour and is defined as

$$h\left(A,B\right)={\text{max}}_{a\in A}\left\{{\text{min}}_{b\in B}\left\{d\left(a,b\right)\right\}\right\}\text{,}$$

where a and b are points of sets A and B, respectively, and d(a,b) is the Euclidean metric between these points.²⁵

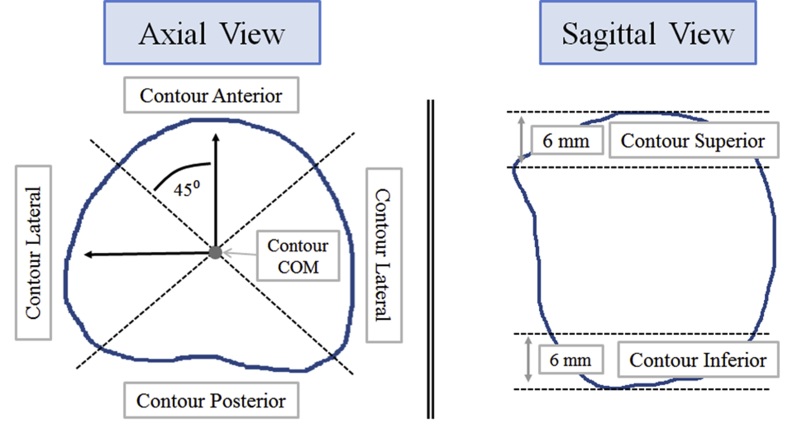
The mean contour distance was used for prostate contours only to evaluate the mean distance error as a function of prostate region (Fig. 1). The mean contour distance was previously used to evaluate prostate contouring variation on CT and CBCT images.²⁶ The mean contour distance was calculated for each region and for the overall contour.

Fig. 1.

Schematic of the framework to calculate mean contour distance. (Left) Axial view. The contour is divided into 3 regions: Anterior, posterior, and lateral. The regions are defined by 2 orthogonal lines with intersection at the center of mass, and oriented 45° relative to the sagittal and coronal planes. (Right) Sagittal view. The superior and inferior regions of the prostate are defined as the superior-most and inferior-most 6 mm regions of the prostate. Figure used with permission.²⁶

Image quality analysis

Image quality evaluation for 10 HN cancer patients and 10 prostate cancer patients was performed in the ARIA (version 13) plan evaluation workspace. For the prostate cohort, 11 observers (4 radiation oncologists, 4 medical physicists, 2 medical dosimetrists, and 1 radiation therapist) performed image evaluations. For the HN cohort, 11 observers (4 radiation oncologists, 4 medical physicists, 2 medical dosimetrist, and 1 radiation therapist) performed image evaluations.

For the image quality evaluations, the observers reviewed the image sets side by side and adjusted window-level settings as needed to visualize the relevant anatomy. The observers were given 2 image sets and were blinded to the image set reconstruction mode. The image sets were labeled _A and _B for each patient to represent the FDK and Iterative data sets (labels were randomly assigned for each patient). The observers were instructed to compare the image sets in all 3 orthogonal views and grade them based on characteristics such as tumor/target visualization, normal organ visualization, sharpness of the image, soft tissue contrast, image noise and uniformity, and overall clinical usability. For each patient in the analysis, the observers provided the label (A or B) of the image set with the better image quality and then provided a score based on a 3-point scale:

• 1.Image quality is similar overall.
• 2.Image quality for the listed image set is slightly superior to those of other image sets.
• 3.Image quality for the listed image set is far superior to those of other image sets.

For cases in which the image quality was deemed to be far different between the 2 image sets (eg, scores of 3), the observers were required to provide comments on the observed differences. For all other image evaluations, observers provided comments on the comparison where appropriate. Once all observers had graded the image sets, the observer score was converted to a 5-point scale as follows:

• 1.Image quality for Iterative image set is far superior to that of the FDK image set.
• 2.Image quality for Iterative image set is slightly superior to the DFK image set.
• 3.Image quality for Iterative image set is similar to that of the FDK image set.
• 4.Image quality for Iterative image set is slightly inferior to that of the FDK image set.
• 5.Image quality for Iterative image set is far inferior to that of the FDK image set.

The 5-point scale was used to report the image quality results. The sequence of scoring (ie, observers selecting the image set with better image quality and then selecting the comparison score) was used to avoid biasing observers based on the grading scale itself.

Results

Contouring variation analysis

Prostate data sets

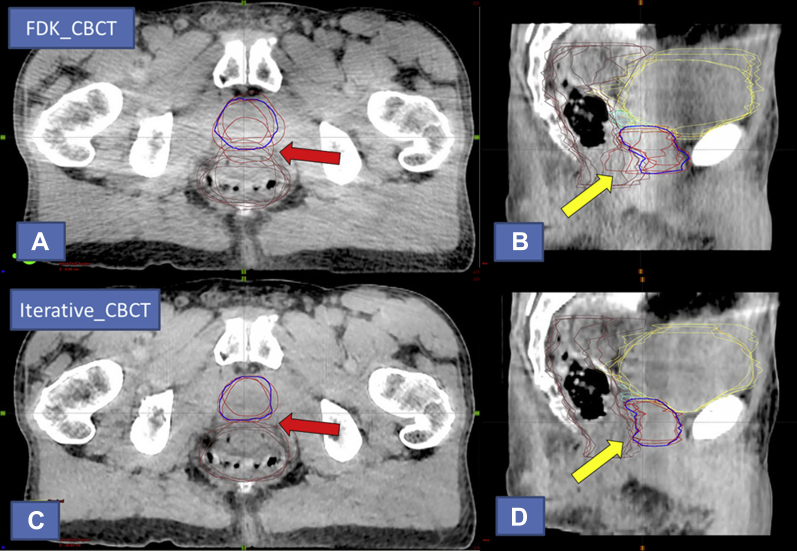
The contouring variation data (Dice coefficient and Hausdorff distance) for all structure types for the prostate data sets is shown in Table 1. For the prostate contours, the Iterative_CBCT data sets resulted in a statistically significant improvement in Dice coefficient of approximately 2.4% (P = .029). For all 9 patients, the average Dice coefficient among all observers was improved for the Iterative_CBCT data sets relative to the FDK_CBCT data sets. For 3 patients, the improvement in average Dice coefficient for the prostate contour was >3%. The largest improvement (approximately 10%) for an individual patient was observed for patient 5 (Fig. 2).

Table 1.

Contouring variation data for all prostate contouring study

Structure	Dice coefficient					Hausdorff distance (mm)
	FDK_CBCT		Iterative_CBCT		P-value	FDK_CBCT		Iterative_CBCT		P-value
	Mean	SD	Mean	SD		Mean	SD	Mean	SD
Prostate	0.853∗	0.075∗	0.877∗	0.047∗	.029∗	8.57	4.63	7.69	2.96	.19
Seminal Vesicles	0.720	0.124	0.703	0.166	.416	10.25	4.70	10.88	4.65	.47
Bladder	0.936	0.033	0.938	0.032	.356	7.17	4.29	6.89	3.04	.35
Rectum	0.893	0.050	0.902	0.044	.120	9.73	6.92	8.72	6.14	.20

Mean contour distance for prostate contours (Mean ± SD) (mm)
	Contour—overall	Superior	Inferior	Anterior	Posterior	Lateral
Iterative_CBCT	1.37 ± 1.62	1.62 ± 1.40	1.40 ± 1.21	1.21 ± 1.87	1.87 ± 1.16	1.16 ± 1.06
FDK_CBCT	1.57 ± 1.74	1.74 ± 1.51	1.51 ± 1.33	1.33 ± 2.12	2.12 ± 1.51	1.51 ± 1.21

Abbreviations: CBCT = cone beam computed tomography; FDK_CBCT = currently available algorithm; Iterative_CBCT = novel iterative algorithm; SD = standard deviation.

^∗Data values that correspond with statistically significant improvement for Dice coefficient and Hausdorff distance.

Fig. 2.

Visual contouring analysis for patient 5 of the prostate study, representing the largest Dice coefficient improvement for prostate contours. Prostate observer contours are shown in red and consensus contour in blue. Overall, the patient appeared to exhibit less inherent soft-tissue contrast than other patients within the study data set. (A) Axial and (B) sagittal views of the currently available algorithm (FDK_CBCT) reconstruction, respectively. Note the variation in the prostate-rectal interface on the axial (red arrow) and sagittal (yellow arrow) views of the contouring; (C) axial and (D) sagittal views of the novel iterative algorithm (Iterative_CBCT) reconstruction, respectively. Note the decreased noise and improved uniformity of the Iterative_CBCT image set relative to FDK_CBCT in both views. Also note the improvement in delineation of the prostate-rectal interface in both views relative to the FDK_CBCT image.

In addition to the improvement in average Dice coefficient value, the Iterative_CBCT data set contours also had less interobserver variation: The standard deviation of the Dice coefficient scores was approximately 60% of the corresponding standard deviation for FDK_CBCT data sets. The Hausdorff distance data for prostate contours indicates a decrease of approximately 1.0 mm, on average, for the Iterative_CBCT data sets, but the difference was not statistically significant.

For seminal vesicle contours, no statistically significant difference in Dice coefficient was found between the FDK_CBCT and Iterative_CBCT data sets. The overall Dice coefficient score for the seminal vesicles (approximately 70%) was lower than that observed for prostate contours (approximately 85%), which is likely due to the nature of the 2 contour types: The seminal vesicles comprise a much smaller volume than the prostate gland, and the Dice coefficient metric is more sensitive to smaller volume structures. The Hausdorff distance data showed no statistically significant difference between the FDK_CBCT and Iterative_CBCT data sets. For organ-at-risk (OAR) contours, no statistically significant difference in contouring variation metrics between the FDK_CBCT and Iterative_CBCT data sets was found for the rectum and bladder contours.

The mean contour distance data are shown in Table 1. On average, the Iterative_CBCT data sets exhibited an improvement in mean contour distance of approximately 0.20 mm for the overall contour, which is an improvement of approximately 15% relative to the overall average contouring uncertainty (estimated using the mean contour distance data for overall contour). For every prostate contour region, the Iterative_CBCT data sets exhibited an improvement in mean contour distance score relative to FDK_CBCT. The largest improvements in mean contour distance were seen in the posterior (0.32 mm improvement) region, but all regions exhibited an improvement within a fairly tight range—from 0.14 mm to 0.32 mm. In addition, the Iterative_CBCT data sets exhibited less variation in mean contour distance across all observers, as indicated by the lower standard deviation values for each prostate region.

Head and neck data sets

The contouring variation data for all structure types for HN is shown in Table 2. For brain stem and spinal canal contours, there was no statistically significant difference between the FDK_CBCT and Iterative_CBCT data sets. For parotid contours, we noted an approximate 2% improvement in the Dice coefficient (P = .03 for left parotid and total contour) and a 2 mm improvement in the Hausdorff distance (on average; P < .01). For submandibular contours, there was no statistically significant difference between the FDK_CBCT and Iterative_CBCT data sets.

Table 2.

Contouring variation data for all head and neck cancer data set structures

Structure	Dice coefficient					Hausdorff distance (mm)
	FDK_CBCT		Iterative_CBCT		P-value	FDK_CBCT		Iterative_CBCT		P-value
	Mean	SD	Mean	SD		Mean	SD	Mean	SD
Brain stem	0.85	0.07	0.85	0.10	.48	7.01	2.34	7.51	2.95	.26
Parotid_L∗	0.83	0.09	0.86	0.07	.03	10.47	5.43	7.75	3.28	<.01
Parotid_R	0.85	0.07	0.86	0.06	.25	9.27	3.71	8.05	3.47	.05
Parotid_Combined∗	0.84	0.08	0.86	0.06	.03	9.87	4.65	7.90	3.35	<.01
SpinalCanal	0.92	0.02	0.92	0.02	.46	5.40	2.56	4.64	1.91	.09
Subman_L	0.83	0.10	0.80	0.12	.28	6.91	4.54	7.26	4.51	.31
Subman_R	0.79	0.21	0.77	0.17	.49	7.52	6.63	8.32	5.55	.16
Subman_Combined	0.81	0.16	0.79	0.15	.39	7.22	5.63	7.79	5.04	.14

Abbreviations: CBCT = cone beam computed tomography; FDK_CBCT = currently available algorithm; Iterative_CBCT = novel iterative algorithm; L = left; R = right; SD = standard deviation.

^∗Data values correspond to statistically significant improvement.

Image quality analysis

Prostate data sets

For the prostate data sets, the mean (standard deviation) score among all observer evaluations was 2.11 (0.68). Observers scored the Iterative_CBCT data sets as equivalent or of better image quality for 107 of 110 image evaluations (97.2%). For 84 of 110 image evaluations (76.4%), observers noted at least a slight improvement in image quality, with significant improvements in image quality for 17 of 110 image evaluations (15.5%). All 10 patients had a mean image quality score of <3 (averaged over all observers), and all observers gave a mean score of <3 (averaged over all patients).

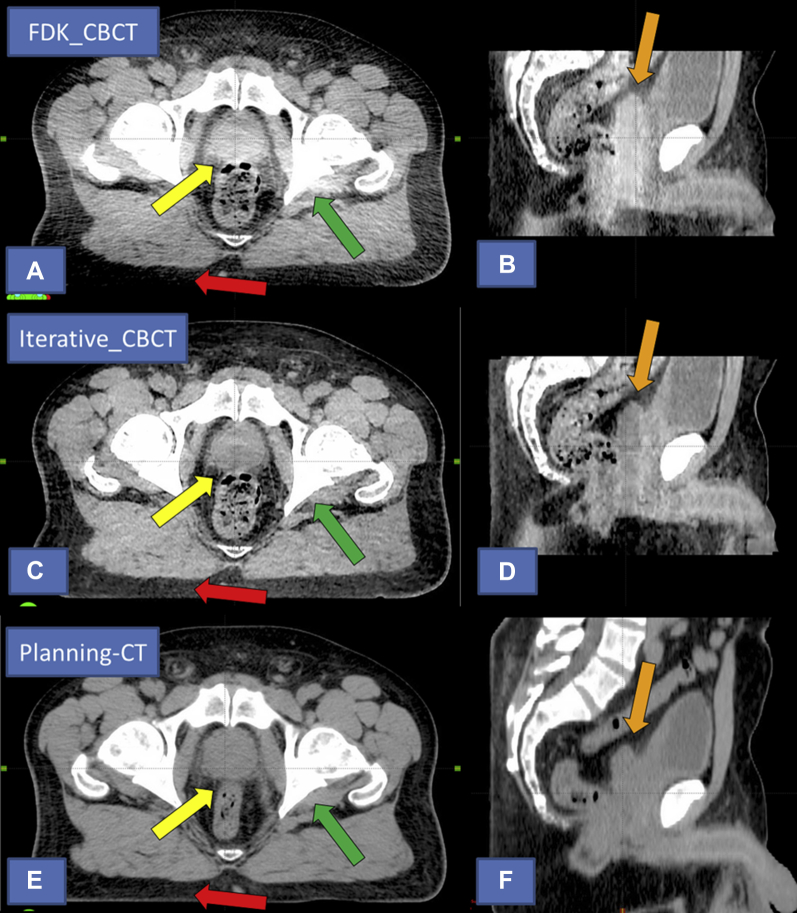
From the observer comments, the following characteristics were commonly used to describe the improvements in Iterative_CBCT image quality for the prostate data sets: sharper image/borders, improvement in the prostate-bladder and prostate-rectum interfaces, rectum and prostate are better defined, less image noise, improved image uniformity throughout the image set, and less streaking from the pelvic bony anatomy. A comparison of the FDK_CBCT, Iterative_CBCT, and planning CT image sets for patient 4 of the prostate study are shown in Figure 3.

Fig. 3.

Comparison of image quality for prostate patient 4. Top images (A) and (B) currently available algorithm (FDK_CBCT). Middle images (C) and (D) novel iterative algorithm (Iterative_CBCT). Bottom images (E) and (F): Planning computed tomography (acquired on different day than the cone beam computed tomography [CBCT] data sets). Note the improvement in image intensity homogeneity in the peripheral portion of the axial field of view (FOV; red arrow), central portion of the axial FOV (yellow arrow), and central portion of the sagittal FOV (orange arrow) in the Iterative_CBCT image. Also note the improved sharpness and image intensity uniformity near bony anatomy (green arrow) and the improved overall image noise for the Iterative_CBCT data set.

Head and neck data sets

For the HN data sets, the mean (standard deviation) score was 2.40 (0.88). Observers scored Iterative_CBCT as equivalent or of better image quality for 99 of 110 image evaluations (90.0%). For 65 of 110 image evaluations (59.1%), observers noted at least a slight improvement in image quality, with significant improvements in image quality noted for 14 of 110 image evaluations (12.7%). Nine of the 10 patients had a mean image quality score of <3.

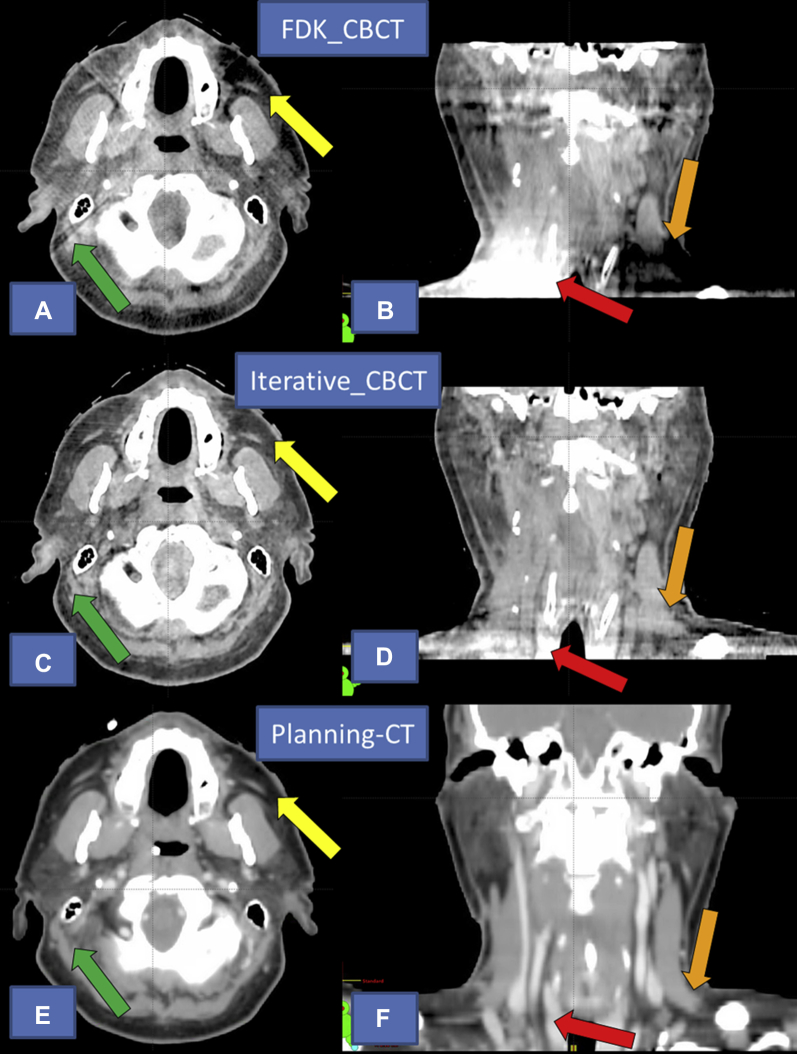
From the observer comments, the following characteristics were used to describe improvements in Iterative_CBCT: fewer artifacts in iterative data set, far superior image quality in inferior portion of the field of view (FOV), improved uniformity, less image noise, better soft-tissue definition near bony anatomy, and better visualization of the parotid glands in iterative. A comparison of the FDK_CBCT, Iterative_CBCT, and planning CT image sets for patient 7 of the HN study are shown in Figure 4.

Fig. 4.

Comparison of image quality for patient 7 with head and neck cancer. Top images (A) and (B): currently available algorithm (FDK_CBCT). Middle images (C) and (D) novel iterative algorithm (Iterative_CBCT). Bottom images (E) and (F) Planning computed tomography (acquired on different day than the cone beam computed tomography data sets). Note the improvement in image intensity homogeneity in the peripheral portion of the axial field of view near the left parotid gland (yellow arrow) and inferior portion of the sagittal field of view (orange and red arrows). Note the lack of streaking artifact in the Iterative_CBCT image near the bony anatomy (green arrow). Also note the improved overall image noise for the Iterative_CBCT data set.

Discussion

The use of CBCT for daily localization is a well-established approach to guide the radiation treatment of many types of cancers, including prostate cancer and HN cancer. The conventional FDK reconstruction algorithm in commercially available CBCT is an improvement relative to the anatomy visualization offered by planar imaging. However, the current CBCT reconstruction algorithms have room for improvement in several areas, including image uniformity, noise, and low-contrast detectability. With these improvements in mind, a novel iterative reconstruction algorithm has been developed for CBCT imaging. In this study, we performed a clinical evaluation of this algorithm.

From the image quality study for prostate data sets, we found that the Iterative_CBCT reconstruction algorithm most notably led to improvements in image noise, image intensity homogeneity, and boundary sharpness. The improvements in uniformity were noted for both the peripheral portion of the data set (in particular, the posterior superficial fat layer of the patient) and the central portion of the data set (within the pelvic rim). These improvements are notable for different reasons. The improved uniformity in the periphery of the image set is not likely to affect visualization of the target or OAR structures for prostate radiation therapy, but it could still help to improve the accuracy of downstream functionality, such as online dose calculation, deformable image registration, and deformable dose accumulation. Improved uniformity in the central portion of the image set, however, has the potential to both aid in the visualization of the target or OAR structures and potentially improve the accuracy of automated online rigid image registration, dose calculation, and deformable registration. Further investigation is warranted to evaluate the sensitivity of the deformable image registration and dose accumulation processes to image quality characteristics, such as image uniformity and noise.

The instructions and methods for the prostate contouring study were the same as those used in a previously published study that included an evaluation of the contouring variation for 5 observers on planning CT, as well as CBCT images acquired with a TrueBeam linear accelerator.²⁶ The commercially available TrueBeam CBCT imaging used in both studies (ie, FDK_CBCT) uses a kernel-based scatter-correction algorithm for the projection data.11, 12, 13 In the previous study, the prostate contour average Dice coefficient results for the planning CT (0.892) were approximately 2% larger than those of the physician observers on CBCT (0.872).

In the current study, we noted a Dice coefficient increase of approximately 2.4% between Iterative_CBCT (0.877) and FDK_CBCT (0.853). Of note, the 2 studies evaluated a different patient sample set, and the current study did not include planning computed tomography data. Nonetheless, we believe our results indicate improvements in visualization of the soft-tissue target (prostate gland) with Iterative_CBCT reconstruction, bridging a large portion of the image quality gap between CBCT and planning CT. The clinical significance of the difference in contouring metrics depends on the intended application.

To provide further context for the observed differences in Dice coefficient, the observers performed repeat contouring for 2 randomly selected patients. After performing the repeat contouring, the difference in average Dice coefficient value difference among all observers was 2.4%. Thus, the observed difference in Dice coefficient for the prostate gland between FDK_CBCT and Iterative_CBCT in this study is similar in magnitude to the Dice coefficient variation observed with repeat contouring (ie, measure of intraobserver variation). The Dice coefficient score is a measure of overall overlap and thus does not pinpoint the region where agreement or disagreement occurs.

However, when the Dice coefficient is supplemented with mean contour distance, the regions of disagreement can be further analyzed. For prostate image guided radiation therapy, our clinical workflow depends on registration based on the prostate-rectum interface. Based on the mean contour distance metric, the confidence interval (μ ± 1.96σ)²⁷ for the posterior region of prostate contours indicates an approximate 0.7 mm difference between FDK_CBCT and Iterative_CBCT. This 0.7 mm value is similar to the magnitude (1.0 mm) of the systematic component of the residual setup variation observed by Mayyas et al.²⁸ For OAR contours, we did not observe any difference in ability to contour the bladder and rectum for observers on Iterative_CBCT and FDK_CBCT. Likewise, the previous study found a Dice coefficient difference of <1% for bladder/rectum contours on planning computed tomography and CBCT.

Recently, studies evaluating contouring for HN cancers have been dominated by autocontouring and/or anatomic change analyses,25, 29, 30, 31, 32, 33, 34, 35, 36, 37 with fewer studies focusing on human-observer contouring.38, 39, 40, 41, 42, 43 The current study appears to be one of very few to evaluate manually segmented contours on CBCT images. There was no statistically significant difference between FDK_CBCT and Iterative_CBCT contours for spinal canal, brain stem, and submandibular contours. The bony border of the spinal canal provides sufficient contrast for both types of CBCT imaging, leaving little room for improvement for Iterative_CBCT. The brain stem was outside of the FOV in some data sets, and was difficult to distinguish in the remaining data sets.

Compared with parotid gland results, submandibular gland contour results were approximately 4% to 7% lower for average Dice coefficient value, which can be attributed to at least 2 factors: (1) Our physicians do not routinely contour the submandibular glands for treatment planning, and (2) the submandibular glands are surrounded by more similar soft tissue than the parotid glands and therefore have less inherent contrast relative to the surrounding anatomy. In fact, for 1 patient, 1 observer declined to contour the submandibular glands on both image sets because of lack of visualization.

We note statistically significant improvements in parotid gland contouring for the Hausdorff distance metric as well as statistically significant improvement for the left parotid gland Dice coefficient value. The anatomic change of the parotid gland during radiation therapy is well documented, and the improved ability to visualize the parotid is an important step toward improving HN CBCT utility. In particular, improved visualization of the parotids has the potential to aid in tracking parotid gland anatomic changes during a patient's treatment course, thereby aiding in clinical decisions with regard to parotid dose reduction and the need for adaptive planning.

At our clinic, we typically use a clockwise direction with half-trajectory for HN CBCT scans to allow for an initial volumetric modulated arc therapy beam gantry angle of 181° (with clockwise delivery), resulting in some projection sampling discrepancy between the left and right sides. This may be the reason for difference in image quality on the patient's left side (Figs. 4A and C) and contouring results for the parotid glands. Overall, there are limitations to the contouring analysis because the gross tumor volume for patients with HN is not well visualized on CBCT, and some image quality improvements in the inferior portion of the image set are not captured by any reasonable OAR contour.

The HN image quality study indicated that Iterative_CBCT reconstruction resulted in improvements that were slightly smaller in magnitude than those seen for the prostate data sets. We believe that this difference in relative improvement is likely because of differences in the employment of the reconstruction algorithm for the 2 sites and inherent differences between the 2 anatomic sites. The Iterative_CBCT reconstruction uses Acuros CTS for the pelvis only, so the improved scatter correction is not used in the HN image sets. The choice to use Acuros CTS for the pelvis only is reasonable because the human pelvis is much larger than the cranium, which results in larger scatter fraction; therefore, Acuros CTS offers more room for improvement with improved scatter correction.

Of course, there are also differences in the configuration of the target and OARs between the 2 anatomic sites, with prostate structures located near the image origin and HN structures scattered throughout the FOV. Overall, the image quality improvements observed for Iterative_CBCT certainly have the potential to affect the current localization paradigm (ie, bony alignment or soft-tissue matching). With that said, we believe the more exciting potential of this novel reconstruction algorithm lies in the domain of automated image analysis and adaptive radiation therapy. With improvements in soft-tissue visualization and image uniformity for the HN and prostate, the potential for improved deformable image registration and deformable dose accumulation warrants further study.

We note 2 main limitations of this study. First, we did not compare the image sets to planning CT, which is the current standard for delineation and treatment planning in radiation therapy. Second, as previously mentioned, we were not able to evaluate visualization of the target for the HN data sets.

Conclusions

A large and diverse group of observers noted improvements in image uniformity, noise level, and overall image quality for the Iterative_CBCT prostate and HN data sets. In addition, expert observers displayed an improved ability to consistently delineate soft-tissue structures, such as the prostate and parotid glands. Thus, the novel iterative reconstruction algorithm analyzed in this study is capable of improving visualization for prostate and HN cancer IGRT.