Machine Learning Methods Uncover Radiomorphologic Dose Patterns in Salivary Glands that Predict Xerostomia in Patients with Head and Neck Cancer

Abstract

Purpose

Patients with head-and-neck cancer (HNC) may experience xerostomia after radiation therapy (RT), which leads to compromised quality of life. The purpose of this study is to explore how the spatial pattern of radiation dose (radiomorphology) in the major salivary glands influences xerostomia in patients with HNC.

Methods and materials

A data-driven approach using spatially explicit dosimetric predictors, voxel dose (ie, actual radiation dose in voxels in parotid glands [PG] and submandibular glands [SMG]) was used to predict whether patients would develop xerostomia 3 months after RT. Using planned radiation dose data and other nondose covariates including baseline xerostomia grade of 427 patients with HNC in our database, the machine learning methods were used to investigate the influence of dose patterns across subvolumes in PG and SMG on xerostomia.

Results

Of the 3 supervised learning methods studied, ridge logistic regression yielded the best predictive performance. Ridge logistic regression was also preferred to evaluate the influence pattern of highly correlated dose on xerostomia, which showed a discriminative pattern of influence of doses in the PG and SMG on xerostomia. Moreover, the superior–anterior portion of the contralateral PG and medial portion of the ipsilateral PG were determined to be the most influential regions regarding dose effect on xerostomia. The area under the receiver operating characteristic curve from a 10-fold cross-validation was 0.70 ± 0.04.

Conclusions

Radiomorphology, combined with machine learning methods, is able to suggest patterns of dose in PG and SMG that are the most influential on xerostomia. The influence pattern identified by this data-driven approach and machine learning methods may help improve RT treatment planning and reduce xerostomia after treatment.

Introduction

Patients with head-and-neck cancer (HNC) are commonly treated with radiation therapy (RT). Of the spectrum of side effects owing to injury to organs at risk (OARs) from RT, xerostomia that arises from the parotid gland (PG) and submandibular gland (SMG) radiation have received significant study. The mean PG and SMG radiation dose is well known to be associated with the risk of developing xerostomia.1, 2, 3, 4 Modern intensity modulated RT techniques provide the opportunity to modify radiation dose distributions in PG and SGM and could potentially avoid radiation-induced xerostomia.

Despite these technological advancements, RT-induced xerostomia continues to be a significant clinical challenge that commonly affects patient-reported quality of life. To study RT-induced xerostomia, most existing literature used aggregated or summarized dosimetric predictors within certain organs, such as mean dose and dose-volume histogram (DVH) metrics in PG.1, 2, 3, 5 The disadvantage of this modeling approach is that the spatial information for the radiation dose within an organ is lost. Different spatial distributions of a dose within an organ can yield the same mean dose and DVH metrics. A previous study by our group using DVH metrics showed that the level of low dose delivered to the combined PGs has a strong influence on xerostomia.⁶ However, this previous study was not able to identify the spatial location of the influential regions using DVH metrics.

On the other hand, spatial information of the dose is key to understand the local dose effect on xerostomia. Preclinical investigations suggest that RT-induced xerostomia may be related to not only PG dosimetry, but also spatial location of secondary radiation damage within the PG.7, 8 In rat models, irradiation of the caudal portion of the PG caused not only xerostomia, but was also associated with salivary function recovery in contrast with irradiation of the cranial portion. The investigators subsequently demonstrated that this recovery may be related to the presence of stem or progenitor cells that are responsible for the recovery of radiation-induced xerostomia.⁹

Data mining investigations by Robertson et al within their informatic infrastructure have demonstrated that the level of low-dose irradiation to PG is associated with xerostomia at 3 to 6 months.10, 11 A pilot study by Quon et al of 30 patients has shown that the cranial half of the PG and its dosimetry may be more important in causing severe xerostomia in patients with HNC, and the current study sought to build on these observations.¹²

To more robustly evaluate the influence of specific subvolumes of the PG and SMG on injury and symptoms of severe xerostomia after RT, we applied supervised machine learning methods and a radiomorphology approach using voxel dose to predict parotid-injury-causing acute xerostomia. Radiomorphology parametrically represents the spatial dose distribution within normalized anatomic structures using voxel- or shaped-based dosimetric predictors, which are consistent across patient cohorts.¹³ The supervised machine learning method that was ultimately used is able to learn the influence of spatial dose patterns across organ subvolumes on xerostomia by assigning higher weights to the voxel dose of the predictive regions and lower weights to less predictive regions. We define the spatial pattern of the learned weights distributed across the voxels as the voxel importance pattern.

Methods and Materials

Patients

Our study population included 427 patients with HNC who were treated with parotid-sparing intensity modulated RT with curative intent between January 2008 and December 2016 and for whom xerostomia scores were available in our database. The data included both single- and double-sided neck treatments. All patients were seen weekly during RT for on-treatment visit assessments, and during the follow-up period typically every 3 to 4 months for the first 3 years and every 6 months thereafter. All study assessments, including the National Cancer Institute Common Terminology Criteria for Adverse Events xerostomia grading, were performed prospectively at the point of care during routine treatment and each follow-up visit. The study cohort excluded patients who did not have all PG and SMG contoured to ensure that every patient in the study cohort had complete radiation dose metrics in these 2 major salivary glands. Data from 427 actual patients were fed into the machine learning models.

Features

The features are predictors and variables we engineered as input data for the prediction model. The features are categorized into 2 parts: planned radiation dose metrics and patient demographic and clinical pathology features. To capture the spatial information of radiation dose explicitly, organs are modeled as voxels, and actual dose in the voxels are used as individual dosimetric predictors, which we call voxel dose. The voxels are linearly interpolated within the dose grid and equally spaced within the organ for the reference patient. The distance between any adjacent 2 voxels along the x, y, and z axes in Figure 1 are 4.68 mm, 4.68 mm, and 3.00 mm, respectively. Specifically, we used voxel-based doses in PG and SMG. The PG and SMG were contoured as part of the routine clinical workflow. In general, the contours of the PG were guided by surrounding anatomic landmarks as follows: Anteriorly and medially (masseter muscle), posteriorly and medially (styloid process), inferiorly and posteriorly (by course of posterior digastric muscle), laterally (by platysma), and inferiorly (after parotid tissues that generally stop at the level of the hyoid bone). For the SMG, the contours were guided laterally by the platysma, superiorly by the medial cortex of mandible, medially by the genioglossus, and by mylohyoid muscles anteriorly. The voxel dose and clinical features were later fed into the supervised learning models as input.

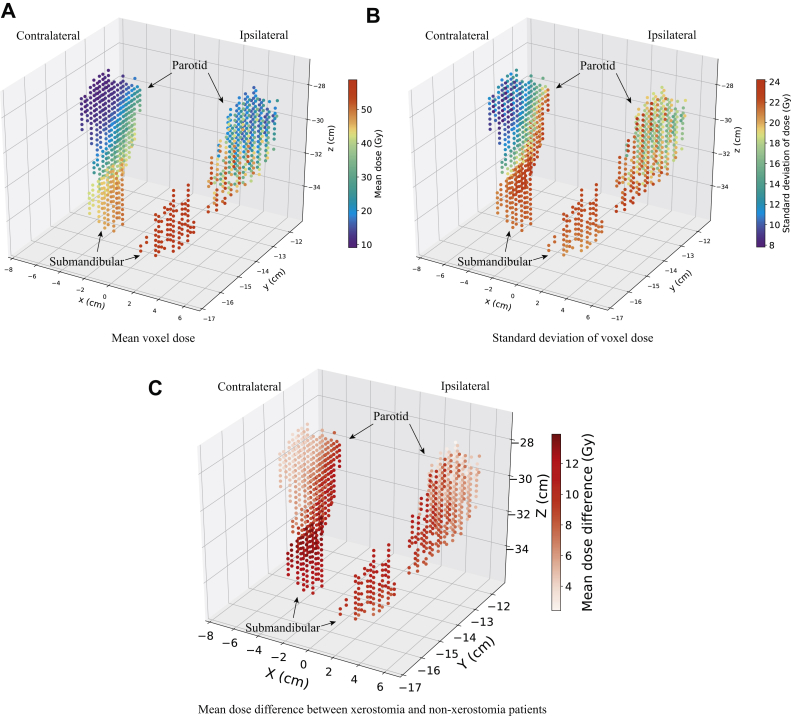
Figure 1.

Distribution of radiation dose in parotid and submandibular glands across the patient cohort. (A) Mean voxel dose, (B) standard deviation of voxel dose, and (C) mean dose of patients who developed xerostomia, minus the mean dose of patients who did not.

Patients' anatomic structures are spatially different. To obtain consistently identifiable doses for all patients, we aligned patients' structures to a common reference frame using a deformable registration technique (ie, Coherent Point Drift algorithm).¹⁴ Furthermore, to consider the factor of tumor location, we mirrored the patients' structures so that the spatial relationship of the organs, which we derived the dose from, was not left versus right, but rather ipsilateral versus contralateral relative to the disease side. The framework and actual steps to generate the voxel dose were described in a prior study.¹⁴ We also included the algorithmic steps to generate the voxel dose in the supplemental material.

The sociodemographic and clinical pathology features included are sex, race, age, attending physician, baseline xerostomia grade, tumor characteristics (TNM stage), chemotherapy (yes/no), human papillomavirus (HPV) status (positive or negative), whether feeding tube was used, and tumor site. Baseline xerostomia grade was measured either before treatment started or during the first week of treatment. Tumor site was characterized by mapping International Classification of Disease, 9th and 10th editions, diagnosis codes to specific site definitions. These features were chosen to capture basic patient characteristics and factors that may relate to xerostomia. There are no missing data in continuous features, and missing data in categorical features were treated as a new missing category. Patient cohort characteristics (ie, summary statistics of the above features) stratified by xerostomia outcome are shown in Table 1.

Table 1.

Patient characteristics at baseline

Predictor	Xerostomia grade ≥2 at 3 mo postradiation therapy		P-value
	No (N = 282)	Yes (N = 145)
Age∗	58.62 (52-67)	58.47 (53-64)	.77
Sex			.61
Male	210 (74.47%)	112 (77.24%)
Female	72 (25.53%)	33 (22.76%)
Race			.24
Caucasian	196 (69.50%)	113 (77.93%)
African American	65 (23.05%)	22 (15.17%)
Asian/Pacific islander	8 (2.83%)	7 (4.83%)
Other	13 (4.61%)	3 (2.07%)
Attending physician			.22
1	143 (50.71%)	69 (47.59%)
2	58 (20.57%)	28 (19.31%)
3	35 (12.41%)	25 (17.24%)
4	3 (1.06%)	3 (2.06%)
Missing	43 (15.25%)	20 (7.09%)
Chemotherapy			< .01
Yes	198 (70.21%)	123 (84.83%)
No	84 (29.79%)	22 (15.17%)
Human papillomavirus			< .01
Positive	185 (65.60%)	74 (51.03%)
Negative	94 (33.33%)	71 (48.97%)
Missing	3 (1.06%)	0 (0%)
Feeding tube used			.06
Yes	196 (69.50%)	88 (60.69%)
No	83 (29.43%)	57 (39.31%)
Missing	3 (1.06%)	0 (0%)
Baseline xerostomia grade			< .01
0	216 (76.60%)	99 (68.28%)
1	63 (22.34%)	33 (22.76%)
2	3 (1.06%)	13 (8.97%)
Primary tumor stage (T stage)			.89
0	12 (4.26%)	6 (4.13%)
1	50 (17.73%)	29 (20.00%)
2	66 (23.40%)	44 (30.34%)
3	47 (16.67%)	23 (15.86%)
4	65 (23.05%)	35 (24.14%)
Missing	42 (14.89%)	8 (2.84%)
Regional lymph nodes stage (N stage)			.11
0	69 (24.47%)	25 (17.24%)
1	33 (11.70%)	25 (17.24%)
2	128 (45.39%)	83 (57.24%)
3	6 (2.13%)	5 (3.45%)
Missing	46 (16.31%)	7 (2.48%)
Distant metastasis stage (M stage)			.51
Yes	16 (5.67%)	6 (4.14%)
No	229 (81.21%)	132 (91.03%)
Missing	37 (13.12%)	7 (2.48%)
Tumor site			< .01
Oral cavity	52 (18.44%)	45 (31.03%)
Oropharynx	54 (19.15%)	42 (28.97%)
Nasopharynx	12 (4.26%)	14 (9.66%)
Larynx	54 (19.15%)	17 (11.72%)
Other	110 (39.01%)	27 (18.62%)
Treatment side			< .01
Unilateral	8 (2.84%)	3 (2.07%)
Bilateral	238 (84.40%)	139 (96.55%)
Lower in the neck	36 (12.77%)	2 (1.38%)

P-value obtained using the 2-sample test.

^∗Summary statistics include the mean and interquartile range for continuous variables and the count and percentage value for categorical variables.

Outcome measure

The outcome measure was Common Terminology Criteria for Adverse Events xerostomia grading, captured prospectively at the start of the first follow-up period, which is 3 months after RT. The xerostomia grade is physician-rated at the clinic during the patient encounter. A prevalence analysis within our database shows that the severity of xerostomia starts decreasing after RT, which is likely owing to recovery. We chose to look at xerostomia 3 months after RT, which is around the time of the second follow-up visit, as an indication of acute xerostomia caused by radiation-induced injury (as opposed to the inclusion of recovery). For predictive modeling, a binary classification problem was created by grouping xerostomia grading into 2 categories: Severe xerostomia if grade 2 or 3, and no or mild xerostomia if grade 0 or 1. The primary endpoint for prediction is whether a patient will develop severe xerostomia 3 months after RT. For patients who did not have a xerostomia measurement at 3 months post-RT, the last xerostomia measure was carried forward. Patients who did not have a xerostomia measurement at 3 months post-RT was mostly due to lost to follow up or inability to get measurements at that time.

Prediction models

Three supervised machine learning algorithms were applied to our data set: ridge logistic regression, lasso logistic regression, and random forest.15, 16 To fit ridge and lasso logistic regression models, features were standardized to have 0 mean and unit variance before input into the prediction models. The area under the curve (AUC) score evaluated using nested 10-fold cross-validation for each model was compared using a pairwise 2-sample t test after fitting each model to our data set. The optimal hyperparameters for those algorithms were chosen using 10-fold cross-validation while maximizing the AUC score on the hold-out data. Furthermore, the cross-validation was repeated 40 times with different random splitting of the data to ensure the learned hyperparameters do not depend on a specific random splitting of the data. To determine the best model, the voxel importance pattern obtained from each algorithm along with the prediction performance was evaluated among the 3 algorithms.

Voxel importance pattern

Lasso logistic regression learns a sparse set of features and assigns 0 weight to nonimportant features. Ridge logistic regression does not learn a sparse solution but assigns a larger weight to more important features. The magnitude of the feature weights learned by regularized logistic regression, combined with hyperparameter tuning using cross-validation, indicates the relative importance of the voxel dose. Moreover, the radiation dose in different voxels are on the same scale (average dose range, 9.09-58.77 Gy), which prevents having very different weights owing to different feature scales. Therefore, the magnitude of the learned weights was used as a measure of voxel importance, which indicates how much a change in the radiation dose in a voxel affects the probability of the patient developing xerostomia. A higher positive voxel importance indicates a larger chance of developing xerostomia if the dose in that voxel was increased.

The voxel importance for random forest was measured by computing how much the squared error decreased during the training process when partitioning data using a certain feature over all trees.15, 17

To visualize the voxel importance pattern, we normalized voxel importance measures to be in the range of 0 to 1 and linearly mapped the normalized voxel importance onto the 3-dimensional PG and SMG structures.

To further check whether the voxel importance pattern is consistent given the sample randomness, the data were randomly separated into 5 folds, and the analysis was repeated (learning step in Fig 2) 5 times on 4 folds. Then, the correlation coefficients of the weights learned from the 5 analyses were computed. High correlation coefficients between the feature weights learned from the 5 analyses indicate that the voxel importance pattern is consistent on different random samples.

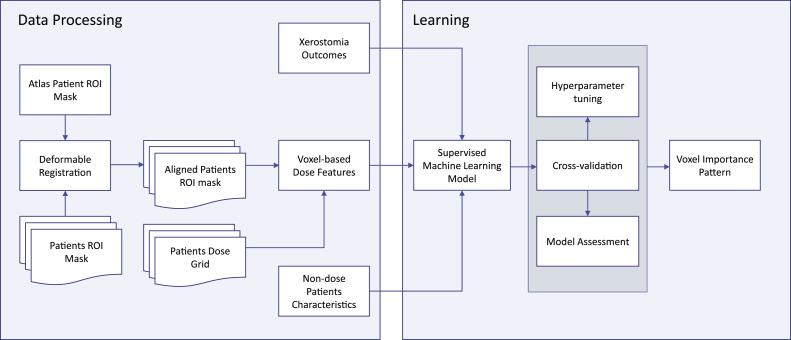
Figure 2.

Flowchart of key steps for this analysis. Abbreviations: ROI = region of interest.

Results

Xerostomia outcome

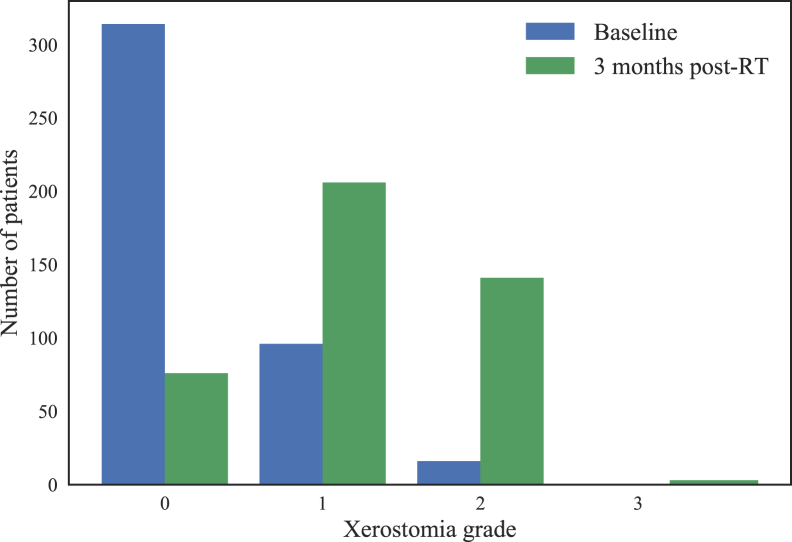
For the xerostomia prediction outcome, 145 patients (34%) had xerostomia (grades 2 and 3) 3 months after RT. Eighty-nine patients (20.8%) did not have a xerostomia assessment at 3 months post-RT, and last observation carried forward was used to obtain the outcome for these patients. The average time point from which the last measurements were carried forward is 67.9 days from the start of RT, and the standard deviation was 38.6 days. Figure 3 shows the distribution of xerostomia grade at baseline and 3 months post-RT and that a large portion of patients developed xerostomia after RT.

Figure 3.

Distribution of xerostomia grade at baseline and 3 months after radiation therapy.

Dose distribution

Figure 1 shows the distribution of mean voxel dose, standard deviation of dose, and mean dose of the patient group that developed xerostomia, minus the mean dose of the patient group that did not develop xerostomia in the total 942 voxels of the PG and SMG across the patient cohort. The mean dose in voxels ranged from 9.09 Gy to 58.77 Gy, and the standard deviation of dose from 7.81 Gy to 24.21 Gy. The ipsilateral SMG had the highest mean voxel doses, and the anterior–superior portion of the 2 PG had the lowest mean voxel doses. The inferior–posterior portion of the contralateral PG and the 2 SMG had the highest variation of dose, and the anterior–superior portion of the contralateral PG had the lowest variation of dose. The patient group that developed xerostomia received a higher mean dose than the patient group that did not develop xerostomia across the entire PG and SMG. In the SMG and inferior portion of contralateral PG, patients who developed xerostomia received a much higher mean dose.

The pattern of mean voxel dose generated is consistent with our clinical practice whereby the dose spectrum decreases more superiorly across the PG. The ipsilateral SMG and the tail of the ipsilateral PG typically receives comparable high doses of radiation owing to the presence of level II cervical nodal metastases.

Model performance

After obtaining the voxel dose, nondose features, and xerostomia outcomes, the AUC scores of ridge, lasso logistic regression, and random forest were evaluated using nested 10-fold cross-validation on the obtained data set. The cross-validation AUC scores (out-of-sample score) for ridge, lasso logistic regression, and random forest were 0.69 ± 0.08, 0.67 ± 0.06, and 0.69 ± 0.07 respectively. The P-values of the pairwise 2-sample t test comparing the AUC scores on the 10 holdout folds between the 3 models were .46 (ridge vs lasso logistic regression), .92 (ridge logistic regression vs random forest), and .48 (lasso logistic regression vs random forest). Therefore, there is no statistically significant difference between the 3 models regarding predictive performance using the significance level of .05.

Voxel importance pattern

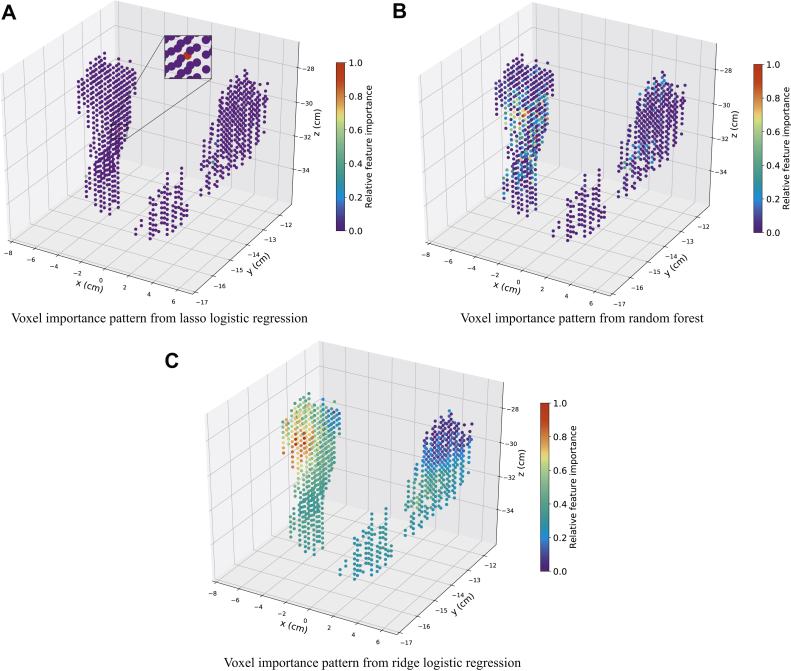
The voxel importance patterns for the 3 methods are shown in Figure 4. The ridge and lasso logistic regression models are both well suited for high-dimensional data, where the number of features is larger than the number of samples or many features are correlated.¹⁸ However, given the highly correlated voxel dose, lasso yields only 1 or a few voxels from the predictive regions owing to the ${\ell }^1$ norm regularization. Random forest produces nonsmooth, relative, variable importance patterns owing to the random selection of a subset of features among the correlated features to grow the trees, but ridge logistic regression produces a smooth solution by shrinking the weights of correlated features close to each other.¹⁸

Figure 4.

Voxel importance patterns learned from the 3 machine learning algorithms where the color corresponds to the relative importance of each voxel.

By reducing the variance of the estimated weights of highly correlated features, ridge regression has been commonly used to address multicollinearity.19, 20, 21 The dimension of the voxel radiation dose features is high (942 voxels), and much larger than the number of patients (427 patients). Moreover, the radiation dose features are highly correlated for voxels that are spatially close. Likely, there is a region of voxels, instead of a single or few voxels, from which the dose has the largest influence on xerostomia, and other regions have less but not 0 influence. The voxel importance patterns in Figure 4 verified the reasoning given earlier in this article.

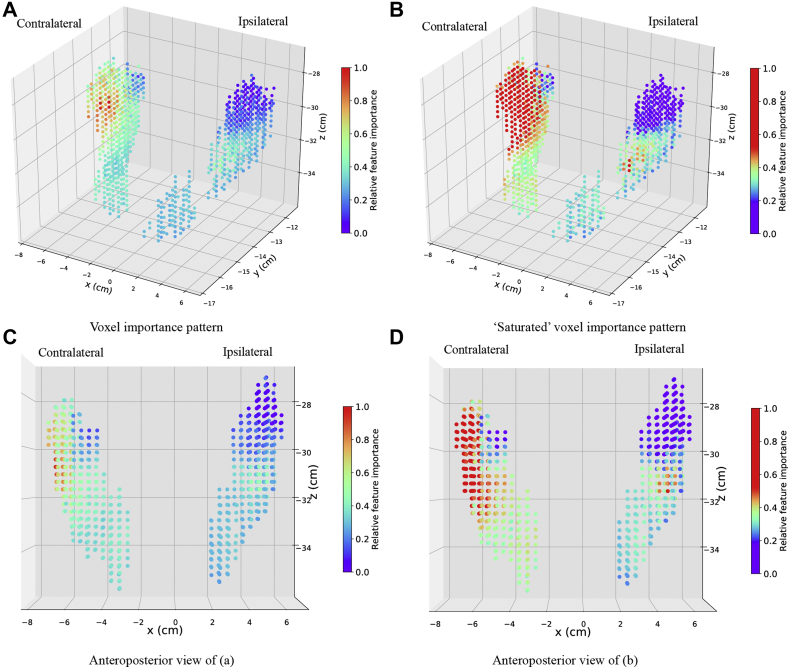
Given the previous characteristics of our voxel dose and 3 supervised learning models, ridge logistic regression is well suited for our study. Therefore, ridge logistic regression was used to study the voxel importance pattern (Fig 5). The AUC score for the final ridge logistic regression model evaluated by nonnested 10-fold cross-validation is 0.70 ± 0.04. The red region represents the most important voxels, and violet represents the least important. Together, the doses in the different subvolumes in PG and SMG all have an effect on xerostomia, but the influence of the dose on xerostomia varies across the different subvolumes. Specifically, the superior–anterior portion of the contralateral parotid is the most influential region. The medial portion of the ipsilateral parotid is also very influential, and the superior portion of the ipsilateral parotid is the least influential region. Figure 6 shows 2-dimensional cross-sectional images from computed tomography of the reference patient that show the colored spatial distribution of influential areas within the anatomic substructures. Model coefficients for clinical features and voxel dose are shown in Tables S.3 and S.4 in the supplemental material. To predict the risk of developing xerostomia for a patient, we use logistic function $\text{p}\left(y\mid X\right)=\frac{1}{1+e^{-{\beta }^{T}X}}\text{,}$ where y is the risk of developing xerostomia, X is the vector of clinical features and voxel dose for the patient, and β is the learned model coefficients in Tables S.3 and S.4.

Figure 5.

(A) Voxel importance pattern from ridge logistic regression and (B) different visualization of the same voxel importance result where voxel importance values that are 1 standard deviation (SD) away from the mean were saturated to increase the resolution of voxel importance closer to the mean value of the voxel importance. The saturated plot was created as the set of voxel importance values that are greater than 1 SD of the mean voxel importance values to be 1 SD of the voxel importance values plus the mean value. As a result, the voxels of which the voxel importance value is greater than 1 SD of the mean voxel importance values are shown in red. Similarly, voxels of which the voxel importance value is greater than 1 SD of the mean voxel importance values are shown in blue. Voxel importance values within 1 SD of the mean value is color coded from blue to red.

Figure 6.

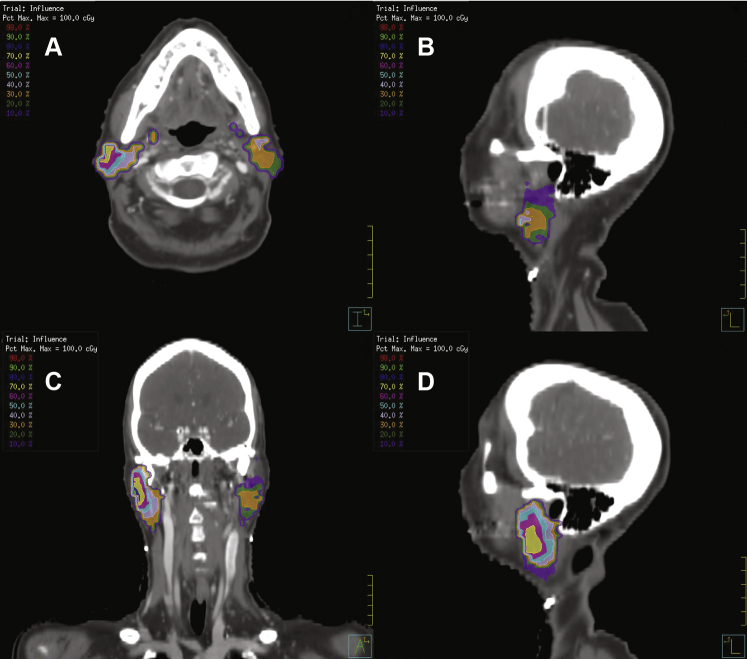
Two-dimensional cross-sectional images from computed tomography scans of the reference patient, displaying the spatial location of the influential area and colored distribution of voxel-based dose feature importance. (A) Axial view of voxel importance pattern, (B) sagittal view of the voxel importance pattern on the contralateral side, (C) coronal view of the voxel importance pattern, and (D) sagittal view of the voxel importance pattern on the ipsilateral side.

The consistency of the voxel importance pattern obtained from the ridge logistic regression was tested on 5 different random samples. The lowest Pearson correlation coefficient among the weights learned from the 5 random samples was 0.85, which indicates that the voxel importance pattern is fairly consistent given the sample randomness.

We also performed the same analysis with only the complete cases (332 patients) where patients who did not have a xerostomia assessment at 3 months post-RT were excluded. The 10-fold cross-validation AUC score for the complete cases using ridge logistic regression is 0.68 ± 0.03, and the voxel importance pattern is the same as in Figure 5. The Pearson correlation coefficient between the voxel importance (feature weights) of the complete cases versus the case where patients who did not have a xerostomia assessment at 3 months post-RT were included is 0.93, which indicates that the voxel importance patterns from the 2 analyses are highly consistent.

Statistically significant features

For a normal regression analysis where the number of features is smaller than the number of samples, confidence interval and P-value can indicate whether a feature is statistically significantly associated with the outcome (feature coefficient is nonzero). However, penalized (ridge/lasso) regression methods do not produce meaningful confidence intervals or P-values. Therefore, to get the P-value for the clinical features and voxel dose, and check if they are statistically significantly associated with outcome, we performed a univariate logistic regression for each clinical feature and voxel dose separately. In other words, for each individual feature, we fitted a logistic regression, using it as the independent variable, and the xerostomia outcome as the dependent variable. The results are shown in Tables S.1 and S.2 in the supplemental material.

Table S.1 shows that, among the clinical features, whether the patient has HPV, completed chemotherapy, their baseline xerostomia grade, tumor site, N stage, and use of feeding tube are statistically significant features at a significance level of .05.

Discussion

The results demonstrate the successful application of the use of spatially explicit dosimetric predictors in predicting xerostomia in patients with HNC, leading to the identification of potential important parotid dose subvolumes associated with the predicted risk of severe xerostomia at 3 months after RT. To the best of our knowledge, this analysis used the largest cohort of patients with xerostomia HNC and prospective point-of-care data in literature, which enables robust modeling results and conclusions. The analysis confirmed evidence that parotid subvolumes are at a greater risk of contributing to radiation-induced xerostomia, as initially proposed in humans by van Luijk et al.⁸

Modeling the radiation dose spatially explicitly provides insights into the spatial dependence of dose in contrast with the use of DVH metrics alone. For instance, we are aware of 1 existing study that used a similar voxel-based dose analysis for acute dysphagia in patients with HNC.²² The authors applied a statistical test to compare the voxel-based dose distribution between patients with grade ≥3 versus <3 dysphagia. Instead of comparing the dose difference between patients who developed xerostomia and those who did not, we combined the voxel-based dose modeling with supervised machine learning algorithms to build a predictive model for xerostomia. We also learned how spatial dose influences xerostomia, highlighting the flexibility of this methodology. Our methodology can also be potentially applied to other RT-related head-and-neck toxicities, such as dysphagia and trismus.

The distribution of average doses shows that the most important region found (ie, superior-anterior portion of the contralateral PG) is within the low-dose region in the patient cohort. This is consistent with the results from a study by Robertson et al using DVH metrics to demonstrate the impact of a low-dose bath to both PG on the risk of grade ≥2 xerostomia.¹⁰ We believe that if this region was treated with a high radiation dose, the other regions were likely treated with an even higher dose, leading to a much higher risk of developing xerostomia.

Furthermore, we would expect the superior portion of the ipsilateral PG also to be more predictive because the region is also low dose. However, the voxel importance pattern result did not reveal this, but rather, the medial portion of the ipsilateral PG was more predictive. We hypothesize that in the ipsilateral PG, the medial portion is more important because of its proximity to the ductal region, and radiation damage to that region will render doses in the superior portion much less important in predicting xerostomia. This is in accordance with the preclinical xerostomia model that has demonstrated that sparing the stem or progenitor cells contained in the ductal region of PG preserves salivary function after RT.⁸

We further investigated whether our current method improves the prediction performance compared with using only conventional dosimetric features. Specifically, we computed the mean dose and DVH features (D5, D25, D50, and D90) over all parotid and submandibular glands. The AUC performance using these conventional dosimetric features and the ridge logistic regression model evaluated with nested 10-fold cross-validation on the same 477 patients is 0.68 ± 0.09, which is not significantly different from using voxel-dose features. Although the current method using voxel-dose features did not significantly improve prediction performance, more insight is provided about the spatial dependency between radiation dose and acute xerostomia, which cannot be achieved using only conventional dosimetric features.

The findings provide insight into the importance of bilateral parotid injury,and underscore the importance of carefully determining the clinical indications for bilateral cervical nodal irradiation along with a careful delineation of how superior and lateral the cervical nodal planning target volumes encroach upon the medial and superior aspects of the PG. Moreover, the analysis also demonstrated (to a lesser degree) the importance of irradiation in the subvolumes in the contralateral SMG contributing to the severity of xerostomia at 3 months post-RT. This highlights the clinical implications and importance of reducing the volume of cervical neck irradiation as a clinical strategy to de-intensify the current chemoradiation treatment paradigm for head-and-neck squamous cell carcinomas, especially for HPV-associated oropharyngeal carcinomas.

Several additional limitations of our analysis need to be recognized. First, the study population consists of patients treated at a single local hospital. The specific voxel importance pattern obtained may be specific for patients at this hospital. Second, for the xerostomia prediction outcomes, we used last observation carried forward to obtain data for patients without xerostomia assessment at 3 months post-RT. Our longitudinal xerostomia outcomes data show that there is minor xerostomia recovery from the end of treatment to 3 months post-RT. Therefore, our prediction outcome data could be slightly biased toward a more severe xerostomia grade.

Third, we believe that the importance pattern identified by our method depends not only on the actual relationship between dose and xerostomia outcome, but also on the range of dose variations in our patient cohort. Most patients have similar patterns of dose; therefore, evaluating dose-response outside of the range of patterns delivered to patients in the database is challenging. Even if we think that areas with low-dose variation are likely to show weak associations, our study still shows that the low-dose region on the contralateral parotid gland, which has a low-dose variation, is the most influential region.

Fourth, the learned influence pattern depends on the specific model we used (ie, ridge logistic regression). The identified important region may be too big if the region that contains highly correlated voxel dose is large. In addition, our results indicate a possible serial component to the behavior within the ipsilateral parotid (ie, high radiation dose delivered to medial portion of ipsilateral parotid [close to ductal region]), and possibly causing an occlusion to the duct, rendering the superior portion less important.

However, we did not explicitly model serial behavior within organs because we modeled voxel dose as independent features. This assumes that doses in different regions within the analyzed organs influence xerostomia in parallel. Explicitly modeling the dependency between doses in different voxels may enable us to model possible serial behavior of dose influence on xerostomia within organs. However, we believe a hypothesis regarding certain serial behavior or dependency between dose influence on xerostomia in different regions is required beforehand to investigate possible serial behavior. Without prior knowledge and a hypothesis about any serial behavior, we adopted the current modeling approach.

Fifth, the pattern of dose effect on xerostomia, as we learned in this study, represents only the association between radiation dose and xerostomia. Sixth, because we treated each voxel independently, we did not explicitly consider the spatial coherence of the dose patterns. However, ridge logistic regression handles the correlations between voxel doses by assigning similar voxel importance to highly correlated predictors, which is inherent in the way we treated patients. Future efforts that explicitly include the spatial coherence between dose voxels in derived features may uncover interdependencies that also relate to the xerostomia outcome. No conclusion on the causal effect between dose and xerostomia was established in this observational study. Finally, this study only included radiation doses in the PG and SMG, but there is a study that reported that the mean dose to oral cavity is associated with xerostomia as well.¹

For future studies, we can apply this approach to patients with HNC at other hospitals that may have different patient characteristics and radiation treatment plans to validate our approach and the voxel importance pattern we learned. Ultimately, we want to learn the causal effect between radiation dose and xerostomia, which is difficult using observational studies. Either an experimental study or advanced causal inference analysis should be conducted. Nabi and Shpitser recently proposed a causal inference technique (ie, causal sufficient dimension reduction) for high-dimensional treatments problems,²³ which we are currently applying to our problem.

In this study, we focused on the methodology to study the spatial pattern of dose influence on xerostomia. To investigate the effect of possible interaction, reserve capacity, and compensation mechanism on xerostomia, we are currently studying the spatial dose influence on xerostomia recovery by comparing its influence pattern with an acute xerostomia analysis. We believe this next study will provide further implications of the biological mechanisms behind dose effect on xerostomia.

Different dose and fractionation schemes are known to have different biologic effectiveness for HNC treatment. For our patient cohort, all 427 patients were treated with 33 to 36 fractions, and the highest dose-planning target volume received was between 200 Gy and 220 Gy. Therefore, fractionation schemes do not vary much among our patient cohort. However, we believe a study of the effect of different fractionation schemes on xerostomia would be interesting for future studies.

In addition, whether the current method combined with conventional dosimetric features will yield better prediction accuracy is another interesting research question for future study. To combine the current method with conventional dosimetric features, we can carve the parotid and submandibular glands into different subregions (larger than voxels), and compute dosimetric features for each of the subregions. Those dosimetric features within the carved subregions can be used to predict xerostomia. Using this approach, we will still be able to capture the spatial dependency between radiation dose and xerostomia and enables a more flexible modeling approach because we can control the sizes of the carved subregions, which may improve xerostomia prediction accuracy. Finally, we will also include dose in oral cavity in our study to investigate how dose in subvolumes in oral cavity is associated with xerostomia.

Conclusions

We have identified that doses to specific subvolumes in the PG and SM (ie, superior-anterior portion of the contralateral PG) are the most predictive of xerostomia and are within the low-dose bath region in our study population. We also found that the medial portion of the ipsilateral PG to be predictive of xerostomia. We believe our methodology and the local dose effect pattern identified can help improve RT planning and reduce xerostomia for patients with HNC.