Subsampling reveals that unbalanced sampling affects Structure results in a multi-species dataset

Abstract

Studying the genetic population structure of species can reveal important insights into several key evolutionary, historical, demographic, and anthropogenic processes. One of the most important statistical tools for inferring genetic clusters is the program Structure. Recently, several papers have pointed out that Structure may show a bias when the sampling design is unbalanced, resulting in spurious joining of underrepresented populations and spurious separation of overrepresented populations. Suggestions to overcome this bias include subsampling and changing the ancestry model, but the performance of these two methods has not yet been tested on actual data. Here, I use a data set of 12 high-alpine plant species to test whether unbalanced sampling affects the Structure inference of population differentiation between the European Alps and the Carpathians. For four of the 12 species, subsampling of the Alpine populations—to match the sample size between the Alps and the Carpathians—resulted in a drastically different clustering than the full data set. On the other hand, Structure results with the alternative ancestry model were indistinguishable from the results with the default model. Based on these results, the subsampling strategy seems a more viable approach to overcome the bias than the alternative ancestry model. However, subsampling is only possible when there is an a priori expectation of what constitute the main clusters. Though these results do not mean that the use of Structure should be discarded, it does indicate that users of the software should be cautious about the interpretation of the results when sampling is unbalanced.

Introduction

Almost all species show some form of genetic structure in the distribution of genetic variation. Be it a herb with an extremely limited distribution (Freville et al. 2001), a widely distributed tree species (Meirmans et al. 2017), or a planktonic species from the open ocean (Peijnenburg and Goetze 2013), there may be surprising genetic discontinuities across a species’ range. Patterns of population structure can take many forms, from simple gradients resulting from limited dispersal to complex hierarchical patterns resulting from ecological adaptation to local conditions. Studying population structure can therefore be used to make inferences about the underlying evolutionary, historical, demographic, or anthropogenic processes, or a mixture of these (Lee and Mitchell-Olds 2011; Orsini et al. 2012; Nadeau et al. 2016).

One of the most widely used statistical tools for assessing population structure based on individual genotypes is the program Structure (Pritchard et al. 2000; Falush et al. 2003). Structure applies assignment of individuals to populations in a Bayesian framework, assuming Hardy–Weinberg equilibrium within clusters. While doing so, it performs a dual role: (1) assigning individuals to clusters, with the possibility of admixture between clusters, (2) finding the most suitable number of clusters (K) given the data. Structure generally performs both tasks very well and often gets results with a very intuitive biological explanation. Nevertheless, the method is not without flaws: Pritchard et al. (2000) themselves already acknowledged that Structure may give rise to spurious clustering in the presence of isolation by distance (see also Frantz et al. 2009; Meirmans 2012). Furthermore, the inference of the number of clusters is difficult as there may not be a single “optimal” value (Meirmans 2015), and different methods (Pritchard et al. 2000; Evanno et al. 2005) may yield different estimates (Janes et al. 2017).

Recently, several papers have pointed out that Structure is particularly sensitive to unbalanced sampling of populations (Kalinowski 2011; Neophytou 2013; Puechmaille 2016). With simulated data, even at the correct value of K, an unbalanced sampling design resulted in incorrect assignment of individuals to clusters; underrepresented populations tended to be clustered together even when they were not genetically more closely related. Conversely, the most sampled populations were often split into two or more spurious clusters with many individuals showing some degree of admixture. Patterns that are remarkably similar to those in Puechmaille’s (2016) simulations can be observed when Structure is run on actual data sets. Puechmaille himself showed such a bias to be present in the analysis of Monarch butterflies. A similar pattern was noted earlier in a study of hybridisation between domesticated and wild species of cabbage, where the most sampled species (Brassica rapa) was split into two almost fully admixed clusters (Luijten et al. 2015). In order to reduce the bias that comes from unbalanced sampling, Puechmaille (2016) suggested subsampling the largest sample to match the size of the smaller ones. This subsampling strategy indeed removed the spurious clustering that was present in the largest sample both in Monarch butterflies (Puechmaille 2016) and in Brassica (P. Meirmans unpublished data).

In response to these simulation papers, Wang (2017) posited that a simple change in the settings of Structure may suffice to resolve the bias resulting from unbalanced sampling. The ancestry model used by Structure has a default setting where it is assumed that all source populations contribute equally to the total sample of individuals. Obviously, this is not the case when sampling is unbalanced. However, an alternative ancestry model can be used where a separate admixture parameter (alpha) is inferred for each cluster. Using simulated data and artificially unbalanced subsets of real data, Wang (2017) showed that changing the ancestry model setting improves Structure’s performance with unbalanced data sets. Furthermore, Wang found that reducing the initial value of alpha, to a value of about 1/K, further improves the results.

In general, it is difficult to assess to what extent a bias that is present in simulated data is also present in real data sets. This is because the true situation cannot be known for real data sets. However, the subsampling strategy suggested by Puechmaille (2016) and the ancestry model settings suggested by Wang (2017) do present an opportunity to assess the incurred extent of the bias since the results of different methods can directly be compared. This is especially the case for species where unbalanced sampling coincides with an a priori hypothesis of divergence: e.g., for species where a large population is geographically widely separated from a much smaller population. Such species allow assessing whether any observed admixture between large and small populations is the result of bias or rather the result of unknown biological processes such as long-distance dispersal, recent fragmentation, or a shared evolutionary history.

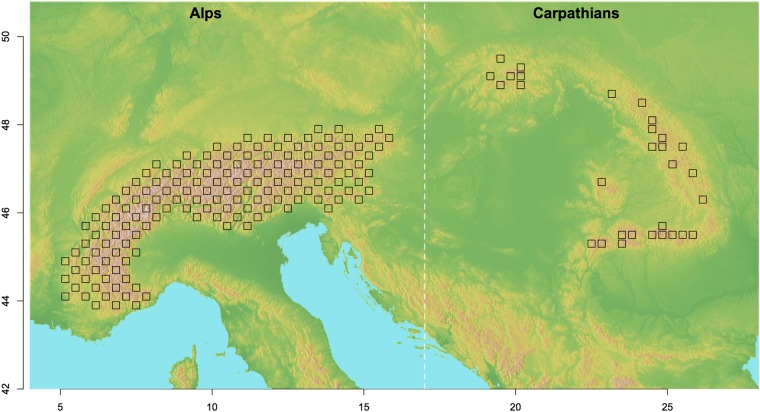
Here, I use a data set of 12 high-alpine plant species to test whether unbalanced sampling affects the Structure inference of population differentiation between the European Alps and the Carpathians. The data set is remarkable in its scope (Gugerli et al. 2008) as all species have been uniformly sampled on the same regular grid in both mountain ranges. Even though the Carpathians are stretched out over a longer arc than the Alps, they have fewer high peaks and therefore fewer habitats for high-alpine species. Therefore, the regular sampling design resulted in an unbalanced data set, with more samples taken from the Alps than from the Carpathians (Fig. 1). The two mountain ranges are clearly geographically separated and also their floristic differences are well described (Tutin et al. 1964–1980). Therefore, it can be hypothesised that the population samples from these 12 species will generally fall into two clusters corresponding to the two mountain ranges. However, Gugerli et al. (2008) found for one of the included species—Carex sempervirens—partial overlap between the clusters between the Alps and the Carpathians. Such mismatch between the Structure results and the expectation may be either because the unbalanced sampling introduces a bias in Structure, or because the true divergence is different than hypothesised. Subsampling the population samples from the Alps should allow a distinction between these two possibilities.

Fig. 1.

Map of Central Europe showing the Alps and the Carpathians. Squares indicate all cells of the main IntraBioDiv grid where populations from the 12 species included here have been sampled

Materials and methods

Data

The data were used from the IntraBioDiv-project (Gugerli et al. 2008; Alvarez et al. 2009; Taberlet et al. 2012), which contains AFLP data from 39 high-alpine species from the Alps and/or the Carpathians. From this data set, a subset of 12 species was selected that had a sufficient number of samples from both mountain ranges. Details of the sampling and AFLP-protocol can be found in Gugerli et al. (2008) and Alvarez et al. (2009). The greatest strength of this data set is that sampling was performed uniformly for all species: the area was divided into a regular grid with cell sizes of 20° longitude by 12° latitude (~20 by 22.5 km) and every second cell was extensively searched for the presence of all species. When a species was present, plant material was sampled from three individuals from a single location within the cell along a horizontal transect with 10 m distance between individuals. The total number of individuals per selected species ranged from 153 to 408 for the Alps and from 18 to 80 for the Carpathians (Table 1). Genotyping of the sampled individuals followed the standard protocol from Vos et al. (1995); bands were visualised either by electrophoresis on 8% polyacrylamide gels or on automatic capillary sequencers. The number of loci ranged from 61 for Geum reptans to 234 for Luzula alpinopilosa.

Table 1.

Overview and results of the Structure analyses of AFLP data from 12 Alpine species from the Alps and the Carpathians

Species	Abbreviation	# loci	# pops Alps	# pops Carp.	F ST	F SC	F CT	β AC (full data)	βAC (Wang, alpha = 1.0)	βAC (Wang, alpha = 0.5)	β AC (mean of subsamples)
Arabis alpina	Aal	151	129	19	0.72	0.67	0.13	0.46	0.44	0.44	0.69
Carex sempervirens	Cse	125	137	22	0.41	0.33	0.12	0.38	0.38	0.38	0.63
Dryas octopetala	Doc	101	124	15	0.37	0.22	0.19	0.64	0.65	0.65	0.92
Geum montanum	Gmo	93	122	19	0.51	0.35	0.25	0.58	0.59	0.59	0.86
Geum reptans	Gre	61	51	8	0.65	0.42	0.39	0.78	0.82	0.82	0.92
Hedysarum hedysaroides	Hhe	123	76	11	0.86	0.86	0.05	0.17	0.17	0.17	0.37
Hypochaeris uniflora	Hun	102	59	27	0.52	0.26	0.36	0.80	0.77	0.78	0.76
Juncus trifidus	Jtr	88	91	23	0.38	0.28	0.14	0.51	0.51	0.51	0.51
Loiseleuria procumbens	Lpr	121	90	13	0.40	0.31	0.13	0.09	0.07	0.07	0.74
Luzula alpinopilosa	Lal	234	82	19	0.45	0.32	0.19	0.76	0.74	0.74	0.69
Saxifraga stellaris	Sst	199	101	12	0.52	0.43	0.16	0.56	0.56	0.57	0.88
Sesleria caerulea	Sco	70	137	7	0.85	0.85	0.02	0.54	0.50	0.50	0.40

Given are the number of loci, the number of populations sampled in the two mountain ranges, the F-statistics from an AMOVA, and the difference in the Structure assignments between the Alps and the Carpathians (β_AC). The β_AC values are given for the analysis of the full data set, the analysis with the alternative ancestry model (with two initial values of the alpha parameter), and for the analysis where the data set was subsampled to balance the number of population samples in the two mountain ranges (average shown over 500 replicate subsamples)

The data used was a slightly expanded version of the version stored in the Dryad database at: 10.5061/dryad/s4q6s. The Dryad version was split into separate data sets for the Alps and the Carpathians and contained for each mountain range only those loci that were polymorphic within that range. Since the sample sizes were much smaller in the Carpathians than in the Alps, the result was that the data set for the Carpathians contained fewer loci than that of the Alps, even though originally, both data sets contained the same set of loci. Since loci that are polymorphic in one range but monomorphic in the other are informative about the differentiation between the two mountain ranges, the original data set was used.

structure analysis

For every species first a Structure (version 2.3.4, Pritchard et al. 2000) analysis was run for the full unbalanced data set, with all populations from the Alps and all populations from the Carpathians. The AFLP data were coded as suggested in the manual by including an extra row at the top that contained for every locus the name of the recessive allele (which was set to “0” for all loci). Since I was only interested in the distinction between the Alps and the Carpathians, which is expected to be the highest hierarchical level of clustering, I focused on the results when Structure was ran with K = 2. Structure was run with the admixture model, with uncorrelated allele frequencies, and without using the sampling locations as prior information. Changing those settings—correlated allele frequencies, no-admixture model, or using the Alps-Carpathian distinction as priors—did not notably change the results. The Monte Carlo Markov Chain was run for 100,000 steps, after a burnin period of 10,000 steps; trial runs suggested that this was enough to reach convergence. Ten replicate analyses were run for every data set, and the results of the run with the highest overall likelihood, according to the ln Pr(X|K) statistic, was used for interpretation.

To assess any bias resulting from sampling more populations in the Alps, I used both the ancestry model settings suggested by Wang (2017) and the subsampling strategy suggested by Puechmaille (2016). The ancestry model was changed by setting the parameter popalphas in the “extraparams” file to a value of 1; in the graphical user interface of Structure this corresponds to checking the box labelled “separate Alpha for each population” under the “Advanced…” ->“Configure” option of the “Ancestry Model” settings. Two values of the initial value of alpha were used—the default of 1.0, and 0.5–, by setting the alpha parameter in the extraparams file (corresponding to “Initial Alpha” in the GUI). Besides these parameters, Structure was run with the same settings as above.

Subsampling was done for every species separately by creating 500 subsampled data sets where the number of sampling locations in the Alps matched the number of locations in the Carpathians. For every subsampled data set all Carpathian populations were included plus a random sample (without replacement) of an equal number of populations from the Alps. For example, for Arabis alpina each subsample consisted of 38 populations: 19 from the Carpathians and 19 from the Alps, the latter randomly sampled from the 129 Alpine populations. Each subsampled data set was analysed in Structure at K = 2 with the same parameter settings as the full data set, using the default option to set the random number seed based on the system clock. Comparing the output of multiple Structure runs can be challenging, as the labelling of clusters is arbitrary in every run. There are algorithmic approaches for solving this (Jakobsson and Rosenberg 2007), but these require that the same individuals are present in every replicate, which is not the case with repeated subsampling. Here, I based the cluster alignment of the subsamples on the results of the analysis with the full data set: for every replicate analysis, I switched the labels in such a way that the sum of squared deviations between the assignments of the subsampled and full data were minimised. I then proceeded by calculating for every location the average assignment to the two clusters over all subsamples in which the location was included. These average assignments were then plotted on a map to provide a visual way to compare them to the assignments from the full, unbalanced, data set.

A simple test statistic was selected to quantify the degree to which Structure returned separate clusters for the Alps and the Carpathians. This test statistic (β_AC) was calculated by taking the absolute value of the variable coefficient (“slope”) of an Analysis of Variance with mountain range as the explanatory variable and the Structure q-values as the response variable (calculated using the lm() function in R). The β_AC-statistic is equivalent to calculating for every mountain range the mean proportion of individuals assigned to the first cluster, and then taking the absolute difference between the two mountain ranges. When the two mountain ranges harbour genetically completely separated clusters, the value of β_AC equals 1; when they contain exactly equal proportions of the two clusters, the value of β_AC equals zero.

For every species, the β_AC statistic was calculated on the Structure results for the full data set and for all 500 replicate subsamples. When the Structure results of the full data set are biased by the unbalanced sampling design, the value of β_AC is expected to be substantially lower for the full data set than for the subsampled data sets. This is not a formal statistical test and cannot be used to calculate p-values, but should nevertheless give a good indication of whether there is a difference between the analyses of the full and subsampled data sets. Note that the β_AC statistic is meant to compare the strength of clustering compared to a priori defined groups (here the two mountain ranges) and should not be confounded with other summary statistics such as ΔK (Evanno et al. 2005) and ln Pr(X|K) (Pritchard et al. 2000) which are meant to compare the clustering at different values of K. Furthermore, neither the coefficient of determination (r²) nor the p-values of the LM can be used to assess the strength of the association between the mountain ranges and the Structure results as the former is affected by unbalanced sampling and the latter by sample size.

For the data analysis, I mostly focused on K = 2 as I explicitly wanted to assess how well the Structure results match the a priori expectation of a differentiation between the Alps & the Carpathians. However, it is also of interest to investigate other values of K, and to assess which value of K has the strongest support in each species. To this end, Structure was run for every species with K values from 1 to 11, for the full data set and for 100 out of the 500 subsampled data sets. The same settings were used as detailed above, so with ten replicate runs per value of K. For every data set, I calculated the ΔK-statistic (Evanno et al. 2005) to select the value of K with the strongest support.

In addition to the Structure analysis, a hierarchical AMOVA (Excoffier et al. 1992) was performed for each species, with the populations clustered into two groups corresponding to the two mountain ranges. The main objective of this AMOVA was to estimate the F_CT-statistic, which quantifies the degree of population divergence between the Alps and the Carpathians. This was done for the full data set and for every subsampled data set, using the function poppr.amova() from the R-package poppr (Kamvar et al. 2014). The Structure and AMOVA analyses were performed and the results were parsed using custom scripts in R; these scripts can be found in Dryad package https://doi.org/10.5061/dryad.nh4366s.

Results

structure with unbalanced data sets

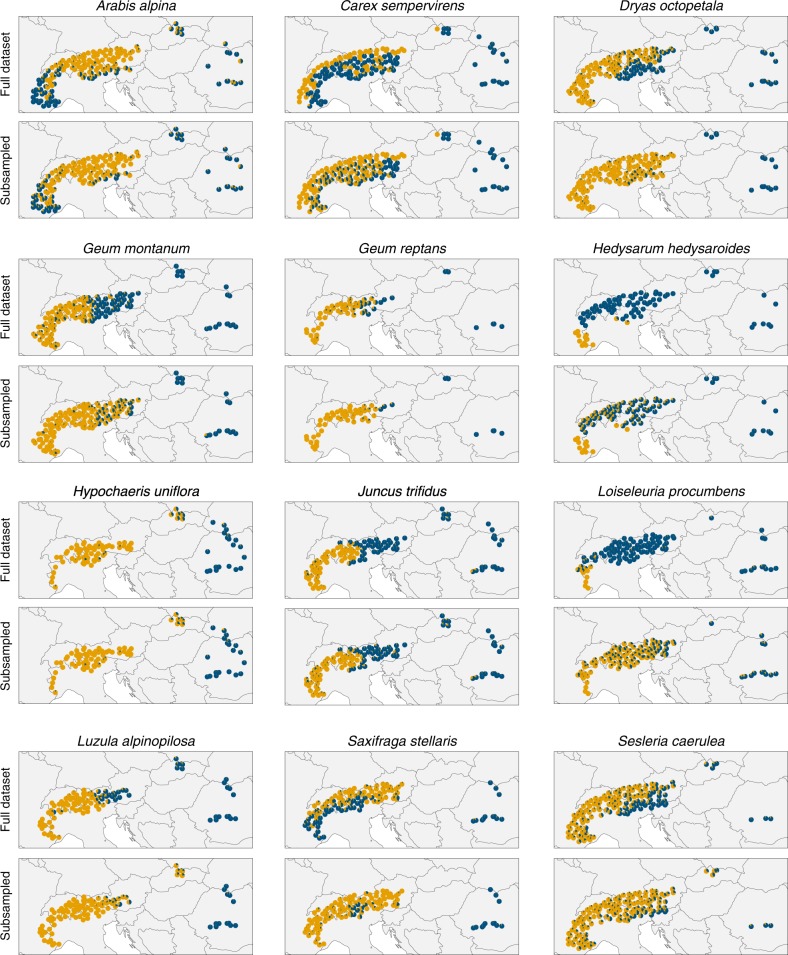
When Structure was run using the full unbalanced data sets, only a few species showed separate clusters for the Alps and the Carpathians (Fig. 2, top graph for every species). Generally, the populations from the Carpathians were all grouped in the same cluster (sometimes with a bit of admixture), but they shared this cluster with multiple populations from the Alps. It was not always the case that the Carpathian populations were grouped together with the populations from the Alps that are geographically the closest. This is most notable in Arabis alpina and Saxifraga stellaris where the Carpathian populations cluster together with the western-most populations from the Alps.

Fig. 2.

Maps showing the results of Structure analyses of AFLP data for 12 alpine species, for both the full unbalanced data sets and subsampled balanced data sets. Pies represent the assignments (q-values) to K = 2 clusters, averaged over the three individuals that were sampled at each location. The maps for the subsampled data sets were calculated by averaging the assignments over 500 replicate analyses per species

One species (Hypochaeris uniflora) showed a pattern that was distinctly different in this respect (Fig. 2): here all populations from the Alps formed a cluster together with the populations from the Western Carpathians, with the rest of the Carpathian populations forming the second cluster. Interestingly, this was also the species where the sampling was most balanced with 27 populations sampled in the Carpathians and 59 in the Alps; this represents a ratio of 1:2.2, whereas over all species this is on average 1:7.2. Hypochaeris uniflora also showed strong genetic differentiation between the two mountain ranges; it had the second-highest F_CT value at 0.36.

structure with alternative ancestry model

Changing the ancestry model to infer a separate value of alpha for each population did not notably change the results. Plotting the assignments yielded almost exactly the same patterns (Fig. S1) as the run with the default ancestry model; the value of the β_AC statistic was also close to the value obtained with the default setting (Table 1). Changing the initial value of alpha from its default value of 1.0 to a value of 0.5 also did not have any affect on the results (Fig. S1).

structure with subsampled balanced data sets

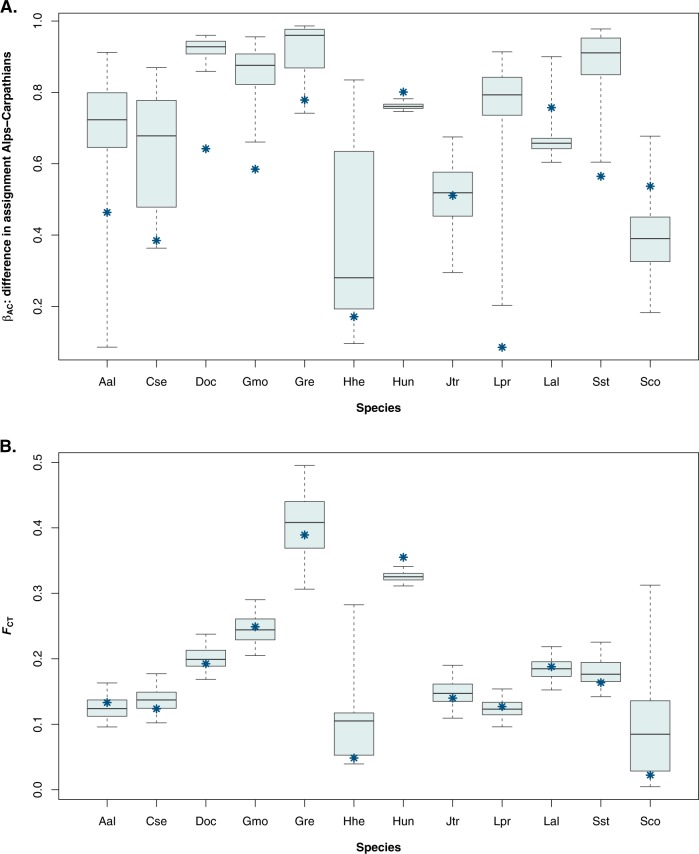
In nine out of the 12 species, subsampling to create balanced data sets increased the separation between the Alps and the Carpathians in the Structure results as quantified by the β_AC statistic (Fig. 3a). Four of those species stood out in that they showed near-complete separation between the two mountain ranges in the subsampled balanced data sets, but not in the full unbalanced data sets (Fig. 2): Dryas octopetala, Geum montanum, Loiseleuria procumbens, and Saxifraga stellaris. For these species, the β_AC statistic for the unbalanced data set was located in the lower 2.5% percentile of the distribution of β_AC scores for the subsampled data sets (Fig. 3a). These species therefore represent cases where the unbalanced sampling design has lead to a consequential difference in the results. However, for the other species the difference between the balanced and unbalanced data sets were only slight. There was also one species, Luzula alpinopilosa, where Structure returned less separation between the two mountain ranges when sampling was balanced. In the subsampled data sets, the populations from the Western Carpathians were clustered together with all populations from the Alps.

Fig. 3.

Divergence between populations from the Alps and from the Carpathians for 12 alpine species based on the results of Structure (a; β_AC statistic) and the results of an AMOVA (b; F_CT). Asterisks represent the results of the full data set with unbalanced sampling; boxplots represent the distribution of the results of the 500 replicate subsamples where sample sizes from the Alps matched those from the Carpathians (thick line gives the median; box gives 25% and 75% percentiles; whiskers give 2.5% and 97.5% percentiles)

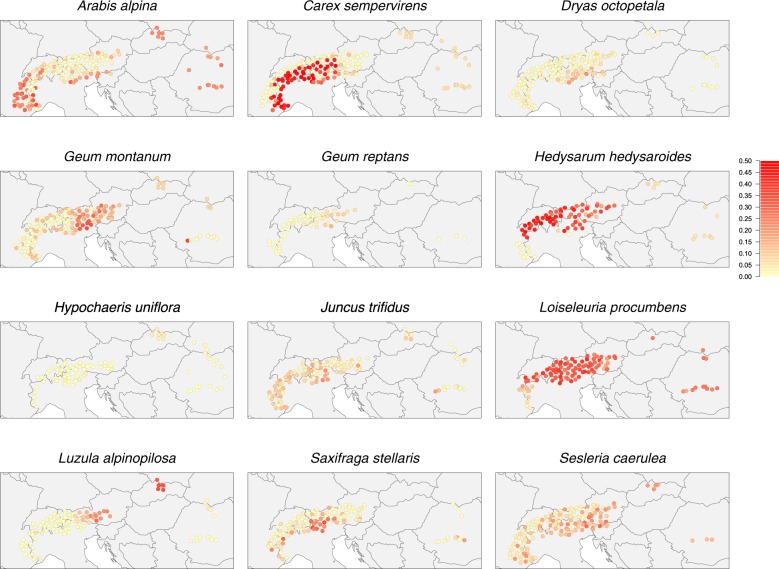
Within several species, there was a large degree of variation in the values of the β_AC scores among the replicate subsamples (Fig. 3a, showing the percentiles of the distribution of q-values across replicates). This variation was largest in Arabis alpina, where β_AC ranged from a minimum of 0.0042 (almost equal assignment to the two clusters in the Alps and in the Carpathians) to a maximum of 0.96 (clustering almost coincided completely with the two mountain ranges). Other species with notably large ranges in β_AC with the subsampled data include Hedysarum hedysaroides (0.092–0.94) and Loiseleuria procumbens (0.15–0.94). The variation in assignments can also be visualised by calculating the standard deviation across replicates for every population separately (Fig. 4). This shows for some species remarkable geographical patterns. In some species—e.g. Dryas octopetala—the standard deviation is uniformly low. In other species—e.g. Carex sempervirens—it was low in some parts of the sampling range but high in other parts. Finally, in some species—most notably Loiseleuria procumbens—it was high throughout almost the whole-sampling range.

Fig. 4.

Maps showing per sampling location the standard deviation in Structure assignment over 500 replicate subsamples, where the number of sampling locations in the Alps was reduced to match the number of locations in the Carpathians

In contrast with β_AC, the variation in F_CT across subsamples was generally much smaller (Fig. 3b; note difference in scale with 3a). For F_CT, the value for the full data set was also generally very close to the median of the values for the subsampled data sets; with the exception of Hypochaeris uniflora.

Other values of K

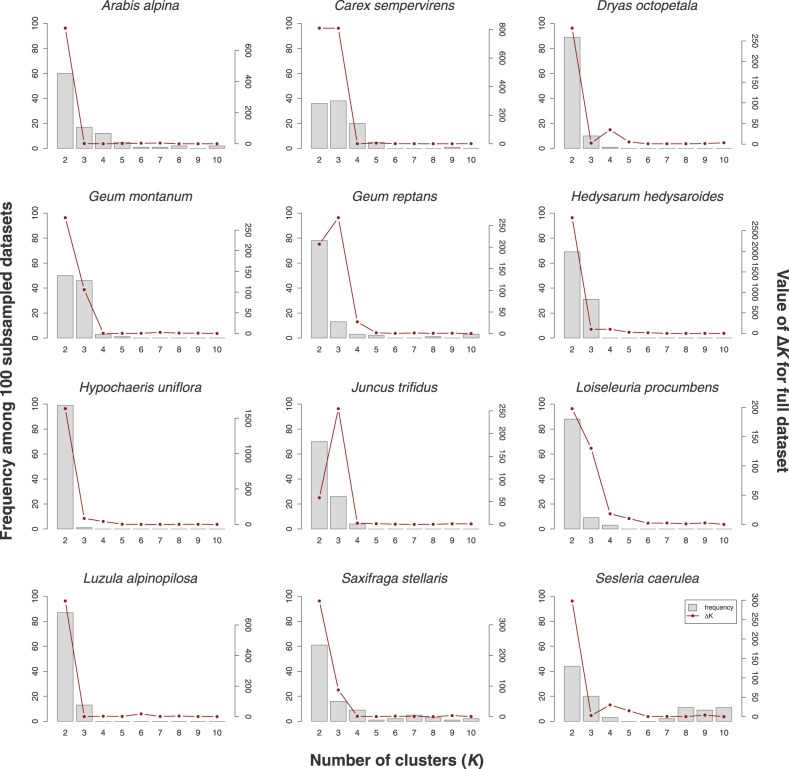
The ΔK-statistic indicated for ten out of the 12 species an optimal value of K = 2 clusters (lines in Fig. 5). The only exceptions were Geum reptans and Juncus trifidus, which both showed the highest value of ΔK at K = 3. In addition, Carex sempervirens showed a ΔK value for K = 3 that was only slightly lower than that for K = 2. Despite the general support for two clusters, most species showed distinct geographical patterns for the clusters at higher values of K (Fig. S2, showing up to K = 5), indicating that these may be well worth a biological explanation, despite not having the strongest support. The histograms in Fig. 5 show how frequently the different values of K were inferred to be the optimal value among 100 of the subsampled data sets. These histograms show that in most species, there was considerable variation in the optimal values of K among the subsampled data sets.

Fig. 5.

Inference of the optimal number of clusters according to the ΔK-statistic (Evanno et al. 2005). For each of the 12 species, the red line shows the value of ΔK for the full data set (secondary Y-axis); the histograms show the frequency at which each value of K was inferred to be the optimal value among 100 of the 500 subsampled data sets (primary Y-axis)

Discussion

The results of the analysis of genetic data from 12 alpine species confirm previous simulation results that Structure (Pritchard et al. 2000) may have a bias when population sampling is unbalanced (Kalinowski 2011; Neophytou 2013; Puechmaille 2016). In four out of the 12 species, the distinction between the Alps and the Carpathians increased drastically when the sample sizes from the Alps were reduced to match those from the Carpathians. Furthermore, there were several other species that showed a more moderate increase in the Alps-Carpathians distinction. Whereas these simulation studies used codominant markers, my analyses used dominant AFLP markers, indicating that the bias is present with both marker types. The underlying cause of this bias is very hard to tell, as determining that would require a very detailed and mechanistic study of how Structure works, which is something that cannot be done with the data used here. In any case, it is important for researchers to realise that the results from a Structure analysis should not be taken at face value, especially when the results do not match an a priori expectation.

The subsampling strategy suggested by Puechmaille (2016) proved very useful for uncovering the bias present in the Structure result of these four species. However, one drawback of this method is that it requires an a priori assumption of what the actual populations are and which populations are underrepresented in the sampling. Of course, if such information is available at the start of the experiment it would be preferable to try to avoid unbalanced sampling in the first place. In practice, however, this may prove to be difficult as access to sampling sites may be restricted or simply beyond the budget of the study. Nevertheless, in any case where Structure gives unexpected or biologically difficult-to-explain results the subsampling strategy should be employed.

When there is an a priori expectation of what the population structure looks like, a Structure analysis should always be accompanied by a direct test of the population structure, for example using an AMOVA (Excoffier et al. 1992). As could be expected, in the data set used here there was a significant positive correlation (Spearman’s r = 0.69; p = 0.013) between the F_CT statistic returned by an AMOVA and the β_AC statistic that quantified whether Structure returned separate clusters for the Alps and the Carpathians. Interestingly, the correlation coefficient was slightly higher (Spearman’s r = 0.72; p = 0.008) with the average value β_AC values from the subsampled Structure analyses then with the full data; suggesting that the subsampled Structure analyses matches the result of the AMOVA slightly better than the Structure results from the full data set.

The alternative ancestry model setting suggested by Wang (2017), where a separate admixture parameter (alpha) is inferred for each cluster, had very little effect on the results returned by Structure. In addition, modifying the alpha setting did not improve, or affect, the result of Structure with unbalanced sampling. The only notable effect was a slight change in the estimation of the number of clusters: Geum reptans, which under the default model had three clusters according to ΔK, showed an optimum of K = 2 under the alternative ancestry model (Fig. S3). The small affect of the alternative model is surprising since Wang found that this method was very effective with simulated genetic data with unbalanced sampling, and also with a real genetic data set from human populations. One explanation may be that Wang focused on data sets with multiple populations—so with higher values of K—whereas I focused almost exclusively on K = 2. Furthermore, the alternative ancestry model assumes simultaneous divergence of the clusters from a unique ancestral pool, which may simply not be applicable to the plant species studied here.

The subsampling analysis also revealed that in some species there is a lot of variation in Structure results, depending on which populations are included (Fig. 4). This large variation is clear from the large range in β_AC values across replicates, which in some species nearly ranged from the minimum value of zero to the maximum value of one. In addition, there were some strong patterns across the sampling range with some populations showing much higher variation in cluster assignment then others. In some species, most notably Geum montanum, the populations with a high variation in assignment corresponded to populations that showed admixture in the analysis of the full data set, nicely illustrating the uncertainty associated with the admixture process. However, this was not the case for all species. For example, in Hypochaeris uniflora the populations from the Western Carpathians are highly admixed in the analysis of the full data set, but show a low standard deviation in the assignment of the subsampled data sets. Conversely in Carex sempervirens (see also Gugerli et al. 2008), the populations from the Southwestern and South-Central Alps showed a high standard deviation in assignment across the subsampled replicates, but little admixture in the analysis of the full data set. In general, visualising the spatial variation in assignments across replicate subsamples may be insightful for pointing out areas where there may be uncertainty in the assignment. For this, the command line version of Structure can be used to automate the process.

In addition to variation in assignments across replicates, the subsampling analyses also showed a large amount of variation in the estimates of K. For the full data set, ten of the twelve species showed an optimal value of K = 2, according to the ΔK-statistic. This corresponds to the observation of Janes et al. (2017) that ΔK has a strong tendency towards K = 2, possibly as it tends to return the highest hierarchical level when there are multiple levels of clustering (Evanno et al. 2005). In contrast with this finding for the full data set, the subsampled data sets showed a range of K-estimates for the subsampled data sets for most species. For two species, Arabis alpina and Sesleria caerulea, the estimates even spanned the whole tested range from K = 2 to K = 10. This dependence on the exact sampling used for a Structure analysis reduces the reproducibility of the results (see also Gilbert et al. 2012): two studies on the same species but with slightly different sampling schemes (even when taken from the same part of the species’ range) may show strikingly different results.

Though four species showed a clear distinction between the Alps and the Carpathians after subsampling, the other eight species showed partial overlap of clusters between the two mountain ranges. This indicates that the demographic history of these species is more complex than a simple Alps-Carpathians dichotomy. The Structure clusters also show many different patterns across species, meaning that there are few generalities in the phylogeography of these species. Using partly the same data, Alvarez et al. (2009) already showed for the Alps that the phylogeographic patterns were strongly dependent on the soil requirements of the species, with species from calcareous soils showing different patterns than species from acidic soils. This was hypothesised to be the result of the different locations of pleistocene refugia containing the different soiltypes. In addition, Meirmans et al. (2011) showed how various ecological and life-history traits differently affected different aspects of the genetic population structure of 27 alpine species. Unfortunately, the IntraBioDiv data set (Gugerli et al. 2008; Taberlet et al. 2012) only has 12 species with sufficient samples in both the Alps and the Carpathians, so tests of the influence of the ecology and life-history of these species on the large-scale genetic patterns would have limited power with n = 12.

The complexity of the demographic history of these species is also apparent when looking at higher values of K (Fig. S2). For some species, shared Alp-Carpathian clusters are no longer present at higher values of K; this is most notably the case for the four species where subsampling drastically changed the Structure results. This reflects patterns that were present in the simulation results of Puechmaille (2016). Of course, unlike with simulated data, for real data sets as were used here, one can never be sure whether results from the subsampled or from the full data are closer to the true situation. Furthermore, though the data set is only a couple of years old, the number of loci used is relatively low compared to today’s standards. Since the simulations of Puechmaille (2016) and Wang (2017) used comparable numbers of loci, it remains to be seen whether substantially larger numbers of loci still lead to bias in the Structure results. Nevertheless, the point remains that for several species Structure gave consistently different results when subsampling than with the full data set. From a statistical point of view these results are jarring since one wishes different permutations of the same data to give more-or-less the same results. This is the basis of many time-tried statistical approaches such as bootstrapping, jackknifing, and separating data sets into a training set and a validation set. AMOVA’s F_CT statistic performed much better in this respect as the values for the subsampled data sets were generally nicely centred around the value for the full data sets.

One of the major limitations of Structure is that it does not take the coordinates of the sampling locations directly into account while clustering. Since in this study the a priori expectation of separation between the Alps and Carpathians is distinctly spatial, there is the possibility that the inclusion of the spatial data could counteract any of the effects of unbalanced sampling is this case. Multiple methods have been developed that explicitly use the spatial data in analyses of population structure (e.g., Dupanloup et al. 2002; Corander et al. 2003; François et al. 2006), and it would be interesting to test whether these methods show similarly biased results as Structure for this set of species. However, doing this requires a considerable extra amount of calculation and is therefore outside of the scope of the current study.

Recommendations

For one-third of the 12 included species, I found that subsampling the populations from the Alps drastically changed the results of the Structure analysis. This confirms previous results with simulated data sets (Puechmaille 2016; Wang 2017) that Structure has difficulties uncovering the true population structure when sampling is unbalanced. To detect such a bias, it is recommended to use the subsampling approach originally suggested by Puechmaille (2016) and expanded upon here. Unfortunately, this method is only applicable when there is an a priori expectation of the population structure that can be used as a basis for the subsampling. Based on the results presented here, using the alternative ancestry model suggested by Wang (2017) is not recommended, as it did not lead to a visible change in the results. This is unfortunate as the alternative ancestry model is much simpler to implement than the subsampling approach and can be applied without any a priori expectation. The results presented here do not mean that the use of Structure should be discarded: there is abundant evidence that Structure can return highly insightful results. However, it does mean that Structure does have its limitations and its results should never be taken at face value. Therefore, the most important recommendation is to always interpret the results with great scrutiny and in the light of available ecological, demographic, and life-history information about the species (Meirmans 2015). Visual inspection of the structure results, and comparison with the spurious patterns shown in the paper by Puechmaille (2016) may also be of great aid in this. In fact, it was such visual inspection of the Structure results for these 12 alpine species that eventually lead to the production of this paper.

Data accessibility

The data used are a slightly extended version of the data present in Dryad packages: 10.5061/dryad.f3rk4 and 10.5061/dryad.s4q6s. The used R-scripts, input files, results files, and associated data can be found in Dryad package: 10.5061/dryad.nh4366s.

Compliance with ethical standards

Conflict of interest

The author declares that he has no conflict of interest.

Electronic supplementary material

The online version of this article (10.1038/s41437-018-0124-8) contains supplementary material, which is available to authorized users.