Structure Learning Under Missing Data

Abstract

Causal discovery is the problem of learning the structure of a graphical causal model that approximates the true generating process that gave rise to observed data. In practical problems, including in causal discovery problems, missing data is a very common issue. In such cases, learning the true causal graph entails estimating the full data distribution, samples from which are not directly available. Attempting to instead apply existing structure learning algorithms to samples drawn from the observed data distribution, containing systematically missing entries, may well result in incorrect inferences due to selection bias.

In this paper we discuss adjustments that must be made to existing structure learning algorithms to properly account for missing data. We first give an algorithm for the simpler setting where the underlying graph is unknown, but the missing data model is known. We then discuss approaches to the much more difficult case where only the observed data is given with no other additional information on the missingness model known. We validate our approach by simulations, showing that it outperforms standard structure learning algorithms in all of these settings.

1. Introduction

Causal discovery is an unsupervised learning problem where the goal is to recover as much structure of a causal graphical model as possible from data generated from a process well-approximated by such a model. A large literature on this problem exists, with causal discovery algorithms falling into three general types. Constraint-based algorithms, such as the PC algorithm and the FCI algorithm (Spirtes et al., 2001), attempt to rule out graphs inconsistent with constraints found in the data, and return the set of remaining graphs. Score-based algorithms, such as GES (Chickering, 2002), rank models with a score that rewards model fit, and penalizes model complexity, and finds high ranking models using exhaustive or local search. Finally, parametric methods such as LiNGAM exploit parametric assumptions to infer causal structure (Shimizu et al., 2006).

Using causal discovery algorithms in applications entails dealing with practical data analysis issues, including missing data. If available data has systematically missing entries, using only fully observed rows (complete cases) forms a biased view of the true underlying data distribution, which can severely affect the performance of causal discovery algorithms, as we later show.

In this paper, we consider the problem of causal discovery under missing data. We make use of a statistical technique called Inverse Probability Weighting (IPW) – first developed in Horvitz and Thompson (1952) and then improved and generalized in Robins et al. (1994) and Scharfstein et al. (1999) – which weights datapoints by their sampling probability to alleviate biases due to imbalances in population classes. IPW has numerous applications when missing data is present, such as improvements to M-estimation (Wooldridge, 2007) and estimating biased population statistics (Vansteelandt et al., 2010), such as the population mean. Our methods also make use of IPW, but do so in a way that takes into account information pertaining to the data generation process and causes of missingness in order to improve causal structure learning.

Via simulations, we show that in settings where the underlying causal graph is unknown, but the missing data model is known, our adjustments based on IPW result in high quality inferences about the underlying graph. We also consider more complicated versions of the problem where neither the underlying graph nor the missing data model are known. In this setting, we give evidence that an algorithm that considers, by brute force, all possible sequences of reweightings of the observed data, will yield the sparsest output graph if it uses reweightings corresponding to the true missing data model. Moreover, this sparsest output will be closer to the true graph than outputs that use reweightings not licensed by the true model. The brute force reweighting algorithm, and the IPW adjusted algorithms can be viewed as using identification results for the full data distribution in missing data problems described in Mohan et al. (2013); Shpitser et al. (2015) to improve performance of structure learning when missing data is present.

For simplicity, we restrict our attention to learning directed acyclic graph (DAG) models using the PC algorithm (Spirtes et al., 2001), the standard constraint-based approach for DAGs. Although we do not pursue this here in the interests of space, our approach generalizes in a straightforward way to learning ancestral graphs (Richardson and Spirtes, 2002) using the FCI algorithm, and to learning nested Markov models (Richardson et al., 2017) using scoring approaches.

Our paper is organized as follows. Section 2 reviews notation and basic preliminaries, Section 3 discusses relevant material for causal discovery under missing data with our novel contributions beginning in subsection 3.3 onward, Section 4 contains our simulation results, and Section 5 contains our conclusions.

2. Notation and Preliminaries

We denote variables (or vertices in a graph) by capital letters V, and sets of variables (or vertices) by bold capital letters V. Values are denoted by lowercase letters v, and sets of values by bold lowercase letters v. For values v of V, and W ⊆ V, denote v_W to be a subset of values in v for variables in W. A directed acyclic graph (DAG) is a graph with directed edges with no directed cycles. Given a DAG $\mathcal{G}$ with a vertex set V, denote the sets of parents, children, ancestors, and descendants of V as as $\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(V)\equiv \{W|W\to V\text{exists}\text{in}\mathcal{G}\}$, $\mathrm{c}{\mathrm{h}}_{\mathcal{G}}(V)\equiv \{W|V\to W\text{exists}\text{in}\mathcal{G}\}$, defined as $\mathrm{a}{\mathrm{n}}_{\mathcal{G}}(V)\equiv \{W|W\to \dots \to V\text{exists}\text{in}\mathcal{G}\}$, and $\mathrm{d}{\mathrm{e}}_{\mathcal{G}}(V)\equiv \{W|V\to \dots \to W\text{exists}\text{in}\mathcal{G}\}$, respectively. By convention, for any $V,V\in \mathrm{a}{\mathrm{n}}_{\mathcal{G}}(V)\cap \mathrm{d}{\mathrm{e}}_{\mathcal{G}}(V)$. For any V, define ${\text{nd}}_{\mathcal{G}}(V)=\mathbf{V}\backslash \mathrm{d}{\mathrm{e}}_{\mathcal{G}}(V)$. Given A ⊆ V, define the induced subgraph ${\mathcal{G}}_{\mathbf{A}}$ to be a DAG containing vertices A and only edges in $\mathcal{G}$ between elements in A.

2.1. Statistical Models, Causal Models, and Causal Discovery of DAGs

A statistical model of a DAG $\mathcal{G}$ with a vertex set V is the set of all distributions p(V) of the form

$$p(\mathbf{V})=\prod _{V\in \mathbf{V}}p(V|\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(V)).$$ (1)

For disjoint subsets A,B,C of V, we say that A is independent of B given C in p(V), written as a shorthand as (A ⫫ B | C)_p if p(A | B ∪ C) = p(A | C).

Conditional independences in a distribution that factorizes as (1) can be read off by the d-separation criterion (Pearl, 1988). We use ${(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{\mathcal{G}}$ as a shorthand for A being d-separated from B given C in a DAG $\mathcal{G}$. In any distribution p(V) that factorizes as (1) according to a DAG $\mathcal{G}$, the following global Markov property holds. For any disjoint subsets A,B,C of V,

$${(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{\mathcal{G}}\text{implies}{(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{p(\mathbf{V})}.$$ (2)

The notion of causality we consider in this paper is based on the intervention operation do(a) (Pearl, 2009). This operation can be viewed as altering a system’s normal state from the outside, in the same way the value of a variable in a normally operating computer program can be altered artificially by a debugger. Given a distribution p(V), a subset A of V, and a value set a, the variation in V \ A after the operation do(a) is performed is called an interventional distribution and is denoted by p(V\A | do(a)). Just as statistical models can be viewed as sets of distributions defined by restrictions, causal models can be viewed as sets of interventional distributions defined by restrictions. In this paper, we define the weakest causal model of a DAG $\mathcal{G}$, which postulates that for any A ⊂ V, and any values a of A, $p(\mathbf{V}\backslash \mathbf{A}|\text{do}(\mathbf{a}))={\prod }_{V\in \mathbf{V}\backslash \mathbf{A}}p(V|{\mathbf{a}}_{{\text{pa}}_{\mathcal{G}}(V)\cap \mathbf{A}},\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(V)\backslash \mathbf{A})$.

The task of causal discovery algorithms is recovering $\mathcal{G}$ given a dataset corresponding to p(V) which factorizes according to $\mathcal{G}$. In fact, in general recovering the complete DAG $\mathcal{G}$ is impossible due to observational equivalence, where two distinct DAGs ${\mathcal{G}}_1$, ${\mathcal{G}}_2$ yield the same statistical model. Because of observational equivalence, a causal discovery algorithm in general cannot distinguish distinct but observationally equivalent DAGs. For this reason, the goal of causal discovery algorithms for DAGs is recovering the true DAG up to its equivalence class.

Regardless of the type of causal discovery algorithm used, assumptions are necessary for inferring causal structure from observational data. The standard assumption in the literature is that any conditional independence that holds in the data corresponds to some structural features of the underlying $\mathcal{G}$. This assumption is called faithfulness. A distribution p(V) is said to be faithful for a DAG $\mathcal{G}$ if for any disjoint subsets A,B,C of V,

$${(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{\mathcal{G}}\text{if}\text{and}\text{only}\text{if}{(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{p(\mathbf{V})}.$$ (3)

2.2. Missing Data and Missingness Graphs

In missing data problems, samples from the full data distribution p(V) are not available. Instead, a subset L ⊆ V is sometimes observed in the data and sometimes missing, while O ≡ V\L is always observed. For each L_i ∈ L there exists an observability indicator R_i, such that L_i is observed if R_i = 1, and L_i is missing if R_i = 0. We define a set of indicators as R ≡ {R_i | L_i ∈ L}. We represent this situation as follows. The variables in L are never observed themselves. However, for each L_i ∈ L there exists a proxy variable $L_i^{*}$ such that $L_i^{*}=L_i$ if R₁ = 1, and $L_i^{*}$ is equal to a special value “?” if R₁ = 0. Thus, the set of observed variables is Z ≡ O ∪L^* ∪ R.

Thus, the full data distribution p(V), and the observed data distribution p(Z) are related by the following identity:p(O,L*,R = 1) = p(V,R = 1) = p(R = 1 | V )p(V). This implies that if p(R = 1 | V) can be shown to be a function g_R|V(p(Z)) of the observed data distribution, then, via IPW, the full data distribution p(V) is identified as $p\left(\mathbf{O},{\mathbf{L}}^{*},\mathbf{R}=1\right)/g_{\mathbf{R}|\mathbf{V}}(p(\mathbf{Z}))$.

A number of missingness models exist which permit identification of the full data distribution. In this paper, we will use graphical models of missingness, introduced in Mohan et al. (2013). A missingness graph ${\mathcal{G}}^m$ is a directed acyclic graph with vertices corresponding to variables O,L,L^*,R with the property that for every $L_i^{*}\in {\mathbf{L}}^{*}$, $\mathrm{p}{\mathrm{a}}_{{\mathcal{G}}^m}\left(L_i^{*}\right)=\left\{L_i,R_i\right\}$, and for every R_i ∈ R, $\mathrm{c}{\mathrm{h}}_{\mathcal{G}}\left(R_i\right)\cap \mathbf{V}=\varnothing$.

Just as with regular DAGs, we associate distributions p(O,L,R,L*) with a missingness DAG ${\mathcal{G}}^m$ with a vertex set O ∪ L ∪ R ∪ L* if it factorizes as (1) with respect to ${\mathcal{G}}^m$:

$$p\left(\mathbf{O},\mathbf{L},\mathbf{R},{\mathbf{L}}^{*}\right)=\prod _{V\in \mathbf{O}\cup \mathbf{L}\cup \mathbf{R}\cup {\mathbf{L}}^{*}}p(V|\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(V)).$$ (4)

Missingness graphs can also be viewed as causal models, with elements in R being particularly useful to subject to the intervention operation, since

$$p\left(\mathbf{O},{\mathbf{L}}^{*}|\text{do}\left({\mathbf{1}}_{\mathbf{R}}\right)\right)=\frac{p\left(\mathbf{O},{\mathbf{L}}^{*},{\mathbf{1}}_{\mathbf{R}}\right)}{{\prod }_{R\in \mathbf{R}}p(1_R|{\mathbf{1}}_{\mathbf{R}\cap {\text{pa}}_{\mathcal{G}}(R)},\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(R)\backslash \mathbf{R})}=p(\mathbf{O},\mathbf{L})=p(\mathbf{V}).$$ (5)

See Mohan et al. (2013); Shpitser et al. (2015) for further details. Even though (5) is a version of the g-formula (in ratio form) for missing data problems, it cannot be applied directly to identify p(V), since elements of $\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(R)\backslash \mathbf{R}$ for some R may intersect L, and thus may not always be observed.

A general algorithm for identifying the full data distribution in missingness graphs was given in Shpitser et al. (2015). This algorithm adapted causal inference ideas for identifying interventional distributions of the form $p(Y|\text{do}(\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(Y)))$ involved in defining controlled direct effects for the task of identifying $p(R=1|\mathbf{R}\cap \mathrm{p}{\mathrm{a}}_{\mathcal{G}}(R)=1,\mathrm{p}{\mathrm{a}}_{\mathcal{G}}(R)\backslash \mathbf{R})$, and then applied (5).

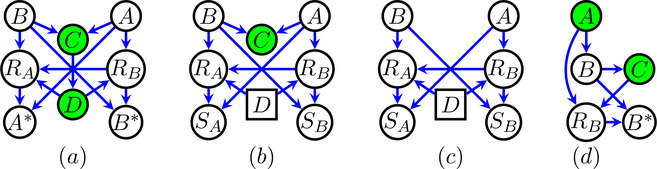
As an example, consider the graph in Fig. 1 (a), where O = {C,D}, L = {A,B}. The application of the algorithm in Shpitser et al. (2015), with certain subproblems arising in the operation of the algorithm shown in Fig. 1 (b),(c), yields $p(A,B,C,D)=p\left(A^{*},B^{*},C,D,1_{R_A},1_{R_B}\right)/\left\{q\left(1_{R_A}|B,D,1_{R_B}\right)\cdot q\left(1_{R_B}|A,D\right)\right\}$, where

$$q(1_{R_B}|A,D)=\frac{{\tilde{p}}_D(A^{*}|1_{R_A},1_{R_B})\tilde{p}(1_{R_B})}{{\sum }_{R_B}{\tilde{p}}_D(A^{*}|1_{R_A},1_{R_B})\tilde{p}(1_{R_B})};q(1_{R_A}|B,D,1_{R_B})={\tilde{p}}_D(1_{R_A}|1_{R_B},B^{*})$$ (6)

and ${\tilde{p}}_D\left(R_A,R_B,A^{*},B^{*}\right)={\sum }_{C}p\left(A^{*},B^{*},R_A,R_B|C,D\right)p(C).$

Figure 1:

Vertices in green correspond to variables that are always observed. (a) An example where the full data distribution p(A,B,C,D) is identifiable from the observed data distribution p(R_A,R_B,A^∗,B^∗,C,D). (b),(c) Graphs corresponding to subproblems considered considered by the identification algorithm. (d) A simple missingness graph, where causal discovery from the observed data distribution leads to recovering an erroneous graph.

3. Causal Discovery Under Missing Data

Having given the necessary preliminaries, we now consider the problem of causal discovery from missing data. We assume the observed data was generated from the observed data distribution p(Z) that was generated from a true missingness graph ${\mathcal{G}}^m$ such that the distribution p(O,L,L^*,R) factorizes according to ${\mathcal{G}}^m$ as in (4)

A simple approach to causal discovery might be to ignore missing data entirely, and use the observed cases in the data as input to a causal discovery algorithm. The problem with this approach is illustrated by Fig. 1 (d), where A and C are always observed, and B is potentially missing, based on R_B which is a function of A and C. Here, the true DAG has a single conditional independence (A ⫫ C | B), which would be easily recoverable if the algorithm were given samples from the full data distribution p(A,B,C). However, in the context of missing data, samples from this distribution are not available. If only samples from p(A,B^*,C,R_B) are available, and we use fully observed data rows, then the algorithm only sees samples from $p\left(A,B^{*},C|1_{R_B}\right)$. This introduces a form of selection bias known as Berkson’s bias in the statistics literature or “explaining away” in the artificial intelligence literature. In this particular case, the result is that A is no longer independent of C given B if we also insist on conditioning on R_B, as easily verified by d-separation in Fig. 1 (d). This version of Berkson’s bias misleads the PC algorithm into returning the complete graph rather than the equivalence class corresponding to A → B → C.¹

A more sophisticated alternative would attempt to approximate the full data distribution first, before applying causal discovery algorithms. The difficulty is that generally in order to identify the full data distribution, we need to know the missingness graph. However, in causal discovery settings the true graph is unknown. In addition, in order to recover the true graph in missing data contexts, we need to introduce an extension of the faithfulness assumption. Before doing so, we introduce necessary conditional graphs, and kernels, which correspond to intermediate worlds after IPW is applied, and the fixing operation, which corresponds to a single application of IPW.

3.1. Conditional Acyclic Directed Mixed Graphs, Kernels and Fixing

A conditional acyclic directed mixed graph (CADMG) $\mathcal{G}(\mathbf{V},\mathbf{W})$ is a graph containing directed (→) and bidirected (↔) edges with no directed cycles such that no edge with an arrowhead into W exists (vertices W are drawn as squares, and meant to denote constants, while V are drawn as circles and meant to denote random variables). A CADMG may contain both a → and ↔ edge between the same pair of vertices. Given a CADMG $\mathcal{G}(\mathbf{V},\mathbf{W})$, and a subset O ⊆ V, define the latent projection (Pearl, 2009) onto O, as a CADMG $\mathcal{G}(\mathbf{O},\mathbf{W})$ with a vertex set O,W, all edges in 𝒢 between elements in O ∪ W, and the following additional sets of edges. First, a directed edge between V₁,V₂ ∈ O∪W is added if there exists a directed path from V₁ to V₂ with all intermediate elements not in O ∪ W. Second, a bidirected edge between V₁, V₂ ∈ O ∪ W is added if there exists a path from V₁ ← ◦…◦ → V₂ with no collider triples, with all intermediate elements not in O ∪ W. The latent projection can be viewed as a graphical analogue of marginalization in distributions, hence the suggestive notation. Note that a latent projection is not a simple graph, e.g. may include both → and ↔ connecting the same pair of vertices.

Given a CADMG $\mathcal{G}(\mathbf{V},\mathbf{W})$, we say a vertex V ∈ V is fixable in $\mathcal{G}$ if no Z ∈ V \ {V } exists such that V ∈ $\mathrm{a}{\mathrm{n}}_{\mathcal{G}}(Z)$, and V ↔ ∘ ↔ ... ↔ ∘ ↔ Z exists in $\mathcal{G}$. For any vertex V fixable in $\mathcal{G}(\mathbf{V},\mathbf{W})$, define a fixing operator ${\varphi }_V(\mathcal{G}(\mathbf{V},\mathbf{W}))$ that produces a new graph ${\mathcal{G}}^{*}$ that removes all arrows with arrowheads into V, and moves V from V to W in ${\mathcal{G}}^{*}$. For {V₁, … V_k} ⊆ V, a sequence 〈V₁, … V_k〉is fixable in $\mathcal{G}$, if V₁ is fixable in $\mathcal{G}$, V₂ is fixable in ${\varphi }_{V_1}(\mathcal{G})$, etc. For such a fixable sequence, define ${\varphi }_{\langle V_1,\dots V_k\rangle }(\mathcal{G})$ as the generalization of 𝜙_V defined via function composition.

Define a kernel q(V | W) as any mapping from values of W to a normalized density over V. Define marginalization and condition in kernels in the natural way. Given a kernel q(V | W) and a CADMG $\mathcal{G}(\mathbf{V},\mathbf{W})$, and V fixable in $\mathcal{G}$, define a fixing operator ${\varphi }_V(q;\mathcal{G})$ that produces a new object $q*(\mathbf{V}\backslash \{V\}|\mathbf{W}\cup \left\{V\right\})\equiv q(\mathbf{V}|\mathbf{W})/q(V|\mathrm{n}{\mathrm{d}}_{\mathcal{G}}(V)\cup \mathbf{W})$. It is not difficult to show this object is always a kernel. For a fixable sequence above, define ${\varphi }_{\langle V_1,\dots V_k\rangle }(q;\mathcal{G})$ as the natural generalization of ${\varphi }_V(q;\mathcal{G})$ defined via function composition.

Given a kernel q(V | W), and any A ⊆ V, B,C disjoint subsets of V∪W such that W ⊆ B∪C, we say (A ⫫ B | C)_q if q(A | B,C) is only a function of A∪C. Given a CADMG $\mathcal{G}(\mathbf{V},\mathbf{W})$, and a kernel q(V | W), we say that q is Markov relative $\mathcal{G}$ if for any A ⊆ V, B,C disjoint subsets of V ∪ W such that W ⊆ B ∪ C, if A is m-separated from B given C in $\mathcal{G}$ then (A ⫫ B | C)_q, where m-separation is a natural generalization of d-separation (Richardson and Spirtes, 2002).

If a CADMG/kernel pair is obtained by applying ϕ to a DAG $\mathcal{G}(\mathbf{V})$ and a distribution p(V) that factories according to $\mathcal{G}$, then the kernel is Markov relative to the CADMG (Richardson et al., 2017). An important result in that reference is that any two fixable sequences in $\mathcal{G}$ on the same set Z ⊆ V applied to a CADMG $\mathcal{G}$ and kernel q Markov relative to $\mathcal{G}$, if they are ultimate derived from hidden variable DAGs and their distributions in an appropriate way, lead to the same CADMG and kernel (Richardson et al., 2017). For this reason, we can redefine fixing operators to apply to sets rather than sequences: ${\varphi }_{\mathbf{Z}}(\mathcal{G})$ and ${\varphi }_{\mathbf{Z}}(q;\mathcal{G})$. A causal way to think about a CADMG $\mathcal{G}(\mathbf{V},\mathbf{W})$ and kernel q(V | W) obtained from p(V ∪ W) via ϕ_W is they represent an interventional distribution p(V | do(w)) (identified from p(V) in a particular way represented by ϕ_W), and a graph representing conditional independences in this distribution.

3.2. Faithfulness in Missing Data Causal Discovery Problems

The standard faithfulness assumption (3) implies all conditional independences are “structural.” For our problem we also need to consider generalized independence constraints, sometimes known as “Verma constraints” (Verma and Pearl, 1990). A simple example of a Verma constraint occurs in Fig. 1 (a). Here, in order to apply missing at random (MAR) approaches, it would be desirable to have R_A be conditionally independent of A given the set of observed variables {C,D} or its subset. However, it’s easy to verify by d-separation in Fig. 1 (a) that this is not true for any such set. However, it is possible to show that in any distribution p(A,B,C,D,R_A,R_B,A*,B*) that factorizes as in Fig. 1 (a), R_A is independent of A conditionally on D,R_B in the kernel ϕ_D(p(A*,B*,C,D,R_A,R_B); ${\mathcal{G}}^m$ (A*,B*,C,D,R_A,R_B)). In the case of Fig. 1 (a), it is these types of generalized independences that result in identifiability of the full data distribution. The type of faithfulness assumption we need states, informally, that generalized conditional independences themselves are also all structural.

Definition 1 (weak generalized faithfulness)

Given a missingness graph ${\mathcal{G}}^m$ with the observed variables Z ≡ O∪L^*∪R, and the corresponding distribution p(R,V), p is weakly faithful to ${\mathcal{G}}^m$ if for any set W ⊆ Z fixable in ${\mathcal{G}}^m(\mathbf{Z})$, and any A ⊆ Z\W, and B,C disjoint subsets of Z\(W∪A) such that W ⊆ B ∪ C, ${(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{{\varphi }_{\mathbf{W}}\left({\mathcal{G}}^m(\mathbf{Z})\right)}$ if and only if ${(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{{\varphi }_{\mathbf{W}}\left(p(\mathbf{Z});{\mathcal{G}}^m(\mathbf{Z})\right)}$.

This assumption is stated on fixing sequences applied to the latent projection onto observed variables Z in a missingness graph ${\mathcal{G}}^m$. All variables involved in fixing operations are also always observed.

3.3. Causal Discovery with Graph-Agnostic Identifiable Models

Aside from generalized faithfulness described above, the simplest additional assumption we can make to make causal inference in the presence of missing data possible is that sufficient information on p(R | V) is available such that (i) p(V) is identified by some function f(p(Z)), and (ii) this function is not sensitive to the structure of ${\mathcal{G}}_{\mathbf{V}}^m$. We call this type of missingness model a graphagnostic identifiable model. A simple example of such a model assumes that for every R_i ∈ R, $\mathrm{c}{\mathrm{h}}_{{\mathcal{G}}^m}\left(R_i\right)=L_i^{*}$, and $\mathrm{p}{\mathrm{a}}_{{\mathcal{G}}^m}\left(R_i\right)\subseteq \mathbf{V}\backslash \left\{L_i\right\}$. In this model, results in Mohan et al. (2013) show that the full data distribution p(V) is identified via IPW as $p\left(\mathbf{O},{\mathbf{L}}^{*},{\mathbf{1}}_{\mathbf{R}}\right)/\{{\prod }_{R_i\in \mathbf{R}}p(1_{R_i}|\mathbf{O},{\mathbf{L}}^{*}\backslash \left\{L_i^{*}\right\},{\mathbf{1}}_{\mathbf{R}\backslash \left\{R_i\right\}})\}$, regardless of what the structure of the edges among V vertices is.

An alternative commonly used missingness model is the sequential monotone missing at random (MAR) model. In this model, variables in V are assumed to be under a total ordering ≺, which induces a total ordering on elements of R, where R_i ≺ R_j if L_i ≺ L_j. For every L_i, define pre_≺(L_i) to be the set of variables in V earlier in the ordering than L_i. Similarly, for every R_i, define pre_≺(R_i) to be the set of variables in R earlier in the ordering than R_i. Monotonicity here means once a variable L_i is missing, then for every L_j such that L_i ≺ L_j, L_j is also missing. We further assume every L_i is independent of R_i = 1, given pre_≺(R_i) ∪ pre_≺(L_i). Under these assumptions, it is well known that regardless of graph structure on V, the full data distribution p(V) is identified as $p\left(\mathbf{O},\mathbf{L}*,\mathbf{R}=1\right)/{\prod }_{R_i\in \mathbf{R}}p\left(R_i=1|\mathrm{p}\mathrm{r}{\mathrm{e}}_{\prec }\left(R_i\right)=1,\left\{L_j^{*}|L_j\prec L_i\right\}\right)$.

Causal discovery in graph-agnostic identifiable missingness models can be addressed by the following modification of the PC algorithm. First, use the structure of the (known) missingness model to obtain an estimator g(D) for p(1_R | V), using an identified functional f(p(Z)) = p(1_R | V). Then, replaced ordinary conditional independence tests in the PC algorithm with IPW-weighted tests, and apply the resulting modified PC algorithm to the observed data. As pseudo-code, we have:

Algorithm 1.

CBR-PC algorithm

Input: Observed dataset D with corresponding variable sets V,O,L,L*, and R; a known estimator g(D) of p(1R | V).

Output: An equivalence class of DAGs over V.

procedure CBR-PC

Construct an IPW-weighted conditional independence algorithm tester(A,B,C; D) for any ${(\mathbf{A}⫫\mathbf{B}|\mathbf{C})}_{p(\mathbf{Z})/p\left(1_{\mathbf{R}}|\mathbf{V}\right)}$ using D and g(D).

return PC-alg(D,tester(A,B,C;D)).

end procedure

⊳ PC-alg denotes the PC algorithm from Spirtes et al. (2001), taking as input a dataset D and an algorithm tester(.) for performing any conditional independence hypothesis test (A ⫫ B | C)p using a dataset D drawn from p.

For example, the finite sample version of the PC algorithm which uses hypothesis tests based on the correlation matrix can be augmented by instead computing an appropriately weighted correlation matrix, while versions which use non-parametric independence tests may augment each test with the appropriate weights. For simplicity, in our simulations we restrict our attention to using weighted correlation matrices. We call this version of PC the correlation-based reweighted PC algorithm (CBR-PC). The following result is straightforward, and generalizes to other versions of the PC algorithm that use IPW with weights given by f(p(Z)) = p(1_R | V).

Theorem 1 The CBR-PC algorithm is asymptotically consistent.

Proof: This follows from asymptotic consistency of the ordinary PC algorithm (Spirtes et al., 2001), and the consistency of IPW estimators for any functional of the full data law, if p(R = 1 | V) is identified (Tsiatis, 2006).

3.4. Causal Discovery with Unknown Identifiable Missingness Models

A much more difficult setting assumes a true underlying missingness graph ${\mathcal{G}}^m$ where p(V) is identifiable, but where no part of ${\mathcal{G}}^m$ is known, including the parts related to the missingness model. There are a number of difficulties in this setting. First, the appropriate (strong) version of weak generalized faithfulness needed in this setting cannot yet be stated precisely. This is because without knowing ${\mathcal{G}}^m$, we cannot be sure attempted divisions by conditional distributions are valid and interpretable causally as was the case with the operator ϕ. In such cases it is an open question whether graphs exist which properly capture independence structure of kernels obtained by such “invalid” operations, and if so what such graphs might look like. Without a characterization of these graphs, it is impossible to state a one to one correspondence between some notion of path separation in such graphs and independence in corresponding kernels formed by “invalid” operations. Second, the space of possible sequences of “invalid” fixing operations is very large. It is not currently known how to minimize the number of hypothesis tests performed, in the way the PC algorithm does, when fixing operations are involved. Third, given that an independence after fixing was found, it is not currently known what the full implications of this are for graphical structure.

Nevertheless, a simple algorithm for learning the graph of an unknown identifiable missingness model, based on conjecture by James M. Robins, is as follows. Given a set of variables, try all possible fixing sequences, apply the PC to the resulting (possibly “non-causal”) kernel, and output the pattern with the fewest edges. As shown in the following section, the sparsest graph found in this way appears to be closest to the true graph, and corresponds to a sequence fixable under the true graph. However, the general validity of this type of algorithm is an open problem due to issues we discuss above.

We now outline in more detail how to implement this algorithm, conjectured to be valid for finding correct structure up to equivalence in unknown identifiable missingness models. Recall that this algorithm applies PC to a kernel obtained by an arbitrary (and not necessarily fixable relative to the true graph) fixing sequence from the observed data distribution p(Z). Since we only have observed data as an empirical approximation of p(Z), we proceed via an iterative resampling scheme suggested by Robins. Assume we are interested in a fixing sequence where we divide by 〈p(H₁ | T₁), … ,p(H_k | T_k)〉. We first learn a model of p(H₁ | T₁;α₁) via maximum likelihood (in our experiments we used a random forest method, but we believe any flexible strategy would be appropriate). Then, we use a weighted bootstrap approach with IPW to select, from the original dataset $\mathcal{D}$ of size n, another dataset ${\mathcal{D}}_1$ of size n. Specifically, we select a row in $\mathcal{D}$ with replacement, such that each row i has a selection probability $\frac{1/p\left(H_1^i|{\mathbf{T}}_1^i;{\widehat{\alpha }}_1\right)}{{\sum }_{j=1}^{n}1/p\left(H_1^j|{\mathbf{T}}_1^j;{\widehat{\alpha }}_1\right)}$. After obtaining ${\mathcal{D}}_1$, we then fit a model p(H₂ | T₂; α₂) by maximum likelihood now using ${\mathcal{D}}_1$, and use this model to select a dataset ${\mathcal{D}}_2$ of size n from ${\mathcal{D}}_1$, where rows are selected with replacement with probability similar to above, except the learned H₁ model is replaced with the learned H₂ model. We iteratively proceed in this way until we obtain ${\mathcal{D}}_k$. In addition, if a fixing sequence p(H_j | T_j) is such that T_j contains all variables, then we ignore the operation (as it corresponds to a marginalization and can be safely skipped without affecting subsequent hypothesis tests). This dataset is used as an empirical approximation of the kernel resulting from applying the above fixing sequence to p(Z).

As an example, of the scheme, assume we are interested in applying (6) to p(Z) given by variables in Fig. 1 (a). For $q\left(1_{R_A}|B,D,1_{R_B}\right)$, we first learn a model p(D | C), then use weighted bootstrap with weights 1/p(D | C) to generate a dataset from which a model for $q\left(1_{R_A}|B,D,1_{R_B}\right)$ is learned (skipping the step of fixing C, since it corresponds to a marginalization). Similarly, for $q\left(1_{R_B}|A,D\right)$ we use weighted bootstrap and IPW with weights 1/p(D | C) to generate a dataset ${\mathcal{D}}_1$, which is used to learn a model for p(R_A | D,R_B). We then use weighted bootstrap and IPW on ${\mathcal{D}}_1$ again, with weights 1/p(R_A | D,R_B), to generate a dataset ${\mathcal{D}}_2$, which is used to learn a model for $q\left(1_{R_B}|A,D\right)$. Finally, both q weights are used to reweigh observed cases, with the resulting weighted correlation matrix given as input to the PC algorithm.

The weighted bootstrap scheme can be viewed as mimicking the fixing operations of the identification algorithm for needed weights for R in Fig. 1 (a), but ignoring all fixing operations that correspond to marginalization. This is due to the fact that marginalizations do not affect independence statements, and all fixing operations can be reordered so marginalizations are computed last, see also Theorem 7 in Shpitser et al. (2009).

4. Simulations

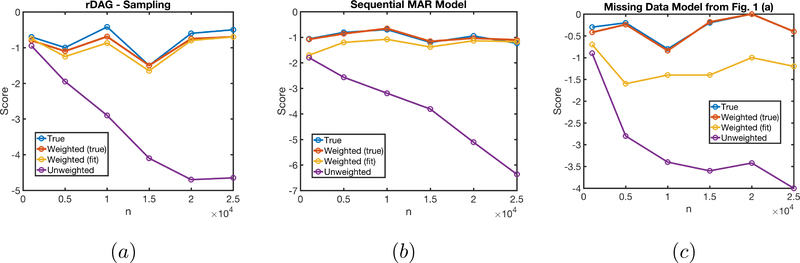
To illustrate the advantages of the CBR-PC algorithm, we focused on cases where the regular PC algorithm performs well given the full data distribution but performs poorly given observed cases only. The CBR-PC algorithm completely reverses this performance gap, learning causal structure given samples from the observed data distribution nearly as well as the the PC algorithm that is given access to samples from the full data distribution.

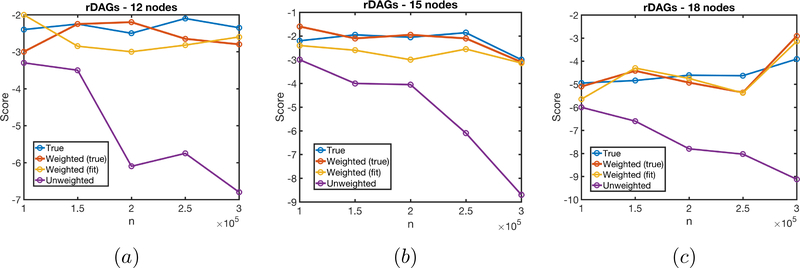
We generated random sparse DAGs of size 9, 12, 15 and 18 of degree 2. The DAGs were parameterized as multivariate normals via the standard parameterization given by the LDL decomposition of the precision matrix (Lauritzen, 1996). For all DAGs, we considered the model with disconnected R variables. For DAGs of size 9, we also considered the sequential monotone MAR model. In all cases, we generated $p(R|\mathrm{p}{\mathrm{a}}_{{\mathcal{G}}^m}(R))$ using a noisy-or model, in order to generate strong Berkson’s bias due to only observing cases where R = 1. For all cases, we generated 10 trials for 20 random DAGs, at sample sizes ranging from 1000 to 30000.

We note that the CBR-PC performance is not significantly affected by percentage of missingness ranging up to around 90%, in which case the small sample size of observed cases starts to negatively affect performance. This in contrast to the original PC algorithm, which performs progressively worse as percentage of missingness increases. For all simulations, we set the percentage of missing rows at around 60% ± 8 for each trial in order to clearly illustrate the negative effects of missing data the original PC algorithm may plausibly face in practical scenarios.

We compared four versions of the PC algorithm. The algorithm that used the true full data distribution, the algorithm that used the observed cases only, and the algorthms that reweighted observed cases using either the true model p(R | V), or the model p(R | V) learned using the random forest method described in Chipman et al. (2010). We scored the output of the algorithms by subtracting one point for every skeleton edge or collider that was different between the output, and the true equivalence class, with the best score corresponding to recovering the true equivalence class thus being 0.

The results are shown in Fig. 2 (a), (b), and Fig. 3 (a), (b) (c),, and show that CBR-PC is generally doing as well as the PC algorithm running on the full data distribution, and the PC algorithm using the observed data distribution doing poorly in general, and more poorly with larger sample sizes. We believe this is due to the fact that some false edges introduced due to Berkson’s bias are “weak,” and thus cannot be detected at low sample sizes.

Figure 2:

A comparison of four versions of the PC algorithm for learning sparse DAGs from observations with missing data. (a) Under the “disconnected R” model with random DAGs (b) Under the sequential MAR model with random DAGs. (c) For the model in Fig. 1 (a). Here the algorithm that learned p(R | V) used weighted bootstrap for reweighting.

Figure 3:

Additional simulations of the “disconnected R” model with random DAGs. (a) 12-node graphs (b) 15-node graphs (c) 18-node graphs

Second, we illustrate how the harder version of the problem, where no information about ${\mathcal{G}}^m$ is known might be approached by learning the graph in Fig. 1 (a). First, we verified that even in cases where p(R | V) is identified via a complex function of the observed data, such (6) for Fig. 1 (a), learning this function correctly and applying CBR-PC to the observed data yields performance that is not much worse than that obtained by running PC on the true data. See Fig. 2 (c) for the summary of our experiments.

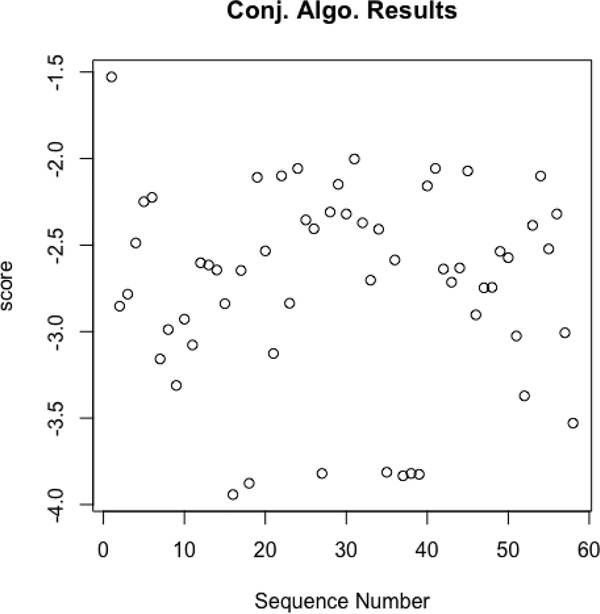
Lastly, we approach the even harder version of the problem where no causal structure is known at all. We applied the pseudo-algorithm outlined in section 3.4 to data generated from the graph in Fig. 1 (a), by trying a random subset of 60 reweighting sequences, including the true sequence licensed by the model. The scores of the resulting graphs are shown in Fig. 4, with the score for the true sequence shown first. It’s clear that given the sequences we tried, the average score of the true sequence is better than all others. We emphasize that while the algorithm we suggest has promising performance in our experiments, it’s formal validity for learning the true structure of a DAG under unknown identifiable missingness models remains an open problem.

Figure 4:

The weighted bootstrap approach applied to a number of fixing sequences on a single dataset size of 10000. The left-most score corresponds to the correct fixing sequence.

5. Conclusions

In this paper we consider the problem of causal discovery from datasets with missing entries. In short, the CBR-PC algorithm outperforms standard structure learning algorithms significantly in all scenarios considered, properly accounting for missing data. Lastly, in addition to considering the problem of causal discovery in missing data problems, we believe this paper is the first time constraint-based causal discovery procedures were adapted to take advantage of generalized independence (or Verma) constraints (Verma and Pearl, 1990; Richardson et al., 2017).