Structural similarity networks predict clinical outcome in early-phase psychosis

Abstract

Despite recent advances, there is still a major need for prediction of treatment success in schizophrenia, a condition long considered a disorder of dysconnectivity in the brain. Graph theory provides a means to characterize the connectivity in both healthy and abnormal brains. We calculated structural similarity networks in each participant and hypothesized that the “hubness”, i.e., the number of edges connecting a node to the rest of the network, would be associated with clinical outcome. This prospective controlled study took place at an academic research center and included 82 early-phase psychosis patients (23 females; mean age [SD] = 21.6 [5.5] years) and 58 healthy controls. Medications were administered in a double-blind randomized manner, and patients were scanned at baseline prior to treatment with second-generation antipsychotics. Symptoms were assessed with the Brief Psychiatric Rating Scale at baseline and over the course of 12 weeks. Nodal degree of structural similarity networks was computed for each subject and entered as a predictor of individual treatment response into a partial least squares (PLS) regression. The model fit was significant in a permutation test with 1000 permutations (P = 0.006), and the first two PLS regression components explained 29% (95% CI: 27; 30) of the variance in treatment response after cross-validation. Nodes loading strongly on the first PLS component were primarily located in the orbito- and prefrontal cortex, whereas nodes loading strongly on the second PLS component were primarily located in the superior temporal, precentral, and middle cingulate cortex. These data suggest a link between brain network morphology and clinical outcome in early-phase psychosis.

Introduction

Finding predictors of response to antipsychotic drug treatment is of critical importance to improving outcomes for psychotic disorders [1, 2]. A priori identification of patients who are not likely to respond to a specific treatment strategy could reduce the number and length of ineffective treatment trials. Moreover, understanding the biological underpinnings of effective treatments may lead to the detection of malleable central nervous system targets for the development of new treatment strategies—a current imperative because of the long-standing dearth of novel antipsychotic treatments.

Although parallel group trials cannot determine treatment response for individual patients in a definite manner, we have previously applied rigorous a priori criteria to distinguish likely responders from non-responders [3, 4] and have shown that functional striatal connectivity was higher in non-responders compared with responders [5] and normalized with antipsychotic treatment [6].

The fact that we found that brain connectivity was related to treatment outcome is not surprising. Schizophrenia has long been considered a disorder involving dysconnectivity in the human brain [7, 8], and graph theory has provided means to characterize the connectivity in the healthy and abnormal human brain [9]. Briefly, graph theory describes brain networks abstractly as a set of nodes and edges, and quantifies their patterns of connectivity [7]. Although normal brain graphs have typical properties (i.e., they are more organized than random graphs), brain graphs of schizophrenia patients may have specific abnormalities.

For example, highly connected nodes in the brain that are also densely connected with one another, so-called rich clubs, are present in schizophrenia but less prominent compared with healthy controls [10]. Other structural imaging studies using graph theory found evidence for less information integration and more clustering of nodes across brain regions [10–12]. Similar findings have emerged in other structural studies [13, 14], but studies based on functional connectivity have not always converged with these structural findings [15–17], and only a minority of studies have demonstrated relevance of these graph metrics for clinical outcome.

Although two prior studies [18, 19] computed group-wise graph metrics in responders and non-responders, we here tested how individual network architecture relates to individual clinical outcome. Previous work has shown that this can be achieved by comparing, in each individual, the statistical similarity between brain regions [20–22] or by assessing their correlations across different imaging domains [23]. Although still speculative, previous studies suggest that statistical similarity networks might capture biologically meaningful correlates of development, aging, and brain disorders [24].

Statistical similarity between brain regions can be used to build similarity matrices across the whole brain for each individual from which a binary graph of nodes and edges can be constructed. This gives a similarity network (or connectome) for each participant, which can then serve as a predictor for individual treatment outcome. This was the approach we used in the current study (Fig. 1). Based on ample evidence that schizophrenia brain abnormalities are primarily located in highly connected nodes in the human connectome [25], we focused our analysis on the hubness (or nodal degree) graph metric, which can be computed from the similarity networks. We hypothesized that the hubness of cortical nodes would be associated with individual treatment outcome in two concatenated early psychosis cohorts. Treatment outcome of positive symptoms was computed using mixed models [26–30].

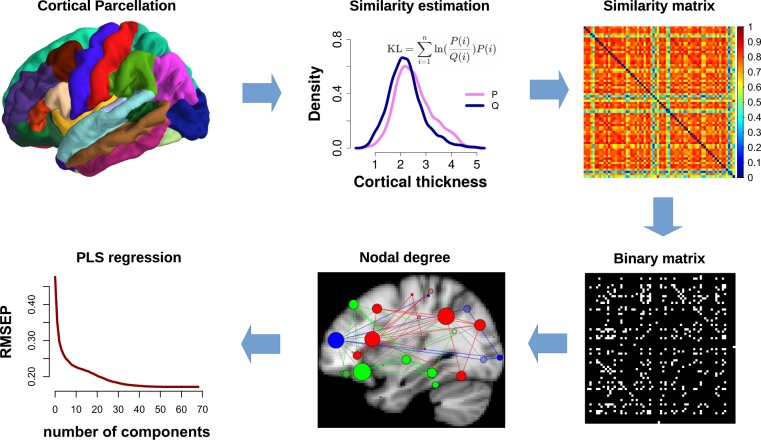
Fig. 1.

Analysis flowchart. Computation of similarity networks in each participant by calculating the statistical similarity between brain regions. First, Freesurfer cortical parcellation was conducted for each individual participant. Cortical thickness was extracted for each vertex within each region and used to estimate the probability distribution function. The similarity between any pair of region was then estimated by calculating the KL divergence of their probability distributions, resulting in a 68 × 68 similarity matrix. The KL divergence computes the loss of information when one distribution is used to approximate another. The similarity matrix was then thresholded into a binary matrix to create a network graph. Graph-based degree (or hubness) for each node was then calculated for each individual participant. Nodal degrees were then entered as predictors into a partial least squares regression, using individual treatment response slopes as outcome measure. KL Kullback–Leibler divergence, PLS partial least squares regression, RMSEP root mean square error of prediction

Materials and methods

Participants

We used two early-phase psychosis cohorts from two separate 12-week clinical trials on second-generation antipsychotics with a similar design and similar treatment effects (Fig. S1). Details have been published previously [31] and are summarized in Table 1, as well as in the Supplementary Information. Importantly, there were no significant differences between studies in duration of untreated psychosis (t (62.48) = 0.72, P = 0.473) and in the proportion of medication naive participants (χ² (1) = 2.66, P = 0.103). Written informed consent was obtained from adult participants and the legal guardians of participants younger than 18 years. All participants under the age of 18 provided written informed assent. The study was approved by the Institutional Review Board (IRB) of Northwell Health, which served as the central IRB for all clinical sites. To replicate previously reported group differences in cortical thickness [32], we also included a sample of 58 healthy controls (Table 1). Healthy controls were recruited at the Zucker Hillside Hospital during the CIDAR trial.

Table 1.

Sample characteristics

Characteristic	PSY	Mean	SD	HC	Mean	SD
Males	59			25
Females	23			33
Age, years	82	21.6	5.5	58	28.1	11.9
Schizophrenia	57
Schizophreniform disorder	15
Psychotic disorder NOS	5
Schizoaffective disorder	2
Bipolar I disorder (with psychotic features)	3
Prior medication exposure	75	8.4	29.4
Medication naive	28
Medication 2 weeks or less	71
Education, years	77	12.2	2.2	58	13.7	2.9
IQ	69	97.9	13.2	49	102.2	10
BPRS total	82	42.7	7.5	0
BPRS TD	82	14.3	3.1	0
DUP, weeks	77	110.9	176.2	0

PSY patients with early psychosis, HC healthy controls, BPRS Brief Psychiatric Rating Scale, BPRS TD Brief Psychiatric Rating Scale Thinking Disturbance, DUP duration of untreated psychosis, NOS not otherwise specified, IQ intelligence quotient

Patients had a current DSM-IV-defined diagnosis of schizophrenia, schizophreniform, schizoaffective disorder, or psychotic disorder not otherwise specified, and bipolar disorder with psychotic features and could have had up to 2 years of antipsychotic treatment. Many but not all subjects were first-episode patients. Note that excluding the patients with a diagnosis of bipolar disorder with psychotic features (N = 3) did not alter the results.

Symptom assessments using the anchored version of the Brief Psychiatric Rating Scale (BRPS-A) were done at baseline, weekly for 4 weeks, every 2 weeks until week 12. To obtain a measure of positive symptoms, we defined thought disturbance [3] as the sum of the following items: conceptual disorganization, grandiosity, hallucinatory behavior, and unusual thought content.

Structural magnetic resonance imaging and analysis

Magnetic resonance imaging (MRI) exams were conducted on a 3-T scanner (GE Signa HDx). All participants were measured on the same scanner. We acquired anatomical scans in the coronal plane using an inversion-recovery prepared 3D fast spoiled gradient sequence (TR = 7.5 ms, TE = 3 ms, TI = 650 ms matrix = 256 × 256, FOV = 240 mm), which produced 216 contiguous images (slice thickness = 1 mm) through the whole brain. Image processing and segmentation were conducted with the Freesurfer 5.1.0 recon-all pipeline and the Desikan-Killiany cortical atlas [33]. All image processing, parcellation, and quality control procedures were conducted while blinded to participants’ demographic and clinical characteristics. Visual inspections for quality assurance were conducted and no manual interventions were necessary. Details on the processing pipeline can be found in the Supplementary Information. We then tested for group differences in cortical thickness for each of the 68 regions as derived from the Freesurfer recon-all pipeline and adjusted this analysis for age, sex, and intracranial volume.

Individual treatment response estimation

Rather than categorizing participants to responders and non-responders, which is statistically inefficient [29], we focused on treatment response as a continuous measure and used mixed models to make efficient use of the full sample and the repeated measures [26, 30, 34, 35].

Individual response was estimated using mixed models with restricted maximum likelihood and used as outcome measure in subsequent analyses. With mixed models, individual responses are estimated to be closer to the average treatment response, an effect that is well known as partial pooling or shrinkage [36]. The partial pooling effect for the two psychosis cohorts can be visualized by showing how individual treatment effects are pulled toward the average treatment effect (Fig. 2). Partial pooling makes the analysis less susceptible to individual outliers by attenuating the impact of participants with only few assessments (Fig. 2), which is of particular importance in estimating treatment response in relatively small samples. Although only 82 participants had MRI baseline data available, the full sample of 248 participants was used to obtain more precise estimates of the individual treatment response slopes. A more detailed description can be found in the Supplementary Information.

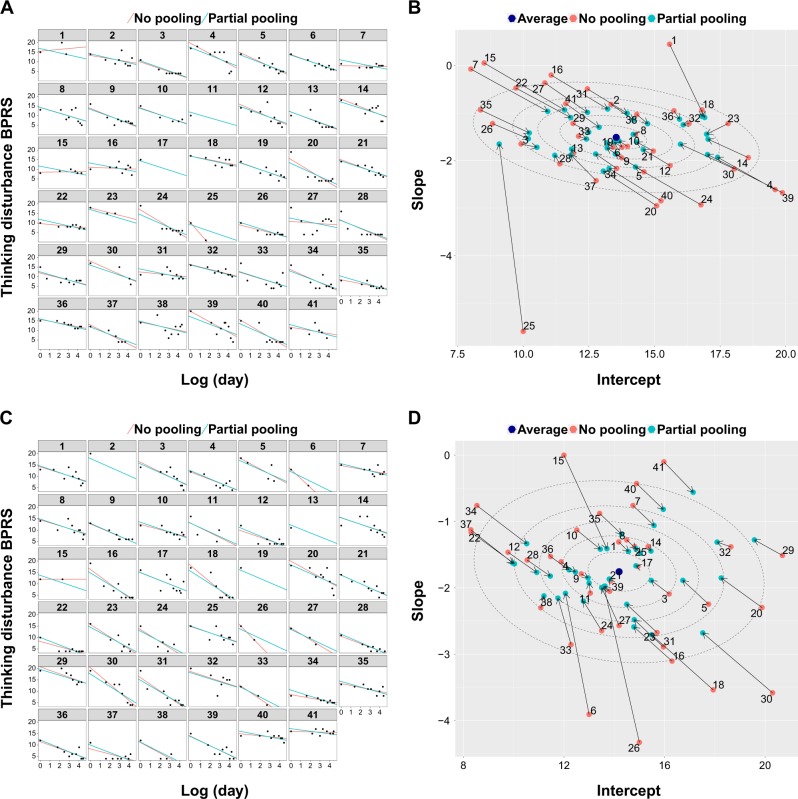
Fig. 2.

Partial pooling to regularize individual response slopes. a Individual time courses for all participants from the first schizophrenia cohort. A log-linear relationship between time as measured in days from baseline and thinking disturbance symptoms was evident. Partial pooling regularized the individual slopes, i.e., the influence of outliers with only few assessments was attenuated. b The partial pooling effect is demonstrated by the individual responses being pulled toward the average treatment effect. As a consequence, outliers are less influential, as is particularly striking for those participants with few assessments. c, d The same is shown for the second schizophrenia cohort. Dotted ellipses indicate confidence regions for the average treatment effect (10, 30, 50, 70, 90%, respectively)

Graph theoretic analysis

Individual network graphs were computed following a new method that estimates statistical similarity across brain regions in each individual participant [20, 21]. The analysis flowchart is shown in Fig. 1. After cortical parcellation into 68 brain regions through the Freesurfer recon-all pipeline, statistical similarity between all pair-wise brain regions was computed in each individual. First, probability density functions were estimated for the cortical thickness distribution in each region, using a Gaussian kernel and 512 sampling points. We followed the comprehensive characterization of structural similarity networks by Wang and colleagues [22] who also investigated the diminishing influence of increasing numbers of sampling points for the probability density function estimation. We then chose a more conservative resolution that the one used by Wang and colleagues [22] of 512 sampling points. This resulted in probability distributions for each of the 68 brain regions. Statistical similarity between each possible pair of distributions was then computed by calculating the Kullback–Leibler (KL) divergence between them [20–22]. The KL divergence measures the difference between two probability distributions (i.e., the loss of information when one distribution is used to approximate another). The KL divergence is thus defined as

$$D_{KL}\left(P∥Q\right)={\sum }_{i=1}^{n}P\left(i\right)log\frac{P\left(i\right)}{Q\left(i\right)}$$ 1

with P and Q being two probability distribution functions and n the number of sample points. Since D_KL(P|Q) is not equal to D_KL(Q|P), a symmetric variation of the KL divergence can be derived as follows:

$$D_{KL}\left(P,Q\right)={\sum }_{i=1}^n\left(P\left(i\right)log\frac{P\left(i\right)}{Q\left(i\right)}+Q\left(i\right)log\frac{Q\left(i\right)}{P\left(i\right)}\right).$$ 2

Finally, the following transformation was used to limit the measure to a range from 0 to 1:

$$\mathrm{KLS}\left(P,Q\right)=e^{-D_{KL}\left(P,Q\right)}.$$ 3

We thus computed the KLS values for all possible pairs of brain regions in each individual participant, resulting in a 68 × 68 similarity matrix S_ij for each subject (Fig. 1). Individual similarity matrices were then binarized by employing a sparsity threshold τ (number of actual edges divided by the maximum possible number of edges in a network), which ensured the same number of nodes and edges for the networks across participants. This resulted in a binary adjacency matrix A_ij [22]:

$$A_{ij}=\left[a_{ij}\right]=\left\{\begin{array}{c}\hfill 1,\mathrm{if}{s}_{ij}>{\mathrm{KLS}}_{\mathrm{th}};\hfill \\ \hfill 0,\mathrm{otherwise,}\hfill \end{array}\right.$$ 4

with KLS_th being a subject-specific KLS threshold that ensured that all networks had the same number of nodes and edges across participants. Following previous work [23], we chose a sparsity threshold of τ = 0.1 for our analysis but also repeated calculations for a range of thresholds (0.1–0.7, with intervals of 0.05). The binary matrices allowed us to construct graphs of nodes and edges.

The graph theoretic measure of primary interest was nodal degree or hubness. The degree, k(i), of a node is the number of edges connecting the i-th region to the rest of the network:

$$k\left(i\right)={\sum }_{i=1}^n{A}_{ij},$$ 5

where A_ij is the binary adjacency matrix, which was computed by thresholding the similarity matrix, S_ij.

Statistical analyses

We used multivariate partial least squares (PLS) regression to test the relationship between nodal degree and individual treatment response. This method is particularly suited for a set of highly correlated predictors. In PLS, the optimal low-dimensional solution for a relationship between a set of correlated predictor variables and a response variable is computed. The 82 × 68 predictor variable matrix comprised estimates of degree (calculated at 10% connection density) for each of 68 nodes in each of 82 participants.

The (82 × 1) response vector comprised individual treatment response slopes. To account for unspecific inter-individual differences, the predictor matrix and the response vector were regressed on potential confounds, including study cohort (CIDAR, OMEGA3), baseline value of thinking disturbance, intracranial volume, age, gender, and age × gender interaction. Residuals of this regression were then used in the actual PLS analysis.

To rank each cerebral node according to its correlation with each PLS component, we used bootstrapping, i.e., drawing 1000 samples with replacement of the 82 individual participants, to compute the error on the PLS weights. A similar procedure has been used in recent graph theoretic work [23, 37, 38].

All analyses were conducted with R version 3.3.2 (2016-10-31) [39]. Mixed models were estimated using the lme4 library [40], PLS regression were computed with the pls library [41], bootstrapping was performed with the boot library [42], and brain graph metrics were computed with the brainGraph [43] and igraph [44] libraries. Python 2.7.15rc1 and pysurfer (0.8.0) were used for visualizing the imaging results.

Results

Nodal degree predicts treatment response

The first two PLS regression components explained 29% (95% confidence interval (CI): 27, 30) of the variance in treatment response after cross-validation, with 1000 sets of five participants held out from the sample. This model fit was significant in a permutation test with 1000 permutations (P = 0.006). Notably, statistical significance (P < 0.05) was maintained when repeating the PLS regression across connection densities (0.1–0.7). The PLS components were positively correlated with treatment response slopes (first PLS component: r = 0.66, P < 0.001; second PLS component: r = 0.4, P < 0.001; Fig. 3). To assess their contribution, we ranked the 68 nodes of the individual networks according to their bootstrap standardized weight on each PLS component [23, 37, 38]. Most importantly, since the sign of the correlation between PLS components and treatment response slopes was positive (Fig. 3), nodes that correlated strongly with PLS scores had a negative relationship with treatment response. We found that they were primarily located in the orbito- and prefrontal cortices and posterior cingulate cortex for the first PLS component and in the superior temporal, precentral, and middle cingulate brain areas for the second PLS component (Fig. 3).

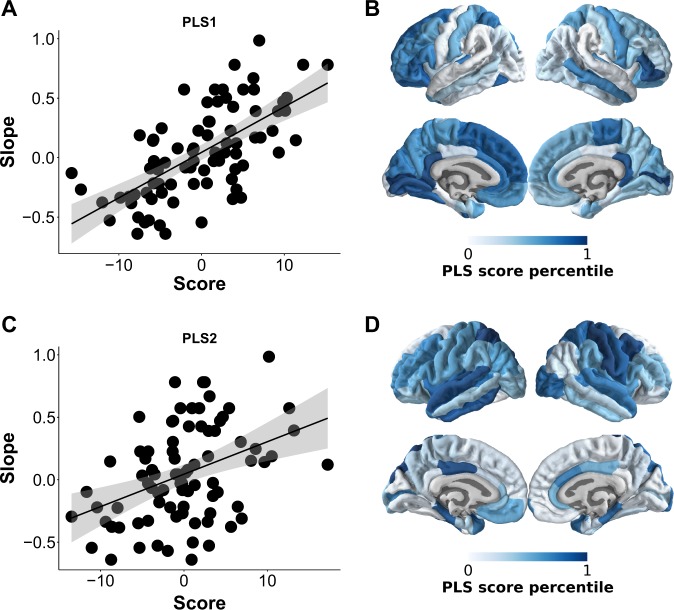
Fig. 3.

Correlations of partial least squares (PLS) scores with individual treatment response and contribution of cortical nodes in the psychosis cohort (N = 82). Nodal degree for each of the 68 was entered into a PLS regression, with individual treatment response slopes as outcome measure. The first two PLS components explained a significant proportion of variance in treatment response. a, b The first PLS component correlated most strongly with nodal degree of orbito- and prefrontal cortices and posterior cingulate cortex. Note that more negative slopes meant better treatment response. c, d The second PLS component correlated most strongly with superior temporal, precentral, and middle cingulate brain areas

In summary, these findings suggest that individual differences in the configuration of structural similarity networks explain a significant proportion of the variance in treatment response.

We then also tested for group differences in nodal degree between psychosis patients and a cohort of healthy controls. Using permutation tests with 1000 permutations for each of the 68 nodes, we found a significant increase in nodal degree in the left orbitofrontal cortex (P < 0.05; Fig. S2).

Validation of results

To verify that our findings held up when using a different cortical parcellation scheme, we repeated the analysis using the Destrieux atlas [45], which comprises 148 nodes. We again found that the first two PLS components explained 30% (95% CI: 28, 31) of the variance in treatment response after cross-validation. In addition, excluding the patients with a diagnosis of bipolar disorder with psychotic features (N = 3) did not alter the results.

Group differences in cortical thickness

For completeness, we also assessed how the psychosis cohorts differed from the control cohort in terms of cortical thickness in all 68 cortical nodes. Confirming previous reports [32], cortical thickness was reduced in patients compared with controls most prominently in the left paracentral and parahippocampal gyrus and increased in the right rostral anterior cingulate cortex (Fig. S3). However, these alterations did not survive correction for multiple comparisons using false discovery rate (q < 0.05).

Discussion

Here we showed that individual differences in structural similarity networks predicted treatment response in early-phase psychosis. The importance of this finding is twofold. First, we used the continuous scale to define treatment response, thereby increasing statistical sensitivity and avoiding power loss through dichotomization [29]. Second, and related, we computed networks for each participant, which allowed us to predict treatment response on the individual level.

We focused our analysis on a specific graph theoretic parameter, namely nodal degree or hubness. The rationale for this decision was that brain networks contain only a minority of highly connected nodes acting as hubs. Hubs are considered to be functionally valuable by supporting information integration [25] but their value comes at a high biological cost due to increased metabolic demand and long-distance connections. Their prominent role suggests that schizophrenia-relevant brain abnormalities should be concentrated in hubs, a prediction that was indeed supported by a large body of meta-analytic evidence [25], where schizophrenia lesions were found most dominantly in frontal and temporal cortical hubs. In line with this notion, we found that nodal degree in orbito- and prefrontal areas contributed most strongly to the prediction of treatment response, with additional contributions from superior temporal regions. Importantly, nodes in the right orbitofrontal cortex have showed reduced degree compared with controls in functional networks in schizophrenia [15]. Our work extends this finding by showing that orbitofrontal nodes appear to impact clinical outcome in early-phase psychosis.

Although previous studies indicated the usefulness of brain morphology and machine learning in predicting response to treatment [46, 47], only one study has investigated the relationship between anatomical networks and clinical outcome [48]. That study used structural covariance of cortical folding to predict treatment response in first-episode psychosis, and found higher segregation, poorer integration, and vulnerable gyrification covariance in non-responders. Specifically, non-responders showed reduced centrality of the left insula and anterior cingulate cortex. In addition, they were also more vulnerable to simulated lesions, i.e., covariance disintegrated after removal of high-degree hubs, supporting the relevance of nodal degree for treatment response [48]. A comparable study that used resting state functional connectivity found reduced global efficiency and increased clustering in patients with schizophrenia that normalized with response to antipsychotic treatment [19].

What is the biological meaning of structural similarity networks? It has been hypothesized that brain regions that grow together should display strong structural covariance across individuals [48, 49]. In line with this hypothesis, previous work has shown that structural networks of regions that grow together shared similar global and nodal topological properties [50]. Thus, a likely interpretation is that structural similarity networks reflect “synchronized developmental change in distributed cortical regions” [50]. Accordingly, structural covariance networks show reorganization during normal development [24, 49, 51], aging [21, 52–54], and disease [12, 55, 56]. This suggests that structural similarity networks capture biologically meaningful correlates of development, aging, and brain disorders. Speculatively, then, these processes may impact distributed and treatment-relevant brain areas.

How can brain regions, similar in their thickness patterns and potentially growing synchronously, influence treatment outcome? Although still speculative, a potential mechanism is through the relationship with cognition. We have previously shown that higher scores in general cognition and reasoning capacity in particular were positive predictors of treatment response [4]. However, since that study did not include any brain imaging data, we could not characterize a potential neural correlate of this effect. Since brain network properties have been shown to be positively correlated with cognition [57], it is possible that they are the biological correlate underlying both cognition and improved treatment outcome.

An important difference between our study and previous attempts to characterize individual treatment response is that we did not dichotomize our sample into responders and non-responders. Although such dichotomization may be appealing and particularly relevant to clinicians, it is statistically inefficient to binarize a continuous measure [29, 58, 59]. The argument that binary decisions are what clinicians ultimately need to make, and therefore research should provide them with binary classifications, can easily be refuted. Indeed, if a binary decision must be made, it must be made at the point of actual clinical care, when all costs and potential benefits are known [59]. For example, the clinician may decide that a probable non-responder may still undergo treatment if the potential benefit outweighs the risk for that particular case. Furthermore, it is generally under-appreciated that it is often difficult to determine whether or not an individual patient responded to the treatment. The reason for this is that one does not know how the patient would have done under placebo. This is often overlooked and can limit attempts at classifying patients based on observed response. Thus, treatment response prediction based on a single-criterion classification in responders and non-responders should be treated with caution [75].

What is thus the potential clinical meaning and application of the current study’s findings? With an approach such as this, the ultimate goal is to provide the clinician with an estimate of response probability for a given patient. As we have just shown, this is different from classifying the patient as a responder or non-responder. After taking all available information into account, it is the clinician (and not the researcher) who ultimately decides whether to treat even a likely non-responder. A study such as this can thus inform the clinician’s decision process by providing individual predictions of treatment response.

The mixed model approach employed in this study is one way to address this problem; it separates random variation from actual treatment variation in each participant [29, 30]. In addition, individual treatment response is estimated more efficiently by utilizing the full data set and more conservatively by applying shrinkage [34, 36].

A few limitations merit comment. First, we did not include a placebo control group, which would have allowed us to compare the overall variability in response between the treatment and the control groups. In principle, such a comparison would need to show that the variability in the treatment arm is higher than the one in the placebo arm, and that the difference is clinically relevant [60, 75]. However, placebo-controlled trials in early-phase psychosis have rarely been conducted. In addition, since the neurobiological underpinnings of graph metrics are still unknown, pathophysiological inferences must be made with caution. Next, we did not include functional connectivity [5] or other potentially predictive data in this study, which means that our findings may not be predictive when other predictors are included in the model. Finally, graph metrics may also vary depending on the parcellation scheme. However, in this study we repeated our analysis with an additional atlas of 148 nodes and found essentially the same results.

In conclusion, this study showed that advanced statistical modeling of treatment response and a relatively novel [20] computation of structural similarity networks established a potential link between brain network morphology and clinical outcome in early-phase psychosis.

Funding and disclosure

This study was presented first at the European Conference of Schizophrenia Research 2017, Berlin, Germany. This work was supported by NIMH grant P50MH080173 to Dr. Malhotra, grant P30MH090590 to Dr. Kane, grant R01MH060004 to Dr. Robinson, grant R01MH076995 to Dr. Szeszko, and grant R21MH101746 to Drs. Robinson and Szeszko. Dr. Homan had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis. Dr. Robinson has served as a consultant for Asubio, Otsuka, and Shire and has received grants from Bristol-Myers Squibb, Janssen, and Otsuka. Dr. Kane has served as a consultant for Alkermes, Eli Lilly, Forest, Forum, Genentech, Intracellular Therapies, Janssen, Johnson & Johnson, Lundbeck, Otsuka, Reviva, Roche, Sunovion, and Teva; he has received honoraria for lectures from Genentech, Janssen, Lundbeck, and Otsuka; and he is a shareholder in MedAvante and Vanguard Research Group. Dr. Lencz is a consultant for Genomind. Dr. Malhotra has served as a consultant for Forum Pharmaceuticals and has served on a scientific advisory board for Genomind. The remaining authors declare no competing interests.

Data and code availability

The data and code supporting the findings of this study are available online at http://github.com/philipphoman/ssn. To ensure reproducibility we included a Makefile, which reflects the dependencies between different analysis modules and allows to run the analysis using the “make” command from the Unix command line.

Supplementary information

Supplementary Information accompanies this paper at (10.1038/s41386-019-0322-y).