Watching microtubules grow one tubulin at a time

Microtubules are mesoscale dynamic noncovalent polymers essential for all eukaryotic life. Their dynamic behavior is crucial for cells to divide, differentiate, and migrate. Microtubules are built through the lateral assembly of linear protofilaments formed through the head-to-tail association of tubulin dimers (1). Lateral association of protofilaments forms the hollow cylindrical microtubule. Microtubules grow through the addition of tubulin dimers at their tips. Observations of individual microtubules using a variety of optical techniques coupled with biochemical analyses and modeling have resulted in a conceptual framework to understand the kinetics and structural transitions that occur during their growth and disassembly. In PNAS, Mickolajczyk et al. (2) harness the power of recent developments in recombinant tubulin engineering (3–6) and interferometric scattering microscopy (iSCAT) (7) to measure directly the association and dissociation constants of single tubulin dimers at the growing microtubule tip (k_On and k_Off, respectively) and advance a model for microtubule growth.

Despite decades of research on microtubule dynamics, basic polymer properties such as rates of tubulin dimer addition and loss at microtubule tips are still controversial and vary by an order of magnitude between studies, even in a simplified in vitro system (1, 8, 9). These uncertainties limit our understanding of tubulin self-assembly and its regulation by the myriad of proteins that associate with microtubules in cells (10). Why do we still lack a detailed view of microtubule assembly when similar efforts in the actin field have yielded a deeper quantitative understanding of actin dynamics (11)? One reason is the multistranded structure of the microtubule. Unlike actin, which consists of two helical strands, microtubules are typically formed by 13 protofilaments that can grow independently from each other. Multiple protofilaments can create different arrangements that can give rise to different association and dissociation kinetics of tubulin dimers at their tips. However, available dynamic imaging methods lack the resolution to distinguish individual protofilaments at the tip, essentially providing only one-dimensional information about microtubule growth. Classic studies using video-enhanced differential interference contrast microscopy to measure growth rates of single microtubules at different soluble tubulin concentrations provided estimates of tubulin k_On and k_Off (8) (Fig. 1). These were inferred assuming a simple one-dimensional Oosawa model in which growth rate varies linearly with tubulin concentration and k_Off is independent of tubulin concentration (12). These studies reported k_On and k_Off values at the growing microtubule end of ∼8.9 μM⁻¹⋅s⁻¹ and 44 s⁻¹, respectively (8).

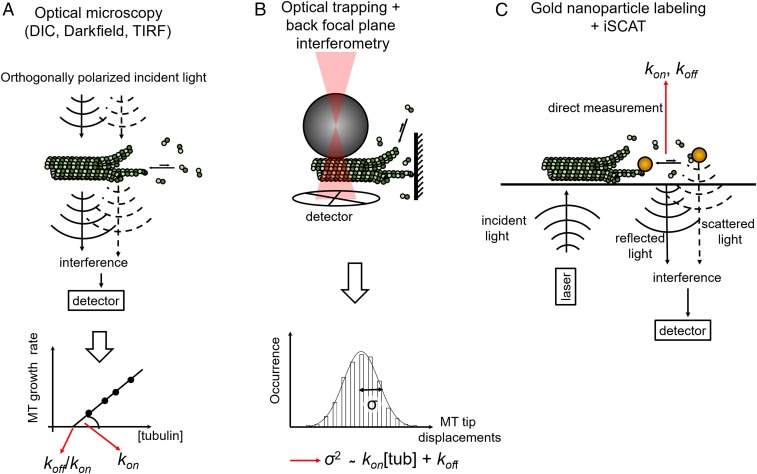
Fig. 1.

Methods for measuring tubulin k_On and k_Off. (A) DIC-based measurements of microtubule growth rates and derivation of k_On and k_Off rates (8). (B) Optical trap-based measurements of tip displacement and inference of k_On and k_Off (13, 14). (C) iSCAT-based observation of single gold-labeled tubulin dimers and direct measurement of association and dissociation kinetics (2). DIC, differential interference contrast; MT, microtubule; TIRF, total internal reflection fluorescence; tub; tubulin.

Detection of the axial position of microtubule tips was enhanced by using optical trapping combined with back focal plane interferometry (13, 14). In these assays, microtubules grew against a barrier, and tip displacement was measured from the motions of trapped microbeads attached at the other microtubule end. Despite higher resolution along the microtubule axis, this method detected only the position of the longest protofilament and could not easily distinguish between tubulin dimer addition/loss to the longest protofilament and changes in microbead position due to protofilament buckling. This may partially explain the difference in observed increments of microtubule length during assembly reported by the two studies (refs. 13 and 14). Despite these limitations, these studies revealed an increase in microtubule tip fluctuations with tubulin concentration and challenged the use of the Oosawa one-dimensional model as an adequate approximation for the microtubule. Indeed, tubulin dissociation from the multiprotofilament lattice may involve several scenarios such as breakage of one longitudinal bond (between two dimers in a protofilament) or additionally one or two lateral bonds (between dimers in neighboring protofilaments) corresponding to progressively lower k_Off values. Hence, the k_Off of tubulin from the microtubule can be expressed as the sum of elemental k_Off values, weighted by the probability of dissociation via each of these different scenarios (9). Thus, if the fraction of tubulins with zero, one, or two lateral bonds changes with tubulin concentration, the k_Off should also change.

To address this limitation, Gardner et al. (9) took into account the fluctuations of the microtubule tips over time (Fig. 1). They did this by assuming that the variance of microtubule growth rates can be described by a Skellam distribution, where tubulin on- and off-rates are treated as two statistically independent Poisson-distributed variables. In this case, the growth rate variance would be proportional to the sum of tubulin on- and off-rates, allowing estimation of k_On and k_Off. However, the rates of tubulin association and dissociation are not completely independent and neither are the dynamics of individual protofilaments. To tackle this problem, one can apply computational models to infer the k_Off from the model fit to the data at different tubulin concentrations (15–17). This strategy is complicated by the fact that different models disagree on assumptions about the bending energies and morphology of protofilaments at the microtubule tip. Three possible tip configurations have been reported based on low-resolution cryo-electron microscopy data: blunt or tapered (18), gently curved sheets (19), or flared (20, 21). Visualization of individual protofilaments at dynamic microtubule tips with higher resolution is a major technical challenge. Postulated tip morphologies and bending energies of protofilaments define lateral and longitudinal bond values in computational models, and hence the k_Off. Indirectly, this also affects the k_On because the models are adjusted to have the right balance between tubulin association and dissociation to recapitulate experimentally observed microtubule growth rates. Moreover, certain tip morphologies may impose different steric constraints for the attachment of new tubulin dimers. Brownian simulations predict significantly different k_On values at the tip of a pioneer protofilament without lateral neighbors, compared with a partially shielded spot between two adjacent protofilaments (22).

Therefore, model-based inference of k_On and k_Off from one-dimensional optical microscopy or optical trapping is dependent on model assumptions and can lead to significantly different outcomes. Studies from the Odde and Gardner groups (9, 15, 23) estimated a k_On of ∼4 μM⁻¹⋅s⁻¹ per protofilament (∼52 μM⁻¹⋅s⁻¹ per microtubule), with lateral and longitudinal bonds of 4.5 to 5 and 9.4 k_BT, respectively. Similar estimates were obtained by Margolin et al. (16). On the other hand, models from Zakharov et al. (17) and McIntosh et al. (21) estimated a lower k_On of ∼0.6 μM⁻¹⋅s⁻¹ per protofilament, with stronger lateral and longitudinal bonds of 5.4 to 9.1 and 15 to 16.6 k_BT, respectively.

The new study from Mickolajczyk et al. (2) provides needed clarity to this problem by making direct single-molecule measurements of tubulin association and dissociation at microtubule tips (2). Using iSCAT (7) and engineered recombinant Saccharomyces cerevisiae tubulins (3), Mickolajczyk et al. are able to observe the incorporation of single gold-labeled tubulin dimers at microtubule tips with high temporal resolution (Fig. 1). The frequency of incorporation of gold-labeled tubulins recapitulates microtubule growth rates with unlabeled tubulin within a factor of 2, suggesting that incorporation is not significantly affected by the 20-nm gold label. This is consistent with theoretical studies indicating that tubulin incorporation into microtubules is not diffusion limited (24). The association rate was measured by counting the number of binding events at the microtubule tip in the presence of the slowly hydrolyzing GTP analog GTPγS, which supports growth and suppresses depolymerization for yeast microtubules. These measurements yielded a k_On of 3.4 ± 1.6 μM⁻¹⋅s⁻¹ per microtubule, or 0.26 μM⁻¹⋅s⁻¹ per protofilament, a value lower than previous experimental measurements for mammalian tubulin and significantly lower than that assessed using tip fluctuation analysis (9). One cannot exclude, however, that the difference reflects different properties of mammalian and S. cerevisiae tubulin.

To estimate tubulin dissociation rates, Mickolajczyk et al. (2) recorded dwell times of individual gold-labeled tubulins at growing microtubule tips. They found two distinct groups of reversible single-tubulin binding events. The authors interpret the group with short dwell times as corresponding to tubulin binding events involving only one longitudinal bond and propose the second group to represent binding events that involve both a longitudinal and a lateral bond. Key to supporting this interpretation is Mickolajczyk et al.’s ability to introduce a destabilizing mutation at the tubulin lateral interface and show that this manipulation makes long dwell times significantly less abundant. Using a simple kinetic Monte Carlo model (15), Mickolajczyk et al. derive elemental dissociation constants corresponding to the breakage of one longitudinal bond (4.9 ± 0.6 s⁻¹) or one longitudinal and one lateral bond (0.13 ± 0.02 s⁻¹). Using the same model and the experimentally determined k_On, the authors calculate lateral and longitudinal bond strengths of 3.6 ± 0.4 and 12.0 ± 0.2 k_BT, respectively. Interestingly, the authors argue that only the combination of relatively strong longitudinal bonds and a low k_On allows microtubule growth with tapered ends, whereas a higher k_On predicts a blunter microtubule tip. This conclusion is in disagreement with previous work that linked fast association kinetics with tapered ends (9, 23).

Clearly, more work is needed to fully understand the kinetics and structural transitions at microtubule ends. This study illustrates how the application of new microscopy techniques and the opportunities provided by the use of recombinant engineered tubulins can finally bring the field of microtubule dynamics to the single-molecule level. The recent exciting developments in interferometric scattering mass spectrometry, which allows simultaneous monitoring of distinct stepwise changes in actin filament length with nanometer precision and the determination of molecular weight distributions without any exogenous label on the actin monomers (25), holds the promise to watch microtubules grow one single tubulin at a time without the need of a gold label. Still lacking are methods to probe the dynamics and conformations of individual tubulins and protofilaments during microtubule assembly, disassembly, and transitions between these states. Combined with single-molecule measurements, these tools will bring invaluable new mechanistic insights into the dynamic behavior of microtubules and their regulation by the diversity of tubulin isoforms and posttranslational modifications as well as associated proteins and chemotherapeutic agents.