Dominant words rise to the top by positive frequency-dependent selection

Significance

Speakers of a language somehow come to use the same words to express particular meanings—like “dog” or “table”—even though there is seldom a necessary connection between a word and its meaning, and there are often many alternatives from which to choose (e.g., “sofa,” “couch,” “settee”). We show that word choice is not just a matter of saying what others say. Rather, humans seem to be equipped with a bias that makes them disproportionately more likely to use the words that most others use. The force of this bias can drive competing words out, allowing a single word to dominate all others. It can also explain how languages spontaneously organize and remain relatively stable for centuries or even millennia.

Abstract

A puzzle of language is how speakers come to use the same words for particular meanings, given that there are often many competing alternatives (e.g., “sofa,” “couch,” “settee”), and there is seldom a necessary connection between a word and its meaning. The well-known process of random drift—roughly corresponding in this context to “say what you hear”—can cause the frequencies of alternative words to fluctuate over time, and it is even possible for one of the words to replace all others, without any form of selection being involved. However, is drift alone an adequate explanation of a shared vocabulary? Darwin thought not. Here, we apply models of neutral drift, directional selection, and positive frequency-dependent selection to explain over 417,000 word-use choices for 418 meanings in two natural populations of speakers. We find that neutral drift does not in general explain word use. Instead, some form of selection governs word choice in over 91% of the meanings we studied. In cases where one word dominates all others for a particular meaning—such as is typical of the words in the core lexicon of a language—word choice is guided by positive frequency-dependent selection—a bias that makes speakers disproportionately likely to use the words that most others use. This bias grants an increasing advantage to the common form as it becomes more popular and provides a mechanism to explain how a shared vocabulary can spontaneously self-organize and then be maintained for centuries or even millennia, despite new words continually entering the lexicon.

In his review of August Schleicher’s 1869 pamphlet Darwinism Tested by the Science of Language (1), the 19th century philologist Max Müller wrote “a struggle for life is constantly going on amongst the words and grammatical forms in each language. The better, the shorter, the easier forms are constantly gaining the upper hand, and they owe their success to their own inherent virtue” (2). Evidently, so taken was Darwin with Müller’s views that just a year later he quoted Müller’s “struggle for life…” passage in his 1871 book the Descent of Man (3), adding “the survival or preservation of certain favored words in the struggle for existence is natural selection” (p. 91).

Linguists since Schleicher’s time have continued to identify regularities in the ways that languages change, including patterns in the replacement of sounds, morphology, syntax, and words (4–6). For instance, frequently used words tend to be replaced less often than infrequently used words (7), and irregular verbs have a greater tendency to become regular than do regular verbs to become irregular (8). Linguistic change such as in these two examples, involves some form of competition among alternative words, but were Müller and Darwin right to assume that the changes are driven by natural selection, that is to say, the changes are driven by the “inherent virtue” of the eventual “winners”?

One of the more significant developments of twentieth century neo-Darwinism was the mathematical formulation of the theory of neutral or random drift (9, 10). This theory, commonly applied to genetic variants, shows that the frequencies of alternative forms change over time simply as a result of random or stochastic effects—no selection need be involved. Applied to language (11, 12), random drift can be used to study changes in the frequencies with which speakers use various words for a given meaning, such as “sofa,” versus “couch” or “settee.” Drift’s importance in population studies, then, is that its mathematical expression provides a precise null expectation against which stronger claims, such as those that Darwin and Müller made, can be assessed (11, 12).

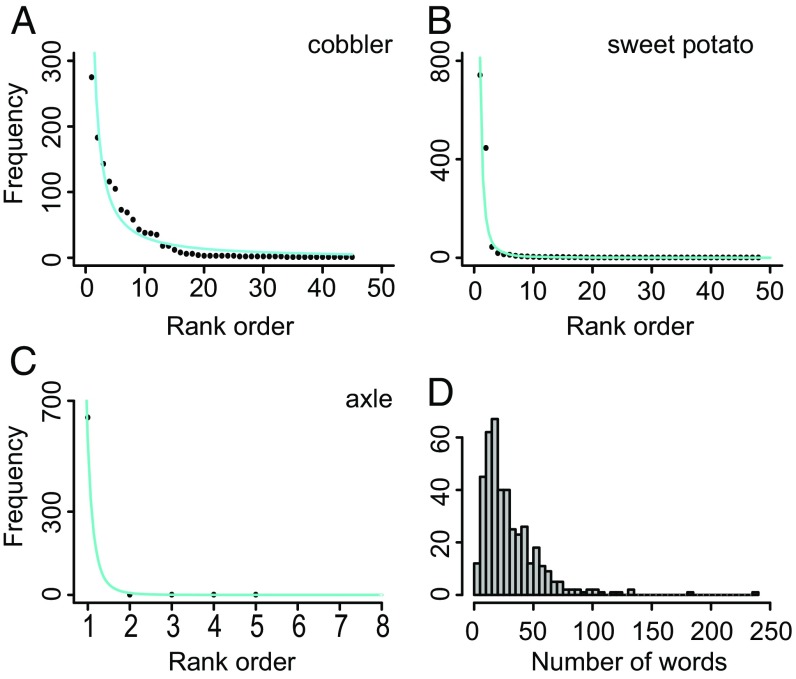
For example, in language, a common observation is that when the number of speakers who use a word is plotted against that word’s rank-order position in a list of words sorted by frequency (e.g., Fig. 1 A–C), sharply down-sloping curves arise that can be described by the form $f\left(k\right)=\alpha k^{-\beta }$, where $f\left(k\right)$ is the observed number of speakers who use a word, and k is its rank order position (1, 2,...k) (13). Studies in linguistic settings have shown that drift can produce curves with these shapes (12, 14–16), even the extreme example in Fig. 1C where, among competing alternatives, one word has risen to the top, dominating all others. On the other hand, while drift can in principal produce any monotonically declining curve, some outcomes of drift are more probable than others (17). So, the real question becomes not whether drift can produce outcomes such as those in Fig. 1 A–C, but whether mechanisms other than drift provide more likely explanations. This is the challenge that claims of selection in language must meet.

Fig. 1.

(A–C) The frequencies (y axis) of alternative words for the meaning denoted by the word in the upper right corner plotted against their rank order within that list of alternatives (x axis), with smooth curve of the form y = ax^−b fitted for descriptive purposes. The exponent b increases (steeper drop off) from A–C, reflecting the decreasing frequency of the second word relative to the first [note: attenuated x axis of C disguises the steepness of the exponent (B)]. (D) Frequency distribution of the number of words per meaning for the n = 418 meanings (mean ± SD = 30.4 ± 25.3, median = 25.3).

Here, we investigate the contributions of random drift (D), along with three forms of selection—directional selection (DS), positive frequency-dependent selection (FDS), and a model that combines directional with positive FDS (FDS+DS) (Materials and Methods). Drift asks what frequency distributions of speakers per word emerge over long periods of time if speakers use words randomly in proportion to the number of other speakers using them. Directional selection incorporates drift but allows some words to be inherently better or worse than others. An example of directional selection is that shorter words, or words that are easier to pronounce, might have an advantage, especially when they are frequently used in speech (18). Alternatively, a word might acquire an advantage from being used by a high-status person. Directional models including various social, phonetic, or other biases have been proposed for linguistic change (19), or, for example, in cultural settings to understand the choice of color terms, musical preferences, or baby names (20).

Positive frequency dependent selection refers to a scenario in which the likelihood that a speaker will use a word increases disproportionately to the number of other speakers using it. Elements of the frequency-dependent process appear in early work in statistics (21), and in cultural settings, positive frequency dependence, or “conformist bias” (22), has been investigated to explain the evolution of cultural forms (23), and the diffusion of innovations (24). Positive frequency dependence is observed in nature for aposematic or warning colors in insects, as the aposematic signal often becomes increasingly effective at deterring predators as it spreads through a population (25).

We implement these models in a computational framework that allows us to assess their relative contributions to explaining word choice in two regional American populations.

Data and Results

Our data come from over 417,000 responses obtained from over 2,000 respondents in two regional surveys conducted as part of the Linguistic Atlas Project (LAP) (26) (SI Appendix): the Linguistic Atlas of the Mid-Atlantic States (LAMSAS) (27) (n = 1,162 individuals) and the Linguistic Atlas of the Gulf-States (LAGS) (28) (n = 914 individuals). The LAP was designed to elicit local and regional variation in the words used for common vocabulary items. Owing to this emphasis on identifying variation among speakers, the LAP does not investigate lexical variation in the number words, words for days of the week or months of the year, or pronouns for which typically a single word is used in each case. To gather information on word use, trained linguist interviewers guided conversations toward predetermined topics (such as weather, food, buildings, and furniture), recording the words their respondents used for concepts or meanings such as sofa, “umbrella,” “chimney,” “canal,” “sit down,” “frost,” and “what” (SI Appendix, Tables S1 and S2, and Open Science Framework Public Project “MotherTongue”).

The LAGS and LAMSAS datasets yielded frequency distributions of the number of speakers per word for 325 and 93 meanings, respectively, including meanings such as “cobbler” (referring to a popular pie-like dessert in North America, as opposed to a shoe repairer), “sweet potato,” and “axle” (Fig. 1 A–C and SI Appendix, Tables S1 and S2). Most meanings are nouns (n = 301, 72%), followed by verbs (n = 53, 12.6%), expressions (n = 34, 8.1%), adjectives (n = 19, 4.5%), and deictics (context-dependent expression; n = 11, 2.6%). The number of words reported per meaning ranges from 2 to 240 with a mean ± SD of 30.4 ± 25.3 (median = 25.3; Fig. 1D). Because LAP meanings were selected to elicit variation among speakers, this figure overestimates the average degree of variation in the lexicon and is probably not representative of what might be thought of as a language’s core vocabulary. However, this bias does not affect our study because our interest is in identifying which processes are responsible for different patterns of word use, not the proportion of meanings explained by drift, directional selection, and frequency dependent selection.

We competed the four models in a Bayesian setting to discover which of the 418 frequency distributions of number of speakers per word (such as Fig. 1 A–C) they best describe (Materials and Methods and SI Appendix). Our Bayesian approach yields a posterior probability for each model for each meaning. Because the posterior probabilities for each meaning sum across models to 1.0, a model’s posterior provides a measure of its relative success for that meaning.

Overall, we find little support for random drift as a description of the process by which words propagate through a population of speakers (Table 1): some form of selection provides the more probable explanation of the word-frequency distributions for over 91% of the meanings we studied, and the results are nearly identical in the two datasets. Drift, or roughly “say what you hear” or “copy others,” does not provide an adequate description of word choice. A recent study of three historical grammatical changes also found mixed support for drift (11).

Table 1.

Percentage of winners by model and their summary statistics

Dataset	D	FDS	DS	FDS+DS
Full dataset, n = 418 meanings	8.6	16.3	35.6	39.5
LAGS, n = 325	8.6	16.9	35.7	38.8
LAMSAS, n = 93	8.6	14.0	35.5	41.9
Full dataset (w/o FDS+DS)	8.8	17.7	73.4
Statistic, mean ± SEM
2/1 ratio	0.70 ± 0.03	0.18 ± 0.03	0.45 ± 0.02
H	0.82 ± 0.01	0.42 ± 0.04	0.58 ± 0.01
Example meanings (SI Appendix, Tables S1, S2, and S4)	Cobbler, parlor, hay shed, relatives	Axle, towel, biscuits, syrup	Sweet potato, sofa, coffin, skunk

Shown are percentage of n = 418 meanings where the model shown has the highest posterior probability (Methods) and means of two key summary statistics (main text) for cases where the model shown above has highest posterior probability.

The FDS+DS model performs best (Table 1), but appears principally to mimic or compete with DS rather than adding a new element to the description of the data: the sum of the FDS+DS and DS posterior probabilities obtained when all four models are considered (Table 1, top row, and Table 1) correlates across meanings r = 0.97 (n = 418) with the DS posterior probabilities obtained in the absence of FDS+DS (“w/o FDS+DS” row in Table 1). Similarly, when we consider the n = 165 FDS+DS winners, 95% (n = 157) of them are DS winners in the absence of FDS+DS. We therefore drop FDS+DS from further consideration and analyze the posterior probabilities obtained when we compete the D, DS, and FDS models.

Our primary interest is in which of the three evolutionary processes (D, DS, or FDS) is most likely to yield strong concordance among speakers as to which word or words to use for a given meaning, as it is these words that probably constitute the majority of everyday speech. In this context, D tends to provide the best explanation for meanings whose frequency distributions imply the least concordance. For these meanings a variety of words is used by speakers, all coexisting at relatively high frequencies, such as is true of cobbler (Fig. 1A). Other meanings whose words were governed by drift include “relatives” and “parlor” (SI Appendix, Tables S1–S3 provide the top 10 words by posterior probability for each model).

Where DS prevails speakers typically report a smaller number of words, but it is often the case that two or three words are found at relatively high frequencies, with a number of other alternatives at much lower frequencies. Thus, DS is the best fitting model for sweet potato (Fig. 1B) for which both sweet potato and “yam” were used at high frequencies. DS was also the best fitting model for sofa (sofa and “lounge/couch” used at high frequencies) and “coffin” (coffin and “casket” used at high frequencies) (SI Appendix, Tables S1–S3). Directional selection, then, yields less variety among speakers than drift but does not seem strong enough in the face of the continual influx of new words to raise one of them to a dominant position.

Where speakers are highly likely to use the same word for a meaning, positive frequency dependent selection provides the most probable explanation of the word frequencies. This is observed for axle (Fig. 1C) where one form (axle) dominates a group of alternatives that only a negligible number of speakers used. Other meanings for which nearly all speakers use the same word and for which FDS also provided the best explanation include “towel,” “syrup,” and “biscuits” (SI Appendix, Tables S1–S3).

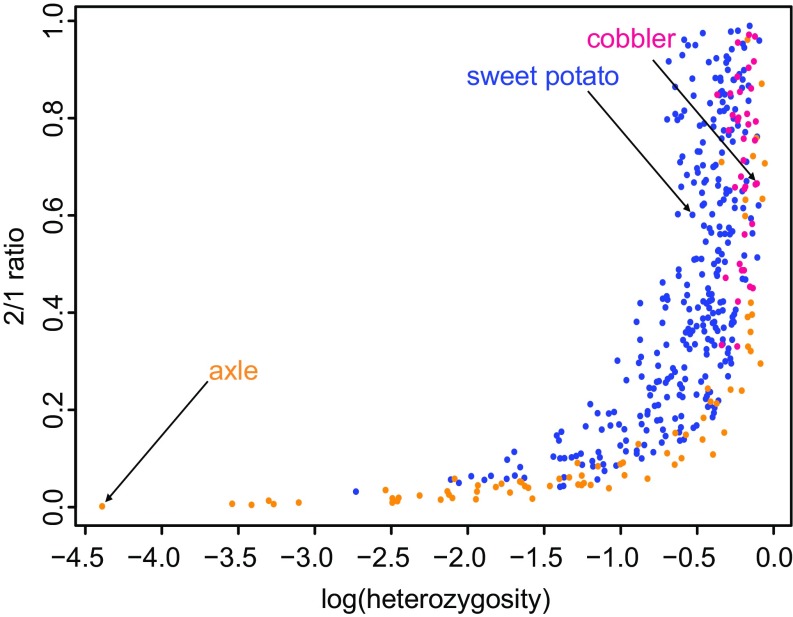
Confirmation that the three different processes yield frequency distributions of word use with the shapes characteristic of Fig. 1 A–C can be seen in Fig. 2 where the models carve out largely nonoverlapping portions of a 2D parameter space defined by two statistics: 2/1 ratio (the ratio of the second most frequent to the most frequently occurring word) and heterozygosity (H), a statistic commonly used in genetics to measure the variation in the frequencies of genetic alternatives, here applied to word frequencies (SI Appendix, Model Selection). A low 2/1 ratio means that the drop off in frequency from the most to the second most frequent form is great and thus is indicative of one word dominating. A low value of H also indicates that one word dominates: if most respondents use the same word, there is little variation among words in their frequencies. Both of these features are true of axle.

Fig. 2.

Ratio of the frequency of the second most commonly used word for a meaning to the highest frequency word (2/1 ratio) plotted against the logarithm of H, showing regions where each of the models performs best (see text): blue, DS; magenta, D; and mustard, FDS. FDS explains word frequencies characterized by high concordance among speakers (low 2/1 ratio and low H), or relatively low 2/1 ratio (low for any given level of H). DS explains intermediate levels of both measures. D best characterizes meanings with a variety of words at relatively high frequencies (low concordance among speakers). Mean 2/1 ratios and mean H differ significantly among the models such that D > DS > FDS (all P values < 0.001).

Random drift best explains those cases with the least concordance among speakers and consequently they have high 2/1 ratio and high H (Fig. 2, Upper Right). Meanings that DS explains best tend to fall in the middle, and FDS governs word choice for meanings that sit in the lower left portion of Fig. 2, corresponding to low 2/1 ratio and low H. Where FDS is dominant, the FDS parameter, s (Materials and Methods), is more than three times higher than for the remaining meanings (FDS meanings: $\overline{s}$± SD= 0.013 ± 0.014, n = 74; D and DS meanings: $\overline{s}$± SD = 0.004 ± 0.002, n = 344; SI Appendix, Fig. S2 left panel). FDS’s posterior probability increases curvilinearly in s (SI Appendix, Fig. S2 right panel), such that when s ≥ 0.006, FDS always provides the best explanation of the data.

FDS can still predominate even when concordance among speakers appears to be lower (Fig. 2, Upper Right). However, these tend to be meanings with two words competing at high frequencies plus an unusually large number of other words at much lower frequencies [F test of log(no. of words)] by winning model for meanings with 2/1 ratio > 0.5, F = 5.12, df = 2, P = 0.007; all P values throughout are two-tailed). As a consequence of the large number of words, high levels of s (F = 4.84, df = 2, P < 0.007) are required to maintain the two dominant words above the others. For example, for the meaning “a little ways,” two phrases—“a little ways” and “a little piece”—were the most commonly used and at nearly equal frequencies.

Characteristics of Words are Only Weakly Related to Word-Use.

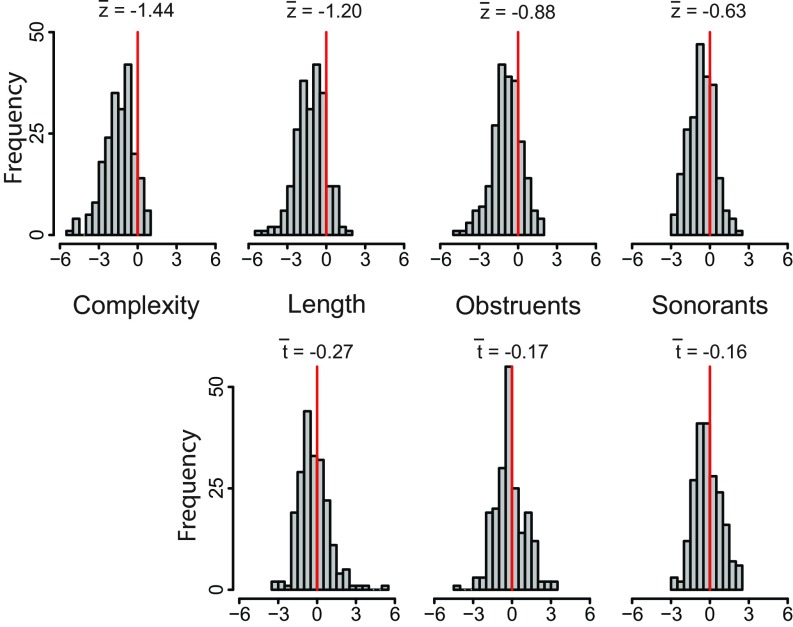
We scored all of the words for a representative sample of n = 232 meanings (totalling n = 252,506 responses; SI Appendix, Word and Meaning Characteristics) on four attributes related to ease of pronunciation: “complexity” (no. of words in the reply: some replies consist of more than one word, such as “help yourself”), “length” (number of sounds or phones in the reply), number of “obstruent” sounds (sounds whose production requires that the airway is obstructed, such as g in “good”) and number of “sonorant” sounds or consonants that do not obstruct the airflow. We then correlated words’ pronunciation scores with the logarithm of the number of speakers who used them, separately for each meaning. This yielded 232 correlations for each attribute, each one of which tests the question of whether speakers tend to use the “better” words more often. We converted the correlations to z scores so as to put them on comparable scales and combined them in histograms (Fig. 3).

Fig. 3.

(Upper) Histograms of z-transformed rank-order correlations between an attribute score and word frequency for four attributes related to ease of pronunciation: complexity, length, obstruents, and sonorants (n = 232 meanings; SI Appendix). All z scores, P < 1⁻¹⁰. (Lower) Histograms of t scores after controlling for complexity (responses with more words have more sounds). Length remains significant (P < 0.002), while effect sizes are small (average t = −0.21) for obstruents (P = 0.06) and sonorants (P = 0.04). Controlling for length, the effect of obstruents and sonorants disappears (P > 0.35).

If word characteristics are unrelated to word choice, we expect the z-score distributions to be centered at zero (corresponding to correlations of zero). Instead, all four distributions are shifted slightly to the left of zero, meaning that the words the majority of speakers used have a weak tendency to be easier to pronounce: they are less complex, they require fewer sounds (shorter length), and they have fewer obstruents and sonorants (Fig. 3, upper row). The effects in the latter three variables might be confounded by complexity: replies with more words will have more sounds. However, we find that even after controlling for complexity (Fig. 3, lower row), the words that are used by more speakers have fewer sounds, including both fewer obstruents and fewer sonorants. Controlling further, for length, the effects of obstruents and sonorants disappears (P > 0.35).

The correlations (z scores) in Fig. 3 are small and frequently reversed (any z score > 0 is opposite to expectation), suggesting only a weak effect of words’ attributes on word use. The weak correlations might reflect the effects of past selection itself: by removing “bad” words the variance among the remaining words in the characteristics related to ease of pronunciation is reduced, as is the covariation of these characteristics with the number of speakers who use them. As a consequence, the correlations are unduly influenced by other, background, random factors that affect how many speakers use a word but which are unrelated to ease of pronunciation—an effect consistent with Robertson’s (29) secondary theorem from population genetics. Nevertheless, even though small, the correlations in Fig. 3 align with the observation from the general lexicon that frequently used words, such as “you,” “me,” “he,” “she,” and “I,” and the number words tend to be short and easy to pronounce (30) and that languages spontaneously adjust to improve their transmissibility (31). However, we find that the highest frequency words for the meanings the FDS, D, and DS models best explain do not differ in their mean scores on the four pronunciation attributes (all P values > 0.18). This suggests that ease of pronunciation of words does not play a strong role in determining the eventual shape of the frequency distributions of numbers of speakers per word.

Characteristics of Meanings Do Not Differ Among Models.

We additionally examined characteristics of the meanings (as opposed to the words). Meanings that D best explained are no more or less likely to be a particular part of speech than expected from the overall data (P = 0.56), and the same is true of DS and FDS meanings (P = 0.87 and P > 0.82, respectively). Meanings’ mean “concreteness” (Materials and Methods) scores (32) are also similar among models (P = 0.73), as are their average ages of acquisition (33) (P > 0.10). However, among FDS meanings, the strength of posterior support positively correlates with its concreteness rating (r = 0.38, P = 0.0004, n = 55), while this relationship is not true of DS (r = 0.10, P = 0.10, n = 262) or D meanings (r = −0.16, P = 0.42, n = 26): concreteness seems to affect how well the frequency-dependent effect works.

We identified for each meaning the word used by the greatest number of speakers (“top word”) and then obtained the frequency of use of that word from the Corpus of Contemporary America Usage (COCA) (34). A word’s COCA frequency is thus not the same as the number of speakers in our study who used a particular word. Rather, a word’s COCA frequency measures how often it appears (relative to words for thousands of other meanings) in a very large sample of word use (SI Appendix, Fig. S1). The top words for the meanings the three models best explained do not differ in their average COCA frequency (geometric mean frequencies in COCA, P = 0.45): thus it is not the case that, say, words that D best explained are used less or more often in general and so on for the other two models. However, across all n = 418 meanings, frequency of use in the COCA (P < 0.0002) and concreteness (P < 0.0003) independently predict that a meaning will have fewer alternative words: speakers are more likely to use the same word for a meaning when that word is used frequently and its meaning is clear.

Discussion

Our results support Darwin’s (3) contention that the words that have survived long enough to become commonplace in everyday speech have got to their positions of favor via a process of natural selection, even if not always by what Müller (2) called their “inherent virtue.” Thus, the nonselective process of random drift, or roughly “say what others say,” although capable of producing distributions such as those seen in Fig. 1 A–C, does not provide a general description of word choice. When new lexical variants are continually being introduced into the vocabulary, as is generally true of language, drift is not strong enough on its own to elevate one or a small number of words to high levels. The answer to the question of how speakers come to use the same words, then, is not that they merely copy each other.

Directional selection can to some degree move people toward using the same words. This is seen in the lower H scores for words that directional selection explained and, more generally, in the weak tendency we observed for speakers to prefer shorter and easier to pronounce words. However, as with drift, speakers’ continual inventiveness with language perhaps removes any simple link between features of words and how often they are currently used: linguistically “good” words might only have arisen recently and therefore not yet achieved a high frequency, or some otherwise good words might be on their way out of use, having been replaced by others.

By comparison, positive frequency dependence provides a mechanism capable of explaining how speakers come to use the same word for a meaning. Under positive FDS a word’s inherent virtue—contra Müller and, we suspect, Darwin—appears to play a relatively small role; instead, words that, even if from random fluctuations, get used at higher frequencies seem to convert listeners’ minds to use them more than would be expected from their frequency alone, a so-called “conformist bias” (22, 35). This bias means that a word’s “fitness” (likelihood that a speaker will use it as opposed to some other word) continues to increase disproportionately as it becomes more common and eventually propels the word to fixation, that is, it becomes the sole word used for that meaning. Unlike with drift or directional selection, the increasing strength of positive frequency dependent selection continues despite the constant influx of new words. Indeed, at fixation, the force of positive FDS is greatest and so positive frequency dependence might give insight into how some words can remain paired with a meaning for hundreds or even thousands of years (7, 36, 37), far exceeding the time span of the possibly three to four generations that might separate the oldest and youngest speakers in a group [frequently used forms are also less buffeted by the effects of drift (11, 12)].

A positive frequency-dependent bias also provides an answer to a key puzzle of language, which is how a shared vocabulary can spontaneously self-organize among a group of speakers even when there are potentially many competing alternative words for each meaning, new words continually arise, and there is no external authority directing word use. Mathematical and computational models that have been proposed to explain this puzzle (38, 39), based on rules of copying and weighting of others’ (agents’) word use, can similarly yield a group of speakers converging on a common vocabulary. Our model shares some similarities with these agent-based models in that our model can be viewed as a version of a “voter” model on a fully connected network (40, 41). In our case, we allow for mutation of word use, and frequency dependence arises as a mean-field approximation rather than via interaction between agents. The existence of robust and undirected processes that can give rise to shared vocabularies helps to explain how a common language can scale up to millions or even billions of speakers (38) and may have applications to “artificial semiotic systems” (38), such as web tools, and the evolution of shared belief systems in society (39).

Our modeling assumes that the number of different word forms for a meaning is in a stochastic equilibrium fluctuating around some average maintained by the loss of existing words and the gain of new ones. This is, of course, an approximation, but consistent with this assumption, the number of different words per meaning correlates r = 0.87 for the 66 meanings that occur in both the LAMSAS and LAGS datasets, and the top two words for many of the meanings are the same (SI Appendix). Nevertheless, it is possible that some of our word distributions in which two or a variety of words is commonly used could eventually resolve to a single dominant word, or, in other cases, a contender to a dominant word might arise. Our modeling also treats each respondent as having just a single word for each meaning, when in fact most respondents would probably recognize all or nearly all of the various words that other respondents reported. Our assumption is that respondents are telling us the word they would be most likely to use.

It does not escape our attention that the mechanism of frequency dependent selection is also the mechanism that would govern most fads or the rapid spread of novel cultural forms and ideas. In this sense, language is laid bare as a cultural phenomenon, subject at least in part to fluctuations in usage that could often be little more than whimsy in origin. Indeed, such linguistic fads are seen, as in the rapid spread of slang and other vernacular elements. Why the core lexicon is relatively shielded from the ephemeral existence of most fads is an intriguing subject for lexicographers, linguists, sociologists, and others interested in cultural change. One possibility is that most language use is designed to convey factual information, while fads are at least partly driven by status and identity signaling that derives it force from novelty and thereby loses momentum as a phenomenon becomes common, and this might give insight into what constitutes a mere fad versus something that will become more lasting.

Materials and Methods

Models.

We suppose that the number of speakers who use each of the i = 1…k different words for a particular meaning (e.g., Fig. 1 A–C) represents the long-term outcome of a mutation-selection balance process in which new words or expressions continually arise at some rate θ and are continually affected by selection.

Let

$$W_i=\frac{x_i^{\left(1+s\right)}{w}_i}{{\displaystyle {\sum }_i\left(x_i^{\left(1+s\right)}{w}_i\right)}},$$ [1]

where x_i is the frequency of speakers in a population who use alternative form i (i = 1…k), s represents the strength of frequency dependent selection acting on i (s ≥ 0), w_i is a coefficient denoting the intrinsic fitness of word i independently of how many speakers use it, and the summation in the denominator is over all forms i. Defined this way, W_i is the expected frequency in the next generation of word i relative to the other words for a particular meaning.

When s = 0 and all w_i = 1, all words are equivalent, and Eq. 1 describes random drift. Drift supposes that a number of neutral alternative words exist for a given meaning, that new forms are continually introduced, and that speakers use words in proportion to the number of other speakers who use them.

Setting s = 0 but allowing w_i to vary among words yields a model of directional selection that incorporates drift but allows some words to be better or worse than others by an amount that depends upon the magnitude of w_i. The w_i values are not optimized or fit to the observed frequencies as this would assume that “better” words have higher frequencies. Rather, they are assigned to words at random as they enter the lexicon (see Model Estimation, below).

If s > 0, but all w_i = 1, Eq. 1 describes positive frequency dependent selection. Under positive FDS, the likelihood that a speaker will use a word increases disproportionately to the number of other speakers using it, an example of a rich-get-richer or preferential attachment mechanism (42). The strength of frequency dependence is characterized by the parameter s (Eq. 1), where positive frequency dependence corresponds to s > 0. Finally, we created a model that combines positive FDS with DS (FDS+DS).

Model Estimation.

We used approximate Bayesian computation (ABC) (43, 44) (SI Appendix) to estimate models’ abilities to predict each meaning’s frequency distribution of speakers. ABC is used widely in population studies because it can incorporate the effects of drift and selection acting within populations. ABC simulates models a large number of times with parameters drawn randomly from prior distributions, retaining the simulations closest to the observations. These retained runs sample from the posterior distribution of model parameters that are most likely to have given rise to an observed set of data, y.

The ABC design is (43):

• i)Draw Θ_I ∼ π(Θ)
• ii)Simulate x_i ∼ p(x| Θi)
• iii)Reject Θ_i if x_i ≠ y, where y are the observed data. The subset of draws from Θ that produce x_i similar to y define the posterior distribution of Θ, p(Θ | y).

Here, Θ is a vector corresponding to the parameters of the evolutionary model, π(Θ) is the prior distribution of Θ (SI Appendix), and the x_i are simulated from this prior. Alternative forms of the vector Θ define the D, DS, and FDS models, according to Eq. 1. The acceptance/rejection at step iii is achieved by use of a set of summary statistics, S(y), defined on the data (SI Appendix).

Simulations (step ii) of the DS model randomly associate the w_i terms with a word when it enters the lexicon, reflecting the possibility that, for example, a word newly entering the lexicon, and thus at low frequency, might nevertheless have w_i > 1. The prior distribution of these weights is centered at 1.0 and then falls away in both directions in a manner roughly corresponding to exponential decline following Ohta (45). The weights then influence, along with the effects of drift, how the word spreads through the population of speakers over generations of word transmission. For a description of the priors on the other parameters, see the SI Appendix.

Our simulations presume a genealogical process (from the perspective of the word) in which words move from speaker to speaker with one of three outcomes: the word might remain unchanged, it can mutate to a new form, or an existing word can replace the word another speaker uses. Over the long term, this leads to an equilibrium distribution of word frequencies that is governed by the forces of drift and selection, as represented in each model. Word frequencies vary from one generation to the next because fitter forms are more likely to be copied or because a speaker’s word might be replaced by another “fitter” word or by mutation, creating a new word.

Model Comparisons.

A model’s performance relative to the other models is assessed by its Bayesian posterior probability, given by

$$P\left(M_i|D\right)=\frac{P\left(D|M_i\right)p\left(M_i\right)}{{\displaystyle {\sum }_{i}P}\left(D|M_i\right)p\left(M_i\right)},$$

where $P\left(M_i|D\right)$is the probability of the data under model i, and $p\left(M_i\right)$ is the prior probability of model i. $P\left(D|M_i\right)$ is calculated as the proportion of simulations in which model i best describes the summary statistics. A model’s posterior probability is proportional to the number of simulations (out of a large number) for which the model best matched the S(y). We then record the “winner” for each meaning as the model with the highest posterior probability.

Linguistic Atlas Project Data.

All raw data are available via the Linguistic Atlas Project websites and handbooks. See SI Appendix, Materials and Methods. In addition, we make available all of our files and filtering criteria available at the Open Science Framework (https://osf.io), public project “MotherTongue.”

Meaning Characteristics.

COCA word frequencies.

We identified the word that was most commonly given for each of the meanings in our sample. We then consulted the COCA (34) and recorded that word’s frequency of appearance (written and spoken use), noting its rank-order position in the list.

Concreteness scores.

We obtained concreteness rankings for 40,000 commonly used English words and two-word expressions (32), where concreteness was defined as the extent to which the meaning refers to something that can be experienced directly through the senses (1–5 scale, where 5 is concrete and 1 is abstract). We found matches or near matches in this list to the highest frequency word for n = 292 of the meanings in our sample of n = 418. The concreteness scores correlate r = 0.94 with concreteness ratings obtained from an earlier study of 4,291 words (46).

Age of acquisition.

We recorded the mean age of acquisition (33) for each of our meanings. We found, as above, matches or near matches to n = 312 of our meanings.