Crowd wisdom enhanced by costly signaling in a virtual rating system

Significance

Costly signaling theory from ecology posits that signals will be more honest and thus information will be accurately communicated when signaling carries a nontrivial cost. Our study combines this concept from behavioral ecology with methods of computational social science to show how costly signaling can improve crowd wisdom in human, online rating systems. Specifically, we endowed a rating widget with virtual friction to increase the time cost for reporting extreme scores. Even without any conflicts of interests or incentives to cheat, costly signaling helped obtain reliable crowd estimates of quality. Our results have implications for the ubiquitous solicitation of evaluations in e-commerce, and the approach can be generalized and tested in a variety of large-scale online communication systems.

Abstract

Costly signaling theory was developed in both economics and biology and has been used to explain a wide range of phenomena. However, the theory’s prediction that signal cost can enforce information quality in the design of new communication systems has never been put to an empirical test. Here we show that imposing time costs on reporting extreme scores can improve crowd wisdom in a previously cost-free rating system. We developed an online game where individuals interacted repeatedly with simulated services and rated them for satisfaction. We associated ratings with differential time costs by endowing the graphical user interface that solicited ratings from the users with “physics,” including an initial (default) slider position and friction. When ratings were not associated with differential cost (all scores from 0 to 100 could be given by an equally low-cost click on the screen), scores correlated only weakly with objective service quality. However, introducing differential time costs, proportional to the deviation from the mean score, improved correlations between subjective rating scores and objective service performance and lowered the sample size required for obtaining reliable, averaged crowd estimates. Boosting time costs for reporting extreme scores further facilitated the detection of top performances. Thus, human collective online behavior, which is typically cost-free, can be made more informative by applying costly signaling via the virtual physics of rating devices.

One of the most appealing features of online communication is the high speed and low cost of sharing unfiltered opinions, ideas, and ratings. But theory predicts a validity crisis of cost-free communication: In both economics and biology, costly signaling theory suggests that to maintain reliability, communication systems must be based on costly signals (1–4), or at least on signals that are costly for dishonest signalers (5). Signaling cost ensures that cheating would not pay (or would not be possible) for signalers that are not strong enough and/or who are not sufficiently motivated to signal. This principle explains, for example, why male peacocks advertise their quality by growing a long-ornamented tail (3, 6), why offspring signal their nutritional needs by costly begging displays (7, 8), why among humans, job candidates advertise their quality by top-school diplomas (1, 9, 10), and why economic wealth may be advertised by conspicuous consumption (11, 12). In all of these cases, if signaling were cost-free, cheating would prevail and the information value of signals would have diminished.

In online rating, one can leverage the “wisdom of the crowd” to improve the quality of information, by exploiting the phenomenon that aggregate subjective ratings can be more accurate than the rating of any individual (13–15). In that case the prediction of costly signaling theory is subtler because signalers do not usually communicate to advertise their own quality or needs to gain something in return (such as a mate, food, or a job). Instead, they express their opinion or share information in an altruistic way, which does not seem to involve the conflict of interests between signaler and receivers that typically motivates cheating. But even if there is no motivation to cheat, there is, at best, ambiguous direct benefit to the rater in providing an accurate assessment of provider quality (16). Therefore, especially in the absence of a conflict or clear, direct benefits, signalers are likely to provide low-quality information. These considerations raise two hypotheses: According to rational action theory (17, 18) in a communication ecology where the benefits are diffuse and the costs are borne by the individual, the best strategy to improve the wisdom of the crowd (19) is to make rating as costless as possible to reduce barriers for raters to provide the best possible information. Alternatively, costly signaling theory would suggest the opposite dynamic (20): By imposing a cost to providing information and especially by imposing higher costs on reporting extreme ratings, only those who are confident in their assessment and highly motivated to share that assessment may be willing to pay. In this way, the cost of signal production can filter out unreliable cooperative signalers (21–25).

We tested these competing hypotheses by deploying costly signaling in the design of a communication system: We developed two online games in which players use services and provide ratings for these services. In the first game, subjects do not expect to gain benefits in return for providing an accurate rating (low incentive game). Such rating systems are ubiquitously deployed for rating goods and services on the internet. In the second game, subjects expect accurate rating scores to increase their financial gains (higher incentive game). Therefore, motivation is expected to be low in the first game and higher in the second one. In both conditions, we examine the effects of signaling time cost on crowd wisdom.

Results

Testing Costly Signaling in a Low Incentive Game.

In our first online game, players maneuvered a simulated car to collect coins. They received one cent for each coin collected. Roads were separated by lakes, and players had to ride a simulated ferry to cross each lake (Fig. 1A). The first two ferry rides were used as a training set, with delays of 20 s and then 4 s, to set a common baseline for ferry performance evaluations. Thereafter, we randomly varied the delays and speeds of ferry services. Some ferries arrived immediately and traversed the lake without delay, allowing subjects to complete the journey within 2 s. Other ferries were delayed in arrival and slow moving, requiring up to 40 s to cross (uniform distribution of times, 2–40 s). At the end of each ferry ride, subjects were prompted to rate their satisfaction with the ferry service on a scale of 0–100 before they could continue to play (Fig. 1A, Right). Total game duration was limited to 15 min. Subjects were therefore motivated to complete their ranking as soon as possible as this subtracted from their time to collect monetary rewards. Before the game, subjects were informed that ferry services will vary in speed and delay and were asked to accurately score their satisfaction after each service event. Game sessions were timed and synchronized to create an experience similar to that of a multiplayer online game (Methods, Synchronization of cohorts). In a survey after game completion, subjects were not able to reliably guess if their rating scores affected ferry performances (Methods, Postgame survey). Each individual used the ferry services several times (mean = 17.6 rides per subject). Thus, we were able to measure correlations between subjective ratings and objective service performance (total time to take the ferry) both within and across subjects (26). Since repeated rating scores are not independent measures, statistical evaluations were done at the subject level (Methods, Shuffle-statistics bootstrap 95% confidence intervals and Shuffle-statistics P values).

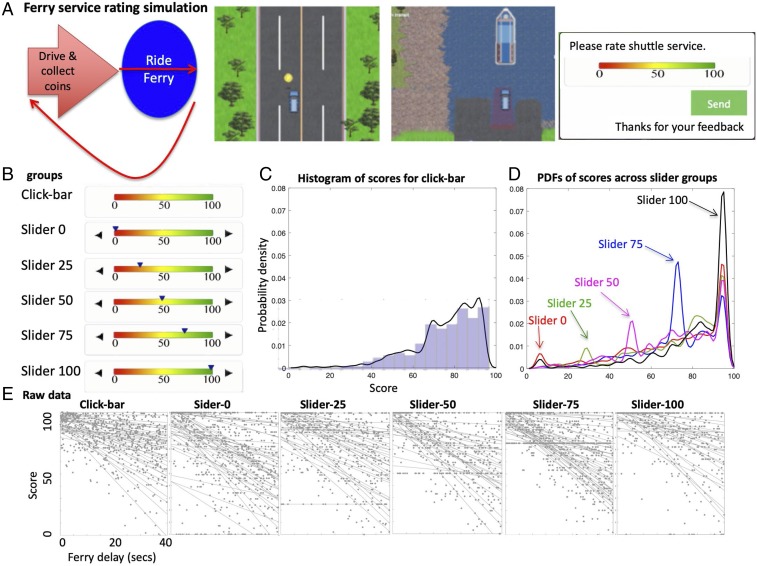
Fig. 1.

Slider initial position affects distribution of rating scores. (A) Ferry-service rating game. (Left) Flowchart of the ferry services simulation game. (Middle) Subject maneuvering a simulated car to collect coins. (Right) Waiting for ferry service to cross a lake. Subsequently, players were asked to rate their satisfaction with the ferry service along an analog visual scale of 0–100. (B) Rating devices of the six experimental groups (n = 40 subjects × 6 groups). (B, Top) Click bar. Sliders, including two push buttons that move the cursor (black triangle) either left or right at a constant velocity. Groups differ in the initial position of the cursor: either 0, 25, 50, 75, or 100. (C) Smoothed histogram of ferry rating scores for the click-bar group. (D) Smoothed histograms of ferry rating for the five slider groups. Peaks represent cases where subjects submitted default scores. (E) Scatterplot of ferry delays versus raw rating scores. Lines represent within-subject regression slopes. Horizontal clusters of markers indicate cases where subjects submitted default scores.

We manipulated signaling time costs via the “physics” of the graphic user interface that recorded the ratings. This allowed us to test if signaling costs can affect the correlation between subjective rating and ground truth. For the control group, we used a click bar where all scores from 0 to 100 could be given by an instant click on the screen (all ratings are equally “cheap”). This represents the conventional cost-free method used in most rating systems. For all other groups we imposed differential signaling time cost using “sliders”: A slider has an initial default position and “velocity,” which can be easily manipulated (Fig. 1B) to impose a feeling of “friction” while moving the slider. After each ferry ride, subjects were prompted to rate their satisfaction with the ferry by adjusting the slider position using two buttons: pressing continuously on either the left or right button moved the slider, at a constant velocity, toward the desired position on the scale. This moderate constant friction allows reporting of scores within less than 3 s. That is, time costs of reporting scores increased linearly with distance from initial slider position at the range of a few seconds.

We tested six groups, with n = 40 subjects per group, and with repeated trials adding to about 600–800 rating scores per group: the control group rated ferry rides using a click bar. The remaining five groups rated ferry rides using the slider with initial default position at 0, 25, 50, 75, or 100 (Fig. 1B). For each group the time cost of rating is proportional to the distance from these defaults. Setting an initial slider position at 0 imposes time costs that are proportional to the reported quality, an initial position at 100 imposes time costs that are inversely proportional to the reported quality, and setting an initial position near the center of the expected distribution of scores imposes time costs that are proportional to the deviation from expectation (either up or down). We planned to test whether each of these conditions differs from the no-cost click-bar condition. Note that the initial slider position also offered a cheap default score: subjects could simply accept it without even touching the slider at no added time cost.

Fig. 1C presents a histogram of ratings for the click-bar (zero cost) group, pooled over all subjects. As shown, the distribution of rating scores is strongly skewed toward the upper end of the scale (mean score = 78.3) despite the uniform distribution of ferry delays. This is a common observation for online rating systems where scores follow a J-shaped distribution (27, 28). In the slider groups, histograms of subjective ratings showed similarly skewed distributions, except that the distributions show a peak at 100 (an upper-edge effect of the device, Fig. 1D) and a second peak at the initial default position of the slider. This second peak represents cases where subjects most likely submitted their scores without changing the default slider position. Note that the height of these “default” peaks increases with the initial slider position (lowest at 0 and highest at 100), most likely due to subjects’ higher tendency to “accept” a default slider position that is similar to the rating score they had in mind. This result is consistent with our working hypothesis according to which the time cost motivates subjects to accept the default unless they have strong contrary opinion. Default ratings are also apparent in the scatterplots of ferry delays versus rating scores for each group (Fig. 1E). Within-subject linear regression estimates are plotted as lines in Fig. 1E. Interestingly, the scatterplots and regression lines appear tightest in the slider-75 group, where the default peak was closest to the population mean (mean score = 76.5, median = 81, pooled over all groups).

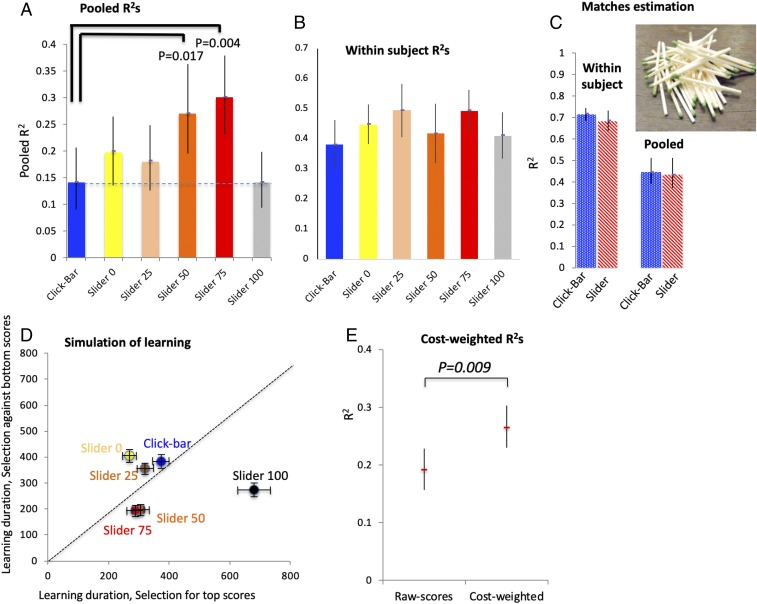
Fig. 2A presents the coefficients of determination, R²s, of ferry delays on rating scores pooled over all subjects. R²s for the slider-50 and slider-75 groups were about twice those in the click-bar group. Planned pairwise comparisons using shuffle statistics (i.e., shuffling subjects across groups; Methods, Shuffle-statistics P values) reveal a statistically significant difference in R²s between the click-bar group and the slider-50 and slider-75 groups (P = 0.017 and 0.004, respectively, Bonferroni adjusted direct P values for five comparisons). Differences in R²s between click-bar and other slider groups were not significant (slider 0: P = 0.203; slider 25: P = 0.3; slider 100: P = 0.104, uncorrected). Interestingly, despite the significant effect on the pooled correlations, R²s obtained within subjects were fairly similar and show no trends across groups (Fig. 2B). Therefore, the advantage of slider 50 and slider 75 appears to be in “calibrating” the rating scores at the crowd level. Since the initial position of slider 75 is close to the center of distribution of scores, this outcome is consistent with the notion that imposing time costs, proportional to deviation from expected reported quality should improve reliability via calibration. However, reliability could have improved for other reasons as well—e.g., slowing the rating action could have evinced increased accuracy. We therefore tested if the phenomenon can be replicated in a very different context, where the physical effect of the slider is preserved but rating is not associated with clear benefits or time costs during a game. To test this, we gave a neutral estimation task to a new group of subjects, by asking them to estimate the number of matches in an image (Methods, Design and programming of matches estimation task and Matches estimation task). We found that correlations between estimates and true number of matches obtained with a click bar were nearly identical to those obtained with a slider with an initial position at the center of the estimate’s distribution (Fig. 2C, n = 40 subjects × 2 groups, not significant). This negative result suggests that there was nothing particular about the rating device that could have driven the differences.

Fig. 2.

Evaluation of crowd wisdom across rating devices. (A) Pooled R² with 95% confidence intervals for each group. P values are Bonferroni adjusted. (B) Within-subject R² with 95% confidence intervals for each group. (C) Pooled and within-subject R² for matches estimation task, comparing click bar (blue, n = 40 subjects), and slider (red, n = 40 subjects). (D) Means and 95% confidence intervals for simulation of learning by an agent that selects and learns to prefer ferry services according to their rating scores. Learning duration is estimated by iterations it takes to reduce selected ferry delays by half. The x axis shows results of an agent that selects for top-scored services, and the y axis shows results for an agent that avoids the bottom-scored services. (E) R²s of raw scores versus weighted R²s of scores by time costs, pooled across all slider groups.

Evaluation of crowd wisdom.

Online rating systems are often used to leverage the wisdom of the crowd (13). Namely, aggregating judgments across subjects can often improve accuracy by balancing idiosyncratic biases across individuals when averaging observations. To determine if costly signaling also benefits these crowd estimates, we binned ferry delays into 20 performance categories according to their time delays (2-s bins: 1–2, 3–4, 5–6,…, 39–40 s). Within each bin we averaged the scores across subjects and calculated the R²s between those averaged scores and ferry delays across bins. As expected, the averaged R²s of the binned data were very high, (about 0.9) in all groups (SI Appendix, Fig. S1A). We can now ask two practical questions: First, how does the rating device affect the sample size needed before objective performance differences can be detected? Second, how does the rating device affect the efficiency of different selection regimes over time? For example, how fast can one learn to select top-performing ferries while sampling rating scores from different bins? We focus on sample size because rating systems are subject to a tradeoff between speed and accuracy: improving accuracy requires aggregating more rating data over time, at the expense of timely response (29).

To estimate the sample size needed for reliably distinguishing across objective performance groupings, we drew random samples of rating scores from binned groups of ferry performances and calculated averaged R²s for different “crowd” (sample) sizes. As shown in SI Appendix, Fig. S1B, in the slider-75 group a sample size of about six rating scores from each bin was sufficient to explain 75% of the variance in rating scores across performance groupings. In contrast, a sample of about 20 ratings from each bin was needed to reach the same level in the click-bar group. SI Appendix, Fig. S1C summarizes the differences in R²s across all sample sizes for each group. Thus, the benefit of costly signaling is also evident with respect to crowd wisdom.

To quantitatively evaluate how costly rating devices may affect the efficiency of different selection policies over time, consider an agent who needs to select ferry services on a regular basis. If service quality fluctuates it is critical to update the selection policy as soon as possible (based on small samples of ferry scores). To simulate such a situation, we consider each ferry performance bin as representing the performance of a particular ferry service provider (i.e., 20 providers with time delays of 1–2, 3–4, 5–6 s, etc.). We then simulated a dispatcher who needs to select the best (or to avoid the worst) provider by evaluating the provider’s rating scores. The dispatcher initially deploys the providers at random with equal probability and, in turn, receives subjective rating scores on user satisfaction. The dispatcher updates the probability of selecting a provider by, either increasing it for providers that received the top scores (selection favoring top ratings), or alternatively, reducing it for those that received low scores (selection avoiding bottom ratings). As an estimate of learning speed, we computed the number of ratings needed for the dispatcher to cut the expected ferry delays by half.

As expected, estimates of learning speed mirrored the correlations presented earlier: the simulated dispatcher learned faster using rating data obtained with slider 75 compared with click bar (Fig. 2D). Learning was particularly slow with slider 100, where time costs were negatively proportional to the reported quality. Interestingly, costly rating devices learning speed varied strongly across selection regimes: Fig. 2D compares learning durations for a dispatcher that favors providers with top ratings (horizontal axis) versus a dispatcher who avoids providers with bottom ratings (vertical axis). We see an asymmetry in learning durations across the slider groups: Mean learning durations for sliders 50, 75, and 100 are below the diagonal, whereas sliders 0 and 25 are above the diagonal. Therefore, simulation suggests that with high initial slider position, it might be easier to avoid poor ferry services, and with low initial position, it might be easier to pick top ferry services. In the absence of cost (click bar) the two selection methods performed the same.

Since scores that took longer to report (due to their distance from initial position) appear to be more informative than scores that took little or no time to report, it makes sense to test, more generally, if weighting each rating score by its time cost can improve correlations. We pooled all data for the slider groups (n = 3,880 scores from 200 subjects), and calculated the R²s between scores and ferry delays either as is, or after giving each rating score a weight based on its time cost (distance from initial slider position). We found that the R²s between ferry delays and rating scores is significantly higher when scores are cost weighted (Fig. 2E, P = 0.009, bootstrap analysis; Methods, Shuffle-statistics P values). Some, but not all of this effect is due to removal of default scores (where time cost is 0). For example, in the slider-75 group, removing default scores increase pooled R² from 0.30 to 0.37, but the cost-weighted correlation increased it further to 0.43.

Manipulations of cost functions.

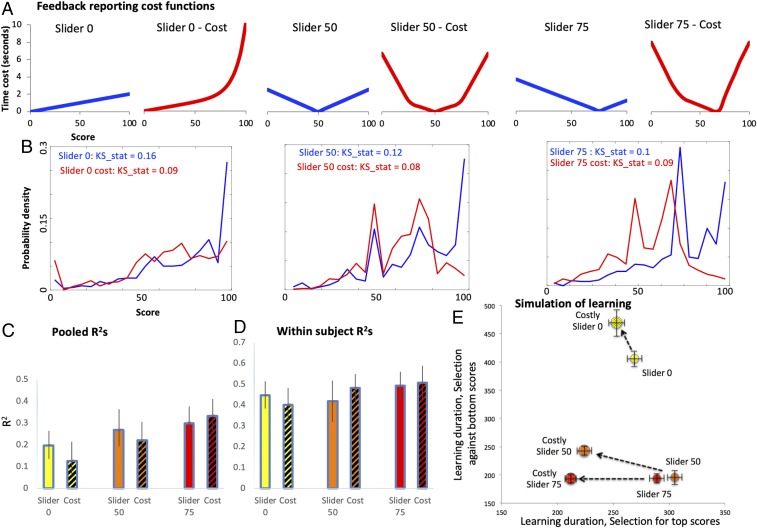
Given that imposing time costs on reporting extreme scores appears to increase reliability, we sought to examine whether imposing even greater time costs might further improve reliability. To do this we experimented with variable-friction sliders as shown in Fig. 3A. For each slider we set friction to be an increasing function of the deviation from its initial position. In this way, we imposed a steep time cost of up to 10 s for reporting extreme deviations from the default. We tested three groups: slider-0 cost, slider-50 cost, and slider-75 cost with n = 40 subjects per group, and compared results to those of the corresponding low-friction slider groups. In all three “slider-cost” groups, imposing higher friction eliminated high concentrations of scores at the top (Fig. 3B and SI Appendix, Fig. S2) and shifted the distributions of rating scores toward a normal distribution, as indicated by the lower Kolmogorov–Smirnov statistics (Fig. 3B). However, despite the improvements in distribution shapes, imposing high time costs on reporting extreme scores did not affect R²s (Fig. 3 C and D). Still, the effect of costs at the margins of the distribution of scores changed the efficiency of different selection policies over time (Fig. 3E): In all groups, increasing time cost shortened simulated learning duration for selecting services based on top scores, compared with baseline (see arrows in Fig. 3E). In contrast, selecting against bottom scores, learning duration was either longer (for slider 0 and slider 50) or unchanged (for slider 75). This asymmetry has a simple explanation: In our ferry simulation game, subjects were willing to pay high time costs for reporting top scores but not for reporting bottom scores (see slider-50 cost and slider-75 cost in SI Appendix, Fig. S2).

Fig. 3.

Evaluation of crowd wisdom using variable-friction devices. (A) Cost functions of scores, comparing constant-friction sliders to variable-friction devices. (B) Probability densities of rating scores that correspond to the cost functions above. Kolmogorov–Smirnov statistics represent deviation from normal distribution. (C) Pooled R²s comparing sliders with the same initial positions but different cost function. (D) Same as in C within subject. (E) Means and 95% confidence intervals for simulation of learning as in Fig. 2D.

Testing Costly Signaling in a Higher Incentive Game.

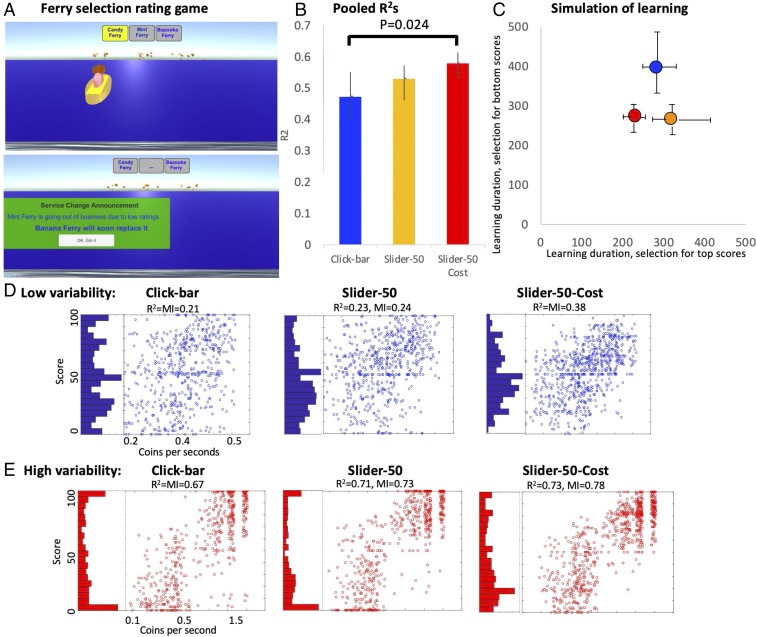
According to costly signaling theory, the failure to improve R²s by imposing higher signaling time costs may be explained by a possible ceiling effect of signaling cost relative to the benefit: In the current game, signalers’ expectation of benefits in return to signaling effort should be low. Therefore, perceived net benefits, and hence motivation, should diminish quickly with signaling costs, making extreme scores too costly (see Discussion). However, if the perceived benefit of signaling can be enhanced, imposing a steeper cost function should improve R²s. To test this prediction, we developed a fast-pace game, where ferries from three different companies bring, in turns, coins to the player (Fig. 4A). As in the previous game, subjects received a one cent bonus for each coin, but here the rate of collecting coins is four times faster, gains are directly linked to ferry companies’ performance, and subjects were instructed to score ferries accurately to maximize their gains. Subjects were not allowed to directly select companies, but companies that perform poorly were occasionally replaced by new ones. This replacement, in addition to changes in ferry performance during the game, were designed to create the false impression that accurate rating scores should increase monetary gains. In a survey after the game, most subjects (incorrectly) guessed that the rating scores they provided had affected, or might have affected ferry performance (Methods, Postgame survey).

Fig. 4.

Evaluation of crowd wisdom in a selection/rating game. (A, Top) Ferries from three different companies bring coins at different rates. (Bottom) Replacement of poorly performing companies creates an impression of selection via players ratings. (B) Pooled R² with 95% confidence intervals for each group. Sliders cost functions are the same as in slider 50 and slider-50 cost in Fig. 3A. P values are Bonferroni adjusted. (C) Simulation of selection regimes (as in Fig. 2D). (D) Histograms and scatterplots of rating scores vs. ferry performance during the first 18 trials with low variability of ferry performance. Performance units are coins per second presented on a log scale. MI, mutual information. (E) Same as in D for trials 19–36 with high performance variability of 0.1–1.5 coins per second.

The game included 36 ferry trips. In trips 1–18 each ferry brought two coins in each trip, and trip durations (ferry speed) varied between 4 and 10 s (0.2–0.5 coins per second). Then, during trips 19–36, we introduced a step increase in variation: We increased the range of trip durations to 1–14 s and introduced variability in the number of coins each ferry brought in each trip in the range of 1–3 (0.1–1.5 coins per second). In a pilot study, we found that the center of the distribution of scores in this game is fairly close to the center of the scale (mean score = 54), and we therefore set the slider default position at 50. We tested three groups with 40 subjects per group: click bar, slider 50 (low friction), and slider-50 cost (high friction), using the same cost functions as in Fig. 3A.

As predicted by costly signaling theory, R²s were highest in the slider-50-cost group (Fig. 4B). Planned pairwise comparisons using shuffle statistics reveal a statistically significant difference in R²s only between the click-bar group and the slider-50-cost groups (P = 0.024, Bonferroni adjusted). We next evaluate the efficiency of different selection policies over time in each group (Fig. 4C). As expected, rating scores obtained from the slider-50-cost group gave the shortest learning durations. Note, however, that both slider groups were superior to the click bar in the selection regime that avoided bottom ratings. In contrast, only slider-50 cost was superior to click bar in the selection regime that favored top ratings. This outcome is similar to that of the previous experiment (Fig. 3E). Here too, subjects were willing to pay high time costs for reporting top scores, but less so for reporting bottom scores.

Finally, we look at rating behavior separately during the low variation trials 1–18 and during the later high-variation trials (Fig. 4 D and E). During the early, low-variation trials, scatterplot of ferry performances (coins per second) versus rating scores show tighter determination of ferry performance on rating scores in the slider-50-cost group compared with both the click bar and the slider 50, with R²s almost two times higher in the cost group (Fig. 4D). In contrast, after the transition from low- to high-variation trials (Fig. 4E) the distribution of rating scores remained broad only in the slider-50-cost group, but became bimodal in the click bar and slider 50, with clustering at the margins. Such polarized distribution of rating scores should decrease information, and indeed, here the benefits of the costly slider are better captured by mutual information compared with R²s (Fig. 4E). In sum, in this dynamic setting the variable-friction slider reduced the scatter in the center of the distribution when variance in service performance was low and prevented clustering at the margins of the distribution after the transition to high variance. It remains to be tested if the benefits of imposing time costs would generalize across different types of dynamic transitions in rating systems.

Discussion

Overall, comparing our results to the predictions implicit in rational action theory and costly signaling theory, the majority of evidence suggests that rising costs for extreme scores yields greater crowd wisdom even when there is no conflict or competition among users. However, there appeared to be an asymmetry: boosting time costs for reporting very low scores had some negative effects, which is consistent with rational action theory. Indeed, if raters have initially little or no motivation to report low scores, increasing the cost of reporting such scores may reduce their rating effort even further. We therefore suggest that tuning signaling time costs should be viewed as an optimization problem of fitting appropriate costs to selection regimes and to the expected motivation of the users (30).

More formally, our approach may be compared with existing models of costly signaling of need (7, 31) where signalers differ in the benefit they expect to gain in return for their signaling efforts. In such models the benefit function increases monotonically with diminishing returns, approaching an asymptote (Fig. 5A). Note that although the asymptote is lower for, say, a moderately hungry bird chick and higher for a very hungry chick, both chicks always want more food (with declining but always positive hunger). In the absence of signaling cost, all chicks would beg with maximal intensity. But since begging calls may be energetically costly, the optimal begging intensity lies at the point where the difference between benefit and cost is maximized (Fig. 5A). Here, signaling cost makes the begging calls honest and meaningful (32), and the parent can distinguish between different levels of needs.

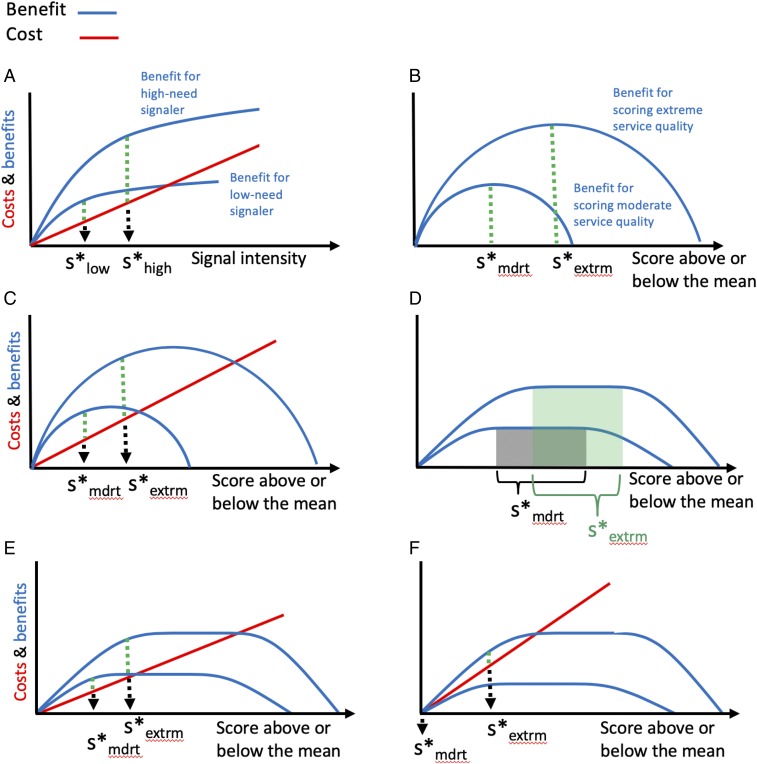
Fig. 5.

A graphic model of costly signaling of need (following ref. 32) adapted to the case of costly scoring of service quality. (A) In the original model (31) the term “need” was derived from the notion that offspring in a great need benefit from receiving extra food more than satiated offspring and can therefore invest more in costly signaling. In a rating system, the differential benefit effect of signaling low and high need may be replaced with scoring two different levels of either low or high service quality satisfaction: moderate versus extreme (e.g., service perceived as 1 versus 2 SD below or above the mean). (B) When raters are motivated to signal reliably they perceive the benefit curves as decreasing beyond the point representing true service quality, forming different peaks, and thus different signaling optima for scoring moderate versus extreme service qualities (S*_mdrt versus S*_extrm, respectively). (C) Under the same conditions as in B, adding cost does not increase reliability (does not increase the distance between S*_mdrt and S*_extrm). (D) When perceived service quality is not clear, the benefit peaks are flattened and there is no single optimum, creating an overlap between the optimal scoring range of moderate and extreme service qualities, which reduces reliability. (E) Under the same conditions as in D, introducing signaling cost sets clear different optima for scoring moderate and extreme qualities. (F) When signaling cost exceeds the benefit for moderate scores, raters may only score extreme qualities and refrain from scoring moderate ones.

In a rating system, we consider signaling intensity as the distance of a rating score from the median score in either direction. In this scenario, if rating behavior were to follow the model of signaling depicted in Fig. 5A, we might expect a bimodal distribution in the absence of cost. That is, each signaler might be motivated to give an extreme rating of 0 or 100 even for slight deviations from average quality under the belief that the benefits to signaling increase with signaling intensity because extreme scores are more likely to affect the behavior of the service provider. However, this is not what we found. Even with the noncostly click bar, the vast majority of rating scores were not at the extremes, suggesting that many raters’ benefit function was unlike that of the “greedy” chick. That is, most raters had no inherent incentive to inflate scores. Rather, it is possible that they tried to signal service quality as reliably as they could, believing that rating accuracy was more effective than extremeness in evincing the best response from the service provider. If this was the case, each rater should expect maximal benefit for giving accurate scores (Fig. 5B). This is akin to assuming that the chick in the “signaling of need” example (Fig. 5A) has an optimal meal size beyond which the benefit of receiving extra food becomes negative (say, through feeling bloated and sick or regurgitating the nutrition). Note that under such a scenario, even in the absence of signaling costs (Fig. 5B), the optimal signaling intensity (score) is clearly different for different service qualities, forming a reliable scoring system. Moreover, adding signaling costs will shift scores closer to the mean, potentially negatively influencing information quality (Fig. 5C). This scenario would be consistent with rational action theory where scoring reliability is optimal in the absence of cost.

That said, it has been suggested that even when signalers have no reason to cheat or to signal unreliably, they are still prone to make errors if they do not have full information (22, 23, 30). In our rating setup this is expected because human perception of service quality is affected by multiple factors, from subjective attitude to perceptual and memory constraints. This implies that raters do not know the accurate location of the peak of the benefit curve for each ferry, which realistically creates a wide flat peak of the benefit curves as described in Fig. 5D. Having such flat peaks results in high variance in rating scores, and since the flat area for moderate and extreme service qualities can partially overlap, it is expected that even small variation in individual attitude toward the service would result in a broad range of scores for the same service quality. Here, introducing a signaling cost becomes beneficial, as it forms clear, different optimal levels of signaling, thus calibrating variation between raters and improving reliability (Fig. 5E). In some other cases, introducing signaling cost can also favor “no scoring” (and accepting the default slider position) unless service quality is clearly good or bad, making scoring sufficiently beneficial to outweigh the cost (as illustrated by Fig. 5F). Although in practice the exact shapes of the benefit curves in rating systems are unknown, it is easy to experiment with different cost functions, as we did in this study, and then design an optimal signaling cost function empirically.

Our study suggests that costly signaling theory may be implemented to design more reliable communication systems. Signaling cost can improve collective estimates and, in turn, smaller sample sizes may be used to detect differences in satisfaction ratings under higher cost regimes. This may be worth further investigation beyond virtual rating systems because the rate of social learning across distributed social networks, where feedback is ongoing, may strongly depend on the reliability of information obtained from small samples (19, 33, 34). In addition to extending costly signaling theory, these results should inform online rating systems currently being deployed in e-commerce and elsewhere, which are currently polluted with low-quality scores (35). We hope that the experimental approach presented here can be replicated, elaborated, and further generalized to improve crowd wisdom in large-scale communication systems.

Methods

Subjects.

A total of 520 subjects were recruited via Amazon Mechanical Turk (M-Turk). We required subjects to be adult (over 18 y old) and to reside in the United States. All subjects remained anonymous, and we did not collect any demographic information. Subjects electronically signed an informed consent before playing the simulation game (or evaluating photos of matches). Once a subject finished the simulated ferry game (or matches evaluation), we assigned him/her with a completion credential, which was used to exclude the subject from participating in the study more than once. These experiments were approved by both the Institutional Review Boards (IRBs) of The City University of New York (IRB 2015–0185) and Princeton University (IRB 0000008221).

In rare cases (1 of 80 in the matches game and 6 of 320 in the ferry game), subjects failed to complete the task. In these cases, we compensated the subjects and excluded the partial data obtained from them.

Design and Programming of Ferry Simulation Game.

Subjects played the games using their web browsers. Games were implemented using WebGL technology. Subject actions were automatically recorded to MySQL database tables for analysis. For the low incentive game, server-side code was programmed using PHP and MySQL. Client-side code was programmed in JavaScript using PIXI-JS library for animation. For the higher incentive game, client side was programmed in Unity.

Synchronization of cohorts.

Game sessions were timed and synchronized to create an experience similar to that of a multiplayer online game. Cohorts of subjects were recruited via M-Turk for each session about 20 min prior to each session onset. Once a subject logged in, a virtual “waiting room” was presented, with a timer countdown to the beginning of the session. At time 0, a “gong” sound was played, and subjects were then presented with a 1-min video with technical instructions for maneuvering the simulated car. The game then started promptly.

Ferry services games.

Low incentive game.

Subjects drove a simulated car on a road, with coins presented in random locations on the road. Subjects used their keyboard to control speed and to steer the car left or right to collect coins. They received a one cent bonus for each coin collected. After driving a fixed distance, where up to 5 coins could be collected (over about 10–25 s), the car reaches a lake. It is then kept on hold until a ferry arrives and carries the car over the lake. The ferry then unloads the car, and the player is prompted to score the ferry. After that, the player gains control of the car, driving on the road again to collect more coins. The game continues for 15 min in this manner, which allows up to 24 ferry rides (trials) and collecting up to 120 coins. We coupled the waiting time with ferry travel speed, such that ferries with short delays moved fast, and those with long delays moved slow, to generate a linear scale of overall service delays. The fastest ferry speed was 2 s, and additional delays varied uniformly between 0 and 40 s. The first 2 ferry rides were used to familiarize the subjects with the game, and were excluded from the analysis: The first was set to a total of 20-s delay and the second to 4-s delay. Thereafter delays were selected at random. Subjects were compensated $2.00 for playing the simulation plus the bonus for collected coins.

Higher incentive game.

Ferries from three different companies were bringing coins to the subject in turn. Each company had a distinct ferry color code. Ferry trips varied in their speed and in the number of coins they carry in each trip. The game was composed of 36 trials. In trials 8, 15, 21, 27, and 32, the ferry company with the lowest performance was replaced with a new company. Replacement was announced one trial before it via a popup message which stated “X ferry is going out of business due to low ratings. Y ferry will soon replace it.” During trials 1–18 all ferries carried 2 coins, and their speed ranged between 4 and 10 s. During trials 19–36, ferries carried between 1 and 3 coins, and their speed ranged between 1 and 14 s. Game duration was about 10 min. Subjects were compensated $2.00 for playing the simulation plus $0.74 bonus for the 74 coins received.

Rating device (slider and click bar).

After each ferry ride subjects were presented a rating device. The click bar allows one to click anywhere on a scale from 0 to 100. The slider requires one to press a button to move the slider left or right in that same range starting from its default starting position. Friction of the slider was set by adjusting the velocity of the moving slider. After selecting a rating, subjects had to click a submit button to continue the game. While all subjects were forced to submit a rating, they were allowed to submit their rating without altering the default value presented to them.

Design of high-friction sliders.

In the slider-0-cost group, slider design and instructions were the same as in the original slider-0 group. In slider-50-cost and slider-75-cost groups, high friction (low velocity of slider) occurs close to the origin and can be confused with a technical glitch (nonresponsive widget). We therefore designed a scale with two distinct ranges: at the center (between 20 and 80), the widget presented a numeric 0–100 scale and friction was low (slider moves faster). At the top and bottom 20% edge, labeled as “super” and “bad,” were given high friction (slider moves slower) (Fig. 3A, Top Right). Subjects (n = 40 per group) were instructed to use these extended ranges to report ferry rides where they were particularly satisfied or frustrated with the ferry service.

Ferry services game groups.

Subjects were instructed to score their satisfaction with ferry services accurately: “Ferry services will change over time and occasionally they may be delayed. In the end of each ferry ride you will be prompted to score your satisfaction of the ferry performance. Please use the rating device to report your satisfaction accurately after each ferry ride.” All subjected were presented with the same scale for rating, ranging between 0 and 100. Each group included 40 subjects. Groups used either the click bar or sliders with starting positions 0, 25, 50, 75, or 100.

Design and programming of matches estimation task.

Piles of matches were placed on a dark surface and photographed by D.C. Images were then cropped and presented serially using the same WebGL mechanism as described above.

Matches estimation task.

Subjects were first presented with a 1-min video with technical instructions. They were then presented serially with the images of matches, ranging between 48 and 1,006, in a pseudorandom order. Each image was presented with a rating device with a scale ranging between 0 and 1,200. Subjects reported their estimate using either a click bar or a slider, and then pressed the submit button to evaluate the next image. Subjects were compensated at the rate of $2.00 for completing this task, which took them about 10–15 min.

Matches estimation groups.

Control subjects were instructed as follows: “Look carefully at each image and try to assess the number of matches displayed. Do not try to count, just estimate by observing. Then click on the bar to report your estimate. You may click again to correct, and once ready click the submit button.” One group of 40 subjects estimated the number of matches using a click bar. A second group of 40 subjects were presented with the same matches estimation task, but estimated the matches using a slider, with initial position set at 500. Instructions for this group were “look carefully at each image and try to assess the number of matches displayed. Do not try to count, just estimate by observing. Then push left and right buttons of the slider to report your estimate. Once ready click the submit button.”

Data Analysis.

All data analysis was done with MATLAB 2017.

Correlation analysis.

Since variables used in this study, ferry speed, duration, and rating scores, are continuous, we used (Pearson R)² to assess accuracy because rating scores are correlated against a continuous (metric) variable (the ferry delay and speed). However, since we evaluate relative service quality, Spearman rank correlations might also be appropriate. In practice, however, in our data Pearson and Spearman correlations give nearly identical results.

Crowd estimates as function of sample size.

Using 20 bins of ferry delays, we randomly draw with replacement from the ratings submitted by subjects, with N = 2, 3, …, 35 per bin (n = 35 was the smallest number of ratings obtained per bin). For each of the 20 bins, we averaged the sampled ratings to obtain “crowd estimates” in each bin. We then computed R²s of these crowd estimates with the delays across the 20 bins. For example, for a sample (crowd) size of n = 30, we averaged the 30 scores for each bin and then computed the R², comparing those average scores to the mean ferry delay over the 20 bins. We repeated this procedure 1,000 times, each time taking a new random sample and computed R². The average of these 1,000 random draws for different sample sizes resulted in the curves shown in Fig. S1B. We also computed the area under this curve (AUC) for a single draw (AUC is the R² value averaged across sample sizes). We then computed the 5% and 95% bounds across 1,000 iterations. This gives a mean and 95% confidence intervals of AUC across the 1,000 draws (Fig. S1C). For the matches estimation task, we calculated AUC as described above, instead of the 20 bins of ferry delays we used the 20 images of matches.

Shuffle-statistics bootstrap 95% confidence intervals.

Bootstrapped error bars for mean R² and for AUC were computed by resampling subjects with replacements within each group. We then computed the 5% and 95% bounds across 1,000 iterations. For example, for computing 95% confidence interval for the pooled R²s in the click-bar group (n = 40 subjects), we randomly selected subjects in this group, with replacements, 40 times. We then computed the pooled R²s for rating scores across those 40 randomly selected subjects. We repeated this to obtain 1,000 pooled bootstrap R²s, sorted them, and set indexes 50 and 950 as the 5% and 95% confidence interval. Note that error bars were often asymmetric, particularly when close to the upper bound.

Shuffle-statistics P values.

To assess statistical significance of pooled R² difference between two groups (say between click bar vs. slider 75), we first computed R² for each group and calculated the absolute difference between them. This baseline difference was then used to judge the differences between random cohorts. For each run, we randomly selected half of the subjects of each group to create a mixed group. We computed R² for this mixed group, and then again for a second randomly mixed group. We then calculated the absolute difference between R² (or AUC). We repeated this 1,000 time to obtain 1,000 estimates of random R² differences, which we then compared with the baseline. The proportion of cases where the bootstrap estimate difference was larger than the baseline was our direct P value estimate. For assessing statistical significance of AUC differences between two groups we repeated the same procedure as above, replacing R² with AUC.

Simulation of learning.

For each experimental group, we simulated a dispatcher who had to select among ferry service providers and observed a subjective rating for each ferry ride. The corresponding objective ferry delays of the provider were invisible to the dispatcher. The task of the dispatcher was to select the ferry providers with the shortest delays or to avoid those with long delays. There were 20 ferry providers spanning the range of delays (the same 20 bins as before). Note that within each bin ferry delays were similar, but the observed rating scores were noisy.

The dispatcher aimed at either choosing the fastest, or at avoiding the slowest ferries by considering (sampling) the rating scores. At any point in time the dispatcher selected a provider i with probability p_i. A rating for this choice was obtained by drawing at random from the subjective rating collected online from the ith delay bin. Initially, p_i = 0.05 for all i = 1, …, 20. After observing 40 ratings the dispatcher iterated on the selection policy by updating the probabilities p_i as follows: for selection for top scores, increment the probability, p_i ← p_i + 0.005, for the provider i with the highest rating among the 40 draws. For avoiding bottom scores, decrement the probability, p_i ← p_i – 0.005, for the provider i with the lowest rating among the 40 draws. Then renormalize the probabilities, p_i ← p_i/sum_{i = 1:20} p_i; compute the expected mean of sample ferry delays according to the current probabilities, and repeat the process by drawing another 40 ratings as before. Keep running iterations, and stop when the expected mean of sampled ferry delays is reduced by half.

Postgame Survey.

Low incentive game.

A random sample of 234 participants was presented with a survey immediately after the game. The survey question stated: “The study design divided players into two groups. In one group, feedback affected ferry performance, in the other group ferry performance was random. To which group do you think you were assigned?” A total of 46% correctly stated that ferry performance in their group was random. A total of 28% stated that rating scores have, or might have affected ferry performance in their group. The remaining 26% could not tell.

High incentive game.

The same question above was asked of sample size = 100. A total of 57% wrongly stated that rating scores have, or might have affected ferry performance in their group. A total of 30% stated that ferry performance in their group was random, and the remaining 13% could not tell.

Data Availability.

All data and code are available at Matlab files at the Harvard Dataverse: Ratings of simulated ferry services and matches estimation (2018); doi: 10.7910/DVN/OCYAPW (https://dataverse.harvard.edu/dataverse.xhtml?alias=AffectiveRatingData) (36).