Direct observation of individual tubulin dimers binding to growing microtubules

Significance

Microtubule polymerization dynamics are fundamental to cell migration and cell division, where they are targets for chemotherapy drugs. Despite significant progress, the precise structural and biochemical events occurring at growing microtubule tips are not well defined, and better understanding is necessary for discriminating mechanisms of microtubule dynamics regulation in cells. Here, we visualize individual tubulin subunits reversibly and irreversibly interacting with dynamic microtubule tips, and thereby directly measure tubulin plus-tip kinetics. By analyzing plus-tip residence times of wild-type and mutant tubulin, we characterize the relative contributions of longitudinal (along protofilaments) and lateral (between protofilaments) bond energies to microtubule growth. This work provides insight into microtubule tip structure and potential modes of microtubule dynamics regulation.

Abstract

The biochemical basis of microtubule growth has remained elusive for over 30 years despite being fundamental for both cell division and associated chemotherapy strategies. Here, we combine interferometric scattering microscopy with recombinant tubulin to monitor individual tubulins binding to and dissociating from growing microtubule tips. We make direct, single-molecule measurements of tubulin association and dissociation rates. We detect two populations of transient dwell times and determine via binding-interface mutants that they are distinguished by the formation of one interprotofilament bond. Applying a computational model, we find that slow association kinetics with strong interactions along protofilaments best recapitulate our data and, furthermore, predicts plus-end tapering. Overall, we provide the most direct and complete experimental quantification of how microtubules grow to date.

Microtubules (MTs) are cytoskeletal polymers of αβ-tubulin that play fundamental roles in cell structure, mitosis, and intracellular trafficking (1, 2). Dynamic instability—the stochastic switching between phases of growing and shrinking—depends on the GTPase activity of tubulin subunits, is essential for MT function, and is directly targeted by multiple anticancer drugs (3–6). A broad understanding of MT dynamics has been established through computational modeling (7–10), structural studies (11, 12), and reconstitution assays (13–16). MTs grow through the net addition of GTP-bound tubulin to the plus-end. Incorporation into the lattice stimulates the GTPase activity of tubulin subunits, destabilizing the lattice behind a stabilizing cap region that is enriched in GTP and GDP-P_i. Loss of this cap exposes the labile GDP lattice and causes catastrophe—the switch from growing to rapid shrinking.

Several basic aspects of MT dynamics remain poorly understood; consequently, a quantitative “microscopic” understanding of MT dynamics remains elusive. Lack of knowledge about structure and biochemistry at the MT end continues to pose major obstacles. MTs typically contain 13 linear protofilaments (head-to-tail assemblies of tubulin) that associate side by side to form a hollow tube. MTs do not grow in an orderly spiral/helixlike manner. Instead they grow raggedly, with some protofilaments extending beyond others (17–20). This variable and uneven end structure means that tubulins landing on the tip can be stabilized to different degrees depending on the number of intra- and interprotofilament contacts they make (13). Adding to this configurational complexity, the tubulin subunits themselves undergo conformational changes during and after their addition to the MT, and these changes modulate their biochemical properties in unknown ways (2). The poorly understood structural and biochemical heterogeneity at the tip makes it difficult to infer microscopic states and biochemical rates from measurements of MT dynamics and structure (13, 21–23).

Computational kinetic models can, in principle, fill this gap by providing a microscopic “movie” of MT dynamics, based on assumptions about the underlying biochemistry. By fitting predicted growth rates to measured ones, recent applications of these kinds of models have provided estimates for the strength of lateral and longitudinal lattice contacts (8, 9). Computational models have also shown how the springlike bending properties of tubulin can influence the structure of MT ends and the kinetics of catastrophe (7–9, 24, 25). However, despite these important contributions, a consensus molecular model is still lacking, in large part because different groups make different and sometimes conflicting assumptions about the biochemical rules governing MT growth, shrinking, and switching (7, 11, 13, 20, 25–27). Even within the same set of assumptions, the predicted strength of longitudinal and lateral interactions in the lattice depend strongly on the assumed rate at which tubulins land on the MT end (8, 28). Thus, there are insufficient experimental constraints for computational models to unambiguously describe the heterogeneous biochemistry that underlies MT growth and dynamics.

Single-molecule measurements have the potential to distinguish kinetically distinct subpopulations that are blurred together in ensemble measurements (29–31), but to date, numerous technical difficulties have prevented the extension of these methods to tubulin and MTs. The free-tubulin concentrations required for growth, the fast kinetics of assembly, and the fact that a focal-limited spot of a MT contains ∼500 tubulins hamper fluorescence measurements. Optical trapping-based methods having better spatiotemporal resolution have been applied, but they detect association events indirectly and have provided conflicting results (15, 21). These experimental limitations mean that it has so far not been possible to resolve the ambiguity inherent to computational models by directly observing, with high temporal resolution, individual tubulins interacting with the growing tip.

In the present work, we overcome the longstanding challenge of single-molecule tubulin measurements by applying two recently developed technologies: recombinant tubulin (32–35) and interferometric scattering microscopy (iSCAT) (36–39). We first created biochemically homogeneous populations of tubulin subunits sparsely labeled with 20-nm gold nanoparticles. We then visualized dynamic MTs label-free using iSCAT, and watched in real-time at high frame rates as the gold-labeled subunits transiently bound to the tips. In this way, we directly quantified the rates of tubulin association and dissociation. Interestingly, the transient dwell times of tip-bound tubulin split into two subpopulations, indicating that our measurements are reporting on two classes of binding sites at the MT tip. Experiments using mutant tubulin demonstrated that perturbing the interprotofilament contacts reduces the fraction of long dwell-time events. We thus interpret our fast and slow events as those having zero and one lateral contact, respectively. Applying a computational kinetic model, we arrived at a self-consistent parameterization of MT growth that supports the formation of ragged and tapered tips. Overall, our approach provides quantitative insight into the long-elusive tubulin–MT interactions that underlie MT growth and dynamic instability.

Results

Monitoring Individual Tubulins Within Growing MTs by iSCAT.

We combined two recently introduced technologies, recombinant tubulin (32) and iSCAT (36–39), to make single-molecule observations of individual tubulin dimers binding to growing MT tips. We first generated a homogenous population of Saccharomyces cerevisiae tubulin biotinylated through a C-terminal KCK epitope (tubulin-KCK) on the β-subunit (Tub2) (Fig. 1A). We then added 20-nm streptavidin-coated gold nanoparticles (1:2,000 gold-to-tubulin ratio) and measured MT dynamics in vitro (Fig. 1B). MTs were detected label-free, as expected (38–40), and tubulin-bound gold nanoparticles (tubulin-gold) appeared as points of high contrast (Fig. 1C). To isolate the growth reaction and avoid more complex behaviors associated with catastrophe, we performed our assays using GTPγS, the hydrolysis-resistant GTP analog that best supports growth and prevents catastrophe for yeast tubulin (41, 42). Individual tubulin-gold landing events at MT tips were clearly observable (Fig. 1C and Movie S1). These landings reflected end-binding events, because no landings were observed along the body of the MT. Thus, our labeling and iSCAT approaches provide a viable approach for studying MT assembly kinetics at the single-molecule level.

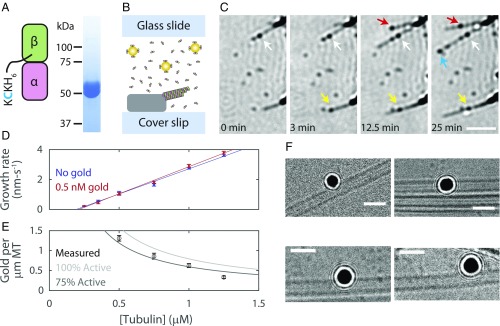
Fig. 1.

Gold nanoparticle-labeled recombinant tubulin incorporates into MTs without perturbing kinetics or structure. (A) Recombinant yeast tubulin was prepared with a biotinylated C-terminal KCK extension. Gel shows tubulin-KCK purity. (B) Diagram of the in vitro reconstitution of MT growth. Sea urchin axonemes seed polymerization; MTs formed from yeast tubulin sparsely tagged with 20-nm gold nanoparticles. (C) Time-lapse iSCAT images of growing MTs and tubulin-gold association. Arrows indicate tubulin-gold incorporation events. MTs readily grow past incorporated tubulin-gold. Axonemes appear as dark structures on the right side of each frame. (Scale bar: 2.5 μm.) (D) MT growth rates for tubulin-KCK with and without 0.5 nM gold nanoparticles. Data shown as mean ± SEM for n = 6 to 27 growing MTs. Solid lines show linear fits to data. (E) The number of gold nanoparticles per micrometer of polymerized MT. All experiments performed with a constant concentration of 0.5 nM gold nanoparticles. Data shown as mean ± SEM for n = 31 to 61 MTs. Lines show the expected number of gold nanoparticles per micrometer of MT given the tublin-to-gold ratio and assuming 8 nm per tubulin and 13 protofilaments per MT. Percent active refers to the portion of the gold nanoparticle pool that is not lost to nonspecific surface binding. (F) Example cryo-EM micrographs showing that gold-labeled tubulin can incorporate into the wall of MT without causing observable defects. (Scale bars: 50 nm.)

Multiple lines of evidence indicate that the gold labeling did not substantially perturb the kinetic or structural properties of the labeled tubulins as they polymerize into MTs. First, the presence of gold did not alter MT growth rates, indicating that tip-bound tubulin-gold did not alter the binding kinetics for subsequent unlabeled tubulin-KCKs (Fig. 1D). Second, tubulin-gold incorporated into the MT lattice at a spatial frequency that closely corresponded to their population as a fraction of total tubulin (Fig. 1E). Thus, tubulin-gold is not disadvantaged relative to tubulin-KCK for incorporating into growing MTs. Finally, cryo-EM imaging of MTs with tubulin-gold polymerized into the wall revealed normal lattices that were free of obvious defects (Fig. 1F and SI Appendix, Fig. S1).

Direct Observation of the Tubulin On-Rate Constant.

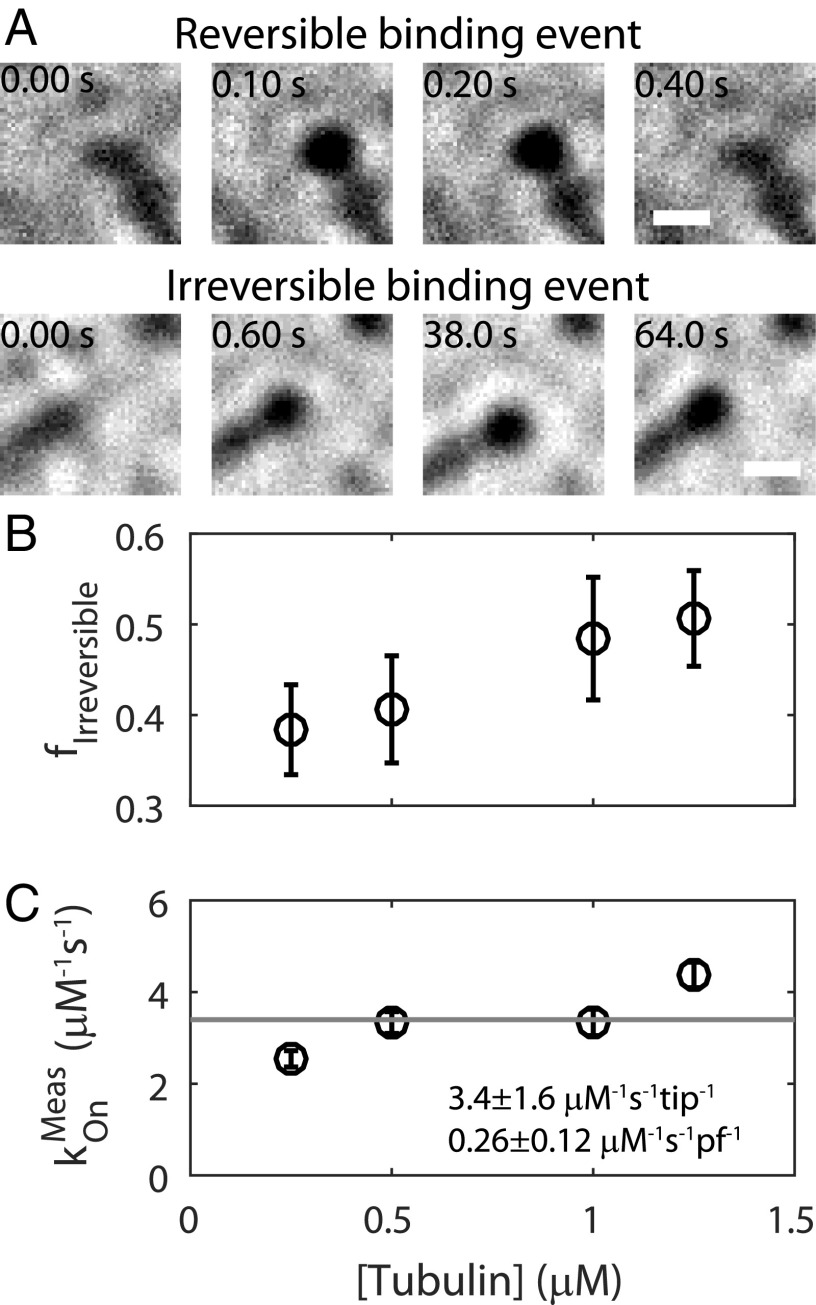
We analyzed individual tubulin-gold binding events as they occurred in real time by recording MT growth at 100 frames per second. We also imaged at 1,000 frames per second, but these data were not usable because the frequency of false-positive events arising from the relatively slow diffusion of gold nanoparticles was too high (SI Appendix, Fig. S2). We observed two classes of binding events: reversible ones in which tubulin-gold transiently dwelled at the MT tip before dissociating (Fig. 2A and Movie S2), and irreversible ones in which the tubulin-gold was integrated into the MT lattice (Fig. 2A and Movie S3). Counting the raw number of irreversible tubulin-gold binding events per tip per second at different total tubulin concentrations allowed us to predict the unlabeled MT growth rate to within a factor of about 2, further validating our single-molecule approach (SI Appendix, Fig. S3). Next, we scored the fraction of observed events that were irreversible at each tubulin concentration (Fig. 2B). This irreversible fraction increased with increasing tubulin concentrations, reflecting a higher likelihood that reversibly bound tubulins are “trapped” by incoming subunits, effectively converting reversible events into irreversible events. Finally, we estimated the on-rate constant (k_On) for tubulin association by counting the total number of binding events (reversible and irreversible) per tip per second and dividing that number by the gold nanoparticle concentration of 1 nM (Fig. 2C). The mean k_On value was 3.4 ± 1.6 μM⁻¹⋅s⁻¹ per tip or 0.26 μM⁻¹⋅s⁻¹ per protofilament (Fig. 2C, fit ± 95% CI) and was independent of the total tubulin concentration, as expected. This is a direct measurement of the tubulin k_On, and does not require fitting to a model (13).

Fig. 2.

Visualization of single tubulin-gold binding events under iSCAT at 100 frames per second. (A) Example images showing reversible and irreversible tubulin-gold binding events. Irreversible events persisted until the end of individual experiments, with polymerization extending beyond them at longer time scales (see Materials and Methods and Fig. 1C). (B) The fraction (f) of irreversible events observed at each free tubulin concentration. Data shown as mean ± SEM for n = 22 to 34 flow cells. (C) Direct measurement of the tubulin-gold k_On, determined by counting the total number of tubulin-gold binding events per second per micromolar gold nanoparticles. Data are shown as mean ± SEM for n = 22 to 34 flow cells. Value converted to per protofilament (pf) basis by dividing by 13. A Pearson correlation test on the data returned a P value of 0.11, where a value of 0.05 or lower is necessary to reject the null hypothesis that the measured k_On is not correlated with tubulin concentration. All measurements used 1 nM gold nanoparticles.

Direct Observation of Tubulin Dissociation Events Reveals Two Reversible Populations.

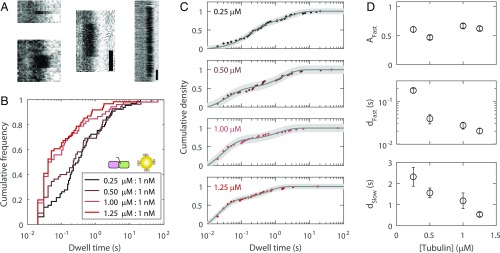
We next characterized tubulin dissociation from the tip by quantifying the dwell times of the reversible tubulin-gold binding events at four different tubulin-KCK concentrations (Fig. 3 A and B). Three trends were apparent from this analysis (Fig. 3B): (i) dwell times spanned 4 orders of magnitude, from 10⁻² to 10² s; (ii) no distribution followed a single-exponential; and (iii) increasing concentrations of tubulin-KCK led to shorter dwell times. To interpret the distribution of measured dwell times, F(τ), the data were fit to a biexponential (Fig. 3C):

$$F\left(\tau \right)=1-A_{fast}{e}^{\frac{-\left(\tau -0.01\right)}{d_{fast}}}-\left(1-A_{fast}\right)e^{\frac{-\left(\tau -0.01\right)}{d_{slow}}}$$

where A_fast is the fraction of fast-phase events, d_fast is the fast-phase characteristic dwell time, d_slow is the slow-phase characteristic dwell time, and the x-offset of 0.01 accounts for the frame rate (residuals in SI Appendix, Fig. S4). Both the fast and slow characteristic dwell times decreased substantially with increasing tubulin concentration (Fig. 3D and SI Appendix, Fig. S5). We speculate that this shift in dwell times reflects a kinetic stabilization by the incoming tubulin, the association of which forms additional contacts that convert fast events to slow events and slow events to irreversible events (i.e., “associative trapping,” investigated in detail below). Thus, the loss of long dwell times at high tubulin concentrations is consistent with the corresponding increase in the fraction of irreversible binding events noted above (Fig. 2B).

Fig. 3.

Quantification of reversible tubulin-gold tip-dwell times. (A) Example kymographs showing reversible tip-dwell events. (White scale bars: 50 ms; black scale bars: 200 ms.) (B) Distributions showing all reversible dwell time data for four tubulin-KCK concentrations, each with 1 nM 20-nm gold nanoparticles (n = 52 to 66 dwell events). Titrating the labeled fraction in this manner modified the landing frequency of free tubulin-KCK, but not that of gold-bound tubulin-KCK. (C) The data were well-fit with biexponentials. Uncertainty in the fit is shown as a shaded gray area. (D) Best parameters determined from the biexponential fit, shown as fit value ± 95% CI. Inverting the characteristic dwell times d_Fast and d_Slow yields characteristic tubulin dissociation rates.

Analysis of Mutant Tubulins with Perturbed Binding Interfaces Reveals That Interprotofilament Bonds Are Necessary for Long Dwell Times at MT Tips.

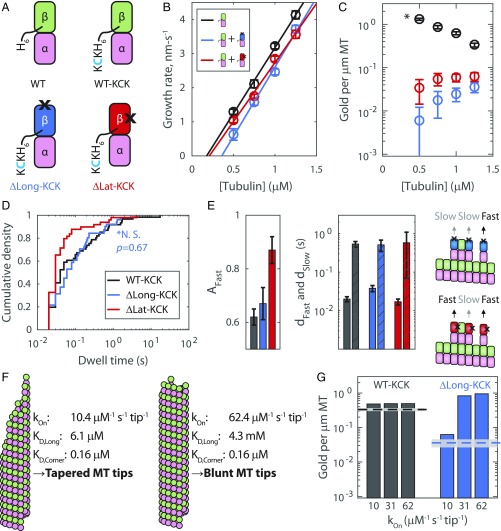
The presence of two reversible dwell time populations suggests that there are (at least) two distinct classes of tubulin-binding sites on the tip. But what intra- or interprotofilament interactions define these classes? To address this question, we took advantage of tubulin mutants with impaired longitudinal or lateral interfaces (Materials and Methods and Fig. 4A): ΔLong-KCK has two mutations at its plus-end that attenuate longitudinal tubulin–tubulin interactions (32), and ΔLat-KCK has a single mutation that weakens the lateral binding interface (43). We measured MT growth at multiple concentrations of wild-type tubulin (no KCK tag, not biotinylated) in the presence of 10 nM biotinylated mutant tubulin and 1 nM 20-nm streptavidin-coated gold nanoparticles (Fig. 4A). Adding gold-labeled mutant tubulin modestly decreased the MT growth rate compared with the control (Fig. 4B); however, it strongly decreased the number of gold counted per micrometer of MT polymer (Fig. 4C). Hence, the mutants tended to transiently “poison” MT tips, with the longitudinal interface mutant yielding a stronger effect. We quantified reversible dwell times for each mutant, focusing on the highest wild-type tubulin concentration (1.25 μM) at which mutant incorporation was highest. The ΔLong-KCK dwell time distribution was not significantly different from that of 1.25 μM tubulin-KCK (Fig. 4 D and E), as expected, since none of the tip-binding interfaces were mutated. This result rules out the possibility that slow-phase dwells were due to transient burying of the labeled tubulin by unlabeled tubulin. The second mutant, ΔLat-KCK, had fast and slow characteristic dwell times identical to those of tubulin-KCK, but the fraction of fast events increased by about 50% (Fig. 4 D and E and SI Appendix, Fig. S6). This shift in the balance of fast and slow dwells indicates that half of the slow dwell events were converted to fast dwell events. Thus, the data are consistent with the slow- and fast-phase dwells differing due to the addition of one lateral bond (Fig. 4E).

Fig. 4.

Experiments and computational modeling with mutant tubulin support tapered tip growth. (A) Library of tubulin species. Only those with a C-terminal KCK can bind to gold nanoparticles. Black X’s indicate the locations of interface-perturbing mutations. (B) Observed growth rate as a function of free wild-type tubulin with or without 10 nM mutant tubulin and 1 nM 20-nm gold nanoparticles. Data shown as mean ± SEM for n = 20 to 29 MTs for wild type alone, n = 9 to 24 for ΔLong-KCK added, and n = 17 to 37 for ΔLat-KCK added. (C) The number of gold nanoparticles per micrometer of MT for tubulin-KCK (mean ± SEM, n = 31, 35, 61, and 47 MTs measured for 0.50, 0.75, 1.00, and 1.25 μM tubulin, respectively); ΔLong-KCK (n = 45, 88, 98, and 92); and ΔLat-KCK (n = 50, 65, 77, and 63). The asterisk indicates that twofold more gold nanoparticles were used in the mutant experiments versus the wild-type tubulin-KCK. (D) Reversible tip dwell times of gold-labeled ΔLong-KCK (blue, n = 51) and ΔLat-KCK (red, n = 49) on wild-type MT tips versus control (tubulin-KCK, black n = 61) at 1.25 μM total tubulin. A Wilcoxon rank sum test shows the tubulin-KCK and ΔLong-KCK distributions are not significantly different (*N.S.). (E, Left and Center) Results of biexponential fits to wild-type and mutant dwell time data (fits ± 95% CIs; colors as in D). Solid bars denote fast-phase characteristic dwell times; bars with diagonal lines denote slow-phase characteristic dwell times. (E, Right) Diagram rationalizing why the fraction of fast dwell time events increased about 50% for ΔLat-KCK: Mutants bound in configurations in which their weakened interface touches another tubulin subunit do not benefit from the extra stabilization from lateral binding. (F) In our computational model, different assumed k_On values yielded vastly different longitudinal affinities, leading to different predicted tip structures. In the cartoon MT ends, the variation in protofilament extension length matches that observed in the respective simulations. (G) Predicted (bars) and experimental (lines, mean ± SEM) number of gold nanoparticles per micrometer of MT at 1.25 μM tubulin. Three different on-rate regimes for the computational model are shown [includes a 0.75× correction factor for percent active (Fig. 1E)].

A Computational Kinetic Model Supports a Slow Tubulin k_On.

The presence of associative trapping means that is not possible to directly convert the fit to observed dwell times into microscopic rate constants. Instead, we used a minimal computational kinetic model of MT elongation to obtain insight into the biochemical mechanisms underlying our observations. This model includes a tubulin k_On and two adjustable parameters that describe the strength of longitudinal and lateral contacts (28, 44). For each simulated k_On, the strength of the two interfaces were refined by global fitting to the experimental growth rates and dwell times (SI Appendix, Fig. S7 and Materials and Methods). A range of k_On values yielded good fits that had similar “corner” affinities (simultaneous longitudinal and lateral interactions) but that varied in the relative strength of longitudinal and lateral interactions. Smaller k_On values (closer to our experimentally measured value; Fig. 2C) required a stronger longitudinal affinity (corresponding to a slower off-rate) and resulted in rough and tapered MT end configurations (Fig. 4F). In contrast, faster k_On values required a weak longitudinal affinity (corresponding to a faster off-rate) and resulted in blunt MT end configurations where growth is dominated by addition at corner sites (Fig. 4F and SI Appendix, Fig. S7).

To choose between these contrasting scenarios, we extended our simulations to model our mutant tubulin experiments (Fig. 4A). We assumed that mutants interacted with the MT identically to wild type, except on their perturbed interface where we imposed a penalty to attenuate the lateral or longitudinal interaction strength. In other words, in the simulations, the wild-type tubulins behaved as before, but the mutants received “attenuation factors” to selectively weaken the mutated interface. We then sought to determine the attenuation factor for each mutant by fitting to the mutant growth rate data (SI Appendix, Fig. S8). For the longitudinal mutant simulations, we obtained an attenuation factor on the order of 10⁶ to 10⁷. This attenuation is consistent with the fact that the mutation adds bulky charged residues in place of smaller neutral ones and with the observation that the mutant cannot assemble MTs by itself (32), and it is plausible, given that single mutations are commonly observed to decrease binding affinity by 3 or more orders of magnitude (45). Even with attenuation factors that completely canceled the lateral interface contribution to binding affinity for the mutant tubulin that is present at <1% of the total, we were unable to recapitulate the decrease in growth rates observed experimentally in the presence of a small fraction of that mutant (SI Appendix, Fig. S8). Consequently, we focused on the simulations with the longitudinal mutant. We used our simulations to predict the expected number of gold nanoparticles per micrometer of MT, and found that only low k_On parameterizations were capable of replicating the experimental data (Fig. 4G and SI Appendix, Fig. S9). Hence, the parameterization that best described our entire dataset was k_On = 10.4 μM⁻¹⋅s⁻¹⋅tip⁻¹, K_D,Long = 6.1 ± 0.7 μM, and K_D,Corner = 0.16 ± 0.02 μM (equivalently, k_Off,Long = 4.9 ± 0.6 s⁻¹ and k_Off,Corner = 0.13 ± 0.02 s⁻¹), consistent with ragged MT tip tapers during growth (Fig. 4F). We note that this upper limit value for k_On is approximately threefold higher than our experimentally measured value but view this as a good match because numerous experimental factors, including loss of gold to nonspecific surface binding, tubulin degradation over time, and slight depression of tubulin diffusion due to the gold label, support the measured value as a lower limit.

Discussion

The current work presents a direct, single-molecule interrogation of the biochemical mechanisms that dictate MT growth kinetics. Our determinations of the tubulin k_On (Fig. 2C) and dissociation rate (Fig. 3) were made by observing the fates of individual tubulins as they transiently interacted with the MT tip, and hence required no model fitting or assumptions. Our dissociation rate measurements provide insight into the complex biochemistry of the growing MT tip: For the reversible associations, two dwell-time populations were observed, consistent with tubulin binding through either a single longitudinal interaction or at a corner site, and these structural interpretations were supported both by results from mutant tubulin and by kinetic simulations.

For the tubulin bimolecular k_On, our experimental and model-derived values can be considered as lower and upper bounds, respectively. It might be expected that attaching a 20-nm-diameter gold nanoparticle to an approximately 4 × 4 × 8 nm tubulin would dramatically slow the on-rate. However, because the diffusion constant scales linearly with diameter and does not depend explicitly on mass or density (Stokes–Einstein equation), the gold-tubulin complex is expected to have only an ∼2.5-fold slower diffusion constant than tubulin alone, and, in any case, the measured tubulin on-rate is more than 2 orders of magnitude below the diffusion limit (46, 47). Furthermore, two critical control experiments confirm that particle attachment does not strongly depress the tubulin on-rate. First, we confirmed that tubulin-gold incorporates into MTs at a spatial frequency that closely corresponds to its fraction of the total tubulin concentration (Fig. 1E). If the gold label substantially depressed the on-rate, then gold-tubulin would be disadvantaged relative to unlabeled tubulin in growth, and the number of gold nanoparticles per micrometer of MT would fall far below the expected trendline. Second, we confirmed that tubulin-gold incorporates into MTs at a temporal frequency that corresponds to the unlabeled MT growth rate (SI Appendix, Fig. S2). We conclude that slowing of diffusion caused by the gold label did not substantially alter tubulin on/off kinetics at the MT tips.

Our k_On is in good agreement with numerous theoretical studies of MT dynamic instability (7–9, 20, 48, 49), and thus should help to build a long-sought consensus value for the field. We note, however, that our value is roughly fivefold slower than the fast k_On deduced from growth rate fluctuations by Gardner et al. (13). Although some of the difference may come from our use of yeast tubulin as opposed to mammalian tubulin, our model, in general, predicts that for a given corner affinity, faster k_On values will lead to blunter MT tips, and slower k_On values will lead to more tapered tips (Fig. 4). Thus, the relatively slow on-rate we observe is consistent with the numerous reports of tapered MT growth in the literature (17–20, 50–53). Attempts to fit experiments that used the plus-end–blocked tubulin mutant also argued against a k_On significantly faster than our measured value (Fig. 4). We note that for our favored k_On regime, very few (about 3%) transient interactions at the tip are expected to be missed at our chosen frame rate, reinforcing that iSCAT is able to capture the transient tubulin interactions that drive MT growth.

Our kinetic measurements provide constraints for the energetics underlying the stability of the GTP cap at dynamic MT tips. While it is established that both lateral and longitudinal tubulin–tubulin interactions contribute to the stability of the MT lattice, the relative contributions of lateral and longitudinal free energy are debated (2). Our single-molecule dwell time measurements describe a fast and a slow population of reversible binding events, and our mutants constrain these to be single longitudinal sites and corner sites, respectively. The dependence of these fast and slow dwell times on the free tubulin concentration (Fig. 3) indicates that there are tubulin-dependent transitions between the different substates at the growing plus-end. These associative trapping events mean that our dwell time measurements only provide an upper limit for tubulin off-rates from these sites. However, we were able to fit the data with our stochastic kinetic model (Fig. 4 F and G) and found that the microscopic rate constants that were most consistent with our data were k_Off,Long = 4.9 ± 0.6 s⁻¹ and k_Off,Corner = 0.13 ± 0.02 s⁻¹. Combining these values with our on-rate, we can calculate a longitudinal bond energy of 12.0 ± 0.2 k_BT and a lateral bond strength of 3.6 ± 0.4 k_BT, values that lie in the middle of the range of published models (7–9, 13, 20). Our value for the lateral bond strength is particularly close to that of VanBuren et al. (8). The large difference between the longitudinal and lateral bond energies measured here approaches (to within ∼3 k_BT) previous values deduced from molecular dynamics simulations (27). This qualitative agreement is encouraging; however, those simulations were carried out before the structural basis for lateral interactions was established and for bovine rather than yeast tubulin, so quantitative comparisons should not be overinterpreted. Overall, the values we obtained suggest that the longitudinal bond energy is strong enough to be a major contributor to MT elongation, but not strong enough to drive the elongation of individual protofilaments or unseeded nuclei at modest tubulin concentrations. While our strong longitudinal bond energies are consistent with the short extended tips as seen in recent cryo-electron tomography work (20), our measurements do not inform on the curvature or mechanical states of the protofilaments at the tip.

A notable result from our kinetic simulations in the identified slow k_On regime is the natural occurrence of tapered tip structures during growth. Tapered end configurations have been observed by EM (17–20, 50, 51), been inferred from fitting the intensity profile of fluorescently labeled MTs (13, 52), and been observed indirectly in the form of EB3 comet splitting in the presence of eribulin (53). Our data now identify the biochemical mechanisms by which these tapers grow. Key to taper formation is the associative trapping of tubulin subunits, described as follows. In our preferred kinetic model, the longitudinal affinity of tubulin is sufficiently strong such that newly bound subunits with no lateral contacts can stay bound for long enough that there is a low but significant probability that a second tubulin will convert the longitudinal association into a corner one by binding at one of the two open neighboring positions. These associative trapping events are relatively rare but occur more often at higher concentrations of tubulin because the rate of association is faster. Once such a trapping event occurs, it leads to longer-lived binding (over a second), and can thereby initiate a new taper. This contrasts with the high k_On model, in which newly bound subunits with no lateral contacts dissociate so quickly that they are not appreciably trapped. In either model, longer-lived corner positions can also be further stabilized by associative trapping: If an incoming tubulin makes a second lateral interaction, the tubulin is effectively buried and becomes irreversibly incorporated into the lattice. These associative trapping events can explain the increase in the irreversible fraction at higher tubulin concentrations (Fig. 2B). They can also explain why the fast and slow characteristic dwell times become shorter at higher tubulin concentrations: Incoming tubulin traps the longer-lived events, and the remaining population has a shorter characteristic dwell time (Fig. 3D). This kinetic race is analogous to fluorescence lifetime measurements, in which the measured lifetime decreases due to nonradiative decay that preferentially affects the longer lifetime events (54). Indeed, the observed decreases in the reversible tubulin characteristic dwell times as a function of free tubulin (Fig. 3D) were quantitatively accounted for by associative trapping in our computational kinetic model (SI Appendix, Fig. S7).

The fundamental tubulin on- and off-rates that we identified in this study form the basis for GTP cap maintenance during MT growth. The on-rate measured here sets an upper limit for the rate at which GTP hydrolysis could be occurring without depleting the cap, but further experiments are necessary to gain a full understanding of how these events coordinate to drive dynamic instability. MT polymerization mechanisms are conserved from yeast to humans, with specific kinetic rates varying with species, isoform, and posttranslational modifications (2, 33, 34). Thus, the single-molecule approach developed here holds promise for discovering the biochemical origin of these differences as well as for defining the mechanisms by which various polymerases, depolymerases, and chemotherapeutic drugs exert their effects by altering tubulin on- and off-rates at the MT plus-end.

Materials and Methods

Protein Preparation.

Plasmids to express wild-type yeast αβ-tubulin were previously described (32, 41, 55). Plasmids to express wild-type yeast αβ-tubulin with a C-terminal KCK tag; a β:F281A mutation of Tub2p (yeast β-tubulin) with C-terminal KCK tag (designated ΔLong-KCK in the text); and a β:T175R, V179R mutation of Tub2p (yeast β-tubulin) with C-terminal KCK tag (designated ΔLatX-KCK in the text) were made by QuikChange (Stratagene) mutagenesis, using the expression plasmid for wild-type Tub2 as template and with primers designed according to the manufacturer’s instructions. The integrity of all expression constructs was confirmed by DNA sequencing. All wild-type and mutant yeast αβ-tubulins (wild-type KCK, β:T175R/V179R-KCK, β:F281A-KCK) were purified from inducibly overexpressing strains of S. cerevisiae using Ni-affinity and ion-exchange chromatography, as previously described (28, 32, 41, 55). After purification, all KCK samples were labeled with EZ-Link Maleimide-PEG2-Biotin (Thermo Scientific). All tubulin samples were incubated with 2 mM Tris(2-carboxyethyl)phosphine (TCEP) for 30 min on ice. Following incubation with TCEP, 20-fold excess of Maleimide-PEG2-Biotin was added and samples were incubated for 2 h at 4 °C. Samples were exchanged into storage buffer [10 mM potassium piperazine-N,N′-bis(2-ethanesulfonic acid) (K-PIPES) pH 6.9, 1 mM MgCl₂, 1 mM EGTA] containing 50 µM GTP with 2 mL, 7K MWCO Zeba Spin Desalting Columns (Thermo Scientific). Tubulin samples were then flash-frozen and stored at −80 °C. The degree of tubulin subunit biotinylation was determined to be within error of 100% (one biotin per tubulin dimer) using a fluorescence biotin quantification kit (46610; Thermo-Fisher). Before any assay, tubulin was thawed and spin-filtered (100-nm pore size) to remove aggregates, and the concentration was remeasured by absorbance at 280 nm.

iSCAT.

An iSCAT microscope was custom-built for this study. The design roughly followed the scanning illumination design suggested by the Kukura laboratory (36, 37), and the system was built around an existing total internal reflection microscope (56). Illumination was provided by a 650-nm laser (OFL384; OdicForce), which was mode-cleaned using a single-mode optical fiber (Thorlabs). Scanning was performed using an acoustooptic deflector (45070-5-6.5DEG-0.633; Gooch and Housego). A 60 × 1.49 numerical aperture objective (Nikon) equipped with an objective heater (Bioscience Tools) was used. Images were taken using a Basler Ace complementary metal-oxide semiconductor camera (AcA2000_165um) accessed by custom-written LabVIEW software. The total microscope magnification was 167×, resulting in an image calibration of 33 nm per pixel. For all experiments performed, unless otherwise stated, the camera exposure time was 9.435 ms, the laser was scanned over the sample 290 times per exposure, and the power incident on the sample was ∼25 W/cm². All images and movies shown in this study were flat fielded (36, 37), and thus pixel intensity represents a percent contrast rather than a raw grayscale count.

MT Growth and Reversible Tubulin Binding Assays.

MT growth assays under iSCAT were based on established protocols (41). MTs were polymerized in flow chambers off of sea urchin axoneme seeds. Coverslips were washed with ethanol and silanized using 1H,1H,2H,2H-perfluorodecyltrichlorosilane (Alfa-Aesar) before being constructed into ∼10-μL flow cells using double-sided tape. Chambers were first washed with 20 μL of Brinkley Reassembly buffer (BRB80) (80 mM K-PIPES, 1 mM EGTA, 1 mM MgCl₂, pH 6.8), and then axoneme seeds were added. After 5 min, a blocking buffer (5 mg/mL BSA and 0.25 mM GTPγS in BRB80) was added. After 10 min, polymerization assay mix was added and the flow chamber was sealed using clear nail polish. The polymerization assay mix included a controlled amount of biotinylated tubulin, 2 mg/mL BSA, 2 mM GTPγS, 0.4 mM MgSO₄, and 0.08% methylcellulose in buffer (100 mM PIPES, 1 mM EGTA, and 1 mM MgSO₄, pH 6.9). Streptavidin-coated 20-nm gold nanoparticles (BBI Solutions) were added to the polymerization assay mix at a final concentration of either 0.5 nM or 1.0 nM. In all cases, streptavidin-coated gold nanoparticles and biotinylated tubulin were premixed on ice for at least 10 min. In all assays, a large stoichiometric excess of tubulin was used (tubulin-to-gold ratios ranging from 10:1 to 2,500:1). In experiments with biotinylated mutant tubulin, mutants were premixed with gold at a 10:1 ratio on ice for 10 min before unbiotinylated wild-type tubulin was added to the polymerization mix (final concentration of 0.25 to 1.25 μM wild-type tubulin, 10 nM biotinylated mutant tubulin, 1 nM 20-nm streptavidin-coated gold nanoparticles). Flow chambers were heated to 30 °C in a mini incubator (Bio-Rad), and loaded onto the iSCAT microscope, where temperature was maintained using an objective heater. Sample temperature was measured periodically using a digital thermometer (Leaton L812) to ensure consistency. Growth rate movies were acquired at two frames per second. To assess gold nanoparticles per micrometer of MT, 20 frame stacks were taken at 100 frames per second (MT fluctuations are visible at that frame rate and aid in distinguishing whether a gold nanoparticle is truly on a MT, or just has stuck to the surface near a MT). Growth rates and the number of gold nanoparticles per micrometer of MT were measured in ImageJ. For all experiments performed, data were taken from at least two flow cells spread over at least 2 separate experimental days.

To measure individual tubulin binding and unbinding events, the tubulin growth assay was repeated with a controlled amount of tubulin-KCK and 1 nM streptavidin-coated 20-nm gold nanoparticles (BBI Solutions). For the mutant tubulin experiments, a 1 nM concentration of gold nanoparticles was covered with 10 nM biotinylated mutant tubulin, and the rest of the tubulin in the pool was nonbiotinylated. Experimentally, a growing tip was located, and a 20,000-frame movie was taken at 100 frames per second. Only axonemes containing clear, single growing MTs (determined by contrast and fluctuations) were recorded. Multiple movies of multiple tips were taken in each flow cell, and no flow cell was imaged for longer than ∼40 min to minimize tubulin loss (to nonspecific surface binding, aggregation, or denaturation). Movies were fed into ImageJ, and kymograph analysis was performed manually. Most movies had 0, 1, or 2 events. An event was labeled as irreversible if the MT was seen to grow past the tubulin-gold, or if the dwell event persisted throughout the lifetime of the flow cell (significantly longer than 200 s). Only events that were at least two frames long were scored.

Cryo-EM.

To view the overall MT architecture in the presence of gold label, biotinylated tubulin was polymerized in a 1× solution of 100 mM PIPES, 2 mM EGTA, 1 mM MgCl₂, and 5% glycerol (pH 6.9) with 1 mM GTPγS and 1 nM 20-nm streptavidin-coated gold nanoparticles at 30 °C for 2 h. The tubulin-to-gold ratio was 1000:1. Cryo-EM grids were prepared by applying 3 µL of MTs to a glow-discharged Quantifoil R1.2/1.3 300-mesh gold holey carbon grid (Ted Pella Inc.) and blotted for 4.0 s under 100% humidity at 30 °C before being plunged into liquid ethane using a Mark IV Vitrobot (FEI). Micrographs were collected on a Talos Arctica microscope (FEI) operated at 200 kV with a K2 Summit direct electron detector (Gatan). SerialEM software (David Mastronarde, J. Richard McIntosh, bio3d.colorado.edu/SerialEM/) was used to manually collect data. Images were recorded at 6,700× and 13,500× magnification using a defocus from −2.5 to −3 µm. All micrographs were dose-fractionated to 20 frames with a dose rate of about six electrons per pixel per second, with a total exposure time of 10 s. Micrographs were processed using RELION v2.1 (57); images were motion-corrected using MotionCor2, and contrast transfer function estimation was performed using CTFFIND4.

Computational Modeling.

We created a computer program to perform kinetic Monte Carlo simulations of growing MT plus-ends. The model is similar to one we have used previously (28, 44) and to an earlier implementation from others (9). Briefly, the MT lattice is represented by a 2D array with a periodic boundary condition to mimic the cylindrical wall of the MT. MT elongation is simulated one biochemical reaction at a time. In this work, the two possible reactions are association and dissociation; we did not include GTPase because our experiments used a hydrolysis-resistant GTP analog. The association can occur at the tip of each protofilament with a rate given by k_On × [tubulin], where k_On is the assumed microscopic (per protofilament end) k_On. Terminal subunits can dissociate from the MT lattice at a rate given by k_On × K_D, where K_D is the affinity determined by the sum of all tubulin–tubulin interactions as described previously (9, 28, 44). Execution times for each event are determined by sampling a random number, x, between 0 and 1, and then calculating the time as −(1/rate) × ln(x), where rate gives the appropriate rate constant as described above. At each step, the event with the shortest execution time is implemented, the simulation time is advanced accordingly, and the list of possible events and their associated rates is updated to account for changes in subunit neighbor state. In this way, we obtain a biochemical movie of elongation. We implemented the Next Reaction Method (58), which increases the speed of simulations by reducing the number of random numbers to be generated, which in turn allows more efficient sorting of the list of possible events. For a given choice of k_On, the strengths of longitudinal and corner (longitudinal + lateral) interactions were determined by jointly fitting model-predicted growth rates and dwell times to the experimentally measured values. We showed previously that longitudinal and corner affinities are the dominant determinants of growth rate (28). The goodness of fit between predicted and measured values was determined using a weighted sum of the squared residuals of both growth rates and dwell times. Because we are fitting our models to different types of data (growth rates and dwell times), we weight the residuals from growth rates and dwell times to give them roughly equivalent impact in terms of the fitting. The weight for growth rate data was $\frac{1}{n_{gr}\sqrt{mean{\left(dat{a}_{gr}\right)}^2+std{\left(dat{a}_{gr}\right)}^2}}$, where n_gr is the number of growth rate data points. The weight for dwell time data point was $\frac{2}{n_{dwell}\sqrt{mean{\left(dat{a}_{dwell}\right)}^2+std{\left(dat{a}_{dwell}\right)}^2}}$, where n_dwell is the number of dwell time data points. The best-fitting parameter set was found using the Gauss–Newton algorithm to minimize the weighted sum of the residuals, using custom routines written for MATLAB. To avoid winding up in a local minimum, the fitting was performed at least 25 times, with each attempt starting from different initial guesses for the fitted parameters. To estimate the error in our fitted parameters, we performed 20 independent minimizations starting from the same initial parameter set. The random nature of the simulation ensures that these 20 attempts can diverge from each other. This process yielded 20 different parameter sets, and we took the SD of the distribution as a measure of the fitting error.

To simulate growth rates in the presence of interface-perturbed mutants, we modified the simulation code to include a second “species” of tubulin with its own user-specified concentration. We assumed that the interface mutants decrease the strength of interaction (affinity) at that interface. This attenuation affects the dissociation rate of the affected subunit, but not its association rate. For ∆Long-tubulin (β:T175R, V179R mutations), longitudinal interactions involving the plus-end of the mutant are attenuated. In other words, these mutants are assumed to bind the MT end equally as tightly as wild type but, once associated, they poison the end of the protofilament where they reside. For ∆Lat-tubulin (β:F281A mutation), lateral interactions involving the right side of the mutant (viewed from the outside of the MT, with plus-end up) are attenuated. In other words, this lateral mutant is assumed to bind less tightly than wild type when its mutated side contacts the lattice but equally tightly when its nonmutated side contacts the lattice (Fig. 4E). Other than the attenuation factors, the mutant subunits are assumed to behave identically to the wild type. Attenuation factors were determined by fitting to the mixed tubulin growth rate data, keeping all other parameters fixed.