Binocular Eye Movements Are Adapted to the Natural Environment

Abstract

Humans and many animals make frequent saccades requiring coordinated movements of the eyes. When landing on the new fixation point, the eyes must converge accurately or double images will be perceived. We asked whether the visual system uses statistical regularities in the natural environment to aid eye alignment at the end of saccades. We measured the distribution of naturally occurring disparities in different parts of the visual field. The central tendency of the distributions was crossed (nearer than fixation) in the lower field and uncrossed (farther) in the upper field in male and female participants. It was uncrossed in the left and right fields. We also measured horizontal vergence after completion of vertical, horizontal, and oblique saccades. When the eyes first landed near the eccentric target, vergence was quite consistent with the natural-disparity distribution. For example, when making an upward saccade, the eyes diverged to be aligned with the most probable uncrossed disparity in that part of the visual field. Likewise, when making a downward saccade, the eyes converged to enable alignment with crossed disparity in that part of the field. Our results show that rapid binocular eye movements are adapted to the statistics of the 3D environment, minimizing the need for large corrective vergence movements at the end of saccades. The results are relevant to the debate about whether eye movements are derived from separate saccadic and vergence neural commands that control both eyes or from separate monocular commands that control the eyes independently.

SIGNIFICANCE STATEMENT We show that the human visual system incorporates statistical regularities in the visual environment to enable efficient binocular eye movements. We define the oculomotor horopter: the surface of 3D positions to which the eyes initially move when stimulated by eccentric targets. The observed movements maximize the probability of accurate fixation as the eyes move from one position to another. This is the first study to show quantitatively that binocular eye movements conform to 3D scene statistics, thereby enabling efficient processing. The results provide greater insight into the neural mechanisms underlying the planning and execution of saccadic eye movements.

Introduction

While investigating the visual environment, humans make two to three fixations per second (Yarbus, 1967). Each fixation involves binocularly coordinated movements of the eyes to acquire the new target in three dimensions: horizontal, vertical, and in-depth. Here we investigate the information used to determine the in-depth component of such fixations. We know the visual system allocates computational resources effectively by exploiting regularities of the natural environment (Field, 1987; Geisler, 2008). For example, the shape of the binocular horopter is consistent with the distribution of naturally occurring binocular disparities (Liu et al., 2008; Sprague et al., 2015; Canessa et al., 2017; Gibaldi et al., 2017a). This is a very useful adaptation because the neural computations involved in stereopsis are challenging. Of particular difficulty is the correspondence problem: Which points in the two eyes' images came from the same feature in the scene? If the natural environment consisted of uniformly distributed small objects, all distances in every direction would be equally probable, and binocular disparities would be very broadly distributed. But the natural environment is not like this. Instead, it contains many opaque objects such that farther objects are often occluded by nearer ones. It is also structured by gravity, so many surfaces are earth-horizontal (e.g., grounds, floors) or earth-vertical (trees, walls). Consequently, the distributions of disparities are constrained and dependent on position in the visual field. The horopter indicates the distance in various visual directions where binocular fusion is guaranteed and stereoacuity is highest. Its shape conforms to the distribution of natural disparity, strongly suggesting that the constraints of environmental statistics are manifested in the brain's search for solutions to binocular correspondence, allowing a much more restricted and efficient search than otherwise needed (Sprague et al., 2015; Gibaldi et al., 2017a).

When executing saccades, the oculomotor system could aim the upcoming movement at the estimated eccentricity of the target, which would minimize error when the eyes land. But saccades generally undershoot the target by 5%–10% followed by a corrective saccade (Becker and Fuchs, 1969; Henson, 1978). This behavior minimizes energy expenditure because an undershoot followed by correction requires less eye rotation than an overshoot followed by correction (Lemij and Collewijn, 1989; Aitsebaomo and Bedell, 1992). Fixations are clearly affected by the 3D structure of the visible scene. For example, people tend to fixate near objects even when many farther objects are visible (Sprague et al., 2015; Gibaldi et al., 2017a). These previous observations and others (Wismeijer et al., 2010) concern the choice of gaze direction for the upcoming fixation and not eye vergence.

We investigated the horizontal vergence associated with saccades to eccentric targets. When vergence is inaccurate, the target has residual binocular disparity and double images are perceived. Accurate vergence produces a single, fused percept of the target. What is the best strategy for guiding vergence when executing a saccade? The distance to an eccentric target is provided by sensed depth information, particularly binocular disparity (Wismeijer et al., 2010). When that estimate is uncertain, the system should use prior information: the central tendency of the distribution of naturally occurring disparities. The least energy would be expended by not changing horizontal vergence at all. Such movements would follow the torus in Figure 1A. Given these constraints, we hypothesize that eye vergence should be aimed at different distances depending on the information available. When distance information is uncertain, vergence should be biased toward the most probable disparity in the stimulated part of the visual field. When distance information is more certain, vergence should be closer to the true target distance.

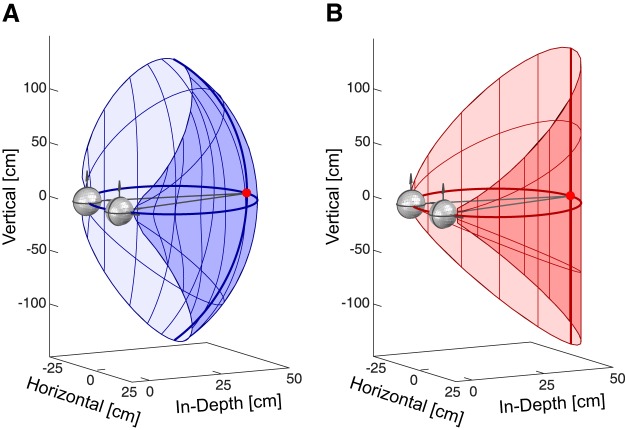
Figure 1.

Theoretical iso-vergence surface and binocular horopter. A, Theoretical iso-vergence surface. Initial fixation is on the red dot. The iso-vergence circle (dark blue circle) goes through the fixation point and the centers of rotation of the two eyes. In Helmholtz coordinates, the set of locations in 3D space that can be reached by eye movements with the same horizontal vergence is a torus (blue grid). The torus serves as the definition of zero change in horizontal vergence when analyzing our intrasaccadic vergence data. B, Theoretical binocular horopter. Initial fixation is again on the red dot. The Vieth–Müller Circle (dark red circle) goes through the fixation point and the optical centers of the two eyes. In Helmholtz coordinates, the set of locations in 3D space that create zero horizontal disparity is a cylinder (red grid). The cylinder serves as the definition of zero horizontal disparity when analyzing our binocular horopter data.

We examined this hypothesis by measuring intrasaccadic vergence as people make saccades to eccentric targets in various conditions. We also measured the distribution of natural disparities in different parts of the central visual field. And we measured the positions of corresponding points in the two retinas across the central field.

Materials and Methods

The present study includes three complementary experiments: Experiment 1 focuses on measuring intrasaccadic vergence for saccades directed to eccentric targets in the visual field. Experiment 2 measures positions of corresponding retinal points (i.e., the binocular horopter) in the field. Experiment 3 measures the distribution of naturally occurring disparities in the same visual field. These data allowed us to compare biases in binocular fixation to the positions of retinal corresponding points and to the distribution of naturally occurring disparities.

Experiment 1: oculomotor horopter

We measured the change in horizontal vergence when subjects make saccades from straight ahead to various secondary and tertiary positions.

Subjects.

Eight subjects (6 females and 2 males, ages 24–38 years) participated. All but one were unaware of the experimental hypotheses. The subject protocol was approved by the Institutional Review Board at the University of California, Berkeley. All subjects gave informed consent before starting the experiment. All had normal stereopsis according to the Stereo Reindeer Test (Stereo Optical).

Apparatus.

Subjects sat in front of a large frontoparallel LCD screen (125 × 77 cm) with HD resolution (1920 × 1080 pixels) (Fig. 2A). The screen was used for calibrating the eye tracker. An array of LEDs was used to produce fixation targets. The subject's head was stabilized with a bite bar. The eyes were positioned very accurately relative to the screen and LED array by using a sighting device (Hillis and Banks, 2001). The midpoint of the subject's interocular axis intersected a surface normal from the center of the display screen and the midpoint of the LED array.

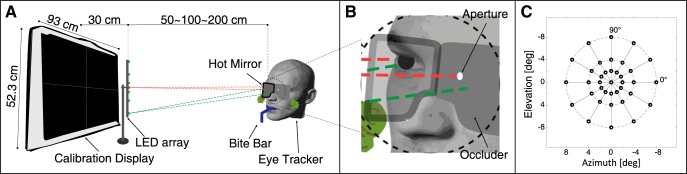
Figure 2.

Apparatus for the oculomotor experiment. A, Display screen, LED array, subject, and eye tracker. The subject was positioned on a bite bar in front of the display screen and LED array. He/she wore the Eyelink II tracker. The display screen was used for calibrating the tracker. The LED array was used to present fixation targets: one straight ahead (red) and the others at six peripheral locations (green). The central LED was colinear with the midpoint of the subject's interocular axis and a normal from the midpoint of the display screen. The distance from the subject to the LED array was 50, 100, or 200 cm. The array could rotate about its midpoint, thereby creating meridians of different orientations. B, Closeup of hot mirrors and aperture-occluder. In the monocular condition, we mounted an annular occluder with a small aperture on the far side of the mirror and in front of the nondominant eye. That eye could see the initial fixation target through the aperture but could not see the peripheral targets. C, Tested field positions: six meridians (0°, 30°, 60°, 90°, 120°, and 150°) each with six eccentricities (±2°, ±4°, and ±8°).

Binocular eye position was measured with a head-mounted eye tracker (Eyelink II). There were monocular and binocular conditions. For the monocular condition, we occluded one eye's view of the stimulus while measuring gaze directions of both eyes. To allow this, we placed a hot mirror (Knights Optical, pass-band 425–675 nm, block-band 750–1150 nm) between each tracker camera and eye (Fig. 2B). These mirrors transmit visible light (∼96%) and reflect infrared (∼98%). The infrared-based tracker cameras could thereby image the eyes while the subject could see the visible-light scene through the mirrors with a nearly unimpeded FOV. We could record the positions of both eyes while stimulating only one eye. Stimulation of one eye only was accomplished by placing a small aperture with an annular occluder on the far side of the mirror and in front of one eye such that that eye could see the initial fixation target but not the saccadic target (Fig. 2B). The occluded eye was always the nondominant eye because the dominant eye usually exhibits better performance in terms of fixation stability (Subramanian et al., 2013) and saccade kinematics (Vergilino-Perez et al., 2012). The occluder was removed for the binocular condition.

Visual stimulation was provided by a linear array of seven LEDs. The array was parallel to the surface of the display screen. The central LED was in the same visual direction (from the midpoint of the interocular axis) as screen center. The peripheral LEDs were at eccentricities of ±2°, ±4°, or ±8°. Testing was done for six orientations of the LED array: 0°, 30°, 60°, 90°, 120°, and 150° (Fig. 2C).

Synchronization between the visual stimuli and eye tracker was done using the Psychtoolbox (Brainard, 1997; Kleiner et al., 2007) (RRID:SCR_002881) together with a toolbox for integration of the Eyelink (Cornelissen et al., 2002). An Arduino board, controlled with a serial port, turned the LEDs on and off.

Procedure.

Each session began with calibration of the eye tracker. The calibration targets subtended 0.6°. Thirteen calibration positions were presented followed by nine new positions for validation (Gibaldi et al., 2017b). The calibration area was determined for each session according to the stimulus distance and orientation of the LED array. To ensure accuracy, calibration was repeated until the validation yielded a mean error <0.5°. Each eye was calibrated separately to improve accuracy for binocular tasks (Svede et al., 2015; Gibaldi et al., 2017b).

After calibration, the display screen was turned off and the experiment began. The room was dark, except for the LEDs. Subjects initiated stimulus presentations. On each trial, the central fixation LED was illuminated for 0.6–1 s and was seen by both eyes. Then that LED was extinguished and one of the six peripheral LEDs was illuminated for 1 s. The subject was instructed to make an eye movement to the peripheral LED as quickly and accurately as possible. To discourage anticipatory movements, the order of presentation of the peripheral LEDs was random, and the time elapsed between a button press and the onset of the peripheral LED was variable. The subject was presented each peripheral target 10 times for a total of 60 trials per session. Different LED array orientations were presented in different sessions, six in all.

The peripheral targets were seen binocularly in some conditions and monocularly in others. In the former condition, the central and peripheral targets were seen by both eyes, so visual feedback (binocular disparity) was available to guide vergence. In the monocular condition, the central target was again seen by both eyes, but the peripheral targets were seen by the dominant eye only, so visual feedback was not available for guiding vergence.

We measured intrasaccadic vergence from fixation straight ahead at one of three initial distances (50, 100, and 200 cm) to secondary positions (0° and 90° along the horizontal and vertical meridians, respectively) at the same distances. We did the measurements at 100 cm twice to assess repeatability. We also measured intrasaccadic vergence from straight ahead at 100 cm to tertiary positions (orientations of 30°, 60°, 120°, and 150°) at the same distance. Those measurements were done with monocular viewing only.

Postprocessing.

On each trial, we measured intrasaccadic vergence, which we define as the change in horizontal vergence from initial central fixation to fixation at the end of the saccade. To ensure accurate measurement of initial fixation position, we applied a drift compensation before each saccade so that the measured gaze vectors intersected the fixation target (Enright, 1989). We had to define start and end positions of each saccade. We used the velocity and acceleration threshold criteria provided by the Eyelink (22°/s and 4000°/s²) to approximately identify those points. When the velocity and/or acceleration first exceeded those values, a preliminary start point was marked. When the velocity and/or acceleration first fell below those values, a preliminary endpoint was marked.

The threshold criteria provided by Eyelink do not take into account the kinematics of saccades of different amplitudes (e.g., larger saccades have greater peak velocities: the main sequence) (Bahill et al., 1975). So we developed a custom technique for further refining start and end positions. The technique involves fitting each position trace with a sigmoid (four parameters: position offset, time offset, slope, and amplitude) (Waitzman et al., 1991). We used a RANSAC algorithm (Gibaldi et al., 2015) to find the best sigmoid using data from 50 ms before the preliminary start point to 50 ms after the preliminary endpoint. We defined start points and endpoints, respectively, as the 2% and 98% of the sigmoid. The change in vergence was the difference in horizontal vergence at the endpoint relative to the start point. The fitting and start point and endpoint calculations were done for each trial. The median intrasaccadic vergence for each eccentricity was computed from the 10 measurements. We determined intrasaccadic vergence for the first saccade only (i.e., not after corrective saccades).

We measured the change in horizontal vergence that occurred for saccades to different eccentricities in different directions. To do so required a quantitative definition of what constitutes no change in vergence. For this, we defined an iso-vergence surface in Helmholtz coordinates (Schor et al., 1994). This surface is the circle containing the point of initial fixation and the rotation centers of the two eyes rotated about the interocular axis (Fig. 1A). The resulting torus was our definition of no change in horizontal vergence. Eye movements that placed the intersection of the lines of sight nearer than the torus had positive vergence change (convergence), and movements that placed the intersection farther than the torus had negative vergence change (divergence).

Experiment 2: binocular horopter

In conditions similar to the oculomotor experiment, we measured the binocular horopter: the positions in 3D space that stimulate corresponding points in the two retinas (Ogle, 1950; Shipley and Rawlings, 1970; Nakayama, 1977; Hillis and Banks, 2001; Schreiber et al., 2008; Cooper et al., 2011).

Subjects.

Five of the subjects from the oculomotor experiment participated: 4 females and 1 male. All but one were unaware of the experimental hypotheses. Again, the protocol was approved by the Institutional Review Board, and subjects gave informed consent before beginning.

Apparatus.

The setup was similar to the one in the oculomotor experiment. Subjects were positioned on a bite bar such that the midpoint of the interocular axis was on the normal from the center of the screen. We stimulated the two eyes separately using red-green anaglyph glasses.

Procedure.

We used a dichoptic, apparent-motion procedure to measure the binocular horopter (Nakayama, 1977; Hillis and Banks, 2001; Schreiber et al., 2008; Cooper et al., 2011). Specifically, we measured the horizontal disparity that yields equal perceived directions in the two eyes and therefore produces no apparent motion. The subject always fixated a target at screen center while dichoptic peripheral stimuli were presented intermittently. The room was dark, except for the fixation target and peripheral stimuli.

The central fixation target was designed to allow subjects to monitor the accuracy of their vergence. It consisted of a binocular fixation cross and a dichoptic Maltese cross. One arm of the Maltese cross was seen by the left eye and the other by the right eye. Horizontal and vertical vergence were appropriate for the distance of the fixation cross when the two arms were perceived as aligned. On each trial, the subject waited until the fixation target was aligned and then initiated presentation of the peripheral stimulus with a button press. The dichoptic peripheral stimuli were vertical ellipses with an aspect ratio of 6. We increased the size of the ellipses in approximate proportion to eccentricity: 20, 30, and 50 minarc tall at eccentricities of 2°, 4°, and 8°, respectively.

The ellipses had the same elevation in the two eyes but were displaced horizontally by equal and opposite amounts relative to the tested azimuth. They were flashed sequentially to the two eyes (50 ms on time, 70 ms interstimulus interval, and 50 ms on time). Half the time the left-eye stimulus appeared first and half the time the right-eye stimulus did. The subject indicated at the end of each presentation whether the ellipses appeared to move leftward or rightward. The horizontal disparity between the ellipses was varied trial by trial according to a QUEST adaptive staircase (Prins and Kingdom, 2009). The staircase ran for 40 trials and converged on the disparity that was perceived as moving neither leftward or rightward.

We tested the same target positions as in the oculomotor experiment: six eccentricities (±2, ±4, and ±8°) for each of six orientations (0°, 30°, 60°, 90°, 120°, and 150°). Fixation distance was 100 cm. Anticipatory eye movements were minimized by presenting different eccentricities along the tested meridian in random order and by making the time to stimulus onset variable. One meridian was tested in each 10 min session. We also made measurements at fixation distances of 50, 100, and 200 cm along the vertical and horizontal meridians only. We made the measurements at 100 cm twice to assess repeatability. Test-retest reliability was excellent: Pearson's correlation in each subject was >0.93 along the vertical meridian and >0.82 along the horizontal.

To quantify the disparities associated with corresponding points, we need a definition of zero horizontal disparity. For this, we used the theoretical binocular horopter (in Helmholtz coordinates). In the plane of fixation, this horopter is the Vieth–Müller Circle (the circle containing the point of fixation and the optical centers of the two eyes). Above and below the fixation plane, it is a cylinder (Fig. 1B). Locations nearer than the cylinder have positive (crossed) horizontal disparity and locations farther than the cylinder have negative (uncrossed disparity).

Experiment 3: natural-disparity statistics

We measured the distributions of naturally occurring disparities across the central visual field while people engaged in everyday activities. The apparatus and procedure were similar to a previous study (Sprague et al., 2015).

Subjects.

Four subjects (1 female and 3 males, ages 25–39 years) participated. All but one were unaware of the experimental hypotheses. The protocol was approved by the Institutional Review Board. All subjects gave informed consent before starting the experiment. All had normal stereopsis.

Apparatus.

We used a mobile scene- and eye-tracking apparatus to measure the 3D structure of the scene and where subjects were fixating in those scenes as they engaged in everyday activities (Fig. 3A). The apparatus consists of two outward-facing cameras that capture stereoscopic images of the scene in front of the subject, and a binocular eye tracker that measures gaze direction for each eye. The eye tracker was a head-mounted SR Research EyeLink II Eye Tracker (RRID:SCR_009602) running at 250 Hz. The cameras were two XCD-MV6 digital video cameras (Sony) recording at 30 Hz with a resolution of 640 × 480. We modified the previous apparatus (Sprague et al., 2015) to expand the stereo camera's FOV to 75° horizontally by 58° vertically. The tracker was synchronized to the stereo camera in a master/slave configuration. The two devices were hosted by two separate computers powered by an external battery. The computers were carried in a backpack worn by the subject.

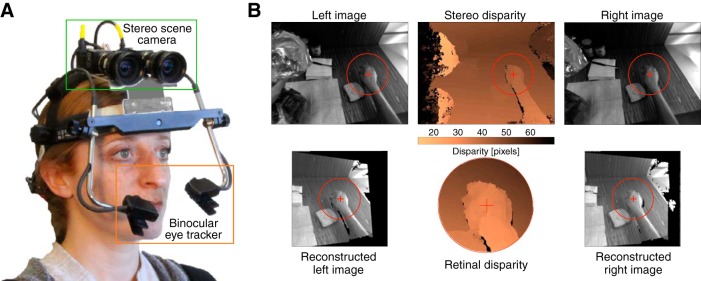
Figure 3.

Apparatus and images in natural-disparity experiment. A, The eye tracker and stereo camera. The subject wears a head-mounted device that consists of a binocular eye tracker and a stereo camera for recording the 3D scene. B, Stereo images from the scene camera, reconstructed images, and disparity map. Top row represents example left and right images from the stereo camera. A disparity map derived from those images is also shown in that row. Bottom row represents left and right images, reconstructed in eye coordinates. Red crosses represent the fixated point. Red circles represent a region with a diameter of 20° centered on that point. Bottom row, middle panel represents the disparity map in cyclopean-eye coordinates for the central 20° of the visual field. Color bar represents horizontal disparity in pixels for the top and bottom rows.

Procedure.

Subjects performed four tasks that were chosen as representative of everyday activities. The tasks were Outdoor walk, in which subjects walked in a natural outdoor area; Indoor walk, in which they walked while looking for an office in a campus building; Order coffee, in which they ordered a coffee at a local café while socializing; and Making sandwich, in which subjects assembled a peanut butter-and-jelly sandwich. Before each session, the eye tracker was calibrated separately for each eye (Svede et al., 2015; Gibaldi et al., 2017b). We then estimated the translation and rotation of viewpoints from the stereo camera to the eyes using a custom 3D registration algorithm (Sprague et al., 2015). The calibration was checked at the end of each session, and the data were discarded if the follow-up calibration was not within 0.8° of the initial calibration.

Postprocessing.

The eye-tracking data and stereo-image pairs were used to reconstruct the 3D geometry of the visible scene in eye coordinates. Figure 3B (top row) shows example images from the stereo cameras. We generated a depth map from those images using an established stereo reconstruction algorithm (Hirschmüller, 2008). We removed some routines from that algorithm because they in effect implemented prior depth distributions. We used the two gaze-direction measurements from the eye tracker to estimate gaze direction in cyclopean-eye coordinates and then imposed the fixation distance according to where the cyclopean gaze vector intersected the reconstructed 3D scene. Using the coordinates of the fixation point, we then transformed the stereo images into cyclopean-eye coordinates and left-eye and right-eye coordinates to compute binocular disparity (Fig. 3B, bottom row). From the current measurements, the resulting database contains 770,000 samples. The postprocessing pipeline is described in detail previously (Sprague et al., 2015).

Data analysis

For each position in the central visual field, we determined the distribution of horizontal disparities experienced by the 4 subjects in the four tasks. The data across subjects were very similar, so we averaged across subjects. The data differed significantly across tasks, so we used a weighted combination of data from the tasks based on a previously developed sampling technique (Sprague et al., 2015). We then sorted the data to determine the disparity distributions for fixation distances similar to those in the oculomotor and horopter experiments: near (40–80 cm), intermediate (80–180 cm), and far (180–360 cm).

Results

Experiment 1: oculomotor horopter

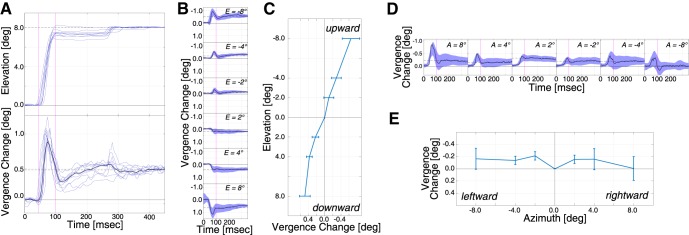
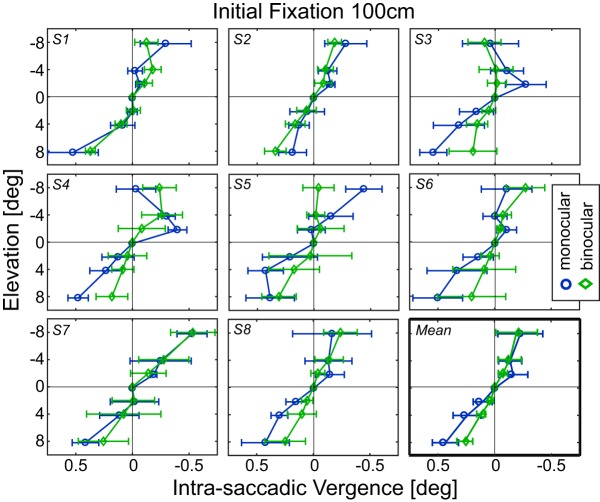
Figure 4A (top) shows one subject's saccade trajectories to a target at an elevation of −8° (i.e., upward). Figure 4A (bottom) shows the change in horizontal vergence for those saccades where 0° represents no change from the vergence associated with the initial fixation target. There was transient divergence as the eyes were in flight followed by smaller divergence when the eyes landed. Figure 4B shows horizontal vergence over time for this subject as he made saccades to targets at various elevations. Divergence occurred with upward saccades and convergence with downward saccades. Again, we observed transient vergence (divergence with upward movements and convergence with downward) that became smaller in magnitude as the eyes landed. We computed the median vergence change from saccadic start point to endpoint for each peripheral stimulus. Figure 4C shows some of those data. It plots the median vergence change as a function of elevation (i.e., for stimuli along the vertical meridian). Clearly, divergence occurred consistently in this subject with upward saccades and convergence consistently with downward saccades. Figure 5 shows the 100 cm data for each subject separately. The data were quite similar from one subject to another: All subjects exhibited divergence with upward saccades and convergence with downward. Those biases were present in the monocular and binocular conditions, but were larger in the monocular condition.

Figure 4.

Intrasaccadic vergence for vertical and horizontal saccades in a representative subject. A, Saccade and vergence trajectories. Top, Eye position over time for 10 upward saccades to a target at −8° eccentricity. Eye position is the average of the two gaze-direction vectors referenced from the midpoint of the interocular axis. Bottom, Vergence change over time for those saccades. B, Horizontal vergence in the same subject to targets at elevations of ±2°, ±4°, and ±8°. Solid lines indicate the mean trajectories. Shaded areas represent 95% CIs. Horizontal vergence is the difference between the azimuths of the two gaze vectors referenced from the midpoint of the interocular axis. C, Intrasaccadic vergence in the same subject for vertical saccades. The means (solid lines) and SDs (error bars) are plotted as a function of elevation. Figure 5 reports data for each subject for the monocular and binocular conditions, and the median computed among subjects. D, Vergence in the same subject to targets at azimuths of ±2°, ±4°, and ±8°. Solid lines indicate the mean trajectories. Shaded areas represent 95% CIs. E, Intrasaccadic vergence in the same subject for horizontal saccades. The means (solid lines) and SDs (error bars) are plotted as a function of azimuth.

Figure 5.

Intrasaccadic vergence for vertical saccades for each subject. Each panel plots intrasaccadic vergence for vertical saccades as a function of elevation for one subject. Bottom right, The data averaged across subjects. Blue lines and symbols represent monocular data. Green lines and symbols represent binocular data. Initial fixation distance is 100 cm.

Figure 4D, E shows the data as a function of azimuth. Figure 4D shows vergence over time for the same subject making saccades to targets at various azimuths. Transient divergence occurred that became smaller as the eyes landed. Figure 4E plots median vergence changes for the various peripheral stimuli along the horizontal meridian. Divergence occurred consistently with leftward and rightward movements.

The vergence bias produced small residual errors relative to the true target location. In the monocular condition, the error was ≤0.1 diopters, so a residual accommodative error would likely have been ∼3 times smaller than the depth of focus of the human eye (Campbell, 1957). In the binocular condition, the residual disparity was ≤20 minarc, so in many cases there was sufficient residual disparity to lead to a correct vergence movement after the eyes landed near the eccentric target (Ogle, 1950). This led to a corrective movement to reduce the disparity to near zero.

Figure 6 shows oculomotor data combined across subjects. Figure 6A plots median intrasaccadic vergence for vertical and horizontal saccades at each of the three initial fixation distances and for monocular and binocular viewing. The top shows vergence with vertical eye movements. Again, there was consistent divergence when making upward saccades. Divergence was significantly greater for −4 vs −2° (p < 10⁻⁴, Wilcoxon signed-rank test) and for −8 vs −4° (p < 10⁻⁵). There was again consistent convergence with downward saccades. Convergence was significantly greater for 4° versus 2° (p < 10⁻⁴) and 8° versus 4° (p < 10⁻⁵). There was also consistent divergence for leftward and rightward eye movements, but no significant effect of eccentricity from ±2 to ±8°.

Figure 6.

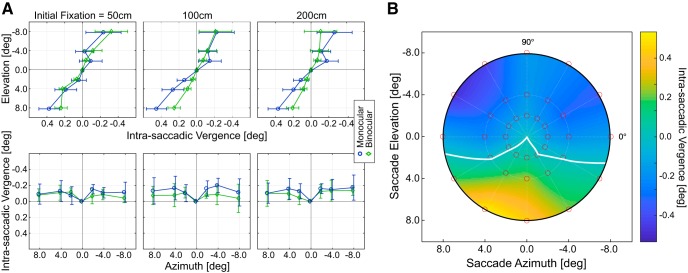
Intrasaccadic vergence across subjects, and fixation distances, and for monocular and binocular viewing. A, Horizontal intrasaccadic vergence for vertical and horizontal saccades. Left to right, Data for initial fixation distances of 50, 100, and 200 cm averaged across trials and subjects. Top, Data for vertical saccades. Bottom, Data for horizontal saccades. The means (solid lines) and SDs (error bars) are plotted as a function of elevation or azimuth. Green symbols and lines represent the data for binocular viewing. Blue symbols and lines represent the data for monocular viewing. B, Intrasaccadic vergence across the central visual field. Initial fixation distance was 100 cm. Monocular condition. The abscissa and ordinate indicate the horizontal and vertical eccentricity, respectively, of the saccadic target. Median horizontal vergence is represented by color: Lighter colors represent more positive values. White curve indicates where vergence changes sign from convergent to divergent. Red dots represent the tested field positions. The heat map was obtained via natural neighborhood interpolation (Sibson, 1981).

There was a small but consistent effect of monocular versus binocular viewing. With binocular viewing, intrasaccadic vergence changed less than with monocular viewing. For vertical saccades, there was less convergence with downward saccades and less divergence with upward (p < 10⁻⁴, Wilcoxon signed-rank test). With horizontal saccades, there was less divergence for leftward and rightward saccades (p < 10⁻⁴). Postsaccadic corrections were larger with binocular viewing, but that is not reflected in these data because we only considered the vergence before correction. There was no consistent effect of fixation distance. Test-retest reliability was quite high. Pearson's correlation was >0.95 for each subject when making vertical saccades and >0.87 when making horizontal saccades.

Figure 6B plots the median intrasaccadic vergence for all 36 peripheral targets for an initial fixation distance of 100 cm and monocular viewing. It shows that the pattern of divergence with upward, leftward, and rightward saccades and convergence with downward saccades generalized to positions off the vertical and horizontal meridians. The pattern of divergence and convergence with upward and downward saccades, respectively, was observed in every subject (Fig. 5). The pattern of divergence with leftward and rightward saccades (data not shown) was also observed in every subject (Fig. 5).

The pattern of convergence with downward movements and divergence with upward is consistent with previous reports (Enright, 1984, 1989; Collewijn et al., 1988; Zee et al., 1992; Oohira, 1993). It means that the 3D landing points of downward and upward saccades are biased, respectively, toward nearer and farther than current fixation. The pattern of divergence with leftward and rightward saccades is also consistent with previous reports (Enright, 1984, 1989; Collewijn et al., 1988; Zee et al., 1992; Oohira, 1993).

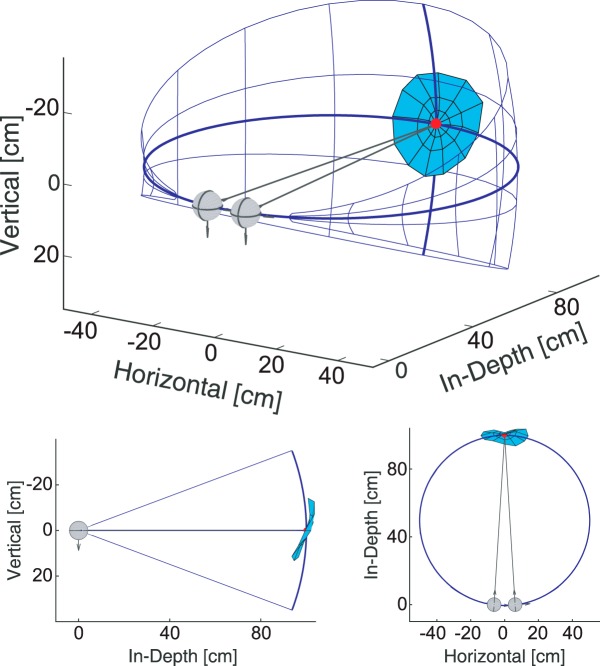
We calculated where in 3D space the lines of sight intersected at saccadic endpoints for all peripheral locations. We call the resulting surface the oculomotor horopter because it corresponds to the 3D positions to which the eyes initially move when stimulated by eccentric targets (Schor et al., 1994). Figure 7 plots the oculomotor horopter in 3D space for an initial fixation distance of 100 cm (the only distance at which we made measurements along all six meridians). The data used to generate the surface are from the monocular condition, averaged across subjects. The oculomotor horopter is pitched top back and has a slightly convex horizontal cross section at the tested fixation distance.

Figure 7.

Empirical oculomotor horopter. The oculomotor horopter is shown from three perspectives. Red dot in each panel represents the initial fixation point. Data are from the initial distance of 100 cm (monocular condition). Blue grid represents the theoretical oculomotor horopter (iso-vergence surface) for that fixation distance. Blue surface represents the empirical oculomotor horopter. Top, View from behind and to the right of the subject. Left bottom, View from the right. Right bottom, View from above the subject.

As we said above, eye trajectories generally contained a large transient vergence when the saccade velocity was highest: divergent for upward and horizontal saccades and convergent for downward (Enright, 1984, 1989; Collewijn et al., 1988; van Leeuwen et al., 1998). The magnitude of the transient vergence was greater at large eccentricities. These transient responses were followed by corrections that reduced the vergence error relative to the true distance of the stimulus as the eyes decelerated to land near the eccentric target. The correction could have been driven by visual feedback in the binocular condition, but not in the monocular condition.

Experiment 2: binocular horopter

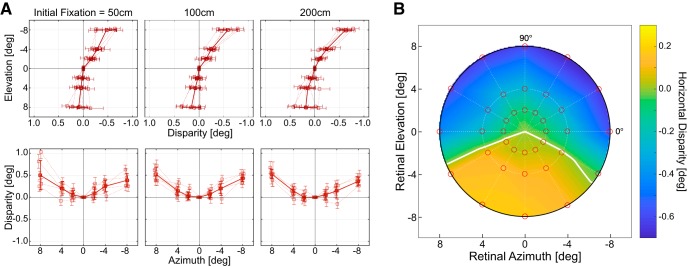
Figure 8A shows the horizontal disparities required to stimulate corresponding retinal points along the vertical and horizontal meridians. The panels from left to right show the disparities for fixation distances of 50, 100, and 200 cm. The top and bottom show the disparities along the vertical and horizontal meridians, respectively. There was very little effect of fixation distance, which is expected because corresponding points are fixed in retinal coordinates (Hillis and Banks, 2001).

Figure 8.

Binocular horopter. A, Binocular horopter along the vertical and horizontal meridians for different fixation distances. Left to right, Data for fixation distances of 50, 100, and 200 cm averaged across trials and subjects. Top, Bottom, Data along the vertical and horizontal meridians, respectively. Thin dotted lines are data from different subjects. The means (solid lines) and SDs (error bars) are plotted as a function of elevation or azimuth. B, Binocular horopter across the central visual field. Fixation distance was 100 cm. The abscissa and ordinate indicate azimuth and elevation, respectively. Median horizontal disparity for corresponding points is indicated by color: darker colors represent greater uncrossed disparity. White curve indicates where disparity changes sign from crossed to uncrossed. Red dots represent the tested field positions. The heat map was been obtained with natural neighborhood interpolation (Sibson, 1981).

As has been reported many times before, the disparities associated with corresponding points near the vertical meridian are uncrossed in the upper visual field and crossed in the lower visual field (Nakayama, 1977; Siderov et al., 1999; Grove et al., 2001; Schreiber et al., 2008; Cooper et al., 2011): thus, the binocular horopter is pitched top back. We calculated the horizontal shear (the angle between meridians that contain corresponding points near the vertical meridian) for our data and obtained an average value of 3.0°, which is consistent with previous reports (Nakayama, 1977; Siderov et al., 1999; Grove et al., 2001; Schreiber et al., 2008; Cooper et al., 2011). We also calculated H (the Hering–Hillebrand deviation) for our data. H is a measure of the deviation, near the horizontal meridian, between the empirical horopter and the Vieth–Müller Circle. We obtained an average value of 0.40, which agrees well with previous findings (Ogle, 1950; Shipley and Rawlings, 1970; Grove et al., 2001; Hillis and Banks, 2001; Schreiber et al., 2008).

Figure 8B shows the horizontal disparities required to stimulate corresponding points across the central visual field. Uncrossed disparities were required in the upper field and crossed disparities in the lower field. Thus, the top-back pitch of the binocular horopter generalizes to positions off the vertical meridian (Grove et al., 2001; Schreiber et al., 2008). Small uncrossed disparities were required in the left and right fields as well, so the binocular horopter is convex for fixation distances ∼>36 cm (Grove et al., 2001; Schreiber et al., 2008).

Experiment 3: natural-disparity statistics

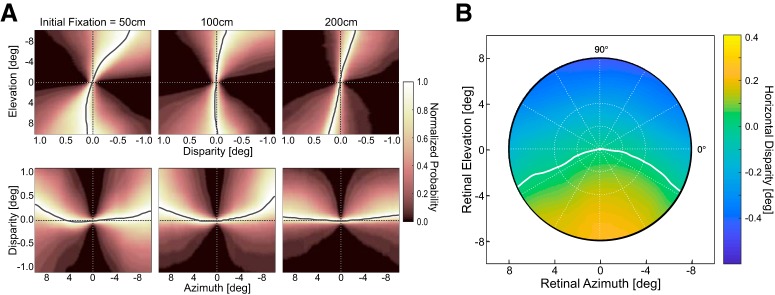
Figure 9A shows some of the data from the natural-disparity experiment. The top row plots the probability distributions and the median for horizontal disparity along the vertical meridian for near, intermediate, and far fixation. At all fixation distances, the central tendency of the distribution is crossed in the lower visual field and uncrossed in the upper field. The spread of the distribution decreases with increasing fixation distance. The bottom row of the figure shows the probability distributions along the horizontal meridian for the three fixation distances. At all fixation distances, the central tendency is uncrossed in the left and right fields. Again, the spread of the distribution decreases with increasing fixation distance. The central tendency is also shifted toward zero disparity at the far fixation distance.

Figure 9.

Natural-disparity statistics. A, Distributions of horizontal disparity along the vertical and horizontal meridians. Each panel plots the normalized probability of different disparities for positions along those meridians. The data from the 4 subjects were averaged. The plotted distributions were derived from weighted combinations of the data from the four tasks using a previous sampling method (Sprague et al., 2015). Left to right, Probabilities for different fixation distances: near (40–80 cm), intermediate (80–180 cm), and far (180–360 cm). Top, Bottom, Probabilities for the vertical and horizontal meridians, respectively. In each panel, brighter colors represent greater probabilities. Solid curves indicate the medians of the disparity distributions at each eccentricity. B, Median horizontal disparity at each position in the central 16° of the visual field for fixation distances in the range 40–8000 cm. Abscissa and ordinate indicate azimuth and elevation, respectively. The disparity values are indicated by color: darker color represents larger uncrossed disparity. White curve indicates where the median disparity changes sign from crossed to uncrossed.

Figure 9B plots median horizontal disparity for each position in the central visual field combined across fixation distances, subjects, and tasks. Clearly, the median disparity shifts from crossed in the lower field to uncrossed in the upper field. Thus, the crossed-to-uncrossed transition is characteristic of the whole central field rather than just the vertical meridian. The median disparity also shifts from slightly uncrossed in the left field to zero near the fovea to slightly uncrossed in the right field, so the transition from uncrossed to zero to uncrossed is observed across the whole field, not just the horizontal meridian.

Comparison of oculomotor data and natural-disparity statistics

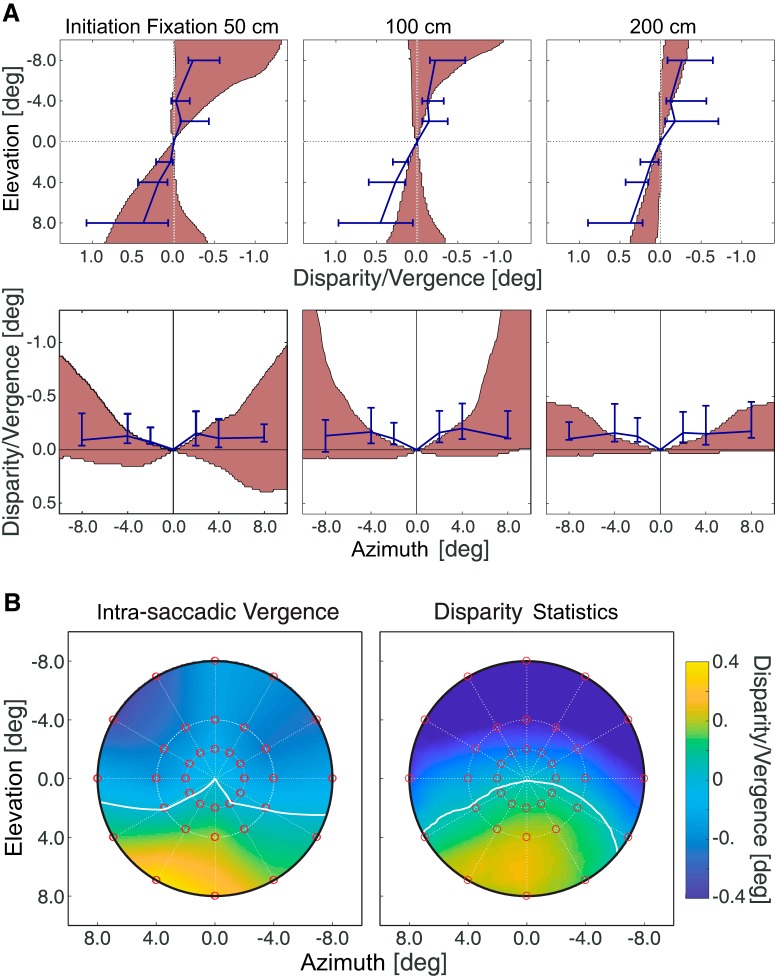
We next examined the degree to which the horizontal vergence associated with different directions and amplitudes of saccades (Figs. 4, 6) conforms to natural-disparity statistics. Figure 10A (top row) plots intrasaccadic vergence and the range of natural disparities as a function of elevation along the vertical meridian. The vergence data are from the monocular condition. Fitting the oculomotor data with a line, we can calculate the angle between the projections of that line into two eyes. Those shear values for the monocular condition were 2.4° (±1.1), 2.3° (±0.7), and 2.7° (±1.1) at initial fixation distances of 50, 100, and 200 cm, respectively. Shear values for the median natural-disparity statistics data were 2.4°, 1.7°, and 1.8° for near, intermediate, and far fixation distances (which correspond to ∼50, 100, and 200 cm, respectively). Thus, the agreement between the oculomotor and natural-disparity data is generally good along the vertical meridian but is best at the near fixation distance. We also examined the degree to which the binocular horopter (Fig. 8) conforms to natural-disparity statistics (Fig. 9). The agreement is good, which replicates earlier reports (Sprague et al., 2015; Gibaldi et al., 2017a).

Figure 10.

Intrasaccadic vergence and natural-disparity statistics. A, Left to right, Data for initial fixation distances of 50, 100, and 200 cm. Top and bottom rows represent the data along the vertical and horizontal meridians, respectively. Blue lines indicate the average change in horizontal vergence. Error bars are the 25th and 75th percentiles. Shaded regions represent the range of natural disparities from 25th to 75th percentiles. To allow fair comparison between the two sets of data comparable, both are referenced to the iso-vergence surface (Fig. 1A). B, Map of intrasaccadic vergence (left) and median horizontal disparity (right) across the central 16° of the visual field. The abscissa and ordinate indicate azimuth and elevation, respectively. The vergence-change and disparity values are indicated by color: Blue represents divergence or uncrossed disparity. Orange represents convergence or crossed disparities. White curves indicate where the median vergence change or disparity reverses sign. The disparity data are for fixation distances of 80–160 cm to be comparable with the vergence data for the fixation distance of 100 cm. Both sets of data are referenced to the iso-vergence surface (Fig. 1A).

Figure 10A (bottom row) plots the oculomotor and natural-disparity data along the horizontal meridian. Again, the vergence data are from the monocular condition. H values for the oculomotor experiment were 0.10 (±0.10), 0.09 (±0.14), and 0.13 (±0.13) for initial fixation distances of 50, 100, and 200 cm, respectively. H values for the median natural-disparity data were 0.17, 0.23, and 0.07 for near, intermediate, and far fixation distances, respectively. The agreement between the oculomotor and natural-disparity data along the horizontal meridian is generally very good.

Figure 10B compares the median intrasaccadic vergences (left) and median natural disparities (right) across the central visual field. The vergence data are for a fixation distance of 100 cm, and disparity data are for fixation distances of 80–160 cm. The agreement between the oculomotor and natural-disparity data is very good for all field positions, which shows that the agreement along the vertical and horizontal meridians generalizes to positions off those meridians.

Discussion

We found that the horizontal vergence that accompanies saccades deviates systematically from the true target distance. The eyes diverge when making upward and horizontal saccades, and converge when making downward saccades. Those effects occur whether the eccentric target is seen monocularly (where there is no computable disparity to signal the correct vergence) or binocularly (where disparity signals the correct vergence); the effects are larger with monocular viewing. These vergence biases are consistent with the distributions of natural disparities, suggesting that the oculomotor system has incorporated those statistics to optimize efficiency.

Visuo-motor optimization

Saccades to eccentric targets generally undershoot slightly followed by corrective saccades to place the foveas on or close to the target. Undershooting minimizes energy expenditure, so it is sensible to do this given uncertainty about target position and saccadic motor error.

What is the best strategy for guiding vergence accompanying saccades? The true distance to the target is the plane of the display screen. The distance for which no vergence change occurs is the iso-vergence surface (Fig. 1A). The most likely distance given no distance information from disparity (i.e., monocular viewing) is the median of the natural-disparity distribution (Fig. 9). To what distance should vergence be aimed? Energy expenditure associated with rotating the eyes to a new vergence posture is lowest on the iso-vergence surface. But moving the eyes there may require a correction, as occurs with saccadic undershoots. The correct distance is that of the display screen, so when that distance is well specified (as in binocular viewing), we expect vergence to be reasonably consistent with it. If target distance is not well specified (monocular viewing), we expect vergence to be biased toward the most likely distance (i.e., the central tendency of the natural-disparity distribution) and/or toward minimum energy (iso-vergence surface). Thus, vergence should lie between the true distance and the median of the natural-disparity distribution: closer to the true distance with binocular viewing and closer to the disparity median with monocular viewing. This is precisely what we observed. This strategy enables accurate binocular movements given uncertainty about the distance of the new fixation target.

Neural mechanisms

Our results are relevant to a long-standing debate between Hering and Helmholtz (King, 2011; Coubard, 2013). Hering said the eyes should be thought of as two parts of one organ rather than two separate organs. Specifically, he stated that fixations from one point in 3D space to another are implemented by one neural activation directing both eyes to move (Hering, 1868). He said there are separate saccadic and vergence command systems that control both eyes. In contrast, von Helmholtz proposed that eye movements are implemented by independent activation of the two eyes (von Helmholtz, 1867): two monocular command systems, each controlling one eye.

We found that saccades to an eccentric target visible in only the dominant eye yields divergence with upward and horizontal saccades and convergence with downward saccades. Assume the right eye is the dominant eye. When the eyes land at the end of a saccade, that eye is usually pointed to the right of targets in the upper, left, and right fields and to the left of targets in the lower field. This is easy to understand from Hering's perspective. The vergence command system has learned from the natural environment that disparities in the upper, left, and right visual fields are mostly uncrossed and that disparities in the lower field are mostly crossed. The system programs divergence and convergence appropriately for saccades into those parts of the field. As a result, the probability that the right and left eyes are aligned with a target of uncertain distance is increased. Our results are difficult to understand from von Helmholtz's perspective. Why would a monocular command system aim the right eye to the right of the target when making upward, leftward, and rightward saccades and to the left of the target when making downward saccades? A monocular command system would aim the eye at the target (or slightly short of it when location is uncertain) instead of aiming systematically right or left of it depending on the direction of the upcoming saccade. Thus, our data are more consistent with Hering's scheme of separate saccadic and vergence command centers.

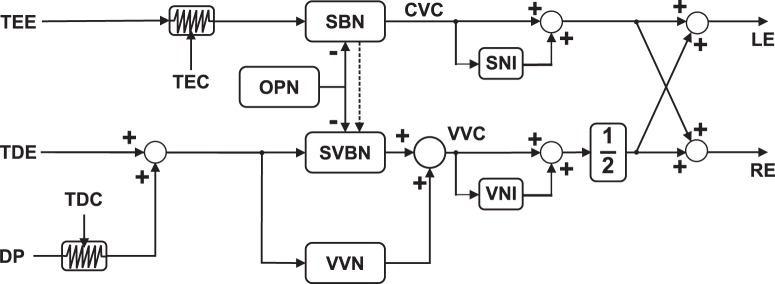
Our results are also consistent with the neural model of saccadic-vergence burst neurons (SVBNs) (Zee et al., 1992; Busettini and Mays, 2005b; Kumar et al., 2006) with a modification to incorporate prior disparity distributions for different parts of the visual field (Fig. 11). Vergence is faster when accompanied by saccades, and saccades are slower when accompanied by vergence (Enright, 1984, 1992; Erkelens et al., 1989; Mays and Gamlin, 1995). To explain eye control for saccades in depth, Zee et al. (1992) proposed the multiply model of SVBNs. The model claims that there are separate burst neurons for pure saccades (saccadic-burst neurons [SBNs]) and pure vergence (vergence-velocity neurons [VVNs]), but also hypothesized a separate class of neurons (SVBNs) to account for saccade-vergence interactions. The SBNs are located in the paramedian pontine reticular formation (Zee et al., 1976; Sparks and Mays, 1990); their discharge rate is proportional to the saccadic target's eccentricity. The model claims that VVNs and SVBNs are different classes of midbrain vergence-burst neurons (Mays et al., 1986). Recent evidence shows that SVBNs may reside in the central mesencephalic reticular formation (Quinet et al., 2017). They receive a target disparity error that may originate from frontal cortex (Gamlin and Yoon, 2000; Gamlin, 2002) or medial superior temporal area (Takemura et al., 2001), and transform it into discharge proportional to the achieved vergence velocity. Omni-directional pause neurons exert inhibitory control on SBN and SVBN activity (Mays and Gamlin, 1995), but not on VVN. SVBNs generate premotor commands for vergence, but only during concomitant saccades. Nonlinear modulation of vergence commands by saccadic peak velocity is modeled by a direct connection between SBNs and SVBNs (Busettini and Mays, 2005a). SVBN output is added to that of VVNs and, in this way, saccades enable faster vergence. The conjugate and disconjugate velocity commands are stabilized by dedicated neural integrators.

Figure 11.

Modification of multiply model of SVBNs (Zee et al., 1992; Busettini and Mays, 2005b; Kumar et al., 2006). The conjugate velocity command (CVC) uses a visual error proportional to target eccentricity (TEE), whereas the disconjugate velocity command (WC) uses target disparity error (TDE). The two commands are generated by cooperation of three types of burst neurons: SBNs for pure saccades, VVNs for pure vergence, and SVBNs for saccade-related vergence. Saccadic activity is gated by omni-directional pause neurons (OPN). Their activity is summed/subtracted to obtain velocity commands for the left (LE) and right eyes (RE). Dashed line and the asterisk indicate a nonlinear effect between SBNs and SVBNs (Busettini and Mays, 2005b; Kumar et al., 2006). The saccade (SNI) and vergence (VNI) neural integrators then stabilize the motor commands. Our modification to the model uses an uncertainty estimate of target eccentricity (TEC) to modulate the TEE signal, which affects the conjugate velocity command. With greater uncertainty, saccadic undershoot increases. Similarly, our modification of the model uses an estimate of the confidence on target disparity (TDC) to affect the vergence velocity command (WC). With greater uncertainty, the disparity prior (DP) has more influence on the vergence response.

In our modification, prior information about natural disparities is incorporated by adding a disparity prior. The influence of the prior on the input disparity estimate is modulated by the uncertainty associated with that estimate (target disparity). This model explains saccade-vergence interactions and how vergence biases come to be compatible with disparities experienced through interaction with the natural environment.

Theoretical and empirical horopters

The theoretical binocular horopter is the locations in 3D space that stimulate identical points (same azimuth and elevation) in the two retinas (i.e., the locations that create zero horizontal and vertical disparity) (Ogle, 1950; Shipley and Rawlings, 1970; Schreiber et al., 2008; Cooper et al., 2011). We limit our discussion to locations that create zero horizontal disparity. In Helmholtz coordinates, the resulting theoretical horopter is a cylinder containing the Vieth–Müller Circle and vertical horopter (Fig. 1B).

The empirical binocular horopter is measured as we did in the binocular horopter experiment. This horopter is the locations in 3D space that create equal perceived azimuths in the two eyes. The empirical binocular horopter is similar but not identical to the theoretical (Fig. 8A): The horizontal component is less concave than the cylinder (Ogle, 1950; Shipley and Rawlings, 1970; Hillis and Banks, 2001) and the vertical component is pitched top back relative to vertical (Nakayama, 1977; Siderov et al., 1999; Schreiber et al., 2008; Cooper et al., 2011).

There are also theoretical and empirical oculomotor horopters. The former is the locations in space for which horizontal vergence is the same. The theoretical oculomotor horopter is a torus: the Vieth–Müller Circle rotated about the interocular axis (Schor et al., 1994) (Fig. 1A).

We measured the empirical oculomotor horopter (Figs. 4, 6): the 3D positions of the new fixation point after execution of vertical, horizontal, and oblique saccades (Fig. 7). As with the binocular horopters, the theoretical and empirical oculomotor horopters differ. In particular, people diverge relative to the theoretical horopter when they make upward and horizontal saccades and converge from it when making downward saccades.

Learning

We found that biases in horizontal vergence accompanying saccades are quite consistent with the pattern of naturally occurring disparities. Horizontal and vertical vergence biases are known to be consistent with the horizontal and vertical disparities that occur in oblique field positions due to binocular geometry (Schor et al., 1994). Vergence biases are adjusted fairly rapidly to compensate for lenses that cause prismatic or magnification changes in one eye (Ellerbrock and Fry, 1942; Henson and Dharamshi, 1982). The adaptation can be nonuniform across the visual field (Graf et al., 2003).

These observations are compatible with the idea that vergence biases are learned through interaction with the environment. Such learning helps maintain efficient oculomotor behavior during development as the separation between the eyes grows and the extraocular muscles change. It also enables efficient behavior when the mapping between the environment and disparity is changed due to new spectacles or contact lenses (Graf et al., 2003; Cooper et al., 2011).