Hybridized Guided-Mode Resonances via Colloidal Plasmonic Self-Assembled Grating

Abstract

For many photonic applications, it is important to confine light of a specific wavelength at a certain volume of interest at low losses. So far, it is only possible to use the polarized light perpendicular to the solid grid lines to excite waveguide–plasmon polaritons in a waveguide-supported hybrid structure. In our work, we use a plasmonic grating fabricated by colloidal self-assembly and an ultrathin injection layer to guide the resonant modes selectively. We use gold nanoparticles self-assembled in a linear template on a titanium dioxide (TiO₂) layer to study the dispersion relation with conventional ultraviolet–visible–near-infrared spectroscopic methods. Supported with finite-difference in time-domain simulations, we identify the optical band gaps as hybridized modes: plasmonic and photonic resonances. Compared to metallic grids, the observation range of hybridized guided modes can now be extended to modes along the nanoparticle chain lines. With future applications in energy conversion and optical filters employing these cost-efficient and upscalable directed self-assembly methods, we discuss also the application in refractive index sensing of the particle-based hybridized guided modes.

Introduction

Optical antennas are the key to confine light energy into a target structure and vice versa.¹ Plasmonic nanoparticles (NPs), in particular, are suitable for collecting light energy into a nanometer-sized volume via oscillation of the free electrons at the particle surface (localized surface plasmon resonance, LSPR) and converting the energy into a current, that is, light harvesting.² Thus, efficient light concentration and hot carrier extraction have led to diverse applications such as photocatalysis,³ photovoltaics,⁴ and photodetection.⁵ Plasmonic NP chains are of special interest as they can excite modes with suppressed radiative losses.^6,7 When a chain is formed from individual NPs, the excited plasmon mode for incident polarization along the chain direction shifts to a lower energy (super-radiant mode) until a certain group velocity of the collective plasmon mode is reached.⁸ This collective plasmon mode along with all higher energy modes can be imagined analogously to a mechanical string vibration model or nondegenerated modes as in quantum mechanics. In theory of plasmonic chains, these energetic higher modes (subradiant) have lower propagation losses than the super-radiant mode.⁹ Recent research topics have focused on the study of these subradiant modes for possible applications in optical sensing,¹⁰ subdiffraction energy transport,^11,12 and plasmonic NP gratings.¹³

However, these NP chain-based plasmonic grating resonant (PGR) modes still have radiative damping, and their resonance wavelength varies greatly because of size and particle spacing.¹³ By incorporating thin-film layers, plasmon modes can be extracted by phase-matching conditions and guided within these layers following the properties of a grating waveguide-based guided-mode resonant^14,15 (GMR) structure. Such waveguide–plasmon polaritons have been intensively studied and can be used to investigate strong coupling,¹⁶⁻¹⁸ to demonstrate light generation,¹⁹ and to show filter properties with high optical transmission.²⁰ All these properties benefit from the hybridized coupling (Fano resonance) of a narrow (waveguide mode) and a broad (plasmonic mode) oscillation.²¹ In most of the cases, these hybrid structures are fabricated using an electron beam and contact lithography followed by physical vapor deposition, sol–gel approach, and a chemical etching step which results in a limited array of polycrystalline NPs that suffer from increased damping. Recent developments in directed self-assembly can solve this bottleneck to realize large-scale assembly of monocrystalline NPs at a reasonable price.²² In particular, the combination of rapid top-down laser interference lithography (LIL) template and bottom-up template-assisted self-assembly (TASA) methods allow the freedom to assemble NPs in various two-dimensional structures.²³ Consequently, development in self-assembly makes it possible to access the plasmon modes along the NP line selectively. Generally, the NP-based pure plasmonic resonance mechanisms are extremely responsive to the change in the surrounding media and thus have significantly contributed toward the fabrication of highly sensitive refractive index²⁴ (RI) as well as biological sensors.^25,26 As broader PGR (super- and subradiant) modes with a larger full width at half-maximum (fwhm) have a higher radiative loss, Q-factor (inversely proportional to fwhm) remains significantly low for their application in the field of sensing. By coupling the plasmonic features to the high “Q” photonic modes (with smaller fwhm) of a dielectric GMR structure, one can increase the sensitivity of the so-obtained hybridized photonic modes as compared to the pure photonic (GMR) case while maintaining the sharpness and “quality”.

In this work, we have applied plasmonic grating, that is, the NP lines (fabricated by LIL and TASA) directly to the waveguide (TiO₂ layer) to save the process steps in constructing the hybridized geometry. A previous work from our group has demonstrated plasmonic studies of NP lines formed by template-assisted colloidal self-assembly, followed by a printing transfer to the target substrate.¹³ Here, we save ourselves from the transfer step by assembling the particles directly into the GMR structure. However, this step is not trivial as the surface chemistry of the particles and the substrate required for an efficient assembly now had to be adjusted to the LIL-fabricated GMR structure. Moreover, this effective fabrication step was not possible in the previous work as those substrates were made by mechanical instability (wrinkling) followed by assembly through spin-coating. For the current work, we have used LIL and convective self-assembly toward the fabrication of the hybrid optoplasmonic structures which till now are limited by “e-beam” fabrication techniques.^16,17 The grating period and waveguide thickness are chosen accordingly to obtain a phase match to favor coupling between the GMR and PGR modes. Experimental and theoretical spectroscopic methods with polarizations both parallel and perpendicular to the chain direction are used to study the plasmonic NP–waveguide polaritons on the centimeter scale. With this simple, cost-efficient, and upscalable fabrication method, we are able to discuss the complete hybrid nature of the resulting modes and show their application as optoplasmonic RI sensors.²⁷

Experimental Section

Fabrication of Dielectric GMR Structure

TiO₂ films are deposited on glass substrates (2.5 × 2.5 cm²) using electron beam evaporation (LAB 500 evaporator, Leybold Optics GmbH) at a rate of 2 Å/s up to a layer thickness of 200 nm. They are divided into individual smaller pieces and spin-coated with the negative photoresist ma-N 405 diluted with ma-T 1050 (MicroChem) in a 1:1 ratio. Optimized spin parameters of 6000 rpm, acceleration of 2000 rpm/s, and a total spin time of 33 s produced a thin film of 150 nm thickness, as confirmed by spectroscopic ellipsometry (RC2-DI, J.A. Woollam Co., Inc.). The coated substrates are further exposed to LIL to obtain a photoresist grating.

Gold Particle Synthesis

Spherical gold NPs with 88 ± 12 nm diameter are synthesized via a colloidal seeded growth process according to the procedure of Bastús et al.²⁸ Citrate-stabilized NPs are coated with bovine serum albumin (BSA) prepared according to already published methods.²⁹ Briefly, 40 mL of the NP solution is added to 4 mL of 1 mg/mL BSA solution with 1 wt % sodium citrate at pH 9. The solution is allowed to incubate overnight. After fourfold centrifugation, the NPs are analyzed with UV–vis spectroscopy and transmission electron microscopy. The NP size of 88 nm is determined by a statistical analysis of 50 particles.

Directed Self-Assembly

The fabricated dielectric GMR sample is UV flood-exposed (UV-15 S/L, Herolab) at 254 nm for 10 min and subsequently hard-baked at 120 °C for 4 min on a hot plate to reduce the swelling and leaching out of the photoresist while in contact with the slightly alkaline particle solution. Oxygen plasma treatment (30 s, 0.2 mbar, 80 W, Flecto 10, Plasma Technology) prior to the convective assembly experiment³⁰ creates good wettability of the substrate that is fixed to a motorized translation stage (PLS-85, Physik Instrumente). A cleaned glass slide (Menzel) is mounted above the GMR sample at a distance of 0.5 mm, and 25 μL of NP solution (0.5 mg/mL gold, pH 9) is placed in between the gap. The elevated pH value ensures a strong negative surface charge of the protein coating (−30 mV)²⁹ to provide electrostatic stabilization of the colloidal suspension. A constant linear motion at the rate of 1 μm/s is imparted to the stage through a computerized software system to recede the contact line in a direction parallel to the channels. The stage temperature is set to 14 K above dew point to control the evaporation rate at the meniscus that drives the transport of NPs toward the three-phase contact line. Lateral confinement by the channel geometry and a vertical one determined by the thickness of the liquid film inside the channels enables the selective crystallization of particles into double (dimer) lines together with the help of attractive capillary forces that arise during drying.

UV–Vis–NIR Spectroscopy

An ultraviolet–visible–near-infrared (UV–vis–NIR) spectrophotometer (Cary 5000, Agilent Technologies) in transmission geometry is used for recording optical responses corresponding to a broad range of 400–2400 nm. A rotatable polarizer is used to investigate the effect of both polarizations, s-pol (transverse electric, TE) and p-pol (transverse magnetic, TM), where the electric fields are out-of-plane and in-plane to the plane of incidence, respectively.

Finite-Difference in Time-Domain Simulations

A commercial-grade simulator based on the finite-difference in time-domain (FDTD) method is used to perform the calculations (Lumerical FDTD,³¹ version 8.16). For the simulation of the optical response, a plane wave source is used and the frequency points are set equal to that of the wavelength span. Monitor boxes (transmission monitors kept normal to the substrate) are used to obtain the optical responses of the systems. For the dielectric properties of gold, data from Palik³² are fitted using six coefficients with a root-mean-square error of 0.2. For the photoresist, TiO₂ layer, and glass substrate, the optical constants are fitted by using the experimentally obtained values through spectroscopic ellipsometry that are available in Supporting Information T1 (see Figure S1). The mesh size in the FDTD region is set to auto-nonuniform with a minimum mesh size of 0.25 nm and an additional mesh overlay of 2 nm applied over the arranged particle geometry. Periodic boundary conditions are applied for X and Z directions with perfectly matching layers along the Y direction.

RI Sensing

Deuterium oxide of 99.9% purity (D₂O), commonly known as heavy water, is used as an initial surrounding medium which is altered with a solution (0.3 g/mL) of sodium chloride (NaCl) in D₂O to slightly increase RI and observe the characteristic spectral change. The RI of pure water and salt solution are initially measured using a digital multiple wavelength refractometer DSR-L (Schmidt + Haensch) and used for the calculation of the sensitivity of different resonant geometries.

Results and Discussion

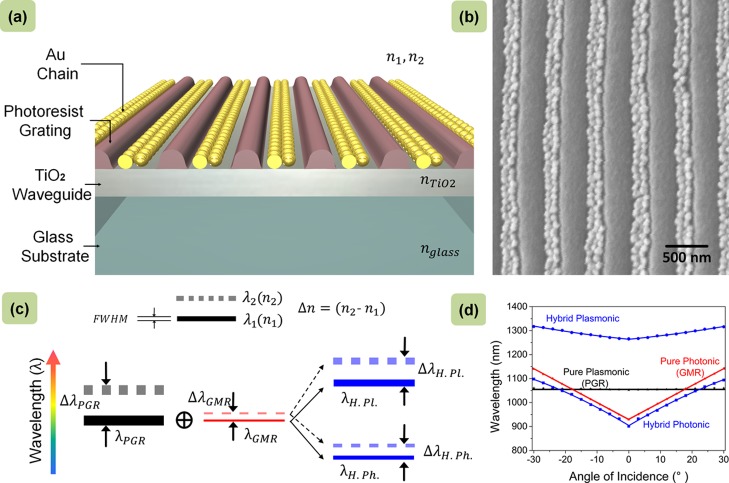
Figure 1a shows a schematic illustration of the hybrid optoplasmonic structure composed of a plasmonic NP grating and a dielectric GMR structure. This GMR structure is a photoresist grating (periodicity, Λ = 520 nm, and thickness, t = 150 nm) on a titanium dioxide (TiO₂) waveguide layer (thickness, d = 200 nm) supported by a glass substrate which forms a resonance between a diffracted and a waveguided mode. More discussion on the GMR structure can be found in Supporting Information T2. Figure 1b shows a scanning electron microscopy (SEM) image of the fabricated hybrid structure in top view. Figure 1c explains the interplay of the pure states into the formation of the hybridized states and their effect on RI variation. The top bars, solid and dotted, denote wavelengths corresponding to the initial (n₁) and final (n₂) indices, respectively. The thickness of the solid bar is used to represent “fwhm” of the resonance mechanism in general instead of referring to each of the individual cases. Sensitivity (S) is generally defined as the rate of change (Δλ) of resonant wavelength (λ_R) in response to change (Δn) in the surrounding index (n₁ to n₂). A plasmonic (PGR) mode with higher “S” and broader “fwhm” couples with the photonic (GMR) mode of relatively lesser “S” and smaller “fwhm” to produce hybrid photonic (H. Ph.) and hybrid plasmonic (H. Pl.) states. Apart from sensitivity, another factor that decides the quality of sensing is the figure of merit³³ (FOM), which can be defined as the ratio between “S” and “fwhm”. As smaller “fwhm” results in sharper curves with better measurement resolution, this is desired in all practical sensors apart from high “S” to maintain a high “FOM”. Thus, as shown in the schematic, the hybridized photonic mode (H. Ph.) can have an enhancement in “S” because of the coupling of plasmonic features while still maintaining lower “fwhm” to have a decent “FOM”. Figure 1d shows the dispersion relation for these pure and hybrid states obtained by plotting the resonant dip wavelength of experimentally observed transmission spectra as a function of the angle of incidence (AOI) in the case of parallel polarization. For both of the pure and hybrid photonic modes, the introduction of oblique incidence lifts the degeneracy of normal incidence through mode splitting; the split resonant dips corresponding to the higher wavelengths are plotted only in this figure. More detailed analysis of the dispersion studies has been elucidated further in this discussion.

Figure 1.

Concept and optical properties of plasmonic self-assembled GMR structure. (a) Plasmonic NP grating self-assembled inside a photoresist template on a TiO₂ waveguide. (b) SEM image of the plasmonic NP grating showing gold NPs within the photoresist grating channels. (c) Schematic illustrating the formation of two hybridized states: plasmonic (H. Pl.) and photonic (H. Ph.) along with the effect of RI variation (n₁ to n₂). The sensitivity (S = Δλ/Δn) and FOM (= S/fwhm) can be obtained from the distance between the solid and dashed lines (Δλ) and line thickness (fwhm), respectively. (d) Dispersion relation for pure photonic (guided-mode resonance), pure plasmonic (plasmonic grating resonance), and their hybridized modes obtained experimentally in air through an AOI scan with polarization along particle chains.

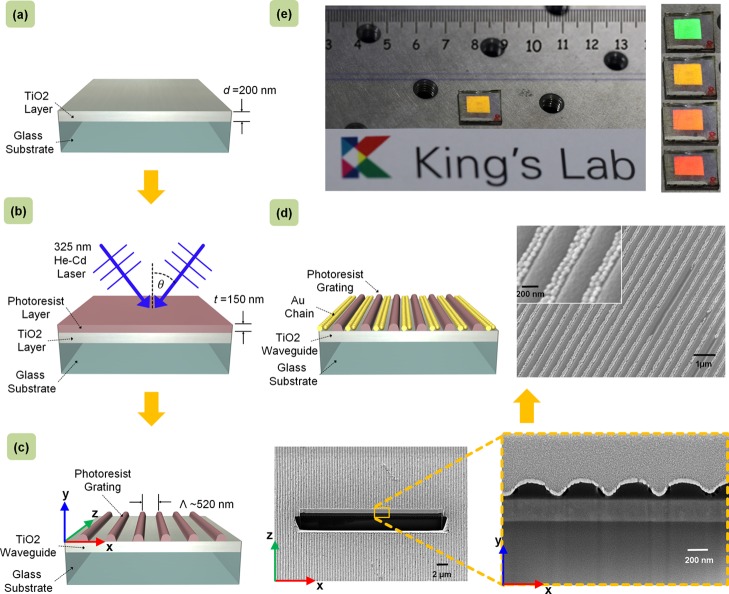
Figure 2 describes the overall fabrication procedure of the desired hybrid geometry, which is a combination of top-down and bottom-up approaches in producing the dielectric GMR structure and plasmonic NP grating, respectively. The details of the Lloyd mirror-based LIL setup corresponding to Figure 2b are given in Supporting Information T3 (schematic in Figure S3). Once the photoresist grating of the GMR structure is formed, the grating channels are filled with synthesized gold NPs through the process of directed self-assembly (TASA). Supporting Information T4 includes more about the TASA setup with a schematic in Figure S4. A movie clip of particle assembly recorded in real time by using an optical microscope in reflection mode is also provided in the Supporting Information (Video V1) that can provide a direct insight into the assembly process. Thus, one can observe a fast filling process of gold NP arrangement in chains over a large area which may be considered superior in comparison to the electron beam deposition techniques. Although grating homogeneity was lacking over a large scale that resulted in partial filling of some grating channels, the overall characteristics remain maintained when compared to the simulative study of ideal homogeneous chains and are discussed in the following sections. Figure 2d shows the finalized structure with an SEM image exhibiting efficient filling of photoresist channels with gold NPs. The magnified view in the inset supports the formation of dimer chains, which is considered during all simulative analyses throughout this report. Thus, our method, in contrast to e-beam techniques provides not only cost efficiency and large area fabrication, but also a plausible effort toward bringing in both the physical and chemical communities to a single productive platform. Moreover, plasmonic NP chains have been directly assembled in different designated geometries for studying both pure and hybrid states. The non-necessity of any molded template and transfer mechanism, unlike previous study,¹³ has indeed made the whole fabrication process even simpler.

Figure 2.

Fabrication of the hybrid optoplasmonic structure: (a) deposition of 200 nm TiO₂ layer onto the glass substrate by electron beam physical vapor deposition. (b) Spin-coating of negative photoresist and LIL using a He–Cd laser. (c) Formation of a GMR structure with a 520 nm periodic photoresist grating. Focused ion beam (FIB) cut reveals grating channels in a magnified view. (d) Directed self-assembly of gold NPs (88 nm in diameter) by the controlled evaporation of particle dispersion (convective self-assembly). An SEM image of the final structure with a magnified view in the inset shows dimer particle chain arrangement within grating channels. (e) Photograph of the fabricated sample on an optical table. Different first-order diffracted wavelengths (colors) at various AOIs appear on reflections from ordinary white room-light source.

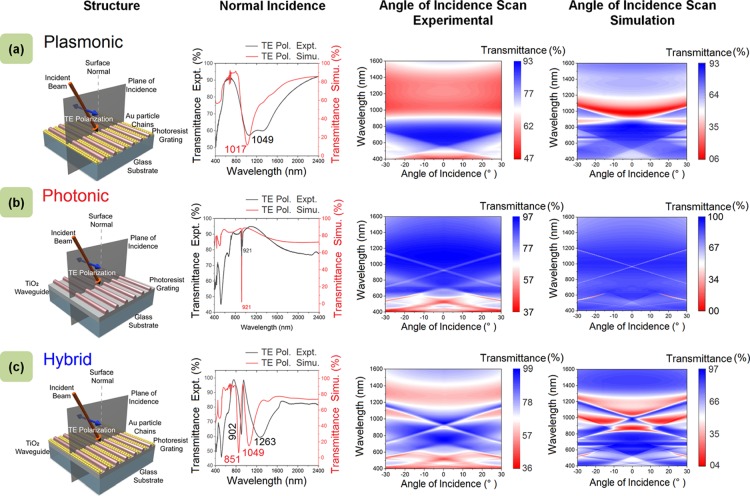
To have a thorough analysis of the fabricated hybrid structure, its optical characteristics in contrast to its constituent pure photonic and plasmonic counterparts are investigated to full extent. Although the “photonic” term is associated with the case of a dielectric GMR structure, “plasmonic” can be referred to a gold NP grating self-assembled directly on a separate photoresist-patterned glass substrate without any waveguide layer. Figure 3a presents studies on such plasmonic blocks excited in parallel polarization, that is, the TE case with respect to the plane of incidence lying normal to the grating lines (shown in the figure). Under normal incidence in air, the experimental spectroscopic data exhibit collective plasmonic resonances around 1049 nm as a broad transmission dip that well-agrees with previously reported findings¹³ and can be identified as the super-radiant mode. For a better understanding of the associated resonance, a simulation model with similar geometry of gold NP dimer chains on a photoresist-patterned glass substrate is considered using FDTD methods, with the specifications given in the Experimental Section. The deviation between the experimental and theoretical transmittance values can be attributed to the nonideal cases of finite chain length along with the missing particles in reality as compared to the modeled ideal case of infinitely chained close-packed structures. Further, studies under the variation of AOI are performed. As the polarization (TE) is fixed parallel to the chain orientation, varying the incident angle keeps the incident electric field intact, thus producing similar transmission spectra over −30° to 30°. The transmittance values as a function of wavelength and incident angle obtained experimentally as well as through simulation are provided in Figure 3a that correspond to the dispersion relation. The effects of polarization perpendicular to the grating lines (TM) are also explored via experiment as well as simulation and presented in Figure S5a of Supporting Information T5. It can be observed that plasmonic bands are formed around 530 nm corresponding to a single NP resonant dip.

Figure 3.

Comparison of optical properties of three different structures in TE mode: (a) plasmonic dimer lines of gold NPs with 520 nm periodicity supported by photoresist gratings on a glass substrate. Both experiment and simulation studies show a broad particle resonance around 1000 nm for excitation with TE polarization along the chain directions. Variation of the incidence angle experimentally exhibits a constant broad dip which is also supported by simulations. (b) Dielectric GMR structure with a photoresist grating (of periodicity 520 nm and thickness 150 nm) on a TiO₂ waveguide (of 200 nm thickness) and a glass substrate. Experimental as well as simulation studies observe transmission dip at 921 nm for normal incidence, whereas splitting of modes occurs on varying the AOI. (c) Hybrid plasmonic–dielectric resonant structure with gold NP dimer lines filled within the grating lines of a dielectric GMR. At normal incidence, two hybrid modes are excited at different wavelengths. Scanning of the incidence angle reveals the interaction of the broad plasmonic mode with the photonic GMR mode at higher angles, as observed from both experimental and simulation data.

Next, in Figure 3b, dielectric GMR with a photoresist grating and TiO₂ waveguide on a glass substrate is studied for optical characterization as well as for comparison with the final hybrid structure. The experimental and simulation transmission spectra match well with a periodicity of 520 nm, waveguide thickness of 200 nm, and a grating amplitude of 150 nm. For normal incidence in air, both the graphs produce a transmission dip at 921 nm for TE polarization, that is, parallel to the grating. However, in contrast to the simulation, the resonant dip in the experimental curve has a shorter depth because of the lesser diffraction efficiency of the fabricated grating. This can be caused by the nonuniformities like the variation in duty cycle (the ratio between the ridge width and the period of grating) and depth over large area unlike the ideal uniform case of simulation. As the incident angle is varied from 0° toward ±30°, we observe a similar splitting of the resonant mode into nondegenerate¹⁴ modes. The purpose of these AOI scans is to observe the effect of the red-shifted order interplaying with the plasmonic band in the final hybrid optoplasmonic structure. Figure S5b of Supporting Information T5 shows similar GMR optical characteristics in the TM mode with a resonant wavelength around 870 nm under normal incidence.

Finally, Figure 3c shows the case of a hybrid structure achieved through the combination of the fabrication processes discussed in this report with 150 nm grating thickness, 520 nm grating periodicity, and 200 nm TiO₂ waveguide layer supported on a glass substrate. The normal incidence spectrum obtained experimentally (black curve) in air contains two resonant dips: the broader one around 1263 nm as a hybrid plasmonic resonant mode along with a sharper hybrid photonic mode at 902 nm corresponding to the GMR phenomenon. The simulation results (red curve) similarly show the presence of both hybrid plasmonic and photonic resonances at 1049 and 851 nm, respectively. The experimentally obtained GMR transmittance dip (photonic) is enhanced in the hybridized photonic state at 902 nm because of the effect of coupling. As AOI is increased from 0° toward ±30°, one of the photonic modes (red-shifted) starts interplaying more with the constant plasmonic band as their spectral positions get closer. Thus, at larger angles, more of the plasmonic features are induced to the photonic mode through an easy exchange of energy, making both the hybrid modes broad as seen from the figure. The simulation results of the AOI scan in Figure 3c also agree to this experimentally observed fact. This hybridization, however, is strictly a feature of the TE modes as no such case is obtained for the TM mode, confirmed by Figure S5c of Supporting Information T5. This is because of the fact that for the TE case, the GMR sharp resonance falls on the left shoulder of the broad PGR mode at normal incidence providing a fair chance of the coupling mechanism. For the TM case (see Figure S5), the plasmonic resonances near 530 nm are the effective contributions of single NPs. As located far away from the photonic resonances (around 870 nm), nonoverlapping of these modes results in noncoupling, making the TE excitation case the only possible way of hybridization. This is contradictory to the case of well-known waveguide–plasmonic structures^16,17 consisting of metallic bar-based grating where plasmonic modes are only excited in the TM polarization, whereas the TE case produces only a grating-like response.³⁴ To compare our plasmonic grating of NP chains with metallic bars, a similar dimension of the grating in the hybrid optoplasmonic geometry for both the polarizations is studied and shown in Figure S6 of Supporting Information T6. This points out that unlike our case, TM excitation instead of TE is indeed required to bring in the hybridization for these types of waveguide–plasmonic structures.

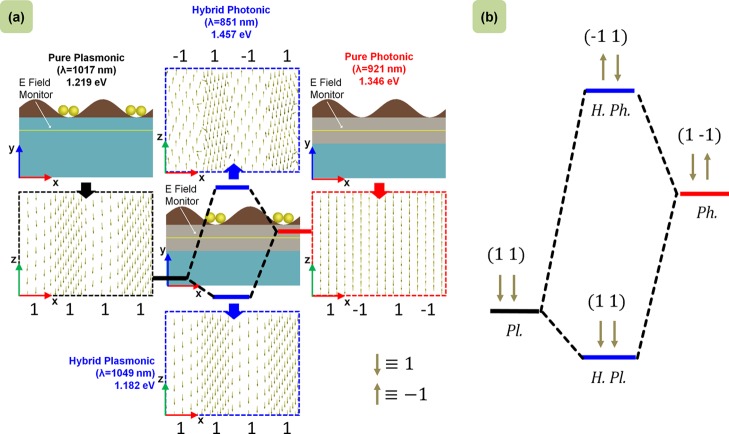
To justify the proper coining of the photonic/plasmonic terms to the observed hybrid modes, the various resonance conditions are studied through simulation by investigating the electric field (|E⃗|) distribution at resonant wavelengths for all of the pure and hybrid structures. Figure 4a shows the different geometries used in simulative studies with the E-field monitors placed below the grating–waveguide/substrate interface. The electric field vectors obtained in these monitors clearly show the basic notion of hybridization in terms of alignment of field vectors for the cases of pure and hybridized geometries. From a simplified model, as shown in Figure 4b, we can write a system of equations to understand the effect of superposition of the pure states |Ph.⟩ and |Pl.⟩ to produce the hybridized ones |H. Ph.⟩ and |H. Pl.⟩, which is

1

Figure 4.

Hybridization model of the plasmonic NP GMR grating by FDTD simulations. (a) Pure plasmonic and photonic modes are excited at PGR (1017 nm) and GMR (921 nm) wavelengths, respectively, in their corresponding setups. Hybridized modes are also excited at their respective resonant wavelengths (851 and 1049 nm) in the hybridized setup. The electric field vector maps (xz-plane) are plotted for all the resonant setups below the grating (fixed y-position). (b) With the vector direction definition downward (↓ ≡ +1) and upward (↑ ≡ −1), the plasmonic NP GMR hybridization model can be represented schematically.

The operators (1 1 and 1 −1 for Pl. and Ph., respectively) used here are identical to the basic states to understand the influence onto one another. The hybridized plasmonic state |H. Pl.⟩ can definitely be identified for its similarity of alignment corresponding to the pure state |Pl.⟩. The mixing of states in hybridization can also be idealized from the spatial distribution of electric field (|E⃗|) that exhibits the resultant hybridized states as the superposition of the pure ones. The field profiles for all the planes of interest can be found in Figure S7 of Supporting Information T7. The similarities in the E-field profiles of the hybridized states to that of the pure counterparts give an initial impression which is further exploited through the vector plot in Figure 4a at our chosen layer of interest. The use of matrix notation in explaining plasmonic lattice resonances³⁵ through a similar hybridization model, previously, included a rigorous mathematical calculation based on dipole–dipole interactions. We, in our hybridization model, have realized the orientations of electric field vectors as a distinctive feature to construct the matrix that can relate the hybridized states to the pure states. This simple yet supportive notation can also be implied on nanoscaled geometries revealing the hybridization of plasmonic dipolar and quadrupolar modes³⁶ and thus bear significant importance toward the generalization of the plasmonic hybridization model.

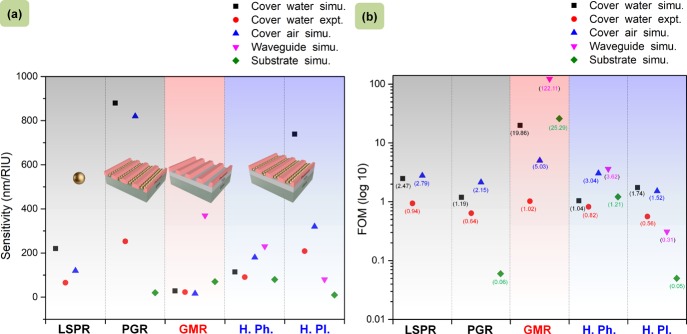
A detailed study on the RI sensing behavior of these pure and hybrid resonant states has been carried out to imply the importance of the hybridized modes using pure water and salt solution. Supporting Information T8 contains RI data (Figure S8) corresponding to the liquids used. For simulation, these RI data are incorporated into the simulation model as surrounding media to obtain spectral feedback for the different resonant geometries. For the experimental realization, three separate custom-made poly(dimethylsiloxane) cuvettes with distinct samples operating in PGR, GMR, and hybrid modes are introduced to the spectrophotometer, and sensing measurements are performed in response to pure D₂O and salt solution. For a comparative isolated particle LSPR measurement, gold NP solutions in glass cuvettes with different suspension media (pure D₂O and salt solution) are used. Supporting Information T9 contains the sensing data for both the simulation and experiment (spectra in Figure S9) of all the resonant geometries with water as a cover medium. Sensitivity (S) and FOM are calculated for the corresponding resonant line shapes and are tabulated in Table S1 of the same section. Figure 5a,b contains the S and FOM values for these cases of water as a cover medium. However, the GMR structure in simulation (cover water simu.) shows a slight deviation from its resonance condition, which can be identified through the oscillations in the transmission spectra (in Figure S9) along with the extreme sharp resonance dip that resulted in high FOM. It is assumed that the associated parameters of the GMR model are meant for operating with the background FDTD index = 1.0, which is the case of air, and have been studied so far in terms of transmittance spectra for different resonance geometries. Hence, a separate study is carried out in FDTD simulation where the background indices are varied from 1.0 to 1.1 for calculating S and FOM and are presented in Supporting Information T10 (Figure S10a) for all the resonant geometries. These are shown in Figure 5 as “cover air simu.” data points. An increase in sensitivity for the hybrid photonic (H. Ph.) state as compared to the pure photonic state (GMR) is evident with a reasonable FOM. There is a certain mismatch in the “S” values between simulation and experiment for the cases of plasmonic (both pure and hybrid) modes, which is due to the nonconsideration of the protein coatings around the NPs in the simulation. These coatings, in reality, have affected the experimental plasmonic sensitivity and can be eliminated out in future by physical means like plasma cleaning or heat treatment. The photonic modes (both pure and hybrid) remain unaffected, showing matching values for experiment and simulation.

Figure 5.

Studies on sensing performance of different resonant geometries: (a) comparison of sensitivity (S) and (b) FOM of different resonance configurations obtained via simulation and experiment.

In particular, the fabricated GMR structure operating in the pure photonic state itself has a lower value (S_avg ≈ 22 nm/RIU) as compared to conventional GMR RI sensors operating in a wavelength-interrogation scheme, which is now increased to a higher value (S_avg ≈ 128 nm/RIU) because of the inclusion of the plasmonic features. “S_avg” is calculated over the three measurement cases of cover index variation, as shown in Figure 5.

The use of plasmonic NP grating in contrast to single NPs for plasmonic coupling has also affected the degree of enhancement as PGR (S_avg ≈ 650 nm/RIU) shows a surprisingly high sensitivity than the single-particle LSPR (S_avg ≈ 135 nm/RIU). This is also the reason behind obtaining high FOM values despite having a low Q factor (Q = λ_R/fwhm). This has been explained in our earlier publication³⁷ as an amplification because of plasmon–plasmon coupling in metallic NPs separated at nanometric distances that showed similar enhancements in RI sensitivity over orders of magnitude. Thus, the choice of PGR modes for the coupling of a highly sensitive plasmonic resonant mechanism into the modes of a relatively lower sensitive dielectric GMR structure is surely justified toward attaining an increased sensitivity. In fact, the reason behind getting a high sensitivity of the PGR mode in comparison to that of GMR as a response to the change in the cover medium can be understood from the electric field distribution for the different resonance mechanisms, as shown in Figure S7 of Supporting Information T7. As we have investigated the change in the cover index, the PGR modes that are located mainly around the particles in the cover region responded effectively to this index variation and resulted in higher S values. On the other hand, the GMR modes that are localized mostly within the waveguide can have the evanescent fields only to sense the change in the cover which resulted in lower sensitivity. The sensitivity of the pure photonic GMR mode can be increased by rigorous optimization of the constituting parameters which however is not the current focus of this article. Rather, we have discussed the possibilities of enhancement of sensitivity by coupling the plasmonic features into the GMR structure. While considering the sensitivity of the hybridized modes, one can locate the field distribution of the hybridized photonic (H. Ph.) modes mostly within the waveguide, whereas the hybridized plasmonic (H. Pl.) modes are localized around the particles that lie in the cover region. Thus, a change in cover medium has resulted in a higher sensitivity of H. Pl. as compared to H. Ph. However, the sensitivity of this H. Pl. mode is lower than that of PGR (pure plasmonic) because of the admixing of GMR features. Nonetheless, the H. Ph. sensitivity is better as compared to GMR, with the FOM values higher than that in PGR (which was our target), and is expected to be even higher if the constituent photonic mode (GMR) itself has a higher sensitivity value.

To prove the influence of the pure modes on the hybrid ones, we have extended our discussion on sensitivity with two simulation cases of index variation by changing the waveguide and substrate indices separately. As the GMR mode (pure photonic) is localized within the waveguide, we have obtained high S values for the case of waveguide index variation. The H. Ph. also being located within the waveguide has shown a higher sensitivity value with a higher FOM than the case of cover index variation (dataset “cover air simu.”) which, yet, is lower than GMR sensitivity because of the admixing of the PGR modes. PGR that was previously sensitive to the cover region now shows lesser sensitivity and lower FOM on the change of medium, that is the substrate index, for the case of pure plasmonic mode. Correspondingly the H. Pl. located mainly in the cover region is now less sensitive to this waveguide index change. Supporting Information T10 contains details of this study with the corresponding plots in Figure S10b. Figure 5 contains the data set “waveguide simu.” that shows S and FOM for the variation of the medium indices. We have also performed a separate study to back up the conclusion where we have changed the substrate index of all the cases (dataset “substrate simu.” in Figure 5). The pure photonic (GMR) and the hybrid photonic (H. Ph.) being located in the waveguide, nearer to the substrate, result in certain sensitivity which however is lesser than the case of the waveguide index variation (waveguide simu.). The pure plasmonic (PGR) and hybrid plasmonic (H. Pl.) modes being away from the substrate show much lesser values of S. Figure S10c of Supporting Information T10 contains the associated plots. The calculated values of S and FOM from the plots in Figure S10 are tabulated in Table S2 of the same section which provides a comparative analysis of the sensitivity of the different resonance geometries for different regions of the resonating structures.

Thus, we can conclude that the sensitivity of the hybridized states is solely dependent on that of the pure states and the medium these pure states are sensitive to. With a proper optimization and choice of these pure states, one can tune between the sensitivity and FOM over a wide spectral range. Thus, a pre-optimized GMR device with an improved “S” (optimization of duty cycle and index contrast) can surely have a further enhanced sensitivity as well as a higher FOM (FOM = S/fwhm) in the hybrid photonic mode as long as the resonant wavelength overlaps with the plasmonic resonance.

Conclusions

In summary, we have demonstrated a new method of combining top-down (LIL) and bottom-up (colloidal synthesis and TASA) approaches for the successful fabrication of hybrid plasmonic–photonic geometry over a large centimeter-scale area. The fabricated structure with a proper choice of design parameters supports coupling of the plasmonic radiant modes of gold NP grating to the photonic modes of TiO₂-based GMR under normal incidence; this results in the formation of hybridized states that can be tuned by varying AOI. The hybridized structure is optically characterized in comparison to its constituent resonant geometries along with an in-depth study of these resonances through numerical simulations to understand the coupling of two resonances. On the basis of the electric field plots, a matrix transfer model is also established that can be applied in general to similar cases of coupling of different resonances. With a system completely new in the field of modal strong coupling, we have realized its potential application in RI sensing where the sensitivity of a GMR device can further be enhanced via admixing of plasmonic signatures without much loss of the resolution. Furthermore, these hybrid structures can set up a new paradigm in the field of strongly coupled systems leading to plasmonic hot electron generation and thus can find application in solar energy harvesting, photovoltaics, photocatalysis, and many others.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.8b20535.

• Real-time video of directed self-assembly of particles under an optical microscope (AVI)

• Optical constants of TiO₂, ma-N 405 photoresist, and glass substrate measured from spectroscopic ellipsometry; concepts of a GMR structure; LIL using Lloyd’s mirror setup; directed self-assembly for the arrangement of particles; optical characteristics of the different resonant geometries in TM mode; comparison of plasmonic bars with similar dimensions in hybrid geometry; electric field plots at resonance for different cross sections; RI measurement for sensing; spectra for sensing measurements with water as a cover medium; and spectra for sensing measurements with air as a cover medium (PDF)

Author Contributions

S.S. has performed the experiments and software-based simulations. S.S. and T.A.F.K. have written the manuscript. S.S., V.G., and M.K. have fabricated the sample. V.G. and M.K. have performed the characterization. J.S. has synthesized the NPs. P.T.P. has operated the assembly process. J.S., P.T.P., and J.J. have contributed to correcting and modifying the manuscript. T.A.F.K. and J.J. have conceived the idea. T.A.F.K. has supervised the whole work. All authors have reviewed and contributed to the final manuscript.

The authors declare no competing financial interest.