Abstract
Photonic
quantum technologies call for scalable quantum light sources
that can be integrated, while providing the end user with single and
entangled photons on demand. One promising candidate is strain free
GaAs/AlGaAs quantum dots obtained by aluminum droplet etching.
Such quantum dots exhibit ultra low multi-photon probability and an
unprecedented degree of photon pair entanglement. However, different
to commonly studied InGaAs/GaAs quantum dots obtained by the Stranski–Krastanow
mode, photons with a near-unity indistinguishability from these quantum
emitters have proven to be elusive so far. Here, we show on-demand
generation of near-unity indistinguishable photons from these quantum
emitters by exploring pulsed resonance fluorescence. Given the short
intrinsic lifetime of excitons and trions confined in the GaAs quantum
dots, we show single photon indistinguishability with a raw visibility
of 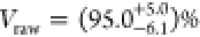 , without the need
for Purcell enhancement.
Our results represent a milestone in the advance of GaAs quantum dots
by demonstrating the final missing property standing in the way of
using these emitters as a key component in quantum communication applications,
e.g., as quantum light sources for quantum repeater architectures.
, without the need
for Purcell enhancement.
Our results represent a milestone in the advance of GaAs quantum dots
by demonstrating the final missing property standing in the way of
using these emitters as a key component in quantum communication applications,
e.g., as quantum light sources for quantum repeater architectures.
Keywords: Semiconductor quantum dot, resonance fluorescence, indistinguishable photons, Al droplet etching
Most applications in photonic
quantum technologies rely on clean quantum interference of deterministically
generated single and entangled photons. Quantum indistinguishability
is a crucial ingredient for the creation of higher N00N states,1,2 quantum teleportation3 and swapping operations,4 boson-sampling,5,6 and photon-based
quantum simulations.7 An ideal quantum
light source thus needs to emit photons on demand, with high purity
and near-unity indistinguishability as well as being scalable and
interconnected with different quantum systems. Semiconductor quantum
dots are proving to be the best sources that fulfill these requirements,8 delivering ultra bright sources of on-demand
single photons at high rates compatible with photonic circuitry. Recently,
GaAs quantum dots obtained by the infilling of nanoholes produced
by local droplet etching9 have emerged
to be one of the most promising deterministic solid-state quantum
light sources, reporting the lowest multi-photon probability10 and the highest degree of polarization entanglement11 while also being the brightest entangled photon
pair source reported.12 Entangled photons
from these quantum dots have also been used to implement quantum teleportation13 and entanglement swapping protocols,14 thus proving their potential for quantum network
applications. Furthermore, their short intrinsic lifetime enables
high-repetition rate single-photon sources and, together with the
high symmetry of the quantum dots, results in improved entanglement
fidelities.11 Another advantage of these
quantum dots is that they have reduced strain gradients compared to
commonly studied dots obtained by the Stranski–Krastanow growth
mode and are expected to have long nuclei ensemble spin coherence,
promising for quantum-dot-based quantum memories.15 Additionally, their emission wavelength range makes them
suitable for hybrid quantum photonic technologies since they can be
tuned into resonance with quantum memories, e.g. rubidium atoms.16,17 However, near-unity indistinguishable photons, a crucial element
for photonic quantum technologies, was missing from this type of quantum
dots until now. Strong charge fluctuations at the vicinity of the
quantum dot,18,19 induced by the droplet growth
method20 and faster phonon-induced pure
dephasing21 and zero-phonon broadening22 were suspected to be the main causes of the
lower quantum interference visibility for these quantum emitters.
In this letter, we apply cross-polarized pulsed resonance fluorescence
to show that quantum dots derived from droplet etching do not suffer
from additional dephasing mechanisms at short time scales and exhibit
near-unity indistinguishability of on-demand generated single photons.
Remarkably, high quantum interference visibility values of 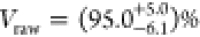 are achieved without
the need of Purcell
enhancement using microcavities.23−25 Instead, we capitalize
on the intrinsically short lifetime of the excited states of these
quantum emitters.26
are achieved without
the need of Purcell
enhancement using microcavities.23−25 Instead, we capitalize
on the intrinsically short lifetime of the excited states of these
quantum emitters.26
For pulsed resonant
s-shell excitation,27 a polarization suppression
setup was constructed similar to that
in ref (28) but with
the second polarizing beam splitter (PBS) replaced by a nanoparticle
linear film polarizer, as illustrated in Figure 1 a. The sample was mounted in a low vibration
closed-cycle cryostat and cooled to 5 K. For excitation, a tunable,
linearly polarized laser was used with a repetition rate of 80 MHz
and pulse duration of 5.0 ps after sending the pulse through a pulse
slicer. The excitation beam was directed onto the sample via the polarizing
beam splitter, through an objective with 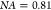 , and focused onto the quantum dot of interest
using a solid immersion lens (SIL), directly attached to the sample
surface. The signal was collected through the same optics in a confocal
geometry and separated from the backscattered excitation laser by
the polarizing beam splitter and a linear polarizer oriented perpendicular
to the laser polarization. Further improvement of the laser suppression
was achieved by spatial filtering since a small portion of the backscattered
laser has a component perpendicular to the original polarization with
a four-leaf clover patterned beam profile.29
, and focused onto the quantum dot of interest
using a solid immersion lens (SIL), directly attached to the sample
surface. The signal was collected through the same optics in a confocal
geometry and separated from the backscattered excitation laser by
the polarizing beam splitter and a linear polarizer oriented perpendicular
to the laser polarization. Further improvement of the laser suppression
was achieved by spatial filtering since a small portion of the backscattered
laser has a component perpendicular to the original polarization with
a four-leaf clover patterned beam profile.29
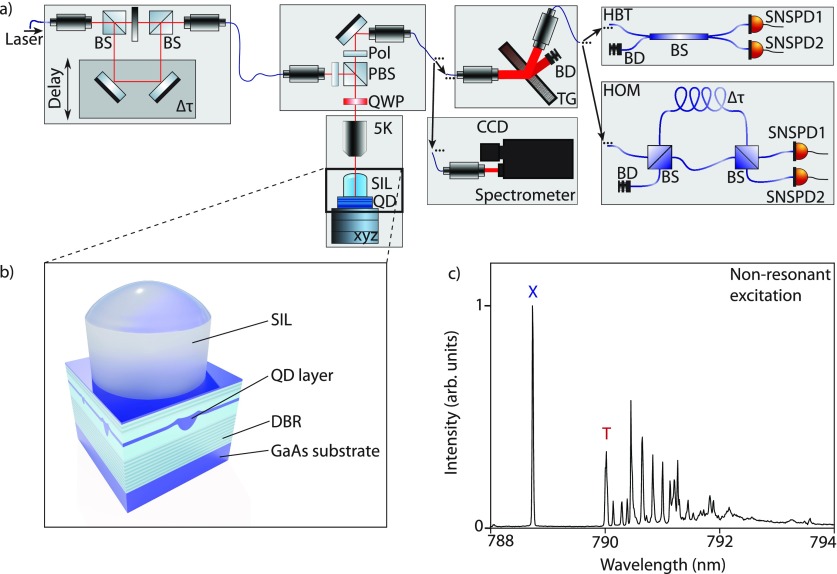
Figure 1.
(a) The modular setup consisting of laser excitation with delay line, the confocal microscopy setup with polarization suppression, the transmission spectrometer, the Hanbury-Brown and Twiss setup (HBT), and the Hong–Ou–Mandel setup (HOM). BS, beam splitter; BD, beam dump; TG, transmission grating; SNSPD, superconducting nanowire single photon detector; Pol, polarizer; PBS, polarizing beam splitter; QWP, quarter waveplate; SIL, solid immersion lens. (b) Schematic illustration of the sample structure. (c) Spectrum of QD1 under non-resonant excitation.
To perform photoluminescence measurements, the signal was coupled through a spectrometer onto a silicon CCD. For correlation measurements, the resonance fluorescence signal was further filtered with a home-built transmission spectrometer having a bandwidth of 19 GHz and an end-to-end efficiency exceeding 60%. Second-order intensity correlation measurements were carried out with a Hanbury–Brown and Twiss type setup realized with a fiber coupled 50:50 beam splitter connected to two superconducting nanowire single photon detectors (SNSPD) with efficiencies of 50% and 60%, a timing jitter of 20 and 30 ps, and dark count rates of 0.006 and 0.017 dcts/s. The detection events are recorded in a timetag file along with laser excitation events and analyzed with our Extensible Timetag Analyzer (ETA) software.30 To determine the indistinguishability of two consecutively emitted photons, two-photon interference was measured in a Hong–Ou–Mandel (HOM) type experiment. In order to interfere, these photons must impinge on a beam splitter with excellent spatial and temporal overlap. The temporal overlap is achieved by sending the signal into an unbalanced fiber-based Mach–Zehnder interferometer with a path-length difference of 2 ns. The two output ports of the Mach–Zehnder interferometer are connected to a SNSPD each. Depending on the paths the photons take, they can arrive on the beam splitter simultaneously or with a time delay of 2 or 4 ns, resulting in the characteristic quintuplet for Hong–Ou–Mandel measurements31 in the histogram. The temporal overlap of the photons on the second beam splitter is ensured by splitting the excitation pulse into two identical pulses using another unbalanced Mach–Zehnder interferometer with variable delay. This delay is precisely tuned to the fixed fiber delay in the Hong–Ou–Mandel setup by measuring the interference of overlapping short laser pulses using the same detectors as for all the correlation measurements. For the best possible time resolution, unsliced laser pulses with a pulse duration of 1.94 ps were used.
The GaAs quantum dot sample investigated
in this work was grown
by molecular beam epitaxy using the aluminum droplet etching technique.
The quantum dot layer was embedded in a λ-cavity made of 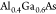 (123 nm) with 9.5 pairs of bottom and 2.5
pairs of top distributed Bragg reflectors (DBR) consisting of
(123 nm) with 9.5 pairs of bottom and 2.5
pairs of top distributed Bragg reflectors (DBR) consisting of  /
/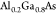
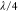 -thick
layers, as depicted in Figure 1 b. The structure was finished
by a 4 nm thick protective GaAs layer. The Al-droplet etching method
allows the growth of highly symmetric quantum dots with a low fine
structure splitting (FSS).32 This sample
structure shows an extraction efficiency of
-thick
layers, as depicted in Figure 1 b. The structure was finished
by a 4 nm thick protective GaAs layer. The Al-droplet etching method
allows the growth of highly symmetric quantum dots with a low fine
structure splitting (FSS).32 This sample
structure shows an extraction efficiency of 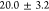 % into the first lens for a quantum dot
well-positioned under the SIL.
% into the first lens for a quantum dot
well-positioned under the SIL.
In Figure 1 c we show the spectrum of QD1 subject to pulsed non-resonant excitation at a wavelength of 781 nm. The neutral exciton (X), emitting at 788.73 nm, is isolated from the rest of emission lines at longer wavelengths, which are attributed to electron-hole recombination in the presence of additional carriers in the quantum dot which stem from nearby confined states due to the weak confinement in shallow quantum dots.33 The trion (T) transition corresponds to the peak at 790.02 nm. To resonantly excite an s-shell transition (X or T), we tune the energy of the excitation laser to the transition energy, ideally resulting in photoluminescence only from this specific transition. Furthermore, the dephasing due to interactions with phonons and nearby trapped charge carriers is reduced.34 To address the electric environment of the dot, we additionally illuminate the sample with a low intensity white light source.35,36 This results in a very clean spectrum with only one prominent line of the exciton transition and minor contribution of less than 2% from the trion transition as shown in a semi-logarithmic plot in Figure 2 a.
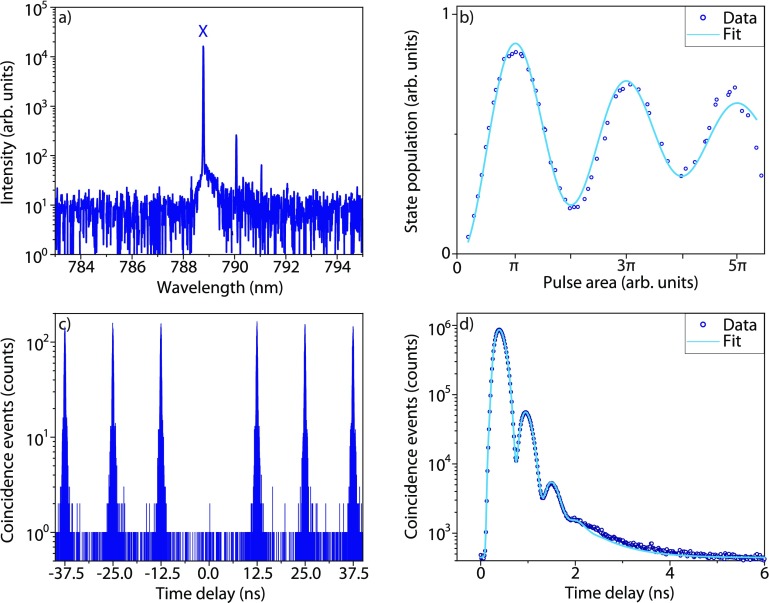
Figure 2.
Characterization of the
neutral exciton under pulsed resonant s-shell
excitation. (a) Resonance fluorescence spectrum in a semi-logarithmic
plot. (b) Excitation laser power-dependent Rabi oscillation up to
a pulse area of 5π. From our fit we extract an occupation probability
of 85% under π-pulse excitation. (c) Second-order intensity
correlation histogram yielding 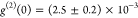 (d) Semi-logarithmic plot of the lifetime
measurement with oscillations due to the fine structure splitting.
The fit gives a lifetime of
(d) Semi-logarithmic plot of the lifetime
measurement with oscillations due to the fine structure splitting.
The fit gives a lifetime of 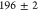 ps and a fine structure splitting of
ps and a fine structure splitting of 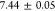 μeV.
μeV.
To show that this excitation scheme addresses the quantum dot coherently, we performed power-dependent pulsed resonance fluorescence measurements. In Figure 2 b, Rabi oscillations of the integrated intensity of the neutral exciton transition as a function of the excitation pulse area are shown. By exciting the quantum dot with a power corresponding to a pulse area of π, the population of the two-level system of the quantum dot is maximally inverted, preparing the quantum dot in the excited state. The procedure used to fit the data is explained in the Supporting Information. We extract a population probability for the neutral exciton state of 85% under π-pulse excitation. For all further measurements, the quantum dot is excited with a π-pulse.
The second-order intensity correlation function shown in Figure 2 c shows nearly background
free single photon emission. By calculating the ratio of the area
of the center peak and average area of eight side peaks in a time
window of 3.2 ns each, a measured degree of second-order coherence
of 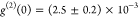 is determined.
We attribute the deviation
from 0 solely to re-excitation37 and conclude
that there is negligible residual excitation laser present in the
correlation measurement.
is determined.
We attribute the deviation
from 0 solely to re-excitation37 and conclude
that there is negligible residual excitation laser present in the
correlation measurement.
Figure 2 d shows
the lifetime measurement of the resonantly excited neutral exciton
in a semi-logarithmic plot. The exponential decay is observed with
a periodic modulation.38 Due to the exchange
interaction between the electron and hole spins, the degeneracy of
the exciton states of the quantum dot is lifted, leading to two linearly
cross-polarized fine structure (FS) states with an energy splitting
of 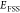 . During excitation, the
spin of the exciton
state is determined by the polarization of the excitation pulse.39,40 Then, the spin starts precessing on the equator of the Bloch sphere,
oscillating between the two orthogonal fine structure states. The
polarization of the emitted photon is set by the spin at the time
of the recombination. Since one polarization component is suppressed
by the polarizers in our setup, the intensity of the detected signal
oscillates with a frequency
. During excitation, the
spin of the exciton
state is determined by the polarization of the excitation pulse.39,40 Then, the spin starts precessing on the equator of the Bloch sphere,
oscillating between the two orthogonal fine structure states. The
polarization of the emitted photon is set by the spin at the time
of the recombination. Since one polarization component is suppressed
by the polarizers in our setup, the intensity of the detected signal
oscillates with a frequency 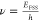 .41 The data
is modeled with a fit explained in the Supporting Information, which yields a lifetime of
.41 The data
is modeled with a fit explained in the Supporting Information, which yields a lifetime of 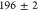 ps and a fine structure splitting of
ps and a fine structure splitting of 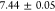 μeV.
μeV.
In order to point out similarities with and differences
to the
neutral exciton, we investigate the resonantly excited charged exciton
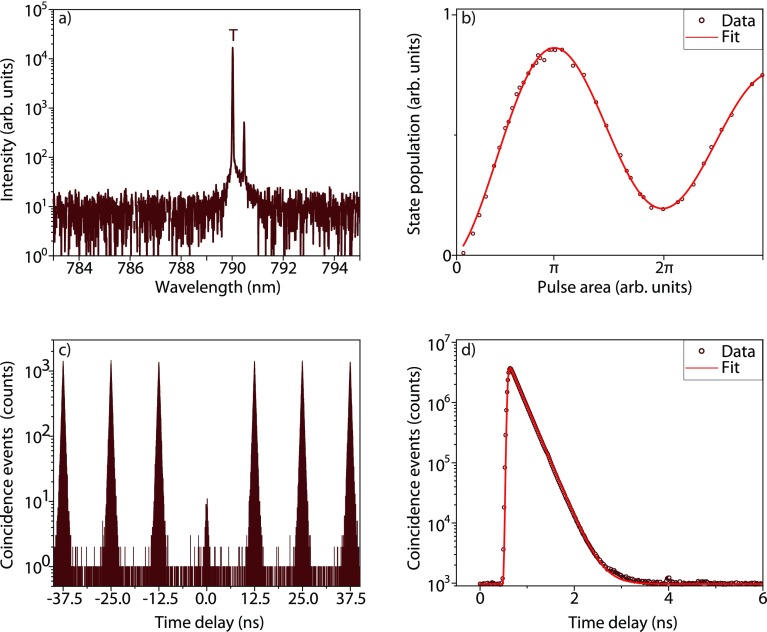
as well. Figure 3 a
shows the spectrum of the trion of QD1 under pulsed resonant excitation.
We observe an additional line close to the trion transition with 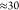 times lower intensity, which might be a
higher charge state emitting after a second capture process. Similar
to the neutral exciton, we observe clear Rabi oscillations as a function
of the excitation pulse area, as shown in Figure 3 b, and a maximum population inversion probability
of
times lower intensity, which might be a
higher charge state emitting after a second capture process. Similar
to the neutral exciton, we observe clear Rabi oscillations as a function
of the excitation pulse area, as shown in Figure 3 b, and a maximum population inversion probability
of 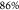 under π-pulse
excitation. The second-order
intensity correlation function yields a measured degree of second-order
coherence of
under π-pulse
excitation. The second-order
intensity correlation function yields a measured degree of second-order
coherence of 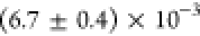 , as shown in Figure 3 c, confirming that the laser suppression
is very good. In Figure 3 d we show a semi-logarithmic plot of a lifetime measurement. A single
exponential fit gives a lifetime of
, as shown in Figure 3 c, confirming that the laser suppression
is very good. In Figure 3 d we show a semi-logarithmic plot of a lifetime measurement. A single
exponential fit gives a lifetime of 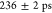 . As opposed to the lifetime measurement
of the neutral exciton in Figure 3 d, this measurement shows no quantum beats, due to
the lack of fine structure splitting of the trion state.42
. As opposed to the lifetime measurement
of the neutral exciton in Figure 3 d, this measurement shows no quantum beats, due to
the lack of fine structure splitting of the trion state.42
Figure 3.
Characterization of the trion under pulsed s-shell resonant
excitation.
(a) Resonance fluorescence spectrum in a semi-logarithmic plot. The
origin of the ≈30× less intense line is discussed in the
main text. (b) Rabi oscillation up to a pulse area of 3π. (c)
Second-order intensity correlation histogram yielding 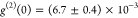 (d) Semi-logarithmic
plot of the lifetime
measurement fitted with a single exponential decay giving us a lifetime
of
(d) Semi-logarithmic
plot of the lifetime
measurement fitted with a single exponential decay giving us a lifetime
of 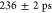 .
.
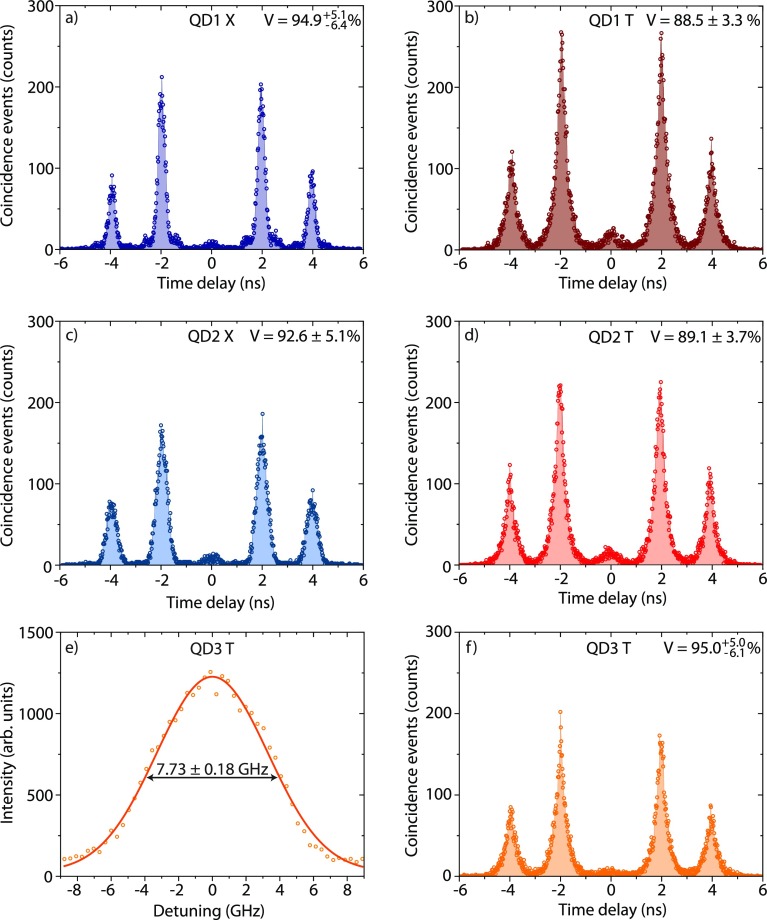
Having confirmed low multi-photon emission probability for both neutral and charged excitons under π-pulse resonant excitation, we continue to investigate the indistinguishability of consecutively emitted photons using a two-photon interference measurement, as described above. In Figure 4 a and b the center peak quintuplet for two-photon interference measurements of the neutral exciton and trion of QD1 are shown. The relative peak heights originate from different combinations of long and short paths in the Mach–Zehnder interferometer two consecutive photons can take. In the Hong–Ou–Mandel measurement of the neutral exciton, the same oscillations as in the lifetime measurements are visible.
Figure 4.
Hong–Ou–Mandel measurements under resonant s-shell
excitation for the (a) neutral exciton of QD1 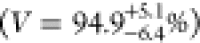 , (b) trion of QD1
, (b) trion of QD1 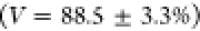 , (c)
neutral exciton of QD2
, (c)
neutral exciton of QD2 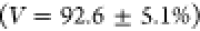 , (d)
trion of QD2
, (d)
trion of QD2 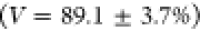 , and (f) trion of QD3
, and (f) trion of QD3 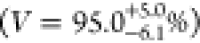 . The visibilities are calculated by summing
up the peak areas of the three center peaks. The method is explained
in more detail in the Supporting Information; (e) line width of the trion of QD3 with a Gaussian fit
. The visibilities are calculated by summing
up the peak areas of the three center peaks. The method is explained
in more detail in the Supporting Information; (e) line width of the trion of QD3 with a Gaussian fit 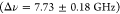 .
.
In the limit of 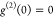 , the visibility of two-photon interference
can be calculated from the area of the three center peaks A1,2,3 by
, the visibility of two-photon interference
can be calculated from the area of the three center peaks A1,2,3 by 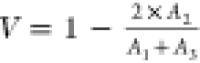 , where
, where 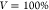 corresponds to perfectly indistinguishable
photons.31 To calculate the peak area of
the three center peaks, the coincidence events are summed up in time
windows which are individual for every transition (see details in
the Supporting Information). The uncorrected
visibilities for QD1 are
corresponds to perfectly indistinguishable
photons.31 To calculate the peak area of
the three center peaks, the coincidence events are summed up in time
windows which are individual for every transition (see details in
the Supporting Information). The uncorrected
visibilities for QD1 are 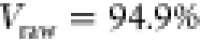 with a statistical error
with a statistical error 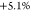 and
and 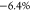 for
the neutral exciton and
for
the neutral exciton and 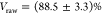 for the trion. To compensate for imperfections
in the setup, we measure the classical interference fringe visibility
with a narrow continuous wave diode laser to be
for the trion. To compensate for imperfections
in the setup, we measure the classical interference fringe visibility
with a narrow continuous wave diode laser to be 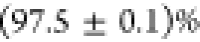 , which yields the upper measurable
bound
of the visibility in this setup. In general, we are able to show very
high indistinguishability visibilities by performing the Hong–Ou–Mandel
measurement on further dots, as shown in Figure 4 c, d, and f. Here we obtain a visibility
of
, which yields the upper measurable
bound
of the visibility in this setup. In general, we are able to show very
high indistinguishability visibilities by performing the Hong–Ou–Mandel
measurement on further dots, as shown in Figure 4 c, d, and f. Here we obtain a visibility
of 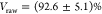 for the neutral exciton,
for the neutral exciton, 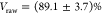 for the trion of QD2, and
for the trion of QD2, and 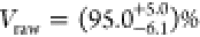 for the trion of QD3. This value
is the
highest obtained visibility for on-demand sources without Purcell
enhancement or more elaborate excitation techniques.43 We would like to note that fitting the Hong–Ou–Mandel
data, instead of summing up the data in specified time windows, very
often overestimates the two-photon interference visibility, in particular
if the data were collected with low timing resolution. Especially
when the low time resolution is masking quantum beats and the dip
at zero time delay, fitting can wrongly increase the visibility and
even lead to unphysical results, i.e., visibilities above
for the trion of QD3. This value
is the
highest obtained visibility for on-demand sources without Purcell
enhancement or more elaborate excitation techniques.43 We would like to note that fitting the Hong–Ou–Mandel
data, instead of summing up the data in specified time windows, very
often overestimates the two-photon interference visibility, in particular
if the data were collected with low timing resolution. Especially
when the low time resolution is masking quantum beats and the dip
at zero time delay, fitting can wrongly increase the visibility and
even lead to unphysical results, i.e., visibilities above 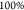 . This result is
even independent of the
used fit function (see details in the Supporting Information). We measure the line width of the trion transition
of QD3 by slowly scanning a Fabry–Pérot interferometer
with a resolution of
. This result is
even independent of the
used fit function (see details in the Supporting Information). We measure the line width of the trion transition
of QD3 by slowly scanning a Fabry–Pérot interferometer
with a resolution of 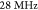 over the line and recording the
signal
on a SNSPD. Fitting the data with a Gaussian peak provides a line
width of
over the line and recording the
signal
on a SNSPD. Fitting the data with a Gaussian peak provides a line
width of 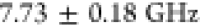 and is shown in Figure 4 e. Considering a
lifetime of
and is shown in Figure 4 e. Considering a
lifetime of 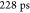 , we show that the line width is a factor
of 10 larger than the Fourier limit. As we are still measuring a very
high HOM visibility for this transition, this indicates negligible
spectral wandering on short time scales.
, we show that the line width is a factor
of 10 larger than the Fourier limit. As we are still measuring a very
high HOM visibility for this transition, this indicates negligible
spectral wandering on short time scales.
We point out that our
two-photon interference visibility value
of 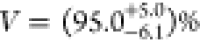 is the highest raw value measured for any
on-demand source without a micro-cavity and marks an important milestone
for quantum dots derived from droplet etching. Near-unity indistinguishability
was the last missing quantum optical property to put GaAs quantum
dots on the horizon for future quantum communication and quantum information
processing applications. On the basis of our results, we foresee that
photonic structures other than cavities, e.g., waveguides, trumpets,
and nanowires44,45 to enhance light extraction efficiency
from solid-state emitters, can be used to achieve even higher levels
of indistinguishability without the need of Purcell enhancement.
is the highest raw value measured for any
on-demand source without a micro-cavity and marks an important milestone
for quantum dots derived from droplet etching. Near-unity indistinguishability
was the last missing quantum optical property to put GaAs quantum
dots on the horizon for future quantum communication and quantum information
processing applications. On the basis of our results, we foresee that
photonic structures other than cavities, e.g., waveguides, trumpets,
and nanowires44,45 to enhance light extraction efficiency
from solid-state emitters, can be used to achieve even higher levels
of indistinguishability without the need of Purcell enhancement.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 Research and Innovation Program (820423; S2QUIP), the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (SPQRel; 679183), the FWF (P 29603, P 30459), the Linz Institute of Technology, the German Federal Ministry of Education and Research via the funding program Photonics Research Germany (13N14846), Q.Com (16KIS0110) and Q.Link.X, the DFG via the Nanosystem Initiative Munich, the MCQST, the Knut and Alice Wallenberg Foundation grant “Quantum Sensors”, the Swedish Research Council (VR) through the VR grant for international recruitment of leading researchers (ref. 2013-7152), and the Linnæus Excellence Center ADOPT. K.D.Z. gratefully acknowledges funding by the Dr. Isolde Dietrich Foundation. K.M. acknowledges support from the Bavarian Academy of Sciences and Humanities. K.D.J. acknowledges funding from the Swedish Research Council (VR) via the starting grant HyQRep (ref. 2018-04812). A.R. acknowledges fruitful discussions with Y. Huo, G. Weihs, R. Keil, and S. Portalupi.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b05132.
Resonance fluorescence of GaAs quantum dots with near-unity photon indistinguishability; Rabi oscillation; time-correlated single-photon counting fit function including convolution with internal response function; polarization-resolved photoluminescence spectroscopy; and analysis of two-photon interference measurements (PDF)
Author Contributions
⊥ E. Schöll, L. Hanschke, and L. Schweickert contributed equally to this work. E.S. and K.D.J. built the setup with the help from K.D.Z., L.S., and T.L., E.S., L.H., L.S., K.D.Z., and K.D.J. performed the measurements. E.S., L.H., L.S., and K.D.Z. carried out the data analysis with help from K.D.J. S.F.C.S. and A.R. designed, optimized, and grew the quantum dot sample. M.R. and R.T. characterized the quantum dot sample, helping to optimize the sample. T.L. fabricated the final device with the help from R.T. E.S. and K.D.J. wrote the manuscript with help from all of the authors. K.D.J. conceived the experiment and supervised the project.
The authors declare no competing financial interest.
Supplementary Material
References
- Walther P.; Pan J.-W.; Aspelmeyer M.; Ursin R.; Gasparoni S.; Zeilinger A. Nature 2004, 429, 158. 10.1038/nature02552. [DOI] [PubMed] [Google Scholar]
- Nagata T.; Okamoto R.; O’Brien J. L.; Sasaki K.; Takeuchi S. Science 2007, 316, 726–729. 10.1126/science.1138007. [DOI] [PubMed] [Google Scholar]
- Bouwmeester D.; Pan J.-W.; Mattle K.; Eibl M.; Weinfurter H.; Zeilinger A. Nature 1997, 390, 575–579. 10.1038/37539. [DOI] [Google Scholar]
- Pan J.-W.; Bouwmeester D.; Weinfurter H.; Zeilinger A. Phys. Rev. Lett. 1998, 80, 3891–3894. 10.1103/PhysRevLett.80.3891. [DOI] [Google Scholar]
- Spring J. B.; Metcalf B. J.; Humphreys P. C.; Kolthammer W. S.; Jin X.-M.; Barbieri M.; Datta A.; Thomas-Peter N.; Langford N. K.; Kundys D.; Gates J. C.; Smith B. J.; Smith P. G. R.; Walmsley I. A. Science 2013, 339, 798–801. 10.1126/science.1231692. [DOI] [PubMed] [Google Scholar]
- Broome M. A.; Fedrizzi A.; Rahimi-Keshari S.; Dove J.; Aaronson S.; Ralph T. C.; White A. G. Science 2013, 339, 794–798. 10.1126/science.1231440. [DOI] [PubMed] [Google Scholar]
- Aspuru-Guzik A.; Walther P. Nat. Phys. 2012, 8, 285. 10.1038/nphys2253. [DOI] [Google Scholar]
- Senellart P.; Solomon G.; White A. Nat. Nanotechnol. 2017, 12, 1026–1039. 10.1038/nnano.2017.218. [DOI] [PubMed] [Google Scholar]
- Huber D.; Reindl M.; Huo Y.; Huang H.; Wildmann J. S.; Schmidt O. G.; Rastelli A.; Trotta R. Nat. Commun. 2017, 8, 15506. 10.1038/ncomms15506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweickert L.; Jöns K. D.; Zeuner K. D.; Covre da Silva S. F.; Huang H.; Lettner T.; Reindl M.; Zichi J.; Trotta R.; Rastelli A.; Zwiller V. Appl. Phys. Lett. 2018, 112, 093106. 10.1063/1.5020038. [DOI] [Google Scholar]
- Huber D.; Reindl M.; Covre da Silva S. F.; Schimpf C.; Martín-Sánchez J.; Huang H.; Piredda G.; Edlinger J.; Rastelli A.; Trotta R. Phys. Rev. Lett. 2018, 121, 033902. 10.1103/PhysRevLett.121.033902. [DOI] [PubMed] [Google Scholar]
- Chen Y.; Zopf M.; Keil R.; Ding F.; Schmidt O. G. Nat. Commun. 2018, 9, 2994. 10.1038/s41467-018-05456-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reindl M.; Huber D.; Schimpf C.; da Silva S. F. C.; Rota M. B.; Huang H.; Zwiller V.; Jöns K. D.; Rastelli A.; Trotta R. Sci. Adv. 2018, 4, eaau1255. 10.1126/sciadv.aau1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basso Basset F.; Rota M. B.; Schimpf C.; Tedeschi D.; Zeuner K. D.; Covre da Silva S. F.; Reindl M.; Zwiller V.; Jöns K. D.; Rastelli A.; Trotta R.. Entanglement swapping with photons generated on-demand by a quantum dot. 2019, arXiv:1901.06646.arXiv.org e-Prints. https://arxiv.org/abs/1901.06646 [DOI] [PubMed]
- Gangloff D. A.; Éthier-Majcher G.; Lang C.; Denning E. V.; Bodey J. H.; Jackson D. M.; Clarke E.; Hugues M.; Le Gall C.; Atatüre M. Science 2019, eaaw2906. 10.1126/science.aaw2906. [DOI] [PubMed] [Google Scholar]
- Akopian N.; Wang L.; Rastelli A.; Schmidt O.; Zwiller V. Nat. Photonics 2011, 5, 230–233. 10.1038/nphoton.2011.16. [DOI] [Google Scholar]
- Schweickert L.; Jöns K. D.; Namazi M.; Cui G.; Lettner T.; Zeuner K. D.; Scavuzzo Montaña L.; Covre da Silva S. F.; Reindl M.; Huang H.; Trotta R.; Rastelli A.; Zwiller V.; Figueroa E.. Electromagnetically Induced Transparency of On-demand Single Photons in a Hybrid Quantum Network. 2018, arXiv:1808.05921.arXiv.org e-Print archive. https://arxiv.org/abs/1808.05921.
- Heyn C.; Zocher M.; Pudewill L.; Runge H.; Küster A.; Hansen W. J. Appl. Phys. 2017, 121, 044306. 10.1063/1.4974965. [DOI] [Google Scholar]
- Liu J.; Konthasinghe K.; Davanço M.; Lawall J.; Anant V.; Verma V.; Mirin R.; Nam S. W.; Song J. D.; Ma B.; Chen Z. S.; Ni H. Q.; Niu Z. C.; Srinivasan K. Phys. Rev. Appl. 2018, 9, 064019. 10.1103/PhysRevApplied.9.064019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyn C.; Stemmann A.; Köppen T.; Strelow C.; Kipp T.; Grave M.; Mendach S.; Hansen W. Appl. Phys. Lett. 2009, 94, 183113. 10.1063/1.3133338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axt V. M.; Kuhn T.; Vagov A.; Peeters F. M. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 125309. 10.1103/PhysRevB.72.125309. [DOI] [Google Scholar]
- Tighineanu P.; Dreeßen C. L.; Flindt C.; Lodahl P.; Sørensen A. S. Phys. Rev. Lett. 2018, 120, 257401. 10.1103/PhysRevLett.120.257401. [DOI] [PubMed] [Google Scholar]
- Somaschi N.; et al. Nat. Photonics 2016, 10, 340–345. 10.1038/nphoton.2016.23. [DOI] [Google Scholar]
- Ding X.; He Y.; Duan Z.-C.; Gregersen N.; Chen M.-C.; Unsleber S.; Maier S.; Schneider C.; Kamp M.; Höfling S.; Lu C.-Y.; Pan J.-W. Phys. Rev. Lett. 2016, 116, 020401. 10.1103/PhysRevLett.116.020401. [DOI] [PubMed] [Google Scholar]
- Bennett A. J.; Lee J. P.; Ellis D. J. P.; Meany T.; Murray E.; Floether F. F.; Griffths J. P.; Farrer I.; Ritchie D. A.; Shields A. J. Sci. Adv. 2016, 2, e1501256 10.1126/sciadv.1501256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiraz A.; Atatüre M.; Imamoğlu A. Phys. Rev. A: At., Mol., Opt. Phys. 2004, 69, 032305. 10.1103/PhysRevA.69.032305. [DOI] [Google Scholar]
- He Y.-M.; He Y.; Wei Y.-J.; Wu D.; Atatüre M.; Schneider C.; Höfling S.; Kamp M.; Lu C.-Y.; Pan J.-W. Nat. Nanotechnol. 2013, 8, 213–217. 10.1038/nnano.2012.262. [DOI] [PubMed] [Google Scholar]
- Kuhlmann A. V.; Houel J.; Brunner D.; Ludwig A.; Reuter D.; Wieck A. D.; Warburton R. Rev. Sci. Instrum. 2013, 84, 073905. 10.1063/1.4813879. [DOI] [PubMed] [Google Scholar]
- Novotny L.; Grober R. D.; Karrai K. Opt. Lett. 2001, 26, 789–791. 10.1364/OL.26.000789. [DOI] [PubMed] [Google Scholar]
- Schweickert L.; Lin Z.; Zeuner K. D.; Lettner T.; Gyger S.; Zichi J.; Schöll E.; Jöns K. D.; Zwiller V.. ETA is a graphical event-driven programming language for time-tag processing. Zenodo: 2018; https://github.com/timetag; 10.5281/zenodo.1495352 [DOI]
- Santori C.; Fattal D.; Vucković J.; Solomon G. S.; Yamamoto Y. Nature 2002, 419, 594–7. 10.1038/nature01086. [DOI] [PubMed] [Google Scholar]
- Huo Y. H.; Rastelli A.; Schmidt O. G. Appl. Phys. Lett. 2013, 102, 152105. 10.1063/1.4802088. [DOI] [Google Scholar]
- Musiał A.; Gold P.; Andrzejewski J.; Löffler A.; Misiewicz J.; Höfling S.; Forchel A.; Kamp M.; Sęk G.; Reitzenstein S. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 045430. 10.1103/PhysRevB.90.045430. [DOI] [Google Scholar]
- Ates S.; Ulrich S. M.; Reitzenstein S.; Löffler A.; Forchel A.; Michler P. Phys. Rev. Lett. 2009, 103, 167402. 10.1103/PhysRevLett.103.167402. [DOI] [PubMed] [Google Scholar]
- Gazzano O.; Michaelis de Vasconcellos S.; Arnold C.; Nowak A.; Galopin E.; Sagnes I.; Lanco L.; Lemaître A.; Senellart P. Nat. Commun. 2013, 4, 1425. 10.1038/ncomms2434. [DOI] [PubMed] [Google Scholar]
- Reindl M.; Jöns K. D.; Huber D.; Schimpf C.; Huo Y.; Zwiller V.; Rastelli A.; Trotta R. Nano Lett. 2017, 17, 4090–4095. 10.1021/acs.nanolett.7b00777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer K. A.; Müller K.; Lagoudakis K. G.; Vučković J. New J. Phys. 2016, 18, 113053. 10.1088/1367-2630/18/11/113053. [DOI] [Google Scholar]
- Dada A. C.; Santana T. S.; Koutroumanis A.; Ma Y.; Park S.-I.; Song J.; Gerardot B. D. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 081404. 10.1103/PhysRevB.96.081404. [DOI] [Google Scholar]
- Kodriano Y.; Schwartz I.; Poem E.; Benny Y.; Presman R.; Truong T. A.; Petroff P. M.; Gershoni D. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 241304. 10.1103/PhysRevB.85.241304. [DOI] [Google Scholar]
- Müller K.; Kaldewey T.; Ripszam R.; Wildmann J. S.; Bechtold A.; Bichler M.; Koblmüller G.; Abstreiter G.; Finley J. Sci. Rep. 2013, 3, 1906. 10.1038/srep01906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flissikowski T.; Hundt A.; Lowisch M.; Rabe M.; Henneberger F. Phys. Rev. Lett. 2001, 86, 3172–3175. 10.1103/PhysRevLett.86.3172. [DOI] [PubMed] [Google Scholar]
- Bayer M.; Ortner G.; Stern O.; Kuther A.; Gorbunov A. A.; Forchel A.; Hawrylak P.; Fafard S.; Hinzer K.; Reinecke T. L.; Walck S. N.; Reithmaier J. P.; Klopf F.; Schäfer F. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 65, 195315. 10.1103/PhysRevB.65.195315. [DOI] [Google Scholar]
- Wei Y.-J. J.; He Y.-M. M.; Chen M.-C. C.; Hu Y.-N. N.; He Y.-M. M.; Wu D.; Schneider C.; Kamp M.; Höfling S.; Lu C.-Y. Y.; Pan J.-W. W. Nano Lett. 2014, 14, 6515–6519. 10.1021/nl503081n. [DOI] [PubMed] [Google Scholar]
- Gregersen N.; McCutcheon D. P. S.; Mørk J.; Gérard J.-M.; Claudon J. Opt. Express 2016, 24, 20904–20924. 10.1364/OE.24.020904. [DOI] [PubMed] [Google Scholar]
- Bulgarini G.; Reimer M. E.; Bouwes Bavinck M.; Jöns K. D.; Dalacu D.; Poole P. J.; Bakkers E. P. A. M.; Zwiller V. Nano Lett. 2014, 14, 4102–4106. 10.1021/nl501648f. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.