Learning curve estimation in medical devices and procedures: hierarchical modeling

Abstract

In the use of medical device procedures, learning effects have been shown to be a critical component of medical device safety surveillance. To support their estimation of these effects, we evaluated multiple methods for modeling these rates within a complex simulated dataset representing patients treated by physicians clustered within institutions. We employed unique modeling for the learning curves to incorporate the learning hierarchy between institution and physicians and then modeled them within established methods that work with hierarchical data such as generalized estimating equations (GEE) and generalized linear mixed effect models. We found that both methods performed well, but that the GEE may have some advantages over the generalized linear mixed effect models for ease of modeling and a substantially lower rate of model convergence failures. We then focused more on using GEE and performed a separate simulation to vary the shape of the learning curve as well as employed various smoothing methods to the plots. We concluded that while both hierarchical methods can be used with our mathematical modeling of the learning curve, the GEE tended to perform better across multiple simulated scenarios in order to accurately model the learning effect as a function of physician and hospital hierarchical data in the use of a novel medical device. We found that the choice of shape used to produce the ‘learning-free’ dataset would be dataset specific, while the choice of smoothing method was negligibly different from one another. This was an important application to understand how best to fit this unique learning curve function for hierarchical physician and hospital data.

1. Introduction

Learning curve effects have been observed to significantly impact the outcomes of medical procedures as well as the effectiveness and safety of medical devices used in the care of patients. Within the domain of surgical procedures, the adoption and dissemination of procedural techniques have been associated with procedural success among stapedotomies [1], cesarean sections [2], total hip arthroplasties [3], laparoscopic rectal cancer excisions [4], and arterial vascular access [5]. In addition, dramatic learning effects have been demonstrated in the use of implantable medical devices, including gastrointestinal stenting [6], carotid arterial stenting [7,8], the treatment of total occlusions in coronary interventional procedures [9], and the use of vascular closure devices [10,11]. Beyond observation of powerful learning impacts on procedural outcomes, learning curves have also been documented in improved accuracy of radiology imaging interpretation with accumulating experience [12].

Understanding the impact of learning on procedural success and device safety has broad impact for clinical care in terms of early adverse outcome rates and implications for training requirements in terms of procedural volume required for independent practice [1,12]. For example, within the medical device learning effects literature, the absolute improvements with increasing use of the devices varied from 1% to 44%, with the most notable increases being the release of an entirely new class of device [10], or the combination of a new procedural technique and new medical device [9]. This also presents statistical challenges for clinical trial analysis [13], surgeon and proceduralist performance ‘score-card’ reporting, and post-marketing surveillance of medical devices and procedural techniques [11].

Several modeling techniques have been proposed to hypothetically quantify the ‘learning curve’ based upon industrial processes [14], and a variety of underlying mathematical forms have been proposed [15]. For illustration, we demonstrate theoretical learning curves for two separate devices with different rates of learning (Figure 1). However, there is no consensus on the choice of underlying learning mathematical form or the most appropriate choice for estimation of these effects [16]. Promising work has shown that generalized estimating equations (GEE) [11,12] and Bayesian hierarchical methods [13] have potential to accurately model and quantify learning effects for medical procedures and implantable devices. One of our authors, Frederic Resnic has previously demonstrated use of the GEE to model learning curve effects for a device [11]. They were able to model the learning curves rates for a vascular closure device using the GEE with clustering by centers. They found overall success rates to increase from 93% to 97% during the study. The GEE and the hierarchical generalized linear models or generalized linear mixed effect models (GLME), as a frequentist alternative, appear to have fine potential to model learning curve effects. At the same time, these methods may have possible disadvantages; for example, the GEE may not work as well in modeling hierarchical data in that it may be sensitive to small cluster effects, and the GLME may have convergence issues for smaller datasets. Although perhaps the basis of either modeling is well understood in the field, the direct comparison of these methods, especially in this regard with learning curves, is not well known.

Figure 1.

Hypothetical learning curves for two devices.

In addition, there is evidence of a center specific learning impact that may be separable from the learning that occurs at the physician level [11,17]. These separate impacts could be due to a number of factors, but one hypothesis is that there are learning effects occurring within supporting staff and services, such as catheterization laboratory nursing and technicians or operating room nurses and anesthesiologists, that may be contributory to procedural success. To our knowledge, separation and formal incorporation of both operator and ‘institutional’ learning curve effects has not yet been explored within the medical literature.

Thus, in order to better understand the impacts of learning amongst the hierarchy of operators and institutions (centers) as well as to evaluate our mathematical method to adjust for these effects, we have conducted a simulation study as well as assessed our techniques on real datasets. In this study, we modeled different scenarios in which we varied the number of centers, the number of physicians per center, the rate of learning amongst physicians as well as centers, and the rate of the outcome (in this case, rate of complications from vascular bleeding), employing novel mathematical modeling to obtain the rates. We modeled the learning curve using methods that incorporate the hierarchical nature of the data, then employed both GEE and GLME for modeling the different shapes, and compared this with the observed results for learning influenced clinical outcomes, as generated by the simulation model. We additionally modeled different shapes of the learning curves and utilized different methods to smooth the curves. We were interested to see how these two modeling approaches compare with one another in this context but mainly to test methods for modeling learning curve effects.

2. Methods

2.1. Model and simulation data

In order to assess the performance of two hierarchical modeling methods within a controlled data environment in which the learning effects were known but that remained grounded in actual clinical data, we developed a simulated data set with hierarchical learning effects based upon historical clinical data. The clinical covariates developed in this data were generated using prior covariate distributions on the basis of historical data among 23,813 percutaneous coronary interventions (PCI) from the statewide Massachusetts angioplasty registry [18] from 2005 to 2007. Covariates were selected on the basis of known association with the risk for vascular complications following the implantation of vascular access site closure devices in cardiac catheterization procedures: age, gender, diabetes, history of myocardial infarction, and the presence of cardiogenic shock at the time of the presentation [18–21]. The variables collected in that dataset were based on the American College of Cardiology National Cardiovascular Registry CathPCI data element definitions v3.x [22]. We chose five patient level variables to simplify the generation of the simulated dataset and based the covariates in the simulated dataset on their distributions. These five variables have been repeatedly demonstrated to be associated with the risk of vascular complications following PCI procedures and used in prior publications [11,23,24]. We could have included many other ‘consensus risk predication variables’ but chose to use only five to simplify the simulation effort, as this was more of a proof of concept to assess the relative strengths and weaknesses of the two modeling approaches than an effort to generate specific populations of real risk of vascular complications.

First, for each PCI case, the event rates of the outcome of interest (vascular complications following the implantation of a vascular closure device) were generated in the range of 3–10% ignoring any learning effects among the physician or institution by assuming a large cumulative experience in using the device (hereafter noted as the ‘steady state’ outcome rate). We obtained this by modeling this probability by a logistic regression as

$$\begin{gathered} logit (p=1)=\text{log}\left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_1*\text{age}+{\beta }_2*\text{gender}+{\beta }_3*\text{diabetes}+{\beta }_4*\text{historyMI}+{\beta }_5*\text{shockstatus} \\ p=\frac{1}{\left(1+e^{-\left({\beta }_0+{\beta }_1*\text{age+}{\beta }_2\text{*}gender +{\beta }_3* diabetes +{\beta }_4*\text{historyMI }+{\beta }_5*\text{shockstatus}\right)}\right)} \end{gathered}$$ (1)

where p is the probability of having a vascular complication. β₀ is the intercept, and β₁, β₂, β₃, β₄, and β₅ are coefficient of age, gender, diabetes, history MI, and shockstatus, respectively. Age is a continuous variable and gender (male/female), diabetes (yes/no), historyMI (yes/no), and shockstatus (yes/no) are all categorical variables. Changing the value of β₀, the intercept, allowed us to affect the steady state rate of complications. We randomly generated cases for each physician at each center so that each physician had a different number of procedures based on an assumed mean experience, per physician, of approximately 300 procedures, based on the volume of procedures performed by the top 80 percent of interventional cardiologists, as measured by annual volume of procedures, performed at our own institution. Therefore, this estimate was meant to be generalizable to the operators at a typical teaching hospital.

We next incorporated the learning effects amongst the physicians into the model while holding the institutional learning at asymptotic steady state. On the basis of historical experience with vascular closure device learning effects in a national cohort [11], we estimated that learning impacts could decrease adverse outcomes by 25%, and therefore assumed that the curve intercept, b₀, to be 25% of the steady state adverse rate. As the learning rate varies from a variety of characteristics of a medical device [25], we allowed the slope to vary to simulate either slow (0.02) or fast learning (0.09), as modeled by b₁. The p₀ are the predicted probabilities derived from (1), which is the asymptotic steady state outcome event rate in the simulation model. We modeled this curve as

$$p_1=p_0-\left(p_0-b_0\right)*\left(e^{\left(-\left(b_1*\text{procedure}\right)\right)}\right)$$ (2)

We assumed the shape of the curve for which there is no specific reference [15]. In order to graphically represent the simulated outcomes, we created bins on the basis of the cumulative number of procedures for each physician and calculated the average success rate among each bin.

Finally, we incorporated the learning effects for centers (hospitals) into Equation (3) on the basis of the hypothesis that institutional learning effects appeared to be significant and distinct from physician learning effects. However, in general, these effects are only a fraction of the physician learning rate and typically represent supporting staff learning and facility/equipment workflow changes that occur over time in response to optimization of the device use. Therefore, we assumed individual learning effects would be the most powerful as compared with institutional effects. For this reason, we selected the institutional learning effects to be about 20% of the overall physician learning impact where 20% of 25% lead to a 5% difference in learning between this rate and the physician rate; we allowed the intercept to be 5% of this rate as c₀. We allowed the slope to vary as either slow (0.005) or fast (0.05) learning as c₁ that affects the center number (centerno), which was generated along with the randomly generated cases per physician. The p₁ are the predicted probabilities from (2) that we can think of as the steady state in the physician learning curve model. We modeled this curve as

$$p_2=p_1-\left(p_1-c_0\right)*\left(e^{\left(-\left(c_1*centerno\right)\right)}\right)$$ (3)

The final outcome was based on a random binomial selection using the final predicted probabilities, p₂ to create a binary outcome. We programmed all this in r 2.13.2 to run all simulations.

A total of 500 iterations for each of 24 separate simulated data sets were generated using the aforementioned methods in order to evaluate the performance of the models on a different adverse event outcome rates (3%, 5%, and 10%), among 5 or 10 institutions, and among 10 or 15 physicians per center with slow or fast rates of learning. A summary of these scenarios is shown in Tables I and II.

Table I.

Description of simulated learning curve scenarios (main).

Scenarios	Number of centers	Number of physicians/center	Percentage of outcome for each scenario	Rate of learning
1,2,3	5	10	3,5,10	Slow
4,5,6	10	10	3,5,10	Slow
7,8,9	5	15	3,5,10	Slow
10,11,12	10	15	3,5,10	Slow
13,14,15	5	10	3,5,10	Fast
16,17,18	10	10	3,5,10	Fast
19,20,21	5	15	3,5,10	Fast
22,23,24	10	15	3,5,10	Fast

Note. From Equation (2), b₁ = 0.02 is slow and b₁ = 0.09 is fast rate of learning and from Equation (3), c₁ = 0.005 is slow and c₁ = 0.05 is fast rate of learning.

Table II.

Description of simulated learning curve scenarios (secondary simulation).

Scenarios	Number of centers (5 or 10)	Percentage of outcome for each scenario (3% or 10%)
1	5	3
2	5	10
3	10	3
4	10	10
5	5	3
6	5	10
7	10	3
8	10	10
9	5	3
10	5	10
11	10	3
12	10	10

In the second part of our simulation, we focused on our GEE methods and considered other shapes besides the exponential for the learning curves, a logarithmic shape and a power series as 1/(1 + x), which is a Maclaurin series. We also considered other smoothing methods besides the smoothing spline, a pspline and a locally weighted scatterplot smoothing (LOWESS) function. The logarithmic series was modeled as

$$\begin{gathered} p_1=(b_{11}*\left(\left({\left(\left((p_0-b_0\right)/p_0\right)}^{*}(\text{log (procedure))})+b_1\right)\right)+b_{12} \\ {p}_2=(c_{11}*\left(\left({\left(\left((p_1-c_0\right)/p_0\right)}^{*}(\text{log (procedure))})+c_1\right)\right)+c_{12} \end{gathered}$$ (4)

for physician, p₁, or institution learning, p₂.

While the power series was modeled as

$$\begin{gathered} p_1=\left(b_{11}*\left(p_0-\left(p_0-b_0\right)*\left(\frac{1}{1-\left(-b_1*\text{procedure }\right)}\right)\right)\right)+b_{12} \\ {p}_2=\left(c_{11}*\left(p_1-\left(p_1-c_0\right)*\left(\frac{1}{1-\left(-c_1*\text{procedure }\right)}\right)\right)\right)+c_{12} \end{gathered}$$ (5)

for p₁ and p₂. A total of 500 iterations were performed, for each of 12 separate scenarios, with four datasets generated for each of the three different learning curve shapes analyzed. Within each cluster of four, we evaluated the performance of the models on a different adverse event outcome rates (3% and 10%), and among 5 or 10 institutions. The final outcome was again based on a random binomial selection using the final predicted probabilities, p₂ to create a binary outcome. We programmed all this in R to run all simulations.

2.2. Statistical analysis

In the main simulation, for each scenario, both the GEE and the GLME modeling methods were applied. The GEE is given by [26]: $u(\beta )=\sum _{i=1}^N{D}_i{V}_i^{-1}\left\{{\mathbf{Y}}_i-{\mu }_i(\beta )\right\}$ where D_i = dμ_i/dβ and V_i = Cov(Y_i).Utilizing the aspects of hierarchical modeling with the GEE [27], for the GEE, we modeled the final outcome as described in Section 3.1, along with the previously created covariates using a binomial distribution and exchangeable correlation structure, because we assumed the responses to be equally correlated, along with the interaction between center and physician to define the hierarchical nature of the model. We used the geepack package in R and the geeglm function within this package to fit the clustered GEE model for each dataset of each scenario.

The GLME is given by Rabe-Hesketh and Skrondal [28] the following functional form for a binary outcome of y ~ h(η) + ε where η = Xβ + Zγ and $h(\eta )=\frac{e^{\eta }}{1+e^{\eta }}$ where the linear predictor is represented of as a combination fixed and random effects as the link function relates the outcome to the linear predictor. For GLME, we modeled the final outcome from Section 3.1, along with the previously created covariates with a random center effect and physician hierarchy. To fit the hierarchical linear mixed effect models, we used the glmer package in r.

Root-mean-square error (rMSE) [29] was calculated between the predictions and the marginal success rates in the observed data to assess performance of the model in predicting learning curve influences. QIC [30], which stands for quasi-likelihood, is an adaptation of Akaike’s information criteria (AIC) for the GEE, was used to judge the goodness-of-fit of a GEE model. Besides the QIC test, there is a QICu, an unadjusted version of the test. We tested goodness-of-fit by the general information criteria (GIC), again similar to the AIC. Overall estimates for each scenario were calculated from performance across the 500 iterations for each scenario.

For graphing the performance of the modeling methods, we used predicted probabilities from the GEE fit or from the GLME fit which we used as success probabilities. These success probabilities were generated from the coefficients of the covariates and intercept terms for each simulated dataset. Both GEE and GLME predicted probabilities were separately smoothed by a smoothing spline [31] technique where all knot points were used for plotting purposes. The probability of success was plotted against institutional volume and overlaid with the observed probability of success. The smoothing spline is of the form, where is it a cubic spline with knots for x: ∑w_i[y_i − f(x_i)]² + λ ∫(f″ (x))²dx.

Finally, in the second simulation, for each of the 12 different datasets created, the GEE predicted probabilities were separately plotted using three separate smoothing techniques: (i) smoothing spline technique (same used in main simulation); (ii) pspline technique; and (iii) LOWESS technique. The pspline or penalized spline is [29]: $s\left(X_i(t)\right)=\sum _{h=1}^n{\beta }_h\cdot B_h(t)$ where the B_h(t) ‘s are the B-spline basis functions and for which it first needs to select a large number, say n of equi-spaced knots and then compute the cubic B-spline basis functions corresponding to these knots. The LOWESS [32] technique refers to locally weighted polynomial regression where it uses a weight function that moves along each ith point and weights based on distance between points, using a classic tricube weight function by default where N represents the neighborhood of points where $w_i={\left({\left(1-\frac{d\left(x_i,x\right)}{\underset{j\in N(x)}{\text{max}}d\left(x_j,x\right)}\right)}^3\right)}^3$. The probability of success calculated from the GEE was plotted with each smoother against institutional volume and overlaid with the observed probabilities of success on the learning curve.

3. Results

3.1. Main simulation results

Overall, both methods performed well in the simulations. We used various parameters and plots to assess their fits in each scenario. A summary of the goodness of fit characteristics is shown in Tables III and A1 contains average coefficient, standard error, and p-value estimates over all iterations per scenario; we see that the covariates that we expect are statistically significant and diabetes, history of MI, and gender tend to adjust for confounding. The magnitude of the coefficients increases for faster learning. For the GLME modeling method, the GIC statistics were consistently superior as compared with the comparable QIC or QICu from GEE modeling in all scenarios, because the values were smaller and typically lower values show a better goodness of fit. Within the GLME modeling method, the GIC values for the GLME are the smallest when the adverse outcome is 3%, as compared with when the outcome is simulated to be at higher rates. This is a consistent pattern seen across the range of scenarios. This method appears to work better for fixed effects rather than also having random effects.

Table III.

Goodness of fit measures for each main simulation scenario.

Scenario	QIC	QICu	GIC	rMSE between observed and GEE	rMSE between observed and LME	rMSE between GEE and LME
1	6419.43	36404.92	−662.02	0.017	0.026	0.012
2	8814.88	38800.08	5221.68	0.020	0.025	0.007
3	10250.37	40235.77	8154.83	0.021	0.025	0.005
4	12827.93	72813.32	−1475.19	0.017	0.026	0.012
5	17617.23	77602.40	10301.11	0.020	0.025	0.007
6	20487.95	80473.24	16163.43	0.017	0.026	0.012
7	9706.82	54692.24	−744.60	0.019	0.029	0.013
8	13284.88	58270.00	7951.46	0.022	0.028	0.007
9	15422.16	60407.40	12288.01	0.023	0.028	0.005
10	19370.19	109355.53	−1735.48	0.019	0.029	0.013
11	26529.17	116514.22	15693.84	0.022	0.028	0.007
12	30812.37	120797.56	24390.93	0.023	0.028	0.005
13	4185.00	34169.87	−8715.24	0.034	0.035	0.002
14	6836.16	36821.87	760.28	0.033	0.034	0.001
15	8409.78	38395.71	4806.69	0.033	0.033	0.001
16	8344.68	68329.38	−17671.79	0.034	0.035	0.002
17	13664.22	73649.81	1376.77	0.033	0.034	0.001
18	16803.39	76789.22	9458.34	0.033	0.033	0.001
19	6301.05	51285.78	−13023.73	0.035	0.037	0.002
20	10285.48	55271.04	1158.48	0.035	0.036	0.001
21	12637.74	57623.55	7198.10	0.034	0.035	0.001
22	12561.49	102546.07	−26325.26	0.035	0.037	0.002
23	20523.88	110509.37	2080.96	0.035	0.036	0.001
24	25230.50	115216.21	14179.06	0.034	0.035	0.001

Comparing the two methods, the rMSE rates between observed data and either the GEE or the GLME are smaller for the scenarios 1–12 where rate of learning is slower. Also, the rMSE error for the GLME is slightly higher than that of the GEE. Varying the number of centers or the number of physicians per center did not appear to make a significant difference in the adequacy of the modeling. The two methods appeared to agree more with each other (smaller rMSE) for the scenarios 13–24 that had a faster rate of learning than for the scenarios with a slow rate of learning. The magnitude of the coefficients increases for faster learning (Table A1) so this translates to probability of success increasing as well.

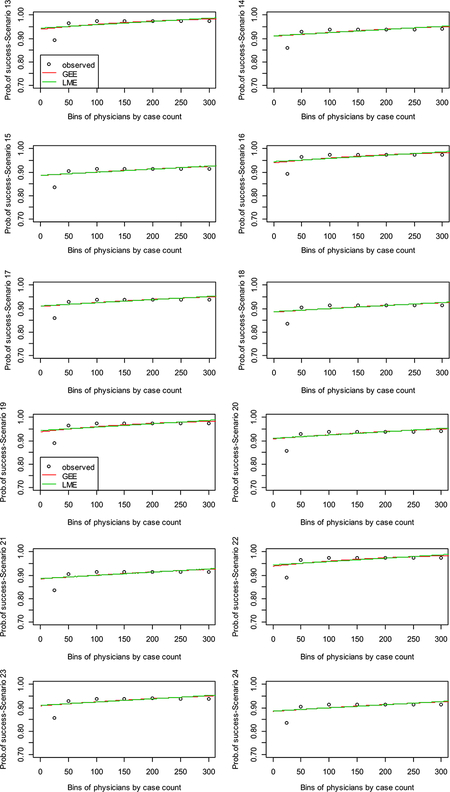
Figure 2a–d reflects the sets of scenarios: 1–6, 7–12, 13–18, and 19–24, respectively. Each figure has the observed binned set of points plotted for the averaged success rate among binned procedures per physician as well as the plots of the fitted curves to the simulated datasets obtained for the GEE and the GLME, with the y-axis as probability of success.

Figure 2.

Learning curve plots from main simulation.

Figure 2a and b reflects slow rates of learning, and Figure 2c and d reflects fast rates of learning (please note scenarios are labelled as Sim in each plot). Figure 2a shows that the curves fit relatively well to the observed data except in the extremes or tails. For Figure 2a, the observed rates seem to be higher in scenarios 1, 4, and 6. The commonality between scenarios 1 and 4 is that the rate of complications is around 3% for both, while for scenario 6, it is 10%. For Figure 2b, the curves fit well to the data except in the lower tail than in Figure 2a. Again the observed rates are higher for scenarios (here 7 and 10) where the rate of complications is around 3%. In both of these figures, the smoothed GEE appears to be taking a more local fit to the data than the smoothed GLME. In Figure 2c and d, the observed rates again seem to be higher for scenarios with rate of complications around 3%. However, both GEE and GLME methods seem to be fitting the observed data except in the lower tail and neither seem to capture this part of the data region in the plots.

3.2. Secondary simulation

First, Table IV shows us the QIC and QICu values for each of the 12 scenarios and Table A2 contains the estimates, standard errors, and p-values; these estimates appear to match what we saw in the main simulation. Comparing respective scenarios between the three shapes, it would seem that the exponential model has the best fit; the power model has the second best fit, distantly followed by the logarithmic model, which has the worst fit. However, if we look at the QICu for the exponential versus power models, we can see that the fits are respectively close to one another. The models for these two different shapes appear to be comparable. Second, when comparing scenarios utilizing 5 centers versus 10, one can generally see that the models using 5 centers has a much better fit than the models utilizing 10 centers. This indicates that the number of centers utilized can have an effect on the fit of the model; specifically, the larger the number of centers included in the model, the worse the associated fit. Finally, increasing the level of the outcome did not seem to have much effect. When comparing respective scenarios utilizing the 3% versus 10% outcomes, we can see that the goodness-of-fit remains relatively unchanged. This indicates that the level of vascular complication inherent to the clinical procedure will not affect our ability to properly model the learning curve.

Table IV.

Goodness of fit measures for each secondary simulation scenario.

Scenarios	QIC	QICu	MSE between observed and GEE model - smooth spline	MSE between observed and GEE model - pspline	MSE between observed and GEE model - LOWESS
1	4184.996	34169.87	0.03475974	0.03531985	0.03456572
2	8409.773	38395.71	0.03677788	0.03688707	0.03675973
3	8344.692	68329.38	0.03382449	0.03455386	0.03387028
4	16803.394	76789.22	0.03285614	0.03264859	0.0323195
5	6192.821	36178.6	0.02730068	0.02850498	0.02712325
6	9980.239	39966.19	0.02695137	0.02735158	0.02682988
7	12367.735	72353.36	0.02241038	0.02403964	0.02248644
8	19946.948	79932.77	0.02293853	0.02326776	0.02254892
9	14045.787	44031.81	0.07119898	0.07744624	0.07074491
10	15621.159	45607.1	0.04959625	0.05016189	0.04863669
11	27957.793	87943.72	0.05465676	0.06163158	0.05422631
12	31143.902	91129.69	0.04536865	0.04674437	0.04470794

GEE, generalized estimating equations; GIC, general information criteria; GLME, generalized linear mixed effect models; LME, linear mixed effect; QIC, quasi-likelihood information criterion; rMSE, root-mean-square error.

Figure 3 shows the shapes of the different learning curves for each of the 12 scenarios, as well as shows the 3 smoothers superimposed upon each scenario. Compared with the other shapes, the exponential model appears to have the steepest slope in phase 2 of the learning curve; this implies that it might be best of the three shapes to model clinical procedures that are learned a reasonably fast pace. The power shape does not have as steep a slope as the exponential model; however, overall, these two learning curve shapes are reasonably similar. The logarithmic model, however, has a much flatter slope in phase 2 than the other two models, requiring a considerable volume of experience to be gained before coming to a plateau. If we compare the respective graphs that utilize 5 centers versus 10 centers, we can see that there does not appear any real difference. For instance, among the four scenarios using the exponential model, scenarios 1 and 3 (whose only difference is scenario 1 utilizes 5 centers, while scenario 3 utilizes 10 centers) look identical to one another; the same pattern goes for scenarios 2 and 4. Hence, changing the number of centers does not seem to alter the learning curve success probability; however, the number of centers seem to affect the goodness of fit.

Figure 3.

Learning curve plots from secondary simulation.

On the other hand, there are differences between respective scenarios that run at 3% versus 10% vascular complication. To start, the expert ‘outcome’ level is different between the two; the plateau being 97% at 3% complication rate, and the plateau being 90% at 10% complication rate. Also, at the very start of the learning curves run at 3%, there is initially a very fast learning rate, which levels off reasonably fast. Therefore, regardless of the level of vascular complication, corresponding graphs appear to plateau at the same level of experience. Finally, regarding Table V, we can come to two conclusions. Firstly, the rMSE values calculated under the three different smoothers seem to be very comparable. Thus, no one smoother stands out as working better than the others. Secondly, the model with the power shapes seems to form the best fit, followed closely by the models with the exponential shape. As was seen when looking at the QIC and QICu, the models with the logarithmic shape remains the worst fit of the three.

Table V.

Real dataset goodness of fit(revised).

Measure	Angiojet			Uncoated BMS
GIC for GLME		343.7695			4728.647
rMSE(s) between* obs and GEE		0.011			0.003
rMSE(s) between* obs and LME		0.029			0.011
rMSE(s) between* GEE and LME		0.027			0.010
Shapes	Exp	PS	Log	Exp	PS	Log
QIC for GEE	2554.595	8255.52	4501.496	4558.572	8677.527	23202.66
rMSE(s) between*:
Obs and spline	0.090	0.029	0.090	0.004	0.009	0.040
Obs and LOWES S	0.089	0.021	0.058	0.004	0.008	0.042
Obs and pspline	0.054	0.015	0.046	0.004	0.008	0.047
Spline and LOWESS	0.069	0.008	0.005	0.0002	0.0003	0.007
Spline and pspline	0.002	0.003	0.034	0.0004	0.0004	0.037
LOWESS and pspline	0.006	0.001	0.030	0.0002	0.0002	0.033
Beta (SE) p-value
Intercept	0.9129 (0.65) <0.1602	2.1220 (0.69) <0.0022	−1.1638 (0.54) <0.0330	5.1014 (0.25) <0.0001	0.3877 (0.16) <0.0001	0.7207 (0.11) <0.0001
Age	0.0290 (0.01) <0.0095	0.0055 (0.01) <0.5845	0.0121 (0.01) <0.3090	−0.0108 (0.01) <0.007	−0.0021 (0.01) <0.3770	−0.0045 (0.01) <0.0019
Sex: male	−0.9445 (0.29) <0.0010	−0.244 (0.26) <0.3533	0.1974 (0.18) <0.2830	−0.5546 (0.09) <0.0001	−0.1474 (0.07) <0.0238	−0.0882 (0.04) <0.0211
Diabetes,y/n	−0.2372 (0.35) <0.4951	−0.423 (0.26) <0.0982	0.2614 (0.34) <0.4440	−0.2729 (0.09) <0.0037	−0.0135 (0.06) <0.8323	−0.0169 (0.04) <0.6526
History MI, y/n)	0.36370 (0.36) <0.3064	−0.3457 (0.34) <0.3147	0.3565 (0.20) <0.0680	−0.7083 (0.09) <0.0001	−0.3480 (0.07) <0.0001	−0.1302 (0.04) <0.0006
Shockstatus, y/n	12.0119 (6.81) <0.0777	0.1677 (0.58) <0.7716	−0.1495 (0.47) <0.7510	−0.9888 (0.22) <0.0001	=0.5686 (0.19) <0.0021	−0.2649 (0.13) <0.0459
Procedure	0.01300 (0.01) <0.2370	0.0064 (0.01) <0.5500	0.1050 (0.04) <0.0110	0.0004 (0.01) <0.4955	−0.0004 (0.01) <4440	0.0221 (0.01) <0.0001

BMS, bare metal stent; GEE, generalized estimating equations; GIC, general information criteria; GLME, generalized linear mixed effect models; LME, linear mixed effect; MI, myocardial infarction; rMSE, root-mean-square error; y/n, yes/no; SE, standard error.

3.3. Real data applications

We used the New York State cardiac dataset collected by their Department of Health containing information on PCI and cardiac surgery reports from 2009 to 2011. From this, we were able to obtain information on cardiac surgery devices to create datasets from which we could employ our learning curve methods. We chose one cardiac device, Angiojet^@ and a stent, uncoated bare metal stent (BMS), to model learning curves, from which there was sufficient information in the dataset for procedures on both.

For both devices, we utilized the first procedure done. For the Angiojet, there were 876 total patients among 109 physicians at 121 centers. For the uncoated BMS stent, there were 24,497 total patients among 391 physicians at 681 centers. We present goodness-of-fit statistics for both datasets in Table V. The QIC for both are smaller than what we obtained in simulations and therefore the GEE seems to be fitting well in these datasets, although better for Angiojet. The AIC from the GLME also appears to be fitting decently for both but not as well for the uncoated BMS. According to the rMSE, the difference between observed and each method tends to be just slightly better for GEE in both methods. The plots in Figure 4 indicate that the GEE is again providing a more on average fit or global fit for both datasets, while the GLME is trying to fit the data except toward the tail end where it diverges in both datasets. Table V reflects that the exponential appears to have best goodness-of-fit that seems to be reflected in the coefficient estimates as well though logarithmic seems better for uncoated BMS, while Figure 5 shows that the power series fits better to the observed data and is closet to other smoothers; the logarithmic appears to fit the learning curve shape the best. The smoothers do not appear significantly different from each other. This appears to align with the simulations as well.

Figure 4.

Real dataset learning curve plots: GEE vs GLME for Angiojet (above) and uncoated BMS (below).

Figure 5.

Real dataset learning curve plots: GEE model with different shapes and smoothers.

4. Discussion

In order to learn more about the learning curve and how it is affected by operator experience and institutional volume, we applied unique mathematical modeling to obtain the rates amongst physicians and allowed this steady state to operationalize the rates amongst institutions. We assumed learning effects at the individual level were stronger than the institutional learning effects. We then incorporated this aspect by allowing the institutional rates to be a percentage of the physician learning rates.

We found that learning curves modeled through our equations and then generated from standard hierarchical modeling with GEE and GLME models fit the data well except for some areas of the tails. It is interesting that the methods are catching the lower tail of the slow rate of learning better than the fast rate of learning. We would expect the opposite. Because the fast rate of learning tends to have a steeper slope, the two methods may partially miss the lower tail but overall they are capturing the correct shape for the learning curve. Varying the number of centers or number of physicians did not appear to improve or worsen the modeling; however, the GEE appeared to have worse goodness-of-fit via AIC but performed better for modeling the observed data on the basis of goodness-of-fit and rMSE. In the case of different shapes, it appeared five centers produced better models than having 10 centers. This implication is that a greater degree of variability is introduced to the model, as we include more centers. A possible explanation might point to the variability of institutional learning between the different centers; there is a significant enough variation between the centers that is not being accounted for and is thus adding to the error of the model. Regarding the outcome, both methods appeared to perform better when the rate of complications was 3%, which was not expected. In terms of fast and slow learning, the GEE appeared to be performing better in the fast learning scenarios than it did in the slow learning and in that sense, was better than the GLME at modeling fast learning, possibly because the fast learning was closer to a linear trend and was easier for the GEE to model than the slow learning, which was more curvilinear. Given the need to explore different shapes and smoothers, we also found that a power series or logarithmic equations could potentially adapt to the learning curve shape better than the exponential and that any of the smoothers could be employed. Of the three different smoothers we employed, no one seemed to outperform the other, so choice of smoother should not be an issue.

There appears to be a threshold in terms of physician volume where the models start to better fit the simulated dataset. The implication of such a threshold effect may be that use of these modeling techniques to assess operator or center performance must be undertaken cautiously at levels below the observed thresholds, as there is significant variation in the predicted success rates. Thus, if one were to incorporate hierarchical learning curve models, such as those studied here, into a study of the performance of operators or centers in the use of a new technology, it would be prudent to avoid making determinations of performance at volumes below the observed thresholds for adequate model fit.

In summary, despite the concern regarding the GEE’s potential limitations at modeling our learning curves, it appeared to well handle the various scenarios with different number of centers, number of physicians per center, rate of complications, and rate of learning, and performed better than GLME in smaller clusters. More complex patient-related risk vectors would likely require more observations in order to yield a stable result, but we prevented this from occurring by using only five covariates. Also we were able to assess modeling various shapes for the learning curve and various smoothers for each shape to further define a paradigm for modeling. With the actual datasets, we were able to demonstrate use of our methodology to generate learning curves and fitting with standard models with either GEE or GLME. We found that the GEE tended to perform better than the GLME again for fitting although it seemed better again for fast learning in the uncoated BMS dataset. The GLME seemed to diverge in the upper tail for both, which could be more related to smoothing. When changing the shapes, it appeared from the graphs that the logarithmic function seemed to better fit an actual learning curve for both devices, even though AIC and rMSE did not seem indicative of that and indicated the exponential or power series was fine. Therefore, it appears important to try all shapes and decide visually as well which learning curve shape will best fit the particular data.

One potential implication of these results are that simulations of learning curve effects may be able to identify the minimum number of training experience needed at the operator and institution level before an acceptable level of proficiency with a new technology should be considered to be possibly attained. In practice, if one could confidently estimate the impact of learning effects on clinical outcomes, informed decision-making (by patients and providers) should incorporate these revised estimates of outcomes in the consideration of the proposed therapy. Separately, understanding the (likely) differences in rates of learning (based on complexity/novelty of procedure or device) may inform the necessary training for an operator or center before they might be considered competent to use the procedure/device independently.

Future clinical studies may be able to determine whether such training experience need be truly ‘hands on’ or based on clinical simulation, case-based learning, or real-time case review so as maximize the learning from the experiences of all operators and institutions. Furthermore, learning curve impacts are essential to interpreting the results of trials of truly novel technologies, even with regards to clinical trials [33–35], and these effects may also be assessed in pre-clinical trial studies before a main confirmatory study. Generally before FDA approval, devices have to undergo extensive clinical trial evaluation, and this would be a good time to assess learning curve effects with our methods. Future work in this area is to directly integrate this new type of learning curve estimation with medical device comparative effectiveness and surveillance analyses in order to separate this effect from device specific effects. Also, given that clinical trials tend to have survival outcomes, there is a need to extend this methodology to modeling survival probabilities and learning curve effects from time-to-event analyses that is possible and can be demonstrated in future work using the basis of our existing methodology of which we have been working.

Appendix A

Table A1.

Main simulation coefficient estimates.

Scenario	GEE Coefficient	GEE Standard error	GEE p-value	GLME coefficient	GLME standard error	GLME p-value
1
Intercept	2.515665727	0.1571844495	<0.0001	0.9165192121	0.008002592	<0.0001
Age	−0.008009532	0.0019552482	<0.0002	−0.0004311956	0.0001016503	<0.0002
Gender	−0.071310514	0.0702294887	<0.4094	−0.0039859843	0.003807215	<0.3848
Diabetes	0.008784372	0.0736203604	<0.5669	0.0005573738	0.003807203	<0.5221
History MI	0.017557799	0.0691947756	<0.4047	0.0009291879	0.003806861	<0.4062
Shockstatus	−0.589672906	0.0648003524	<0.0001	−0.0314656442	0.003807094	<0.0001
Procedure	0.008654075	0.0004578533	<0.0001	0.0004345792	0.00002178888	<0.0000
2
Intercept	2.858963	0.1254721621	<0.0001	0.9392237897	0.009818854	<0.0001
Age	−0.01127062	0.0015742184	<0.0001	−0.0009135975	0.0001247487	<0.0001
Gender	−7.930853	0.0623678458	<0.2645	−0.0065703224	0.004672391	<0.2202
Diabetes	−0.02.659063	0.0573038277	<0.4080	−0.0021177893	0.004672389	<0.3805
History MI	−0.00006.9721	0.0566531204	<0.1788	0.0001344426	0.004671987	<0.2151
Shockstatus	−0.09410704	0.0574647780	<0.0001	−0.0744616368	0.004672222	<0.0001
Procedure	0.005075167	0.0003601513	<0.0001	0.0004054232	0.00002674024	<0.0001
3
Intercept	2.9010430681	0.1090571424	<0.0001	0.9522793548	0.01090536	<0.0001
Age	−0.0125365009	0.0013700091	<0.0001	−0.0012518970	0.0001384004	<0.0001
Gender	−0.0755417993	0.0564761258	<0.2215	−0.0077030228	0.005183825	<0.1774
Diabetes	−0.0395048540	0.0513274007	<0.4559	−0.0039343021	0.005183803	<0.4298
History MI	0.0007025009	0.0533047840	<0.2114	0.0001032001	0.005183245	<0.2229
Shockstatus	−1.0878881801	0.0525021415	<0.0001	−0.1057929177	0.005183002	<0.0001
Procedure	0.0038995025	0.0002929313	<0.0001	0.0003881011	0.00002900010	<0.0001
4
Intercept	2.592400520	0.1071534020	<0.0001	0.9209000313	0.005723777	<0.0001
Age	−0.000500105	0.0013108223	<0.0004	−0.0003520345	0.00007215059	<0.0001
Gender	−0.110074395	0.0477810901	<0.0481	−0.0004570994	0.002707115	<0.0497
Diabetes	−0.042050797	0.0502945297	<0.3590	−0.0021404830	0.002707309	<0.3234
History MI	−0.035247910	0.0500354935	<0.3280	−0.0019040135	0.002707214	<0.3519
Shockstatus	−0.041737002	0.0520283714	<0.0001	−0.0344325730	0.002707340	<0.0001
Procedure	0.007974190	0.0003392025	<0.0001	0.0004091027	0.00001540930	<0.0001
5
Intercept	2.940120798	0.0941788304	<0.0001	0.9454550759	0.000979728	<0.0001
Age	−0.010057524	0.0011117220	<0.0001	−0.0008004170	0.00008818701	<0.0001
Gender	−0.125927784	0.0397398255	<0.0038	−0.0104011038	0.003308733	<0.0027
Diabetes	−0.052884837	0.0399305058	<0.2050	−0.0041872389	0.003308973	<0.3079
History MI	−0.050957232	0.0437703040	<0.2955	−0.0041814302	0.003308784	<0.2525
Shockstatus	−0.993109083	0.0435931045	<0.0001	−0.0782294895	0.003309009	<0.0001
Procedure	0.004895782	0.0002457409	<0.0001	0.0003927125	0.00001890849	<0.0001
6
Intercept	2.987082375	0.0849705727	<0.0001	0.9588458050	0.007008372	<0.0001
Age	−0.011755408	0.0010018802	<0.0001	−0.0011500037	0.00009090074	<0.0001
Gender	−0.120815048	0.0347058072	<0.0027	−0.0120705452	0.003035937	<0.0020
Diabetes	−0.073034155	0.0370057008	<0.1197	−0.0071727948	0.003030209	<0.1205
History MI	−0.055212478	0.0393899380	<0.2347	−0.0054427850	0.003030102	<0.1899
Shockstatus	−1.137312492	0.0395048228	<0.0001	−0.1080317580	0.003030202	<0.0001
Procedure	0.003851802	0.0002143289	<0.0001	0.0003704348	0.00002077824	<0.0001
7
Intercept	2.583543000	0.1270830010	<0.0001	0.9193409549	0.000070094	<0.0001
Age	−0.008300521	0.0015257503	<0.0001	−0.0004750474	0.00008479195	<0.0001
Gender	−0.002754105	0.0500088540	<0.2801	−0.0034452000	0.003179013	<0.3000
Diabetes	−0.019400114	0.0012010827	<0.2315	−0.0013390783	0.003179013	<0.1740
History MI	−0.071050531	0.0550404085	<0.2515	−0.0041358955	0.003179231	<0.2430
Shockstatus	−0.030040703	0.0587389055	<0.0001	−0.0353728870	0.003179109	<0.0001
Procedure	0.008474005	0.0004000082	<0.00001	0.0004477242	0.00001819219	<0.0001
8
Intercept	2.800900042	0.1153887300	<0.00001	0.9405732001	0.008000037	<0.0001
Age	−0.011851314	0.0012370412	<0.00001	−0.0009897121	0.0001028538	<0.0001
Gender	−0.047525581	0.0455911108	0.34001	−0.0038587950	0.003850203	<0.3533
Diabetes	−0.023455532	0.0474943551	<0.09701	−0.0022204097	0.003850231	<0.0857
History MI	−0.081227470	0.0423051004	<0.0000	−0.0008049921	0.003850440	<0.0828
Shockstatus	−0.940100719	0.0471442110	<0.0001	−0.0759715100	0.003850348	<0.0001
Procedure	0.005254874	0.0002982255	<0.0001	0.0004291998	0.00002200032	<0.0001
9
Intercept	2.883493907	0.1092470100	<0.0001	0.9508023711	0.008804037	<0.0001
Age	−0.012528435	0.0011733011	<0.0001	−0.0012010312	0.0001130249	<0.0001
Gender	−0.053229807	0.0443572081	<0.3214	−0.0052701350	0.004237549	<0.2942
Diabetes	−0.025738733	0.0414743050	<0.1399	−0.0028287892	0.004237570	<0.1330
History MI	−0.094241340	0.0392854028	<0.0193	−0.0094940218	0.004237805	<0.0281
Shockstatus	−1.070209044	0.0445491191	<0.0001	−0.1048557890	0.004237707	<0.0001
Procedure	0.004185374	0.0002701391	<0.0001	0.0004175208	0.00002424858	<0.0001
10
Intercept	2.520207000	0.0923910290	<0.0001	0.9101520074	0.004092401	<0.0001
Age	−0.007258102	0.0010503807	<0.0001	−0.0004020385	0.00005941422	<0.0001
Gender	−0.042204430	0.0380285005	<0.3239	−0.0024052740	0.002220890	<0.3285
Diabetes	−0.052045410	0.0395078140	<0.3585	−0.0028851000	0.002220970	<0.3700
History MI	−0.048881815	0.0390002150	<0.2300	−0.0025072479	0.002227000	<0.2054
Shockstatus	−0.010750254	0.0411321191	<0.0001	−0.0337481820	0.002220870	<0.0001
Procedure	0.008500528	0.0002935800	<0.0001	0.0004400225	0.00001274529	<0.0001
11
Intercept	2.849024904	0.0770041045	<0.0001	0.9381831015	0.005095040	<0.0001
Age	−0.011010140	0.0008077974	<0.0001	−0.0009039759	0.000072308	<0.0001
Gender	−0.003819981	0.0315017784	<0.1082	−0.0053808425	0.002710202	<0.1228
Diabetes	−0.000770507	0.0321830814	<0.0753	−0.0054003113	0.002710258	<0.0795
History MI	−0.058029904	0.0337050759	<0.1709	−0.0047211185	0.002710337	<0.1738
Shockstatus	−0.958705938	0.0349535392	<0.0001	−0.0704034708	0.002710190	<0.0001
Procedure	0.005345945	0.0002107990	<0.0001	0.0004307734	0.000015511	<0.0001
12
Intercept	2.897750901	0.0725472904	<0.0001	0.9507003348	0.000249509	<0.0001
Age	−0.012588974	0.0008020125	<0.0001	−0.0012543778	0.000079083	<0.0001
Gender	−0.003132083	0.0289737909	<0.0958	−0.0004400308	0.002980030	<0.1027
Diabetes	−0.000012074	0.0290220300	<0.0904	−0.0000058088	0.002980701	<0.0920
History MI	−0.050420104	0.0300521217	<0.1004	−0.0049535490	0.002980778	<0.1703
Shockstatus	−1.104503281	0.0318757770	<0.0001	−0.1007200189	0.002980035	<0.0001
Procedure	0.004314411	0.0001875288	<0.0001	0.0004207052	0.000017093	<0.0001
13
Intercept	4.008202894	0.2372098090	<0.0001	0.9930229003	0.0002100305	<0.0001
Age	−0.015890170	0.0023020095	<0.0001	−0.0005070499	0.0000785820	<0.0001
Gender	−0.103550385	0.0805179281	<0.2313	−0.0034485380	0.0029431051	< 0.2423
Diabetes	−0.031930004	0.0902137104	<0.0580	−0.0010423002	0.0029432125	<0.0780
History MI	−0.011085020	0.0907153273	<0.4085	−0.0004487707	0.0029429101	<0.3553
Shockstatus	−1.415005285	0.1102929319	<0.0001	−0.0400302903	0.0029428970	<0.0001
Procedure	0.005125792	0.0000055523	<0.0001	0.0001001887	0.0000108447	<0.0001
14
Intercept	4.551480422	0.1008020757	<0.0001	1.0214807583	0.008491357	<0.0001
Age	−0.017783855	0.0017893521	<0.0001	−0.0010050850	0.0001074978	<0.0001
Gender	−0.114139813	0.0059100980	<0.1958	−0.0009295929	0.004020380	<0.1900
Diabetes	−0.008520007	0.0719458793	<0.4855	−0.0005297953	0.004020470	<0.4123
History MI	−0.019715240	0.0052508411	<0.3240	−0.0010504305	0.004020057	<0.3027
Shockstatus	−1.074255521	0.0774309403	<0.0001	−0.0889894300	0.004020171	<0.0001
Procedure	0.002209320	0.0003877574	<0.0001	0.0001358052	0.00002304308	<0.0001
15
Intercept	4.405229335	0.1305770001	<0.0001	1.0405028294	0.009741412	<0.0001
Age	−0.018707142	0.0014812087	<0.0001	−0.0014955753	0.0001239114	<0.0001
Gender	−0.085519574	0.0590302980	<0.2978	−0.0009407822	0.004041213	<0.2803
Diabetes	−0.042402355	0.0022187243	<0.4948	−0.0034120317	0.004041245	<0.4300
History MI	−0.020820405	0.0541800343	<0.1238	−0.0015552471	0.004040757	<0.1890
Shockstatus	−1.783254373	0.0091387511	<0.0001	−0.1272041784	0.004040939	<0.0001
Procedure	0.001070302	0.0003202708	<0.0001	0.0001332434	0.0002055903	<0.0001
16
Intercept	4.747402223	0.1599823780	<0.0001	0.9982144001	0.004338139	<0.0001
Age	−0.014289153	0.0017107559	<0.0001	−0.0004531141	0.00005518938	<0.0001
Gender	−0.192710409	0.0040899227	<0.0102	−0.0002129244	0.002.070738	<0.0100
Diabetes	−0.021223900	0.0719900928	<0.7707	−0.0000307507	0.002070802	<0.7098
History MI	−0.083749409	0.0054387900	<0.4522	−0.0027491048	0.002070791	<0.4377
Shockstatus	−1.429087888	0.0780157095	<0.0001	−0.0404900927	0.002070870	<0.0001
Procedure	0.004024540	0.0004418071	<0.0001	0.0001201420	0.00001183203	<0.0001
17
Intercept	4.002003588	0.1134232150	<0.0001	1.0275111742	0.005990270	<0.0001
Age	−0.010482018	0.0012737937	<0.0001	−0.0009904351	0.00007593950	<0.0001
Gender	−0.187921084	0.0458730000	<0.0002	−0.0114818023	0.002849272	<0.0005
Diabetes	−0.009889248	0.0488837150	<0.2917	−0.0042903383	0.002849410	<0.2880
History MI	−0.009107251	0.0507131440	<0.2140	−0.0041040151	0.002849315	<0.1750
Shockstatus	−1.727048070	0.0599130407	<00001	−0.0908354079	0.002849405	<0.0001
Procedure	0.001894331	0.0002759950	<0.0001	0.0001140483	0.00001028001	<0.0001
18
Intercept	4.489402090	0.104084759	<0.0001	1.0439531514	0.000821830	<0.0001
Age	−0.017001309	0.001137049	<0.0001	−0.0013371759	0.00008070031	<0.0001
Gender	−0.100184410	0.038038410	<0.0001	−0.0131713928	0.003255542	<0.0003
Diabetes	−0.085737513	0.042900295	<0.1153	−0.0009100333	0.003255727	<0.1082
History MI	−0.081005734	0.042308022	<0.1259	−0.0003994048	0.003255593	<0.1051
Shockstatus	−1.830029250	0.053700133	<0.00001	−0.1208472347	0.003255737	<0.0001
Procedure	0.001438302	0.000240591	<0.0001	0.0001128409	0.00001800173	<0.0001
19
Intercept	4.040000977	0.1854213828	<0.0001	0.9901724232	0.005104038	<0.0001
Age	−0.015771890	0.0020431810	<0.0001	−0.0005207035	0.00000488440	<0.0001
Gender	−0.097797040	0.0724150158	<0.2139	−0.0031782103	0.002432508	<0.2288
Diabetes	0.008588859	0.0728040147	<0.4849	0.0001802518	0.002432005	<0.4773
History MI	−0.074032474	0.0713902494	<0.4123	−0.0025000204	0.002432774	<0.4001
Shockstatus	−1.389382340	0.0918201041	<0.0001	−0.0410141103	0.002432083	<0.0001
Procedure	0.004479585	0.0005172517	<0.0001	0.0001452383	0.00001392077	<0.0001
20
Intercept	4.589100202	0.1393000243	<0.0001	1.0241985880	0.000932008	<0.0001
Age	−0.017455112	0.0014902220	<0.0001	−0.0010700299	0.00008850100	<0.0001
Gender	−0.117172909	0.0528303522	<0.0430	−0.0071441259	0.003318147	<0.0575
Diabetes	−0.031589017	0.0550002093	<0.4479	−0.0020213238	0.003318174	<0.4700
History MI	−0.079904732	0.0504074415	<0.1535	−0.0048957205	0.003318330	<0.1708
Shockstatus	−1.718470544	0.0095084754	<0.0001	−0.0923201290	0.003318280	<0.0001
Procedure	0.002200024	0.0003302317	<0.0001	0.0001401115	0.00001898081	<0.0001
21
Intercept	4.410019710	0.1258513845	<0.0001	1.0398251792	0.007928090	<0.0001
Age	−0.017740785	0.0013417523	<00001	−0.0014125403	0.001007744	<0.0001
Gender	−0.090880110	0.0490807555	<0.1415	−0.0070723890	0.003778194	<0.1302
Diabetes	−0.035082725	0.0492322720	<0.4092	−0.0028504440	0.003778222	<0.4102
History MI	−0.105209284	0.0459081550	<0.0340	−0.0083915004	0.003778471	<0.0393
Shockstatus	−1.795053050	0.0009534179	<0.0001	−0.1205953123	0.003778311	<0.0001
Procedure	0.001008958	0.0002777902	<0.0001	0.0001344035	0.00002102098	<0.0001
22
Intercept	4.033098998	0.1294352245	<0.0001	0.9947008510	0.003528715	<0.0001
Age	−0.014213785	0.0013897752	<0.0001	−0.0004487102	0.00004490991	<0.0001
Gender	−0.083300072	0.0519570381	<0.2485	−0.0027070514	0.001085543	<0.2390
Diabetes	−0.078594045	0.0515422893	<0.3810	−0.0024077551	0.001085574	<0.3708
History MI	−0.009023255	0.0527747022	<0.2589	−0.0021528077	0.001085018	<0.2557
Shockstatus	−1.393351325	0.0043417428	<0.0001	−0.0395007849	0.001085531	<0.0001
Procedure	0.004422452	0.0003701089	<0.0001	0.0001377459	0.000009040030	<0.0001
23
Intercept	4.532570391	0.0900091807	<0.0001	1.0212709049	0.004913104	<0.0001
Age	−0.010977959	0.0010150074	<0.0001	−0.0010254277	0.00000224509	<0.0001
Gender	−0.094077078	0.0309031942	<0.0543	−0.0058357389	0.002333054	<0.0540
Diabetes	−0.073144380	0.0373878715	<0.0510	−0.0044151270	0.002333104	<0.0001
History MI	−0.080907827	0.0393328981	<0.2507	−0.0048730375	0.00 2333158	<0.2338
Shockstatus	−1.005372090	0.0459301398	<0.0001	−0.0891313200	0.002333037	<0.0001
Procedure	0.002325805	0.0002430729	<0.0001	0.0001415557	0.00001335250	<0.0001
24
Intercept	4.379757505	0.0850288042	<00001	1.0374887320	0.005578758	<0.0001
Age	−0.017795048	0.0008937280	<0.0001	−0.0014053534	0.00007114408	<0.0001
Gender	−0.088902810	0.0331301111	<0.0454	−0.0072070079	0.002000010	<0.0503
Diabetes	−0.007400005	0.0332247408	<0.0743	−0.0053038925	0.2000009	<0.0700
History MI	−0.002783728	0.0340280240	<0.2735	−0.0049579799	0.002000735	<0.2502
Shockstatus	−1.777041770	0.0400374090	<0.0001	−0.1252245884	0.002000004	<0.0001
Procedure	0.001702828	0.0002021070	<0.0001	0.0001404271	0.00001520133	<0.0001

GEE, generalized estimating equations; GLME, generalized linear mixed effect models; MI, myocardial infarction.

Table A2.

Secondary simulation coefficient estimates.

Scenarios	Coefficient	Standard error	p-value
1
Intercept	4.008202894	0.237209870	<0.0001
Age	−0.015890170	0.002302009	<0.0001
Gender	−0.103550385	0.080517928	<0.2313
Diabetes	−0.031930004	0.090213710	<0.0580
History MI	−0.011085020	0.090715327	<0.4085
Shockstatus	−1.415005285	0.110292932	<0.0001
Procedure	0.005125792	0.000005552	<0.0001
2
Intercept	4.405229335	0.130577000	<0.0001
Age	−0.018707142	0.001481209	<0.0001
Gender	−0.085519574	0.059030298	<0.2978
Diabetes	−0.042402355	0.002218724	<0.4948
History MI	−0.020820405	0.054180034	<0.1238
Shockstatus	−1.783254373	0.009138751	<0.0001
Procedure	0.001070302	0.000320277	<0.0001
3
Intercept	4.747402223	0.159982378	<0.0001
Age	−0.014289153	0.001710750	<0.0001
Gender	−0.192710409	0.004089923	<0.0102
Diabetes	−0.021223900	0.071990093	<0.7707
History MI	−0.083749409	0.005438797	<0.4522
Shockstatus	−1.429087888	0.078015770	<0.0001
Procedure	0.004024540	0.000441807	<0.0001
4
Intercept	4.489402090	0.104084759	<0.0001
Age	−0.017001309	0.001137049	<0.0001
Gender	−0.100184410	0.038038410	<0.0001
Diabetes	−0.085737513	0.042900295	<0.1153
History MI	−0.081005734	0.042308022	<0.1259
Shockstatus	−1.830029250	0.053700133	<0.0001
Procedure	0.001438302	0.000240591	<0.0001
5
Intercept	3.095737510	0.172180104	<0.0001
Age	−0.008898887	0.001994331	<0.0001
Gender	−0.090402340	0.073200973	<0.2491
Diabetes	−0.000704383	0.074458395	<0.3730
History MI	−0.020749405	0.072299182	<0.4077
Shockstatus	−0.084990190	0.075215708	<0.0001
Procedure	0.005404245	0.000473584	<0.0001
6
Intercept	3.309000154	0.118283024	<0.0001
Age	−0.013090270	0.001327998	<0.0001
Gender	−0.085010910	0.057130394	<0.2753
Diabetes	−0.033578100	0.055285554	<0.4043
History MI	0.000753710	0.052987234	<0.2424
Shockstatus	−1.190331777	0.055095019	<0.0001
Procedure	0.002298124	0.000284230	<0.0001
7
Intercept	3.171131983	0.111817305	<0.0001
Age	−0.007092740	0.001390319	<0.0001
Gender	−0.139193004	0.049917804	<0.0293
Diabetes	−0.030423032	0.054892731	<0.3990
History MI	−0.043800090	0.053210089	<0.5100
Shockstatus	−0.730448431	0.054012028	<0.0001
Procedure	0.004002413	0.000304040	<0.0001
8
Intercept	3.373877794	0.090184078	<0.0001
Age	−0.012345709	0.001019030	<0.0001
Gender	−0.133502770	0.035175350	<0.0004
Diabetes	−0.070742507	0.037584784	<0.1402
History MI	−0.002950072	0.039079480	<0.1350
Shockstatus	−1.253401070	0.043310192	<0.0001
Procedure	0.002305019	0.000218744	<0.0001
9
Intercept	0.893158047	0.085180985	<0.0001
Age	−0.007084153	0.001108010	<0.0001
Gender	−0.029349082	0.038310249	<0.4439
Diabetes	−0.054955117	0.044002548	<0.3101
History MI	−0.000353925	0.039333379	<0.2875
Shockstatus	−0.010541842	0.038754004	<0.0001
Procedure	0.008901034	0.000250017	<0.0001
10
Intercept	2.403059281	0.083270370	<0.0001
Age	−0.025180011	0.001013912	<0.0001
Gender	−0.142559835	0.038493394	<0.0005
Diabetes	−0.041280027	0.039929002	<0.1250
History MI	−0.087320572	0.034203477	<0.2207
Shockstatus	−1.570090044	0.041093005	<0.0001
Procedure	0.000407032	0.000237340	<0.0001
11
Intercept	0.89057001	0.007482717	<0.0001
Age	−0.00730511	0.000803903	<0.0001
Gender	−0.04413338	0.029044975	<0.1073
Diabetes	−0.04949420	0.029830302	<0.1508
History MI	−0.01870048	0.029145059	<0.5407
Shockstatus	−0.59928018	0.028740158	<0.0001
Procedure	0.00905537	0.000190500	<0.0001
12
Intercept	2.37727417	0.004809878	<0.0001
Age	−0.02451301	0.000800542	<0.0001
Gender	−0.15017421	0.028419520	<0.0001
Diabetes	−0.09100045	0.028008515	<0.0020
History MI	−0.00058005	0.027201199	<0.0482
Shockstatus	−1.52285410	0.030349755	<0.0001
Procedure	0.00021937	0.000159480	<0.0001

MI, myocardial infarction.