Abstract
Developing temperature transferable coarse-grained (CG) models is essential for the computational prediction of polymeric glass-forming (GF) material behavior, but their dynamics are often greatly altered from those of all-atom (AA) models mainly because of the reduced fluid configurational entropy under coarse-graining. To address this issue, we have recently introduced an energy renormalization (ER) strategy that corrects the activation free energy of the CG polymer model by renormalizing the cohesive interaction strength ε as a function of temperature T, i.e., ε(T), thus semiempirically preserving the T-dependent dynamics of the AA model. Here we apply our ER method to consider—in addition to T-dependency—the frequency f-dependent polymer viscoelasticity. Through smallamplitude oscillatory shear molecular dynamics simulations, we show that changing the imposed oscillation f on the CG systems requires changes in ε values (i.e., ε(T, f)) to reproduce the AA viscoelasticity. By accounting for the dynamic fragility of polymers as a material parameter, we are able to predict ε(T, f) under coarse-graining in order to capture the AA viscoelasticity, and consequently the activation energy, across a wide range of T and f in the GF regime. Specifically, we showcase our achievements on two representative polymers of distinct fragilities, polybutadiene (PB) and polystyrene (PS), and show that our CG models are able to sample viscoelasticity up to the megahertz regime, which approaches state-of-the-art experimental resolutions, and capture results sampled via AA simulations and prior experiments.
Graphical Abstract
INTRODUCTION
Predictive multiscale modeling is a prerequisite for the computational study and design of glass-forming (GF) materials such as polymers. All-atom (AA) molecular simulations can provide insight into complex relaxation dynamics and mechanical properties of GF liquids. However, it is challenging to apply these simulations with limited computational speed to study thermomechanical behaviors over extended time and length scales. This is especially prominent at lower temperatures, where the onset of collective motion gives rise to relaxation phenomena of great interest in the engineering application of polymers and other GF liquids.1–6 For instance, the onset of viscoelasticity in the GF regime governs the performance of polymers in dynamic mechanical applications, such as automotive tires,7 dampers,8,9 structural coatings and barriers,10 and energy-dissipating armors.11 Predictive understanding of GF dynamics is of great importance for the computational design of these materials, which necessitates coarse-grained (CG) modeling of the component polymers.
Coarse-graining techniques offer access to extended spatiotemporal scales by reducing atomistic degrees of freedom and thereby increasing computation speed. However, the chemical specificity of the AA system is partially lost. Approaches such as the inverse Boltzmann, multiscale coarse-graining, and relative entropy coarse-graining methods can be employed to retain the potential of mean force (PMF) of the system, thus retaining key chemical features of the AA system under coarse-graining.12–14 However, the dynamics of CG models developed from these methods is highly difficult to retain as the thermodynamic properties, e.g., the configurational entropy sc and the cohesive energy, are invariably lost upon coarse-graining. This in turn gives rise to an increase in the difference in the activation free energy Ea of relaxation in glass formation between the AA and CG models, as the smoother potential energy landscape of the CG model is expected to yield a lower Ea than that of the AA model.15
Prior works have proposed several strategies to correct the accelerated dynamics that manifest in CG models. One strategy is to use “dynamic” scaling factors.8–12 Such dynamic scaling factors are empirically derived from the ratio of the meansquared displacement (MSD) or diffusivity between AA and CG models. They are effective at reproducing AA dynamics at a given state point, particularly at high temperature, but must be recalibrated for different temperatures. Moreover, recent work by Agrawal et al.10 found that a constant MSD scaling factor is unable to capture the relaxation of CG polymers at longer times. They found that a bimodal time-dependent scaling function was effective in capturing the relaxation dynamics in the temperature range of their study. Although effective in capturing long-time relaxation in an empirical sense, this approach does not provide a theoretical framework for determining the scaling factor at different temperatures, ultimately restricting its usage in the prediction of properties. Another strategy is to use “friction” factors within the framework of dissipative particle dynamics,16–18 which can be used in conjunction with those methods described above to capture both structure and dynamics of the AA counterpart. A demonstration of this strategy was shown by Davtyan et al. for example at relatively higher temperatures,19 although it is not yet known whether friction factors alone can be used on a CG model to capture the slowdown in the dynamics of polymers approaching, or existing below, the glass-transition temperature, Tg.20 Recent works have shown that the entropic contribution to the free energy must also be rescaled in the CG model to properly account for the slowdown in dynamics close to the Tg, and that perhaps a combination of entropic and Langevin-type frictional correction was sufficient to capture the T-dependent diffusive dynamics of polymer systems.21,22 These works adopted potentials that utilized the Ornstein−Zernike equation23 and have demonstrated success in replicating structural properties, thermodynamic properties such as isothermal compressibility,24 and diffusive properties.21 These approaches as well as the aforementioned PMF-based approaches represent innovative solutions by the CG modeling community to capture both the structural and dynamic properties of atomistic polymers, especially in a transferable manner. As hinted earlier, the current demonstration of their success has been on polymers in the melt regime (well above Tg) where liquidlike behaviors prevail. It would be of great interest to explore transferability of CG force fields in capturing atomistic dynamics in the low-T limit, where polymers start exhibiting GF behaviors and eventually become amorphous glassy solids.
Here, we take an alternative approach to the PMF or Langevin type methods in order to achieve transferability in dynamics into the deeply supercooled regime and thus cover all three aforementioned temperature regimes. In our prior works, we demonstrated that by borrowing ideas from the generalized entropy theory (GET) and the Adam−Gibbs theory of glass formation, we could correct the accelerated dynamics of the CG model in a temperature-transferable manner.25,26 This was done by realizing that Ea can be “renormalized” by tuning the cohesive interaction strength parameter ε, which is readily accessible in commonly used nonbonded potentials such as the Lennard-Jones (LJ) potentials. The influence of ε on polymer dynamics has been vindicated in recent simulations.27–29 By systematically varying ε through a renormalization factor α(T), i.e., , our energy-renormalization (ER) approach was able to replicate the dynamics of the AA model at temperature regimes relevant for an amorphous polymer—including the supercooled glass regime, the GF regime, and the melt regime—which was a feat yet to be demonstrated in a CG model. While the renormalization process was empirically donee, it was noted that the sigmoidal trend of the resulting α(T) was exactly consistent with the differences in Ea between AA and CG models and with the shape of the CRR size evolving with T (i.e., Adam−Gibbs’ measure of Ea).30
Here, we follow up on a crucial question concerning what α(T) must look like when sampling rate or frequencydependent rheological behaviors are probed, and whether our ER strategy can be extended to describe viscoelastic response of polymers involving large scale chain motions. This question is of obvious importance in polymer science since one of the foundational properties of polymers is their frequency-dependent dynamic mechanical properties, i.e., linear viscoelasticity, which take on greater importance at larger time scales beyond the glassy relaxation regime. At the outset, we may hypothesize that the frequency-related effects must have a coupled effect on α(T) due to the so-called time−temperature equivalence of linear polymers; however, how exactly this coupling is manifested remains unclear. We also know from the experimental studies of Sokolov and co-workers31–33 that the fragility of GF polymer materials is generally length scale dependent. This observation would appear to require an energy renormalization that depends on frequency (or scattering wave vector q) to describe the viscoelastic response of polymers.
To examine these questions, we perform oscillatory shear using molecular dynamics (MD) simulations and show that changing the imposed oscillation f on the system results in a horizontal shift of α(T), which is proportional to the polymer’s dynamic fragility. By accounting for the dynamic fragility of polymers as a material parameter, we are able to predict how much α(T) must shift with respect to f (in a manner similar to time−temperature superposition) in order to capture AA viscoelasticity, and thus Ea, across a wide range of T and f, i.e., ε(T, f), relevant to the α-relaxation regime. We demonstrate this achievement on two polymers of well-known differences in fragilities: 1,4-cis-polybutadiene (PB) and atactic PS. The more “fragile” PS exhibits a steeper increase in relaxation times with respect to temperature near the glass transition temperature Tg, whereas the more “strong” PB shows a comparatively more linear increase in relaxation times with respect to temperature. We show that in spite of this difference in T-dependent dynamics, the CG models developed from our ER method can predict viscoelasticity for both PS and PB over a wide range of T and several decades of f, which are consistent with both AA simulation results and earlier experimental measurements. Our results show promises of applying CG modeling for the study of time- and temperature-dependent behaviors of polymers and soft matter.
COARSE-GRAINING METHOD
Overview of the Energy Renormalization Strategy.
We recently proposed an energy-renormalization (ER) approach to capturing AA polymer dynamics under coarse-graining25,26 by renormalizing the cohesive interaction strength parameter ε (via the “entropy−enthalpy compensation” effect)34–38 in a temperature-dependent manner, i.e., where α(T) is a renormalization factor and ε0 is a constant value. The sigmoidal variation of α(T) [and ε(T)] obtained from our ER method is consistent with the variation of the extent of collective motion (or alternatively, the size evolution of the cooperatively rearranging regions) predicted by the GET of glass formation.30 A similar operation on the cohesive interaction length-scale parameter σ is also performed to preserve the density. This is important as density is increasingly recognized as a crucial parameter for describing polymeric fluids, for instance, their vibrational dynamics,39,40 which are in turn related to long-time relaxation dynamics.41 Recent coarsegraining efforts have also elucidated the importance of maintaining density as an active variable for capturing structural and thermodynamic properties of polymeric fluids.23 The estimate of σ yields a weakly T-dependent linear function β(T), wherein . Using the ER scheme, we could capture AA dynamics under coarse-graining over the entire temperature range of glass formation, ranging from the high-T melt to the segmental and low-T glassy regimes. Some sacrifices in structural and thermodynamic information were made to achieve this, such as the isothermal compressibility and the full radial distribution function (RDF). However, we were still able to preserve some key thermodynamic and structural properties such as density, strain energy density (proportional to the modulus), and also the primary peak location of the RDF.25 Capturing both thermodynamics and dynamics accurately at different state points remains a challenging endeavor.
To coarse-grain PB and PS polymer models using the ER approach, we first build atomistically informed CG models, where the force centers of the corresponding CG beads are shown in Figure 1A. For this study, we utilize polymer models of N = 10 repeat units per chain to illustrate our coarse-graining approach for computational expediency, since increasing N can significantly increase relaxation time and thus computational cost—a critical problem particularly for atomistic simulations. The probability distributions are used to derive the CG potentials of the bond, angle, and dihedrals for the 1-bead CGPB model via the inverse Boltzmann method (IBM),14 while those of the 2-bead CG-PS model are adopted from our prior work.42 The resulting CG structures of PB and PS are illustrated in Figure 1B, and a detailed treatment of the coarsegraining procedure of the bonded interactions can be found in the Supporting Information.
Figure 1.
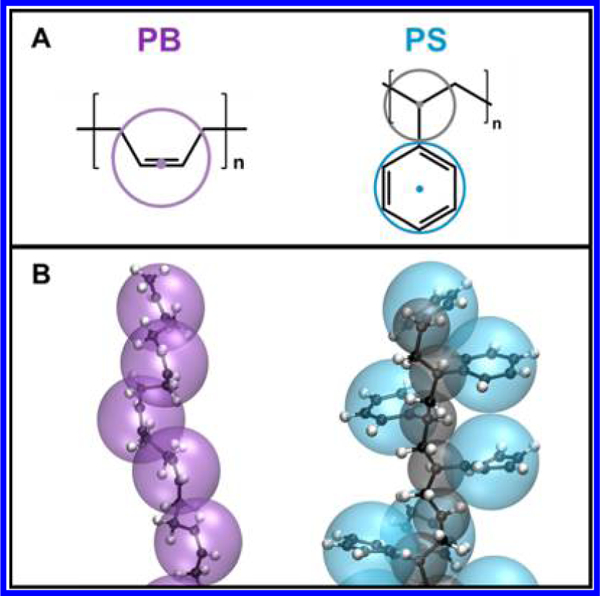
(A) CG mapping scheme for cis-PB and atactic-PS illustrated on their respective repeat units. The PB CG beads are centered on the double bonds in the monomers. The PS CG backbone beads are centered on the alkyl carbon bonded to the phenyl ring, while the side-group beads are centered on the center of mass of the phenyl ring. (B) CG structures of PB and PS, superimposed over their respective AA models.
This leaves the parametrization of the nonbonded potentials via the ER factors α and β for the cohesive interaction strength and length-scale parameters (i.e., ε and σ), respectively, in the 12−6 Lennard-Jones (LJ) potentials. In our prior work of CG PS, α was taken to be temperature-dependent based on calculations of the diffusivity D and segmental relaxation time τα, i.e., α(T), while β was determined by preserving the Tdependent AA density ρ under coarse-graining, i.e., β(T).25 It was found that α(T) had a significant effect on the dynamics of the CG polymer, while β(T) could be estimated roughly at first and then readjusted after calibrating α(T) as to bring the CG model density into alignment with the AA model. As mentioned above, the results of this operation for PS yield a sigmoidally T-dependent function for α(T) and a linear Tdependent function for β(T).25 To generalize our results for the second polymer in question, PB, we perform the similar renormalization procedures based on the criteria mentioned above (the methods are detailed extensively in section 4 of the Supporting Information). Our results show that PB also exhibits a sigmoidally T-dependent function for α(T) and a weakly T-dependence for β(T) which ends up as a single value (i.e., σ = 0.45 nm) to a good approximation (Figure S3 in the Supporting Information). The functional forms of α(T) and β(T) for both PS and PB are listed in Table S2 of the Supporting Information.
We note that the calculations are based on what we henceforth refer to as equilibrium molecular dynamics (EMD) simulations; these refer to simulations involving equilibration without any applied external stresses or deformation to the polymers, wherein D, τα, and ρ are measured. By contrast, viscoelastic properties such as the complex shear modulus G* are obtained by externally deforming the simulation box at a prescribed strain rate, which necessitates nonequilibrium molecular dynamics (NEMD) simulations. In particular, viscoelastic properties of the polymers obtained by performing oscillatory shear via the NEMD simulations are dependent on shear frequency f. This complicates our approach of using ER factors α(T) and β(T) to capture dynamics, as the sampling f is intrinsically related to the thermal state (i.e., T) of the polymer, a phenomenon called “time−temperature superposition”. This is because polymer relaxation typically exhibits a strong dependence on the chain segment size (manifested, for example, in intermediate scattering measurements where τα is highly dependent on the magnitude of the wave vector q),43 and relaxation processes of different number of segments are activated at different frequency f. Thus, for obtaining properties that require NEMD studies such as linear viscoelasticity, the ER factor for cohesive interactions must be tuned with respect to both T and f, i.e., α(T, f).44–46
To streamline our definition for both polymers, we define α(T, f) such that , where εA is the plateau value of ε in the high-T Arrhenius regime for each polymer (more details in section 3 of the Supporting Information on nonbonded potential definitions). The Arrhenius regime represents the T range where the activation energy of GF system is temperature independent, and its onset can be approximated by the temperature where the α(T, f) function reaches a plateau value.25 For subsequent NEMD studies and parametrization of α(T, f), we use β(T) values obtained from EMD simulations.
Energy Renormalization for Viscoelastic Properties.
To determine α(T, f) for studying viscoelasticity, we perform AA and CG measurements of viscoelasticity (i.e., the complex shear moduli G*) at various T and f in the GF regime via smallamplitude oscillatory shear (SAOS) simulations as illustrated in Figure 2A. We sample approximately 40 oscillatory shear cycles and process the sinusoidal stress output σxy(t) (Figure 2B) to obtain the complex shear modulus G* through the relation , where σ0 and γ0 are the stress and strain amplitudes, respectively. The real-part storage modulus G′ and the imaginary-part loss modulus G″ can be calculated by the relations and sin(δ), respectively, where δ is the phase lag between stress and strain (Figure 2B). A caveat to this procedure is that the viscoelastic stress outputs can only be assumed to be linear when the prescribed γ0 is sufficiently small. Thus, we first perform amplitude sweep tests on AA-PB to find the limit of the linear viscoelastic regime, which is estimated to be γ0 ≤ 0.03, as shown in Figure S4. More details on the amplitude sweep test as well as the fitting procedure used to identify viscoelastic parameters such as σ0 and δ are discussed in section 5 of the Supporting Information. Systematic NEMD simulations for CG-PB using different α values at f = 1010 Hz and at T = 140 to 300 K for PB indicate that cohesive interactions have a prominent effect on G* (Figure 2C), which is consistent with recent work that showed a predominant role of ε in capturing dynamic and mechanical behaviors of polymers.42 It is evident that to match AA-PB’s G* values, ε must be renormalized at each temperature in the nonArrhenius GF regime, where the ER factor α must increase as temperature is lowered.
Figure 2.
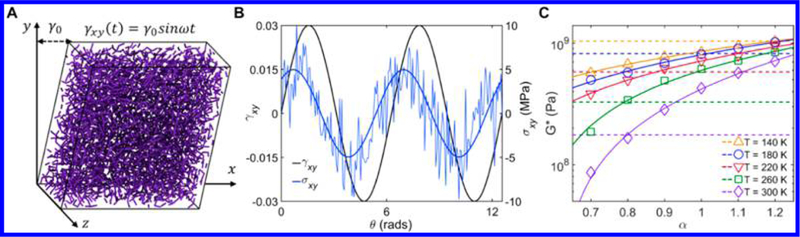
(A) Simulation snapshot of the NEMD oscillatory shear simulation performed on CG-PB. A sinusoidal strain in the form of γ(t) = γ0 sin ωt is imposed in the xy plane. (B) A typical shear stress−strain plot obtained from NEMD. The shear stress outputs are fitted with a sinusoidal function σxy = σ0 sin(ωt + δ). 40 cycles are performed per data point. (C) Complex shear modulus G* of PB measured at f = 1010 Hz for AA (dashed lines) and CG (open symbols) models as a function of α. The solid lines are used to show the trend for CG model data.
Figure 3A shows the α values obtained for PB at T from 100 to 320 K and f from 2.0 × 109 to 2.0 × 1010 Hz by matching AA G* values; Figure 3B shows the α values for PS at T from 350 to 530 K and f from 3.3 × 109 to 2.0 × 1010 Hz. All results are obtained from three trials with random initial configurations. In a similar vein as the sigmoidal α(T) from EMD, we find that α from NEMD also takes a sigmoidal functional form, where the magnitude of α increases from a nearly constant value in the high-T Arrhenius regime to plateaus approaching the glassy state upon cooling. As we hypothesized earlier, we find that α(T) exhibits frequency dependence (see insets in Figure 3A,B). From an isothermal perspective, this translation is nearly vertical. Indeed, the magnitudes of NEMD εA at f = 1010 Hz are observed to be larger than those derived from EMD calculations (detailed in the Supporting Information): they are 1.22 and 1.33 times larger for PB and PS, respectively. This suggests that a higher strain rate necessitates a greater ER factor, which is largely consistent with our sigmoidal representation of α in the GF regime since glassy states require a larger α. The differences in αA between EMD and NEMD may also arise from the effect of applied flow fields on the system’s entropy and the alteration of bonded potentials, which may alter Ea beyond those governed by the cohesive interactions.47
Figure 3.
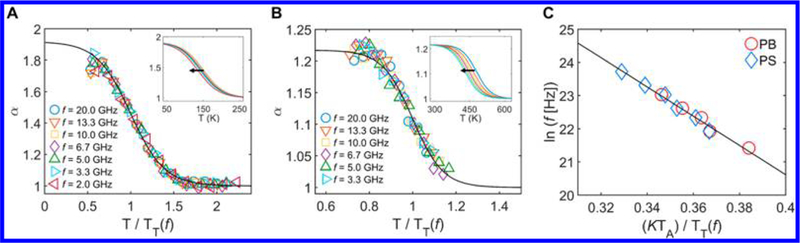
Time- and temperature-dependent energy renormalization factor α(T, f) for CG (A) PB and (B) PS from matching AA G* values. Different open symbols show α determined from using different f. The solid curve shows the functional form of α(T, f). The insets for (A) and (B) show α(T, f) without normalizing the temperature by TT(f) [i.e., α(T)] and thus shows the f-dependence of the sigmoid. Symbols are removed, and only the sigmoidal fits are shown for visual clarity. The arrows indicate the direction of the sigmoidal shift with decreasing f. (C) Collapsed transition temperatures TT(f) of PB and PS (normalized by TA and K) as functions of f. The solid line shows the Arrhenius fitting of both PB and PS data, which is extrapolated for lower f oscillatory shear measurements to obtain α(T, f).
In the non-Arrhenius relaxation regime of glass formation, it is convenient to visualize the shift in α as being horizontal, wherein higher frequency readings will shift α to the right, and vice versa. This can readily be captured by the T and f dependent ER factor α(T, f)
| 1 |
where αg and αA refer to α values in the glassy and Arrhenius regimes, respectively, and Φ is the two-state logistic function taking the form ,48 where k is a fitting parameter describing the breadth of the transition of α(T, f) and TT is the transition temperature separating the Arrhenius and glassy regimes. Note that the same functional form captures α(T) in the absence of f effects as discussed above. Employing this function allows for the collapse of the α curves of PB and PS into single sigmoidal curves that accounts for the f-dependence of α(T) by normalizing T with TT (Figure 3A,B), which scales with f (Figure 3A,B inset). Representative T sweeps for the α-tuned CG models of PB and PS with respect to G′, G″, and G* measured at two different f are shown in Figure S5.
Obtaining viscoelastic properties at lower f requires predictive extrapolation of TT(f). Several prior studies have noted that the f-dependence of a polymer’s dynamics can be well described by an Arrhenius relationship of the form
| 2 |
where f 0 is a prefactor, ΔHa is an apparent activation energy, and Tchar is a characteristic temperature, for instance, Tg.45,46 Similarly, as TT(f) describes approximately the midpoint of the GF regime, we should expect this quantity to follow a similar Arrhenius dependence. Figure 3C shows the plot of TT(f) for PB and PS, normalized by the onset Arrhenius temperature TA and the fragility parameter K. TA is defined by the temperature where α(T, f = 1010 Hz) shown in Figures 3A and3B reaches within 1% of αA, while K is inversely related to D (i.e., K = D−1) obtained from the Vogel−Fulcher−Tammann49 (VFT) fits of the AA segmental relaxation data shown in Figure S3. As discussed in the Introduction, a highly fragile polymer with large K will experience a larger variation in dynamics with respect to T during glass formation. These procedures, i.e., plotting ln f vs , collapse all our data for both polymers, T fT( ) which are then described by a linear Arrhenius fit (solid line) from eq 2 (Figure 3C). These results suggest that TT can be considered as a characteristic temperature associated with GF behavior and also that the f-dependence of α bears close relationship with the GF liquid’s fragility. This latter conclusion is intuitive as α(T, f) is predicated on correcting the diverging GF dynamics between AA and CG models, the extent to which will differ depending on the polymer’s fragility. The Arrhenius assumption of TT(f) is expected to hold over a moderate range of frequency,45 and crucially, these fits for TT(f) can be extrapolated to estimate low-frequency renormalization factor α(T, f) for both polymer systems. All the parameters used in eqs 1 and 2, including the values of TA and K for PB and PS, are listed in Table 1.
Table 1.
Functional Forms of CG Model Cohesive Interactions and Fitting Parameters Used in NEMD Studies of PB and PS
| Function | Polybutadiene Parameters | Polystyrene Parameters |
|---|---|---|
| αA = 0.7866 | αA = 3.232 | |
| αg = 1.509 | αg = 3.923 | |
| k = 0.0343 K−1 | k = 0.03167 K−1 | |
| f0 = 4.13 × 1016 Hz | f 0 = 4.13 × 1016 Hz | |
| ΔHa = 18.61 kJ/mol | ΔHa = 61.27 kJ/mol | |
| TA = 281.0 K | TA = 549.0 K | |
| K = 0.1838 | K = 0.2874 |
RESULTS
We now use the derived α(T, f) as T- and f-dependent renormalization of the cohesive interaction parameter ε for our two polymer models and sample viscoelasticity by measuring G* in the GF regimes for AA and CG systems of both polymers. To do so, we perform SAOS analysis at T = 220−320 K and f = 107−1010 Hz for CG-PB and T = 370−530 K and f = 108−1010 Hz for CG-PS. We note that the ranges explored by the CG-PB model approaches frequency regimes of experimental rheology setups, such as the quartz crystal microbalance, which can sample viscoelasticity at f = 1.5 × 107 Hz.50 For the AA models, the accessible f range is slightly smaller than those of the CG-PB model due to the more fine-grained bead definitions (Figure S2).
Figure 4A shows the G* master curves for AA and CG models of PB and PS at reference temperatures Tref = TA by shifting the data vertically with bT and horizontally with aT values shown in Figure 4B. The vertical shifting factor bT is obtained using AA density ρ results and is defined by the relation, , where ρref is the ρ value at Tref. The horizontal shifting factor aT is the scaling required to converge the different T data into a single master curve and is related to a polymer’s glass-transition.51 The AA density values are later shown in Figure 6. The horizontally shifted frequencies in Figure 4A are then normalized with respect to a reference maximum frequency f max and the logarithmic frequency is then multiplied by the fragility parameter K, in similar vein as the normalization function in eq 2. f max is defined to be the shifted frequency where AA-PB and AA-PS share AA-PS’s maximum Pa. The normalization procedure shifts the data to the same f domain, while the multiplication operation collapses the fragility-dependent softening that manifests in the GF regime of the viscoelastic master curves upon cooling. Both the AA and CG data for the two polymers are reasonably well captured by the master curve, which indicates that the models retain the fragility-dependent viscoelasticity of the two polymers. Figure 4B shows the collapsed aT values for all four systems, with the temperature normalized by TA and the logarithmic shift factor multiplied by K. AA-PB, AA-PS, and CG-PS values can be described with a single Williams−Landel− Ferry (WLF) function:52(fitting parameters are listed in Table S3). However, for the CG-PB, the values of shift factor aT diverge below T ≈ 260 K for reasons we discuss later.
Figure 4.
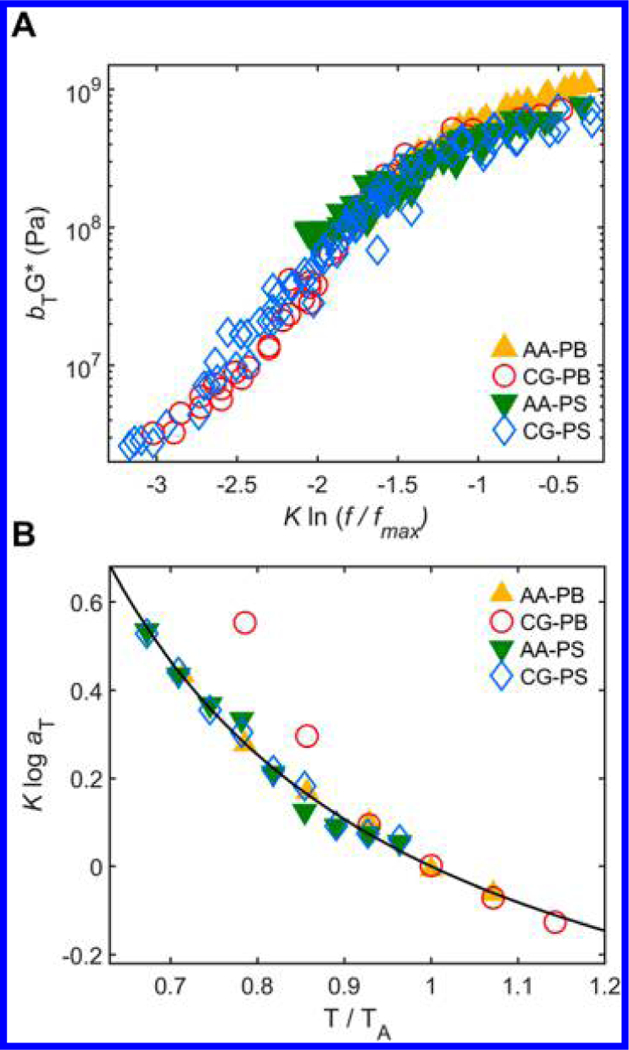
Collapsed representation of (A) complex shear modulus G* and (B) horizontal shift factor aT for AA and CG models of PB and PS. The solid line in (B) represents the collapsed WLF fits. Both figures show the direct relationship between K and viscoelastic behavior of polymers in the glass-forming regime.
Figure 6.
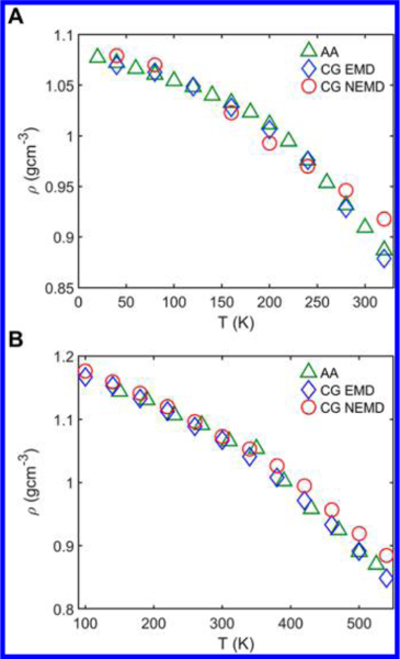
Density sweeps as a function of temperature for (A) PB and (B) PS AA and CG models. The densities of CG models with α(T) derived from EMD as well as α(T, f = 1010 Hz) derived from NEMD are shown up to the temperature used in the oscillatory shear simulations (T = 320 and 530 K for PB and PS, respectively).
In Figures 5A and5B, we show Van Gurp—Palmen plots53—a plotting method that compares G* with δ and thus removes aT from consideration—that compare our AA and CG model results with experimental results. Specifically, we compare our results with those measurements of PB by Palade et al. (Mn = 70 000 g mol−1 and Mw = 70 600 g mol−1, with a mixed microstructure of 41% cis, 48% trans, and 11% vinyl)54 and of PS by Tao et al. (Mn = 92 800 g mol−1 and Mw = 221 000 g mol−1, with an atactic microstructure).55 Direct comparisons cannot be made here as there are substantial differences as follows. First, there are differences in molecular masses, which can cause divergences in relaxation times and fragility parameter K, and thus the maximum δ of the polymers. This can be more obvious for more fragile polymers such as PS. Second, there are differences in microstructure content, particularly for PB. Third, there are differences in cooling rates, which can cause different GF dynamics as discussed by many prior studies. Nevertheless, there are no precedents that have probed GF viscoelastic behavior in similar computational settings as our study, and thus a reasonable agreement observed here is a promising sign for the efficacy of our CG modeling strategy. Indeed, as shown in Figures 5A and5B, the CG models can capture general characteristics of the respective polymers in the GF regime, such as the peak of δ and the softening dispersions in the case of PS that follow. This softening behavior is evident in both experimental and CGNEMD results. The softening dispersion manifests as a large variation in δ observed in experimental measurement,55 and this problem is exacerbated in our CG systems. Noisier δ values are observed in our polymer samples at lower frequencies (Figures 5A and5B) as the SAOS fitting analysis must deal with more thermal noise at lower frequencies and higher temperatures.CG-PS and CG-PB throughout the NEMD calibration of α(T, f). Although the reasoning was that the density ρ is invariant of the sampling f, as our α(T, f) function variation in δ observed in experimental measurement,55 and this problem is exacerbated in our CG systems. Noisier δ values are observed in our polymer samples at lower frequencies (Figures 5A and5B) as the SAOS fitting analysis must deal with more thermal noise at lower frequencies and higher temperatures.
Figure 5.
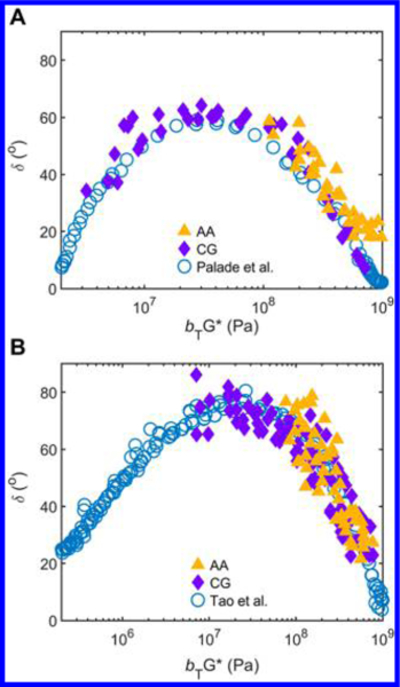
Van Gurp-Palmen Plots of (A) PB and (B) PS comparing NEMD results (filled symbols) with experimental results for PB54 and PS55 (open symbols). Note the softening dispersion in both PB and PS that manifests at lower frequencies due to an onset of thermal noise.
It was mentioned that we used f-independent β(T) for both CG-PS and CG-PB throughout the NEMD calibration of α(T, f). Although the reasoning was that the density ρ is invariant of the sampling f, as our α(T, f) function necessarily changes cohesive energy with f, we may expect that ρ must also change as a result. We find however, that our approach of using an findependent β(T) yields a decent prediction of ρ across all temperatures (Figure 6A for PB and Figure 6B for PS). We see that NEMD systems are slightly denser, particularly at higher T, at f = 1010 Hz, which is consistent with the aforementioned fact that NEMD α(T, f = 1010 Hz) are 1.2−1.3 times higher in magnitude than EMD α(T) (from which β(T) were derived) for both polymers. Nevertheless, cohesive interaction strength ε has a much weaker effect on density compared to the lengthscale parameter σ,25 and accordingly we find that the NEMDbased ρ values are still within ± 0.05 g cm−3 of AA ρ values. Therefore, our approximation for using β(T) seems to yield a fairly accurate representation of ρ, particularly in intermediate and lower temperatures.
DISCUSSION
We have shown that an explicit parametrization and extrapolation scheme for α(T, f) as a function of the polymer’s fragility K yields a CG force field that is able to reproduce the viscoelastic properties of the atomistic polymer in the glassforming regime. These studies were conducted with a chainlength of N = 10 for mainly computational expediency, since larger N requires significantly longer computation time to properly execute (section 7 of the Supporting Information). We may expect, however, that G* from the CG models should deviate slightly from the AA models using the same α(T, f) but with increasing N, as the glass-transition phenomenon of polymers is N-dependent. Thus, it would seem appropriate to make some modifications to α(T, f) (eq 1) based on N, as parameters like TT, describing the crossover temperature between a glass and a melt, are Tg-dependent. Our follow-up simulations based on our current computational resources based on α(T, f) as derived via N = 10 for PB suggest that the difference should not be major (Figure S7), but a more comprehensive follow-up study would be worthwhile to properly assess the N-dependence of α(T, f).
Throughout the present study, we have shown that the fdependent behavior of α(T, f) follows the expected fragility dependence, wherein the variance in TT(f) for the more fragile PS is greater than that for PB (Figures 3A,B). We note, however, that this fragility dependence does not hold for the Tdependent behavior of α(T, f), despite the same glass formation physics that is at play. Should it hold, a larger sigmoidal scaling for PS relative to PB would have been observed, wherein αg for PS > αg for PB. However, the trend is actually the opposite as shown in Figures 3A,B. These are two different polymers, and universality is not necessarily expected a priori, but the reversal of the expected trend is still a curious result. We hypothesize that this contrasting behavior arises from the larger degree of coarse-graining λ for the 1-bead PB relative to 2-bead PS (the difference in bead sizes are demonstrated by the differences in CG model bonded potentials in Figure S2), which has affected many of our results thus far. First, we observe that CG-PB generally samples a lower range of frequency (f = 107−1010 Hz) compared to CG-PS (f = 108−2.0 × 1010 Hz and potentially higher). Beyond f = 1010 Hz, α is nearly independent of frequency for CG-PB, which indicates that the CG-PB is unable to capture relaxations at ultrahigh frequencies. These highfrequency dynamics are primarily associated with the Johari− Goldstein56 type β-relaxation (or even γ-relaxation at even higher frequencies57), which are much more intramolecular in nature compared to α-relaxation.58,59 Thus, it is expected that coarser descriptions of the bonded potentials may cause a loss of resolution in β-relaxation.
This problem is apparent in Figure 4B, which shows a deviation of the WLF function for the CG-PB relative to all other systems at T = 260 K. This temperature coincides with the temperature at which the AA-PB begin to fall out of equilibrium (T at which τ ≈ 1 ns as shown in Figure 4C) and also when the G″ becomes unresolvable with the fully parametrized α(T, f) (Figure S5) or with different iterations of ε and σ (Figure S6). All of these results indicate that upon approaching vitrification, the CG-PB model with higher degree of coarse-graining λ (i.e., number of atoms per CG bead in average) is less capable of capturing its localized dynamics. We note, however, that the reverse also applies—that is, the more “fine-grained” CG-PS model with less λ is less able to capture segmental dynamics in the α-relaxation regime as it cannot access lower frequencies and also exhibits larger noise (Figures 5A,B). Recent studies have confirmed the importance of λ on large-scale diffusive dynamics60 and have investigated how λ changes the temperature-dependent dynamics in CG models in the high-temperature regime.61 Yet, to our knowledge, no recent work has quantitatively addressed how this effect may manifest near the glass-transition temperature where relaxation dynamics become more local in nature. We may hypothesize that λ, and bonded potentials derived via IBM, becomes increasingly important near lower temperatures due to localized glassy dynamics, and our results are consistent with this idea. More quantitative assessment of the relationship between the resolution limits provided by different λ at different temperatures is worthy of future investigation. With this being said, the loss of resolution in high-frequency glassy regimes may be trivial for CG modeling purposes. After all, the AA model should be sufficient for sampling dynamics in these fast regimes. Our findings indicate that the larger scaling of the α(T, f) for CG-PB at lower temperatures may be compensatory in nature with λ. Thus, we expect that reducing λ would decrease the magnitude of α(T, f) scaling in PB, in a manner largely consistent with its fragility relative to PS. It would be worthwhile to confirm these hypothesis and open a pathway for developing universal CG model energetic parameters of glass formers based on K and λ.
Lastly, we wish to discuss the generality of our findings with respect to alternative approaches to capturing the dynamics of CG models. In the Introduction, it was mentioned that previous studies have utilized kinetic scaling factors,61 frictional factors (following the Mori−Zwanzig formalism),16–19 and also a combination of frictional and entropic factors21,22 to correct for T-dependent dynamics of polymers in T-regimes that are primarily characterized via self-diffusion coefficients. With our finding that the cohesive energy parameter can be tailored to capture dynamics into the deeply supercooled amorphous solid regime—in particular, in a sigmoidal manner—it would be of great interest to see how these alternative scaling factors must evolve with decreasing T to capture atomistic dynamics.
CONCLUSION
In this work we have presented a generalized framework for capturing the viscoelastic properties of polymers in the α relaxation regime, demonstrated on disparate polymers PB and PS. By employing a theoretically informed calibration of the activation energy of glass formation via cohesive interaction strength parameter ε and taking dynamic fragility into account, we have shown that we can capture viscoelastic dynamics in the megahertz frequency regime—a regime approaching experimental resolutions—and capture important dynamical properties in this regime such as the maximum in tan δ. The efficacy of our strategy suggests that renormalization of cohesive energy can be generalized to different GF polymers based on parameters such as fragility and degrees of coarse-graining. Such universalization of the energy renormalization in CG model development would be promising in achieving the predictive and multiscale modeling of GF polymer materials over a wide temperature range. The work presented in this study represent an important stride toward such goals.
Supplementary Material
ACKNOWLEDGMENTS
The authors acknowledge support by the National Institute of Standards and Technology (NIST) through the Center for Hierarchical Materials Design (CHiMaD) as well as a computational grant from Quest HPC Systems at Northwestern University. The authors also acknowledge support from the Department of Materials Science and Engineering, the Department of Civil and Environmental Engineering, and the Department of Mechanical Engineering at Northwestern University. S.K. acknowledges support from the Presidential Early Career Award for Scientists and Engineers (PECASE). W.X. gratefully acknowledges the support from NIST-CHiMaD Fellowship. J.S. thanks Dr. Liviu L. Palade (University of Lyon), Dr. Vincent Verney (Blaise Pascal University), and Dr. Sindee L. Simon and Dr. Ran Tao (Texas Tech University) for kindly sharing their experimental work with us. J.S. also expresses gratitude to Dr. Ronald G. Larson (University of Michigan), Dr. Kathleen A. Stair (Northwestern University), Dr. Pavan Kolluru (Northwestern University), Mr. Guobiao Li (Northwestern University), and Mr. David Delgado (Northwestern University) for helpful correspondence throughout the work.
Footnotes
Notes
The authors declare no competing financial interest.
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.macromol.7b02560.
Additional information on simulation protocol, coarsegrained model potentials, linear viscoelastic property calculations, molecular weight effects on viscoelastic properties, and viscoelastic shift factor parameters (PDF)
REFERENCES
- (1).Lacevic NM; Sader JE Viscoelasticity of Glycerol at UltraHigh Frequencies Investigated Via Molecular Dynamics Simulations. J. Chem. Phys. 2016, 144 (5), 054502. [DOI] [PubMed] [Google Scholar]
- (2).Debenedetti PG; Stillinger FH Supercooled Liquids and the Glass Transition. Nature 2001, 410 (6825), 259−267. [DOI] [PubMed] [Google Scholar]
- (3).Li Y; Abberton BC; Kroger M; Liu WK Challenges in Multiscale Modeling of Polymer Dynamics. Polymers 2013, 5 (2), 751−832. [Google Scholar]
- (4).Brennan JK; Lísal M; Moore JD; Izvekov S; Schweigert IV; Larentzos JP Coarse-Grain Model Simulations of Nonequilibrium Dynamics in Heterogeneous Materials. J. Phys. Chem. Lett. 2014, 5 (12), 2144−2149. [DOI] [PubMed] [Google Scholar]
- (5).Fritz D; Koschke K; Harmandaris VA; van der Vegt NF; Kremer K Multiscale Modeling of Soft Matter: Scaling of Dynamics. Phys. Chem. Chem. Phys. 2011, 13 (22), 10412−10420. [DOI] [PubMed] [Google Scholar]
- (6).Agrawal A; Aryal D; Perahia D; Ge T; Grest GS CoarseGraining Atactic Polystyrene and Its Analogues. Macromolecules 2014, 47 (9), 3210−3218. [Google Scholar]
- (7).Wood CD; Chen L; Burkhart C; Putz KW; Torkelson JM; Brinson LC Measuring Interphase Stiffening Effects in StyreneBased Polymeric Thin Films. Polymer 2015, 75, 161−167. [Google Scholar]
- (8).Wu J; Huang G; Qu L; Zheng J Correlations between Dynamic Fragility and Dynamic Mechanical Properties of Several Amorphous Polymers. J. Non-Cryst. Solids 2009, 355 (34), 1755−1759. [Google Scholar]
- (9).Hartmann B Relation of Polymer Chemical Composition to Acoustic Damping. Sound and Vibration Damping with Polymers 1990, 424, 23−45. [Google Scholar]
- (10).Agrawal V; Holzworth K; Nantasetphong W; Amirkhizi AV; Oswald J; Nemat-Nasser S Prediction of Viscoelastic Properties with Coarse-Grained Molecular Dynamics and Experimental Validation for a Benchmark Polyurea System. J. Polym. Sci., Part B: Polym. Phys. 2016, 54 (8), 797−810. [Google Scholar]
- (11).Veysset D; Hsieh AJ; Kooi S; Maznev AA; Masser KA; Nelson KA Dynamics of Supersonic Microparticle Impact on Elastomers Revealed by Real−Time Multi−Frame Imaging. Sci. Rep. 2016, 6, 25577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Noid WG; Chu JW; Ayton GS; Krishna V; Izvekov S; Voth GA; Das A; Andersen HC The Multiscale Coarse-Graining Method. I. A Rigorous Bridge between Atomistic and Coarse-Grained Models. J. Chem. Phys. 2008, 128 (24), 244114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Shell MS Coarse-Graining with the Relative Entropy In Advances in Chemical Physics; John Wiley & Sons, Inc: 2016; pp 395− 441. [Google Scholar]
- (14).Reith D; Putz M; Muller-Plathe F Deriving Effective Mesoscale Potentials from Atomistic Simulations. J. Comput. Chem. 2003, 24 (13), 1624−36. [DOI] [PubMed] [Google Scholar]
- (15).Adam G; Gibbs JH On the Temperature Dependence of Cooperative Relaxation Properties in Glass-Forming Liquids. J. Chem. Phys. 1965, 43 (1), 139−146. [Google Scholar]
- (16).Junghans C; Praprotnik M; Kremer K Transport Properties Controlled by a Thermostat: An Extended Dissipative Particle Dynamics Thermostat. Soft Matter 2008, 4 (1), 156−161. [DOI] [PubMed] [Google Scholar]
- (17).Soddemann T; Dünweg, B.; Kremer, K. Dissipative Particle Dynamics: A Useful Thermostat for Equilibrium and Nonequilibrium Molecular Dynamics Simulations. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2003, 68 (4), 046702. [DOI] [PubMed] [Google Scholar]
- (18).Khani S; Yamanoi M; Maia J The Lowe-Andersen Thermostat as an Alternative to the Dissipative Particle Dynamics in the Mesoscopic Simulation of Entangled Polymers. J. Chem. Phys. 2013, 138 (17), 174903. [DOI] [PubMed] [Google Scholar]
- (19).Davtyan A; Dama JF; Voth GA; Andersen HC Dynamic force matching: A method for constructing dynamical coarse-grained models with realistic time dependence. J. Chem. Phys. 2015, 142 (15), 154104. [DOI] [PubMed] [Google Scholar]
- (20).Rosch TW; Brennan JK; Izvekov S; Andzelm JW Exploring the ability of a multiscale coarse-grained potential to describe the stress-strain response of glassy polystyrene. Phys. Rev. E 2013, 87 (4), 042606. [DOI] [PubMed] [Google Scholar]
- (21).Lyubimov I; Guenza M Theoretical reconstruction of realistic dynamics of highly coarse-grained cis-1, 4-polybutadiene melts. J. Chem. Phys. 2013, 138 (12), 12A546. [DOI] [PubMed] [Google Scholar]
- (22).Lyubimov I; Guenza M First-principle approach to rescale the dynamics of simulated coarse-grained macromolecular liquids. Phys. Rev. E 2011, 84 (3), 031801. [DOI] [PubMed] [Google Scholar]
- (23).Dinpajooh M; Guenza MG On the Density Dependence of the Integral Equation Coarse-Graining Effective Potential. J. Phys. Chem. B 2018, 122 (13), 3426. [DOI] [PubMed] [Google Scholar]
- (24).McCarty J; Clark A; Copperman J; Guenza M An analytical coarse-graining method which preserves the free energy, structural correlations, and thermodynamic state of polymer melts from the atomistic to the mesoscale. J. Chem. Phys. 2014, 140 (20), 204913. [DOI] [PubMed] [Google Scholar]
- (25).Xia W; Song J; Jeong C; Hsu DD; Phelan FR; Douglas JF; Keten S Energy-Renormalization for Achieving Temperature Transferable Coarse-Graining of Polymer Dynamics. Macromolecules 2017, 50 (21), 8787−8796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Xia W; Song J; Hansoge N; Phelan JF; Keten S; Douglas J Energy Renormalization for Coarse-Graining the Dynamics of a Model Glass-Forming Liquid. J. Phys. Chem. B 2018, 122 (6), 2040− 2045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Xu W-S; Douglas JF; Freed KF Influence of Cohesive Energy on Relaxation in a Model Glass-Forming Polymer Melt. Macromolecules 2016, 49 (21), 8355−8370. [DOI] [PubMed] [Google Scholar]
- (28).Xu W-S; Douglas JF; Freed KF Influence of Cohesive Energy on the Thermodynamic Properties of a Model Glass-Forming Polymer Melt. Macromolecules 2016, 49 (21), 8341−8354. [Google Scholar]
- (29).Xia W; Song J; Hsu DD; Keten S Side-Group Size Effects on Interfaces and Glass Formation in Supported Polymer Thin Films. J. Chem. Phys. 2017, 146 (20), 203311. [DOI] [PubMed] [Google Scholar]
- (30).Pazmiño Betancourt BA; Douglas JF; Starr FW String Model for the Dynamics of Glass-Forming Liquids. J. Chem. Phys. 2014, 140 (20), 204509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Sokolov AP; Schweizer KS Resolving the mystery of the chain friction mechanism in polymer liquids. Phys. Rev. Lett. 2009, 102 (24), 248301. [DOI] [PubMed] [Google Scholar]
- (32).Ding Y; Pawlus S; Sokolov AP; Douglas JF; Karim A; Soles CL Dielectric Spectroscopy Investigation of Relaxation in C60− Polyisoprene Nanocomposites. Macromolecules 2009, 42 (8), 3201−3206. [Google Scholar]
- (33).Ding Y; Sokolov AP Breakdown of Time− Temperature Superposition Principle and Universality of Chain Dynamics in Polymers. Macromolecules 2006, 39 (9), 3322−3326. [Google Scholar]
- (34).Betancourt BAP; Hanakata PZ; Starr FW; Douglas JF Quantitative relations between cooperative motion, emergent elasticity, and free volume in model glass-forming polymer materials. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (10), 2966−2971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Douglas JF; Dudowicz J; Freed KF Crowding Induced Self-Assembly and Enthalpy-Entropy Compensation. Phys. Rev. Lett. 2009, 103 (13), 135701. [DOI] [PubMed] [Google Scholar]
- (36).Yelon A; Movaghar B Microscopic Explanation of the Compensation (Meyer-Neldel) Rule. Phys. Rev. Lett. 1990, 65 (5), 618−620. [DOI] [PubMed] [Google Scholar]
- (37).Yelon A; Movaghar B; Crandall RS Multi-Excitation Entropy: Its Role in Thermodynamics and Kinetics. Rep. Prog. Phys. 2006, 69 (4), 1145. [Google Scholar]
- (38).Jeong C; Douglas JF Mass Dependence of the Activation Enthalpy and Entropy of Unentangled Linear Alkane Chains. J. Chem. Phys. 2015, 143 (14), 144905. [DOI] [PubMed] [Google Scholar]
- (39).Puosi F; Leporini D Communication: Correlation of the Instantaneous and the Intermediate-Time Elasticity with the Structural Relaxation in Glassforming Systems. J. Chem. Phys. 2012, 136 (4), 041104. [DOI] [PubMed] [Google Scholar]
- (40).Puosi F; Chulkin O; Bernini S; Capaccioli S; Leporini D Thermodynamic scaling of vibrational dynamics and relaxation. J. Chem. Phys. 2016, 145 (23), 234904. [DOI] [PubMed] [Google Scholar]
- (41).Douglas JF; Pazmiño Betancourt BA; Tong X; Zhang H Localization Model Description of Diffusion and Structural Relaxation in Glass-Forming Cu−Zr Alloys. J. Stat. Mech.: Theory Exp 2016, 2016 (5), 054048. [Google Scholar]
- (42).Hsu DD; Xia W; Arturo SG; Keten S Thermomechanically Consistent and Temperature Transferable Coarse-Graining of Atactic Polystyrene. Macromolecules 2015, 48 (9), 3057−3068. [Google Scholar]
- (43).Horbach J; Kob W Relaxation Dynamics of a Viscous Silica Melt: The Intermediate Scattering Functions. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2001, 64 (4), 041503. [DOI] [PubMed] [Google Scholar]
- (44).Ngai K; Plazek D; Rizos A Viscoelastic Properties of Amorphous Polymers. 5. A Coupling Model Analysis of the Thermorheological Complexity of Polyisobutylene in the GlassRubber Softening Dispersion. J. Polym. Sci., Part B: Polym. Phys. 1997, 35 (4), 599−614. [Google Scholar]
- (45).Bai Y; Jin L Characterization of Frequency-Dependent Glass Transition Temperature by Vogel−Fulcher Relationship. J. Phys. D: Appl. Phys. 2008, 41 (15), 152008. [Google Scholar]
- (46).Lewis AF The Frequency Dependence of the Glass Transition. J. Polym. Sci., Part B: Polym. Lett. 1963, 1 (12), 649−654. [Google Scholar]
- (47).Harmandaris VA Quantitative Study of Equilibrium and NonEquilibrium Polymer Dynamics through Systematic Hierarchical Coarse-Graining Simulations. Korea-Australia Rheology Journal 2014, 26 (1), 15−28. [Google Scholar]
- (48).Lin DC; Douglas JF; Horkay F Development of minimal models of the elastic properties of flexible and stiff polymer networks with permanent and thermoreversible cross-links. Soft Matter 2010, 6 (15), 3548−3561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Vogel H The temperature dependence law of the viscosity of fluids. Phys. Z. 1921, 22, 645−646. [Google Scholar]
- (50).DeNolf GC; Sturdy LF; Shull KR High-Frequency Rheological Characterization of Homogeneous Polymer Films with the Quartz Crystal Microbalance. Langmuir 2014, 30 (32), 9731−9740. [DOI] [PubMed] [Google Scholar]
- (51).Dealy J; Plazek D Time-Temperature Superposition—a Users Guide. Rheol. Bull. 2009, 78 (2), 16−31. [Google Scholar]
- (52).Williams ML; Landel RF; Ferry JD The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am. Chem. Soc. 1955, 77 (14), 3701− 3707. [Google Scholar]
- (53).Trinkle S; Friedrich C Van Gurp-Palmen-Plot: A Way to Characterize Polydispersity of Linear Polymers. Rheol. Acta 2001, 40 (4), 322−328. [Google Scholar]
- (54).Palade L; Verney V; Attane P Time-Temperature Superposition and Linear Viscoelasticity of Polybutadienes. Macromolecules 1995, 28 (21), 7051−7057. [Google Scholar]
- (55).Tao R; Simon SL Bulk and Shear Rheology of Silica/ Polystyrene Nanocomposite: Reinforcement and Dynamics. J. Polym. Sci., Part B: Polym. Phys. 2015, 53 (9), 621−632. [Google Scholar]
- (56).Johari GP; Goldstein M Viscous Liquids and the Glass Transition. Ii. Secondary Relaxations in Glasses of Rigid Molecules. J. Chem. Phys. 1970, 53 (6), 2372−2388. [Google Scholar]
- (57).Lusceac S; Gainaru C; Vogel M; Koplin C; Medick P; Rössler E Secondary Relaxation Processes in Polybutadiene Studied by 2h Nuclear Magnetic Resonance and High-Precision Dielectric Spectroscopy. Macromolecules 2005, 38 (13), 5625−5633. [Google Scholar]
- (58).Arbe A; Richter D; Colmenero J; Farago B Merging of the A and B Relaxations in Polybutadiene: A Neutron Spin Echo and Dielectric Study. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1996, 54 (4), 3853. [DOI] [PubMed] [Google Scholar]
- (59).Hansen C; Richert R Dielectric Anomalies in the B-Relaxation of Glassy 1, 4-Polybutadiene. Acta Polym. 1997, 48 (11), 484−489. [Google Scholar]
- (60).Salerno KM; Agrawal A; Perahia D; Grest GS Resolving Dynamic Properties of Polymers through Coarse-Grained Computational Studies. Phys. Rev. Lett. 2016, 116 (5), 058302. [DOI] [PubMed] [Google Scholar]
- (61).Peters BL; Salerno KM; Agrawal A; Perahia D; Grest GS Coarse Grained Modeling of Polyethylene Melts: Effect on Dynamics. J. Chem. Theory Comput. 2017, 13 (6), 2890−2896. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


