Evaluation and environmental correction of ambient CO₂ measurements from a low-cost NDIR sensor

Abstract

Non-dispersive infrared (NDIR) sensors are a low-cost way to observe carbon dioxide concentrations in air, but their specified accuracy and precision are not sufficient for some scientific applications. An initial evaluation of six SenseAir K30 carbon dioxide NDIR sensors in a lab setting showed that without any calibration or correction, the sensors have an individual root mean square error (RMSE) between ~5 and 21 parts per million (ppm) compared to a research-grade greenhouse gas analyzer using cavity enhanced laser absorption spectroscopy. Through further evaluation, after correcting for environmental variables with coefficients determined through a multivariate linear regression analysis, the calculated difference between the each of six individual K30 NDIR sensors and the higher-precision instrument had an RMSE of between 1.7 and 4.3 ppm for 1 min data. The median RMSE improved from 9.6 for off-the-shelf sensors to 1.9 ppm after correction and calibration, demonstrating the potential to provide useful information for ambient air monitoring.

1. Introduction

Carbon dioxide (CO₂) is a major greenhouse gas, with fundamental importance to Earth’s climate. Since measurements started at the Mauna Loa Observatory in the 1950s (Keeling et al., 2005), the global mean concentration of CO₂ has steadily risen from the preindustrial mole fraction of approximately 280 μmol mol⁻¹ of dry air (parts per million, or ppm) to today’s level exceeding 400 ppm. These observations, both from flask samples and state-of-the-art continuous measurement instruments, have a typical compatibility goal of ~ 0.1 ppm, recommended for observations at background global network sites (World Meteorological Organization, 2013). Flask-based measurements require observers to collect samples, which are subsequently transported to a lab for analysis, at significant cost. Continuous in situ CO₂ analyzers located at towers do not suffer from these regular costs, but these high-precision analyzers can cost upwards of USD 100 000 per site, plus any additional costs for calibration gases and installation of equipment and inlet lines. High-accuracy CO₂ observations are thus relatively sparse compared to other climatological variables such as temperature and precipitation.

Recent research efforts have focused more locally and on the use of networks of observing sites that use instrumented towers similar to what is used for global monitoring, but applied to the urban environment (Pataki et al., 2003; Briber et al., 2013; Kort et al., 2013; McKain et al., 2012; Turnbull et al., 2015). High-accuracy observations from these tower sites are then used to create inversions to estimate the total greenhouse gas flux from the urban area in question (McKain et al., 2012; Bréon et al., 2015; Lauvaux et al., 2016). However, due to the cost of these networks being comparable to ones at the global scale, the observation towers are still sited at a relatively low density of typically 3 to 12 sites in a sin gle metropolitan area (McKain et al., 2012; Kort et al., 2013; Turnbull et al., 2015; Bréon et al., 2015). Observing system simulation experiments have found that, depending on the methodology used, a higher spatial density of observations in these urban regions has been shown to better constrain the inversion estimates, even if the absolute uncertainty of the observations is higher (Turner et al., 2016; Wu et al., 2016; Lopez-Coto et al., 2017), but a trade-off between total network cost and inversion constraint must be balanced.

Recently, a wave of small, low-cost sensors, some of which measure trace gases or particulate matter, in addition to traditional meteorological variables, using various technologies have become commercially available. Evaluation and implementation of some of these new low-cost sensors demonstrate their promise for ambient air monitoring (Eugster and Kling, 2012; Holstius et al., 2014; Piedrahita et al., 2014; Young et al., 2014; Wang et al., 2015; Shusterman et al., 2016). Many of these instruments are based on electrochemical reactions to measure the concentrations of trace gases. With the advent of widely available and low-cost mid-infrared light sources and detectors, a small group of non-dispersive infrared (NDIR) CO₂ sensors have also become commercially available. They are designed for use in a number of applications including ventilation control, agricultural and industrial applications, and inclusion in stand-alone commercial products. Additionally, with the high volume of possible applications, these small NDIR CO₂ sensors are affordably priced on the order of USD 100 to 200 per sensor. Previous studies have compared some of these NDIR CO₂ devices and concluded that, after application of some type of calibration procedure, some of these devices can provide reasonably accurate measurements (±3–5 ppm) of ambient CO₂ concentrations (Hurst et al., 2011; ± Yasuda et al., 2012; Shusterman et al., 2016).

In this paper, one of these small NDIR CO₂ devices is assessed by determining its accuracy with and without environmental corrections. Section 2 describes the CO₂ sensor and its Allan variance, the other instruments included in the system, and the data collection and processing methodology. Section 3 describes the calibration and shows the stability of the reference high-precision gas analyzer, and the initial results from the NDIR sensor are shown in Sect. 4. In Sect. 5, two methods are described to determine functional relationships and coefficient values to correct the observed values of the instrument for environmental variables and Sect. 6 discusses the potential utility of observations from this sensor after correction and temporal averaging.

2. Instruments and methods

To test the validity of using low-cost sensors for scientific applications, a sensor package was implemented consisting of various off-the-shelf components. The K30 sensor module (K30) from SenseAir (Sweden) is the low-cost NDIR CO₂ observing instrument used in this study¹. The K30 is a microprocessor-controlled device with on-board signal averaging and has a measurement range of 0 to 10 000 ppm, observation frequency of 0.5 Hz, and resolution of 1 ppm. The manufacturer’s stated accuracy of the K30 sensor is 30 ppm ±3 % of reading (SenseAir, 2007) for the 0.5Hz ±raw output. Additional NDIR sensors were initially evaluated before selecting the K30, including the COZIR ambient sensor and Telaire T6615, which have manufacturer-specified accuracies of ±50 ppm ±3 % and 75 ppm, respectively (Gas Sensing Solutions, 2014; General ± Electric, 2011). The K30 was chosen not only because it has the highest manufacturer-specified accuracy but also because initial testing showed reliability and consistency when compared to higher-quality observations. In addition to CO₂, temperature, relative humidity and pressure readings are recorded using a breakout board purchased from Adafruit. This board features a Bosch Sensortec BME280, which according to the manufacturer’s datasheet has an average absolute accuracy of ±1 °C, 3 % and ±1 hPa and an output resolution of 0.1 °C, 0.008 % ±and 0.01 hPa for temperature, relative humidity and pressure, respectively (Bosch Sensortec, 2015).

To compare the performance of the K30 to better-performing research instrumentation, a greenhouse gas analyzer based on cavity-enhanced absorption spectrometry (CEAS) was used as the control. The LGR-24A-FGGA fast greenhouse gas analyzer from Los Gatos Research (LGR, San Jose, CA) provides CO₂, CH₄ and water vapor mixing ratios at a frequency of 0.5 Hz and has an un-calibrated uncertainty of < 1 % (Los Gatos Research, 2013). The LGR was connected to a tee connection to allow either ambient air or a calibration source (during calibrations) to be sampled continuously by the analyzer at a flow rate of 400 standard mL min⁻¹. Calibrations for CH₄ and CO₂ were conducted using several NIST-certified standard mixtures every 23 to 47 h for a period of 1 month with molar mixing ratios ranging from 1869.6 parts per billion (ppb) to 2159.4 ppb for CH₄ and from 369.19 to 429.68 ppm for CO₂. See Sect. 3 for details and results of this calibration period.

It is important to note that there are differences in how CEAS works compared to NDIR, most notably that the LGR and other CEAS instruments have a controlled cavity where pressure and temperature are kept nearly constant (with a standard deviation of under 0.5 torr and 0.1 °C for 2 s data), removing potential environmental interference and the need for corrections, whereas the NDIR K30 works in the ambient environment without any mechanism for keeping temperature or pressure constant. Additionally, the LGR implements a water vapor correction on its greenhouse gas concentrations to estimate the dry gas mixing ratio, while the K30 makes no water vapor corrections. A difference between the two analyzers with regard to their sensitivity to the isotopes of CO₂ is expected to be small because the standards used to calibrate the LGR account for all CO₂ isotopes. To increase the effective path length, both the K30 and LGR use mirrors, but the LGR system uses highly reflective mirrors that allow for an effective path length that is many times longer than that of the K30. Additionally, the CEAS instrument determines the concentration of a gas by how long it takes for the signal to degrade inside the cavity (the e-folding time), whereas an NDIR sensor merely measures the intensity of the signal received relative to the total intensity emitted.

For data collection, a Raspberry Pi (RPi) computer is used (Raspberry Pi Foundation, 2015). The RPi is a credit-card-sized (approximately 6×9 cm) computer running a full Linux distribution, allowing for easy customization and usability, that is priced at around USD 25. The K30 is connected to the RPi over universal asynchronous receiver/transmitter (UART) serial and the BME280 over Inter-Integrated Circuit (I²C) serial. An image of the complete sensor package is available in Fig. 1. Data are archived on the RPi and uploaded to a centralized data storage and processing server. The LGR collects and archives its own data, but an RPi is used here as well to collect the data from the LGR over a local area network and transfer them to the same centralized server. The added computational power of an RPi over traditional data loggers allows for the ability to archive two levels of data: the raw data collected every 2 s and 1 min averages.

Figure 1.

Photograph of a Raspberry Pi computer (top), a SenseAir K30 (NDIR) CO₂ sensor (bottom center), a Bosch BME280 temperature and pressure sensor (bottom left) and a ruler for size reference.

Archiving and comparing multiple datasets proved to be challenging, so steps are taken to ensure that each compared value is at the same observed time. All of the RPis use an internet server to synchronize their time, and the LGR uses an internal clock with battery that was set to the same time as the RPis at the beginning of the experiment. Because of various complications including the exact LGR start time and the potential for delays in the RPi’s Linux operating system, the data collection times of each K30 sensor package and the LGR are asynchronous. Additionally, power issues can corrupt parts of the plain text data files stored on the RPi’s SD card with random characters. Thus, a post-processing procedure has been developed that filters extraneous characters, and then each dataset is synchronized based on recorded time stamps and averaged over selected time periods. These new datasets can then be directly compared without missing or out of phase data points.

2.1. K30 Allan variance

Allan variance (Allan, 1966) is a measure of the time-averaged stability between consecutive measurements or observations, often applied to clocks and oscillators. In addition, an Allan variance analysis can be used to determine the optimum averaging interval for a dataset to minimize noise without sacrificing signal. Figure 2 shows the Allan deviation (the square root of the variance) for one K30’s raw 2 s data when exposed to a known reference gas. The original 2 s data show the maximum noise, with a standard deviation comparable to the manufacturer’s specifications of ±30 ppm, but averaging for even 10 s drops the variance significantly. According to this analysis, the optimum averaging time, when the Allan variance is at a minimum (Langridge et al., 2008), is approximately 3 min; longer averaging times do not reduce the noise. The other sensors were found to perform similarly. For the subsequent analysis, an averaging time of 1 min is used, as the Allan variance is only slightly higher than for 3 min, and 1 min observations allow for resolution of atmospheric variability at shorter timescales.

Figure 2.

Allan variance analysis for an NDIR (K30) CO₂ sensor when introduced to breathing air from a high-pressure cylinder of a constant and known CO₂ concentration. Averaging times between 10 and 1000 s are shown. The black line (slope –0.5) shows where the noise is white or Gaussian. Averaging times−greater than about 200 s produce no improvement.

2.2. Experiment

The need to quickly and effectively evaluate a relatively large number of sensors under conditions with relatively stable CO₂ led to the use of a rooftop observation room on the University of Maryland campus in College Park, Maryland. Because this rooftop room had limited access, and it was not part of the building’s HVAC system, it served as an ambient evaluation chamber with minimal influence from human respiration. The room was slightly ventilated for the entire evaluation period to allow outside air to slowly diffuse into the room, with a small household box fan also in the room to ensure that the air was well mixed. The room also fea tures a small, independent heating and cooling unit, but it was only used to keep the room from exceeding a certain temperature, and thus the room was not fully temperature controlled. Even with this control, the diurnal fluctuations of temperature in the room were similar to that of the outdoor environment. This ventilation strategy was intentional so that the room then mimicked the ambient CO₂ concentration of the surrounding atmosphere and approximated the outdoor temperature and humidity, while protecting instruments from direct sunlight, extreme temperatures and inclement weather. This provided an advantage over controlled tests in a laboratory setting in that rather than just a multi-point calibration, comparing datasets over ambient concentrations and environmental conditions allowed for a realistic evaluation of these instruments in more real-world scenarios.

For a continuous period of approximately 4 weeks in spring 2016, six K30 sensor packages as described in Sect. 2 were deployed alongside the LGR in the rooftop room, all sampling room air. The LGR was also connected to a mass flow controller and standard tank to periodically provide a reference for stability (details in Sect. 3). For the reference dataset, the dry CO₂ (CO₂dry) output calculated by the LGR was used. This output includes an applied correction to the mole fraction of CO₂ to give the dry air mole fraction in ppm. The raw CO₂ values were recorded from each K30, temperature and pressure were recorded from each BME280 sensor and water vapor mole fraction was also recorded by the LGR. All of the observations were recorded every 2 s and averaged into 1 min values. The next two sections describe the stability of the LGR as well as the initial comparison between the K30 and LGR observations.

3. Los Gatos evaluation and correction

To evaluate the K30 NDIR sensor performance compared to a research-grade analyzer, first the control dataset needs to be calibrated and corrected for drift. To calibrate the LGR, after the experiment concluded the dataset was corrected using a two-point calibration curve derived from using two NIST-traceable gas standards, one with a CO₂ mole fraction of 369.19 ppm and the other with a mole fraction of 429.68 ppm. A linear fit was then assumed between the two calibration points, with the recorded values as the dependent variable and the NIST-assigned tank values as the independent variable. In addition, three cylinders of breathing air with higher CO₂ mole fractions of 449.73, 486.53 and 516.41 ppm (that are NIST-traceable) were also previously used to calibrate the LGR and showed its linearity. Once the coefficients were determined, the entire LGR dataset was then corrected for further analysis.

In addition to the calibration described above, there was a need to quantify any drift in the LGR analyzer. During the experiment period, the LGR was attached to a tee connector, which pulled ambient air from the aforementioned evaluation chamber using its included pump most of the time, but received periodic calibration every 23 to 47 h for a period of 1 h, initially, and later 10 min, to conserve the tank, using a reference tank of breathing air connected to a Dasibi model 5008 calibrator, which was used to schedule the input of calibration gas. This breathing air tank is assumed to have a fixed CO₂ mole fraction, which was estimated by using the LGR to be 463.7 ppm and was used to quantify and subtract the drift of the LGR over the comparison period.

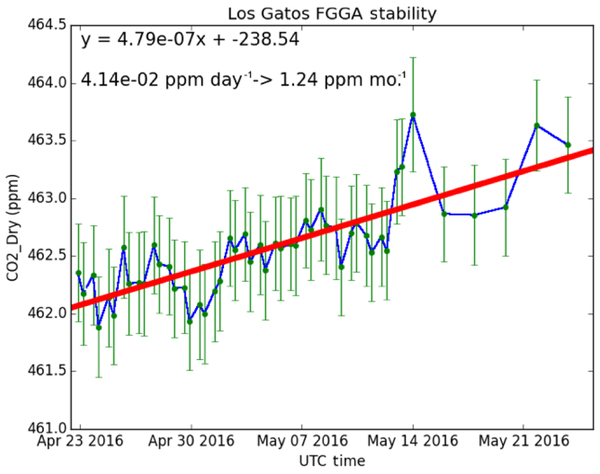
In Fig. 3, the ambient data from the LGR have been filtered out to show only each calibration period performed during the month-long experiment. The data during each calibration period were averaged (either a total of 10 min or 1 h depending on the calibration period) and the averages are plotted on Fig. 3. While there is some small variation in the mean mole fraction observed during each calibration from day to day, there was an upward trend in the recorded value, by over 1.2 ppm over a 30-day period. This observed drift, while not insignificant, is well within the manufacturer’s specifications for this analyzer. However, the observed standard deviation of the 2 s points used in each average (the error bars on Fig. 3) remained relatively constant throughout the period with a mean standard deviation of ±0.3 ppm, which is the manufacturer’s specified repeatability for 2 s data. This high-frequency noise is not a problem for the analysis with the K30 sensor because both datasets are averaged to 1 min values, which removes most, if not all, of this noise. For comparisons between the K30s in the remainder of this paper, the LGR drift is corrected by first computing a linear fit to the calibration points in time (red line, Fig. 3) and then subtracting from the LGR dataset the difference of this fit line from the tank’s assigned value of 463.7 ppm. After this linear correction, the means of each calibration had a root mean square error (RMSE) of 0.2 ppm from the fit line.

Figure 3.

Stability of the Los Gatos Fast Greenhouse Gas Analyzer shown over a 30-day period. Excess breathing air with a fixed CO₂ concentration was introduced periodically using a mass flow controller. The mean of each calibration period is plotted in green with the standard deviation as error bars. The blue line is the linear interpolation between each calibration point, and the red line is a linear fit of each calibration point over the entire time series. The red line is subtracted from the dataset to account for the drift of the analyzer over this period.

4. Initial K30 results

Figure 4 shows the original time series of data recorded during the evaluation experiment described in Sect. 2.2. The top panel shows raw CO₂ mole fractions reported by six K30 sensors as well as the LGR analyzer, each of which is located in the same rooftop evaluation chamber. The middle panels show the reported atmospheric pressure and temperature values from one BME280 sensor and the water vapor mole fraction from the LGR. Then, the bottom panel is the difference between the original recorded K30 value and the corrected LGR recorded CO₂ mole fraction with the calibration periods removed.

Figure 4.

Continuous 1 min time series data during the evaluation experiment. (a) CO₂ observed by six K30 sensors as well as the Los Gatos Research Fast Greenhouse Gas Analyzer. (b, c, d) Observed atmospheric pressure, temperature and water vapor mixing ratio, respectively. (e) Difference of each K30 from the Los Gatos instrument.

Over this 4-week period, the LGR observed an ambient variation of CO₂ with an average value of just over 423 ppm and a standard deviation of just under 21 ppm. There is dis tinct synoptic variation in the diurnal cycle observed, with the magnitude varying from as little as 10 ppm over 24 h to more than 100 ppm. Each of the K30s was successfully able to resolve the ambient variations in CO₂ over this evaluation period, although none of the K30s matched the LGR perfectly in both absolute concentration and relative change. However, without any correction or calibration, each K30 was well within the manufacturer’s stated uncertainty of ±30 ppm ±3 % of the reading for 1 min values.

From the difference plot (Fig. 4, bottom panel), there are some important things to note. First and foremost, each individual K30 sensor has a distinct zero offset. A few of the sensors are approximately the same as the LGR, but many can have an offset that is as much as 5 % (20 ppm) from the LGR. The differences between each K30 and the LGR all have standard deviations between 4 and 6 ppm and RMSEs between 5 and 21 ppm. This means that after accounting for the offset of each individual K30, the practical accuracy of the K30 CO₂ sensor can be within 1 % of the observed concentration. Secondly, each K30 difference time series appears to feature two wave patterns, one with a period of around 1 week and another with a period of approximately 1 day. Given that the cycles seem fairly consistent and are present in each K30, this suggests that the difference between the recorded values from the LGR and each K30 is not random, but instead that there are external factors that can be assessed for potential compensation in the K30 response.

5. Environmental correction

In Fig. 4, the difference between the LGR and each K30 is shown in the bottom panel below time series of environmental data from the evaluation chamber. Just like in the difference plot, each of the environmental variables features two distinct timescales of variability. There is a diurnal cycle of each variable, as well as synoptic-scale variability attributed to weather systems that occurs on the order of 1 week. Because the observed CO₂ differences and the environmental variables are correlated on both short and long timescales, statistical regression methods were used to correct the observed concentration of CO₂ from the K30 sensor to a value approximately that of the concentration determined from the calibration-corrected LGR measurements. Generally, a multivariate linear regression is of the form shown in Eq. (1):

$$y=a_1{x}_1+a_2{x}_2+\dots a_n{x}_n+{\epsilon }_n.$$ (1)

In this case, the measured value y is influenced by the “true” CO₂ value (taken as the value from the LGR instrument), pressure and other environmental variables as the dependent variables x₁,x₂,x_n. A multivariate regression analysis can then be used to find the corresponding coefficients. In addition, in order to better identify the contribution from each individual factor, the data were also analyzed in a successive regression analysis, as described below.

5.1. Successive regression method

Each individual K30 sensor’s original observed CO₂ dataset is first regressed to the LGR dry CO₂ dataset. This regression accounts for the traditional zero and span corrections made during an instrument calibration. The calibration curve of one K30 for just zero and span is shown in Fig. 5. When biases are included due to environmental factors, then the residual, epsilon (“), is calculated in Eq. (2) as

$$\epsilon =y-ax-b,$$ (2)

where in this instance x, the independent variable, is the LGR dataset and y, the dependent variable, is the K30 dataset.

Figure 5.

Calibration curve of K30–1 vs. LGR for 1 min averages without any environmental correction, only span and zero offset are corrected. Solid line is the best fit; dashes represent the 1 : 1 line.

This process is repeated for each environmental variable pressure (P), temperature (T) and water vapor (q), where (P,T,q) is the independent variable, x, and the “ from the previous step is the dependent variable, y. This linear regression method leads to eight correction coefficients of the form a_n and b_n, where n is from 0 to 3 representing each of the independent variables included in the regression. These coefficients can then be used in Eq. (3) along with the environmental variables to correct K30 CO₂ observations for environmental influences.

$$y_{\text{corrected}}=\frac{y-b_0-\left(a_1{x}_1+b_1\right)-\left(a_2{x}_2+b_2\right)-\dots -\left(a_n{x}_n+b_n\right)}{a_0}$$ (3)

For one typical K30, the initial standard deviation of the difference between the K30 and LGR, the RMSE of the data was 6.9 ppm. Using the cumulative univariate regression method described above for the entire evaluation period, the RMSE decreased after each step. After the span and offset regression, it dropped significantly to 3.3 ppm. Then after correcting for atmospheric pressure, the RMSE dropped even lower to 2.7 ppm. Furthermore, including air temperature and water vapor mixing ratio resulted in an RMSE of 2.7 and 2.1 ppm, respectively. It is important to note that the temperature regression did slightly reduce the RMSE but not significantly enough to be resolved with only two significant figures. Therefore, using the successive regression method, the RMSE of the observed difference dropped from 6.9 to 2.1 ppm, a reduction of the error by over a factor of 3. Figure 6 shows the results and scatter plots for each step of the correction for this K30; Fig. 7 shows a difference plot at each step for this same K30 unit. Similar results were observed for each K30 sensor evaluated and a summary can be found in Table 1.

Figure 6.

A continuous time series of 1 min averages as well as scatter plots for K30–1 compared to the LGR instrument during each step of the successive regression described in Sect. 5.1. Cumulative, in order from top to bottom: the original dataset, after correcting for span and offset, after correcting for pressure, after correcting for temperature and, finally, after correcting for water vapor. The root mean square error (RMSE) of the K30 data compared to the LGR at each step is annotated to the upper left of the scatter plot. This regression contains all data points observed in the evaluation period.

Figure 7.

Difference plots for K30–1 compared to the LGR during each step of the successive regression described in Sect. 5.1 and shown in Fig. 6 for 1 min averages. Cumulative, in order from top to bottom: the original dataset, after correcting for span and offset, after correcting for pressure, after correcting for temperature and, finally, after correcting for water vapor.

Table 1.

Root mean square error in ppm between the CEAS LGR and each K30 NDIR sensor’s 1 min averaged data for the original dataset before correction, at each step of the successive regression correction (correcting for (1) zero/span, (2) atmospheric pressure, (3) temperature and (4) water vapor mixing ratio) and after the multivariate regression correction. Each value shown is for a regression calculated using data from the entire evaluation period.

	Original	Zero/span	Pressure	Temp.	q (final)	Multivariate
K30–1	6.9	3.3	2.7	2.7	2.1	1.8
K30–2	5.4	3.5	2.2	2.2	1.9	1.7
K30–3	10.9	6.0	5.0	4.9	4.5	4.3
K30–4	20.8	3.7	2.5	2.4	1.9	1.7
K30–5	8.3	3.7	2.6	2.6	2.2	2.0
K30–6	15.2	4.9	3.6	3.5	2.7	2.2

5.2. Multivariate linear regression method

Alternatively, a multivariate linear regression statistical method can be used to calculate the regression coefficients for each K30 sensor. This results in five correction coefficients a_n and b where n represents each independent variable, the dry CO₂ from the LGR, pressure P, temperature T and water vapor mixing ratio q. Like the successive method above, these coefficients can be used in Eq. (4) along with the original K30 data, y, and the environmental variables to predict the true CO₂ concentration observed.

$$y_{\text{corrected}}=\frac{y-b-\left(a_1{x}_1\right)-\left(a_2{x}_2\right)-\dots -\left(a_n{x}_n\right)}{a_0}$$ (4)

Using the multivariate regression function provided by Python SciPy-Stats (Jones et al., 2001), differences from the LGR of the same K30 described in Sect. 5.1 were reduced to an RMSE of 2.1 ppm, slightly better than the iterative method. This consistently better performance from the multivariate method is shown in the other K30 sensors evaluated. Figure 8 shows the final results of the multivariate regression for the same K30 as in Figs. 6 and 7, as well as the difference between the corrected K30 dataset and the LGR. As with the univariate method, similar results were observed from each K30 sensor evaluated and a summary can also be found in Table 1.

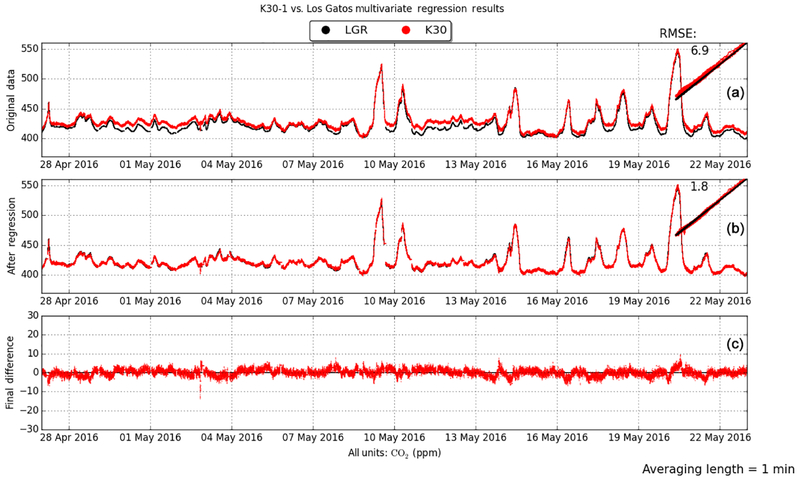
Figure 8.

A continuous time series of 1 min averages as well as scatter plots for K30–1 compared to the LGR for the multivariate regression described in Sect. 5.2. (a) The original data, (b) final time series after correction and the (c) difference plot between the corrected K30 dataset and the original LGR dataset. The root mean square error (RMSE) of the K30 data compared to the LGR before and after the regression is annotated to the upper left of the scatter plot.

6. Discussion

6.1. Time averaging

There are two observations to note based on the evaluation and analysis. First, both before and after the multivariate regressions, there are frequent shifts in the sign of the difference between each K30 and the LGR; these sudden changes occur at or around sunrise most days. Because of the rapid change in atmospheric CO₂ concentration at this time, the ambient calibration chamber may not be well mixed during this time period. Each K30 is located in a slightly different location in the ambient calibration chamber and is approximately 1 to 2 m away from the LGR inlet. This effect, combined with the different response time of the K30s compared to the LGR, can lead to dramatic differences between what each K30 observes and what the LGR observes at the same timestamp for a short period of time each day.

Atmospheric inversion methods often use hourly-averaged data from tower observations (McKain et al., 2012; Bréon et al., 2015; Lauvaux et al., 2016), so after the multivariate regression was applied the K30 and LGR datasets were further averaged to 10 min and hourly datasets. The average RMSE for the six K30s with the 1 min data is 2.3 ppm, 2.0 ppm for 10 min averages and 1.8 ppm for hourly-averaged data. Throughout this analysis period, one of the six K30s evaluated performed consistently worse than the others, and after removing it from the averages the RMSE values dropped to 1.9, 1.6 and 1.5 ppm for 1 min, 10 min and hourly averages, respectively. Thus, by using hourly averages and discarding underperforming sensors, the average RMSE of the difference between the LGR and a K30 NDIR sensor can be reduced to approximately 1.5 ppm.

6.2. Regression period

The RMSEs described above and in Table 1 are for regressions calculated over the entire experiment period of approximately 4 weeks. One goal of this work is to develop a methodology to evaluate individual sensors quickly so that they can be used in scientific applications. In Fig. 9 the average RMSE calculated over the entire month of all six K30s is plotted with respect to the number of days used in the multivariate regression from Sect. 5.2. While the RMSE is generally minimized with increasing regression length, after a regression period of just a few days the RMSE drops significantly from its initial values. Once a few diurnal cycles of varying amplitude have been incorporated, as well as the synoptic-scale variations in the atmosphere (with a timescale of around 1 week), the regression stabilizes. Thus, a regres sion length of around 2 weeks is recommended to maximize correction while minimizing the required amount of time the sensor needs to run concurrently with the LGR.

Figure 9.

The RMSE of all six K30 NDIR sensors when compared to the LGR over the entire experiment as a function of how many days the regression analysis was performed. The colored dots represent each K30’s RMSE, and the box plot shows the median in red, the first and third quartiles within the box and the min and max values on the whiskers.

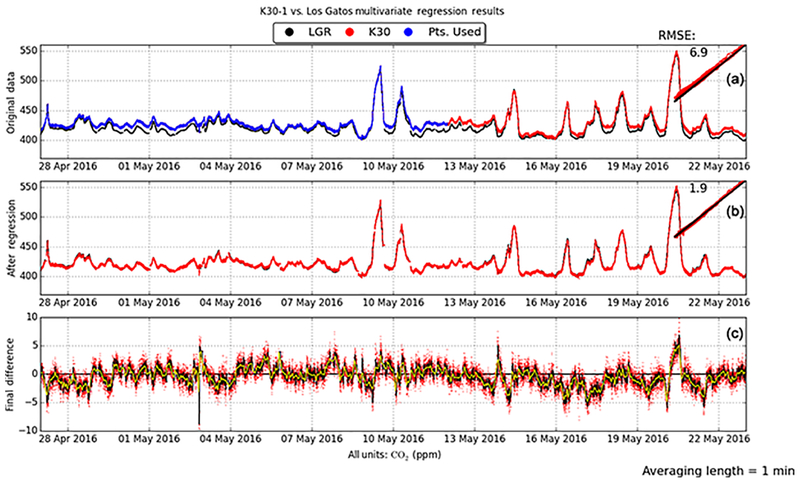
In Fig. 10, a multivariate regression is applied to the same K30 as described in the aforementioned sections and shown in Figs. 6, 7 and 8, but the coefficients are calculated using only data from the first 15 days. The change in the RMSE between the two regressions is 0.1 ppm, going from 1.8 ppm when using all data points to 1.9 ppm when using only approximately the first half. This small but not insignificant change is most likely attributed to the fact that during the first half of the evaluation period, the ambient CO₂ concentrations do not vary significantly, especially relative to the second half, where both the minimum and maximum values occur. In fact, when instead regressing for the last 15 days of the period, the RMSE is 1.8 ppm, a difference not distinguishable with only one decimal place. So as stated above, the diurnal cycles act as a range of calibration points, but values above and below what is included in the regression period may cause the corrected data to still have large errors during these periods, increasing the RMSE for the entire evaluation cycle. Based on these results, it is reasonable to assume that there is either no noticeable baseline drift or that it is assumed to be linear and removed by the multivariate regression in the sensors observed on the weekly to monthly timescales. The longer-term drift of the sensors for periods greater than 1 month is not known at this time, however, and would require a longer evaluation period of at least 6 months.

Figure 10.

As depicted in Fig. 8, a continuous time series as well as scatter plots for K30–1 compared to the LGR for the multivariate regression described in Sect. 5.2. (a) The original data, (b) final time series after correction and the (c) difference plot between the corrected K30 dataset and the original LGR dataset. However, this regression only includes the first 15 days of data (regression training data in blue, the entire dataset in red) to compute the correction coefficients. The difference plot (c) also shows running means for 10 min (black) and hourly (yellow) averages.

6.3. Generalized regression coefficients

All of the final RMSEs calculated in this analysis are from using individual regression coefficients for each K30 sensor. However, it would be beneficial to determine if a generalized set of regression coefficients could be applied to any K30 sensor and what the RMSEs over the evaluation period would be. To calculate the generalized coefficients, the four slopes for each variable as well as the intercepts for each of the five remaining sensors were averaged together, K30–3 was omitted due to the fact that it was the poorest performing sensor and that its coefficients were significantly different from the other five. After correction using the same set of coefficients, the RMSEs of the six sensors ranged from 3.1 ppm to as high as 23.9 ppm. The final RMSEs in some cases were higher than with the original, uncorrected data. Similar results were observed when the multivariate regression coefficients were calculated using the mean concentration of the five sensors. Thus, it appears that for each K30 sensor, an independent evaluation must be completed to provide observations with a sufficient level of quality.

7. Conclusions and future work

The K30 is a small, low-cost NDIR CO₂ sensor designed for industrial OEM applications. Each of the sensors tested falls within the manufacturer’s stated accuracy range of ±30 ppm ±3% of the reading when compared to a high-precision CEAS analyzer, but these ranges are not particularly useful for scientific applications aimed at measuring ambient atmospheric CO₂. If these sensors are individually calibrated, selected for stability and corrected for sensitivity to temperature, pressure and RH, the practical error of these sensors is < 5 ppm, or approximately 1 % of the observed value. The final RMSEs of the six K30 ranged between 1.7 and 4.3 ppm for 60 s averaging times. Averaging for 200 s further reduces the noise by about 30 %, but longer times did not further improve precision. With errors in this range, these instruments could be used in a variety of scientific applications, including observations at high spatial density to better represent the range and distribution of an urban or natural region’s CO₂ concentration.

In the future, further analysis will be performed evaluating the K30 as well as other low-cost CO₂ sensors in a laboratory setting with controlled temperature, pressure and relative humidity. A Picarro cavity ring-down spectroscopic greenhouse gas analyzer will be used as a high-precision control and the various instruments will be subjected to ambient air as well as periodic reference gases. From this lab analysis, we hope to determine the theoretical maximum performance of these sensors in a controlled environment. This subsequent study will additionally attempt to quantify any long-term drift over the course of multiple months.