Abstract
Breast cancer is the most common cancer among women and is considered a major public health concern worldwide. Biogeography-based optimization (BBO) is a novel metaheuristic algorithm. This study analyzed the relationship between the clinicopathologic variables of breast cancer using Cox proportional hazard (PH) regression on the basis of the BBO algorithm. The dataset is prospectively maintained by the Division of Breast Surgery at Kaohsiung Medical University Hospital. A total of 1896 patients with breast cancer were included and tracked from 2005 to 2017. Fifteen general breast cancer clinicopathologic variables were collected. We used the BBO algorithm to select the clinicopathologic variables that could potentially contribute to predicting breast cancer prognosis. Subsequently, Cox PH regression analysis was used to demonstrate the association between overall survival and the selected clinicopathologic variables. C-statistics were used to test predictive accuracy and the concordance of various survival models. The BBO-selected clinicopathologic variables model obtained the highest C-statistic value (80%) for predicting the overall survival of patients with breast cancer. The selected clinicopathologic variables included tumor size (hazard ratio [HR] 2.372, p = 0.006), lymph node metastasis (HR 1.301, p = 0.038), lymphovascular invasion (HR 1.606, p = 0.096), perineural invasion (HR 1.546, p = 0.168), dermal invasion (HR 1.548, p = 0.028), total mastectomy (HR 1.633, p = 0.092), without hormone therapy (HR 2.178, p = 0.003), and without chemotherapy (HR 1.234, p = 0.491). This number was the minimum number of discriminators required for optimal discrimination in the breast cancer overall survival model with acceptable prediction ability. Therefore, on the basis of the clinicopathologic variables, the survival prediction model in this study could contribute to breast cancer follow-up and management.
1. Introduction
Breast cancer is the most common cancer among women worldwide, with an estimated 1.67 million newly diagnosed cases each year, ranking second for cancer incidence rate and fifth for cause of death from cancer [1]. Worldwide increase in breast cancer incidence represents a sizeable burden on public health services [2]. Consequently, the diagnosis, treatment, and prognosis of breast cancer has become a vital research concern [3]. Previous studies have reported various prognosis factors for susceptibility [4–9] and the overall survival of patients in breast cancer [3, 10–12].
The clinicopathologic factors for breast cancer prognosis and overall survival include both tumor burden and tumor molecular biological factors. Tumor burden factors are usually defined as tumor size, lymph node invasion, and lymph vascular and dermis invasion, and tumor molecular biological factors usually include tests for hormonal status—including estrogen receptor (ER), progesterone receptor (PR), and human epidermal growth factor receptor 2 (HER2)—combined with fluorescence in situ hybridization and immunochemistry test results. The Nottingham prognostic index (NPI) was developed to predict prognosis outcomes for various tumor burden situations [13, 14], and the breast cancer severity score was developed for the same purpose but depends mainly on both tumor burden and tumor molecular biological factors [15]. Age at diagnosis is also a factor that is associated with breast cancer prognosis outcome and overall survival [16]. The effect of age on breast cancer progression and mortality might be affected by other clinicopathologic factors [17, 18]. Although various treatments for breast cancer can result in favorable prognosis and survival rates for breast cancer patients [19–23], the radiotherapy, chemotherapy, hormonal therapy, and targeted therapy are highly reliant on clinicopathologic factors [10].
Formerly, analysis of survival benefit or long-term follow-up of breast cancer was based mainly on the common statistical analysis strategy. Along with the improvements in data volume and complex disease causality, machine learning and optimization algorithms have emerged as novel strategies for analyzing breast cancer survival [24–27]. Both statistical and machine learning and optimization algorithm approaches provide theoretical and acceptable explanations for the association between clinicopathologic factors and breast cancer survival benefit. The combined and hybrid use of both statistical and machine learning approaches is a trend in modern biological research.
Biogeography-based optimization (BBO) is a metaheuristic algorithm that was proposed by Simon in 2008 to solve global optimization problems [28]. BBO is an evolutionary algorithm that was inspired by the migration of species between habitats. Specifically, it was inspired by biogeography, which describes (i) the speciation and migration of species between isolated habitats and (ii) the extinction of species [29]. In recent years, the BBO algorithm has been widely used in a myriad of fields, such as to solve the engineering optimization problem. Various BBOs have been proposed to enhance the BBO search ability in specific problems, including blended BBO [30], localized BBO [31], and ecogeography-based optimization [32]. The BBO algorithm is a powerful search technique because it contains both exploration and exploitation strategies based on migration [33].
To explore the clinicopathologic variables of the overall survival of patients with breast cancer, this study analyzed the relationship between the clinicopathologic variables of breast cancer by using a BBO algorithm. We sought to (i) assess the relationship between the clinicopathologic characteristics of overall survival among patients with breast cancer and (ii) to demonstrate the optimization of the overall survival prediction model on the basis of the clinicopathologic variables of breast cancer.
2. Material and Methods
2.1. Data Source and Patients
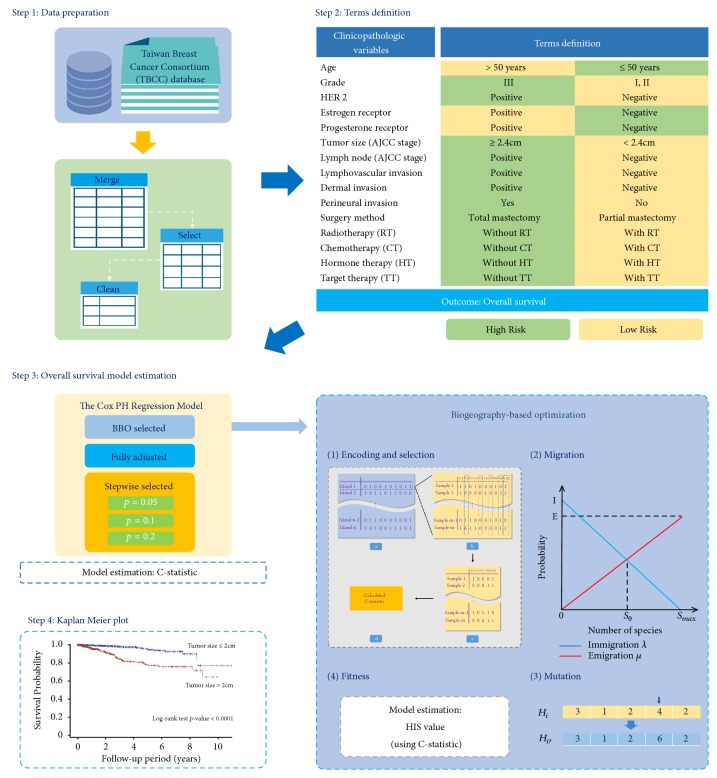
All data were collected from the single-center Taiwan Breast Cancer Consortium (TBCC) database, which is prospectively maintained by the Division of Breast Surgery at Kaohsiung Medical University Hospital, Taiwan. Patients who were diagnosed with ductal carcinoma in situ were excluded. In total, 1,896 patients with breast cancer were included and tracked from 2005 to 2017. The prognosis variables in this dataset included age at diagnosis, grade, tumor size (American Joint Committee on Cancer [AJCC] stage), estrogen receptor (ER), progesterone receptor (PR), human epidermal growth factor receptor 2 (HER2), lymph node (AJCC stage), lymph vascular invasion (LVI) status, dermal invasion, perineural invasion, surgical method, radiotherapy, chemotherapy, and hormone therapy. The overall survival term of all participants with breast cancer was tracked from the date of first diagnosis until participant death or study conclusion. The proposed analysis procedure for TBCC dataset is summarized in Figure 1.
Figure 1.
Summary of the proposed analysis approaches for Taiwan Breast Cancer Consortium (TBCC) database.
2.2. Biogeography-Based Optimization
The BBO algorithm is a population-based optimization algorithm inspired by the natural biogeographical distribution of species [28], which simulates biogeographical species distribution in accordance with the insular migration of species. In biogeography, an area's quality is evaluated by considering suitability index variables (SIVs), including climate, temperature, and humidity. The habitat suitability index (HSI) represents insular quality. A high HSI value indicates that an area is a superior habitat, whereas a low HSI value indicates that an area is an unsuitable habitat. Higher HSI value areas are usually saturated, which means that species encounter difficultly in migrating to these areas and species currently living in these areas are likely to migrate to other areas. By contrast, low HSI value areas are likely to acquire many migrant species come to here. In the BBO algorithm, an unsatisfactory solution results in an area with a low HSI value, whereas a satisfactory solution results in an area with a high HSI value. According to the BBO mechanism, satisfactory solutions are likely to share their SIVs with other solutions and are unlikely to accept SIVs from other solutions. The BBO migration model depicts the migration of species in a habitat. I is the maximum immigration rate (λ), E is the maximum emigration rate (μ), Smax is the maximum number of species that an island can host, and S0 is the number of species that causes the immigration rate to equal the emigration rate. The immigration rate increases as the solution quality decreases, whereas the emigration rate decreases with species quantity. This linear model describes the way for simulating species migration. The BBO algorithm comprises two primary stages: migration and mutation.
2.2.1. Migration
In migration, the probabilistic model can be used to represent the concepts of emigration and immigration. Consider the probability Ps that a habitat contains S species; Ps changes from time t to time t + Δt, which can be formulated as
| (1) |
where λS and μS are, respectively, the immigration and emigration rates when S species are present in the habitat. Equation (1) holds because, to have S species at time (t + Δt), one of the following conditions must be true [28]:
S species were present at time t, and no immigration or emigration occurred between t and t + Δt.
S − 1 species were present at time t, and one species immigrated.
S + 1 species were present at time t, and one species emigrated.
Suppose that time Δt is sufficiently small; the probability of more than one immigration or emigration occurring can be ignored. Subsequently, taking the limit of (1) as Δt → 0 provides the following equation:
| (2) |
From the migration operation curves, where k number of species are present, the emigration μk and immigration λk rates can be formulated as (3) and (4), respectively:
| (3) |
| (4) |
where I and E are the maximal immigration and emigration rates, respectively. The pseudo code of the migration operator is depicted in Algorithm 1.
Algorithm 1.

Pseudo code for migration of BBO.
Consider the special case E = I; (3) and (4) can be combined as
| (5) |
2.2.2. Mutation
In the BBO algorithm, some events, such as the wind carrying seeds or flotsam, provide more favorable features that allow an island to generate superior solutions with statistically significant enhancements. Through species count probabilities Ps, the mutation rate mi can be determined as
| (6) |
where mmax is a user-defined maximal mutation rate that m can reach, and Pmax = max(Ps). The mutation scheme tends to increase diversity among the population. Highly probable solutions tend to be more dominant in the population. Thus, the high HSI solutions likely mutate, which increases the probability that they will improve even more than they already have. The pseudo code of the mutation operator is depicted in Algorithm 2.
Algorithm 2.

Pseudo code for mutation of BBO.
The BBO algorithm can be described using the following steps:
Initialize the BBO parameters, which include a problem-dependent method for mapping problem solutions to SIVs and habitats, the modification probability Pmod, the maximal species count Smax, the maximal migration rates E and I, the maximal mutation rate mmax, and elite number p.
Initialize the habitats, which depend on the population size and problem to determine what habitat is a potential solution.
Calculate the HSI of each habitat, emigration rate μ, immigration rate λ, and species S.
Identify the elite habitats depending on the HSI value.
Migration operation: Modify each nonelite habitat by immigration and emigration rates. The probability that a habitat Hi is modified is proportional to its immigration rate λi, and the probability that the source of the modification comes from a habitat Hj is proportional to the emigration rate μi. After modification of each nonelite habitat using the migration operation, each HSI is recomputed.
Update the species count probability within the habitat according to (2). The mutation operation is performed on each nonelite habitat, and compute each HSI value.
Go to step (3) for the next iteration. The BBO operation is terminated if the criteria are satisfied.
The BBO parameters, habitats, and HSI value evaluations for identifying the relationship between the clinicopathologic variables of breast cancer are explained in Section 2.2.4.
2.2.3. Initializing the BBO Parameters and Habitats
In this study, the BBO algorithm parameters were set as follows: habitat size = 50, number of generation = 100, maximum immigration and emigration rates for each island = 1, elite number = 2, and mutation probability = 0.04 [30].
The solution H comprises hi (i = 1 to population number) as in (7), each habitat h consists of SIVn (n = 1 to number of problem dimensions) as in (8), and each SIVn consists of a randomly generated 0 or 1 as in (9).
| (7) |
| (8) |
| (9) |
2.2.4. Evaluation of HSI Values
We use the C-statistic (or “concordance” statistic) as the HSI values in the BBO algorithm; the C-statistic value is calculated according to linear prediction estimated through Cox proportional hazard (PH) regression. The C-statistic's goodness of fit can be measured for binary outcomes in a regression model. The value of the C-statistic indicates the probability that a patient who had experienced an event had a higher mortality risk than one who had not experienced the event. C-statistics were used to test the predictive accuracy of survival models. The value of the C-statistic equals the area under the receiver operating characteristic curve. A C-statistic value of 0.5 indicates that a model predicts the outcome by chance, 0.7–0.8 indicates acceptable discrimination, 0.8–0.9 indicates excellent discrimination, 0.9–0.99 indicates outstanding discrimination, and 1.0 is perfect prediction [34].
Harrell [35] defined the C-statistic as the ratio of all sample pairs for which the predictions and real outcomes are concordant. Assume a sample data of M items is given. Let X1, X2, X3,…, XM indicate the survival times, and Y1, Y2, Y3,…, YM indicate the predicted probabilities of survival. Given that Xi ≠ Xj, each concordant pair is assigned 1 point, and each discordant pair is assigned 0 point [36].
| (10) |
Subsequently, the C-statistic is calculated using the following equation:
| (11) |
where uij is the number of all usable pairs, and U is a set of all usable pairs of participants (i, j).
2.3. Statistical Analysis
The differences in the distribution of the clinicopathologic variables between surviving and deceased participants were estimated using chi-squared tests. A univariate Cox PH regression model was used to evaluate the hazard function of each clinicopathologic variable in the overall survival of patients with breast cancer. A fully adjusted multivariate Cox PH model was used to estimate the association of all clinicopathologic variables in overall survival among patients with breast cancer. We applied the three stepwise selection Cox PH models by adjusting the selective criteria where p < 0.05, 0.1, and 0.2 for clinicopathologic variable inclusion. By contrast, the BBO–Cox PH model included only the clinicopathologic variables selected using the BBO algorithm. The performance of each Cox PH multivariate model was determined using the C-statistics value. The hazard ratio (HR), 95% confidence interval (95% CI), and p-value were computed. The overall survival function of the statistically significant variables in the selected BBO model was visualized using a Kaplan–Meier curve to establish the effects of each individual clinicopathologic variable on overall survival. The differences in overall survival function between different strata were tested using the log-rank test; p = 0.05 indicated statistical significance for all results of statistical analysis. The statistics were analyzed using SAS 9.3 software (SAS Institute Inc., Cary, NC, USA).
3. Results
3.1. Clinicopathologic Characteristics and Survival of Patients with Breast Cancer
A comparison of the clinicopathologic variables between surviving and deceased patients is presented in Table 1; it shows that 1830 (96.52%) and 66 (3.48%) of the 1896 patients with breast cancer survived and died, respectively. Compared with the survival group, a greater proportion of the death group was HER2 positive (p = 0.040), ER positive (p < 0.001), PR positive (p = 0.001), with tumor size ≥ 2.0 cm (p < 0.001), lymph node positive (p < 0.001), LVI positive (p < 0.001), with dermal invasion (p = 0.009), with perineural invasion (p < 0.001), with total mastectomy (p < 0.001), without chemotherapy treatment (p = 0.004), and without hormone therapy (p < 0.001).
Table 1.
Comparison of clinicopathologic variables between the surviving and deceased patients.
| Variable | Total | Survival | Expired | p-value∗ | |||
|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | ||
| Age (years) | 0.123 | ||||||
| ≤ 50 | 719 | 37.92 | 688 | 37.60 | 31 | 46.97 | |
| > 50 | 1177 | 62.08 | 1142 | 62.40 | 35 | 53.03 | |
| Grade | 0.122 | ||||||
| I, II | 1286 | 67.83 | 1247 | 68.14 | 39 | 59.09 | |
| III | 610 | 32.17 | 583 | 31.86 | 27 | 40.91 | |
| Her 2 | 0.040 | ||||||
| Negative | 1230 | 64.87 | 1195 | 65.30 | 35 | 65.30 | |
| Positive | 666 | 35.13 | 635 | 34.70 | 31 | 46.97 | |
| Estrogen receptor | <0.001 | ||||||
| Negative | 510 | 26.90 | 476 | 26.01 | 34 | 51.52 | |
| Positive | 1386 | 73.10 | 1354 | 73.99 | 32 | 48.48 | |
| Progesterone receptor | 0.001 | ||||||
| Negative | 701 | 36.97 | 664 | 36.28 | 37 | 56.06 | |
| Positive | 1195 | 63.03 | 1166 | 63.72 | 29 | 43.94 | |
| Tumor size (AJCC stage) | <0.001 | ||||||
| ≤ 2 cm | 1161 | 61.23 | 1142 | 62.40 | 19 | 28.79 | |
| > 2 cm | 735 | 38.77 | 688 | 37.60 | 47 | 71.21 | |
| Lymph node (AJCC stage) | <0.001 | ||||||
| Negative | 1265 | 33.72 | 1240 | 67.67 | 25 | 37.88 | |
| Positive | 631 | 33.28 | 590 | 32.24 | 41 | 62.12 | |
| Lymphovascular invasion | <0.001 | ||||||
| Negative | 1326 | 69.94 | 1293 | 70.66 | 33 | 50.00 | |
| Positive | 570 | 30.06 | 537 | 29.34 | 33 | 50.00 | |
| Dermal invasion | 0.009 | ||||||
| Negative | 1798 | 94.83 | 1740 | 95.08 | 58 | 87.88 | |
| Positive | 98 | 5.17 | 90 | 4.92 | 8 | 12.12 | |
| Perineural invasion | <0.001 | ||||||
| Negative | 1659 | 87.5 | 1610 | 87.98 | 49 | 74.24 | |
| Positive | 237 | 12.50 | 220 | 12.02 | 17 | 25.76 | |
| Surgery method | <0.001 | ||||||
| Partial mastectomy | 1133 | 59.76 | 1113 | 60.82 | 20 | 30.30 | |
| Total mastectomy | 763 | 40.24 | 717 | 39.18 | 46 | 69.70 | |
| Radiotherapy (RT) | 0.050 | ||||||
| With RT | 1194 | 62.97 | 1160 | 63.39 | 34 | 51.52 | |
| Without RT | 702 | 37.03 | 670 | 36.61 | 32 | 48.48 | |
| Chemotherapy | 0.004 | ||||||
| With CT | 1140 | 60.13 | 1089 | 59.51 | 51 | 77.27 | |
| Without CT | 756 | 39.87 | 741 | 40.49 | 15 | 22.73 | |
| Hormone therapy | <0.001 | ||||||
| With HT | 1265 | 69.13 | 28 | 42.42 | 1265 | 69.13 | |
| Without HT | 565 | 30.87 | 38 | 57.58 | 565 | 30.87 | |
| Target therapy | 0.232 | ||||||
| With TT | 302 | 15.93 | 288 | 15.74 | 14 | 21.21 | |
| Without TT | 1594 | 84.07 | 1542 | 84.26 | 52 | 78.79 | |
∗ p-value is estimated using the chi-squared test.
HER2: human epidermal growth factor receptor 2.
3.2. Univariate Clinicopathologic Variables
The 15 clinicopathologic variables included age, grade, tumor size, ER, PR, HER2, lymph node, LVI, dermal invasion, perineural invasion, surgery method, radiotherapy, chemotherapy, hormone therapy, and target therapy. Each clinicopathologic variable is dichotomized into low- and high-risk characteristics in Table 2, which lists the clinical characteristics for low- and high-risk breast cancer progression; these characteristics were identical to those used in previous studies. The univariate Cox regression analysis of the clinicopathologic variables in overall survival of patients with breast cancer is presented in Table 2. Grade (HR = 2.169, p = 0.002), ER (HR = 0.4, p < 0.001), PR (HR 0.494, p = 0.005), tumor size (HR = 4.362, p < 0.001), lymph node (HR = 2.689, p < 0.001), LVI (HR = 2.960, p < 0.001), dermal invasion (HR = 3.060, p = 0.003), perineural invasion (HR = 2.558, p < 0.001), surgical method (HR = 2.981, p < 0.001 ), and hormone therapy (HR = 2.666, p < 0.001) were significantly associated with breast cancer progression, including mortality and disease progression.
Table 2.
Univariate Cox regression analysis of clinicopathologic variables in breast cancer overall survival.
| Variable | Comparison | Univariate | |||
|---|---|---|---|---|---|
| HR | 95% CI | p-value∗ | |||
| Age | >50 years | ≤50 years | 0.789 | 0.486-1.281 | 0.338 |
| Grade | III | I, II | 2.169 | 1.332-3.558 | 0.002 |
| HER 2 | Positive | Negative | 1.036 | 0.638-1.683 | 0.887 |
| Estrogen receptor | Positive | Negative | 0.400 | 0.246-0.650 | <0.001 |
| Progesterone receptor | Positive | Negative | 0.494 | 0.304-0.804 | 0.005 |
| Tumor size (AJCC stage) | ≥ 2.4 cm | < 2.4 cm | 4.362 | 2.556-7.448 | <0.001 |
| Lymph node (AJCC stage) | Positive | Negative | 2.689 | 1.631-4.434 | <0.001 |
| Lymphovascular invasion | Positive | Negative | 2.960 | 1.825-4.801 | <0.001 |
| Dermal invasion | Positive | Negative | 3.060 | 1.453-6.445 | 0.003 |
| Perineural invasion | Yes | No | 2.558 | 1.473-4.444 | <0.001 |
| Surgery method | Total mastectomy | Partial mastectomy | 2.981 | 1.761-5.047 | <0.001 |
| Radiotherapy (RT) | Without RT | With RT | 1.446 | 0.891-2.348 | 0.135 |
| Chemotherapy (CT) | Without CT | With CT | 0.782 | 0.438-1.397 | 0.406 |
| Hormone therapy (HT) | Without HT | With HT | 2.666 | 1.636-4.345 | <0.001 |
| Target therapy (TT) | Without TT | With TT | 0.779 | 0.432-1.704 | 0.409 |
∗p-value is estimated using the Cox PH regression.
HR: hazard ratio; HER2: human epidermal growth factor receptor 2.
3.3. Multivariate Clinicopathologic Variables
We compared the fully adjusted Cox PH model, three stepwise selection Cox PH models with different p-value inclusion levels (0.05, 0.1, and 0.2), and BBO–Cox PH model. The performance of each model is summarized in Table 3. The fully adjusted Cox PH model included all 15 clinicopathologic variables. The fully adjusted Cox PH model indicated that older age (adjusted HR = 0.515, p = 0.015) was correlated with a high risk of mortality for patients with breast cancer, whereas tumor sizes greater than 2 cm (adjusted HR = 2.430, p = 0.005) and LVI (adjusted HR = 1.776, p = 0.046) were significantly correlated with a high risk of breast cancer progression.
Table 3.
Multivariate Cox regression analysis of clinicopathologic variables in breast cancer overall survival.
| Variable | Comparison | Fully adjusted | Stepwise selected | BBO selected | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 11 | Model 22 | Model 33 | ||||||||||
| C-statistic | 76% | 78% | 78% | 77% | 80% | |||||||
| p-value∗ | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |||||||
|
| ||||||||||||
| HR | p-value∗ | HR | p-value∗ | HR | p-value∗ | HR | p-value∗ | HR | p-value∗ | |||
|
| ||||||||||||
| Age | >50 years | ≤50 years | 0.515 | 0.015 | 0.589 | 0.036 | 0.523 | 0.003 | ||||
| Grade | III | I, II | 1.524 | 0.132 | 1.830 | 0.026 | 1.642 | 0.073 | ||||
| Her 2 | Positive | Negative | 0.103 | 0.103 | ||||||||
| Estrogen receptor | Positive | Negative | 0.506 | 0.195 | 0.451 | 0.003 | ||||||
| Progesterone receptor | Positive | Negative | 0.801 | 0.595 | ||||||||
| Tumor size (AJCC stage) | ≥ 2.4 cm | < 2.4 cm | 2.430 | 0.005 | 3.017 | <0.001 | 2.435 | 0.004 | 2.436 | 0.004 | 2.372 | 0.006 |
| Lymph node (AJCC stage) | Positive | Negative | 1.511 | 0.103 | 1.301 | 0.038 | ||||||
| Lymphovascular invasion | Positive | Negative | 1.776 | 0.046 | 1.878 | 0.016 | 1.642 | 0.068 | 1.753 | 0.038 | 1.606 | 0.096 |
| Dermal invasion | Positive | Negative | 1.549 | 0.298 | 2.152 | 0.048 | 1.722 | 0.188 | 1.548 | 0.028 | ||
| Perineural invasion | Yes | No | 1.745 | 0.081 | 1.994 | 0.028 | 1.827 | 0.060 | 1.546 | 0.168 | ||
| Surgery method | Total mastectomy | Partial mastectomy | 1.735 | 0.087 | 1.869 | 0.031 | 1.848 | 0.066 | 1.633 | 0.092 | ||
| Radiotherapy | Without RT | With RT | 1.299 | 0.378 | ||||||||
| Chemotherapy | Without CT | With CT | 1.338 | 0.379 | 1.234 | 0.491 | ||||||
| Hormone therapy | Without HT | With HT | 1.022 | 0.962 | 2.231 | 0.002 | 1.918 | 0.014 | 2.178 | 0.003 | ||
| Target therapy | Without TT | With TT | 0.859 | 0.697 | ||||||||
1Stepwise selection met the p = 0.05 level for entry into the model; 2 Stepwise selection met the p = 0.1 level for entry into the model; 3 Stepwise selection met the p = 0.2 level for entry into the model.
∗p-value is estimated using Cox PH regression.
HR: hazard ratio; HER2: human epidermal growth factor receptor 2.
In the stepwise selection Cox PH model with inclusion at p = 0.05, tumor sizes greater than 2 cm (adjusted HR = 3.017, p < 0.005), LVI (adjusted HR = 1.878, p = 0.016), dermal invasion (adjusted HR = 2.152, p = 0.048), and without hormone therapy (adjusted HR = 2.231, p = 0.002) were significantly correlated with a high risk of breast cancer progression. In the stepwise selection Cox PH model with inclusion at p = 0.1, older age (adjusted HR = 0.589, p = 0.036) was correlated with a high risk of mortality for patients with breast cancer, whereas grade III (adjusted HR = 1.830, p = 0.026), tumor sizes greater than 2 cm (adjusted HR = 2.435, p = 0.004), perineural invasion (adjusted HR = 1.994, p = 0.028), total mastectomy (adjusted HR 1.869, p = 0.031), and without hormone therapy (adjusted HR = 1.918, p = 0.014) were significantly correlated with a high risk of breast cancer progression. In the stepwise selection Cox PH model with inclusion at p = 0.2, age (adjusted HR = 0.523, p = 0.003), PR (adjusted HR = 0.451, p = 0.003), tumor size (adjusted HR = 2.436, p = 0.004), and LVI (adjusted HR = 1.753, p = 0.038) were significantly correlated with breast cancer progression.
The BBO–Cox PH model included tumor size, lymph node, dermal invasion, surgery method, chemotherapy, and hormone therapy as breast cancer progression predictors. Tumor sizes greater than 2 cm (HR = 2.372, p = 0.006), lymph node metastasis (HR = 1.301, p = 0.038), dermal invasion (HR = 1.548, p = 0.028), and without hormone therapy (HR = 1.178, p = 0.003) were significantly correlated with breast cancer progression.
The C-statistic values were 76%, 78%, 78%,77%, and 80% in the fully adjusted Cox PH model, three stepwise selection Cox PH (with inclusion at p = 0.05, 0.1, and 0.2) models, and BBO–Cox PH model, respectively. The BBO–Cox PH model obtained the highest C-statistic value of all the models, which indicated higher concordance for predicting the overall survival of patients with breast cancer.
We present the survival curves of various clinicopathologic characteristic categories using Kaplan–Meier method. The difference between each clinicopathologic variable in the survival curves was estimated using the log-rank test. The BBO–Cox PH model included tumor size, lymph node, dermal invasion, surgery method, chemotherapy, and hormone therapy as breast cancer progression predictors, and the results revealed that all BBO-selected clinicopathologic variables were statistically significant in different categories within each individual clinicopathologic variable. The Kaplan–Meier curves are presented in Figure 2.
Figure 2.
Kaplan–Meier curve of BBO-selected clinicopathologic variables including (a) tumor size, (b) lymph node status, (c) lymphovascular invasion status, (d) dermal invasion status, (e) perineural invasion status, (f) surgical methods, (g) chemotherapy status, and (h) hormone therapy status.
4. Discussion
Overfitting is a limitation that must be faced for conventional statistical approaches, such as regression models. The principal reason is that regression-based selection approaches provide analysis results that depend mainly on the distribution of a population in associated variables. BBO is similar to evolutionary algorithms, such as the genetic algorithm (GA) [37] and particle swarm optimization (PSO) [38]. GA, PSO, and BBO are all inspired by nature and perform information sharing between solutions (i.e., genes for GA, particles for PSO, and habitats for BBO) [39]. A GA solution will “die” at the end of each generation, and PSO and BBO solutions will continue to exist as the optimization process progresses. PSO solutions tend to be clustered together in similar groups, whereas GA and BBO solutions do not necessarily have any clustering tendencies. BBO has unique features, and a BBO solution shares its content (SIV) directly with other solutions. This feature leads to BBO having better performance than GA and PSO in optimization problems [39]. BBO has been successfully applied to several engineering problems, including global benchmark functions and economic load scheduling [33]. In this study, BBO was successfully applied to select clinicopathologic variables that resulted in superior performance compared with other Cox regression models (i.e., the fully adjusted Cox regression model and three stepwise-selected Cox regression models). BBO is a mechanism of the Cox regression model that improves the ability to explore C-statistics and variables. By using BBO, the migration operator shared more accurate information than with other solutions, and including randomization for the mutation operator at the mutation stage partly resolved the overfitting problem.
The BBO-selected model included tumor size, lymph node metastasis, lymphovascular invasion, perineural invasion, dermal invasion, surgery method, hormone therapy, and chemotherapy as predictors for the overall survival of patients with breast cancer. This optimization model obtained superior prediction results and concordance compared with the fully adjusted Cox PH model in the assessment of C-statistics. The fact that the BBO algorithm considers the internal relationship between clinicopathologic variables may explain why it increases the discriminant ability of the final BBO model.
In addition, we reevaluated the individual HR for each selected variable in the BBO model through multivariate Cox PH regression analysis. The results revealed that not all of the selected variables provided a significant individual HR in the Cox PH model. Only tumor size, lymph node metastasis, dermal invasion, and hormone therapy had a significant correlation with the overall survival of patients with breast cancer. These factors had been previously reported as associated with the overall survival of patients with breast cancer.
Tumor size and lymph node are frequently used to predict the overall survival and prognosis of patients with breast cancer [40]. The NPI index is a benchmark for breast cancer prognoses that includes these two main factors [13, 41]. The extended use of the NPI index for various breast cancer prognostic purposes remained contributed and widespread in recent studies such as including the hormone status (ER, PR, and Her2) [42–44]. Dermal invasion, also known as dermal lymphatic invasion, is generally associated with inflammatory breast cancer [45]. Breast cancer characterized by dermal invasion is generally correlated with inferior overall survival. Hormone therapy is an effective therapy for hormone-positive patients with breast cancer [46]. Therefore, the decision to commence hormone treatment mainly relies on the ER and PR status of patients with breast cancer. Although ER and PR were not included in the BBO-selected model, hormone therapy (an effective treatment options for patients with ER positive or PR positive breast cancer) could partially explain the beneficial effect of ER and PR positive case with hormone therapy in breast cancer overall survival. However, the retrospective nature of our study might have limited the analysis of various covariates that have been previously reported as correlated with overall breast cancer survival rates.
5. Conclusion
This study used the BBO algorithm to search for combinations of clinicopathologic variables that can facilitate prediction of the overall survival of patients with breast cancer. Compared with the fully adjusted multivariate Cox regression model and stepwise selection Cox regression model, the BBO-selected model had a higher C-statistic value for predicting overall survival. This study determined that the BBO algorithm could select only 8 variables from 15 clinicopathologic variables, which is the minimum number of discriminators required for optimal discriminant effectiveness when predicting the overall survival of patients with breast cancer accurately and with concordance. This model may have vital implications for the selection of clinicopathologic variables for breast cancer.
Acknowledgments
This work was partly supported by the Ministry of Science and Technology (105-2221-E-151-053-MY2, 107-2811-E-992-500-, 105-2314-B-037-038-MY3, and 105-2314-B-037-037-MY3), Taiwan.
Contributor Information
Ming-Feng Hou, Email: mifeho@kmu.edu.tw.
Cheng-Hong Yang, Email: chyang@cc.kuas.edu.tw.
Data Availability
The data used to support the findings of this study have not been made available because of the institution regulation.
Conflicts of Interest
The authors declare that they have no competing interests or other financial motivations.
References
- 1.Health Promotion Administration M. o. H. a. W. Cancer registry annual report, 2015. 2017.
- 2.Jemal A., Bray F., Center M. M., Ferlay J., Ward E., Forman D. Global cancer statistics. CA: A Cancer Journal for Clinicians. 2011;61(2):69–90. doi: 10.3322/caac.20107. [DOI] [PubMed] [Google Scholar]
- 3.Bundred N. J. Prognostic and predictive factors in breast cancer. Cancer Treatment Reviews. 2001;27(3):137–142. doi: 10.1053/ctrv.2000.0207. [DOI] [PubMed] [Google Scholar]
- 4.Fu O. Y., Lin Y. D., Chuang L. Y., Chang H. W., Yang C. H., Hou M. F. The combinational polymorphisms of ORAI1 gene are associated with preventive models of breast cancer in the Taiwanese. Biomed Research International. 2015;2015:7. doi: 10.1155/2015/281263.281263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chuang L.-Y., Lin Y.-D., Chang H.-W., Yang C.-H. An improved PSO algorithm for generating protective SNP barcodes in breast cancer. PLoS ONE. 2012;7(5) doi: 10.1371/journal.pone.0037018.e37018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chang W.-C., Fang Y.-Y., Chang H.-W., et al. Identifying association model for single-nucleotide polymorphisms of ORAI1 gene for breast cancer. Cancer Cell International. 2014;14(1, article 29) doi: 10.1186/1475-2867-14-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yang C.-H., Lin Y.-D., Chuang L.-Y., Chang H.-W. Double-bottom chaotic map particle swarm optimization based on chi-square test to determine gene-gene interactions. BioMed Research International. 2014;2014:10. doi: 10.1155/2014/172049.172049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang C.-H., Lin Y.-D., Chuang L.-Y., Chang H.-W. Evaluation of breast cancer susceptibility using improved genetic algorithms to generate genotype SNP barcodes. IEEE Transactions on Computational Biology and Bioinformatics. 2013;10(2):361–371. doi: 10.1109/tcbb.2013.27. [DOI] [PubMed] [Google Scholar]
- 9.Fu O.-Y., Chang H.-W., Lin Y.-D., Chuang L.-Y., Hou M.-F., Yang C.-H. Breast cancer-associated high-order SNP-SNP interaction of CXCL12/CXCR4-related genes by an improved multifactor dimensionality reduction (MDR-ER) Oncology Reports. 2016;36(3):1739–1747. doi: 10.3892/or.2016.4956. [DOI] [PubMed] [Google Scholar]
- 10.Decker T., Hungermann D., Böcker W. Prognostische und prädiktive Faktoren invasiver Mammakarzinome. Der Pathologe. 2009;30(1):49–55. doi: 10.1007/s00292-008-1105-0. [DOI] [PubMed] [Google Scholar]
- 11.Ibrahim E. M., Al-Foheidi M. E., Al-Mansour M. M., Kazkaz G. A. The prognostic value of tumor-infiltrating lymphocytes in triple-negative breast cancer: a meta-analysis. Breast Cancer Research and Treatment. 2014;148(3):467–476. doi: 10.1007/s10549-014-3185-2. [DOI] [PubMed] [Google Scholar]
- 12.Stevens K. N., Vachon C. M., Couch F. J. Genetic susceptibility to triple-negative breast cancer. Cancer Research. 2013;73(7):2025–2030. doi: 10.1158/0008-5472.can-12-1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Anderson T. J. Breast cancer prognostication in the 21st century and the Nottingham prognostic index. Journal of Clinical Pathology. 2002;55(2):86–87. doi: 10.1136/jcp.55.2.86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fong Y., Evans J., Brook D., Kenkre J., Jarvis P., Gower-Thomas K. The nottingham prognostic index: five- and ten-year data for all-cause survival within a screened population. Annals of the Royal College of Surgeons of England. 2015;97(2):137–139. doi: 10.1308/003588414X14055925060514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jimenez-Lee R., Ham B., Vetto J., Pommier R. Breast cancer severity score is an innovative system for prognosis. The American Journal of Surgery. 2003;186(4):404–408. doi: 10.1016/S0002-9610(03)00283-6. [DOI] [PubMed] [Google Scholar]
- 16.Brandt J., Garne J., Tengrup I., Manjer J. Age at diagnosis in relation to survival following breast cancer: a cohort study. World Journal of Surgical Oncology. 2015;13(1):p. 33. doi: 10.1186/s12957-014-0429-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Partridge A. H., Hughes M. E., Ottesen R. A., et al. The effect of age on delay in diagnosis and stage of breast cancer. The Oncologist. 2012;17(6):775–782. doi: 10.1634/theoncologist.2011-0469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Purushotham A., Shamil E., Cariati M., et al. Age at diagnosis and distant metastasis in breast cancer - a surprising inverse relationship. European Journal of Cancer. 2014;50(10):1697–1705. doi: 10.1016/j.ejca.2014.04.002. [DOI] [PubMed] [Google Scholar]
- 19.Yu X., Zhou S., Wang J., et al. Hormone replacement therapy and breast cancer survival: a systematic review and meta-analysis of observational studies. Breast Cancer. 2017;24(5):643–657. doi: 10.1007/s12282-017-0789-5. [DOI] [PubMed] [Google Scholar]
- 20.Inwald E. C., Ortmann O., Zeman F., et al. Guideline concordant therapy prolongs survival in HER2-positive breast cancer patients: results from a large population-based cohort of a cancer registry. BioMed Research International. 2014;2014:10. doi: 10.1155/2014/137304.137304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Makanjuola S. B. L., Popoola A. O., Oludara M. A. Radiation therapy: a major factor in the five-year survival analysis of women with breast cancer in Lagos, Nigeria. Radiotherapy & Oncology. 2014;111(2):321–326. doi: 10.1016/j.radonc.2014.03.013. [DOI] [PubMed] [Google Scholar]
- 22.Chang B., Sokhn J., James E., Abu-Khalaf M. Prolonged progression-free survival in a patient with triple-negative breast cancer metastatic to the liver after chemotherapy and local radiation therapy. Clinical Breast Cancer. 2014;14(2):e61–e64. doi: 10.1016/j.clbc.2013.11.007. [DOI] [PubMed] [Google Scholar]
- 23.Sofi A. A., Mohamed I., Koumaya M., Kamaluddin Z. Local therapy in metastatic breast cancer is associated with improved survival. American Journal of Therapeutics. 2013;20(5):487–492. doi: 10.1097/MJT.0b013e31822119c5. [DOI] [PubMed] [Google Scholar]
- 24.Ritchie M. D., Hahn L. W., Roodi N., et al. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. American Journal of Human Genetics. 2001;69(1):138–147. doi: 10.1086/321276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Montazeri M., Montazeri M., Montazeri M., Beigzadeh A. Machine learning models in breast cancer survival prediction. Technology and Health Care. 2016;24(1):31–42. doi: 10.3233/THC-151071. [DOI] [PubMed] [Google Scholar]
- 26.Vanneschi L., Farinaccio A., Mauri G., Antoniotti M., Provero P., Giacobini M. A comparison of machine learning techniques for survival prediction in breast cancer. BioData Mining. 2011;4(12) doi: 10.1186/1756-0381-4-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Modiri A., Kiasaleh K. Permittivity estimation for breast cancer detection using particle swarm optimization algorithm. Proceedings of the 2011 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society; August 2011; Boston, Mass, USA. pp. 1359–1362. [DOI] [PubMed] [Google Scholar]
- 28.Simon D. Biogeography-based optimization. IEEE Transactions on Evolutionary Computation. 2008;12(6):702–713. doi: 10.1109/TEVC.2008.919004. [DOI] [Google Scholar]
- 29.Christy A. A., Raj P. A. D. V. Adaptive biogeography based predator-prey optimization technique for optimal power flow. International Journal of Electrical Power & Energy Systems. 2014;62:344–352. doi: 10.1016/j.ijepes.2014.04.054. [DOI] [Google Scholar]
- 30.Ma H., Simon D. Blended biogeography-based optimization for constrained optimization. Engineering Applications of Artificial Intelligence. 2011;24(3):517–525. doi: 10.1016/j.engappai.2010.08.005. [DOI] [Google Scholar]
- 31.Zheng Y.-J., Ling H.-F., Wu X.-B., Xue J.-Y. Localized biogeography-based optimization. Soft Computing. 2014;18(11):2323–2334. doi: 10.1007/s00500-013-1209-1. [DOI] [Google Scholar]
- 32.Zheng Y.-J., Ling H.-F., Xue J.-Y. Ecogeography-based optimization: enhancing biogeography-based optimization with ecogeographic barriers and differentiations. Computers & Operations Research. 2014;50:115–127. doi: 10.1016/j.cor.2014.04.013. [DOI] [Google Scholar]
- 33.Ma H. P., Simon D., Siarry P., Fei M. R. Biogeography-based optimization: a 10-year review. IEEE Transactions on Emerging Topic in Computational Intelligence. 2017;1(5):391–407. doi: 10.1109/TETCI.2017.2739124. [DOI] [Google Scholar]
- 34.Hosmer Jr. D. W., Lemeshow S., Sturdivant R. X. Applied Logistic Regression. John Wiley & Sons; 2013. [Google Scholar]
- 35.Harrell F. E., Jr., Lee K. L., Mark D. B. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Statistics in Medicine. 1996;15(4):361–387. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 36.Pencina M. J., Agostino R. B. Overall C as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Statistics in Medicine. 2004;23(13):2109–2123. doi: 10.1002/sim.1802. [DOI] [PubMed] [Google Scholar]
- 37.Holland J. H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. MIT Press; 1992. [Google Scholar]
- 38.Eberhart R. C., Kennedy J. A new optimizer using particle swarm theory. Proceedings of the 6th International Symposium on Micromachine and Human Science; October 1995; Nagoya, Japan. pp. 39–43. [Google Scholar]
- 39.Hordri N., Yuhaniz S., Nasien D. A comparison study of biogeography based optimization for optimization problems. International Journal of Advances in Soft Computing and its Applications. 2013;5:1–16. [Google Scholar]
- 40.Cortesi L., Marcheselli L., Guarneri V., et al. Tumor size, node status, grading, HER2 and estrogen receptor status still retain a strong value in patients with operable breast cancer diagnosed in recent years. International Journal of Cancer. 2013;132(2):E58–E65. doi: 10.1002/ijc.27795. [DOI] [PubMed] [Google Scholar]
- 41.Lee A. H., Ellis I. O. The nottingham prognostic index for invasive carcinoma of the breast. Pathology & Oncology Research. 2008;14(2):113–115. doi: 10.1007/s12253-008-9067-3. [DOI] [PubMed] [Google Scholar]
- 42.Winzer K.-J., Buchholz A., Schumacher M., Sauerbrei W. Improving the prognostic ability through better use of standard clinical data - the nottingham prognostic index as an example. PLoS ONE. 2016;11(3) doi: 10.1371/journal.pone.0149977.e0149977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhen H., Yang L., Li L., et al. Correlation analysis between molecular subtypes and nottingham prognostic index in breast cancer. Oncotarget. 2017;8(43):74096–74105. doi: 10.18632/oncotarget.18242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kwon J., Eom K.-Y., Koo T. R., et al. A prognostic model for patients with triple-negative breast cancer: importance of the modified nottingham prognostic index and age. Journal of Breast Cancer. 2017;20(1):65–73. doi: 10.4048/jbc.2017.20.1.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Abramowitz M. C., Li T., Morrow M., et al. Dermal lymphatic invasion and inflammatory breast cancer are independent predictors of outcome after postmastectomy radiation. American Journal of Clinical Oncology. 2009;32(1):30–33. doi: 10.1097/COC.0b013e31817b6073. [DOI] [PubMed] [Google Scholar]
- 46.Reinert T., Barrios C. H. Overall survival and progression-free survival with endocrine therapy for hormone receptor-positive, HER2-negative advanced breast cancer: review. Therapeutic Advances in Medical Oncology. 2017;9(11):693–709. doi: 10.1177/1758834017728928. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used to support the findings of this study have not been made available because of the institution regulation.