Dynamic magnetic characterization and magnetic particle imaging enhancement of magnetic-gold core-shell nanoparticles

Abstract

Multi-functional nanoparticles with a magnetic core and gold shell structures are emerging multi-modal imaging probes for disease diagnosis, image-guided therapy, and theranostic applications. Owing to their multi-functional magnetic and plasmonic properties, these nanoparticles can be used as contrast agents in multiple complementary imaging modalities. Magnetic particle imaging (MPI) is a new pre-clinical imaging system that enables real-time imaging with high sensitivity and spatial resolution by detecting the dynamic responses of nanoparticle tracers. In this study, we evaluated dynamic magnetic properties and MPI imaging performances of core-shell nanoparticles with magnetic core coated with gold shell. A change in AC hysteresis loops was detected before and after the formation of gold shell on magnetic core nanoparticles, suggesting the influence of core-shell interfacial effect on their dynamic magnetic properties. This alteration in the dynamic responses resulted in an enhancement of MPI imaging capacity of magnetic nanoparticles. The gold shell coating also enabled a simple and effective functionalization of the nanoparticles with a brain glioma targeting ligand. The enhanced MPI imaging capacity and effective functionality suggest the potential application of the magnetic-gold core-shell nanoparticles for MPI disease diagnostics.

Introduction

Multifunctional core-shell nanoparticles are emerging nanomaterials with a wide range of applications in various fields such as biomedical, catalysis, and electronics.¹ They possess multiple characteristics including magnetic, electric, and plasmonic properties assembled in a single nanostructure, which make them potential candidates for various biomedical applications. The versatility of such multi-functional core-shell nanoparticles has rapidly expanded the scope of their applications in molecular imaging, image-guided therapy, and theranostics which offers precise and effective treatment by combining therapeutic and diagnostic approaches.^2,3 Among various nanoparticles, core-shell nanoparticles composed of magnetic nanoparticle core capped with gold shell (MNP@Au) play a key role due to the combination of magnetic and plasmonic features, biocompatibility, and great surface reactivity.⁴ MNP@Au based contrast agents are promising for multi-modal imaging systems including magnetic resonance imaging (MRI), magnetic particle imaging (MPI), X-ray computed tomography (CT), and photoacoustic imaging (PAI).^5,6 By incorporating multiple imaging modalities in a single nanoparticle system, multi-modal imaging allows more precise and reliable diagnostics for various diseases.^7,8 Moreover, image-guided therapies such as image-guided drug delivery and hyperthermia have shown potential for more effective and accurate treatment.^9,10

MPI is a new imaging modality which detects magnetic nanoparticles (MNPs) with high image contrasts and sensitivities.^11,12,13 Compared to MRI which generates contrasts based on the relaxation of hydrogen protons and utilizes MNPs contrast agents to perturb the spin relaxation, MPI directly detects non-linear magnetization responses of MNPs. Under a time-varying magnetic field (i.e. drive field), MNPs produce an inductive signals in the receiver coils based on their non-linear magnetization properties.^14,15 An additional static field (selection field) provides a single field-free point (FFP) with zero magnetic field, while the field is non-zero outside of FFP.¹⁶ The magnetization of MNPs easily aligns with the drive field and produces a signal within FFP. In contrast, the magnetization of MNPs is saturated outside of FFP, and they do not produce any signal. Therefore, the signal localization is achieved by scanning over the entire object using FFP. Since surrounding tissues are diamagnetic, there is no background contrasts from anatomical structures. Moreover, MPI signal is linearly dependent on concentration of MNPs, which allows quantitative and real-time imaging.^17,13

Owing to its detection principle, MPI imaging performance is highly dependent on dynamic magnetic responses of MNPs-based MPI tracers.^18,13 It is well known that dynamic magnetic properties of MNPs differ from static magnetic responses primarily due to the phase delay of magnetization under a time-varying magnetic field. This phase delay is associated with relaxation mechanisms of MNPs, Néel relaxation and Brownian relaxation.¹⁹ Néel relaxation is contributed by the rotation of internal magnetic moment, whereas Brownian relaxation is contributed by the rotation of magnetic moment along with the rotation of the entire particle. Since magnetic relaxation is affected by physical parameters of MNPs including particle size and magnetic anisotropy as well as particle interactions such as dipole–dipole interaction, it is critical to understand the relaxation mechanism of MNPs-based MPI tracers. Previously, our group developed magnetic core-gold shell magneto-plasmonic nanoparticles for multi-modal imaging and image-guided drug delivery.^5,6 However, the effect of gold shell on dynamic magnetic properties and MPI imaging performances has not been explored. In this study, we investigated the dynamic magnetic properties of MNPs and MNP@Au, and evaluated the influence of gold shell on MPI imaging performance.

Experimental

Materials

Iron(III) chloride hexahydrate (ACS reagent, 97%), Iron(II) chloride tetrahydrate (ReagentPlus^®), 98%, hydrochloric acid (36.5–38.0%, BioReagent, for molecular biology), ammonium hydroxide (28% NH₃ in H₂O, ≥99.99% trace metals basis), sodium citrate dihydrate (≥99%, FG), Gold(III) chloride trihydrate (ACS reagent, ≥49.0% Au basis), holo-Transferrin, XTT sodium salt (BioReagent), and phenazine methosulfate were purchased from Sigma-Aldrich. Traut’s reagent and RIPA buffer were purchased from Thermo Fisher. Ultra Pure Agarose was purchased from Invitrogen. The human microglia cell line (CHME-5) was purchased from Applied Biological Materials.

Synthesis of MNPs and MNP@Au

Magnetic nanoparticles (MNPs) were synthesized by co-precipitation method.⁶ Briefly, Iron(III) chloride hexahydrate (FeCl₃·6H₂O) dissolved in water and Iron(II) chloride tetrahydrate (FeCl₂·4H₂O) dissolved in 2M hydrochloric acid solution with a molar ratio of 2:1 were mixed and the temperature of the solution was increased to 70 ˚C under stirring at 200 rpm. Ammonium hydroxide solution was added dropwise to the mixture solution and stirred for 30 min. After the reaction, a sodium citrate aqueous solution was added and the temperature of the solution was increased to 90 ˚C. This reaction was continued for 30 min under stirring at 400 rpm. The synthesized citrate coated MNPs were purified with water by using a centrifugal filter (Amicon Ultra-15 Centrifugal Filter, MilliporeSigma).

The synthesis method of MNP@Au nanoparticles was reported previously.^5,6 Briefly, MNPs was dispersed in 5 mM sodium citrate and sonicated using a probe sonicator at 20% amplitude. The solution was heated to boiling temperature and 85 µmol of HAuCl₄ was added. After 6 min reaction under stirring at 300 rpm, the resulting red-color nanoparticles (MNP@Au) were collected using a permanent magnet and re-dispersed into distilled water.

Characterization of MNP@Au nanoparticles

A transmission electron microscopy (TEM) image was acquired using a Phillips CM-200 200 kV transmission electron microscope operated at 80 kV. X-ray powder diffraction (XRD) patterns of MNP and MNP@Au were recorded with Bruker GADD/D8 X-Ray system with Mo anode (wavelength: 0.708 Å). The magnetization curve of MNP@Au was measured at room temperature using a vibrating sample magnetometer (VSM-3, Toei Kogyo) equipped with anelectromagnet (TEM-WFR7, Toei Kogyo) and a gaussmeter (Model 421, Lake Shore Cryotronics, Inc.). The iron and gold concentrations of MNP@Au were determined using an Inductively Couple Plasma mass spectrometer (ICP-MS, Perkin Elmer Sciex, model ELAN DRC-II). Samples were dissolved in aqua regia and diluted by deionized water prior to the measurement.

AC hysteresis measurement of MNPs and MNP@Au

AC hysteresis loops of MNPs and MNP@Au were measured using a custom-built Magnetic Particle Spectrometer (MPS) which contains a receiver coil and a cancel coil placed in an excitation coil.²⁰ The excitation coil generates an alternating magnetic field, and the time-varying magnetic response of magnetic core is measured by a receiver coil. The AC hysteresis loops were measured under an alternating magnetic field with an amplitude at 4 kA/m (5 mT) and frequencies varied from 10 to 80 kHz.

Numerical simulation

The magnetic core diameters and anisotropy constants of MNPs and MNP@Au were estimated from a numerical simulation using Landau-Lifshitz-Gilbert (LLG) equation. The differential equation of the magnetization is given by ^21,22,23:

$$\frac{d\mathbf{m}}{dt}=-\frac{\gamma }{1+{\alpha }^2}\left\{\mathbf{m}\times {\mathbf{H}}_{\text{eff}}+\alpha \mathbf{m}\times \left(\mathbf{m}\times {\mathbf{H}}_{\text{eff}}\right)\right\}$$ (1)

where m is the magnetic moment, γ is gyromagnetic ratio, α is damping parameter (α = 0.1), and H_eff is the effective field. Magnetic moment was calculated as the value normalized by saturated magnetic moment M_s. The gyromagnetic ratio is estimated as $\gamma ={\mu }_0{M}_{\text{s}}{V}_{\text{M}}\left(1+{\alpha }^2\right)/\left(2\alpha {\tau }_{\text{N}}{k}_{\text{B}}T\right)$, where μ₀ is the permeability of free space, V_M is the volume of a single-domain particle, τ_N is the Néel relaxation time, k_B is the Boltzmann constant 1.38 × 10⁻²³ J/K, and T is the temperature of 300 K. The effective field is composed of the excitation field H_ex, anisotropy field H_an, and fluctuating field H_th. The anisotropy field is estimated as $H_{\text{an}}=2K_{eff}\left(m·n\right)n/\left({\mu }_0{M}_{\text{s}}\right)$, where K_eff is the effective anisotropy constant including crystal, surface, and shape effects, and n is the unit vector of the easy axis. The fluctuating field from thermal noise satisfies the following equations:

$$\langle H_{th,i}\left(t\right)\rangle =0$$ (2)

$$\langle H_{th,i}\left(t\right)H_{th,j}\left(t\text{'}\right)\rangle =\frac{2\text{α}}{1+{\alpha }^2}\frac{k_{\text{B}}T}{\gamma {\mu }_0{M}_{\text{s}}{V}_{\text{M}}}{\delta }_{ij}\delta \left(t-t\text{'}\right)$$ (3)

where i and j are Cartesian indices of different particles. δ_ij is the Kronecker delta function, and δ is the Dirac delta function. In the numerical simulation, 28672 particles were set, and the saturation magnetic moment of the experimental values was applied.

Magnetic particle imaging

MPI images of MNPs and MNP@Au were acquired with the projection Field Free Line (FFL) Momentum MPI scanner (Magnetic Insight Co.). An aqueous solution of nanoparticles (100 μl) was placed into a polymerization chain reaction (PCR) tube and fixed with 1 wt% agar. The MPI scanner was operated with a magnetic field gradient strength of 6, 6, and 6 T/m along x-, y- and z-axes of the instrument with an excitation field of peak amplitude 20 mT at 45 kHz along z-axis. Overlap fraction and harmonic bandwidth were 90% and 1000 kHz. 2D images were captured with a field of view (FOV) of 6 × 8 cm² and acquisition time of 10 seconds per projection.

Functionalization of MNP@Au and in vitro study

Transferrin was conjugated on MNP@Au using Traut’s reagent. Briefly, Traut’s reagent (17.2 µg) was added to 1 mg transferrin in PBS and mixed for 1h. The resulting thiolated transferrin was mixed with MNP@Au with weight ratios of 1:50 in 10 mM HEPES buffer overnight at room temperature. Un-conjugated transferrin was removed using a centrifuge and transferrin-conjugated MNP@Au (Tf-MNP@Au) was re-dispersed in 10 mM HEPES buffer. The conjugation efficiency was evaluated by measuring the concentration of un-conjugated transferrin in the supernatant using Bradford assay. The hydrodynamic sizes and zeta potentials of MNP@Au and Tf-MNP@Au were measured using a Zetasizer Nano-ZS (Malvern instruments). 10 μl of nanoparticles were dispersed in 1 ml PBS, and experiments were performed in duplicate.

The cytotoxicity study of Tf-MNP@Au was conducted on a human microglia cell line (CHME-5) using XTT assay. Cells were seeded in 96-well cell culture plates at a density of 4×10⁴ cells/well. After 24h of incubation at 37 °C, the medium was replaced with 100 μl of fresh medium containing Tf-MNP@Au with a concentration of 1‒50 μg/ml. After 24h and 48h incubation, cells were washed with PBS and 100 μl of fresh medium was added. A mixture solution of XTT and phenazine methosulfate (PMS) was added to each well and incubated at 37 °C for 2h. Absorbance was measured at 450 nm using a microplate reader (Synergy HT, multi-mode microplate reader, BioTek). Experiments were performed in quadruplicate (N=2). The results are represented as the mean ± standard deviation. Statistical analysis was performed using one-way analysis of variance (ANOVA) and difference was considered significant at P<0.05.

Results and discussion

Characterization of MNPs and MNP@Au

MNPs coated with sodium citrate were synthesized by co-precipitation method and followed by gold coating to form magnetic core and gold shell structure (MNP@Au).⁶ Successful gold shell coating on MNPs was confirmed through TEM images and X-ray diffractions. A TEM image of MNP@Au in Figure 1 (a) shows sphere morphology and the average particle size of 30.6 nm. The nanoparticles with weaker contrasts and small sizes show the existence of uncoated MNPs. Figure 1 (b) shows X-ray diffraction patterns of MNPs and MNP@Au. The peaks from MNPs were indexed to the (2 2 0), (3 1 1), (4 0 0), (4 2 2), (5 1 1), (4 4 0) and (5 3 3) planes, which correspond to the inverse cubic spinel phase of Fe₃O₄. MNP@Au showed sharp peaks from gold shell which can be indexed to the (1 1 1), (2 0 0), (2 2 0), (3 1 1), and (2 2 2) planes, as well as slight peaks which correspond to Fe₃O₄. The gold shell thickness of MNP@Au was calculated by applying Scherrer’s equation on the diffraction peaks.²⁴ The crystallite size d is given by

$$d=\frac{K\times \lambda }{\beta \times cos\theta }$$ (4)

where λ is the X-ray wavelength, β is the full-width at half-maximum of the X-ray diffraction peak, and K is a constant related to crystallite shape, equals to 0.90.²⁵ The size d was calculated at each peaks which correspond to the (1 1 1), (2 0 0), (2 2 0), and (3 1 1) planes, and the average shell thickness was calculated to be 8.2 nm. Based on the size of MNP@Au (30.6 nm) and gold shell thickness calculated from XRD data, it is estimated that MNPs formed a cluster with the size of 22.4 nm within a gold shell with a thickness of 8.2 nm. Figure 1 (c) shows the magnetization curves of MNPs and MNP@Au. MNPs and MNP@Au showed superparamagnetic behavior which has no coercivity or remanent magnetization at room temperature without an external magnetic field. The saturation magnetization of MNPs and MNP@Au were 84 emu/g-Fe (Am²/kg-Fe) and 72 emu/g-Fe (Am²/kg-Fe), respectively. It is known that saturation magnetization of magnetic materials is dependent on the crystal lattice.^26,27 Since lattice mismatch at the interface between MNPs and Au can cause structural strain, it is likely that the spin disorder or canting induced by the interfacial strain contributed to the reduction of the saturation magnetization after gold shell coating.²⁸

Fig. 1.

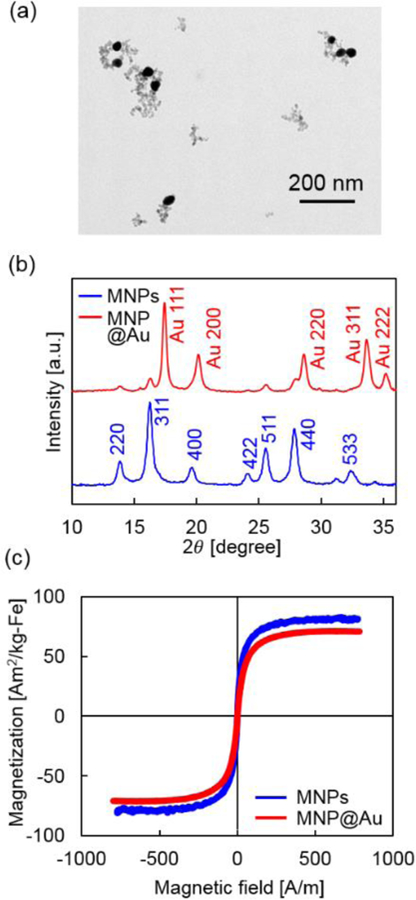
Characterization of MNP@Au. (a) A transmission electron microscopy (TEM) image of MNP@Au, (b) X-ray diffraction (XRD) patterns of MNPs and MNP@Au, and (c) magnetization curves of MNPs and MNP@Au.

Dynamic magnetic characterization of MNPs and MNP@Au

Dynamic magnetic characterization of MNPs and MNP@Au were conducted using our custom-built MPS. The dynamic response of MNPs dramatically changes based on their sizes, compositions, surrounding environment, and the amplitude and frequency of external magnetic fields. MPS excites MNPs by applying an alternating magnetic field and measures the voltage induced in a receiver coil due to a time-varying magnetization of MNPs. The peak voltage and full width at half maximum (FWHM) determine the signal intensity and the spatial resolution of MNPs, respectively.²⁹ The acquired voltage is proportional to the time derivative of the magnetic flux according to Faraday’s law of induction.^30,31 Therefore, the voltage signal can be reconstructed to net magnetic moment and magnetization by integrating the induced voltage. Figure 2 shows differential susceptibility (dm/dH) and corresponding AC hysteresis loops of MNPs and MNP@Au fixed with agar. The nanoparticles were excited under external magnetic fields at a fixed field amplitude (4 kA/m or 5 mT) with three different frequencies (10, 50, and 80 kHz). The voltage signal and AC hysteresis loops were normalized by the saturation magnetization of MNPs and MNP@Au, accordingly. Overall, MNP@Au showed higher dm/dH at all three frequencies when it was compared to dm/dH of MNPs. Lower dm/dH was observed for both of MNPs and MNP@Au under external magnetic fields with higher frequencies. The signal peak of MNPs and MNP@Au shifted to higher magnetic field amplitude when the frequency of magnetic field was increased.

Fig. 2.

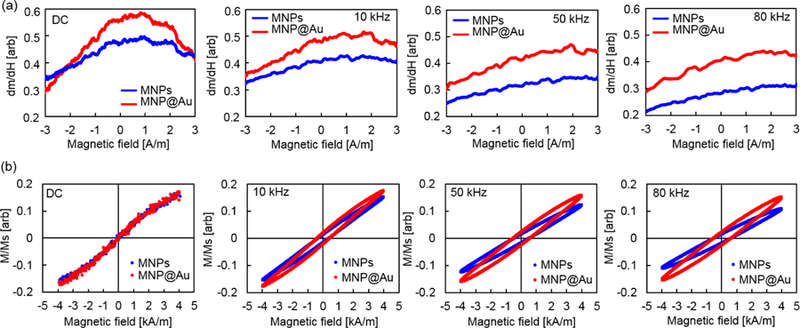
(a) Differential susceptibility (dm/dH) and (b) AC hysteresis loops of MNPs and MNP@Au. Nanoparticles were fixed in agar gel. The amplitude of an external magnetic field was fixed at 4 kA/m (5 mT) and the frequencies were varied from 10 to 80 kHz.

In Figure 2 (b), closed hysteresis loops were observed for MNPs and MNP@Au under a static magnetic field. On the other hand, open hysteresis loops were observed for both particles under magnetic fields with all three frequency conditions. MNPs and MNP@Au showed greater coercivities and lower susceptibilities under magnetic fields with higher frequencies. This change in coercivities corresponds to the signal peak shift of dm/dH under magnetic fields with higher frequencies. When AC hysteresis loops of MNPs and MNP@Au were compared, MNP@Au showed higher susceptibility, although the coercivities were nearly the same. It is clear that the higher susceptibility of MNP@Au contributed to the greater dm/dH compared to MNPs, shown in Figure 2 (a). Figure 3 (a) shows the intensity of the third harmonic of nanoparticle magnetization. Owing to the nonlinear magnetization profile of MNPs under an external magnetic field, the induced signal contains not only a peak at the fundamental frequency but also harmonics of the excitation frequency, which can be calculated by Fourier transformation.³² By incorporating higher-order harmonics, the signal from the excitation field can be removed, thus back ground free detection can be achieved. The third harmonic signal is commonly used for image reconstruction for MPI since the even harmonics are less prominent and the third harmonic is the largest among the odd harmonics.³³ Figure 3 (a) shows that the third harmonic signals from MNP@Au were greater than the third harmonics from MNPs at the frequencies between 1 to 80 kHz. These results indicate the enhanced imaging capacity of MNP@Au compared to MNPs. The ferromagnetic behavior of MNPs under an alternating magnetic field is dominated by a relaxation mechanism which is the delay of the magnetization in aligning with an alternating magnetic field.^34,35 Brownian relaxation is associated with the rotation of magnetic moments due to the rotation of the entire particle. In contrast, Néel relaxation is associated with internal magnetic moment rotation without physical motion of the particle.¹⁹ The Brownian relaxation time τ_B and Néel relaxation time τ_N are given by

$${\tau }_B=\frac{3\eta V_H}{k_{B}T}$$ (5)

$${\tau }_N={\tau }_0\text{exp}\left(\frac{K_{eff}{V}_M}{k_{B}T}\right)$$ (6)

where η is the viscosity of the suspended fluid, V_H is the hydrodynamic volume of magnetic nanoparticles, and τ₀ is the attempt time of ~10⁻⁹ s. Although Brownian and Néel relaxations can occur in parallel, the contribution from Brownian relaxation is negligible for fixed nanoparticles due to the restriction of Brownian rotation. As shown in equation (6), Néel relaxation varies exponentially with the anisotropy constant and magnetic volume.

Fig. 3.

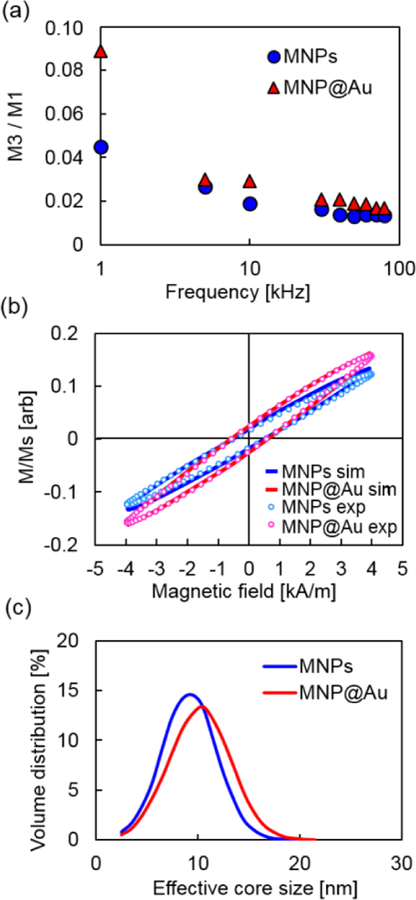
(a) The intensity of the third harmonics of nanoparticle magnetization (M3) normalized to the value of the first harmonics (M1). (b) The AC hysteresis loops and (c) the effective magnetic core sizes of MNPs and MNP@Au calculated using LLG equation.

The magnetic anisotropy energy is the energy barrier that needs to be overcome to reverse the magnetization from its easy axis.³⁶ The magnetic anisotropy energy per particle is given by

$$E_a=K_{eff}{V}_{M}si{n}^2\theta$$ (7)

where θ is the angle between the magnetization and the easy axis of the particle. It is contributed by various factors such as magnetocrystalline anisotropy which primarily arises from spin-orbit coupling and shape anisotropy which originates from dipole-dipole interactions.^37,38 Therefore, the magnetic anisotropy energy of nanoparticles is affected by various parameters including particle size, dipole-dipole interactions, distortions, and electronic hybridization at the nanoparticle interface, assuming a fixed chemical composition.^39,40 The anisotropy constant of MNPs has been reported to differ from that of bulk and varies with the particle size.^41,42 The formation of nanoparticle clusters also affects the anisotropy constant resulting from the increase in dipole-dipole interactions.⁴³ Moreover, it is known that the surface effect on magnetic anisotropy becomes more significant when the particle size is reduced due to the large surface-to-volume ratio of nanoparticles.⁴⁴

To evaluate the effect of gold shell on magnetic anisotropy constant, we conducted a numerical simulation using Landau–Lifshitz–Gilbert (LLG) equation. Stochastic LLG has been widely used to model the magnetization dynamics of magnetic nanoparticles.⁴⁵ This equation describes a non-linear time evolution of magnetization with a phenomenological damping term at the nano-scale.^46,47 The anisotropy constants and effective magnetic core sizes of MNPs and MNP@Au were calculated by fitting the theoretically calculated dynamic hysteresis loops to the experimentally measured hysteresis loops (Figure 3 (b) and (c)). They were estimated under an assumption that the anisotropy energy of MNPs and MNP@Au is comparable based on the identical coercivities of MNPs before and after gold coating. The calculated anisotropy constants and effective magnetic core sizes are summarized in Table 1. The anisotropy constant of MNPs decreased from 11.5 kJ/m³ to 8.0 kJ/m³ after gold coating. The effective magnetic core size of MNP@Au was estimated to be 10.2 ± 3.0 nm, which was larger than that of MNPs (9.2 ± 2.7 nm). The magnetic properties of nanoparticles are known to be significantly affected by the surface condition owing to their high surface-to-volume ratio. It has been reported that magnetic moments of Fe₃O₄ core-Au shell nanoparticles increased due to the trapping of conduction electrons from the gold part at the Fe₃O₄-Au interface.⁴⁸ However, as mentioned in previous section, the saturation magnetization of MNPs was reduced after gold coating possibly due to the strain induced by the lattice mismatch at the interface between magnetic core and gold shell. The lower saturation magnetization of MNP@Au compared to MNPs suggests that the effect of strain at the interface contributed dominantly over the interfacial hybridization. The interfacial effect of core-shell nanoparticles can also alter other parameters such as magnetic anisotropy. It has been reported that the hybridization of 3d electronic states at the interface between Co core and noble metal capping increased magnetic anisotropy of metal-capped Co nanoparticles.³⁹ In contrast, Au capping of Co nanodots decreased blocking temperature due to the strain induced inside the Co nanodots, and it was estimated to reduce magnetic anisotropy based on the atomic relaxations calculated by a molecular dynamics simulation.⁴⁹ The reduction of magnetic anisotropy constant after Au coating corresponds to our simulation results, and it suggests a predominant contribution of core-shell interfacial strain on the magnetic anisotropy. The numerical simulation also indicates the presence of a tight magnetic core cluster within a gold shell, which resulted in the increase of effective magnetic core size of MNP@Au.

Table 1.

The saturation magnetization of MNPs and MNP@Au measured by VSM, and anisotropy constant and effective magnetic core size calculated using LLG equation.

	MNPs	MNP@Au
Saturation magnetization Ms	84 emu/g Fe	72 emu/g Fe
Anisotropy constant K	11.5 kJ/m3	8.0 kJ/m3
Effective magnetic core size	9.2 ± 2.7 nm	10.2 ± 3.0 nm

Magnetic particle imaging

Figures 4 (a) and (b) shows MPI images and MPI signal intensities of MNPs and MNP@Au with different concentrations measured under a magnetic field (field strength: 20 mT, frequency: 45 kHz). MNPs and MNP@Au both showed enhanced contrasts by increasing the concentration, and the corresponding signal intensities increased linearly with the nanoparticle concentration. Moreover, MNP@Au exhibited brighter MPI images compared to MNPs counterparts with similar concentrations. The higher MPI signal intensities of MNP@Au corresponds to the differential susceptibilities (dm/dH) and AC hysteresis loops measured by MPS under the excitation field with a field frequency at 50 kHz. The greater differential susceptibilities and third harmonics of MNP@Au compared to MNPs support the brighter MPI contrasts of MNP@Au. As discussed in previous section, this brighter contrast can be explained by a contribution from the surface interface between the magnetic core and gold shell.

Fig. 4.

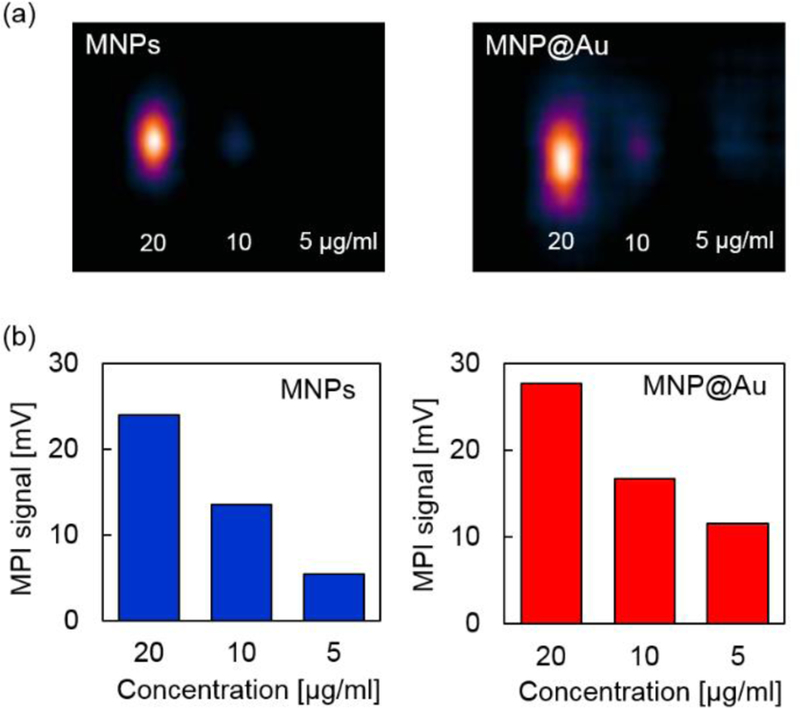
(a) MPI images and (b) MPI signals of MNPs and MNP@Au measured under a magnetic field at 20 mT and 45 kHz. The concentration was varied from 5 µgFe/ml to 20 µgFe/ml.

In vitro study of MNP@Au

MPI is suitable for molecular imaging owing to its high sensitivity and transparent background. Non-invasive diagnostic imaging using MPI has a great promise for early disease diagnosis with high accuracy. To achieve MPI diagnostic imaging, it is essential to demonstrate the biocompatibility of the imaging tracers, as well as to introduce disease or cell-specific targeting capacity to the tracers. In our previous report, we conducted cellular viability study after the exposure of MNP@Au and demonstrated no cytotoxicity effect of MNP@Au up to the concentration of 50 μg/ml.⁵ Therefore, we evaluated functionalization efficiency of MNP@Au with a targeting ligand, and the cellular viability of the functionalized MNP@Au. We chose transferrin as a model targeting ligand and CHME-5 cell line as model cells to evaluate the cytotoxicity. Transferrin is a widely used ligand for diagnostic and therapeutic applications targeting brain glioma due to the high expression of transferrin receptors on the surface of brain capillary endothelial cells and glioma cells.⁵⁰ Various nanoparticles functionalized with transferrin have shown targeting specificity to brain glioma and capability for effective brain glioma imaging.^51,52,53 Figure 5 (a) shows the schematic illustration of the functionalization process. Sulfhydryl (-SH) groups were introduced on transferrin using Traut’s reagent, followed by the conjugation of the thiolated transferrin on MNP@Au via Au-S covalent bonds.⁵⁴ The conjugation was confirmed by evaluating the hydrodynamic size, zeta potential (electrokinetic potential), and the conjugation efficiency (the percentage of transferrin conjugated) using a protein assay. The hydrodynamic size of MNP@Au increased from 39 nm to 45 nm after the functionalization of MNP@Au. A slight increase in zeta potential was also observed from −30.6 mV to −25.5 mV after the functionalization. The negative zeta potential of MNP@Au is contributed from the deprotonated carboxyl groups of sodium citrate on the nanoparticle surface. The slight change in the zeta potential indicates the partial coverage of Au shell surface after transferrin conjugation. The conjugation efficiency of transferrin to MNP@Au was estimated to be 58%. Figure 5 (b) shows the viability of microglia cell line after an incubation with transferrin-conjugated MNP@Au. No significant decrease in the viability of microglia cells was observed within the concentration range between 1−50 μg/ml for up to 48h incubation. This viability data corresponds to our previous report which showed no cytotoxicity effect of non-functionalized MNP@Au. Taken together, these results confirmed an effective functionality of MNP@Au with a targeting ligand and the biocompatibility of the functionalized MNP@Au.

Fig. 5.

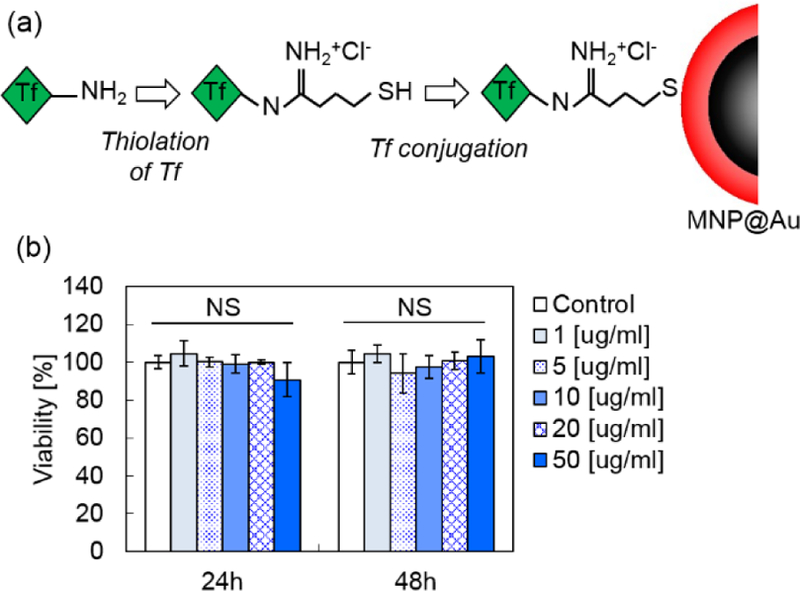
(a) The process for transferrin conjugation on MNP@Au (Tf-MNP@Au) and (b) viability of CHME-5 cells after Tf-MNP@Au exposure (NS, not significant, P > 0.05).

Conclusions

The influence of gold shell coating on dynamic magnetic properties and MPI imaging capacity was studied. An increase in the susceptibility of AC hysteresis loops was detected after gold shell coating on magnetic core nanoparticles. Based on the numerical simulation, it is suggested that the anisotropy constant decreased after gold shell coating, which contributed to the change in the dynamic responses of MNP@Au. We observed an increase in the third harmonic of the nanoparticle magnetization after gold shell coating. This increase agreed with the brighter contrasts and enhanced imaging signals generated from MNP@Au in MPI scanning. Cellular viability study also demonstrated no cytotoxicity effect of functionalized MNP@Au. These results suggest the potential use of MNP@Au as an excellent MPI imaging tracer for disease diagnostic applications.