Multi-Atlas Tool for Automated Segmentation of Brain Gray Matter Nuclei and Quantification of their Magnetic Susceptibility

Abstract

Quantification of tissue magnetic susceptibility using MRI offers a non-invasive measure of important tissue components in the brain, such as iron and myelin, potentially providing valuable information about normal and pathological conditions during aging. Despite many advances made in recent years on imaging techniques of quantitative susceptibility mapping (QSM), accurate and robust automated segmentation tools for QSM images that can help generate universal and sharable susceptibility measures in a biologically meaningful set of structures are still not widely available. In the present study, we developed an automated process to segment brain nuclei and quantify tissue susceptibility in these regions based on a susceptibility multi-atlas library, consisting of 10 atlases with T1-weighted images, gradient echo (GRE) magnitude images and QSM images of brains with different anatomic patterns. For each atlas in this library, 10 regions of interest in iron-rich deep gray matter structures that are better defined by QSM contrast were manually labeled, including caudate, putamen, globus pallidus internal/external, thalamus, pulvinar, subthalamic nucleus, substantia nigra, red nucleus and dentate nucleus in both left and right hemispheres. We then tested different pipelines using different combinations of contrast channels to bring the set of labels from the multi-atlases to each target brain and compared them with the gold standard manual delineation. The results showed that the segmentation accuracy using dual contrasts QSM/T1 pipeline outperformed other dual-contrast or single-contrast pipelines. The dice values of 0.77±0.09 using the QSM/T1 multi-atlas pipeline rivaled with the segmentation reliability obtained from multiple evaluators with dice values of 0.79±0.07 and gave comparable or superior performance in segmenting subcortical nuclei in comparison with standard FSL FIRST or recent multi-atlas package of volBrain. The segmentation performance of the QSM/T1 multi-atlas was further tested on QSM images acquired using different acquisition protocols and platforms and showed good reliability and reproducibility with average dice of 0.79±0.08 to manual labels and 0.89±0.04 in an inter-protocol manner. The extracted quantitative magnetic susceptibility values in the deep gray matter nuclei also correlated well between different protocols with inter-protocol correlation constants all larger than 0.97. Such reliability and performance was ultimately validated in an external dataset acquired at another study site with consistent susceptibility measures obtained using the QSM/T1 multi-atlas approach in comparison to those using manual delineation. In summary, we designed a susceptibility multi-atlas tool for automated and reliable segmentation of QSM images and for quantification of magnetic susceptibilities. It is publicly available through our cloud-based platform (www.mricloud.org). Further improvement on the performance of this multi-atlas tool is expected by increasing the number of atlases in the future.

1. Introduction

Tissue magnetic susceptibility is a physical parameter indicating how the local magnetic field in tissue changes in response to an external applied magnetic field. Quantification of tissue magnetic susceptibility can provide unique information about tissue composition and many recent studies have demonstrated that physiologically significant tissue components including iron and myelin are dominant sources that influence the bulk tissue magnetic susceptibility in brain (Duyn and Schenck, 2016; Langkammer et al., 2010; Liu et al., 2011; Liu et al., 2015; Schweser et al., 2011; Wang and Liu, 2015). Abnormal changes in the concentration and distribution of these tissue components have been linked to different neurodegenerative diseases. For example, abnormal focal accumulations of iron in the brain have been reported in Alzheimer’s disease (AD) (Acosta-Cabronero et al., 2013; Ayton et al., 2017; Bartzokis et al., 1994; Connor et al., 1992; van Bergen et al., 2016b; van Bergen et al., 2018; Yamamoto et al., 2002), Parkinson’s disease (PD) (Barbosa et al., 2015; Dexter et al., 1989; Du et al., 2016; Graham et al., 2000; He et al., 2015; Lotfipour et al., 2012; Martin et al., 2008) and Huntington’s disease (HD) (Browne and Beal, 2006; Dominguez et al., 2015; Dumas et al., 2012; Muller and Leavitt, 2014; Rosas et al., 2012; van Bergen et al., 2016a). Similarly, iron content changes in the basal ganglia have been observed in multiple sclerosis (MS), in which the demyelination process may also be potentially better characterized by tissue magnetic susceptibility (Absinta et al., 2013; Bagnato et al., 2011; Chen et al., 2014; Haacke et al., 2009; Hagemeier et al., 2018; Langkammer et al., 2013; Li et al., 2016; Schweser et al., 2018; Wiggermann et al., 2013; Wisnieff et al., 2015; Yao et al., 2012; Zhang et al., 2016). Since non-invasive measurement of changes in brain iron and myelin content using MRI can give important insight into the normal and pathological processes during aging, quantitative magnetic susceptibility contrast may become a measure to monitor neurodegenerative diseases and, potentially, to test new therapeutics and their efficacy.

Recent advances in high field MRI and quantitative susceptibility mapping (QSM) techniques have led to exciting research possibilities and attracted much research interest in assessing tissue magnetic susceptibility at high spatial resolution through MR phase measurement (Bilgic et al., 2012; Cheng et al., 2009; de Rochefort et al., 2008; Deistung et al., 2017; Duyn et al., 2007; Haacke et al., 2015; Lim et al., 2013; Liu et al., 2015; Liu et al., 2009; Schweser et al., 2011; Shmueli et al., 2009; Wang and Liu, 2015; Wharton and Bowtell, 2010; Yoon et al., 2018). However, besides the complicated phase processing and ill-conditioned phase to susceptibility inverse problem, condensed, reliable and consistent reference susceptibility metrics derived from QSM in a biologically meaningful set of structures that are universal and sharable, are still not widely available. This is partly due to the lack of robust brain segmentation tools for extracting the susceptibility measures from a broad range of healthy and diseased populations with large anatomical variations.

Currently, quantification of QSM in anatomical structures relies either on manual definition of regions of interest (ROI) which is extremely time consuming and evaluator-dependent (He et al., 2015; Li et al., 2014) or on automated brain mapping to available brain atlases. However, the most commonly used brain atlases are mainly based on T1 contrast (Lancaster et al., 2000; Mazziotta et al., 2001). Automatic analysis on QSM images using these atlases and standard whole brain registration and segmentation methods usually gives poor performance in iron-rich deep gray matter nuclei with low T1 contrast and thus poorly guided delineation and registration (Cobzas et al., 2015; Feng et al., 2017; Lim et al., 2013). This problem may be solved by building human brain atlases based on magnetic susceptibility contrast using high-quality QSM images of whole brain from a single subject (Lim et al., 2013) or multiple subjects with a multi-contrast multi-atlas approach, e.g. with dual QSM and T1 contrast multi-atlases (Cobzas et al., 2015) or using well registered group-wise averaged QSM images (Acosta-Cabronero et al., 2016; Hanspach et al., 2017; Keuken et al., 2014; Keuken and Forstmann, 2015; Schweser et al., 2018; Visser et al., 2016). The superior susceptibility contrast sensitive to tissue iron content may also be used to build susceptibility-based atlases of certain iron-rich structures, such as the hippocampus and dentate nucleus (Goubran et al., 2014; He et al., 2017). Individual QSM images under testing can then be normalized to these susceptibility templates for more reliable segmentation and quantification as has been exemplified in some recent studies (Cobzas et al., 2015; He et al., 2017; Lim et al., 2013; Schweser et al., 2018).

One well-known limitation of the single or averaged susceptibility atlases, however, is that the segmentation accuracy is closely dependent on their anatomical similarity to the subject in question (Collins and Pruessner, 2010; Iglesias and Sabuncu, 2015). This is particularly an issue when studying populations with a large age range, e.g. in studies of brain iron change during the whole life span, or when studying patients with a large degree of anatomical variation, e.g. pediatric patients or elderly patients with severe neurodegenerative diseases. In order to overcome this limitation, anatomical variations have to be taken into account in the atlases themselves. One possible option would be to build a longitudinal age-dependent group-wise averaged susceptibility atlases as those developed very recently for studying brain iron changes during both development and aging using QSM (Zhang et al., 2018). Such longitudinal susceptibility atlases have indeed shown superior performance over previous single subject susceptibility atlas and an appropriately selected age-matched QSM template can be used for the target population under investigation. An alternative approach to tackle this problem is by using so-called multi-atlas segmentation, which utilizes a set of atlases covering sufficiently large anatomical variations rather than some model-based average representation of the training datasets. Such multi-atlas approaches have been shown to have the flexibility to better capture anatomical variations through normalization to a sufficiently large number of atlases with accurate manual delineation and multi-label voting fusion (Tang et al., 2015) and usually offer superior segmentation accuracy at the expense of higher computational cost (Iglesias and Sabuncu, 2015).

The goal of the present study was to achieve a more reliable and more accurate automated tissue susceptibility quantification using a similar multi-atlas approach extended from previous study (Cobzas et al., 2015) using 10 pre-selected adult human whole brain atlases built on both magnetic susceptibility contrast and T1 contrast with sufficiently large anatomical variations. Based on QSM contrast, we built the susceptibility atlases for 10 major deep gray matter nuclei, including caudate nucleus (CN), internal globus pallidus (GPi), external globus pallidus (GPe) putamen (Put), thalamus (Thal), thalamic pulvinar (Pulv), red nucleus (RN), substantia nigra (SN), subthalamic nuclei (STN) and dentate nucleus (DN) in both left and right hemispheres. We also developed an automated registration and segmentation pipeline using such multi-atlases based on QSM and T1-weighted image (T1WI). We tested the reliability of this QSM/T1 multi-atlas pipeline in the atlas set and compared its segmentation performance with other multi-atlas pipelines using different combinations of contrast channels, e.g. using gradient echo magnitude with T1WI (GRE/T1) dual contrast channels etc. In addition, the segmentation and quantification accuracy in certain subcortical regions including CN, Put, GP and thalamus was further compared to those obtained using the standard FSL FIRST package (Patenaude et al., 2011) and another recent multi-atlas based package called volBrain (Manjon and Coupe, 2016). The reliability and reproducibility of the QSM/T1 multi-atlas was also tested on susceptibility MRI data acquired using two different scanning protocols, on two different scanner platforms, and eventually on data acquired at a different site. Furthermore, we have made the developed QSM/T1 multi-atlas segmentation pipeline publicly available through our MRICloud platform: www.mricloud.org, which has a simple web-based interface and does not require any installation or advanced computational equipment.

2. Material and Methods

2.1. Data acquisition and QSM processing

Our multi-atlas dataset was developed using a collection of MRI images from 10 healthy individuals, with an age range of 26 to 73 years old (mean ± standard deviation of 59.6 ± 16.3 y/o, 5 male and 5 female). Three of them were collected from a reproducibility study described later in this paper and seven of them were collected from the BIOCARD study conducted at Johns Hopkins University on elderly subjects (Soldan et al., 2017). The protocols were approved by the Johns Hopkins University Institutional Review Board, and written informed consent was obtained from all participants. These ten subjects were selected to include variable anatomic patterns, expressed by different degrees and locations of brain atrophy (Fig. 1). All MRI images were acquired on a 3T Philips Achieva scanner (Philips Healthcare, Best, Netherlands) equipped with a 32-channel receive head coil (Nova Medical, Wilmington, Massachusetts). The susceptibility weighted MRI data were acquired on each subject in the supine position using a multi-echo 3D gradient echo (GRE) sequence with 1.0 mm isotropic resolution (transverse orientation, TE1/∆TE/TR=6/6/40 ms, 6 unipolar echoes, FOV=224×224×140 mm³, flip angle 15°, bandwidth 217 Hz/px, SENSE factor of 2×1×2, scan time 7 min 19 sec). A high resolution T1-weighted MPRAGE image was also acquired for each subject with 1X1X1.2 mm³ resolution (sagittal orientation, TE/TR=3.1/6.8 ms, flip angle 8°, TI=847 ms, Turbo Field Echo (TFE) factor of 240, SENSE factor 2×1×1, scan time 5 min 56 sec).

Fig. 1:

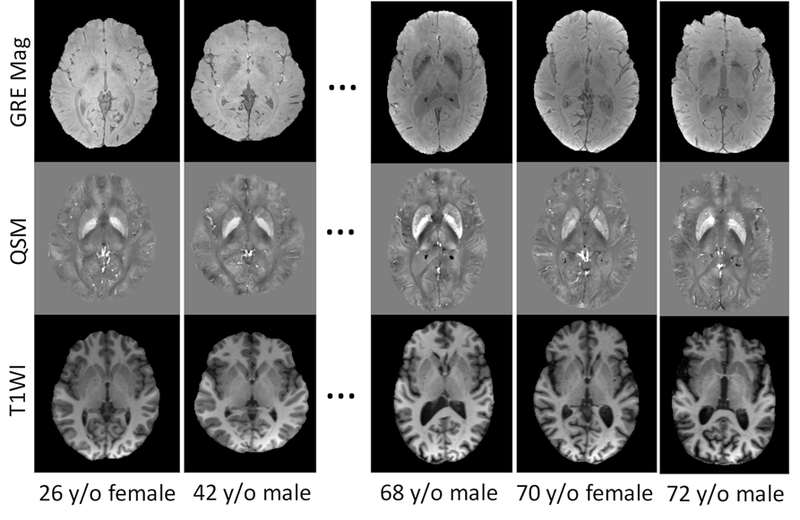
Example source images showing the GRE Magnitude, QSM and T1 weighted MPRAGE images of 5 out of the 10 subjects selected to generate the susceptibility multi-atlases. Variable anatomical patterns and different degrees of brain atrophy can be seen among these atlases. The GRE Magnitude images are averaged across different TEs (6ms to 36ms). Gray scales in QSM images are all in [−0.2, 0.2] ppm.

Susceptibility MRI phase data were preprocessed using Laplacian based phase unwrapping and V-SHARP method for removing background gradient with a maximum spherical mean value kernel radius of 6 mm and a truncated singular value decomposition (SVD) regularization threshold of 0.05 (Li et al., 2011; Wu et al., 2012). After removal of the background field, the resulting local frequency shift maps of the last four echoes (with TE of 18 ms to 36 ms) were averaged to obtain a higher signal-to-noise ratio (SNR) as compared to single-echo reconstruction. The ill-conditioned QSM dipole inversion was solved by using a modified structural feature based collaborative reconstruction algorithm (SFCR) (Bao et al., 2016) with only L1-norm based regularization i.e. λ₁ = γ₁ = 100 and λ₂ = γ₂ = 0. QSM images used to build the multi-atlas dataset and the quantitative susceptibility values reported in this study were not explicitly referenced to tissue susceptibility value of any selected structures, which is equivalent to referencing to the mean susceptibility of the whole brain (Li et al., 2014). Besides the QSM image, a GRE magnitude image averaged over all the echoes was also generated as a separate alternative contrast channel for testing the multi-atlas pipelines (Fig. 1).

2.2. Atlas generation

For generating the multi-atlases, T1WI of each subject was first put in the QSM space by co-registering to GRE magnitude image using FSL FLIRT and skull stripping was then performed with FSL BET (Smith et al., 2004). The final atlases were created in MNI space. The co-registered T1WI in the QSM space was brought to the JHU_MNI_SS template (Mori et al., 2008) by sequential 6, 9, and 12 parameters linear transformations. The same transformations were then applied to QSM and GRE magnitude images (Fig. 2, Multi-atlas Generation).

Fig. 2:

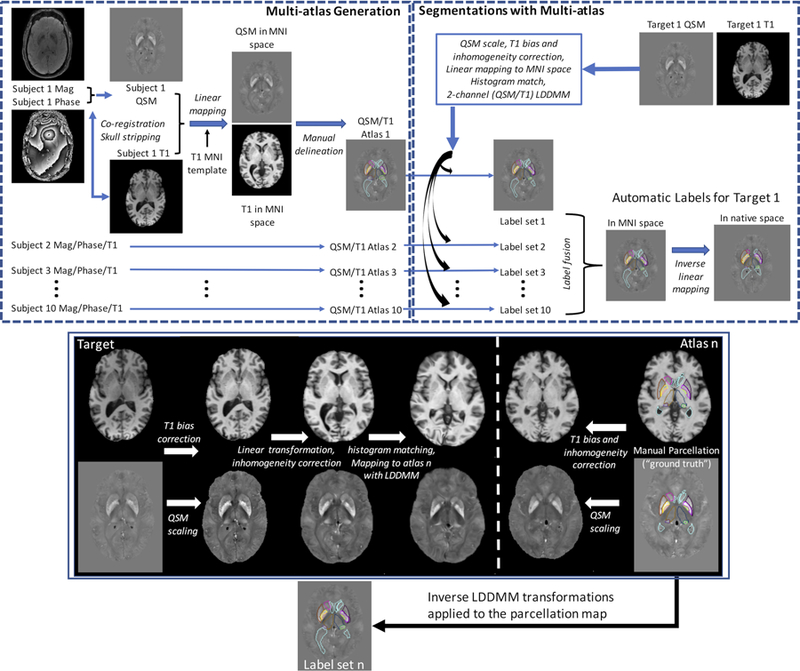
Schematic representation of the QSM/T1 multi-atlas generation (top row left) and automated segmentation pipeline (top row right). Some detailed processing steps, including preprocessing and coregistration with multi-contrast multi-atlas and LDDMM nonlinear warping used in the segmentation pipeline (box with blue border), are illustrated in the bottom panel.

Two human evaluators (both with more than 10 years of experience in computational anatomy) created the multi-atlases based on collected images. First, based on QSM contrast, a neuroanatomist (AVF, MD, neuroradiologist, PhD in Neurosciences with 17 years of experience) delineated the following deep gray matter structures: CN, GPi/GPe, Put, Thal, Pulv, RN, SN, STN and DN with general guidance of the ICBM probabilistic atlas (Mori et al., 2008). The parcellation of RN and SN were mainly defined based on QSM contrast on axial view, while the definition of STN was done on the coronal view, based on its position relative to SN with guidance from previous reported studies (Ewert et al., 2018; Keuken et al., 2014; Visser et al., 2016). The parcellation of thalamus and DN was done following the guidance of (Behrens et al., 2003; He et al., 2017; Lim et al., 2013; Morel et al., 1997; Zhang et al., 2010). Ventricles were delineated based on T1WI and GRE images. White matter and cortex were defined in the remaining tissue (not classified as any of the ROIs above) with the guidance of T1w tissue probabilistic map. A second evaluator (JH, Master in health sciences with 12 years of experience in computational anatomy) reviewed the delineations and ultimate decisions were achieved by consensus between the two evaluators if changes or modifications were needed.

2.3. Segmentation with multi-channel multi-atlas pipeline

The method and processing setups involved in the automated segmentation pipeline using the multi-channel multi-atlas are illustrated in Fig. 2 and described as follows. Let $\left[A^1,\dots ,A^n\right]$ be a set of n atlases where $A^i=\left(A_{QSM}^i,A_{T1}^i,A_S^i\right)$ denotes the i_th atlas with QSM, T1WI and the corresponding manual segmentation image in MNI space. Similarly, let $T=\left(T_{QSM},T_{T1}\right)$ be the target QSM and T1W images that will be segmented. In the multi-channel multi-atlas pipeline, the target images are mapped to the atlas image coordinates using a combination of affine transformation and large deformation diffeomorphic mapping (LDDMM) transformation. Then, atlas manual segmentations are transferred to the target image coordinates and combined via a multi-atlas fusion algorithm to create a target segmentation. The workflow is similar to what was created before for T1 and DTI multi-atlas pipelines (Ceritoglu et al., 2009; Tang et al., 2013; Tang et al., 2014) and is illustrated in Fig. 2. Briefly, it involves the following steps.

1. Target pre-processing steps:

   1. Scaling of $T_{QSM}$ to remove negative values; This was done by normalizing QSM values in the range of −0.15 to 0.25 (ppm) to nonnegative values (0 to 255). QSM values outside this range were cropped to the minimum or maximum of this range i.e. −0.15 or 0.25. Such a range was selected based on the typical range of susceptibility values of major brain tissue as reported in a previous study (Hanspach et al., 2017)
   2. Bias correction of T_T1 using the N4 algorithm as described in (Tustison et al., 2010);
   3. Calculation of a 12 parameter or affine transformation matrix M₁₂ between T_T1 and JHU_MNI_SS MNI atlas using the AIR program (Woods et al., 1998a; Woods et al., 1998b).
   4. Deformation of $T=\left(T_{QSM},T_{T1}\right)$ onto MNI space with M₁₂
2. Target to atlas registrations: For each atlas contrast image $A^i=\left(A_{QSM}^i,A_{T1}^i\right)$ and target contrast image $T=\left(T_{QSM},T_{T1}\right)$ MNI space, the following steps are performed.

   1. Scaling of $A_{QSM}^i$ to remove negative values similar as in step 1a. Bias correction of $A_{T1}^i$ similar as in step 1b.
   2. Histogram matching between $A_{QSM}^i,T_{QSM}$ and $A_{T1}^i,T_{T1}$ pairs. (Coltuc et al., 2006).
   3. Calculation of a 12 parameter affine transformation Mⁱ between T_T1and $A_{T1}^i$ via AIR.
   4. Deformation of $T=\left(T_{QSM},T_{T1}\right)$ with Mⁱ
   5. Calculation of a diffeomorphic transformation ${\phi }^i$ between $T=\left(T_{QSM},T_{T1}\right)$ and $A^i=\left(A_{QSM}^i,A_{T1}^i\right)$ using multi-channel LDDMM.
   6. Further deformation of $T=\left(T_{QSM},T_{T1}\right)$ onto atlas image space with ${\phi }^i.$.

   The LDDMM algorithm calculates diffeomorphic transformations between images of anatomical configurations by computing the geodesic flow in the space of diffeomorphisms between these images. The optimal transformation, $\text{φ}$, is generated as the end point of the flow of a smooth time-dependent vector field, $v_t\in \text{V}$ using a gradient descent algorithm. The two most important parameters that affect the smoothness of the computed diffeomorphism and the registration accuracy are α (controls smoothness of ν_t) and T (number of time steps for discretization of ν_t). The parameters used in our pipeline are modified from Ceritoglu 2009, with two sequential transformations ${\phi }_1={\phi }_{\alpha =0.01,T=2},{\phi }_2={\phi }_{\alpha =0.005,T=2}$ and these transformations are cascaded to compute the final diffeomorphism $\phi ={\phi }_1^{-1}.{\phi }_2^{-1}$. The inverse LDDMM transformation was then used to bring the atlas segmentation $A_S^i$ to the target coordinates in MNI space. Further details of LDDMM-based image registration and normalization accuracy can be found in our previous publications (Beg et al., 2005; Ceritoglu et al., 2009; Ceritoglu et al., 2013; Faria et al., 2011; Faria et al., 2010; Klein et al., 2009). The theory and details of the multichannel LDDMM are described in (Ceritoglu et al., 2009).

3. Segmentation via multi-atlas fusion

   The multi-atlas fusion algorithm (Tang et al., 2013; Tang et al., 2014) used in the pipeline can be briefly summarized as follows: The atlas set $\left[A^1,\dots ,A^n\right]$ contains a collection of locally-defined charts for each atlas generated from manual segmentation images $\left[A_S^1,\dots ,A_S^n\right]$ The algorithm computes maximum a posteriori (MAP) estimates of the high dimensional segmentations from the class of generative models representing the observed target image T, which is assumed to be Gaussian random field conditioned on the atlas charts as well as diffeomorphic changes of coordinates for each chart. The charts and their diffeomorphic correspondences are unknown and viewed as latent or hidden variables. The expectation-maximization (EM) algorithm yields the likelihood-fusion equation and it is maximized by the a-posteriori estimator of the segmentation labels for the target image. The fused likelihoods are modeled as conditional Gaussian random fields with mean fields as a function of each atlas chart under its diffeomorphic change of coordinates onto the target. The conditional-mean in the EM algorithm specifies the convex weights with which the chart-specific likelihoods are fused. In the implementation of the algorithm, main computational steps are

   1. In target image space T, computation of posterior probability $p\left(l|x,T\right),$ where x is the spatial coordinate and $l=1,\dots ,M$ is the label number and M is the total number of labels.
   2. To get a smoother boundary on segmentations, filtering of posterior probability with iterated conditional modes(ICM) algorithm (Besag, 1986) with a neighbouring probability of 0.65.
   3. Computation of target segmentation image $T_S\left(x\right)={\mathit{argmax}}_l\left(p\left(l|x,T\right)\right)$

4. Post-processing: Transformation of T_S from MNI space to its native space using the inverse of the affine transformation M₁₂ computed in step 1.

2.4. Performance testing of the multi-atlas pipeline

The performance of automated segmentation of subcortical gray matter nuclei using the QSM/T1 multi-atlas was first tested on the same atlas dataset in a leave-one-out (LOO) test manner. For this, each atlas was considered as a target brain and mapped to the other nine atlases using both QSM and T1 contrasts and the final labels were defined using the multi-atlas label fusion (MALF) algorithm as also described above (Tang et al., 2015).

For quantitative assessment of the segmentation performance, we calculated the indices of agreement (Dice) between the manual delineations (gold standard) in the atlases and the ones obtained with the QSM/T1 multi-atlas pipeline. Metrics of surface displacement between the manual and QSM/T1 delineations were further calculated as an alternative measure. Such displacements between pairs of ROIs were computed using the following procedure. Surfaces were first generated from each ROI using a restricted Delaunay triangulation. The first set of minimum distances was computed using the distances between each vertex belonging to the first surface and those belonging to the second surface. The second set of minimum distances was generated for vertices belonging to the second surface using the same method. The mean distance was found by averaging these minimum distances. The Hausdorff distance was found by taking the maximum of the suprema of the first and second set of minimum distances. It was considered as the maximum surface distance between the pair of ROIs.

In order to assess the relative performance of the QSM/T1 multi-atlas pipeline with respect to the different choices of image contrast channels, we conducted a similar LOO test using different combinations of available contrast channels including 1) QSM/GRE/T1, 2) QSM/GRE, 3) GRE/T1, 4) QSM only and 5) T1 only. Here QSM/T1 refers to using dual contrast channels with QSM and T1 contrast, while T1 only refers to using the single T1 contrast channel. The segmentation pipelines were modified accordingly to utilize different contrast channels. To gauge the performances, the Dice metrics between the manual delineations and all the delineations obtained with different segmentation pipelines were compared for each deep gray matter region with left and right side combined. In addition, a third evaluator (LC, with 3 years of experience) delineated all the structures of interest in all the 10 atlases independently, blinded from the labels created by the first two evaluators, allowing a comparison of the inter-evaluator agreement with the manual vs. automated agreement.

Besides the Dice metrics of agreement, quantitative values of tissue structure volume and tissue magnetic susceptibility extracted with the QSM/T1 delineation were compared with those extracted with manual delineation. Pearson correlation coefficients were calculated between these quantitative measures. Bland-Altman analysis was also performance to test the agreement between these measures.

The performance of the QSM/TI multi-atlas pipeline was further compared with respect to the standard package of FSL FIRST (Patenaude et al., 2011) and a more recent multi-atlas based package volBrain (Manjon and Coupe, 2016) using the 10-atlas data set. Dice metrics with respect to the manual delineations were compared in common subcortical regions generated by all three packages (FIRST, volBrain and QSM/T1), including CN, Put, GP and thalamus. For this comparison, regions of GPi/GPe generated by the QSM/T1 pipeline were combined into a single GP region, while thalamic pulvinar was combined with thalamus. Tissue structure volumes and magnetic susceptibility values extracted from these ROIs were also compared.

2.5. Robustness over protocols and scanners from different vendors

In order to test the reproducibility of QSM measures over scan protocols and platforms and the robustness of the multi-atlas pipeline, we acquired susceptibility MRIs in 6 healthy subjects (mean age 37.2 ± 11.8 y/o, 4 male and 2 female) using two different protocols and platforms from two different manufacturers, thereby creating 3 susceptibility scans for each subject. The first protocol (Philips Protocol A) was the same one used for acquiring the images of the atlases; the second protocol (Philips Protocol B) used a single echo SWI protocol with 0.9×0.9×1.5 mm³ resolution (TE/TR=20/27ms, FOV=220×220×168 mm³, flip angle 15°, bandwidth 120 Hz/px, SENSE factor of 2, scan time 7 min 51 sec) on the same Philips scanner; the third scan was obtained on a 3T Siemens Magnetom Skyra scanner (Siemens Healthcare, Erlangen, Germany) with parameters matched to the Philips Protocol B (Siemens Protocol B). All three scans for each subject were acquired within 6 months. QSM images were calculated using similar methods and procedures as described above for the atlas dataset except that no echo averaging was performed for single-echo SWI data. GRE magnitude images were used to co-register scans acquired on each subject with different protocols and scanner platforms using 9 parameter linear transformation and the transformation matrices were applied on the QSM images to put them into the same frame of reference.

Using the QSM/T1 multi-atlas segmentation pipeline, each QSM image acquired for each subject using each protocol was treated as a target brain and was automatically segmented and the mean QSM-based magnetic susceptibility value and corresponding tissue structure volume were extracted for each ROI. A manual label was also generated for each of the six subjects drawn on QSM images acquired using Philips Protocol A by one human rater (LC). Dice metrics of agreement with respect to the manual label were then calculated for the three automatically generated brain segmentations from the three different acquisition protocols. Similarly, Dice metrics were also calculated in an inter-protocol manner between the QSM/T1 brain segmentations obtained from each pair of scan data, e.g. from QSM data acquired using Philips Protocol A vs. Philips Protocol B etc. The extracted tissue structure volumes and quantitative susceptibility measures from each dataset using either the manual label or the QSM/T1 multi-atlas approach were further used to test the reproducibility of QSM and the multi-atlas pipeline using a linear correlation analysis and a Bland-Altman analysis.

2.6. Testing the pipeline in an external dataset

To further test the applicability and performance of our susceptibility multi-atlas tool, we applied it on a subset of a QSM dataset from a previously published study (Li et al., 2014) collected at an external site. The susceptibility weighted images were acquired on a 3T Siemens TimTrio scanner on 17 healthy subjects, 8 M/9 F, with age from 47 to 78 y/o (mean 64.9 ± 9.7 y/o) using a 3D GRE sequence with 0.9×0.9×2 mm³ resolution, TE1/∆TE/TR=4.92/4.92/35 ms, six echoes. QSM was calculated by using Laplacian based phase unwrapping, VSHARP and LSQR method as described in (Li et al., 2014). Frequency map or local field changes from all echoes were averaged to gain higher SNR.

Using the QSM/T1 multi-atlas pipeline, each brain was automatically segmented. Manual delineation was also performed by one human evaluator (LC). However, due to the lower resolution of this dataset, manual delineations of GPi and Gpe in GP and STN from SN could not be performed. Dice metrics of agreement between the automated segmentation and the manual delineation were calculated. For this, the GPi and GPe generated from the QSM/T1 pipeline were combined, while STN and SN were combined. Tissue structure volume and magnetic susceptibility values extracted from the two sets of ROIs, i.e. manual versus QSM/T1 multi-atlas approach were also compared.

3. Results

Figure 3 illustrates example manual delineation and parcellation maps obtained using the multi-atlas approach with different combinations of contrast channels overlaid on QSM images of a 46 y/o male participant. The three axial slices show clearly the structures of CN, putamen, GPi/GPe, thalamus, pulvinar, RN, SN and DN, while the coronal slice shows the STN on top of SN. It was observed that both the QSM/GRE/T1 and QSM/T1 multi-atlas pipeline gave results close to manual delineation and outperformed all other automated methods using either dual channels, e.g. QSM/GRE and GRE/T1, or a single contrast channel, e.g. QSM only or T1 only pipelines. As marked by the arrows in Fig. 3, segmentations that exclude T1 contrast tend to have inferior performance around the ventricles and its surrounding structures e.g. CN and thalamus. On the other hand, segmentations excluding QSM contrast tend to have inferior performance in structures that have weak T1 contrast, e.g. RN, DN, or pulvinar.

Fig. 3:

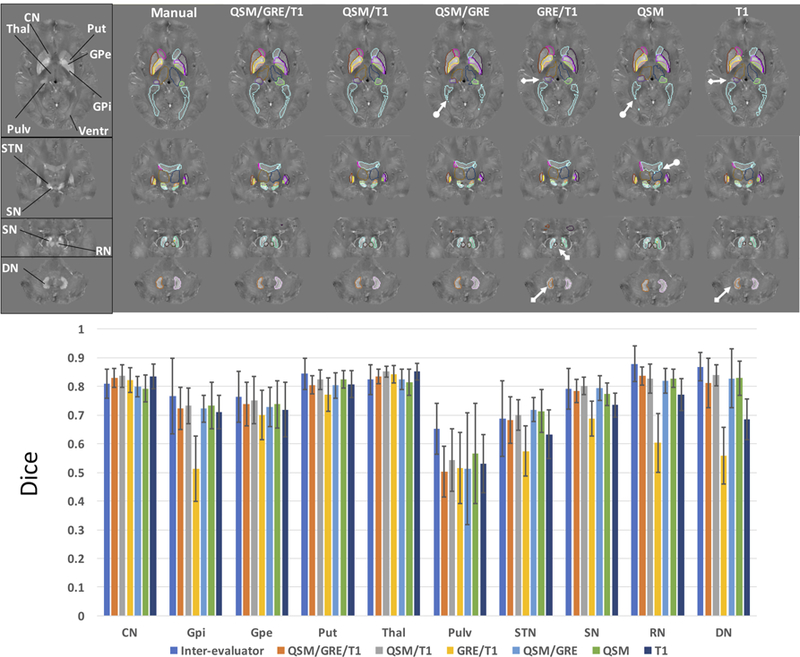
Top row shows the comparisons of the segmentation performances of different multi-atlas pipelines using different combinations of contrast channels, i.e. QSM/GRE/T1, QSM/T1, QSM/GRE, GRE/T1, QSM and T1, to the manual delineation overlaid on QSM images of an example subject. Bottom row shows the Dice metrics of agreement with respect to the manual delineation of all the automated brain delineations using these pipelines in the leave-one-out test on the atlas set (n=10) as compared to the inter-evaluators Dice. CN: caudate nucleus, GPi: globus pallidus internus, GPe: globus pallidus externus, Put: putamen, Thal: thalamus, Pulv: thalamic pulvinar, Ventr: ventricles, STN: subthalamic nucleus, SN: substantia nigra, RN: red nucleus, DN: dentate nucleus. Arrows with circular tails mark the inferior delineation performances around ventricles by pipelines that do not utilize T1 contrast, while arrows with square tails mark inferior delineation performances in DN, RN and pulvinar by pipelines that do not utilize QSM contrast.

The Dice metrics for all deep gray matter nuclei were calculated with respect to the manual delineation in the atlases (consensus by evaluators AVF and JH). As shown in Fig. 3, the QSM/T1 multi-atlas pipeline gave the overall (average over all structures) best performance (Dice of 0.77±0.09) among all of the automated segmentation pipelines and rivaled with the inter-evaluator Dice (0.79±0.07). Using three contrast channels i.e. QSM/GRE/T1, performed comparably (Dice of 0.75±0.10) to the QSM/T1 multi-atlas for all ROIs, but required longer computational time to segment each target brain (2.6±0.5 hours with QSM/GRE/T1 versus 1.6±0.5 hours with QSM/T1 on our cluster). The QSM/GRE and QSM-only pipeline gave comparable performance in most regions to the QSM/T1 pipeline (Dice of 0.75±0.10 and 0.76±0.08, respectively), but inferior performance in CN and thalamus. In comparison, the T1-only and GRE/T1 pipelines performed closely to the QSM/T1 multi-atlas in the caudate, putamen and thalamus (Dice values of 0.73±0.10 and 0.66±0.12, respectively), but gave inferior performance in STN, SN, RN and DN. These results are in general consistent with what we have observed in the example delineations shown in Fig. 3. Since the QSM/T1 pipeline was found to give the best performance among all the tested contrast channel selections, the further tests conducted in this study used the QSM/T1 multi-atlas pipeline.

In terms of regional performances using the QSM/T1 pipeline, the segmentation of most subcortical regions gave Dice values above 0.8, with Dice values between 0.7 and 0.8 for small structures or certain substructures like GPi, GPe or STN. Delineations of the thalamic pulvinar however, showed only moderate agreement between automated and manual segmentation (Dice of 0.54), with a relatively low inter-evaluator Dice of 0.65. The surface displacement metric between the automated and manual segmentation (Table S1) gave a similar indication, with the mean distance in most ROIs below 1.0 mm suggesting an overall distance smaller than one voxel, except in the pulvinar where the mean distance reached 1.7 mm.

The extracted tissue structure volumes (in mm³) and magnetic susceptibility values (in ppm) using either the manual delineation or the QSM/T1 pipeline are summarized in Table 1. Volume and susceptibility values extracted using the QSM/T1 pipeline are in general consistent and significantly correlated with those extracted using manual delineation with most correlation coefficient larger than 0.7, except in the small structure of STN (correlation coefficient smaller than 0.7, but still significant) and in pulvinar (volume measure found not significantly correlated). The overall correlation between the volume measures and susceptibility measures extracted using the QSM/T1 segmentation and manual labels in all the ROIs are 0.97 and 0.96, respectively (Figs. S1a and S1c). QSM/T1 approach showed some volume underestimation especially in CN, putamen and pulvinar (Fig. S1b). The corresponding susceptibility measures extracted from QSM/T1 approach showed a 95% limits of agreement of 0.0030±0.025 ppm with respect to the manual approach (Fig. S1d).

Table 1:

Structure volumes (in mm³) and tissue susceptibility values (in ppm) in the selected bilateral regions of interest obtained by manual delineation and the QSM/T1 multi-atlas approach in the leave-one-out test using the atlas set (subject n=10) and the corresponding correlations between these measures. Volume and susceptibility values are presented as mean ± standard deviation.

Measures	Volume (mm3)		Correlation	Susceptibility (ppm)		Correlation
ROIs	Manual	QSM/T1	R	Manual	QSM/T1	R
CN	4357±1174	3884±782	0.84	0.035±0.013	0.039±0.011	0.91
GPi	642±168	615±118	0.77	0.083±0.020	0.087±0.010	0.70
GPe	1793±688	1932±335	0.71	0.114±0.024	0.120±0.023	0.74
Putamen	4219±1123	3918±542	0.82	0.043±0.019	0.042±0.012	0.87
Thalamus	5431±845	5147±544	0.82	−0.013±0.011	−0.014±0.010	0.97
Pulvinar	991±630	835±336	−0.11†	0.021±0.021	0.026±0.023	0.74
STN	190±66	184±51	0.49	0.092±0.021	0.089±0.019	0.67
SN	724±226	704±179	0.90	0.107±0.019	0.114±0.021	0.82
RN	339±65	307±80	0.77	0.095±0.026	0.101±0.023	0.94
DN	941±335	873±229	0.86	0.085±0.017	0.089±0.016	0.77

CN: caudate nucleus, GPi/GPe: globus pallidus internus/externus, STN: subthalamic nucleus, SN: substantia nigra, RN: red nucleus, DN: dentate nucleus.

R; Pearson’s correlation coefficient. All correlations are significant with p < 0.05, except

^†: not significant with p > 0.05.

The delineations of subcortical regions of CN, putamen, GP and thalamus using FSL FIRST, volBrain and QSM/T1 pipeline are illustrated in Fig. 4a. With respect to the gold standard manual delineation, comparable Dice metrics of agreement were observed between the three methods in CN and putamen, while the QSM/T1 pipeline significantly outperformed FSL FIRST and volBrain in GP (with p<0.05 and p<0.001, respectively) and in thalamus (with p<0.001 and p<0.05, respectively) as in Fig. 4b. It was further observed (Figs. 4c,d) that volBrain tended to underestimate the GP volume and overestimate the magnetic susceptibility in GP. In addition, FSL FIRST was observed to underestimate the GP volume and overestimate the thalamic volume.

Fig. 4:

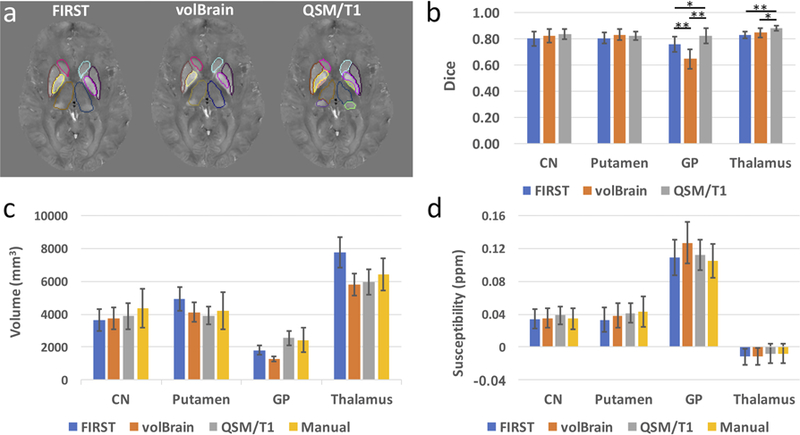
Example segmentations of common subcortical regions, including caudate, putamen, globus pallidus and thalamus, generated by the QSM/T1 multi-atlas pipeline, FSL FIRST and volBrain (a). Dice metrics of agreement between these automated delineations with respect to the manual delineation in those ROIs on the atlas set (n=10) are shown in (b). The segmented GPi and GPe obtained by QSM/T1 multi-atlas approach were combined for calculating the Dice in GP, while thalamic pulvinar was combined with thalamus for calculating Dice in the whole thalamus. The structure volumes (c) and tissue susceptibility values (d) extracted in these deep gray matter regions using the three automated methods are also compared to those obtained nusing manual delineation. CN: caudate nucleus, GP: globus pallidus. *: p<0.05, **: p<0.001 for two-way t-test after correction for multiple comparison.

Test results on the reproducibility of the QSM/T1 multi-atlas pipeline and the QSM magnetic susceptibility measures over scan protocols and platforms are illustrated in Table 2 and Figs. 5 and 6. Figure 5a shows example delineations over QSM images acquired on a 57 y/o male subject using different protocols as compared to the manual delineation drawn on Philips protocol A. The automatically generated ROIs showed almost perfect agreement in an inter-protocol manner, i.e. between-scan-protocols and between-platforms, with excellent segmentation reproducibility indicated by the high inter-protocol Dice values (0.89±0.04, with most of them over 0.85 except in certain small structures such as GPi and STN) and good dice metrics of agreement (0.79±0.08) with respect to the manual labels (Table 2). In addition, excellent correlations were observed between the QSM-based tissue susceptibility measures extracted from these three different scans using the QSM/T1 pipeline in an inter-protocol manner (Figs. 5b-d, correlation coefficient all above 0.97) and with respect to those extracted using the manual labels (Fig. 6c, correlation coefficients all above 0.95). Similar reproducibility and high correlations were also observed in the tissue volume measures in an inter-protocol manner (Fig. 6b, correlation coefficient all above 0.99) and between tissue volume measures extracted from the QSM/T1 pipeline versus those from the manual labels (Fig. 6a, correlation coefficient all above 0.98). The corresponding Bland-Altman analysis results are shown in Figs. S2 and S3 on volume and susceptibility, respectively. In general, the inter-protocol comparisons on tissue magnetic susceptibility have smaller difference variations (95% limits about ±0.015 ppm) than the comparisons between QSM/T1 approach with respect to the manual labels (95% limits about ±0.023 ppm). Similar observations were made for volume measures.

Table 2:

Dice metrics of agreement for the automated segmentations of QSM images acquired with different protocols and platforms (PhilA, PhilB and SiemB) using the QSM/T1 multi-atlas pipeline. Left three columns show comparison with manual delineation drawn on Philips protocol A. Right three columns show the inter-protocol comparison.

Dice	With Respect to Manual			Inter-protocol
ROIs	PhilA	PhilB	SiemB	PhilA&PhilB	PhilA&SiemB	PhilB&SiemB
CN	0.85±0.02	0.86±0.02	0.85±0.02	0.93±0.01	0.94±0.01	0.94±0.02
GPi	0.70±0.06	0.70±0.07	0.71±0.07	0.82±0.05	0.85±0.04	0.85±0.05
GPe	0.81±0.03	0.79±0.03	0.80±0.04	0.88±0.02	0.90±0.02	0.90±0.03
Putamen	0.83±0.03	0.83±0.04	0.82±0.04	0.92±0.02	0.93±0.02	0.93±0.02
Thalamus	0.85±0.03	0.85±0.03	0.85±0.03	0.95±0.01	0.95±0.01	0.96±0.01
Pulvinar	0.80±0.04	0.78±0.06	0.79±0.05	0.88±0.03	0.89±0.02	0.91±0.03
STN	0.60±0.10	0.60±0.09	0.60±0.11	0.81±0.04	0.84±0.05	0.82±0.06
SN	0.77±0.03	0.76±0.05	0.74±0.04	0.87±0.01	0.87±0.02	0.87±0.03
RN	0.84±0.03	0.83±0.03	0.83±0.04	0.87±0.03	0.87±0.03	0.88±0.03
DN	0.87±0.02	0.86±0.03	0.86±0.02	0.89±0.02	0.88±0.01	0.89±0.03

Dice metrics are presented as mean ± standard deviation (subject n=6). CN: caudate nucleus, GPi/GPe: globus pallidus externus/internus, STN: subthalamic nucleus, SN: substantia nigra, RN: red nucleus, DN: dentate nucleus

PhilA: Philips protocol A; PhilB: Philips protocol B; SiemB: Siemens protocol B

Fig. 5:

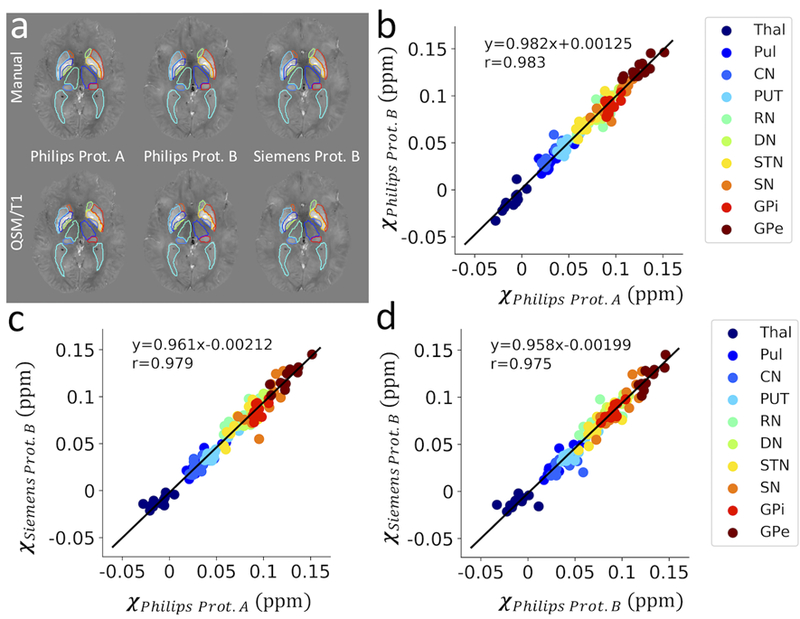
Segmentation performance of the QSM/T1 multi-atlas pipeline (bottom row in a) on QSM data acquired using different protocols and platforms are compared to the manual label (top row in a). Scatter plot of quantitative susceptibility values (in ppm) per structure extracted from these data are shown in (b-d) in an inter-protocol manner with corresponding linear regression lines. Thal: thalamus, Pul: thalamic pulvinar, CN: caudate nucleus, PUT: putamen, RN: red nucleus, DN: dentate nucleus, STN: subthalamic nucleus, SN: substantia nigra, GPi/GPe: globus pallidus internus/externus.

Fig. 6:

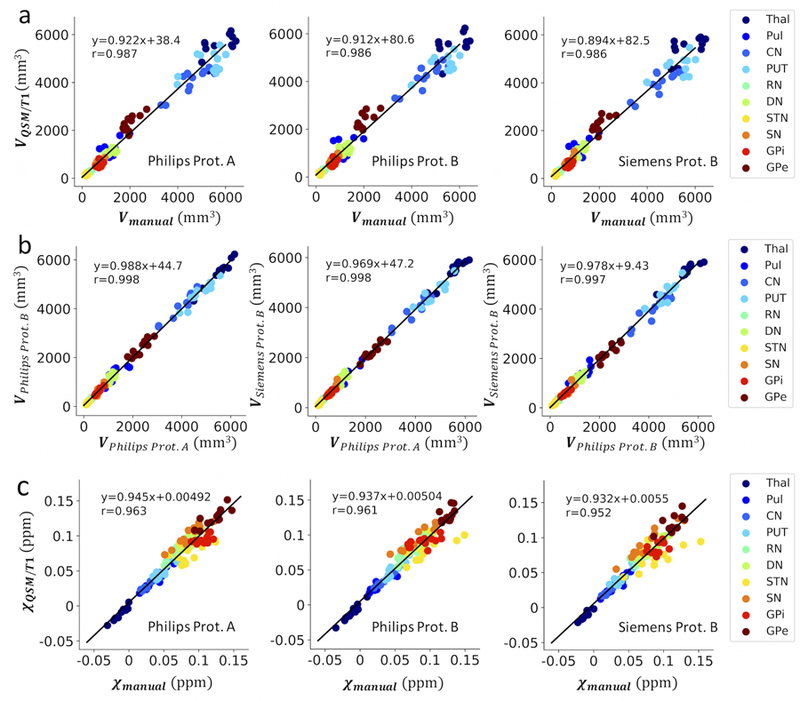
Scatter plot of segmented tissue structure volumes (in mm³) using the QSM/T1 multi-atlas approach on data obtained with different acquisition protocols as compared to the manual delineation drawn on Philips protocol A (a) and in an inter-protocol manner (b) with corresponding linear regression lines. The quantitative susceptibility values (in ppm) per structure extracted from these data acquired using different protocols with the QSM/T1 multi-atlas approach are also compared to those obtained using the manual delineation (c).

To assess its general applicability, the QSM/T1 pipeline was tested on an external dataset. The results are shown in Fig. 7 and the corresponding Dice metrics and extracted tissue structure volumes and susceptibility values are summarized in Table 3. The segmentation by QSM/T1 multi-atlas pipeline in most selected structures agreed well with the manual delineation (Fig. 7a). An average Dice metric of 0.79±0.03 was observed over all ROIs (Table 3), with good performance (Dice values of 0.8 and above) observed in the basal ganglia and midbrain, while slightly inferior performance was observed in putamen, dentate, thalamus and thalamic pulvina (Dice of 0.74–0.78). The extracted tissue structure volume and magnetic susceptibility values in the deep gray matter nulcei using the automated segmentation were found to be consistent with those obtained using manual delineation (Table 3), with overall correlation coefficient above 0.97 for the structure volume measures (Fig. 7b) and above 0.94 for the tissue susceptiblity measures (Fig. 7c). The corresponding Bland-Altman plots of the volume and susceptiblity meaures between the QSM/T1 approach and manual labels are shown in Fig. S4. The limits of agreement for tissue magnetic susceptibility are 0.0024±0.018 ppm.

Fig. 7.

(a) Example manual and automated delineation using the QSM/T1 approach on a subject selected from the external dataset. Manual delineations of the sub-structures, i.e. GPi/GPe and STN, were not performed due to the lower resolution of the QSM images in this dataset and thus insufficient information to identify these sub-structures (marked by arrows with circular tail). The SN region therefore contains both SN and STN. The extracted tissue structure volumes (in mm³) (b) and quantitative susceptibility values (in ppm) (c) using the QSM/T1 approach were compared to those obtained using the manual labels.

Table 3:

External data set results for deep gray matter nuclei: Dice metrics (between manual delineation and automated segmentation using the QSM/T1 multi-atlas approach), extracted structure volumes (in mm³) and tissue susceptibility values (in ppm)

Measures	Dice	Volume (mm3)		Susceptibility (ppm)
ROIs		Manual	QSM/T1	Manual	QSM/T1
CN	0.81±0.05	4068±449	4048±444	0.039±0.005	0.038±0.006
GP	0.83±0.03	2218±239	2589±261	0.094±0.021	0.096±0.017
Putamen	0.77±0.03	3778±293	3819±326	0.053±0.012	0.041±0.007
Thalamus	0.78±0.04	4716±679	4704±473	−0.003±0.006	−0.003±0.006
Pulvinar	0.75±0.05	919±149	973±208	0.038±0.013	0.038±0.011
STN/SN	0.81±0.04	809±118	663±78	0.060±0.016	0.069±0.013
RN	0.82±0.04	300±42	264±38	0.052±0.012	0.060±0.011
DN	0.74±0.07	1023±249	677±208	0.038±0.014	0.051±0.014

CN: caudate nucleus, GP: globus pallidus including both globus pallidus externus and internus (GPe/GPi), STN/SN: subthalamic nucleus and substantia nigra, RN: red nucleus, DN: dentate nucleus.

We have made the developed QSM/T1 multi-atlas segmentation pipeline publicly available through our MRICloud platform: www.mricloud.org, which has a simple web-based interface and does not require any installation or advanced computational equipment. Users can simply upload the co-registered QSM and T1 images through the website and download the results after the calculation is finished. The output results include the segmentation in both native and MNI space with a summary of tissue structure volumes and magnetic susceptibility measures extracted for each label.

4. Discussion

In the present study, we developed a human brain multi-atlas tool utilizing both QSM and T1 contrast for reproducible region selection and magnetic susceptibility quantification of iron-rich subcortical gray matter nuclei. This was demonstrated for different imaging protocols and anatomical variations. Such a multi-atlas tool, currently not available, is an endeavor to address the increasing interest in studying aging and neurodegeneration using magnetic susceptibility as a quantitative MRI that can provide information about important tissue components such as iron and myelin. With the simple single-echo SWI acquisition widely available on clinical scanners and multi-echo GRE sequences increasingly used for QSM, existing and future studies are expected to benefit from such automated, reliable and freely accessible analysis tools for extracting clinically relevant quantitative susceptibility metrics from imaging data.

Previous and recent studies on automated analysis of QSM images have demonstrated the limitation of commonly used T1 based registration and segmentation approaches in quantifying QSM measures mainly due to the low T1 contrast in iron-rich deep gray matter nuclei (Cobzas et al., 2015; Lim et al., 2013). Many research efforts have therefore been devoted to the development of brain atlases and segmentation pipelines based on susceptibility contrast or on fused or combined contrast of susceptibility and T1 contrast (Cobzas et al., 2015; Feng et al., 2017; Garzon et al., 2018; Hanspach et al., 2017; Lim et al., 2013; Zhang et al., 2018). A very recent study has shown that in order to build an averaged susceptibility template with the best overall performance in terms of co-registering all QSM images, it is necessary to use either a hybrid QSM/T1 contrast or a multi-contrast optimization taking into account these two contrasts (Hanspach et al., 2017). The performance is however region dependent with pure QSM contrast being superior in the basal ganglia and thalamus and the hybrid or multi-contrast methods being superior in the motor cortex region and veins. A similar approach was also used to build longitudinal QSM atlases recently (Zhang et al., 2018).

Previously, we were successful in developing a susceptibility single-atlas for automated segmentation (Lim et al., 2013). However, the accuracy of brain mapping to a single atlas or a group-average is largely dependent on the similarity between the atlas and the subject brain in question. Therefore, when studying populations with large anatomical variations; e.g. with characteristic morphological changes associated with age, notably enlarged ventricles, widened sulci and cortical atrophy; accurate cross-subject registration may be hard to achieve (Diaz-de-Grenu et al., 2014) even with highly elastic diffeomorphic transformations, such as LDDMM (Miller et al., 2005; Wang et al., 2007). Consequently, automated analysis of quantitative magnetic susceptibility measures in elderly or patients with neurodegenerative diseases using the single-atlas is not very robust and reliable. In addition, for model-based group-averaged QSM atlas, an appropriate age-matched QSM template needs to be selected for segmenting the target brain (Zhang et al., 2018) and segmentation performance may still be not very robust if large anatomical variations exist in the same age group, e.g. due to pathological reasons (Iglesias and Sabuncu, 2015). As what happens for other image contrasts (Tang et al., 2015; Tang et al., 2013), the robustness of the registration and segmentation can be substantially improved by using a multi-atlas approach, which employs a set of human brain atlases covering sufficient anatomical variations with each atlas having accurate manual parcellation of similar brain structures.

One limitation of the QSM/T1 multi-atlas is of course the need to obtain both T1 and QSM images, which might not be available in all studies involving QSM e.g. iron studies. However, anatomical T1 weighted scans (MPRAGE) are routinely collected in research studies and often in clinical practice and, as shown in our study, the QSM/GRE multi-atlas might also give satisfactory segmentation in case a T1 scan is not available. T1 images have been widely used in MRI volumetric studies for years, with QSM images rarely collected in addition, which might be an even more important limitation for the wide use of our multi-atlas tool. Yet considering the fact that QSM techniques have not been developed until the recent decade, it is believed that there will be an increasing interest and use of the automated multi-atlas segmentation pipelines in the coming future. In this study, a GRE magnitude image averaged over echo times was used as one contrast channel to get a trade-off between the different contrast weightings over short and long echo times. In practice, for single-echo SWI data, using GRE magnitude images with matched TE might further improve the registration and segmentation accuracy, at least at a similar field strength.

In the current susceptibility multi-atlases, we used QSM maps reconstructed from the single supine head position, which is in principle inferior as compared to the QSM map calculated using COSMOS (Calculation of Susceptibility through Multiple Orientation Sampling)(Liu et al., 2009) that was used in a previous susceptibility single-atlas acquired on a healthy young subject (Lim et al., 2013). This is due to the unavailability of the susceptibility weighted scans in multiple directions for the selected elderly subjects and the fact that for most current and future clinical studies, multi-orientation QSM probably won’t be available anyway. However, the SFCR analysis approach was recently shown to have near-perfect agreement with COSMOS for magnetic susceptibility quantifications in deep gray matter regions when using supine data (Bao et al., 2016) and its use in the atlases in the present study again provided good segmentation/normalization results. Even better image quality of single-orientation QSM and better correspondence with respect to COSMOS can be expected in the near future with recent developments of more sophisticated phase preprocessing techniques (Fang et al., 2017) and deep learning techniques(Yoon et al., 2018).

While the agreement indices of the automated segmentation with respect to manual delineation and the inter-evaluator agreement were satisfactory in the LOO test, they were both relatively low in the thalamic pulvinar, which is partly due to the low QSM contrast in the pulvinar of several subjects in our current atlas set. This is of course an issue intrinsic to the QSM/T1 approach, i.e. segmentation of structures with poor contrasts in both QSM and T1 images would be purely based on prior knowledge and prone to errors. The thalamic pulvinar contrast varied between subjects in our atlas set, most likely due to different tissue iron content. Prospectively, the addition of extra-channels of contrast, e.g., contrast derived from DTI, may help ameliorate this issue in these cases. Better segmentation performance and higher Dice values in pulvinar were observe in the protocol reproducibility tests and tests on the external dataset. Our current study has also shown that segmentations of certain substructures e.g. the GPi and GPe and STN might be possible with the developed QSM/T1 multi-atlas tool if high resolution QSM images are available.

Compared to standard FSL FIRST and the recently developed multi-atlas based volBrain method, the presented QSM/T1 multi-atlas showed comparable or superior performance in segmenting several common subcortical regions, i.e. CN, putamen, GP and thalamus. However, it should be noted that our manual delineation was obtained by using both QSM and T1 contrast, while the training data or atlases in both FSL FIRST and volBrain were based on T1 contrast only. Since both manual and automated segmentation depends on the image contrast, there might be slight inconsistency between the delineation or definition of certain brain structures, e.g. definition of GP and thalamus, using combined QSM and T1 contrast versus T1 contrast only. Such inconsistency would therefore favor our QSM/T1 approach.

The susceptibility multi-atlas was also demonstrated to be very stable among platforms and protocols. Tests using the dataset acquired from the external study site employing a different acquisition protocol, a different scanner and a different QSM reconstruction further validated the reliability of our multi-atlas tool. Using these multi-atlas tools for normalization, the magnetic susceptibility values in most selected gray matter nuclei, which are known to be proportional to the tissue iron content, showed good reliability and reproducibility. Such stable results would allow combination of data from different sources into large databases and would help provide universal and generalizable metrics. These in turn could then be used for automated patient analysis, e.g. with the use of big data and machine learning approaches.

It should be noted that explicit QSM referencing to selected brain tissue was not used in the multi-atlases and all our conducted tests. Therefore, all the tissue magnetic susceptibility values reported in this study is equivalent to referencing to the whole-brain. The same way of referencing is also used in the summary output from our shared online pipeline (available at www.mricloud.org). However, this should not limit the use of other options of QSM referencing e.g. referencing to the ventricle CSF or overall WM as they are also provided in the multi-atlas segmentation. Users can also use other selected region of referencing for final QSM quantification.

Strategies to further improve the automated segmentation include the expansion of the atlas library, i.e. to include more atlases that cover broader anatomical variations and different patterns of iron deposition thus QSM contrast especially in the basal ganglia and thalamus, which is known to change during aging (Li et al., 2014; Zhang et al., 2018). Such contrast changes make it easier to delineate certain structures at younger age, e.g. the GPi and GPe, and other structures at later age, e.g. the pulvinar. While the number of atlases to be used varies according to the contrasts and the subjects in question, previous observations by our group and others have shown that the segmentation accuracy may start to converge by using about 10 atlases if an appropriate atlas pre-selection can be done (Ma et al., 2015; Ye et al., 2018). The criteria for pre-selection is the anatomical similarity between atlases and target. Factors such as age and pathology are also great determinants of anatomical similarity and therefore must be considered when selecting the proper atlas library. In addition, as the multi-atlas approach is critically dependent on the manual labels, certain systematic errors may exist if the original manual labels in the atlas are incorrect and have some common and consistent biases. Adding a step similar to “corrective learning” explained in (Wang and Yushkevich, 2013) after computing the label fusion might further improve the segmentation accuracy and help removing systematic manual segmentation errors in the original labels.

For the sake of cohort studies on brain volumetric change or iron deposition across the lifespan and among neurodegenerative diseases, the number of atlases used in the current study are still quite limited and probably account for only part of the expected variability. While more atlases will be added in the future, the 10 datasets we pre-selected to build this first version of the QSM/T1 multi-atlas pipeline does contain a reasonable amount of anatomical variation, e.g. with asymmetry, atrophy etc. that is essential for the multi-atlas method and showed reasonably good performance and robustness in all tested datasets (mainly healthy adults of middle to old age). Of course, for brains during neurodevelopment, i.e. infant, kids, teenagers, separate brain atlases are definitely needed. Increasing the number of atlases, especially with larger anatomical and susceptibility contrast variations in the future is expected to further improve the segmentation performance.

5. Conclusion

A magnetic susceptibility human brain multi-atlas quantification tool with improved accuracy and reliability for automated segmentation and quantification of QSM-based magnetic susceptibility measures was developed, which is expected to facilitate future individual analysis and studies on aging and neurodegeneration employing QSM. Further improvement on the performance of this tool is expected by increasing the number of atlases in the future.