Abstract
An air-conduction circuit model was developed for the chinchilla middle ear and cochlea. The lumped-element model is based on the classic Zwislocki model of the same structures in human. Model parameters were fit to various measurements of chinchilla middle-ear transfer functions and impedances, using a combination of error-minimization-driven computer-automated and manual fitting methods. The measurements used to fit the model comprise a newer, more-extensive data set than previously used, and include measurements of stapes velocity and inner-ear sound pressure within the vestibule and the scala tympani near the round window. The model is in agreement with studies of the effects of middle-ear cavity holes in experiments that require access to the middle-ear air space. The structure of the model allows easy addition of other sources of auditory stimulation, e.g., the multiple sources of bone-conducted sound—the long-term goal for the model's development—and mechanical stimulation of the ossicles and round window.
I. INTRODUCTION
Middle-ear models have been used for many years to investigate how the ear transforms sound pressure at the tympanic membrane to sound pressure in the inner ear. The lumped-element circuit model developed by Zwislocki (1962) was designed to fit measurements of middle-ear input impedance in humans in response to air-conducted sound and is the starting point for more-recent models (Kringlebotn, 1988; O'Connor and Puria, 2008). One benefit of these models is that the effects of pathological changes in ear structure can be predicted by altering the circuit element values and structure (Rosowski and Merchant, 1995; Songer and Rosowski, 2007a). Kringlebotn (1988) built on the Zwislocki model, with a focus on the effect of acoustic energy reflectance at the ear drum and the mechanical coupling between the eardrum and its suspension. In another variation of the Zwislocki model, O'Connor and Puria (2008) modeled the tympanic membrane (TM) as a distributed-parameter transmission line to account for phase delays seen in the middle-ear gain and other transfer functions with an output at the cochlea. While finite-element models have also been used to investigate sound transduction to the inner ear by the tympanic membrane and the ossicular chain (Funnell et al., 1992; Koike et al., 2002; Gan et al., 2004; Higashimachi et al., 2013; Motallebzadeh et al., 2017a), circuit models require less computational power and allow easy specification of the location and output of different sources of sound and vibration. Although various mathematical representations of chinchilla middle ears exist (Songer and Rosowski, 2007b; Wang and Gan, 2016), a lumped-element circuit model of the chinchilla middle ear has only been published recently (Lemons and Meaud, 2016).
While our model is similar in structure, it is unique to that of Lemons and Meaud (2016). Significant differences in parameter values occur because different data sets were used for fitting: Lemons and Meaud (2016) fit the data of Songer and Rosowski (2007b), while the current model is fit to a more-extensive set of middle-ear and inner-ear data with all measurements made in the same set of ears (Ravicz and Rosowski, 2012, 2013a,b). Moreover, the error-minimization methodology we use, although used elsewhere (Puria and Allen, 1998; Keefe, 2015), was not employed for determining lumped-element model parameters in past models of the chinchilla middle ear and cochlea.
Similarities between chinchilla and human auditory peripheries make the chinchilla a good choice of animal model for hearing research, where the intent is to adapt the model for study of the human auditory system. The behavioral frequency range of hearing in chinchilla extends from approximately 50 Hz to 33 kHz, while the range of hearing in a young, normal-hearing human is approximately 20 Hz to 20 kHz. The surface area of the human TM and stapes footplate are approximately 0.68 and 0.030 cm2 (Hemila et al., 1995), respectively, while those of the chinchilla are approximately 0.56 and 0.020 cm2, respectively (Vrettakos et al., 1988). While the chinchilla has a relatively large middle-ear air volume (2 cm3) (Ruggero et al., 1990), which like that of human is broken into multiple air spaces (Browning and Granich, 1978), the total volume is about a third of that of the average human air spaces (Molvaer et al., 1978) and there is no region that contains the small interconnected air cells found in the human mastoid.
The long-term goal of this research is to use this new model to guide investigations of the multiple mechanisms by which body vibrations (conducted to the inner ear via bone conduction) stimulate the inner ear. This goal has shaped this investigation, primarily in our concentration on sounds of frequencies of 10 kHz and lower.
II. METHODS
A. Basic circuit model and model transfer functions
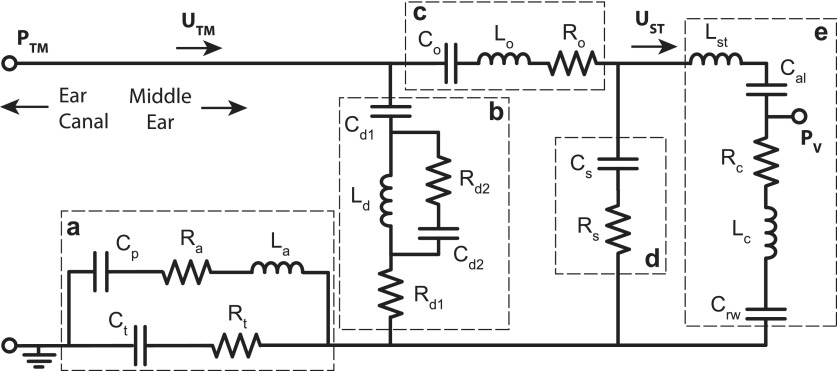
The air-conduction circuit model for chinchilla (Fig. 1) is a modification of the Zwislocki (1962) model with that model's simple form and a relatively small number of elements. The model has five anatomically distinct segments: (a) the air-filled middle-ear cavity, (b) ossicle-uncoupled TM, (c) ossicle-coupled TM, malleus, and incus, (d) incudostapedial joint (ISJ), and (e) the stapes, cochlea, and cochlear windows.
FIG. 1.
Circuit model of the intact chinchilla middle ear. Anatomically distinct segments are (a) middle-ear cavity, (b) ossicle-uncoupled TM, (c) ossicle-coupled TM and malleus-incus complex, (d) incudostapedial joint, and (e) stapes, cochlea, and cochlear windows. Parameter subscripts—a: aditus to the superior cavity, t: tympanic cavity, p: superior cavity, d#: ossicle-uncoupled TM, o: ossicle-coupled TM and malleus-incus complex, s: incudostapedial joint, st: stapes, al: annular ligament, c: cochlea, rw: round window.
The circuit model is a ladder network with combinations of series and parallel elements arranged in several branches. The parallel branches (b and d) model divergent paths for stimulus energy within the eardrum and ossicular joints, both of which “shunt” a fraction of the stimulus away from the inner ear. These shunt paths account for relative motions within the TM and the ossicular chain (Huber et al., 2001; Rosowski et al., 2003; Nakajima et al., 2005). Humans have potentially two ossicular shunts: the incudomalleolar joint (IMJ) and the incudostapedial joint (ISJ). In the chinchilla, the IMJ is ankylosed, therefore shunting within the ossicles in chinchilla is attributed to compliance in the ISJ or the ossicles themselves due to bending (Funnell et al., 1992). Shunts of the latter type would be included in model branch b. The model was solved in the sinusoidal steady state, and while its parameter values are all real numbers, the branch and nodal currents and voltages are complex numbers with both a magnitude and a phase.
The model represents sound pressures as voltages and volume velocities as currents. Descriptions of middle-ear function usually include the transformation of sound energy that reaches the inner ear by the ratio of the areas of the TM and stapes footplate (), and the ratio of the lengths of the malleus and incus lever arms () (Dallos, 1973). However, Fig. 1 includes no explicit transformers. Instead, the transformers are implicitly included in the model parameters and the internal circuit volume velocities () and sound pressures () values. To compute the actual scala vestibuli sound pressure and stapes volume velocity (i.e., and ), one needs to remove the transformation, e.g.,
| (1) |
| (2) |
The model variables with the transformers removed are used to compute two transfer functions [the middle-ear gain (GME) and the stapes-velocity transfer function (SVTF)] and the cochlear input impedance ZC, specifically,
| (3) |
| (4) |
where the velocity of the stapes is divided by the area of the stapes footplate, and
| (5) |
The model directly defines (without the need for transformers) the volume velocity at the TM, UTM, and the sound pressure at the TM in the ear canal, PTM. The ratio of these variables describes the middle-ear input impedance
| (6) |
All four of these system functions [Eqs. (3)–(6)] are implicit functions of frequency.
B. Modification of the middle-ear cavity model to fit measurement conditions
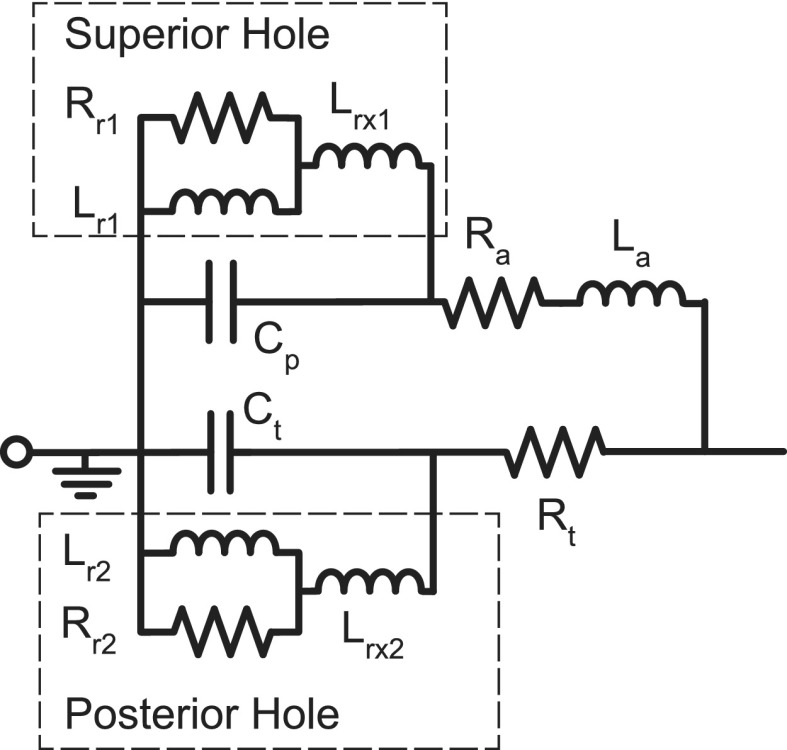
The model of the middle-ear air spaces in branch a of Fig. 1 describes the circumstance where the middle-ear cavity is split between two major air spaces: one directly behind the TM with compliance Ct, and a second superiorly positioned space with compliance Cp that is connected to the first by a foramen, or aditus, with resistance Ra and inertance La. This description can be generally applied to the chinchilla, even though the two model volumes actually represent the combined volumes of multiple inter-connected air spaces (Browning and Granich, 1978). The model of Fig. 1 represents air-filled cavities that are naturally closed to the outside via bony walls; however, most measurements of middle-ear function require opening the bony walls for manipulations of middle-ear muscles, observation of the ossicles, or the placement of microphone probes within the inner ear (Songer and Rosowski, 2006; Ravicz and Rosowski, 2013a,b). Modeling this “open cavity” condition requires adding elements to model the inertances (acoustic masses) associated with sound flow through the openings in the bone, and the radiation impedances from these openings to the outside world (Fig. 2).
FIG. 2.
The addition of six elements to the cavity model of branch (a) in Fig. 1 to account for (1) the placement of a hole into the superior cavity of the chinchilla middle ear (subscript 1), and (2) the placement of a hole into the posterior wall of the tympanic cavity (subscript 2). Each hole is modeled by the addition of an inertance (Lrx#) that models sound flow through the hole, placed in series with a parallel inertance and resistance (subscript r#) modeling the impedance associated with radiation of the sound into the atmosphere (Beranek, 1993).
C. Parameter values set by anatomy and structure
Where possible, model parameters were determined from anatomical values. The compressibility (compliance) of air within closed and nearly closed cavities, and the compliances of membranes and joints are described by electrical capacitors. Translationally oscillating media of known mass (i.e., inertance) and moments of inertia of mechanical masses that undergo rotational motion are represented as inductances. Damping and energy absorbance within the ear are represented by resistors. The middle-ear cavity compliances were constrained by the measurements of the equivalent volume of the combination of the two compliances made by Rosowski et al. (2006),
| (7) |
where ρair is the density of air, cair is the speed of sound in air, Vp and Vt are the volumes of the superior and tympanic cavities, and Vtotal = 2 cm3. The masses of the malleus-incus complex and the stapes are related to the inertances Lo and Lst by the appropriate transformer values
| (8) |
| (9) |
As the stapes inertance Lst is in series with that of the cochlear inertance Lc, and the Zwislocki model does not distinguish between the two, the early optimization passes (steps 1–5 described below) were made with Lst set to zero. Later, the stapes inertance was constrained by Eq. (9).
D. Computer-automated objective optimization procedures
As is described in more detail below, the techniques for estimation of circuit model parameters included multiple passes through a computer-automated objective optimization procedure. This fitting procedure involved iterative perturbations of model parameters to produce a “best” fit of model outputs to the magnitude and phase of experimentally determined system functions. The matlab function fminsearch was adapted for this purpose. The computed outputs of either the entire circuit model or particular model segments were fit to experimental data describing the magnitude and phase of system equations relevant to either the complete model or the studied segment, using the Nelder-Mead simplex method (Nelder and Mead, 1965) for solving multidimensional optimization problems invoked by fminsearch. This iterative method produced an “optimum” parameter set associated with a minimum in a “cost” function.
Ideally, the cost associated with the fit to each data set is the mean of the square of the difference between the model output and the experimental data normalized by the experimental data at each frequency point summed over m frequencies [Eq. (10)], where y is the model output and yo is the experimental data. This normalization converts the deviation into a fraction of the measured values. This generalized formula was sufficient for fitting the model to phase data (after adding 2π to each of the phases as described below). In the case of magnitudes, because the experimental data range over several orders of magnitude, the logarithm (base 10) of both the experimental and model magnitudes were used to estimate the cost [Eq. (11)], as non-logarithmic cost estimates that include normalization by the target value emphasized the fit at data regions with small magnitude and high signal-to-noise ratios. The calculation of the logarithmic magnitude costs in Eq. (11) did not include explicit normalization to the experimental data, as the calculation of the logarithm provided an implicit normalization to the common reference value, where the log quantities were implicitly referenced by a value of 1 of the same units (e.g., a reference value of 1 mm s−1 Pa−1 was used to convert the model and measured |SVTF| to log values). The total cost [Eq. (12)] is the root-mean-square of the costs associated with the n = 6 system equations (3 magnitude and 3 phase). Equal weight was given to the cost of the magnitude and phase of the transfer functions, and each transfer function was weighted equally,
| (10) |
| (11) |
| (12) |
The measured and model phases in some frequency ranges originally included zero as a possible value. Since normalization by a measured phase near zero would greatly increase the cost [Eq. (10)], a + 2π shift was applied to the wrapped experimental and model phases before the cost was calculated. This cycle phase-shift was undone before plotting the results.
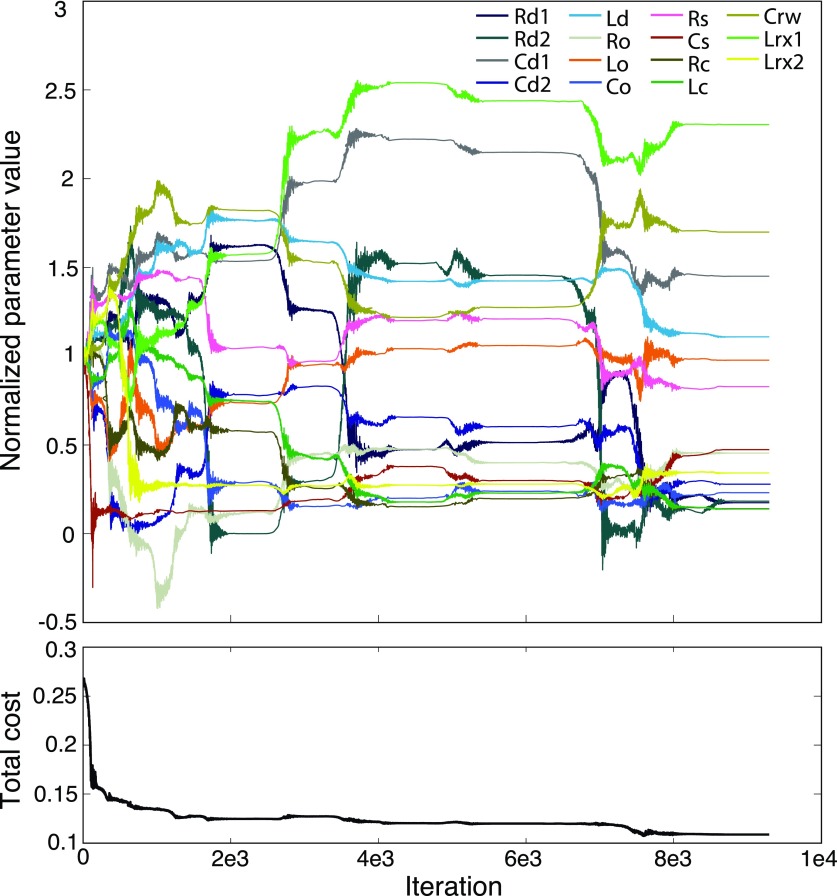
The first set of parameter values for the initial iteration of the model were based on an optimized version of the Zwislocki human middle-ear model parameters (Bowers and Rosowski, 2016). The application of fminsearch results in the iteration of perturbations of all variable parameter values simultaneously, and the calculation of the total cost associated with the updated parameter set.1 For each run, this repeated perturbation and recalculation of the cost was iterated (on the order of 10 000 times) until the predicted parameters stabilized at an “optimum” value. An example of how the parameter values were altered during a single optimization run is illustrated in Fig. 3.
FIG. 3.
(Color online) An example of a single automated objective optimization run of the matlab fminsearch algorithm. Parameter values normalized by their starting “initial” value are shown as a function of the number of iterations of the algorithm. Total cost is calculated using Eq. (12) and accounts for fitting the model to the magnitude and phase of ZME, SVTF, and ZC. Significant changes in parameter values occurred during the first 8000 iterations, but stability was achieved by 9500 iterations.
Due to the high probability of multiple local minima in the total cost associated with optimization of the 14 or more variable model parameters solved for in each iteration, hundreds of automated optimization runs (each of which included thousands of iterations) were performed after forced variations in the starting parameter values: before each run, we applied a separate randomized multiplication factor (over a specified range) to each of the parameter values used to initiate the optimization run. Each of these runs resulted in a unique set of parameters and a cost value. The final output of the hundreds of runs was the stable parameter set with the lowest cost.
A complication of the Nelder-Mead simplex method is that limits cannot be placed on possible parameter value solutions. In order to prevent negative parameter values (i.e., negative compliances, masses, or resistances), the absolute values of those chosen by the algorithm were used to calculate the system outputs at each iteration of the automated process.
E. Manual optimization procedures
To supplement the computer-automated objective optimization procedures, manual fitting procedures were implemented. The purpose of manual fitting was either to test whether the model could be improved beyond what the automated process produced, or to correct the objectively fit parameters to anatomically realistic values. The manual fitting procedures were guided by (i) visual inspection of the model outputs relative to the experimental data and (ii) “sensitivity analyses” that tested how controlled changes in each of the parameter values altered the cost of the model.
Visual inspection was performed via a graphical user interface (GUI). The GUI allowed adjustment of individual parameter values while displaying in real-time the predicted model transfer functions superimposed on the measured data, and the cost associated with the adjusted model parameter set.
The sensitivity analyses tracked how the total cost was affected by isolated ±5%, ±10%, and ±20% changes in each of the individual parameters. Those changes in parameter values that led to decreases in cost indicated a less-than-optimal fit to the data. The single parameter that produced the largest alterations in cost was identified and its value set to minimize cost. The analysis was repeated until the parameters appeared optimum. The change in cost as a function of parameter value perturbation is not necessarily monotonic, hence it is important to examine varying degrees of change. For example, increasing a parameter by 5% may increase cost, but further increases in the same parameter value may result in a cost reduction. If all parameter changes increase the cost, the given parameter set is judged a potential globally optimal set.
F. Estimation of round-window compliance
After multiple sets of automated and manual optimizations determined an optimum set of model parameters for the elements described in Figs. 1 and 2, the cochlear network of the original Zwislocki model was expanded to include several new elements that allowed model estimates of scala tympani sound pressure (PST). Fitting the expanded model to PST measurements helps constrain the round-window compliance, and allows future model calculations of the pressure difference across the cochlear partition. In experiments by Ravicz and Rosowski (2013a), sound pressures were measured simultaneously in the ear canal near the TM and in the two cochlear scalae, including the sound pressure in the scala tympani near the round window.
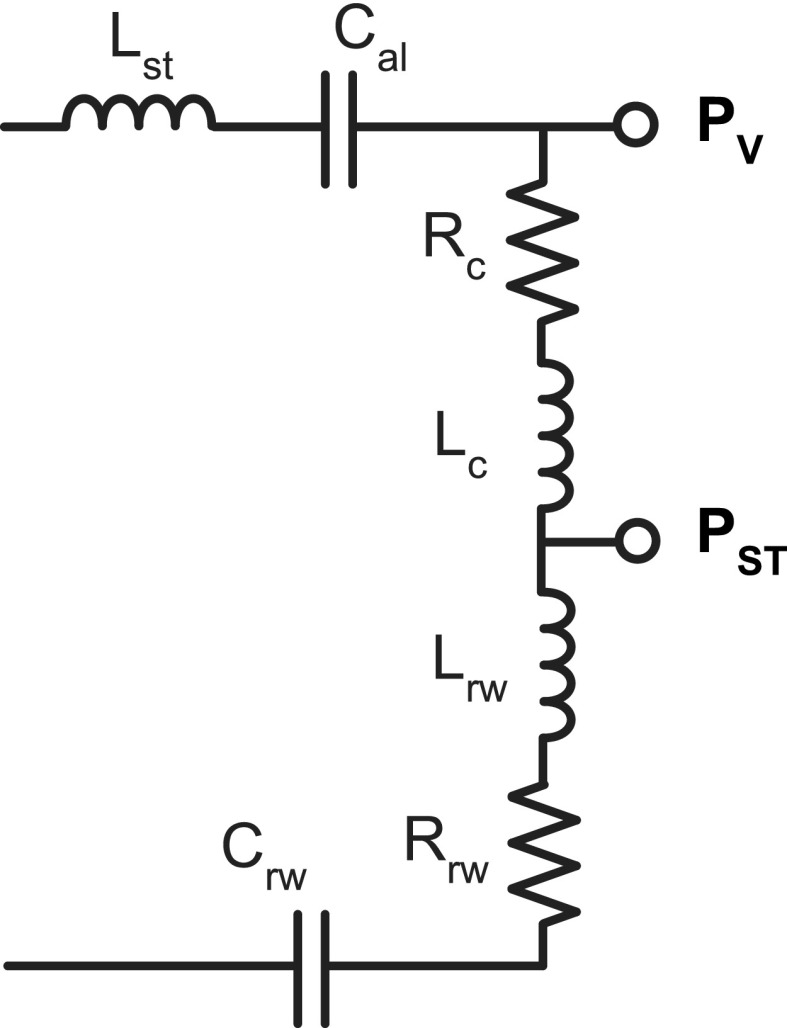
To enable accurate estimation of PST, two elements were added to the cochlear network (Fig. 4): an inertance to model the mass of a column of water-like perilymph between the scala tympani sound-pressure sensor and the round window (Lrw), and an associated resistance (Rrw). Such elements have been introduced in multiple previous studies that modeled measurements of Pst (Nedzelnitsky, 1980; Olson, 2001; Nakajima et al., 2009; Frear et al., 2018).2 As was the case for the vestibule sound pressure, the prediction of the target was calculated by removing the implicit effect of the middle-ear transformers on the model representation of PST,
| (13) |
FIG. 4.
Expanded cochlear network. An inertance Lrw and resistance Rrw were added to the cochlear network, allowing calculation of the sound pressure in the scala tympani PST.
A single automated optimization run was used to find the values of Crw, Lrw, and Rrw that best fit measurements of normalized by the sound pressure in the ear canal PTM (Ravicz and Rosowski, 2013a).
G. Complete procedure for fitting model elements
The procedures for determining the model parameters that best describe the transmission of air-conducted sound through the chinchilla middle ear are summarized in Fig. 5. Our process tries to minimize the number of free parameters that are subject to optimization by exploring different sections and elements by optimization while separated from other parts of the circuit. Figure 5 describes 12 steps.
FIG. 5.
Flow chart of model development.
Steps 1 through 3 describe the initial concentration on an accurate and complete model of the air-filled middle-ear cavity based on the model structure and published measurements of the acoustic impedance of the cavities (Rosowski et al., 2006). (Optimization of nine model parameters.) In step 1, measurements of the cavity impedance at low and middle frequencies were used to fix values of the cavity volumes (directly related to Cp and Ct) and inertance La of the aditus that connects them. In step 2, the circuit structure of branch a in Fig. 1 with circuit parameters defined by step 1, and initial parameters for Ra, Rt, and La from the Zwislocki circuit were used as inputs to 200 automated optimization runs used to fix Ra, Rt, and La for later fitting procedures. In step 3, estimates of the radii of the two openings into the middle-ear cavity were used to fix the four radiation impedance parameters included in Fig. 2 (Lr1, Lr2, Rr1, and Rr2). The additional inertances in Fig. 2 (Lrx1 and Lrx2) were set to zero.
Steps 4 and 5 are independent sets of 200 computer-automated objective optimization runs to fit the magnitude and angle of ZME, SVTF, and ZC measured with the middle-ear cavities in the open state. In these steps, the cavity model parameters were fixed at the values defined by steps 1 through 3, and AR and LR (area and lever ratios) were fixed at their anatomically defined values. For reasons described above, the inertance associated with the stapes mass Lst was also fixed at zero. The 14 other elements in branches b through e of Fig. 1 were adjusted in both steps. In Step 4, human-defined initial values were used for all varied elements, and each initial value was individually randomly varied (by a factor between 0.001 and 1000) before each of a series of 200 optimization runs. The 14 resultant parameters of the run with the lowest cost were used as initial values to step 5. In step 5, as above, before each of 200 optimization runs, each initial parameter value was individually varied by a random factor between 0.001 and 1000. The 14 resultant parameters of the step 5 run with the lowest cost define these elements in further stages.
Steps 6 through 8 were manual adjustments of the model parameters guided by calculations of the cost of the fit. Step 6 introduced new model elements. The inertance of the stapes Lst was fixed at a value derived from its anatomical mass and the contribution of the two transformers [Eq. (9)]. Additional cavity parameters Lxr1 and Lxr2 were added to the circuit, with initial values set by manual adjustments in the next step. Step 7 was a manual adjustment of the circuit values using the GUI to provide visual comparisons of the model predictions and the measured magnitude and phase of ZME, SVTF, and ZC with middle-ear cavities in the open state. Twenty-six parameters could be adjusted including: the two radii that fix the four radiation impedance elements in Fig. 2, the other 22 elements of Figs. 1 and 2 (including those added in Step 6), the TM area, and malleus-incus lever ratio. Step 8 was a complete sensitivity analysis on the individual effects of variations in each of the 26 model parameters to fine-tune the manual adjustments of step 7.
In steps 9a–9e, computer-automated objective optimization runs were performed. Each substep of step 9 allowed the optimization process to explore a unique range of initial values. Sixteen of the circuit parameters (including Lrx1 and Lrx2 introduced in step 6) were variable, while the 9 middle-ear cavity parameters, the stapes inertance (Lst), and the two transformer ratios (AR and LR) were fixed at the values defined by step 8. All sub-steps of step 9 used the fixed and modified parameter values of step 8 as initial values, but a varying range of randomization factors (10±n) was applied to the initial variables: in step 9a, n = 0.25 (200 runs); in step 9b, n = 0.5 (100 runs); in step 9c, n = 1 (100 runs); in step 9d, n = 2 (100 runs); in step 9e, n = 3 (100 runs). The purpose of these repeated optimization-run sets was to search for the true global minimum in cost.
Steps 10 and 11 were manual adjustments. In step 10, the GUI was used to manually adjust Lrx1 and Lrx2, as the value of Lrx1 from step 9 was not anatomically realistic and because of the interplay between Lrx1 and Lrx2 and their effects on the middle-ear transfer-function outputs. All other parameters were fixed by the result of step 9. The modification of Lrx1 and Lrx2 in step 10 required adjustment of certain parameters; in step 11, Lrx1 and Lrx2 were maintained at their manually set values, but the other 24 model parameters (including those associated with the middle-ear transformer ratios) were subjected to repeated manual sensitivity analyses for fine-tuning.
In step 12, the cochlear network was expanded to allow predictions of the sound pressure in scala tympani near the round window (Pst) by adding the inertance Lrw and resistance Rrw in series with Crw. The values of Lrw and Rrw were constrained along with the values of Lc and Rc so that the total cochlear inertance and resistance were unchanged from that defined in step 11. Specifically, the value of Lrw plus the new value of Lc must equal the value of Lc defined in the previous step. A similar constraint was placed on Rrw and Rc. New parameter values for Lrw, Lc, Rrw, Rc [indirectly by varying Lratio = Lrw/(Lrw + Lc) and Rratio = Rrw/(Rrw + Rc)] and an updated value of the round-window compliance Crw were determined—optimization of three model parameters—by a single computer-automated optimization run (randomization of initial values did not produce different results) that fit the model outputs to the /PTM measurements of Ravicz and Rosowski (2013a). All other parameter values were fixed.
III. MODEL FITS
A. Model of the middle-ear air spaces
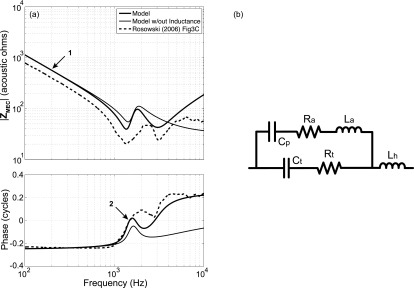
The parameters of the two inter-connected chambers of the intact middle-ear cavity (branch a of Fig. 1) that incorporate the tympanic and superior cavities (the former with volume approximately 3 times that of the latter, and both totaling approximately 2 cm3) were independently analyzed from the rest of the model (TM, ossicles, and cochlea). Step 1 fixed the model parameters that describe the cavity compliances (Ct and Cp) and the inertance of the aditus (La) that connects them, based on a combination of manual and automated fittings to measurements of the input impedance of the cavity, with intact walls, made at frequencies between 0.1 and 2 kHz [Fig. 6(a)]. The low-frequency impedance [at 0.2 kHz, arrow 1 in Fig. 6(a)] can be attributed to the parallel compliances of the two air-filled cavities, with the relationship described by the following equation:
| (14) |
where ZMEC is the impedance of the middle-ear cavity, Ct is the compliance of tympanic cavity, AV is the compliance ratio of the superior cavity Cp to the tympanic cavity Ct (which equals the ratio of the volumes of the superior and tympanic cavities), and the angular frequency is ω = 2πf. Unlike human (Molvaer et al., 1978), there is little inter-individual variation in the total volume of the chinchilla middle-ear cavity (Vrettakos et al., 1988).
FIG. 6.
Middle-ear cavity. (a) Impedance of the fitted intact (no holes) middle-ear cavity superimposed on the averaged data of Rosowski et al. (2006). The middle-ear cavity model parameters were defined by fitting its parameter values to the measured data using a combination of observations from the mean impedance data and the automated optimization technique. Arrow 1 indicates the frequency at which the summed cavity compliances were estimated. Arrow 2 indicates the frequency at which the inertance La was calculated; (b) middle-ear cavity network with a series TM hole inertance that was included in the middle-ear cavity network during this step to represent the perforation in the TM (Voss et al., 2001) that was present during the experimental measurements.
The process of determining the middle-ear cavity parameter values was repeated with AV values between 0.2 and 0.4 with AV = 0.35 yielding the lowest cost and best fit. The inertance La associated with the aditus between the two cavity regions was estimated from the frequency near the lower-frequency minimum in magnitude where the angle of the measured cavity impedance is zero [at 1.49 kHz, arrow 2 in Fig. 6(a)]. The minimum in magnitude and zero angle of the impedance are due to the series resonance between La and Cp (step 1); at the resonant frequency ωo, the imaginary part of the cavity impedance is zero and La can be calculated from Cp and the square of the resonance frequency,
| (15) |
As noted by the thin solid line in Fig. 6(a), the cavity model described by branch a of Fig. 1 explains many of the features of the cavity impedance measurements made in chinchilla [the dashed line in Fig. 6(a)] at frequencies below 2.5 kHz, but it does not explain the second minimum in impedance magnitude and the increasing angle seen at higher frequencies. This difference probably occurs because the cavity impedance measurements were performed in chinchillas with large (∼4 mm2) TM perforations (Rosowski et al., 2006). An appropriately valued inertance (Lh) [Fig. 6(b)] associated with such large perforations (Voss et al., 2001) improved the model fit to the impedance at higher frequencies [thicker solid line of Fig. 6(a)]. In step 2, the automated optimization process was used to determine a resistance of the tympanic cavity (Rt), resistance of the aditus (Ra), and the inertance Lh that best fit the measurement in Fig. 6(a), while Ct, Cp, and La were held constant with the values defined in step 1. The magnitude of Lh determined by the optimization is 3.8e−3 kg m−4, and is consistent with a perforation size of 1.7 mm in radius [Eq. (16); a and l are the radius and length of the perforation],
| (16) |
Equation (16) assumes that the inertance Lh accounts for the mass of air within the perforation as well as the mass portion of a radiation impedance at both ends of the perforation; the resistance portion of the radiation impedance is not considered. While the contribution of Lh was important to fit the cavity model to the cavity impedance measurements of Rosowski et al. (2006) at the higher frequencies, the measurements used to describe branches b through e of the model were made with an intact TM, and the perforation inertance (Lh) was not included in our later analyses.
While the TM was intact in the measurements used to define the rest of the model, two holes were made in the middle-ear cavity to access structures within it: one hole opened the superior cavity to the outside (and allowed access to the tensor tympani tendon, which was cut in all of the measurements), and a second posterior hole opened the tympanic cavity to the outside (and allowed access for stapes velocity and inner-ear sound pressure measurements). In step 3, we amended the cavity model structure to the model of Fig. 2 that includes the effects of the holes and the impedance associated with sound radiation from the holes. The radiation impedances were defined by two elements in parallel (Fig. 2), having parameter values that depend on the radius of the holes,
| (17) |
| (18) |
where Rr and Lr are the resistance and inertance associated with the radiation impedance, and r is the radius of the hole. Middle-ear cavity subscripts 1 and 2 note the superior cavity and tympanic cavity, respectively. Radii of 3.9 and 2.5 mm, estimated from a specimen used in the experiments of Ravicz and Rosowski (2013b), were used to calculate the radiation impedance parameters of the superior cavity and tympanic cavity holes, respectively.
B. Original automated fitting of 14 middle-ear and cochlea parameters: Steps 4 and 5
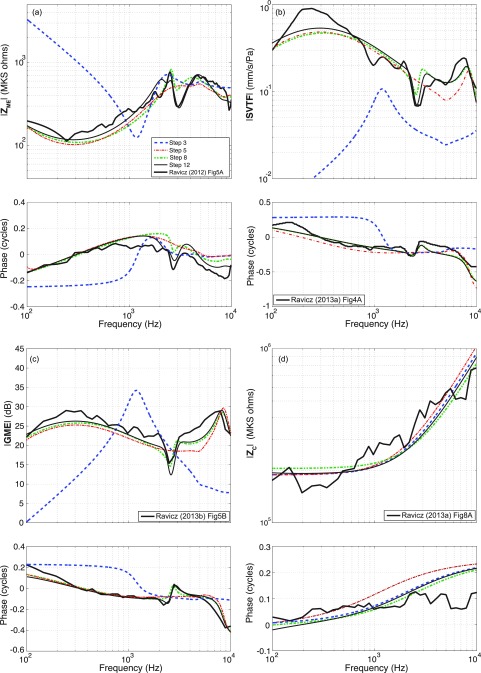
With branch a of Fig. 1 replaced by the circuit of Fig. 2, and with most elements of that branch fixed by steps 1–3 (at this point Lrx1 and Lrx2 were set to zero), the parameters of the ossicularly uncoupled TM (branch b), ossicle-coupled TM and malleus-incus complex (branch c), incudostapedial joint (branch d), and the series combination of the stapes inertance, annular ligament and oval window compliances, and cochlear elements (branch e) were approximated by automated fitting (steps 4 and 5) to measured ZME, SVTF, and Zc data (Ravicz and Rosowski, 2012, 2013a,b). (The stapes inertance was set to zero and unchanged throughout this fitting step.)
The initial values for the automated optimizations of branch b, c, and d elements were from an optimized version of the human middle-ear model of Zwislocki (1962) (Bowers and Rosowski, 2016). Initial values of the cochlear resistive and inductive parameters (in branch e) were determined by manual fitting to the cochlear input impedance (Zc) data [Fig. 7(d)]. The magnitude of the measured cochlear input impedance (Ravicz and Rosowski, 2013b) is relatively flat up to approximately 600 Hz, after which it increases with increasing frequency. This frequency dependence suggests the series combination of a resistance Rc = 1.88e6 kg s−1 m−4 and inertance Lc = 1.46e2 kg m−4, where their values in the model depend on the middle-ear transformer ratios. The resistive effect is assumed to result from the distributed mass and stiffness of the scala fluids and basilar membrane, while the inertance term describes the effect of a mass of fluid between the stapes footplate and the cochlea, as described by Zwislocki (1962). The stapes footplate mass was set to zero, and any inertance in branch e determined by the iterative process was attributed to Lc. The annular ligament (Cal) and round window (Crw) compliance initial values were defined by the optimized Zwislocki model (Bowers and Rosowski, 2016), as there is no obvious compliance-dominated region in the cochlear input impedance data [Fig. 7(d)]. The transfer-function predictions produced by these mixed human and chinchilla initial values of the 14 middle-ear elements are illustrated as the step 3 predictions in Fig. 7, where the large deviations between the measured and step 3 model ZME, SVTF, and GME are the direct result of the use of human model parameters at this stage.
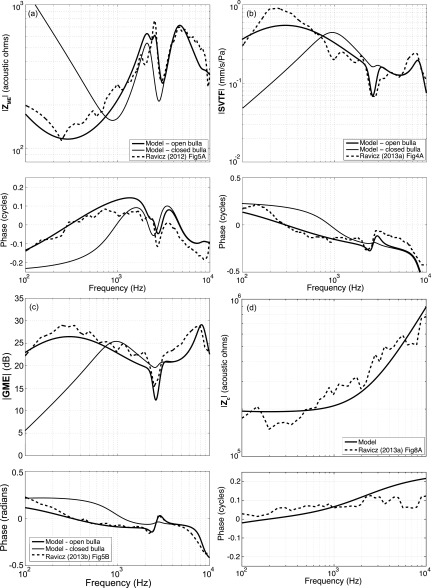
FIG. 7.
(Color online) Outputs of model steps 3, 5, 8, and 12 with superimposed experimental data. Model fits are compared to experimental data of Ravicz and Rosowski (2012, 2013a,b).
During the step 4 and 5 automated fittings, the middle-ear lever ratio LR and stapes footplate area were fixed at 2.84 and 0.0198 cm2, respectively (Vrettakos et al., 1988). The effective TM area was constrained to a pars tensa area of 0.70 cm2 (maximum; Rosowski, 1994), such that AR = 35.3. The transformer ratios have a large effect on both the element predictions and the target data [e.g., Eqs. (3), (4), and (5)], and allowing them to vary freely led to highly inconsistent element definitions.
Two sets of 200 computer-automated optimization runs fit the element-dependent transfer functions of the model to the six target system equations, including: the magnitude and phase of the input impedance of the ear [ZME: Fig. 7(a)], the magnitude and phase of the stapes velocity transfer function [SVTF: Fig. 7(b)], and the magnitude and phase of the cochlear input impedance [Zc: Fig. 7(d)]. The measured middle-ear gain [GME: Fig. 7(c)] was used in the manual fitting procedures, but was excluded from the automatic fitting, as GME is directly related to the combination of Zc and SVTF. The system functions with the model parameters produced by step 5 (Fig. 7) were better fits to the target data than the system functions produced by the model with human-based elements (step 3 in Fig. 7).
C. Introduction of additional model parameters and manual fitting: Steps 6, 7, and 8
Two shortcomings of the model results of step 5 are its lack of an explicit stapes inertance, and the poor fit of the model predictions to the prominent notch in the magnitude and phase near 2.7 kHz seen in the middle-ear dependent transfer functions [Figs. 7(a), 7(b), and 7(c)]. To address the first weakness, step 6 partitioned the branch e inertance into the cochlear inertance Lc and the inertance of the stapes Lst, where the latter was initially set by the transformer ratios and a stapes mass of 0.52 mg using Eq. (9).
The 2.7 kHz notch in the measured magnitude and phase of ZME, SVTF, and GME is thought to result from an anti-resonance that results from the parallel combination of the compliances of the middle-ear cavity and inertances associated with sound flow out the cavity holes (Fig. 2) that were introduced to observe and manipulate the middle ear (Rosowski et al., 2006). While the model used in step 5 contains an anatomically defined radiation inertance, that inertance neither produces the notch seen in the data, nor does it account for the fraction of air within the cavities that is accelerated by sound flow out the cavity hole. This additional inertance at the two cavity holes was added in step 6 by including non-zero Lrx1 and Lrx2 into the cavity model with holes in the cavity wall (Fig. 2).
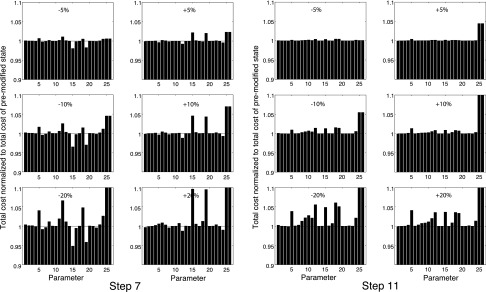
After introducing these new elements, the model parameters were refined using the GUI to visually fit the model predictions to data from ZME, SVTF, Zc, and GME simultaneously (step 7). All 26 model parameters introduced by this point (22 circuit-model element values, 2 middle-ear transformer ratios, and the 2 radii of the cavity holes that controlled the radiation impedances) could be varied. In step 8, repeated sensitivity analyses were performed in which the parameter with the greatest impact was altered to minimize the cost. These cost-guided manual adjustments were repeated until the cost associated with each of the parameters appeared to be minimum. The initial sensitivity analyses of step 8, which tested the sensitivity of the cost to the parameters defined in step 7, are illustrated on the left in Fig. 8. The panels illustrate the fractional change in cost due to ±5%, ±10%, and ±20% variations in individual parameters while all other parameters were held constant. The 26 parameters are arranged along the horizontal axis, where the correspondence between the 26 sensitivity-analysis numbers (SA #) and the parameter names are included in Tables II and III. The existence of decreases in cost associated with changes in the 26 parameters in these panels indicate that step 7 did not produce an optimum parameter set.
FIG. 8.
Sensitivity analyses. Parameters were altered ±5%, ±10%, and ±20% and the change in cost was calculated. Shown is the change in cost produced by perturbations in each of the 26 parameters; the SA # of each parameter, which describes its position along the horizontal axes, is in Tables II and III. The sensitivity analysis of resulting parameter set of step 7 is shown on the left; the deviations from unit values demonstrate some residual non-optimum parameter values. The step 11 results on the right are consistent with an optimum parameter set as the perturbations do not decrease the cost. Parameters 25 and 26 are the transformer ratios.
TABLE II.
Middle-ear cavity network parameter values of step 12 output. All values are in MKS units. Resistance values have units of kg s−1 m−4, inertances have units of kg m−4, and compliances have units of m4 s2 kg−1. SA # is the number assigned to the parameter for the sensitivity analysis. The paired radiation resistances and inertances Rrx and Lrx are linked in the SA by the radius of the holes.
| Parameter | Output of Step 12 | SA # |
|---|---|---|
| Ra | 3.83 e7 | 1 |
| La | 3.18 e2 | 2 |
| Cp | 3.62 e−12 | 3 |
| Rt | 1.60 e6 | 4 |
| Ct | 1.04 e−11 | 5 |
| Rr1 | 8.23 e6 | 21 |
| Lr1 | 7.39 e2 | 21 |
| Rr2 | 2.69 e7 | 22 |
| Lr2 | 1.33 e2 | 22 |
| Lrx1 | 2.53 e2 | 23 |
| Lrx2 | 2.59 e2 | 24 |
TABLE III.
Middle-ear and cochlea parameter values of Step 12 output. All values are in MKS units. Resistance values have units of kg s−1 m−4, inertances have units of kg m−4, and compliances have units of m4 s2 kg−1. SA # is the number assigned to the parameter for the sensitivity analysis.
| Parameter | Output of Step 12 | SA # |
|---|---|---|
| Rd1 | 8.34 e6 | 6 |
| Rd2 | 8.29 e6 | 5 |
| Cd1 | 1.36 e−12 | 8 |
| Cd2 | 2.05 e−12 | 9 |
| Ld | 1.02 e3 | 10 |
| Ro | 7.51 e6 | 11 |
| Lo | 21.0 e3 | 12 |
| Co | 2.07 e−6 | 13 |
| Rs | 3.18 e5 | 14 |
| Cs | 1.70 e−12 | 15 |
| Lst | 15.0 | 16 |
| Cal | 1.10 e−10 | 17 |
| Rc | 3.15 e6 | 18 |
| Lc | 2.27 e2 | 19 |
| Crw | 2.89 e−9 | 20 |
| Rrw | 6.24 e4 | NA |
| Lrw | 68.8 | NA |
| TM area | 0.668 cm2 | 25 |
| Lever | 2.83 | 26 |
| FP Area | 0.0198 cm2 |
The transfer functions predicted by the parameter set defined by step 8 show a clear notch near 2.7 kHz in the magnitude and phase of SVTF, GME, and the phase of ZME, but the notch in ZME magnitude is less well-defined [Figs. 7(a)–7(c)].
D. Step 9: Final automated optimization
Our sensitivity analyses do not guarantee the resulting parameter set is the “best” fit, therefore additional automated fitting steps were performed. Middle-ear cavity parameters, the middle-ear transformer ratios, and the value of Lst were fixed at the values defined in the previous step, and 16 parameters (including Lrx1 and Lrx2) were variable. In steps 9a–9e, a set of automatic fits were performed in which unique, random multiplication factors were applied to the parameter initial values of step 8. The purpose was twofold: (i) to search in the nearby cost-function space for a lower-cost parameter set, where the resulting parameters are not significantly different from the initial values (small randomization factors), and ii) to search for an equally good, or better set of system parameters that could be significantly different than those determined heretofore (large randomization factors). A multiplication factor having a range of 10±n was applied to each parameter, where n = 0.25, 0.5, 1, 2, or 3. A set of 200 optimization runs was performed for n = 0.25, while 100 optimization runs were performed for n = 0.5, 1, 2, and 3. The optimization runs of these two steps produced little change in the model parameter set and the predicted transfer functions.
E. Steps 10 and 11: Final manual fitting and sensitivity analysis
Step 10 invoked the GUI to adjust any parameters defined by step 9 that were inconsistent with anatomical values. Specifically, step 9 defined inertance Lrx1, representing the air mass of the superior cavity resulting from the bulla hole, with a mobile volume of air of 23.5 cm3, which is an order of magnitude greater than the volume of the cavity itself. Manual fitting guided by the dimensions of the cavity resulted in an Lrx1 with a radius and length consistent with a volume of 0.53 cm3. This alteration emphasized the 2.7 kHz dip in the magnitude of ZME. In step 11, a final sensitivity analysis that investigated alterations in all 26 defined model parameters led to other small adjustments. The final outcome of this analysis was a stable cost value that could only be increased by changes in parameter values (Fig. 8, right).
F. Step 12: Expansion of cochlear network to better define Crw
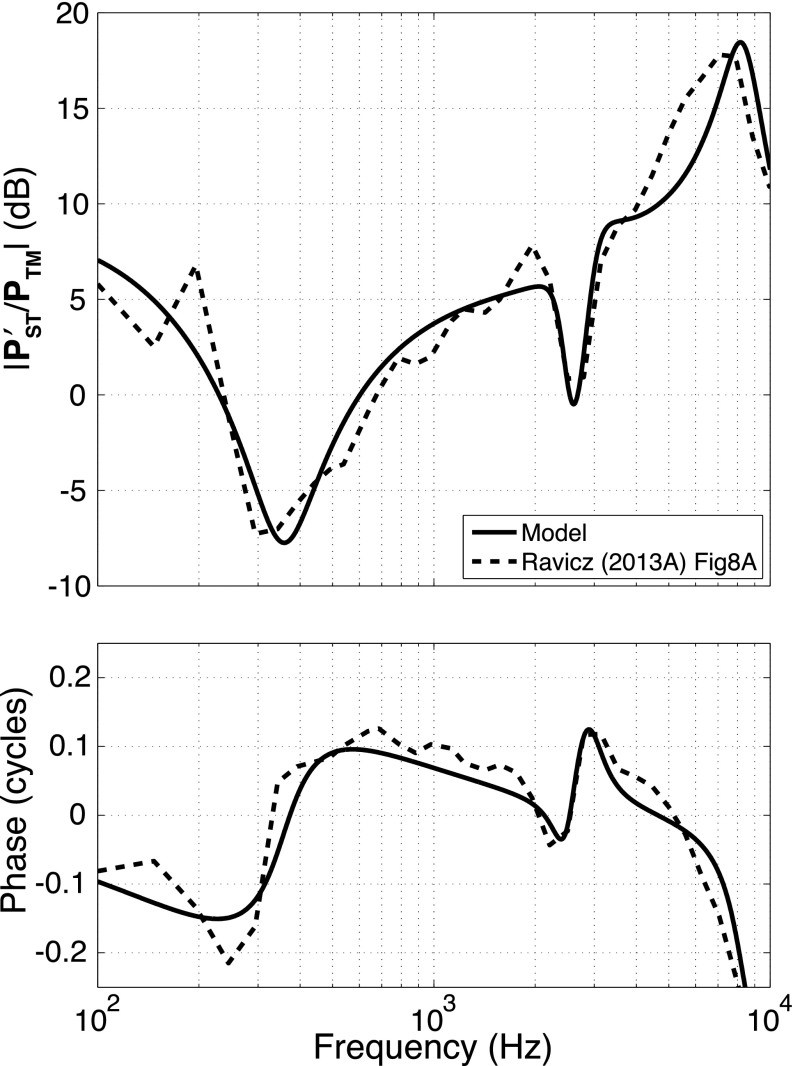
By the end of step 11, most of the parameters of the model were well-defined by a combination of anatomy and the repeated manual and automated optimization steps. An exception was the round-window compliance Crw whose value had little influence on any of the transfer functions used to estimate the model parameter. The lack of a well-defined Crw would interfere with the model's ability to predict the sound pressure in the scala tympani (Fig. 4), a value needed to define the sound pressure across the cochlear partition, a good indicator of the acoustic stimulus to the organ of Corti (Olson, 1999; Nakajima et al., 2009). Direct measurements of normalized by sound pressure in the ear canal at the TM do exist (Ravicz and Rosowski, 2013a) and a last optimization run was used with the target data described in Fig. 9.
FIG. 9.
Fitting the model prediction of normalized by ear canal sound pressure, based on the parameter set determined from step 12. The data are from Ravicz and Rosowski (2013a).
An additional complication in modeling measurements is that the physical location of these measurements is some small distance from the round window, therefore, we separated out a fraction of the cochlear inertance and resistance (Lc and Rc), determined by the first 11 steps of our fitting procedure, to describe the inertance and resistance (Lrw and Rrw) of a small column of perilymph between the measurement location and the round window (Nedzelnitsky, 1980; Olson, 2001). These terms would also account for any inertance or resistance associated with the RW membrane (Nakajima et al., 2009; Frear et al., 2018).
A single run of the automated fitting procedure was used to determine Crw and what portions of Lc and Rc can be attributed to Lrw and Rrw; values of Lrw and Rrw were determined indirectly by optimizing the percent of Lc and Rc, respectively, they were assigned. (Optimization of 3 model parameters.) Lrw and Rrw were initialized at 10% of the total cochlear inertance and resistance. All parameters of the middle ear, Lst, Crw, and transformer ratios were fixed. A single automated optimization run with thousands of iterations was performed, with initial parameter values taken from step 11, and with target data of the measured magnitude and phase of /PTM. Test randomizations of the initial values of the variable parameters did not alter the stable values that resulted from the one optimization run. Figure 9 illustrates an excellent fit between the target and the predicted sound-pressure ratios. The transfer functions predicted by the expanded model parameter set produced by Steps 11 and 12 show a good match to much of the data set (Fig. 7).
G. Fitness of parameter sets
The total costs associated with the different modeling steps are listed in Table I, and show a general improvement of the fit of the model ZME, SVTF, and Zc to the target data (Fig. 7). The large cost from step 3 reflects a combination of chinchilla middle-ear cavity and optimized human middle-ear parameters (Bowers and Rosowski, 2016). The first optimizations of the parameters of Fig. 1 branch b–e, produce a large reduction in cost (steps 4 and 5). Cost in general continued to decrease as the original model was refined. The lowest cost was produced by the final manual adjustments and the introduction of a realistic Crw by the additional fitting to the data of Fig. 9.
TABLE I.
Total cost of the fit after steps 3 through 12.
| Output of step | Cost | Output of step | Cost |
|---|---|---|---|
| 3 | 0.703 | 8 | 0.0985 |
| 4 | 0.111 | 9 | 0.0971 |
| 5 | 0.106 | 10 | 0.0900 |
| 7 | 0.113 | 12 | 0.0818 |
H. Final model parameters
The model parameters that resulted from step 12 are listed in Table II (middle-ear cavity) and Table III (middle ear, cochlea, and transformer ratios). Resistance values have units of kg s−1 m−4, inertances have units of kg m−4, and compliances have units of m4 s2 kg−1. The anatomical equivalents of parameters that can be directly related to anatomical features, such as cavity volumes, introduced hole sizes, and ossicular mass, are listed in Table IV.
TABLE IV.
Anatomical equivalents for parameters of step 12 output. Anatomical equivalents of middle-ear cavity parameter values are listed below, as well the effective malleus-incus complex mass and the mass of the stapes.
| Anatomy | Output of step 12 |
|---|---|
| Tympanic cavity volume | 1.47 cm3 |
| Tympanic cavity hole area | 0.490 cm2 |
| Superior cavity volume | 0.513 cm3 |
| Superior cavity hole area | 0.150 cm2 |
| Malleus-incus mass | 7.56 mg |
| Stapes mass | 0.616 mg |
| Volume of Lrx1 | 0.531 cm3 |
| Volume of Lrx2 | 0.0509 cm3 |
IV. DISCUSSION
A. Degree of fit of the different parameter sets
Outputs from step 3 in Fig. 7 indicate that constraining the middle-ear cavity based on middle-ear impedance data and initializing the cochlear parameters based on cochlear input impedance data is not sufficient for producing a good fit to middle-ear transfer-function data when the remaining parameters are set to values determined for the human middle ear.
Outputs of the first automated fitting steps (step 5 in Fig. 7) are already quite similar in magnitude and phase to the experimental data (Ravicz and Rosowski, 2012, 2013a,b), with a few exceptions: (i) the notches seen in GME and SVTF at approximately 2.7 kHz are not captured, (ii) the model does not capture the two distinct |ZME| maxima at approximately 1.3 and 4.2 kHz (a broad peak is predicted), (iii) the model underpredicts middle-ear transfer function magnitudes at frequencies below 600 Hz, and (iv) the model does not fit the angle of Zc well at frequencies above 1 kHz.
The addition of Lrx1 and Lrx2 in manual fitting steps 7 and 8 reproduces the 2.7 kHz notch in the middle-ear transfer functions. The further addition of an inertance to model the stapes mass shifts the high-frequency maximums of |SVTF| and |GME| to a lower frequency, however, this is not obvious in step 8, as the effect of the stapes addition was balanced by a decrease in cochlear inertance Lc.
As with earlier steps, the model of step 12 underpredicts the magnitude of SVTF and GME at frequencies below 600 Hz, with the largest discrepancy located about the peaks, between 200 and 300 Hz and at 300 Hz, respectively. The magnitude of these transfer functions are directly related to the middle-ear transformer ratios, and the resistive component of the cochlea. It is unclear as to why the automated-optimization method was unsuccessful in generating a parameter set that better fits the magnitude of SVTF at lower frequencies (the cost of the automated process did not account for the fit to GME), but it may be due to the fixing of the middle-ear transformer ratios. During the manual fitting procedure, although the transformer ratios could be adjusted, it was not possible to improve the fit to the low-frequency magnitudes of SVTF and GME simultaneously. The final model underpredicts both, as altering the transformer ratios to better fit one transfer function magnitude caused a worse fit to the other.
There is also a tradeoff in the model fit to the magnitude and angle of the cochlear input impedance above a few kHz. The series combination of Rc and Lc can be set to produce a reasonable fit to the magnitude of Zc [as in Fig. 7(d)], but at the cost of overestimating the angle of Zc above 3 kHz. A reduction in Lc can produce a better fit to the Zc angle, but will lead to a decrease in the fit of the magnitude.
B. Comparison of model parameters to known structures
Compliance of the total middle-ear cavity volume is described in the model by the parallel compliances of Ct and Cp with volumes of 1.47 and 0.513 cm3, respectively, resulting in a total middle-ear cavity volume of approximately 1.98 cm3. Average chinchilla middle-ear volumes of (1.2, 1.5, 2.0, 2.2, 2.8) cm3 have been cited (von Bismarck, 1967; Drescher and Eldredge, 1974; Teas and Nielsen, 1975; Vrettakos et al., 1988; Rosowski et al., 2006). The volume of the superior cavity was measured in two chinchillas (one ear each). The individual measurements were 0.527 and 0.680 cm3. Our fitting results that describe the ratio of the two cavity volumes AV as 0.35 and the sum of the volumes as 2 cm3 are roughly consistent with this anatomical observation AV = Vp/Vt = 0.6/(2 − 0.6) = 0.42.
From Eq. (8), the inertance of the coupled TM, malleus, and incus, Lo is related to the effective ossicular mass Mo, where Mo = Lo(ATM)2 and ATM is the tympanic-membrane area. With ATM = 0.60 cm2 and Lo = 1.9 × 103 kg m−4, the predicted malleus-incus mass from step 12 is 7.56 mg. Thirteen chinchilla malleus-incus complexes (with intact manubrium) from experiments were stored in saline and later weighed. The average mass was 12.9 mg. Since this malleus-incus mass (along with the mass of the coupled TM) rotates around supporting ossicular ligaments near its center of gravity (Sim et al., 2007), the calculated Mo is reasonable.
The inertance representing the stapes mass was added to the circuit in step 6 with a value of 13 kg m−4, which is equivalent to a stapes mass of 0.52 mg with LR = 2.86 and ATM = 0.70 cm2 [Eq. (9)]. This inertance was modified in step 8 to a value of 17.5 kg m−4 (equivalent to a mass of 0.65 mg) and remained fixed in step 9. Because step 11 included adjustments of ATM, LR, and Lst, the final stapes mass became 0.62 mg, which is 55% greater than the 0.4 mg measured by Vrettakos et al. (1988).
The area of the tympanic cavity hole was also modified during the final manual fitting process (step 11) from 0.190 cm2, based on the measured tympanic cavity hole of a single representative chinchilla ear, to 0.150 cm2. This is a reasonable change given the amount of variation expected in cavity hole size across experiments.
The inertance terms in the cochlear input impedance can be described in terms of quantities of water-like fluid. Zwislocki (1962) suggested Lc corresponded to a small column of fluid between the footplate and the cochlear partition, and Nedzelnitsky (1980) and Olson (2001) suggest that some component of Lrw may be attributed to a small column of RW-entrained fluid positioned between the measurement site and the RW. Using the model transformer ratio, we can convert the acoustic inertances seen at the TM to those that appear at the footplate. These acoustic inertances can then be converted to mechanical masses by multiplying by the square of the area of the footplate (Zwislocki, 1962). After these transformations, the masses associated with the optimized Lc and Lrw are 8.11 and 2.46 mg, respectively. Assuming these correspond to volumes of water-like fluid, the volumes are 8.11 and 2.46 microliters, respectively. If we assume these volumes are cylindrical with a cross-section equal to that of the footplate area, ∼2 mm2, the length of the cylinders are 4.05 and 1.23 mm, respectively. The first is about twice the distance between the footplate and the cochlear partition in chinchilla, while the second is a reasonable estimate of the distance between the measurement site and the RW.
C. Effect of closing and opening the cavity on middle-ear sound transmission
While we have fit the middle-ear model to data gathered with the middle-ear air cavity open to enable ossicular manipulations and measurements, the air cavity is closed in the intact animal. Closing the chinchilla air cavity is expected to have two effects (Rosowski et al., 2006): (i) an increase in the stiffness of the ear at low frequencies that results in an increase in the magnitude of the middle-ear impedance at low-frequencies, and a concomitant decrease in the magnitude of SVTF and GME, as sound transmission to the inner ear is reduced; (ii) a change in the frequency and depth of the near 2.7 kHz notches in middle-ear transmission that result from an interaction of the cavity compliance and the inertance of the introduced holes.
Closing the cavity holes in our model by replacing the cavity model of Fig. 2 with that of Fig. 1 produces such effect, as observed in Fig. 10. In that figure, we compare the model predictions based on the parameter values from step 12, with the open cavity data, and model predictions made after closing the model's cavities as described above. The model changes are consistent with both an increase in the stiffness of the ear that increases |ZME| and reduces |SVTF| and |GME| at frequencies below 800 Hz, alters the frequency and depth of the mid-frequency notches in ZME magnitude and phase, and nearly eliminates the mid-frequency notches observed in SVTF and GME magnitude and phase.
FIG. 10.
Chinchilla ME transfer functions with the middle ear closed or with two holes in the cavities. Shown are magnitude and phase of model outputs (thick solid line) of step 12 and experimental data (dashed line) of (a) ZME, (b) SVTF, (c) GME, and (d) Zc. Data are from Ravicz and Rosowski (2012, 2013a,b). In (a)–(c), the model outputs of step 12 with the middle-ear cavity parameters set to the closed-bulla (no hole) condition (thin solid line) are shown as a comparison of middle-ear conditions.
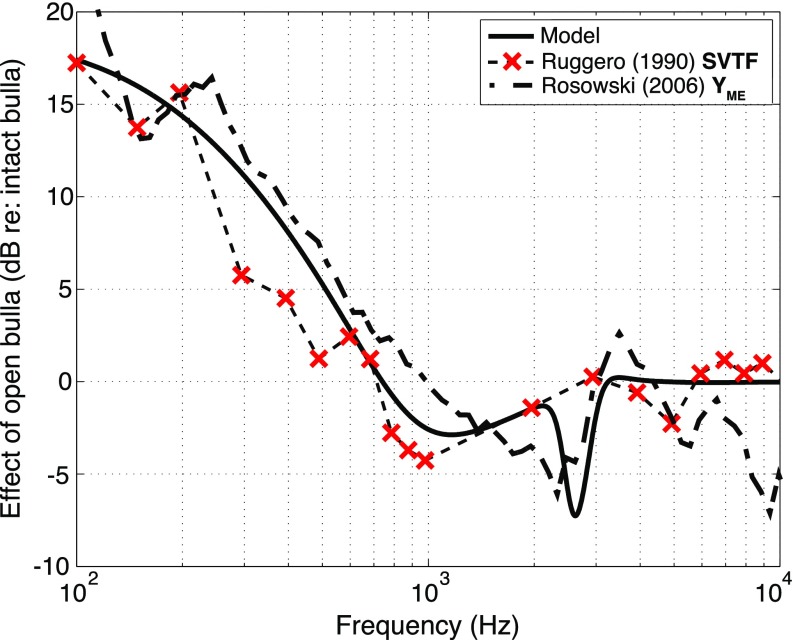
To further compare the cavities contribution to middle-ear function, we compare the model predictions to measurements of the effect of opening holes in the walls of the chinchilla middle-ear cavity, which has been evaluated by multiple investigators (Dallos, 1970; Drescher and Eldredge, 1974; Teas and Nielsen, 1975; Ruggero et al., 1990; Rosowski et al., 2006). In all of these studies, at frequencies below 0.7 to 1 kHz the effect of the opening the middle ear was an increase in the magnitude of middle-ear sound transmission by as much as 20 dB at 100 Hz. Figure 11 shows the effect of opening cavity holes on the magnitude of the model SVTF along with the SVTF data of Ruggero et al. (1990) and YME (1/ZME) of Rosowski et al. (2006). (The Y ratio is computed from YME measured with middle-ear cavity holes similar to those in the Ravicz studies, set 2 of Fig. 12 of Rosowski et al., divided by the mean admittance measured with intact but vented middle-ear cavities, Fig. 3A of that paper.) There is much in common between the model prediction and the data sets, but some differences. In the 2 to 3 kHz region, the model predicts opening the cavities introduces a narrow notch (a narrow-band decrease) in the magnitude. This notch is not seen in the Ruggero et al. data, which did not have a high enough frequency resolution to see such a notch, while in the Rosowski et al. data, which is based on mean data, the notch is somewhat spread in the frequency domain.
FIG. 11.
(Color online) The effect of opening the cavity on middle-ear transmission: the dB difference between the intact and opened cavities in either |SVTF| or |YME|. The effect in the model is shown as a solid line (step 12), the effect measured by Rosowski et al. (2006) is dash-dotted line, and the effect measured by Ruggero et al. (1990) is shown as a dashed line. The × markers show the frequency resolution in the Ruggero data.
Such a notch, and an accompanying rapid change in phase angle is a common observation of the effect of placing holes in the cavity wall (Guinan and Peake, 1967; Ravicz et al., 1992; Rosowski et al., 2006). In chinchilla, the frequency of the notch has been demonstrated to depend on the size of the cavity holes (Rosowski et al., 2006). The ZME, SVTF, and GME data and fits in Fig. 10 demonstrate the model was able to match the magnitude notch and phase change after the introduction of the additional hole associated inertances Lrx1 and Lrx2 in step 6.
The dependence of the notch on the addition of Lrx1 and Lrx2 points out that simply including anatomically correct cavity hole radiation impedances in the model did not produce the notch. We associate the necessary inertances Lrx1 and Lrx2 with some fraction of the formerly enclosed air volumes being accelerated by sound as the sound particles move in and out of the holes. If we assume these air columns have a cross-sectional area equal to the area of the opening of the middle-ear cavities Ah, the volume of the accelerated air columns can be calculated by the following equation:
| (19) |
These hypothetical accelerated air volumes after the manual fitting of step 11 are 0.531 cm3 for Lrx1 and 0.0509 cm3 for Lrx2. These volumes are about 1/3 of the Ct volume and about a tenth of the Cp volume. Our fitting procedure has not reduced the compliant air volumes by these fractions.
D. Possible additional complexity needed to model the low-frequency cochlea
The lumped-element model of the cochlea used in the fitting procedure is based directly on the simple cochlear model proposed by Zwislocki (1962) of a series resistance Rc and inertance Lc. Such a model does a good job of matching the load the cochlea places on the middle ear at frequencies between 0.1 and 3 kHz [Fig. 7(d)]. However, there are cochlear structures with effects not included in our model that may contribute to the cochlear load on sound transmission, in particular, the helicotrema, which is thought to affect the cochlear input impedance at low frequencies (Dallos, 1970; Lynch et al., 1982; Motallebzadeh et al., 2017b). Dallos (1970) attributed variations in the frequency dependence of the cochlear microphonic in chinchillas that occurred at frequencies below 0.3 kHz to the helicotrema. Consistent with such an effect, irregularities in the frequency-dependence of the chinchilla middle-ear impedance were observed in the same low-frequency range (Rosowski et al., 2006), and these irregularities were decreased by removal of the cochlear load. It is possible that the lack of a helicotrema in our model contributes to the model's failure to precisely fit both ZME and SVTF data at frequencies of 0.3 kHz and below. The significance of such low-frequency effects in our future bone-conduction model is reduced by the limited bandwidth, 0.2 to 8 kHz, of our bone-conduction stimuli.
Step 12 was performed to determine the round-window compliance, as automated optimizations did not predict a value that contributed to the resulting transfer function and impedance outputs in any way. The final value of Crw, although being important for fitting the model to the normalized scala tympani sound pressure measurements, had little impact on the cochlear input impedance and middle-ear transfer functions.
E. Comparison to the model of Lemons and Meaud (2016)
As noted above, Lemons and Meaud (2016) used the Songer and Rosowski (2007b) data to produce circuit-element and two-port transmission-matrix descriptions of the chinchilla middle ear that they modified to investigate inter-species difference in middle-ear function. A significant difference between our and the Lemons and Meaud approach is that they chose significantly different transformer values (TM to footplate area ratios AR = 0.8/0.0198, and malleus-incus lever ratio LR = 3.7) that they fixed before fitting the model. While we fixed our model representation of the footplate area to the same value (0.0198 cm2), we initiated LR = 2.86 and ATM = 0.7 cm2 with different values from the literature, and we used sensitivity analyses to direct manual adjustments in LR and ATM. As noted previously, the cost of the different model fits was quite sensitive to LR and ATM, and the fitting procedure led to downward adjustments in both of these quantities. The result of this different approach is a sizeable difference between the overall transformer ratio of our [(ATM/AFP) × LR = 78.8] and the Lemons and Meaud models [(ATM/AFP) × LR = 148]. This difference, coupled with differences in model structure, make it difficult to compare the element values of the two models.
F. Model limitations and weaknesses
1. Cochlear network
Much of the finer frequency dependence in the experimental Zc data (Ravicz and Rosowski, 2013b) is not captured by the model, nor is the less than quarter cycle phase at higher frequencies, as these behaviors cannot be reproduced by a simple series RLC network. Some of the complexity in the data may be associated with the shunting of volume velocity through additional sound pathways such as the cochlear and vestibular aqueducts. Such additional complexity in Zc could explain similar differences between the measured and the model-predicted |GME| and |SVTF| (Ravicz and Rosowski, 2013a,b). A more-complicated representation of the cochlea will be necessary to model the mechanisms of the inner-ear bone-conduction source (Stenfelt, 2016).
2. 3D motion of ossicular chain
Our lumped-element model does not account for observations of complex 3D motion of the ossicular chain (Decraemer et al., 1994). This limitation is shared by the experiments of Ravicz and Rosowski (2013a,b), in which the stapes velocity was measured only in the direction normal to the stapes footplate. In human, over the range of 0.5 to 8 kHz, rocking motions of the stapes are on the same order of magnitude as its linear motion along an axis perpendicular to the stapes footplate (Sim et al., 2010). Puria and Steele (2010) suggest that in larger mammals, such as in human and cat, asymmetry in TM area with respect to the axis defined by the length of the manubrium may cause rocking motion of the ossicles. This differs from smaller mammals such as the guinea pig and chinchilla, in which there is symmetry of the TM area about this same axis. It may then be the case that complex motions of the ossicular chain of the chinchilla are limited to complex modes of motion of the TM resulting from other asymmetries in the membrane.
V. CONCLUSION
A relatively simple circuit of the middle ear and cochlea that is developed from air-conduction hearing data will serve as the basis for a model for bone-conduction hearing in chinchilla. The model was developed by fitting various model outputs to middle-ear input impedance, middle-ear cavity, and transfer-function data, and cochlear input impedance. Parameters that are direct circuit analogs of anatomical features served as model constraints. The model captures the salient features of the data and predicts the effects of middle-ear cavity holes. The greatest difference between the model output and experimental data is in the cochlear input impedance.
Automatic fitting procedures were used that led to decreases in the squared difference (the cost) between target data and model predictions. A GUI also allowed manual fitting that was guided by the quantified total cost of the model fit to the experimental data, and sensitivity analyses that quantified the effect of parameter changes on cost. In some cases, automatic fitting produced erratic results, such as when the stapes mass, transformer ratios of the middle ear, and the annular ligament compliance were allowed to vary. The final parameter values make sense both anatomically and mechanically and are in general agreement with those found in literature. Our model fits middle-ear transfer functions and impedances (Ravicz and Rosowski, 2012, 2013a,b) at frequencies below 10 kHz. No attempt was made to fit to higher-frequency data; we expect phase discrepancies above 10 kHz because our model does not contain any explicit delay term, and such delays have been observed in chinchilla middle-ear data at higher frequencies (Ravicz and Rosowski, 2013a,b).
ACKNOWLEDGMENTS
This work was funded by RO1DC0000194 (J.J.R.), and T32DC000038 and F31DC015915 (P.B.). The authors would also like to thank Mike Ravicz, Melissa McKinnon, Heidi Nakajima, and Sunil Puria for contributions to this work.
Footnotes
At the start of an optimization run, a set of n + 1 vertices is created in an n-dimensional space, where n is the number of parameters being optimized. Each vertex comprises the initial parameter values, with a single, unique parameter value adjusted by 5%. The set also includes a vertex having coordinates of the initial parameter set without adjustment. The cost resulting from each vertex (parameter set) is calculated, and the centroid of the n lowest-cost vertices is calculated. The highest-cost vertex is subjected to multiple transformations, about the centroid of the other vertices. The possible transformations include: reflection, expansion, contraction (outside and inside), and shrink. The lowest-cost vertex produced by these transformations replaces the highest-cost vertex of the original set. The process is repeated: a new centroid is calculated from the updated set of the n lowest-cost vertices, and transformations are applied to the highest-cost vertex, about the centroid, that is then replaced by the lowest-cost vertex produced by the transformations.
The physical cause of these additional elements has been associated with either the force used to move the small column of fluid between the PST measurement point and the round window (RW), the mass and resistance of the RW, or some combination. The fitted acoustic inertance we define as Lrw can be attributed to a cylinder of water of cross-section equal to the RW area and length of 1.25 mm. The computed length is a good approximation of the distance between the RW and the PST measurement location (Ravicz and Rosowski, 2013a).
References
- 1. Beranek, L. L. (1993). Acoustics ( Acoustical Society of America, Cambridge, MA: ). [Google Scholar]
- 2. Bowers, P. , and Rosowski, J. J. (2016). “ Optimization of Zwislocki's human middle-ear circuit model to fit modern data,” Poster presented at the Association for Research in Otolaryngology conference, San Diego, CA. [Google Scholar]
- 3. Browning, G. C. , and Granich, M. S. (1978). “ Surgical anatomy of the temporal bone in the chinchilla,” Ann. Otol. Rhinol. Laryngol. 87, 875–882. 10.1177/000348947808700616 [DOI] [PubMed] [Google Scholar]
- 4. Dallos, P. (1970). “ Low-frequency auditory characteristics: Species dependence,” J. Acoust. Soc. Am. 48, 489–499. 10.1121/1.1912163 [DOI] [PubMed] [Google Scholar]
- 5. Dallos, P. (1973). The Auditory Periphery Biophysics and Physiology ( Academic, New York: ). [Google Scholar]
- 6. Decraemer, W. F. , Khanna, S. M. , and Funnell, W. R. (1994). “ A method for determining three-dimensional vibration in the ear,” Hear. Res. 77, 19–37. 10.1016/0378-5955(94)90250-X [DOI] [PubMed] [Google Scholar]
- 7. Drescher, D. G. , and Eldredge, D. H. (1974). “ Species differences in cochlear fatigue related to acoustics of outer and middle ears of guinea pig and chinchilla,” J. Acoust. Soc. Am. 56, 929–934. 10.1121/1.1903350 [DOI] [PubMed] [Google Scholar]
- 8. Frear, D. L. , Guan, X. , Stieger, C. , Rosowski, J. J. , and Nakajima, H. H. (2018). “ Impedances of the inner and middle ear estimated from intracochlear sound pressures in normal human temporal bones,” Hear. Res. 367, 17–31. 10.1016/j.heares.2018.06.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Funnell, W. R. , Khanna, S. M. , and Decraemer, W. F. (1992). “ On the degree of rigidity of the manubrium in a finite-element model of the cat eardrum,” J. Acoust. Soc. Am. 91, 2082–2090. 10.1121/1.403694 [DOI] [PubMed] [Google Scholar]
- 10. Gan, R. Z. , Feng, B. , and Sun, Q. (2004). “ Three-dimensional finite element modeling of human ear for sound transmission,” Ann. Biomed. Eng. 32, 847–859. 10.1023/B:ABME.0000030260.22737.53 [DOI] [PubMed] [Google Scholar]
- 11. Guinan, J. J., Jr. , and Peake, W. T. (1967). “ Middle-ear characteristics of anesthetized cats,” J. Acoust. Soc. Am. 41, 1237–1261. 10.1121/1.1910465 [DOI] [PubMed] [Google Scholar]
- 12. Hemila, S. , Nummela, S. , and Reuter, T. (1995). “ What middle ear parameters tell about impedance matching and high frequency hearing,” Hear. Res. 85, 31–44. 10.1016/0378-5955(95)00031-X [DOI] [PubMed] [Google Scholar]
- 13. Higashimachi, T. , Shiratake, Y. , Maeda, T. , Sug, K. , and Toriya, R. (2013). “ Three-dimensional finite element analysis of the human middle ear and an application for clinics for tympanoplasty,” WIT Trans. Eng. Sci. 78, 61–72. 10.2495/SECM130061 [DOI] [Google Scholar]
- 14. Huber, A. M. , Schwab, C. , Linder, T. , Stoeckli, S. J. , Ferrazzini, M. , Dillier, N. , and Fisch, U. (2001). “ Evaluation of eardrum laser Doppler interferometry as a diagnostic tool,” Laryngoscope 111, 501–507. 10.1097/00005537-200103000-00022 [DOI] [PubMed] [Google Scholar]
- 15. Keefe, D. H. (2015). “ Human middle-ear model with compound eardrum and airway branching in mastoid air cells,” J. Acoust. Soc. Am. 137, 2698–2725. 10.1121/1.4916592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Koike, T. , Wada, H. , and Kobayashi, T. (2002). “ Modeling of the human middle ear using the finite-element method,” J. Acoust. Soc. Am. 111, 1306–1317. 10.1121/1.1451073 [DOI] [PubMed] [Google Scholar]
- 17. Kringlebotn, M. (1988). “ Network model for the human middle ear,” Scand. Audiol. 17, 75–85. 10.3109/01050398809070695 [DOI] [PubMed] [Google Scholar]
- 18. Lemons, C. , and Meaud, J. (2016). “ Middle-ear function in the chinchilla: Circuit models and comparison with other mammalian species,” J. Acoust. Soc. Am. 140, 2735–2753. 10.1121/1.4964707 [DOI] [PubMed] [Google Scholar]
- 19. Lynch, T. J., III , Nedzelnitsky, V. , and Peake, W. T. (1982). “ Input impedance of the cochlea in cat,” J. Acoust. Soc. Am. 72, 108–130. 10.1121/1.387995 [DOI] [PubMed] [Google Scholar]
- 20. Molvaer, O. I. , Vallersnes, F. M. , and Kringlebotn, M. (1978). “ The size of the middle ear and the mastoid air cell,” Acta Otolaryngol. 85, 24–32. 10.3109/00016487809121419 [DOI] [PubMed] [Google Scholar]
- 21. Motallebzadeh, H. , Maftoon, N. , Pitaro, J. , Funnell, W. R. , and Daniel, S. J. (2017a). “ Finite-element modelling of the acoustic input admittance of the newborn ear canal and middle ear,” J. Assoc. Res. Otolaryngol. 18, 25–48. 10.1007/s10162-016-0587-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Motallebzadeh, H. , Maftoon, N. , Pitaro, J. , Funnell, W. R. J. , and Daniel, S. J. (2017b). “ Fluid-structure finite-element modelling and clinical measurement of the wideband acoustic input admittance of the newborn ear canal and middle ear,” J. Assoc. Res. Otolaryngol. 18, 671–686. 10.1007/s10162-017-0630-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Nakajima, H. H. , Dong, W. , Olson, E. S. , Merchant, S. N. , Ravicz, M. E. , and Rosowski, J. J. (2009). “ Differential intracochlear sound pressure measurements in normal human temporal bones,” J. Assoc. Res. Otolaryngol. 10, 23–36. 10.1007/s10162-008-0150-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Nakajima, H. H. , Ravicz, M. E. , Merchant, S. N. , Peake, W. T. , and Rosowski, J. J. (2005). “ Experimental ossicular fixations and the middle ear's response to sound: Evidence for a flexible ossicular chain,” Hear. Res. 204, 60–77. 10.1016/j.heares.2005.01.002 [DOI] [PubMed] [Google Scholar]
- 25. Nedzelnitsky, V. (1980). “ Sound pressures in the basal turn of the cat cochlea,” J. Acoust. Soc. Am. 68, 1676–1689. 10.1121/1.385200 [DOI] [PubMed] [Google Scholar]
- 26. Nelder, J. A. , and Mead, R. (1965). “ A simplex method for function minimization,” Comput. J. 7, 308–313. 10.1093/comjnl/7.4.308 [DOI] [Google Scholar]
- 27. O'Connor, K. N. , and Puria, S. (2008). “ Middle-ear circuit model parameters based on a population of human ears,” J. Acoust. Soc. Am. 123, 197–211. 10.1121/1.2817358 [DOI] [PubMed] [Google Scholar]
- 28. Olson, E. S. (1999). “ Direct measurement of intra-cochlear pressure waves,” Nature 402, 526–529. 10.1038/990092 [DOI] [PubMed] [Google Scholar]
- 29. Olson, E. S. (2001). “ Intracochlear pressure measurements related to cochlear tuning,” J. Acoust. Soc. Am. 110, 349–367. 10.1121/1.1369098 [DOI] [PubMed] [Google Scholar]
- 30. Puria, S. , and Allen, J. B. (1998). “ Measurements and model of the cat middle ear: Evidence of tympanic membrane acoustic delay,” J. Acoust. Soc. Am. 104, 3463–3481. 10.1121/1.423930 [DOI] [PubMed] [Google Scholar]
- 31. Puria, S. , and Steele, C. (2010). “ Tympanic-membrane and malleus-incus-complex co-adaptations for high-frequency hearing in mammals,” Hear. Res. 263, 183–190. 10.1016/j.heares.2009.10.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Ravicz, M. E. , and Rosowski, J. J. (2012). “ Chinchilla middle-ear admittance and sound power: High-frequency estimates and effects of inner-ear modifications,” J. Acoust. Soc. Am. 132, 2437–2454. 10.1121/1.4750487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Ravicz, M. E. , and Rosowski, J. J. (2013a). “ Inner-ear sound pressures near the base of the cochlea in chinchilla: Further investigation,” J. Acoust. Soc. Am. 133, 2208–2223. 10.1121/1.4792139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Ravicz, M. E. , and Rosowski, J. J. (2013b). “ Middle-ear velocity transfer function, cochlear input immittance, and middle-ear efficiency in chinchilla,” J. Acoust. Soc. Am. 134, 2852–2865. 10.1121/1.4818745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Ravicz, M. E. , Rosowski, J. J. , and Voigt, H. F. (1992). “ Sound-power collection by the auditory periphery of the Mongolian gerbil Meriones unguiculatus. I: Middle-ear input impedance,” J. Acoust. Soc. Am. 92, 157–177. 10.1121/1.404280 [DOI] [PubMed] [Google Scholar]
- 36. Rosowski, J. J. (1994). “ Outer and middle ear,” in Springer Handbook of Auditory Research: Comparative Heraing: Mammals, edited by Popper F. R. ( Spring-Verlag, New York: ), pp. 172–247. [Google Scholar]
- 37. Rosowski, J. J. , Mehta, R. P. , and Merchant, S. N. (2003). “ Diagnostic utility of laser-Doppler vibrometry in conductive hearing loss with normal tympanic membrane,” Otol. Neurotol. 24, 165–175. 10.1097/00129492-200303000-00008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Rosowski, J. J. , and Merchant, S. N. (1995). “ Mechanical and acoustic analysis of middle ear reconstruction,” Am. J. Otol. 16, 486–497. [PubMed] [Google Scholar]
- 39. Rosowski, J. J. , Ravicz, M. E. , and Songer, J. E. (2006). “ Structures that contribute to middle-ear admittance in chinchilla,” J. Comp. Physiol. A: Neuroethol. Sens. Neural Behav. Physiol. 192, 1287–1311. 10.1007/s00359-006-0159-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Ruggero, M. A. , Rich, N. C. , Robles, L. , and Shivapuja, B. G. (1990). “ Middle-ear response in the chinchilla and its relationship to mechanics at the base of the cochlea,” J. Acoust. Soc. Am. 87, 1612–1629. 10.1121/1.399409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Sim, J. H. , Chatzimichalis, M. , Lauxmann, M. , Roosli, C. , Eiber, A. , and Huber, A. M. (2010). “ Complex stapes motions in human ears,” J. Assoc. Res. Otolaryngol. 11, 329–341. 10.1007/s10162-010-0207-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Sim, J. H. , Puria, S. , and Steele, C. (2007). “ Calculation of inertial properties of the malleus-incus complex from micro-CT imaging,” J. Mech. Mater. Struct. 2, 1515–1524. 10.2140/jomms.2007.2.1515 [DOI] [Google Scholar]
- 43. Songer, J. E. , and Rosowski, J. J. (2006). “ The effect of superior-canal opening on middle-ear input admittance and air-conducted stapes velocity in chinchilla,” J. Acoust. Soc. Am. 120, 258–269. 10.1121/1.2204356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Songer, J. E. , and Rosowski, J. J. (2007a). “ A mechano-acoustic model of the effect of superior canal dehiscence on hearing in chinchilla,” J. Acoust. Soc. Am. 122, 943–951. 10.1121/1.2747158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Songer, J. E. , and Rosowski, J. J. (2007b). “ Transmission matrix analysis of the chinchilla middle ear,” J. Acoust. Soc. Am. 122, 932–942. 10.1121/1.2747157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Stenfelt, S. (2016). “ Model predictions for bone conduction perception in the human,” Hear. Res. 340, 135–143. 10.1016/j.heares.2015.10.014 [DOI] [PubMed] [Google Scholar]
- 47. Teas, D. C. , and Nielsen, D. W. (1975). “ Interaural attenuation versus frequency for guinea pig and chinchilla CM response,” J. Acoust. Soc. Am. 58, 1066–1072. 10.1121/1.380766 [DOI] [PubMed] [Google Scholar]
- 48. von Bismarck, G. (1967). The Sound Pressure Transformation Function from Free Field to the Eardrum of Chinchilla ( Massachusetts Institute of Technology, Cambridge, MA: ). [Google Scholar]
- 49. Voss, S. E. , Rosowski, J. J. , Merchant, S. N. , and Peake, W. T. (2001). “ Middle-ear function with tympanic-membrane perforations. II. A simple model,” J. Acoust. Soc. Am. 110, 1445–1452. 10.1121/1.1394196 [DOI] [PubMed] [Google Scholar]
- 50. Vrettakos, P. A. , Dear, S. P. , and Saunders, J. C. (1988). “ Middle ear structure in the chinchilla: A quantitative study,” Am. J. Otolaryngol. 9, 58–67. 10.1016/S0196-0709(88)80009-7 [DOI] [PubMed] [Google Scholar]
- 51. Wang, X. , and Gan, R. Z. (2016). “ 3D finite element model of the chinchilla ear for characterizing middle ear functions,” Biomech. Model Mechanobiol. 15, 1263–1277. 10.1007/s10237-016-0758-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Zwislocki, J. (1962). “ Analysis of the middle-ear function. Part I: Input impedance,” J. Acoust. Soc. Am. 34, 1514–1523. 10.1121/1.1918382 [DOI] [Google Scholar]