Developing prediction models for clinical use using logistic regression: an overview

Abstract

Prediction models help healthcare professionals and patients make clinical decisions. The goal of an accurate prediction model is to provide patient risk stratification to support tailored clinical decision-making with the hope of improving patient outcomes and quality of care. Clinical prediction models use variables selected because they are thought to be associated (either negatively or positively) with the outcome of interest. Building a model requires data that are computer-interpretable and reliably recorded within the time frame of interest for the prediction. Such models are generally defined as either diagnostic, likelihood of disease or disease group classification, or prognostic, likelihood of response or risk of recurrence. We describe a set of guidelines and heuristics for clinicians to use to develop a logistic regression-based prediction model for binary outcomes that is intended to augment clinical decision-making.

Introduction

Prediction models are designed to assist healthcare professionals and patients with decisions about the use of diagnostic testing, starting or stopping treatments, or making lifestyle changes (1). While not a substitute for clinical experience, they can provide objective data about an individual’s disease risk and avoid some common biases observed in clinical decision making (1). Conversely, biases in the way the data are collected or filtered for use by the model can introduce other types of biases, and so the choice of underlying data and cohort selection are paramount. In addition, information generation in health care is growing very quickly and outstripping the capacity of human cognition to adequately manage. Support of human cognition by allowing models to inform decision-making is a scalable way to manage growing data volumes and information complexity (2).

Risk prediction models use patient characteristics to estimate the probability that a certain outcome is present or will occur within a defined time period (3). For example, the TREAT model (Thoracic Research Evaluation And Treatment model) estimates the risk of a lung nodule being cancer using information most likely available to evaluating surgeons (4). A prognostic model such as the ACS NSQIP Surgical Risk Calculator predicts the likelihood of early mortality or significant complications after surgery (5) [see Table 1 for further examples of risk prediction models that will be used throughout this review (6-9)]. This article intends to provide an overview of prediction model development using logistic regression, including identifying and selecting classifying variables, assessing model performance, performing internal and external validation, recalibrating the model, and assessing the clinical impact of the model.

Table 1. Prediction model examples (listed in order of appearance).

Model	Outcome	Type of model	Study design	Population
TREAT model (Deppen et al.) (4)	Lung cancer in indeterminate pulmonary nodules	Logistic regression	Retrospective cohort	Patients with indeterminate pulmonary nodules presenting to thoracic surgery clinics (high prevalence of lung cancer)
ACS NSQIP Mortality (5)	Mortality after surgery	Logistic regression	Retrospective cohort	Low-risk patients referred for general surgery procedures
Mayo Clinic model (Swensen et al.) (6)	Lung cancer in solitary lung nodules	Logistic regression	Retrospective cohort	Pulmonary clinic patients with solitary pulmonary nodules (low prevalence of lung cancer)
Farjah et al. (7)	Presence of N2 nodal disease in lung cancer	Logistic regression	Retrospective cohort	Patients with suspected or confirmed non-small cell lung cancer and negative mediastinum by PET
Liverpool Lung Project (LLP) model (Cassidy et al.) (8)	Lung cancer development	Logistic regression	Retrospective case control	Patients at high risk of developing lung cancer
Tammemagi model (9)	Lung cancer screening-detected pulmonary nodules	Logistic regression	Prospective cohort	High-risk patients undergoing screening CT scan

TREAT, Thoracic Research Evaluation And Treatment; PET, positron emission tomography.

Goal of the model

The most crucial step of developing a prediction model is determining the overall goal of the model: what specific outcome in which specific patient population will the model be predicting, and for what purpose? Carefully choosing the cohort from the population of interest, as well as the outcome and how it is ascertained, not only directs the identification of applicable source data, predictor selection, and model development but helps define the generalizability of the final product. Defining the purpose of the model (and its intended use and audience) would link the information it generates to a clinical action that will presumably benefit the patient. In Steyerberg’s Clinical Prediction Models (2), this is the first of seven steps in developing a risk prediction model (see Table 2).

Table 2. Seven steps for developing valid prediction models.

(I) Determine the prediction problem: defining predictors and outcome of interest

(II) Code predictors

(III) Specify a model

(IV) Estimate model parameters

(V) Model evaluation

(VI) Model validation

(VII) Presentation of the model

From Steyerberg’s Clinical Prediction Models (2).

For example, in the TREAT model the goal was to predict lung cancer in patients with indeterminate pulmonary nodules who presented to a thoracic surgery clinic, a population with a high prevalence of lung cancer (4). The Mayo Clinic model has the same goal, predicting lung cancer in pulmonary nodules; however, it was developed in patients presenting to any outpatient clinic with a pulmonary nodule (8), a population with a lower prevalence of lung cancer (40%) compared to that being evaluated by surgeons (66%). Both models have merit as predictive models, but they are generalizable to different clinical settings and contexts. One can see that effort must be spent at the beginning of the development process to define these goals.

Data

Source of data

Ideally, model development arises from a prospectively collected cohort so that subjects are well defined, all variables of interest are collected, and missing data are minimized (1-3,10). However, primary data collection is expensive. Therefore, pre-existing datasets (e.g., retrospective and/or large database studies, secondary analyses of randomized trial data, etc.) are commonly used for model development, but these may have multiple issues as the data were not collected with model development or a specific clinical question in mind (1). For example, important predictors may not have been collected or could be missing from a large number of subjects. Relevant predictive variables must be reproducible in practice, which is not always true of data derived from randomized trials. Additionally, the subjects in the sample may not be well defined or not representative of the underlying population in which inferences are to be made [see above discussion of TREAT and Mayo Clinic models (4,8)]. Such data inherently have selection biases in their collection, and model development must consider such issues.

Outcome definitions

When defining an outcome it is best to choose one that is clinically relevant and meaningful to patients (1,10). For logistic regression prediction models, these include binary outcomes such as death, lung cancer diagnosis, or disease recurrence. The method of outcome determination, like that of predictor collection, should be accurate and reproducible across the relevant spectrum of disease and clinical expertise (10).

Missing data

Missing values in a dataset is a commonly encountered problem in applied clinical research (1,2). Missing data may be missing at random, but the reason the data are missing is more often related, either directly or indirectly, to predictors and/or the outcome under investigation (3,11). Therefore, simply excluding subjects with missing values can insert unforeseen biases into the modeling process whose impact on the model’s accuracy or validity is difficult to assess. However, if a particular variable is frequently missing one must consider that it may also frequently be unobtainable in the general population for which the model is intended and thus may not be an ideal predictor to include in the model (3,10). For example, excluding patients who did not have a pre-operative positron emission tomography (PET) scan from the population during the development of the TREAT model would have biased the model toward higher risk patients, as they were more likely to have undergone PET for pre-operative staging (4).

Imputation techniques are commonly used to estimate missing values using existing data to predict what the missing value most likely would be. This avoids the biases inherent with simply removing subjects with missing data (3,10,12). Mean imputation, a historically popular method, simply inserts the mean value of the observed data for a missing continuous variable (for example, body mass index). Unfortunately, adding these mean values incorrectly reduces the variance within the population (11). Additionally, ordinary formulas to calculate standard errors and other statistics on the predictive performance of the model are invalid unless they account for imputation techniques, irrespective of the imputation method (3).

In multiple imputation, a multivariable imputation model using the observed data is developed for any independent variable with a missing value (3,10). Statistically, a multiply-imputed value uses random draws from the conditional distribution of the missing variable (given the other variables observed both in the individual and in the overall model). These sets of draws are repeated multiple (≥10) times to account for variability due to unknown values and predictive strength of the underlying imputation model (1,12). The resulting complete datasets with imputed data can then be used for model development as well as for variance and covariance estimates adjusted for imputation. Multiple imputation using a predictive mean matching method was used in the TREAT model to account for both missing pulmonary function tests and PET scans (4). Further information on multiple imputation techniques can be found through the following references (3,11,13,14).

Model development

Identification of predictors

Once the dataset has been cleaned and imputed data generated (when necessary), formal model development begins. Inherent model development begins at the point of data collection, as a well-performing risk prediction model requires some number of strong predictors being present (2,15). Candidate predictors are variables that are studied for their potential performance. Predictors can include any information that precedes the outcome of interest in time and information that is believed to predict the outcome of interest. Examples include demographic variables, clinical history, physical examination findings, type and severity of disease, comorbid conditions, and laboratory or imaging results. For example, in the TREAT model demographics such as age and sex, clinical data such as BMI and history of COPD, evidence of symptomatic disease (hemoptysis or unplanned weight loss), and imaging findings such as nodule characteristics and FDG-PET avidity are some of the predictors included in the final model (4).

Predictors must be clearly defined and measured in a standardized and reproducible way or the risk prediction model will not be generalizable (2,3). For example, a variable such as smoking history has a variety of definitions. The TREAT model includes smoking history using pack-years as a non-linear continuous variable (4), the Mayo model includes smoking history as a binary value (yes/no) (8), and the Tammemagi model uses a combination of pack-years and years since quitting (9).

Predictors that are strongly correlated to the outcome, explain observed variation in the outcome, or interact in combination with other variables become candidates for inclusion in the model (2,3). As the word candidate implies, not all variables may be considered as having utility in a multivariable clinical prediction model. For example, two variables that are highly correlated with one another, like predicted flow expiratory volume in one second (FEV1) and a diagnosis of emphysema when looking at lung cancer, may be individually correlated to the outcome of interest. However, when combined in a multivariable model each becomes a weaker predictor. In essence, the variables under investigation contain very similar information regarding the outcome and only one is needed to capture that information. Under circumstances of extreme correlation (termed multi-collinearity) including both may be detrimental to the model’s specification (1,2).

There are two main strategies for identifying predictors: clinically-driven and data-driven. In clinically-driven predictor identification, candidate predictors are selected either by clinical experts in the research group or by literature review (1,2). In data-driven identification, all predictors are initially included and predictor selection (see below) occurs during the machine-learning based model development phase (11).

Predictor selection methods

When building a model, often the predictors to be included in the model are pre-specified by clinical experts in the field (1,3). The reduction of candidate predictors to simplify the model is often referred to as parsimony. Having a limited number of predictors is beneficial both statistically by decreasing computational time and resources and clinically by improving interpretability. Having fewer inputs improves user experience and therefore the likelihood of routine use in clinical practice (11,16).

Theoretically every variable collected in the study could be a candidate predictor. However, to reduce the risk of false positive findings and improve model performance, the events per variable (EVP) rule of thumb is commonly applied and at a minimum set to 10 (2,3). This rule of thumb recommends that at least 10 individuals need to have developed the outcome of interest for every predictor variable included in the model. Candidate predictors are reduced in relation to the frequency of the outcome (1). For example, a model developed to predict mortality after surgery, a rare outcome, should only include a few predictors. However, this method has largely been replaced as models with higher and lower EVP are all susceptible to bias (17).

There are multiple methods used for eliminating candidate predictors and choosing the variables to be included in the final model without introducing bias into the analysis. In the full model approach, all a priori selected candidate predictors are included in the multivariable analyses and thus in the final prediction model; no candidate predictors are eliminated (1,3). This avoids predictor selection bias and overfitting of the model. However, this requires prior knowledge of which candidate predictors are the most likely to create a meaningful risk prediction model and use of a limited number of predictors (1).

To simply reduce the number of candidate predictors, one may consider combining similar predictors to a single one (for example, combining coronary artery disease, peripheral vascular disease and hypercholesterolemia into “cardiovascular disease history”) or exclude predictors that are highly correlated with others (for example, not including both total cholesterol and LDL cholesterol). Additionally, one could exclude predictors that are frequently missing in the dataset and therefore may not be commonly available in clinical practice (1). Or if candidate predictors have limited variability among the study population (for example, narrow range of BMI 22–25), they can be eliminated.

Alternatively, candidate predictors that do not significantly correlate with the outcome can be removed from the model. This is commonly done with a univariate analysis; predictors that do not have a significant p-value are discarded. However, this is likely to significantly reduce the performance of the model and does not account for interaction between different variables (11). Furthermore, models created using this method are often unable to be validated in new populations, and the use of this method is discouraged.

Predictor selection can also be performed by analyzing the multivariate model and removing predictors that do not significantly impact the final outcome. Backward elimination starts with all candidate predictors in the multivariate model and sequentially removes or keeps variables based on a predefined significance parameter (for example, using the log likelihood ratio test for comparing two models) (3).

In forward elimination, the model is built up sequentially from an initial few predictors using similar significance testing. However, unlike backwards elimination forward elimination does not provide for simultaneous assessment of the effects of all candidate variables, and correlated variables may not remain in the model (3). Thus, forward selection is discouraged in prediction model development as it results in models that are difficult to reproduce, that may not account for predictor interactions, and where important predictors may be erroneously eliminated.

There are also numerous machine learning techniques for predictor selection, also termed feature reduction techniques. These commonly utilize univariate analysis techniques and either produce a single output for each predictor (e.g., “significant” or “not significant”) or rank the predictors according to a certain statistic, leaving the ultimate choice of how many of the top ranked predictors to include up to the analyst (11). There are also feature subset selection techniques that can further break down the predictors and outcome variables (for example, splitting “disease recurrence” into “loco-regional recurrence”, “distant metastases”, etc.). Finally, tree-based models and random forests inherently utilize predictor selection as a part of the model building process. However, these techniques are “black box” approaches where not all of the relationships may have been anticipated and may not be easily interpretable.

Regardless of the predictor selection technique employed, the choice of significance level for inclusion will affect the final model. A smaller significance value (such as P<0.05) will result in a model with fewer predictors but could exclude potentially important predictors. A larger significance value (such as P<0.020) increases the risk for selecting less important predictors (2,10). Overfitting models can occur in both cases, especially if using a smaller dataset. Overfitting occurs when the model fits the data “too well” in that the fit includes the noise from the dataset as well as the true signal. The overfitting model will likely not perform well on predictions with new data, thus failing in external validation (1,2).

Another parameter gained from the multivariate analysis is the baseline risk or hazard. This is the risk to an individual with all predictor values being zero. In logistic regression this is indicated by the model’s intercept; in Cox survival models the baseline event risk can be estimated separately (3).

Variable types (continuous vs. categorical)

Relationships among variables are rarely linear. However, the presence of non-linearity should not be dealt with by simply partitioning continuous variables into intervals (dichotomization or categorization) (1). Estimated values will have reduced precision and associated tests will have reduced power, and adding multiple categories spends more degrees of freedom. Categorization also assumes that the relationship between the predictor and the outcome is flat within each interval. Additionally, if the cut points between categories are not determined in a blinded fashion to the outcome, it can lead to overfitting of the model (1,3,10).

Predictor interactions

Interaction occurs when the effect of two predictor variables cannot be separated, in that the effect of one variable on the outcome is dependent on the value of another variable (1). Common interactions that have been found to be important in predicting outcomes (and thus may be pre-specified) include interactions between treatment and the severity of disease being treated, between increasing age and other risk factors (older subjects less affected by certain risk factors), between age and type of disease, between a measurement and the state of a subject during that measurement (respiratory rate during sleep vs. during activity), between menopausal status and treatment or risk factors, between race and disease, between month of the year and other predictions, between the quality and quantity of a symptom, and between study center and treatment (1).

To test for interaction, a new term must be added to the model for each two predictors for which interaction is being assessed. The coefficient of this term is then analyzed to see if the combination of the predictors has an effect on the outcome. This can quickly become complicated with a higher number of predictors and with continuous predictors. For further information on modeling with and testing for interactions, see the following references (1,2).

Choice of the model

While this article focuses on logistic regression models, many other options for model choices exist. Unfortunately, consensus methods for choosing the type of statistical model do not exist. However, several guidelines should be followed during model selection (1). First, the model must use the data efficiently. The model should fit the overall structures likely to be present in the data and whose mathematical forms are appropriate for the response being modeled (linear, quadratic, etc.). This should minimize the need for interaction terms that are included only to address a lack of fit. Finally, the process of developing the model should be transparent and detailed enough to be reproducible by another analyst (16). Models are either chosen out of a statistical model (such as regression analysis and survival analysis) or via machine learning techniques (such as artificial neural networks, support vector machine models, and tree-based models). Machine learning techniques for model development are beyond the scope of this overview but are well described elsewhere (11).

Logistic regression is a widely used statistical model that allows for multivariate analysis and modeling of a binary dependent variable; linear regression is a similar model for a continuous dependent variable. The multivariate analysis estimates coefficients (for example, log odds or hazard ratios) for each predictor included in the final model and adjusts them with respect to the other predictors in the model. The coefficients quantify the contribution of each predictor to the outcome risk estimation (3,11). Table 1 contains multiple examples of predictive models developed using logistic regression, such as the TREAT model which predicts the likelihood of indeterminate lung nodules being lung cancer, a binary outcome (4).

Model performance

In general, the overall model performance is evaluated by the difference between the predicted outcome and the actual outcome. These differences are related to the concept of “goodness of fit” of a model, with better models having smaller distances between predicted and observed outcomes (1,18). However, this commonly evaluates the fit of the model using the original data while performance of the model should be evaluated on a new dataset.

The Brier score is commonly used to assess performance for models that predict a binary outcome. For example, a model may predict a 10% risk of dying after an intervention, but the actual outcome is either death or survival. The Brier score compares the squared differences between actual and predicted binary outcomes, with scores ranging from 0 for a perfect model to 0.25 for a non-informative model with a 50% incidence of the outcome (18). The Brier score can also be adapted for application to survival outcomes. When evaluating the TREAT model, a boxplot was used to illustrate differences between the Mayo Clinic model and the TREAT model both on the initial data and the external validation data (see Figure 1) (4).

Figure 1.

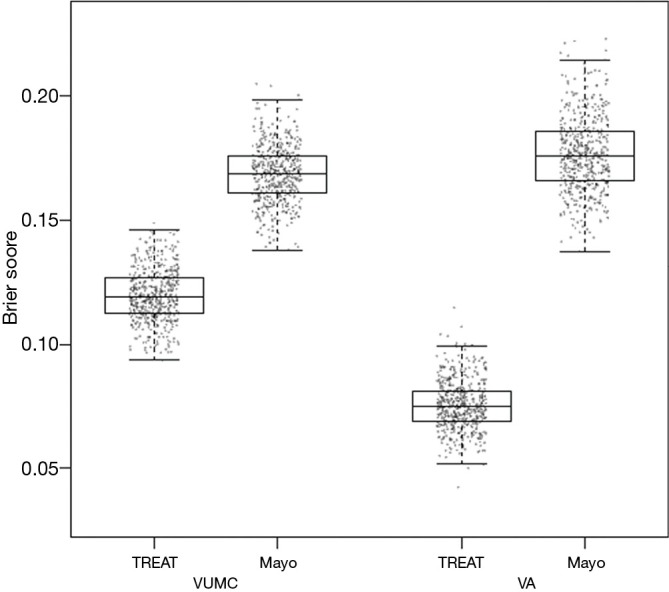
Comparing performance of TREAT model to Mayo Clinic model using Brier scores. From ref (4). TREAT, Thoracic Research Evaluation And Treatment.

Overall performance can be broken down into two characteristics of performance, calibration and discrimination, which can be assessed separately as well.

Calibration

Calibration can also be assessed visually by plotting the observed outcomes (x-axis) against the predicted outcomes (y-axis), with perfect predictions falling along a 45° line. For a linear regression, this would be shown as a scatter plot; for a binary outcome, smoothing techniques may be used to create a slope. This can also be done within subgroups of participants that are ranked by increasing estimated probability, i.e., different risk groups (3,18). Visually assessing calibration can be useful as a predictive model may not perform equally across all risk groups.

A common summary measure of calibration is the Hosmer and Lemeshow test or the “goodness of fit” test (18). This test evaluates calibration (agreement between observed and expected event rates) across each decile of risk values (e.g., <10%, 10–20%, etc.) and compares them for significant differences. A significant P value on the Hosmer-Lemeshow test implies that the model is not well calibrated as it performs differently for different risk categories (3). However, having a non-significant P value does not imply that the prediction model is well calibrated, but rather that there is no evidence that the model is uncalibrated. These “goodness of fit” tests provide a summary statistic, and while it may appear that a model is well calibrated, more information can often be found by examining the calibration plot. For example, there may be certain risk categories for which the model significantly over- or under-estimates risk that are not elucidated by the summary statistic.

Discrimination

Discrimination is the ability of a model to distinguish individuals who developed the outcome from those who remained event free. Discrimination can be evaluated through several methods, the most common of which is the concordance index (c-index or c-statistic) (11,18). The c-index is the chance that given two individuals, one of whom will develop the outcome and one who will not, the model will correctly assign a higher probability to the individual who develops the outcome. For regression models, the c-index is equal to the area under the receiver operating characteristic curve (AUC), and ranges between 0.5–1. A c-index of 1 indicates a model that is perfectly discriminating, and a value of 0.5 would indicate the model is unable to discriminate between these two groups.

The receiver operating characteristic curve (ROC) plots the true positive rate (sensitivity) over the false positive rate (1-specificity). A 95% confidence interval typically accompanies this graph, with wide confidence intervals indicating a less discriminating model. The TREAT model uses AUC to illustrate improvement in discrimination from the Mayo Clinic model both in its original dataset and in the external validation data (see Figure 2) (4).

Figure 2.

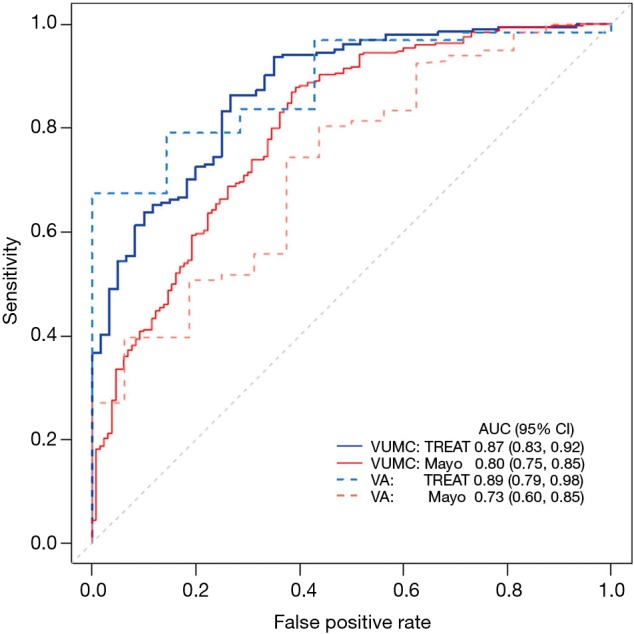
Comparing discrimination of TREAT model to Mayo Clinic model using AUC. From ref (4). TREAT, Thoracic Research Evaluation And Treatment; AUC, area under the receiver operating characteristic curve.

In addition to the c-index, the discrimination slope is a useful and simple measure for how well the individuals who develop the outcome are separated from those who remain event-free (18). Visualization of the amount of overlap between the two groups is easily accomplished with a box plot or histogram; less overlap between the two groups illustrates a better discriminating model.

Model validation

Internal validation

Internal validation of a prediction model estimates the potential for overfitting the model and optimism in the model’s performance, using no other data than the original study sample. The prediction model can be expected to perform optimistically when the data are from the population used to create the model compared to its performance in a different but similar population (1).

In its simplest form, internal validation could be performed by randomly splitting the sample data into two subsets and using half as the development or training subset and half as the validation subset. However, this method is inefficient as not all data collected are used to develop the prediction model. Additionally, this method has replication instability in that different random splits of the data will lead to different prediction models. Internal validation does not address selection bias with recruitment, missing data, or measurement errors as validation is performed within the study population (1).

To avoid these issues, other methods of internal validation are typically employed. In k-fold cross-validation the sample is divided into k subsets or folds (most commonly 5 or 10 folds). One subset is chosen as the validation subset, and the remainder of the k-1 subsets are used for model development or “training”. The validation subset is then used to calculate the prediction error of the model. Once completed, the process restarts holding out a different subset as the validation subset and using the remaining subsets to calculate a new model. This is repeated k times and the model’s performance is calculated by averaging the errors calculated in each step. The advantage of this method is that each observation is used for both training and validation, and each observation is only used once for validation (16).

Bootstrapping is another method of internal validation and is an ideal method for smaller sample sizes or for larger numbers of candidate predictors (3). In general, study populations represent a random sample drawn from a larger target population. Repeated sampling would result in similar but different study populations and may lead to slightly different predictor-outcome associations and model performances. Bootstrapping aims to replicate this process by sampling with replacement within the study population to create multiple training subsets (11). In each bootstrap sample, the data are analyzed as in the original study sample, repeating each step of the model development including applied predictor selection strategies. This will likely yield a different model from each bootstrap sample with a corresponding c-index. Subsequently these bootstrap models are applied to the original study sample, yielding a difference in c-index. The bootstrap sample is then returned to the pool (sampling with replacement), a new random bootstrap sample is drawn, and the process is repeated often 100 or 500 times. The average of these differences in c-index calculated in each round indicates the optimism of the original prediction model. This method allows all of the original data to be used in model development while providing insight into the extent to which the original model is overfitting or too optimistic (1,2). The TREAT model used 500 bootstrap samples with replacements for internal validation, with each bootstrap plotted as a data point to create the boxplots in Figure 1 (4).

External validation

When applied to new individuals, a prediction model generally performs worse than with its original study population, even after internal validation procedures to correct for optimism and overfitting (1). Thus, before a new prediction model is accepted into practice it must also be externally validated to demonstrate its predictive value in a similar population with different individuals. In order to externally validate a predictive model, an independent sample from a comparable population (in terms of inclusion and exclusion criteria) with the same predictor and outcome data available is needed. The model is then applied to the data from external population to estimate their risk of the outcome, compared to the observed outcome, and the performance of the model calculated.

The external validation study can be done retrospectively, with an already existing dataset, or prospectively, by enrolling new individuals with the purpose of validating the model (19,20). In general, the likelihood of finding a lower predictive accuracy after external validation increases as more stringent forms of validation are used. The TREAT model used a retrospectively collected dataset from a different hospital (nearby Veterans Affairs Hospital) for external validation (4); this was a similar cohort to the original dataset but with a higher prevalence of lung cancer.

Temporal validation is one method of external validation in which individuals from the same institution are sampled from a different (usually later) time period (20). This is occasionally accomplished by non-random splitting of the original study sample so that individuals from a later time period are not included in model development. However, these patients have the same inclusion and exclusion criteria as the original study population and likely have the same measures of predictors and outcomes. Thus, they may not be a sufficiently different population for comparison and may not truly indicate the generalizability of the model.

Geographical validation studies involve testing the model at a different institution or in a different country. This can be accomplished in a similar method to temporal validation with non-random splitting of the original study dataset by study center if the original study was multicenter. Alternatively, the model can be tested in a study designed expressly for validation that would likely allow for greater variation of individuals, predictors, and outcomes due to different inclusion and exclusion criteria (20).

Domain or setting validation allows for model validation in populations of individuals that are very different than the original study population. For example, validating a model developed in healthy patients in patients with type 2 diabetes or validating a model developed in adults in children (1,20).

Generalizability

Generalizability is the degree to which the study sample characteristics accurately reflect the new target population. A validated prediction model with excellent calibration and discrimination may not be generalizable to a clinician’s patient population. For example, the well-validated Mayo Clinic model for lung cancer prediction in single pulmonary nodules has been shown to have limited generalizability to a surgical population due to the higher prevalence of lung cancer seen in surgical clinics (8,21). The TREAT 2.0 model was designed to address this issue and was developed in a population of thoracic surgery clinic patients being evaluated for pulmonary nodules (4,22,23). This is a population with a high prevalence of lung cancer and the majority of these patients underwent resection.

Updating or recalibrating the model

When a low predictive accuracy is found after an external validation study, researchers are left with the decision to reject the model or to update the model to improve its predictive accuracy. The model can be adjusted or recalibrated for local circumstances by combining information captured in the original model with information from new individuals from the validation study. The updated model will then have improved transportability to other individuals in new settings (20).

Multiple methods have been proposed for updating models. A common reason for poor predictive performance in a new population is due to a difference in baseline risk or hazard. By adjusting the baseline risk of the original prediction model to that of the new population, calibration can be easily improved (20). Further methods of recalibration included adjusting all predictor weights simultaneously, adjusting only a single predictor weight, or adding a new predictor or marker to the existing model. Updating the model requires either access to individual level data in the validation sample or accurate information about the frequency of the outcome and mean levels of the predictor in the new population. Applying these methods lead to improvement of the predictive power in the validation sample; however, further testing and recalibration may be required before the model is more generalizable.

Adding new predictors to models

As new tests are developed, such as new imaging studies or biomarkers, one may want to include them in new or existing predictive models. However, a good predictive value of the new test itself is no guarantee that it will give added predictive value when in combination with the standard predictors (10). The performance of the model should be evaluated before and after adding in the new test and several methods have been proposed to accomplish this. Measures discussed above such as the AUC can be used to compare the discrimination of the model before and after the addition of the new test and are widely used (20,24). However, this can be insensitive to detecting small changes in model performance, especially if the AUC of the model is already large, and the information may not be clinically relevant (24,25).

Reclassification tables show the extent to which patients are correctly classified (diseased vs. non-diseased, high risk vs. low risk, etc.) before and after the addition to of the new test (10). The net reclassification index (NRI) is a method of quantifying the added value of the new test and has been widely reported along with its associated p-value. However, this is not a reliable measure of improvement as it can be artificially inflated with a high rate of false positive conclusions. Pepe et al. demonstrated that when a non-informative biomarker (one that does not improve prediction on its own) is added to a prediction model the NRI can still show statistically significant improvement, which is highly troubling (24,25). They recommend simply reporting the regression coefficients for the expanded prediction model along with standard tests of significance and presenting reclassification information in risk classification tables.

Assessing impact

Once a prediction model has been validated and is being implemented, the impact of the actual use of the model on the behavior and management of healthcare professionals and/or individual patients should be investigated through a model impact study (20). There are two main approaches to impact studies: assistive and directive. Assistive approaches provide estimated probabilities of the outcome without recommending a decision. In directive approaches, a decision is explicitly recommended or specific therapeutic management is prescribed for each probability category. The assistive approach provides more autonomy to healthcare professionals, while the directive approach may have greater clinical impact (20).

The study design of a model impact study is ideally a randomized control trial where individuals, providers, or centers are either randomly assigned to the intervention (risk-based management using the prediction model) or to usual care (18). This may be done as a stepped-wedge cluster randomized trial where at some point in time each cluster switches between usual care to the intervention. Impact studies can be non-randomized as well, with before-after studies comparing patient outcomes before the intervention (those treated with usual care) to patient outcomes after the prediction model is implemented. Or, a health care provider’s decision making is documented for each individual before and after being exposed to the model’s predictions (20).

Conclusions

To be useful, a prediction model must provide accurate and validated estimates of the risks to the individual and ultimately improve an individual’s outcome or the cost-effectiveness of care. This review outlines the process for development of a logistic regression risk prediction model, from choosing a data source and selecting predictor variables to assessing model performance, performing internal and external validation, and assessing the impact of the model on outcomes.

Disclosure: The content is solely the responsibility of the authors and does not necessarily represent the official views of AHRQ or the Department of Veterans Affairs. The funding agency had no role in the preparation, review, or approval of the manuscript or in the decision to submit the manuscript for publication.