Using Structural Equation Modeling to Examine the Influence of Social, Behavioral, and Nutritional Variables on Health Outcomes Based on NHANES Data: Addressing Complex Design, Nonnormally Distributed Variables, and Missing Information

Abstract

Background

Structural equation modeling (SEM) is a multivariate analysis method for exploring relations between latent constructs and measured variables. As a theory-guided approach, SEM estimates directional pathways in complex models based on longitudinal or cross-sectional data where randomized control trials would either be unethical or cost prohibitive. However, this method is infrequently used in nutrition research, despite recommendations by epidemiologists for its increased use.

Objectives

The aim of this study was to explore 3 key methodologic areas for consideration by researchers when conducting SEM with complex survey datasets: the use of sampling weights, treatment of missing data, and model estimation techniques.

Methods

With the use of data from NHANES waves 2005–2010, we developed an SEM to estimate the relation between the latent construct of depression and measured variables of food security, tobacco use (serum cotinine), and age. We used a hierarchic approach to compare 5 SEM model iterations through the use of: 1 and 2) complete cases without and with the application of sampling weights; 3) an applied missingness dataset to test the accuracy of multiple imputation (MI); 4) the full NHANES dataset with imputed data and sampling weights; and 5) a final respecified model. Each iteration was conducted with maximum likelihood (ML) and quasimaximum likelihood with the Satorra-Bentler correction (QML) to compare path coefficients, standard errors, and model fit statistics.

Results

Path coefficients differed between 15.68% and 19.17% among model iterations. Nearly one-third of the cases had missing values, and MI reliably imputed values, allowing all cases to be represented in the final model iterations. QML provided better model fit statistics in all iterations.

Conclusions

Nutrition epidemiologists should use complex weights, MI, and QML as a best-practices approach to SEM when conducting analyses with complex design survey data.

Introduction

National health surveys can provide nutrition epidemiologists with access to data containing comprehensive biological, psychosocial, behavioral, and demographic variables of interest to public health. These surveys are often conducted with the use of complex sampling designs, which allow for analyses that can be generalizable to the population. As more researchers seek to understand complex relations between determinants of health and associated behaviors through an integrated lens, structural equation modeling (SEM) is one method for answering theory-guided research questions (1). This statistical approach uses a combination of techniques that include regression (path analysis) and factor analysis to explore multivariate, directional pathways between categoric variables, measured variables, and latent constructs (2–4) (see Table 1 for definitions of statistical terms). Either longitudinal or cross-sectional data can be used when conducting SEM, thereby providing researchers with an alternative method for delineating causal relations when randomized control trials would either be unethical or cost prohibitive (2).

Applications for SEM in medical research have been clearly described elsewhere (4). The development of a structural equation model requires 5 essential steps: 1) identification of the research problem, 2) identification of the model, 3) estimation of the model, 4) determination of the model's goodness of fit, and 5) respecification of the model, if necessary and theoretically justified. However, when complex survey design datasets are used (2, 11), SEM analysts must make important decisions regarding model estimation techniques, the use of weighted data, and the treatment of missing data. These decisions have important implications for the interpretation and generalization of analyses, and are inconsistently applied and described in the literature (5, 12, 13).

TABLE 1.

Applied definitions for select statistical terms used in this paper¹

Term	Applied example
Measured variable	A construct that can be directly measured, such as age, blood pressure, height, weight; or biomarkers, such as serum cotinine (a measure of cigarette smoking)
Latent construct	A construct that cannot be directly measured, but that can be reliably assessed through a combination of validated measured variables, such as the construct of depression based on the 9-item PHQ
Factor analysis (measurement model)	A statistical technique used to identify latent constructs, such as depression, through multiple measurable items, such as the PHQ. In SEM, items from the survey are assessed through factor analysis to confirm their reliability and validity as a measure of the intended construct
Path analysis (structural model)	A series of independent linear regressions between multiple variables to test a causal pathway, such as the relation from age to food security to cotinine
Structural equation modeling	A theory-guided approach for regressing pathways among latent constructs and measured variables, such as socioeconomic status, to predict health (1)
Complex survey design	A method of sampling from a population applying stratification and clustering to achieve statistical and practical efficiency (5) For example, NHANES uses a 4-stage sampling design. The primary sampling unit, county, is segmented into smaller units such as city blocks, then dwelling units, and finally selection of individuals within the household (6)
Simple imputation	Simple imputation strategies for data missingness, such as mean imputation, last observation carried forward, and hot-deck imputation strategies, can provide the researcher with a full dataset, but may artificially reduce variability or yield results that are much more precise than they should be, which can lead to inflated type I error rates (7)
Multiple imputation	An alternative approach to simple imputation, where each missing value is computed independently under a Bayesian model that includes an estimation of uncertainty about the missing data, The datasets are analyzed individually and then combined to give an appropriate pooled estimate. The combined procedure produces more accurate standard errors than simple imputation strategies (7–9)
Maximum likelihood	An iterative approach that uses probability density functions to find the parameter estimates that result in a best fit to the observed data (2)
Quasimaximum likelihood	An iterative approach that approximates the likelihood function based on the use of approximated nonnormal density functions, making better estimations for nonnormally distributed variables and sampling weights (10)
Satorra-Bentler correction	A sandwich estimator that is used in conjunction with QML which relaxes the assumption for multivariate normal data, creating robustness to nonnormal distributions and providing better chi-square goodness-of fit statistics and better estimates of other fit indices (10)

¹PHQ, Patient Health Questionnaire; QML, quasimaximum likelihood; SEM, structural equation modeling.

This article will demonstrate best practices for conducting SEM with complex survey data.

Background

The following background is designed to provide the reader with a basic overview of the statistical concepts that are the focus of this methodologic manuscript. The reader is encouraged to review Table 1 for applied definitions of statistical terms and concepts used in this paper.

Complex survey designs

Most large-scale, federally funded surveys are conducted through the use complex, multistage, probability sampling designs, such as NHANES (9) and the Behavioral Risk Factor Surveillance System Survey (14). These surveys are used to report national- and state-level data on various nutrition intake and related health outcome measures, which are used to inform many health policy decisions. Within these complex survey designs (Table 1), methods of stratification and clustering are applied to achieve both statistical and practical efficiency through the use of primary sampling units (PSUs) (5, 6). NHANES sampling design uses counties as the PSU, and its 4-stage sampling structure has been extensively described elsewhere in the literature (3, 6). Each year, only ∼15 PSUs are selected from throughout the United States (6). From these PSUs, ∼5500–6000 persons in total are selected for participation; therefore, individual cycle datasets have limited generalizability and require additional variance adjustments. Merging >1 cycle is recommended in order to achieve a more representative sample of the US population (15), and requires appropriate adjustment of the sampling weights by dividing by the number of cycles being merged. The variance adjustments and weightings can be achieved with the use of software designed for complex survey design analysis (e.g., SUDAAN, SAS, Stata, or R). However, studies that use complex survey data often do not incorporate the sampling weights (5, 13), which may have significant impacts on variable distribution (5) and lead to biases in statistical results and limit finding generalizability.

Missing data

Missing data are common in nearly every form of survey research, especially those with large-scale, complex survey designs (7). When SEM is being used, missingness in any item that comprises a latent construct has the capacity to greatly reduce the power of its tests (11). Therefore, researchers must first explore patterns of missingness for categorization, such as missing completely at random (MCAR), missing at random (MAR), or not missing at random (NMAR) (7). MCAR may occur as a result of random data entry errors that follow no specific pattern (7). If the missing data can be explained by other variables captured in the survey, they are classified as MAR (8). MAR may occur when a specific group or subpopulation chooses not to answer a portion of the survey, and these differential response patterns can be identified through other variables in the dataset, such as demographics. If missing data depend on an unobserved predictor (e.g., travel distance to survey site) or on the variable itself, (e.g., underage drinkers may be less likely to answer alcohol-related questions), they are NMAR, and the missingness must be either modeled, which is imprecise and difficult, or acknowledged as a source of bias in the interpretation of the study's findings (7, 8).

If the missingness is either MCAR or MAR, multiple imputation (MI) (Table 1) has been shown to be an effective method to account for missing data (8, 9, 16), and is currently supported by most statistical software packages. Auxiliary variables, which are variables correlated with the variables of interest yet not part of the specified analysis, can be used in the MI process to increase the validity of the imputed data (9, 16). Other criteria for MI procedures can be found elsewhere (9, 17–19).

SEM estimation

Maximum likelihood (ML) estimation (Table 1) is the default estimator in statistical software packages that accommodate SEM analyses, including STATA and MPLUS. Generally, ML is consistent in producing true values as the sample size gets larger and is considered efficient, with typically smaller standard errors than other estimation techniques when assumptions are met. ML requires relatively large sample sizes and normally distributed variables, and although there are varied recommendations, a generally accepted minimum is 200 observations (2).

Quasimaximum likelihood (QML) (Table 1) estimation has the same sample size requirements as ML, and was developed for use with SEM with nonnormally distributed variables and higher-order effects (10). The specific calculations of QML estimations (20) and QML techniques with regard to SEM are fully described elsewhere (10, 21). QML is more robust than ML to violations of statistical assumptions (10, 22, 23), and is often used in conjunction with the Satorra-Bentler correction (10), which corrects for heteroscedasticity and adjusts standard errors (24), resulting in better model fit statistics, such as the chi-square test, the root mean square error of approximation (RMSEA), the standardized root mean square residual (SRMR), the comparative fit index (CFI), and the Tucker-Lewis Index (TLI) (2–4, 11, 10). QML has also been proposed as the most appropriate estimator for complex survey analyses (10, 20, 22, 25).

Thus, the purpose of this study is to identify a best-practices approach to conducting SEM with large complex survey design datasets when applying survey weights and handling of missing data. Specifically, we compare iterations of an SEM with the following properties: 1) it ignores compared with incorporates complex survey weightings, 2) it uses complete case analysis compared with MI to handle missing data, and 3) it uses ML and QML with Satorra-Bentler correction estimation methods. These iterations will be used to identify which approaches result in better estimations and model fit statistics.

Methods

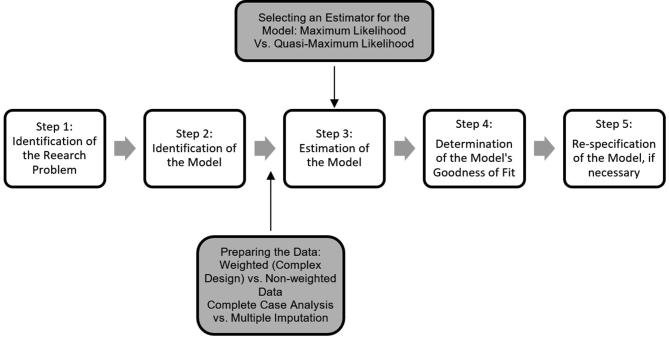
We used a multicycle NHANES dataset to test the hypothesized best practices for SEM (Figure 1). We merged 2005–2010 NHANES cycles to obtain a sample of 17,132 subjects aged >20 y who attempted the interview and examination (15). We summarized the sample's range, mean, and median for age with the R package “psych” (26). We assessed gender and race as a percentage of the sample and of the population. Survey weightings and variance estimates for clustering of strata and PSUs were applied in select iterations of the SEM model and we determined the populations’ weighted mean for age with the “Survey” package (27). Because 3 cycles of data were combined, weighting estimates per observation were reduced by one-third (6).

FIGURE 1.

Steps for conducting SEM analysis with important steps highlighted that researchers should consider when they use complex survey data and handle missing data as explored in this manuscript. SEM, structural equation modeling.

Identification of the research problem and the model (steps 1 and 2)

Food insecurity, a household-level condition of limited or uncertain access to adequate food supply, is increasingly recognized by public health stakeholders for its health, economic, and social implications (28). We explored the theoretical relations of age, food security, depression, and tobacco use within the US population, as shown in the recursive model in Figure 2. These relations are based on previous empirical findings linking food insecurity to depression (29–34) and tobacco use (35), and depression to tobacco use (36).

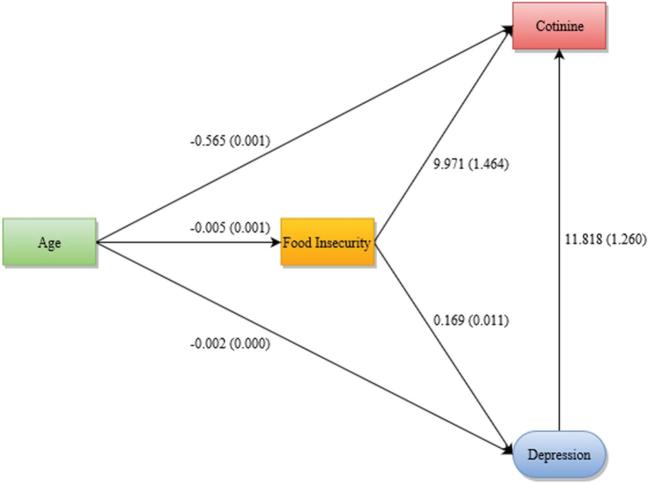
FIGURE 2.

Final adjusted structural equation model of the effects of age on cotinine with mediating factors of food security and depression based on the use of the QML estimation with Satorra-Bentler correction with the NHANES data (n = 17,132 sample size of people aged >20 y; total population = 214,755,655). QML, quasimaximum likelihood.

Measures

The 10-item US Adult Food Security Survey Module assesses household food adequacy in the preceding 12 mo by order of increasing severity, ranging from reports of worry about running out of food to physical symptoms of hunger, with higher scores indicative of higher food insecurity. This survey can be used as either a latent construct or a measured item (37). For these analyses, food insecurity is used as a measured item with a sum score of 0–10. The Patient Health Questionnaire (PHQ) is a 9-item screening instrument used to identify depressive symptoms occurring in the previous 2 wk (38) with a symptom frequency Likert scale rating for each item that ranges from 0 (not at all) to 3 (nearly every day). Although this survey can be used as a measured item for diagnostic purposes in clinical settings, for population-level analyses, it should be treated as a latent construct (39). Cotinine is a validated serum measure of current nicotine use and current smoking behavior (40). Finally, a race/ethnicity variable was used as an auxiliary variable to determine missingness patterns in the data and during the MI procedures.

Structural equation modeling

We used the “lavaan” package in R (41) to build the SEM model for all iterations described in the sections below. For iterations involving weighted data, sampling weights were added through the use of the package survey (27), and then combined with the “Lavaan.Survey” (25) package to complete the estimation.

Preparation of the dataset: applying sample weightings (methods research question 1)

To evaluate the influence of sampling weights on SEM path coefficients, we compared 2 iterations of the SEM model without weighting (iteration 1) and with weighting (iteration 2). Because complete case analysis is a common practice (13), the first 2 iterations of the model used complete cases, with and without complex survey design, to illustrate the changes that can occur in variable distribution, thereby affecting the statistical results.

Preparation of the dataset: assessing missing information and using MI (methods research question 2)

We computed missingness for each SEM variable from the full NHANES dataset. We then explored patterns of missingness for the SEM variables of food security, cotinine, and depression by the auxiliary variable of race/ethnicity. Figures of these patterns were generated with the R package “VIM” (42). These patterns helped to determine whether the incomplete information is MCAR, MAR, or NMAR.

Next, the complete case dataset was modified to match the missingness from the full dataset by applying relevant percentage of missingness to each of the variables by race/ethnicity. Then, 5 imputations, processed with 5 iterations, which have been shown to be sufficient (43), were generated with the “mitools” (44) package and the “mice” (45) package (iteration 3). The final estimated model (iteration 4) used the full NHANES dataset with the MI strategy and complex survey design. Path coefficients were estimated to determine the absolute change between these model iterations.

Estimation and model fit statistics (steps 3 and 4)

Selection of estimation technique (methods research question 3)

Prior to model estimation, distributions of variables were assessed for normality. We then used ML and QML with Satorra-Bentler correction estimation techniques to compare the difference in coefficients and standard errors. Additionally, model fit statistics were compared between these two estimation methods.

Respecification of the model (step 5)

For the final iteration of the model (iteration 5), appropriate covariance paths among the depression screener items with Lagrange multiplier values (2) >50 were respecified to improve model fit.

Results

Demographics

Fewer than two-thirds of the 17,132 participants had complete information (n = 10,574, 61.70%) (Table 2). The full dataset was comprised of 8303 males (48.45%) and 8829 females (51.52%), which represented 48.17% and 51.83% of the population after weighting, respectively. The complete case sample's gender ratio differed slightly from the full dataset, including 5291 (50.04%) males and 5283 (49.96%) females. The mean and median age in the sample was 49.64 and 49.0 y, respectively. When sampling weights were added, the mean ± SE age decreased to 46.79 ± 0.3259 y. Demographics are fully described in Table 2 including the percentage with complete cases in each demographic group.

TABLE 2.

Demographics from NHANES unweighted raw data (n = 17,132), with 6-y weighting (total sample = 214,755,655), and complete cases (n = 10,574), for participants >20 y of age

	NHANES unweighted		NHANES weighted		Complete cases sample
	No.	%	No.	%	No.	%	% completing survey
Ethnicity
Mexican American	3176	18.54	18,000,000	8.38	1526	14.43	48.05
Other Hispanic	1452	8.48	9500,000	4.42	761	7.20	52.41
Non-Hispanic white	8232	48.05	150,000,000	69.85	5929	56.07	72.02
Non-Hispanic black	3472	20.27	24,000,000	11.18	1929	18.24	55.56
Other, including multiracial	800	4.67	13,000,000	6.05	429	4.06	53.63
Age group, y
20–29	3006	17.55	41,000,000	19.09	1581	14.95	52.59
30–39	2910	16.99	40,000,000	18.63	1660	15.70	57.04
40–49	2899	16.92	44,000,000	20.49	1766	16.70	60.92
50–59	2520	14.71	39,000,000	18.16	1619	15.31	64.25
60–69	2648	15.46	25,000,000	11.64	1817	17.18	68.62
70–79	1891	11.04	16,000,000	7.45	1337	12.64	70.70
≥80	1258	7.34	9,500,000	4.42	794	7.51	63.12
Food security (raw: n = 12,797; with weighting n = 175,724,587)
High food security	12,558	98.13	170,000,000	96.74	10,392	98.28	82.75
Marginal food Security	10	0.08	120,000	0.07	8	0.08	80.00
Low food security	108	0.84	900,000	0.51	79	0.75	73.15
Very low food security	121	0.95	1100,000	0.63	95	0.90	78.51

Variable characteristics

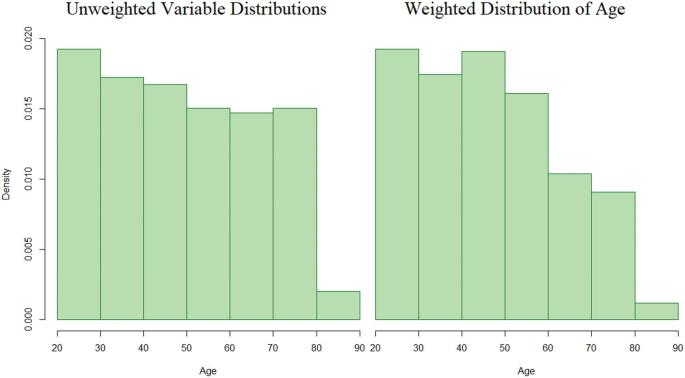
The skewness and kurtosis of age, and 2 of the items that comprise the PHQ (DPQ030 and DPQ040), were within accepted values for ML; however, all other variables were outside of the normally accepted values. Table 3 provides means, ranges, and normality values for each variable included in the analyses. Histograms of age (Figure 3) show a shift in distribution when sampling weights are applied.

TABLE 3.

Descriptive statistics of variables from the NHANES sample¹

Variable	Mean	SD	Min	Max	Skew	Kurtosis
Age	49.64	18.31	20	85	0.14	−1.12
Cotinine	59.78	129.2	0.01	1438	2.60	8.11
Food security	0.24	1.45	0	10	5.94	33.85
DPQ010: …little interest or pleasure in doing things?	0.34	0.71	0	3	2.27	4.71
DPQ020: …feeling down, depressed, or hopeless?	0.36	0.72	0	3	2.24	4.58
DPQ030: …trouble falling or staying asleep, or sleeping too much?	0.63	0.95	0	3	1.41	0.84
DPQ040: …feeling tired or having little energy?	0.74	0.93	0	3	1.18	0.46
DPQ050: …poor appetite or overeating?	0.37	0.76	0	3	2.24	4.30
DPQ060: …feeling bad about yourself—or that you are a failure or have let yourself or your family down?	0.25	0.63	0	3	2.88	8.20
DPQ070: …trouble concentrating on things, such as reading the newspaper or watching TV?	0.25	0.64	0	3	2.88	8.13
DPQ080: …moving or speaking so slowly that other people could have noticed? Or the opposite—being so fidgety or restless that you have been moving around a lot more than usual?	0.16	0.52	0	3	3.73	14.61
DPQ090: …thoughts that you would be better off dead or of hurting yourself in some way?	0.06	0.31	0	3	6.81	52.02

¹DPQ, NHANES depression screener questionnaire.

FIGURE 3.

Histograms of age from NHANES data cycles 2005–2010 showing the shift in distribution with unweighted observations (left) and when sampling weights are applied (right).

Comparing SEM model iterations with and without weightings (methods research question 1)

The first 2 iterations were compared to illustrate how SEM estimates and fit statistics differ when sample weightings are applied. The complete case population sample size with weightings represented 153,038,278 persons.

The first SEM iteration included complete cases without weightings. This model revealed significant relation between all variables, with the largest path coefficients between food security score and cotintine (mean ± SE 8.561 ± 1.219) and between cotinine and depression (mean ± SE10.264 ± 1.392). When weightings were added to the complete cases (Iteration 2), all relations remained significant and the strongest relations remained between food security score and cotinine, and between cotinine and depression. However, for all relations, except for depression and age, the path coefficients differed between iteration 1 and 2 (absolute average change of 15.78%). This difference is due the change in variable distributions and demonstrates how the application of sampling weights may alter the strength of the relations between variables.

Research question 2: missing data

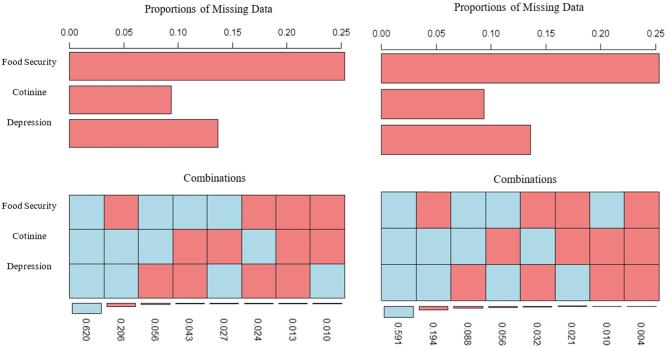
The amount of missing data for the SEM variables ranged from 0.00% to 25.30% (Figure 4, top). Missingness for the individual variables of cotinine and depression score was evenly dispersed by race/ethnicity; however, missingness for the food security variable was missing more often among Mexican-Americans and other Hispanics (Figure 5), confirming there were data missing at random, and race will be included in the imputation process as an auxiliary variable. We did not find any distinguishable missingness patterns for the combinations of food security, cotinine, and depression (Figure 4, bottom).

FIGURE 4.

Proportion of missing data from the full NHANES dataset (left) and modified complete cases data (right) with percentage of component missingness (top) and patterns (bottom) of component missingness among NHANES participants.

FIGURE 5.

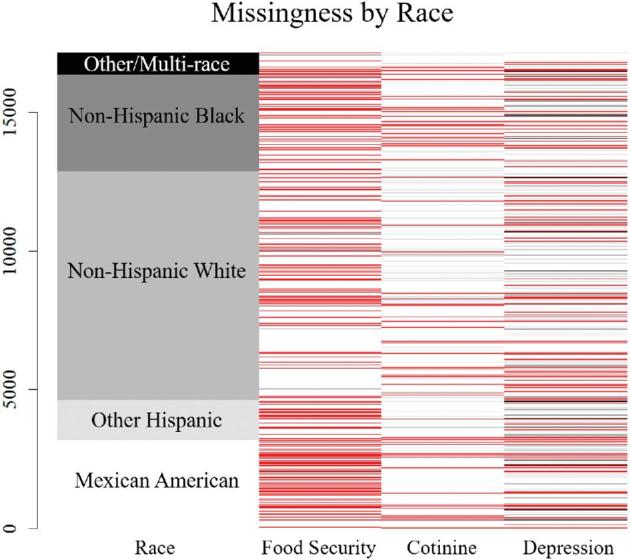
Patterns of missing data by race from the full NHANES data. Mexican-Americans and other Hispanics were far less likely to complete the Food Security Survey Module.

When comparing the path coefficients for iteration 2 (weighted complete case dataset) with iteration 3 (weighted complete case dataset with simulated missingness and MI), there were minimal to no differences (absolute average change of 7.18%). This demonstrates that for this SEM model, MI is an appropriate method for addressing missing data.

When comparing iteration 4 (weighted full dataset with MI) with iteration 2, the average absolute path coefficient difference was 19.17% (Table 4). Iteration 4 confirmed significant relations between all variables with the highest path coefficients between food security score and cotintine (mean ± 9.918 ± 1.407), which was lower than that for iteration 2, whereas the relation between cotinine and depression (mean ± SE 11.170 ± 1.128) was higher than that for iteration 2. Another noticeable difference between the 2 iterations were that the highest relation between variables in the model changed from food security score and cotinine in iteration 2 to cotinine and depression in iteration 4.

TABLE 4.

Comparison of unstandardized coefficients and standard errors for the structural model of each SEM iteration¹

	Iteration 1		Iteration 2		Iteration 3		Iteration 4
	Complete cases without weightings (n = 10,574)		Complete cases with weightings (n = 10,574, total sample = 153,038,278)		Imputed complete cases with weightings (n = 10,574, total sample = 153,038,278)		Full dataset with weightings and MI (n = 17,132, total sample = 214,755,655)
	Coefficient	SE	Coefficient	SE	Coefficient	SE	Coefficient	SE
Food security on age	−0.006	0.001	−0.004	0.001	−0.004	0.001	−0.006	0.001
Cotinine on age	−0.475	0.056	−0.540	0.086	−0.569	0.085	−0.544	0.075
Cotinine on food security	8.561	1.219	10.807	2.035	10.63	1.828	9.918	1.407
Depression on age	−0.003	0.001	−0.003	0.001	−0.002	0.001	−0.002	0.000
Cotinine on depression	10.264	1.392	9.719	1.526	9.668	1.696	11.17	1.128
Depression on food security	0.155	0.014	0.180	0.018	0.176	0.018	0.166	0.011

¹All coefficients were statistically significant P < 0.001. MI, multiple imputation; SEM, structural equation modeling.

Estimation and model fit statistics

Selection of estimation technique (methods research question 3)

The path coefficients produced in each iteration were the same under both QML and ML. QML with Satorra-Bentler correction produced larger SEs (Table 4), but produced better model fit values for each iteration (Table 5). The average increase of SEs of variables was 94% between ML and QML when the complete case dataset was used. The SE increases were greater after applying the weightings, which resulted in an average increase of 154.26%.

TABLE 5.

Comparison fit statistics between ML and QML with Satorra-Bentler correction among model iterations

	Iteration 1		Iteration 2		Iteration 3		Iteration 4		Iteration 5
	Complete cases without weightings (n = 10,574)		Complete cases with weightings (n = 10,574, total sample = 153,038,278)		Imputed complete cases with weightings (n = 10,574, total sample = 153,038,278)		Full dataset with weightings and MI (n = 17,132, total sample = 214,755,655)		Final respecified model (n = 17,132, total sample = 214,755,655)
	ML	QML	ML	QML	ML	QML	ML	QML	QML
Chi-square test P value	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
Root mean square error of approximation (RMSEA) (90% CI)	0.062 (0.0590, 0.064)	0.0611 (0.0570, 0.064)	0.066 (0.063, 0.068)	0.0641 (0.060, 0.068)	0.064 (0.062, 0.067)	0.0631 (0.059, 0.067)	0.062 (0.061, 0.064)	0.0621 (0.059, 0.065)	0.024
Standardized root mean square residual (SRMR)	0.035	0.032	0.037	0.035	0.034	0.034	0.032	0.032	0.012
Comparative fit index (CFI)	0.925	0.9271	0.914	0.9161	0.916	0.9191	0.928	0.9301	0.971
Tucker-Lewis Index (TLI)	0.903	0.9061	0.888	0.8921	0.891	0.8951	0.907	0.9091	0.986

¹Denotes robust statistic for QML with Satorra-Bentler correction as produced by the Lavaan package in R. MI, multiple imputation; ML, maximum likelihood; QML, quasimaximum likelihood.

Comparisons of model fit indices between the ML and QML with Satorra-Bentler correction showed similar differences among each iteration. The chi-square test was significant across all iterations, regardless of estimator used. Because the chi-square test is sensitive to large sample sizes, other indices of fit were used to examine model fit (Table 5). The RMSEA was 0.01–0.02 points lower with the QML estimate than in the ML models, indicating a better absolute model fit for the QML. The 90% CI was wider for the QML estimate, although the increase in spread was to the lower end compared with their ML counterpart. Additionally, the SRMR was lower, whereas the CFI and TLI were higher in the QML compared with ML estimation, all indicating better model fit for QML.

Respecification of model

Evaluation of the Lagrange multiplier values suggested that the model fit could be improved by allowing depression items that comprise the PHQ to covary. All relations in this respecified model (iteration 5) remained significant (Figure 2). Iteration 5 indicates that the total effect of a 1-y increase in age will result in a decrease of serum cotinine of 0.644 ng/mL of blood, which includes the direct path between age and cotinine and indirect paths through food security and depression (Table 6). For each 1-point reduction in food insecurity score, serum cotinine decreases an average of 9.171 ng/mL, whereas for each 1-point reduction in depression, serum cotinine decreases on average 11.818 ng/mL. The total effect of a 1-point decrease in food insecurity leads to a reduction of 11.968 ng/mL in serum cotinine, when including direct and indirect paths. These findings indicate positive independent relations for both food insecurity and depression as predictors of smoking.

TABLE 6.

Respecified SEM model with unstandardized coefficients and standard errors based on the use of QML with the Satorra-Bentler correction for the NHANES cycles 2005–2010 (n = 17,132, total sample = 214,755,655)¹

	Estimate	SE	z	P
Measurement model
Depression on
DPQ010	0.425	0.012	55.242	<0.001
DPQ020	0.483	0.012	49.53	<0.001
DPQ030	0.478	0.014	40.028	<0.001
DPQ040	0.546	0.012	48.576	<0.001
DPQ050	0.415	0.011	56.587	<0.001
DPQ060	0.396	0.011	54.356	<0.001
DPQ070	0.368	0.012	50.414	<0.001
DPQ080	0.238	0.011	34.862	<0.001
DPQ090	0.123	0.01	21.413	<0.001
Structural model
Food security on age	−0.005	0.001	−7.333	<0.001
Cotinine on age	−0.565	0.078	−7.232	<0.001
Cotinine on food security	9.171	1.464	7.049	<0.001
Depression on age	−0.002	0.000	−4.011	<0.001
Cotinine on depression	11.818	1.260	9.902	<0.001
Depression on food security	0.169	0.011	15.143	<0.001
Variances
DPQ010	0.234	0.009	25.420	<0.001
DPQ020	0.179	0.007	26.810	<0.001
DPQ030	0.590	0.016	37.445	<0.001
DPQ040	0.505	0.015	34.272	<0.001
DPQ050	0.348	0.011	31.230	<0.001
DPQ060	0.186	0.007	26.755	<0.001
DPQ070	0.230	0.008	27.312	<0.001
DPQ080	0.159	0.006	25.369	<0.001
DPQ090	0.059	0.005	12.948	<0.001
Food security	1.785	0.127	14.060	<0.001
Cotinine	16,680.716	739.710	22.550	<0.001

¹DPQ, NHANES depression screener questionnaire; QML, quasimaximum likelihood; SEM, structural equation modeling.

Discussion

This paper provides nutrition and other public health epidemiologists with an empirical example of how SEM can be used to explore complex relations between social, behavioral, and nutritional variables. We further provide evidence that support best practices when SEM is used with complex datasets that have missing data. The evidence supporting the use of survey weighting and MI procedures when conducting SEM in large survey data has been explored separately in previous literature; however, this paper provides evidence to support their use in conjunction with QML estimation. Our findings have important implications for the design and interpretation of future studies that aim to inform programmatic and policy decisions in the field of public health nutrition.

Although strongly encouraged by the CDC (6), many researchers conduct analyses without applying sample weightings, or may apply weights, but not address missing data. Although these decisions did not change the directionality of the relations between variables in the SEM iterations tested here, they did alter the path coefficients. Thus, these analytic decisions can have an impact on the final model iteration, which may have consequences on how health policy-makers and program-planners prioritize efforts to address food insecurity and depression as important contributors to smoking in the United States.

The different results of the model iterations tested here illustrate how missing data can still occur in well-designed studies, such as NHANES. In our dataset, nearly one-third of the data would be excluded due to ≥1 missing variable if a complete cases analysis approach was used. This missingness occurred mostly within the Hispanic participants, which may bias interpretations for this ethnic group, as well as for the general US population. Our results supported the approach of using MI to handle this missingness, which allowed all cases to be represented in the analysis in proximity to those shown in previous studies comparing QML and ML simulations based on the use of unweighted, complete case datasets (10, 22).

Finally, although the focus of this manuscript was the testing of various analytic approaches to identify best practices for SEM, the findings of our example model are worth noting. The causal pathways linking food insecurity and depression to smoking provide further support for the evidence for these variables as important psychosocial factors that may influence cigarette use and cessation. Health advocates working on tobacco cessation initiatives should explore collaboration opportunities with the food security and mental health sectors to develop integrative programs that address food access and depression as potential root causes of smoking. Such initiatives may help to improve nutritional, mental health, and smoking cessation disparities within vulnerable populations that may not respond to traditional tobacco cessation programs.

Limitations

The model tested in these analyses contained only continuous variables. Researchers who use SEM to explore other continuous variables, such as dietary intake of food groups or nutrients, and other laboratory values, such as glucose or cholesterol, could apply the best practices identified here. However, the model presented in this paper did not contain categoric variables, such as gender or genetic information, which can also be incorporated into SEM models. Therefore, best practices for conducting SEM using weighted data and MI with categoric variables still need to be confirmed. Additionally, the generalizability of any data is dependent upon sampling methods; therefore, bias in sampling frames may bias the sample, regardless of weighting.

Conclusions

The use of SEM, although still applied sparsely in nutritional epidemiology, has the potential to expand knowledge of complex relations among social and behavioral constructs and measured variables (4). Nutrition epidemiologists who wish to use SEM to explore such relations should apply sample weightings, use MI for handling missing data, and use QML with Satorra-Bentler correction. These steps may help to ensure a more accurate depiction of relations among the variables at a population level to more appropriately inform the translation of findings to nutrition-related policies and programs.

Notes

Research reported in this paper was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number P20GM109097. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Author disclosures: the authors declare no conflicts of interest.

Abbreviations used: CFI, comparative fit index; EM, expectation maximization algorithm; FIML, full information maximum likelihood; MAR, missing at random; MCAR, missing completely at random; MI, multiple imputation; ML, maximum likelihood; NMAR, not missing at random; PHQ, Patient Health Questionnaire (depression screener questionnaire; NHANES variable prefix: DPQ); PSU, primary sampling unit; QML, quasimaximum likelihood with Satorra-Bentler correction; RMSEA, root mean square error of approximation; SEM, structural equation modeling; SRMR, standardized root mean square residual; TLI, Tucker-Lewis Index.