Abstract
One of the key uses of causes is to explain why things happen. Explanations of specific events, like an individual’s heart attack on Monday afternoon or a particular car accident, help assign responsibility and inform our future decisions. Computational methods for causal inference make use of the vast amounts of data collected by individuals to better understand their behavior and improve their health. However, most methods for explanation of specific events have provided theoretical approaches with limited applicability. In contrast we make two main contributions: an algorithm for explanation that calculates the strength of token causes, and an evaluation based on simulated data that enables objective comparison against prior methods and ground truth. We show that the approach finds the correct relationships in classic test cases (causal chains, common cause, and backup causation) and in a realistic scenario (explaining hyperglycemic episodes in a simulation of type 1 diabetes).
Introduction
The past two decades have seen significant progress in computational discovery of causal relationships at the population level. Given a database of medical records, we can find causal relationships between variables like medications, lifestyle, and disease. Yet while causal inference can tell us what causes heart failure in general, it cannot tell us that a specific patient’s heart failure is caused by their thyroid disfunction rather than their uncontrolled diabetes — that is the role of causal explanation. One of the core approaches to explanation is based on counterfactuals, which capture that without the cause the effect would not have happened. However, this approach and other solutions have been primarily theoretical and since we only see what actually happened, it is difficult to determine what would have happened had things been different. Since the solutions to explanation have been mainly theoretical, computational methods for explanation have lagged behind those for inference.
The primary shortcoming of existing explanation methods is their handling of time. Methods either ignore event timing entirely (e.g. Bayesian networks) or add time ad-hoc (e.g. dynamic Bayesian networks) at the expense of computational complexity and large amounts of required input. However if we want to tell an individual why their blood sugar is low at 4 PM, we need to be able to automatically determine that it is due to the race they ran the day before plus their current insulin dosing. Runs from a week ago are not important here, but neither is a brief jog that morning.
To accurately and automatically explain events, we need to handle both continuous time and state (e.g. glucose level), and go beyond only looking at whether an event happens and instead identify causes that change when and how the event happens. Perhaps an individual had a genetic disposition toward lung cancer, but smoking led to diagnosis at a much earlier age than otherwise would have happened. It may be that two arsonists individually didn’t change whether a fire happened (since either would have brought it about), but they increased the intensity of the fire and prevented it from being extinguished.
In this work, we show how to compute answers to counterfactual queries in continuous-time systems using probability trajectories. We then show how to test whether one event changes the probability, time, or intensity of another event and compute quantitative strengths for these relationships. We first evaluate our method in a continuous-time simulation of billiard ball collisions, showing that it rejects spurious correlations when there is a common cause, finds hastening despite probability lowering in cases of backup causation, and identifies the most direct relationships in causal chains. Finally, we use it to explain a hypoglycemic episode in a simulation of Type 1 Diabetes, demonstrating the technique’s readiness for real-world use.
Related Work
Causal explanation has been studied in philosophy, computer science, and other fields including law (determining fault and culpability), medicine (diagnosing individuals to identify the cause of their symptoms), and software engineering (finding causes of program bugs). We focus on reviewing the work in the first two areas since they provide insight into what constitutes a causal explanation and how we can realistically find these.
Philosophy
We draw inspiration from two approaches to causal explanation, or token causality, that aim to evaluate or quantify how much of a difference a cause made to its effect.
The first approach, due to Eells (1991), looks at the probability of the effect over time (its probability trajectory) and examines how this changes after the cause happens up until the time of the effect. For example, if the probability of hypoglycemia is raised after a run, and remains high until hypoglycemia actually happens, then it is because of the run. The probability trajectory approach explicitly incorporates the timing of events, but it requires selecting so-called background contexts to hold fixed. This requires extensive background knowledge that we normally do not have, making it difficult to translate into a computable model.
Counterfactual methods, such as the concept of counterfactual dependence introduced by Lewis (1973), stipulate that a cause is something without whose presence the effect would not have occurred. An event B is said to be caused by A if both A and B occur in the actual world but B does not occur in the not-A world most similar to the actual world. Despite the intuitive appeal of this approach, it is not directly reducible to an algorithm because the similarity function is not specified by the theory. Furthermore, the main counterfactual methods cannot handle overdetermination (when multiple causes occur). If a person who smokes is exposed to asbestos, each factor individually may be enough to bring about lung cancer, leading to no counterfactual dependence. Yet it may be that exposure to both risk factors led to a more aggressive case of cancer or made it happen sooner than it otherwise would have (thus the cause changed the way in which cancer occurred). Paul (1998) and Lewis (2000) later extended the counterfactual theory to capture these types of changes, though without a way of quantifying the similarity between events, these approaches remained incomputable.
We take inspiration from both of these approaches, using change in probability to find relations such as because of and despite (making an event that actually occurs more or less likely, respectively), and changes in timing (hastening, delaying) and manner (intensifying, attenuating) to capture other types of difference-making. This lets us find that while an event may have been inevitable, and a cause made no change to whether it occurred, it can still change when and how it happens. For example, if we have a continuous variable that assesses severity of cancer, we can test how much this is changed by each exposure in the prior example. Similarly, a genetic predisposition may make cancer extremely likely, but an environmental exposure may bring it about much earlier. By looking at changes in probability, timing, and intensity, we can capture these differences.
Computer Science
Causal explanation has received significantly less attention than causal inference (finding causal relationships and structures from data), but a few key advances have been made. Halpern and Pearl (2005a; 2005b) introduced a method (henceforth “HP”) for explanation that links structural equation models (SEMs) and counterfactuals. This approach is designed for deterministic systems and does not explicitly model time. Furthermore, which token causes are found depends on which auxiliary variables are included in the model (Halpern 2014). These features of the approach mean that it can only be used to guide human evaluation, rather than to provide causal explanations automatically. Consider a model that shows that smoking causes lung cancer. A user must interpret what it means for smoking to be true for an individual and which instances are relevant. Some issues with the approach can be resolved by introducing variables to model time (cf. the revised rock throwing model of (Halpern 2014)), but this becomes more difficult in cases like finding why a person’s blood glucose is raised since people tend to give too much credence to recent events in causal explanation. As a result, the approach is susceptible to the same biases as human reasoning, and it has only been evaluated conceptually.
One of the few computational methods for explanation that has been implemented and evaluated on simulated data encodes the processes underlying relationships with logical formulas (Dash, Voortman, and De Jongh 2013), links these with a Bayesian network (BN), and then finds the most likely path through the structure to the effect. However, this approach does not explicitly model the timing of events and cannot handle cases where multiple causes are responsible for an effect. Rather the approach finds only the most likely causal sequence. Further, it does not distinguish between the significance of each component of the sequence. Another logic-based approach (Kleinberg 2012) can handle the case of multiple causes, but it aims to rank the significance of causes rather than test counterfactual queries. Methods for fault detection (Poole 1994; Lunze and Schiller 1999; Chao, Yang, and Liu 2001) aim to find why a system is behaving incorrectly, but are computationally complex and rely on an accurate mechanistic model. Finally, the causal impact method of Brodersen et al. (2015) computes the effect of an intervention (advertising campaign) on a continuous variable (market response), but requires a specified alternative to the intervention rather than supporting general counterfactual queries.
Motivating Example
As a running example, we discuss how to explain changes in blood glucose (BG) of a person with type 1 diabetes mellitus (T1DM). This is challenging, since many factors affect BG and can do so many hours after they occur. For example, moderate exercise can lead to heightened insulin sensitivity for up to 22 hours (Dalla Man, Breton, and Cobelli 2009). Being able to find this and tell an individual why they have low blood glucose (hypoglycemia) can help them prevent this in the future, such as by reducing their insulin doses after exercise or increasing carbohydrate intake.
For example, suppose that Frank is a runner who manages his T1DM using a continuous glucose monitor (CGM) and insulin pump. One day, Frank goes for a morning run, and later has lunch. To avoid a spike in BG from lunch, he gives himself a bolus of insulin. Later that afternoon, his CGM alerts him to warn that he has hypoglycemia. Frank already knows that exercise and insulin can each lead to hypoglycemia, but that does not tell him what caused this afternoon’s hypoglycemia – or how to prevent it the next time he goes for a run. A better personal health device would tell Frank not only what is happening (hypoglycemia) but also why it is happening. We will show how such a device could compute the impact of the morning run on the hypoglycemia as part of providing a better explanation.
Methods
We begin by formally defining stochastic models, events, and the causal explanation problem. We define three causal relations among particular events, relating to changes in probability, timing, and intensity, before introducing an algorithm for estimating the strength of these relationships.
Model Definition
In our running biological example, we can model the body’s state as a collection of continuous valued variables (such as glucose and insulin concentrations), which change continuously across time. We now define these models.
Definition 1.
The state ψ ∈ Ψ of a model is the collection of all variable values at a moment in time.
Definition 2.
A world w is a function which specifies the state of the model at each time point. We denote the set of all possible worlds as W.
Definition 3.
The actual world, denoted w0, is the time-series of states which actually occurred.
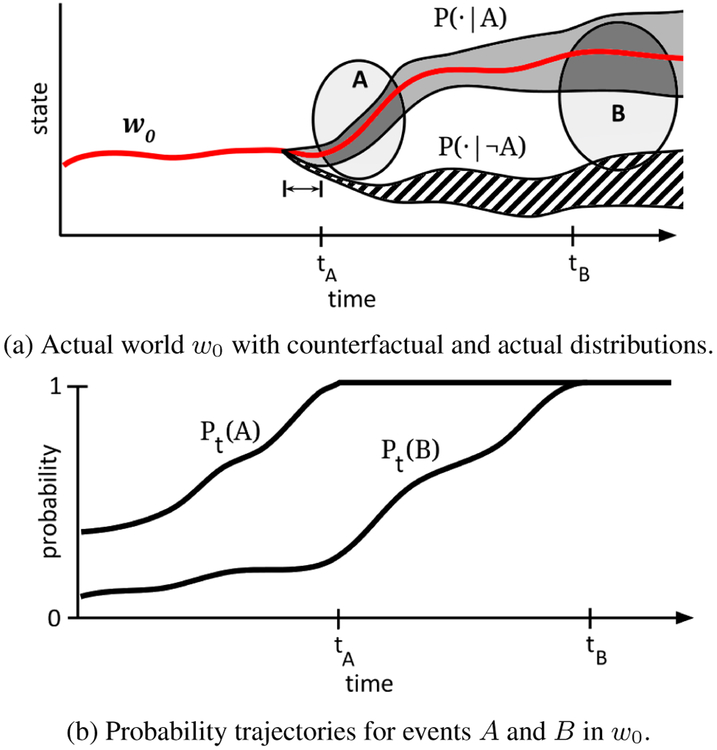
While the true state space may be multidimensional, we can visualize the actual world as a progression of states through time in one dimension as shown by the red line in Figure 1a. We represent an event as the set of worlds where the event occurs. If hypoglycemia, H, is defined as BG being below 70 mg/dL, then then H is the set of all worlds for which BG ever drops below that threshold. The set representation is appropriate because we explain specific instances (tokens) of events rather than event types.
Figure 1:
Schematic depiction of the formalism.
Definition 4.
An event A ⊆ W is a set of worlds. The event A occurs in world w if w ∈ A. We write ¬A to mean the event that A does not occur, which in set notation is A’s complement in W.
Definition 5.
An event A is actual if w0 ∈ A, i.e. if it occurs in the actual world.
In the case of Frank, the actual world w0 contains his specific history of blood sugar levels, heart rate, glucose ingestion, insulin administration, and blood sugar levels.
Figure 1b shows how the probabilities of the two actual events A and B in Figure 1a changed as a function of time. In this figure an event occurs if a world passes through the corresponding ellipse in state-time space. Initially the probabilities were low as w0 could have taken many possible paths. As time progressed, the probability of the world passing through event A become higher, ultimately reaching probability 1 when w0 entered the ellipse labeled A.
Definition 6.
The probability trajectory1 Pw,t(A) gives the probability of the event A eventually occurring in world w given the state of w up to time t.
To simplify notation, we will write Pt(A) for Pw0,t(A), i.e. the reference to the actual world will be understood.
While representing events as sets of worlds is sufficient for a probability-raising theory, we must introduce two additional notions to handle hastening and intensifying effects.
Definition 7.
The timing of an event A in world w, written tA(w), gives the time that the event A occurred in w if w ∈ A, and is undefined otherwise. We will write tA for tA(w0).
Definition 8.
The intensity of an event A in world w, written mA(w), is a real number representing the magnitude of the event A if w ∈ A, and is undefined otherwise.
Explaining Probability-Raising
Imagine three billiard balls on a table, labeled 6, 7, and 8. Initially the ball labeled 6 is rolling towards 7, while 7 and 8 are initially at rest. Then 6 strikes 7, 7 rolls towards and strikes 8, and finally 8 rolls into a corner pocket. The actual world is the time series of positions and velocities for each ball. Now, what would have happened had 7 not struck 8? This is a counterfactual query, in which the event that 7 does not strike 8 is known as the antecedent. In the absence of any other forces, 8 would have stayed at rest and not entered the pocket. But what would have happened to 7? We propose to answer this question not with a single world w in which 7 does not strike 8, but rather with a distribution that assigns a probability to sets of outcomes where 7 does not strike 8.
We generate this distribution by simulating alternative possible worlds which were identical to w0 until some short time τ > 0 prior to the antecedent event, and keeping only those simulated worlds where the antecedent occurs. This is analogous to the do-calculus approach (Pearl 2000) of cutting incoming causal arrows to a variable and fixing the variable’s value. Our method differs in that we use the stochasticity present in the system model to generate ways in which the antecedent could have come about, rather than prescribing the values of particular variables. The result is that counterfactual worlds are just as plausible as the actual world because they are generated by the same stochastic process.
Definition 9.
The counterfactual distribution for actual event A with respect to the actual world gives the probability of an event B if A had not occurred and is given by
where τ is the time horizon constant.
To appreciate the role of the time horizon τ, consider the billiards example above. If C78 is the event that 7 strikes 8, and C8P is the event that 8 enters the pocket, then P(C8P∣¬C78) is the probability that 8 still enters the pocket had 7 not struck 8. If τ is very small, say 1 millisecond, then the denominator PtC78–τ (¬C78) is also small, as there was a very small chance of 7 not striking 8 just 1 millisecond prior to the collision. The result is that only extremely improbable alternatives to actuality are considered in evaluating the counterfactual such as 7 abruptly coming to a halt or 8 spontaneously flying out of the way. If τ is large, say 1 minute, then the alternatives considered differ unduly from the actual world, and dependence of past events on future antecedents may be found, an undesirable feature called backtracking. In general, τ should be as small as possible to limit backtracking, but large enough to allow plausible alternatives to arise from stochasticity in the system.
Consider how to compute the probability of Frank’s afternoon hypoglycemic episode had he not run. If we let R represent those worlds in which Frank runs and H those worlds where he experiences hypoglycemia, then for an appropriately chosen time horizon (which can be arbitrarily small if the decision to run is spontaneous), the probability of hypoglycemia if he had not run is simply P(H∣¬R).
Now, to determine whether R had a probability raising effect on H, we cannot compare against just the actual world w0 because H has probability 1 there: it actually occurred. Instead we need to compare P(H∣¬R) to the probability of H in another distribution (which we term the actual distribution of R) where Frank does run, with the same time of divergence tR — τ.
Definition 10.
The actual distribution for actual event A with respect to the actual world gives the probability of an event B given that A occurs and is given by
Finally we can compute the probability change for the consequent event due to the antecedent event.
Definition 11.
The probability change of B due to A is
When the probability change is positive we say B occurred because of A, and if it is negative B occurred despite A.
Explaining Timing and Intensity Changes
Not all causes raise the probability of their effects. When explaining an event B, we should look not only for events A that raised the probability of B, but also for events that caused B to occur sooner or increased its expected intensity.
To assess whether A hastened the occurrence of B, we use the counterfactual and actual distributions to evaluate the expected difference in the timing of B due to A.
Definition 12.
The timing change of B due to A is
where the expectations may be written as Lebesgue integrals
When the timing change is negative we say that B was hastened by A, and when the change is positive that B was delayed by A.
The definition for intensity change is parallel:
Definition 13.
The intensity change of B due to A is
When the intensity change is positive we say that B was intensified by A, and when the change is negative that B was attenuated by A.
Computing Explanations
We present Algorithm 1 for computing an explanation for event B in terms of event A given the actual world w0 and a subroutine for sampling worlds from the probability trajectory Pt. To approximate probabilities of the form Pt(A), we repeatedly sample worlds w from the distribution Pt(⋅), counting the number of w which fall in A.
In the glucose-insulin example, the actual world w0 is represented as a list of vectors, each containing the concentrations of glucose, insulin, and other state variables at a point in time. To evaluate a single point along the probability trajectory for hypoglycemia Pt(H), we feed the state w0(t) into a model of the glucose-insulin system — which is just a set of stochastic differential equations — and generate n solutions (i.e. other possible worlds). Our estimate for Pt(H) is just the proportion of those solutions in which hypoglycemia occurs, i.e. where blood sugar ever drops below 70 mg/dL. The strength of probability raising, hastening, and intensifying can be computed in this way, with sampling replaced by simulation and the integrals for expectation replaced with sums.
While the algorithm converges to the probabilistic formulation in the large sample limit, in practice we have only a finite number of samples and so statistical tests are required. The significance of a probability change is assessed by the log-likelihood ratio test, chosen because whether an event occurs is categorical, while Welch’s t-test is used to assess significance of timing and intensity change, chosen because the variances of timing and intensity may vary between the actual and counterfactual distributions.
| Algorithm 1 Causal Explanation in Stochastic Processes | |
|---|---|
|
|
All simulations in the paper took < 60sec on a workstation using a python implementation2 of the algorithm. The algorithm’s time complexity is
linear in the user-specified number of samples n and inversely related to the probability of A τ seconds before it actually occurred. The latter term is not a limiting factor in practice, as we are concerned with causes that can be intervened upon, rather than inevitable events.
Experiments
We now demonstrate explanation of events in a simulated physical system implementing difficult cases from the philosophy literature and then show how the process can be applied to explanation of a hypoglycemic episode. As existing methods are not applicable to these data, we provide conceptual rather than quantitative comparisons.
Difficult Cases
We use an idealized model of billiards as a setting for testing difficult cases. Circular balls numbered with single digits which move around a table, interacting via totally elastic collisions, with a single pocket into which balls may fall. The variables are continuous and include ball positions, velocities, and time. Stochasticity is introduced as small perturbations to balls’ direction of motion, and a frictional term gradually slows the balls until they come to rest. We write Cij for the event that the ith ball collides with the jth ball, and CiP for the event that the ith ball enters the pocket.
We apply Algorithm 1 to three test cases using 1000 samples and a time horizon of 20 time steps. The results are summarized in Table 1. Values indicate probability and timing change with asterisks denoting changes significant at the p < 0.05 level.
Table 1:
Explanation results in billiard ball examples.
| Scenario | Relationship | Probability | Timing |
|---|---|---|---|
| common cause | true | +0.334* | - |
| spurious | −0.011 | −0.08 | |
| causal chain | direct | +0.527* | −8.91* |
| indirect | +0.262* | −7.56* | |
| backup cause | true | −0.147* | −5.50* |
Common Cause:
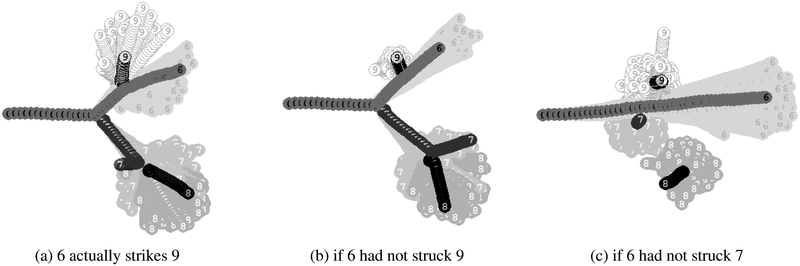
A first test case is a single cause having multiple effects. The actual world, shown in Figure 3a, has four balls labeled 6, 7, 8, and 9. The event C67 causes both C69 (which occurs first) and C78 (which occurs later), while C69 and C78 do not cause one another. The event to be explained is C78.
Figure 3:
Visualization of actual and counterfactual distributions for common cause example.
Results:
Only the true cause C67 is found and the spurious explanation C69 is correctly rejected as insignificant. Figure 3b shows the evaluation of P(C78∣¬C69): no significant change is observed in C78. Then figure 3c shows how if the 6 ball fails to hit the 7, only then is there a significant change in whether 7 hits 8. While HP cannot be applied directly to the billiards model (as it does not handle continuous time and states), after reducing the continuous model to an SEM with similar structure (C69 ← C67 → X → C78), HP also finds the correct result. Regularity-based methods are likely to erroneously detect the spurious relationship however, due to the strong correlation and precedence of the events.
Causal Chain:
Next we test two consecutive relationships forming a causal chain. There are three balls: 6, 7, and 8, with 6 initially moving while 7 and 8 are initially at rest. The actual events are C67, C78, and C8P, and the event to be explained is C8P.
Results:
In the causal chain case, we find both the direct (C78 → C8P) and indirect (C67 → C8P) relationships. The indirect relationship is found to be weaker than the direct one in terms of both probability raising and hastening. In the similar SEM chain C67 → C78 → C8P, HP also finds the direct and indirect relationships, however it cannot differentiate by strength.
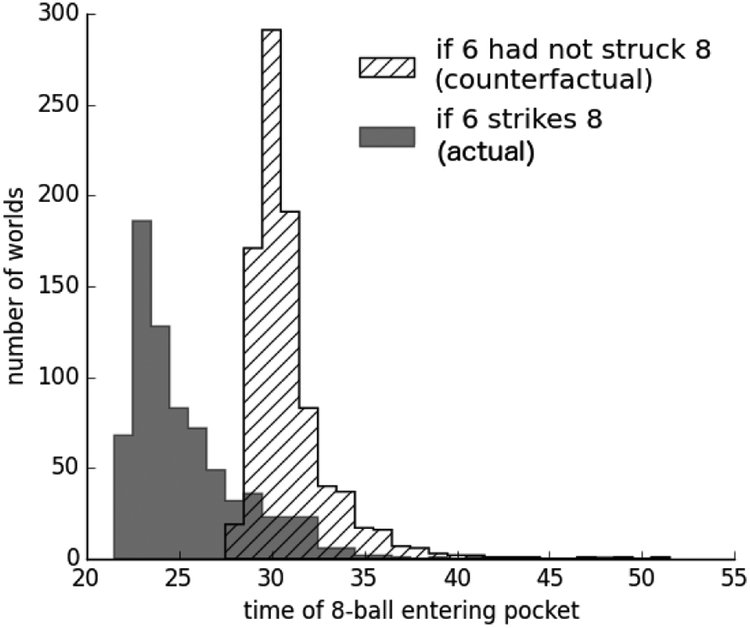
Backup Causation:
Lastly we test an unreliable cause that preempts a reliable backup. There are again three balls: 6, 7, and 8. This time both 6 and 7 are initially moving towards 8, but with 7 ahead of 6 and slightly off-course. The actual events are C78 and C8P, and if 7 had not struck 8, then 6 almost certainly would have.
Results:
In the backup cause case we find a nuanced result. The event C8P occurred despite C78 and was also hastened by C78. In Figure 2 we see how the probability and timing of C8P compare between the counterfactual distribution (where 7 does not strike 8) and the actual distribution (where 7 does strike 8). Both a probability lowering and hastening effect are observed.
Figure 2:
Distribution of timing of 8-ball entering pocket in backup causation example.
This backup example is related to a case of royal poisoning (Hitchcock 2010)3. A first assassin puts a weak poison (30% effective) in the king’s wine and the king actually dies, but if the first assassin had not poisoned the drink, a second assassin would have added a stronger poison (70% effective). Our algorithm finds that death is despite the weak poison. Intuitively, if the first assassin wanted the king to survive, he chose the correct action (preventing the stronger poison from being used). We aim to inform decision making so this interpretation helps devise better strategies for bringing about outcomes. This is in contrast to HP which conditions on the contingency that the second assassin does not act and would find the weak poison causing the king’s death.
Medicine Example
Using a simulation of the human glucose-insulin system (Dalla Man, Rizza, and Cobelli 2007; Dalla Man et al. 2007; Dalla Man, Breton, and Cobelli 2009), we explain a hypoglycemic episode H in terms of lunch L and a run R earlier the same day. We use the cited simulation with the introduction of stochasticity using small Brownian noise applied to slowly equilibrating glucose concentration. This stochasticity models our uncertainty in model accuracy and leads to more natural results.
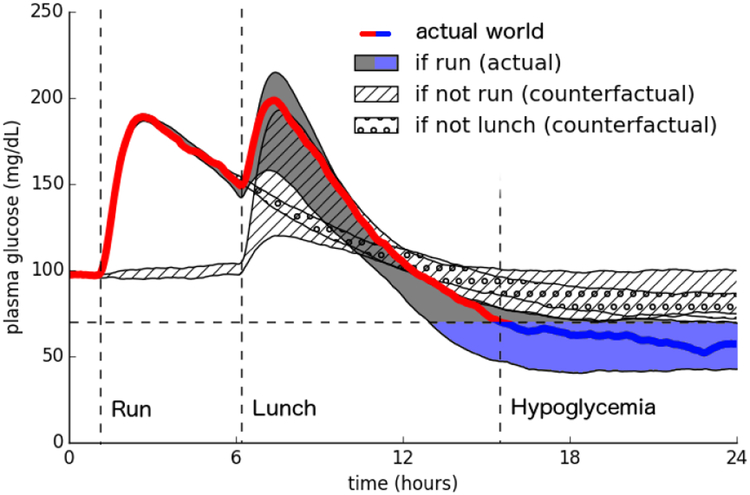
We simulate a 60 kg patient with T1DM wearing an insulin pump delivering a basal insulin infusion of 3.5 pmol/kg/min. The patient goes for a run R at 7 AM whereby heart rate is increased from 60 bpm to 90 bpm for 30 minutes and a snack containing 27.5 g of glucose is consumed to offset the glucose consumed by the exercise. Without any further action, glucose levels would have remained normal. However, the individual later has lunch L at 12 PM containing 50 g of glucose preceded by an insulin bolus of 750 pmol/kg, computed based on the size of the lunch without taking the run into account. After lunch, hypoglycemia H occurs with glucose falling below 70 mg/dL at 9:31 PM and reaching a minimum of 51.4 mg/dL. The glucose over time is shown as the bold trace in Figure 4. We model the decisions to run and have lunch as spontaneous events with probabilities 50% and 80% respectively.
Figure 4:
Comparison of actual and counterfactual traces of blood glucose.
We apply Algorithm 1 to explain H in terms of R and L, using 1000 samples and a time horizon of 15 minutes. The counterfactual and actual distributions for R and the counterfactual distribution for L are plotted in Figure 4 with the shaded regions indicating ±σ error bars. The resulting strengths of causal relationships of R and L on H are given in Table 2. We find that both the run and lunch had strong probability raising, hastening, and intensifying effects on the hypoglycemia. It is unsurprising that L caused H, because it is the insulin in the lunch-time bolus which drives the mechanism for glucose lowering. What is significant however, is that we are able to compute the strength of causal effects of the earlier event R on H, finding that the run did indeed play an important role in causing the hypoglycemic episode, raising the likelihood of glucose under 70 mg/dL by 64.2%.
Table 2:
Results for medical example.
| Relationship | Probability | Timing | Intensity |
|---|---|---|---|
| R → H | +0.642* | −3.14h* | +27.5 mg/dL* |
| L → H | +0.721* | −10.3h* | +28.0 mg/dL* |
Conclusion
Explanations are needed to assign blame, learn from our actions, and make better future decisions. Yet while many fields such as computer science, epidemiology, and political science regularly use methods for causal inference to learn how systems work, explanation has remained in the domain of theory. One of the primary impediments to this is the difficulty of formalizing methods for explanation, and capturing the nuanced ways we explain events. We developed a method for evaluating counterfactual queries that 1) makes this process computable and 2) finds causes for changes in the probability, timing, and intensity of events. Through evaluation on simulated data, we show that this approach can handle difficult cases for other methods and can explain changes in blood glucose in a realistic simulation of T1DM. While our method requires a model and cannot yet handle deterministic systems, it provides a tangible step towards automated explanation without human input.
Acknowledgments
This work was supported in part by NSF Award #1347119 (methods), and by the NLM of the NIH under Award Number R01LM011826 (data simulation).
Footnotes
This term is due to (Eells 1991).
See also the equivalent and less violent “two vandals” example of (Schaffer 2003).
References
- Brodersen KH; Gallusser F; Koehler J; Remy N; and Scott SL 2015. Inferring Causal Impact Using Bayesian Structural Time-Series Models. Annals of Applied Statistics 9:247–274. [Google Scholar]
- Chao CS; Yang DL; and Liu AC 2001. An Automated Fault Diagnosis System Using Hierarchical Reasoning and Alarm Correlation. Journal of Network and Systems Management 9(2):183–202. [Google Scholar]
- Dalla Man C; Raimondo DM; Rizza RA; and Cobelli C 2007. GIM, Simulation Software of Meal Glucose-Insulin Model. Journal of Diabetes Science and Technology 1(3):323–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalla Man C; Breton MD; and Cobelli C 2009. Physical Activity into the Meal Glucose-Insulin Model of Type 1 Diabetes: In Silico Studies. Journal of Diabetes Science and Technology 3(1):56–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalla Man C; Rizza R; and Cobelli C 2007. Meal Simulation Model of the Glucose-Insulin System. IEEE Transactions on Biomedical Engineering 54(10):1740–1749. [DOI] [PubMed] [Google Scholar]
- Dash D; Voortman M; and De Jongh M 2013. Sequences of Mechanisms for Causal Reasoning in Artificial Intelligence. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (AAAI; 2013). [Google Scholar]
- Eells E 1991. Probabilistic Causality. Cambridge University Press. [Google Scholar]
- Halpern JY, and Pearl J 2005a. Causes and Explanations: A Structural-Model Approach. Part I: Causes. British Journalfor the Philosophy of Science 56(4):843–887. [Google Scholar]
- Halpern JY, and Pearl J 2005b. Causes and Explanations: A Structural-Model Approach. Part II: Explanations. British Journal for the Philosophy of Science 56(4):889–911. [Google Scholar]
- Halpern JY 2014. Appropriate Causal Models and Stability of Causation. In Principles of Knowledge Representation and Reasoning: Proceedings of the Fourteenth International Conference, (KR; 2014). [Google Scholar]
- Hitchcock C 2010. Probabilistic Causation. Stanford Encyclopedia of Philosophy. [Google Scholar]
- Kleinberg S 2012. Causality, Probability, and Time. Cambridge University Press. [Google Scholar]
- Lewis D 1973. Causation. The Journal of Philosophy 70(17):556–567. [Google Scholar]
- Lewis D 2000. Causation as Influence. Journal of Philosophy 97:182–97. [Google Scholar]
- Lunze J, and Schiller F 1999. An Example of Fault Diagnosis by Means of Probabilistic Logic Reasoning. Control Engineering Practice 7(2):271–278. [Google Scholar]
- Paul LA 1998. Keeping Track of the Time: Emending the Counterfactual Analysis of Causation. Analysis 191–198. [Google Scholar]
- Pearl J 2000. Causality: Models, Reasoning and Inference. Cambridge University Press. [Google Scholar]
- Poole D 1994. Representing Diagnosis Knowledge. Annals of Mathematics and Artificial Intelligence 11(1-4):33–50. [Google Scholar]
- Schaffer J 2003. Overdetermining Causes. Philosophical Studies 114(1):23–45. [Google Scholar]