On the nature and use of models in network neuroscience

Abstract

Network theory provides an intuitively appealing framework for studying relationships among interconnected brain mechanisms and their relevance to behavior. As the space of its applications grows, so does the diversity of meanings of the term “network model.” This diversity can cause confusion, complicate efforts to assess model validity and efficacy, and hamper interdisciplinary collaboration. Here we review the field of network neuroscience, focusing on organizing principles that can help overcome these challenges. First, we describe the fundamental goals in constructing network models. Second, we review the most common forms of network models, which can be described parsimoniously along three primary dimensions: from data representations to first-principles theory, from biophysical realism to functional phenomenology, and from elementary descriptions to coarse-grained approximations. We identify areas of focus and neglect in this space. Third, we draw on biology, philosophy, and other disciplines to establish validation principles for these models. We close with a discussion of opportunities to bridge model types and point to exciting frontiers for future pursuits.

WHAT IS A NETWORK MODEL?

Over a century ago, Camillo Golgi used blocks of brain tissue soaked in a silver-nitrate solution to provide among the earliest and most detailed views of the intricate morphology of nerve cells. Santiago Ramon y Cajal then combined this technique with light microscopy and an artist’s eye to draw stunning pictures that helped to establish that these nerve cells do not constitute a single reticulum. Instead, they are individual, anatomically defined units with complex interconnections. This idea, known as the Neuron Doctrine, soon came to encompass not just the structure but also the function of the nervous system and provides the foundation for modern neuroscience [1].

It is upon this foundation that modern network neuroscience thrives. This field uses tools developed in physics and other disciplines but has a natural relationship to the study of the brain. As in the Neuron Doctrine, network neuroscience seeks to understand systems defined by individual, functional units, often called nodes, and their relations, interactions, or connections, often referred to as edges. Together, the units and interactions, as well as any associated dynamics, form a network model that can be used to describe, explain, or predict the behavior of the real, physical network that it represents (Fig. 1). Many network models draw direct associations between these conceptual quantities and groups of anatomically defined, interconnected neurons in real brains [2–7]. These network models can then be analyzed using a host of quantitative techniques. For example, pairwise interactions can be described using an N × N adjacency matrix, where N is the number of nodes in the network, and each ij^th element of the adjacency matrix gives the connection strength between node i and node j [8]. The architecture of the adjacency matrix can then be characterized using a set of mathematical approaches known collectively as graph theory, which was not developed explicitly to understand the brain but has a natural synergy with network neuroscience [9]. Many other approaches, including generalizations of graphs known as hypergraphs (an edge can link any number of vertices) and simplicial complexes (higher-order interaction terms become fundamental units) along with non-graph-based techniques, likewise can be used to analyze networks of neurons that constitute biological nervous systems [10–12].

FIG. 1. Schematic of network models used in neuroscience.

(Left) The simplest and most commonly used network model for neural systems is one that represents the pattern of connections (edges) between neural units (nodes). More sophisticated network models can be constructed by adding edge weights and node values, or explicit functional forms for their dynamics. Multilayer networks can be used to represent interconnected sets of networks, and dynamic networks can be used to understand the reconfiguration of network systems over time. (Right) Common measures of interest include: degree, which is the number of edges emanating from a node; clustering, which is related to the prevalence of triangles; cavities, which describe the absence of edges; hubness, which is related to a node’s influence; paths, which determine the potential for information transmission; communities, or local groups of densely interconnected nodes; shortcuts, which are one possible marker of global efficiency of information transmission; and core-periphery structure, which facilitates local integration of information gathered from or sent to more sparsely connected areas.

These approaches can be applied to other network models of the brain, as well, not just those made up of interconnected neurons in vivo. For example, network models can be constructed across spatial scales that encompass pieces of chromatin, neuroprogenitor or neuronal cell cultures, cerebral organoids, cortical slices, and small volumes of human or non-human tissue [13–19]. Nodes can be chosen to reflect anatomical or functional units such as cell bodies at the microscale, cy-toarchitectonically or functionally distinct volumes at the macroscale, or more arbitary delineations like voxels [20–30]. Edges can be chosen to reflect anatomical connections based on identified synapses, white matter tracts, structural covariance, physical proximity, or functional relations such as statistical similarities in activity time series [31–36].

Even more sophisticated network models can be constructed to include heterogeneous and dynamic elements. For example, multilayer and multiplex network models can be constructed using multiple types of nodes and edges, such as those obtained from distinct neuroimaging modalities [37–39]. Annotated networks can be used to assign properties to nodes, such as cerebral glucose metabolism estimates from fluorodeoxyglucose (FDG)-positron emission tomography (PET), blood- oxygen-level dependent (BOLD) contrast imaging, mag- netoencephalographic (MEG) or electroencephalographic (EEG) power, gray matter volume or cortical thickness, cytoarchitectonic properties, measurements of oxidative metabolism, or estimates of coding capability, and to understand their relationships to nodal properties and internodal connectivity [40, 41]. Temporal dynamics can be applied to both nodes and edges, enabling studies of networks as reconfigurable dynamical systems that evolve over time [42–46].

Once constructed, these network models can be used to obtain deeper insights into how patterns of relationships between units support emergent function and behavior. For example, clustered connections can be used to identify locally efficient subgraphs or larger scale modules that can subserve specialized functions [47]. The conspicuous absence of connections can indicate holes or cavities in the architecture that could be conducive to information segregation [48, 49]. Topological shortcuts may support unusually long-distance interactions and generally efficient large-scale information transmission [50, 51]. At a more local level, nodes in a network that are more connected than the average are called hubs, which can be either localized or connected globally with one another to form a rich-club or network core [52, 53]. Important questions then follow regarding how the specific pattern of edges between nodes supports or hinders critical neu-rophysiological processes related to synchrony, communication, coding, and information transmission [54–57].

However, despite these clear benefits of using the evergrowing suite of network-based approaches to better understand the brain, the rapid growth of this field also brings major challenges. The sheer number of different kinds of network models used continues to grow, and their relationship to the kinds of relatively simple networks of interconnected neurons seen under Cajal’s microscope becomes increasingly distant. Consequently, different investigators use the term “network model” with different sets of assumptions about what the term means, which systems are most amenable to these kinds of analyses, and what sorts of conclusions can be drawn from the results (Box 1). These different assumptions can hamper communication, collaboration, and discovery. We therefore aim here to synthesize a set of organizing principles that govern how to define, validate, and interpret the different kinds of models encompassed by modern network neuroscience.

BOX 1: MODEL THEORY - A PHILOSOPHICAL PERSPECTIVE.

Recent model theory aims both to distinguish unique types of models from one another and to identify structural elements of models that are generalizable across scientific subfields. A model is a functional representation of a feature of the world. That is, it depicts what something is in terms of some of its measurable aspects to yield insights into how it works. There are at least four basic sorts of models [202, 203]. Some models are scalar, illuminating a feature by reducing or expanding it. Some are idealized, creating simplified, abstract representations. Other models are analogical, generating comparative structures at either the material or formal level. And still others are phenomenological, depicting merely observable elements. Insofar as all models are representations, they face the difficult task of defining the relation they have to the feature they model. What makes them heuristic devices? How is their accuracy or truth determined? Are functional models less true, given their distance from material substructures? Or are physical models less accurate, given their inability to account for higher level system dynamics?

All models represent reality in some sense and fail to represent reality in another sense. They are, therefore, akin to literary fiction. Models mobilize a creative approximation of some world-feature for an identifiable end. As such, they are perhaps best interpreted as imaginative objects and evaluated pragmatically. Theorizing models as fictions involves reframing them as imagined entities that aid in the narrativizing of a physical system [204–208]. As with any fiction, the community or discipline in question provides the principles that define how the model is generated and used. The model thus explores possible interpretations that are of value and interest to the community that uses it to gain insights that will move the field forward [209, 210]. Moreover, insofar as different models represent different features of a system, they may be used conjunctively to construct complementary narrative schemas. Whether taken together or separately, models clarify the anatomy and the architecture of a thing, precisely through the exercise and further provocation of scientific imagination.

WHAT KINDS OF MODELS ARE USED IN NETWORK NEUROSCIENCE?

We begin by reviewing efforts to understand mechanisms of brain structure, function, development, and evolution in network neuroscience. We organize these efforts in terms of three key dimensions of model types that define the state-of-the-art in the field (Fig. 2). The first dimension is a continuum that extends from data representation to pure (or “first-principles”) theory. The second dimension is a continuum that extends from biophysical realism to phenomenological estimates of functional capacity (“functional phenomenology”). The third dimension is a continuum that extends from elementary descriptions to coarse-grained approximations. For each dimension, we discuss the rationale for its construction, several common forms, and major contributions. We then use this classification scheme to provide a vision for how future work might bridge network model types and provide integrative explanations for the diverse parts, processes, and principles of neural systems.

FIG. 2. Three dimensions of network model types.

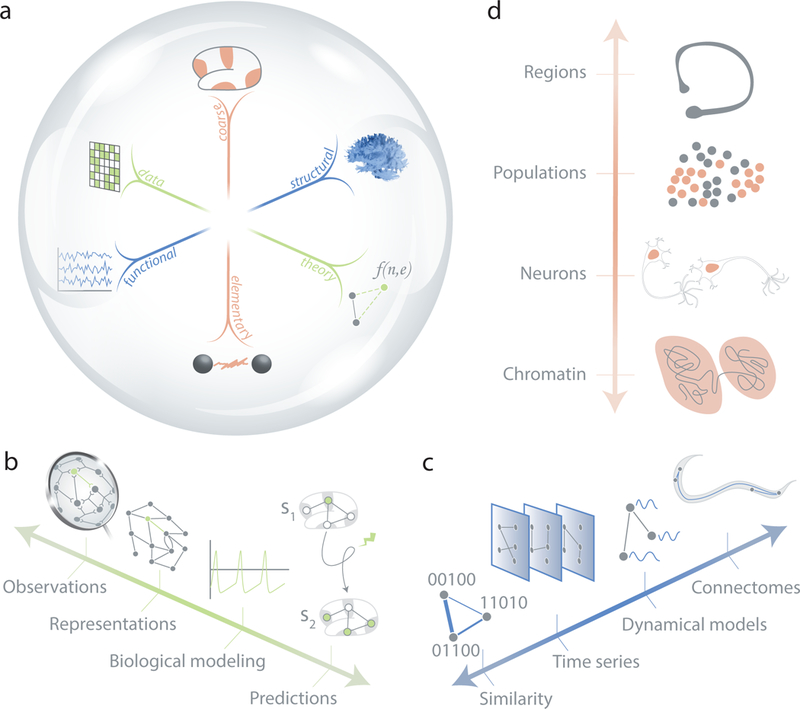
(a) We posit that efforts to understand mechanisms of brain structure, function, development, and evolution in network neuroscience can be organized along three key dimensions of model types. (b) The first dimension extends from data representation to first-principles theory. (c) The second dimension extends from biophysical realism to functional phenomenology. (d) The third dimension extends from elementary descriptions to coarse-grained approximations.

From data representation to first-principles theory

Perhaps the first and most fundamental question that one can ask about a network model is whether it is a simple representation of data or a theory of how the system behind the data might work [58]. A straightforward way to operationalize the difference between these types is that a pure data representation cannot make a prediction about how the system came to be or what the system will become, whereas a first-principles theory explicitly sets out to do so. Mathematically, a data representation can be stored as a simple, temporal, multilayer, or annotated graph. In contrast, a theory-based model must combine a graph with a difference or differential equation specifying dynamics, evolution, or function of the nodes, edges, or both. This distinction is important because data-driven network models may have more biological realism but are less amenable to claims regarding mechanism or dynamics than theory-based models.

Data-based network models were first built using the detailed descriptions of brain structure by Cajal and his successors. For example, a synthesis of extensive prior work in the macaque suggested that the pattern of 305 structural connections among 32 visual and visual-association areas is consistent with a distributed hierarchy of information processing [59]. Complementary work in the mammalian cortex, especially the cat, distinguished between central and peripheral brain areas, in concert with their role in sensory processing [60–62]. As tools from the mathematical study of graphs became more commonly used to formalize the study of connectivity patterns in neural systems, efforts expanded across species from C. elegans to human, from macroscopic to microscopic scales, and from structural to functional data [16, 63–70]. These data-based network models were initially simple graphs that lacked any formal specification of dynamics. Later work extended these efforts to include other sorts of temporal, multilayer, multiplex, and annotated graphs. These models continue to provide new insights into how structural and functional connectivity are conserved and varies across species, depend on the spatial scale of measurement, and relate to cognition and disease [43, 71–77].

Theory-based models combine a network architecture with a model of dynamics that occurs at each node, at each edge, or across both nodes and edges. The most common forms of such models are those that define dynamics for each node. At the microscale, relevant dynamics include Hodgkin-Huxley, Izhikevich, and Rulkov map neuronal dynamics [78–81]. For neuronal ensembles, phenomenological models span FitzHugh-Nagumo, Hindmarsh-Rose, and Kuramoto oscillators [82–84]. For larger volumes of tissue, neural mass models have been used, for example in combination with coupling patterns derived from white-matter tractography to provide insights into neural underpinnings of synchronization, plasticity, and neurological disease [46, 85–89]. Another type of theory-driven model predicts how exogenous input to a neural system impacts its dynamics in a network- dependent manner, a form of network control [90–92]. Less common, but potentially useful, theory-based models define edge dynamics, for example as generative network models [93]. These models could be profitably extended by recently developed dynamic extensions of the classic random graph, including the configuration model, the stochastic block model, and the block-point process model [94, 95].

Network models at the two extremes of this dimension have both advantages and disadvantages. Data representations have the benefit of tracking closely with experimental findings but cannot alone be used to make formal, model-based predictions about a neural system’s growth, evolution, or dynamics. In contrast, theory-based models are explicitly built to make such predictions but typically must abstract away many neurophysiological and neuroanatomical details to ensure that the mathematics is manageable and the results are interpretable [96]. Intermediate models along this dimension try to combine the advantage of the extremes, often by defining theories whose parameters or functions are specified by data. For example, an intermediate model could specify first-principles dynamics on units that are linked by data-based estimates of large-scale patterns of connectivity. In general, models distributed along this dimension are synergistic, because data representations inform theories, and theories produce predictions that can be tested in new data representations [97].

From biophysical realism to functional phenomenology

A second dimension that is useful for differentiating network models spans structural to functional realism. Network models on the extreme end of structural, biophysical realism include physically true elements, such as neurons, represented as nodes; physically true axonal projection patterns, represented as edges; and, should dynamics be included, biophysically accurate descriptions of, for example, developmental, regenerative, or experience-dependent changes in neuronal morphology and projections [98]. In contrast, network models on the extreme end of functional phenomenology include nodes and edges that do not necessarily have exact physical counterparts, such as noise correlations in cellular neuroscience or functional connectivity in human neuroimaging, and, if dynamics are included, laws of network evolution that capture an observed phenomenon in a more abstract or conceptual sense. In the context of network neuroscience, this distinction is important because it often determines whether a particular model can be used to infer the functional capacities of realistic, physical structures or the structural demands of certain functions.

Perhaps the quintessential biophysical network model of a neural system is the C. elegans structural con-nectome, a data representation in which nodes represent neurons and edges represent chemical or electrical synapses [2, 33, 99]. Such models have recently been extended to first-principles theories of network control using a simplified noise-free, linear, discrete time, timeinvariant model of dynamics [92, 100–102]. At larger spatial scales, the structural connectomes of the mouse, macaque, and human brain are also biophysical network models providing a data representation of the white matter tracts (edges) linking volumes of tissue (nodes) [3, 64, 70]. Network models with biophysically realistic components can also be constructed according to theoretical principles. For example, simple theories of network control have been studied using network models composed of biophysically realistic white-matter tracts [103]. Likewise, complex theories of long-distance coordination have been studied using theory-driven oscillatory cortical-circuit models that use biophysically realistic components including synaptically couple excitatory and inhibitory neurons [45, 104]. Other efforts to include more biophysical realism in network models have focused on morphological diversity, arborization patterns, chemical gradients and physical barriers, cell-type specific connectivity rules, synaptic plasticity, and cytoarchitecture [5, 105–109].

Conversely, network models of functional phenomenology have edges that are defined by measures of functional connectivity or statistical similarities in node time series [36]. Functional edges have informational rather than physical meanings, including synchronization, phase locking, coherence, and correlation [110, 111]. Such edges also provide information about the properties of one time series that can be inferred or predicted from another [112]. Commonly, these kinds of functional edges are combined with nodes corresponding to exact physical volumes and locations to produce functional network models at the level of cells or large-scale brain regions [16, 67]. It is also possible to construct network models where the nodes are defined by non-physical rules. For example, at the cellular level, a node can be defined as an entity that produces a time series of spiking that is statistically different than other entities; e.g., by a principal components analysis [113]. At a larger scale, a node can be defined by the output of a sensor that is sensitive to brain activity from a distributed area with ill-defined physical boundaries because of artifacts of volume conduction through tissue and bone with complex morphologies, as in EEG, MEG, or electrocor- ticography (ECoG) [18, 114–116]. There also exist network models of functional phenomenology that incorporate explicit formulations of dynamics, such as: (i) the packet-switching model of information transmission in the structural connectome, which draws inspiration from queuing theory applied to the Internet [117]; and (ii) the pairwise maximum-entropy model of collective behavior across neurons or large-scale brain areas, which draws inspiration from statistical mechanics [118–121]. Studies of this type are often more focused on understanding the brain as an information-processing system than on understanding its specific physical instantiation.

Network models at the extremes of this dimension have both advantages and disadvantages. Biophysically realistic models incorporate rich empirical observations regarding the physical nature of the brain. They are concrete but can be computationally expensive and are sometimes difficult to interpret because of a plethora of parameters needed to describe the network structure. In contrast, network models that emphasize functional phenomenology incorporate rich empirical observations regarding the informational nature of the brain but are less easily mapped onto brain structure. They are not concrete in the physical sense but can provide simplicity, interpretability, and formal links to non-physical theories such as information theory (Box 2). These fundamental differences are particularly important to keep in mind when network models at these two extremes have apparently similar properties. For example, in some imaging modalities edge strength as measured by structural connectivity is correlated with edge strength as measured by functional connectivity [121–124]. However, a structural connection inferred from a physical measurement should be interpreted differently than a functional connection inferred from statistical similarities in time-series data [120, 125–127]. Accordingly, it is often useful to generate intermediate models along this dimension that combine approaches from the extremes. For example, an intermediate model could estimate functional interactions between units that are linked by biophysical estimates of inter-neuronal (synaptic) connectivity.

BOX 2: FUNCTIONAL PHENOMENOLOGY AND INFORMATION THEORY.

Common network models of functional phenomenology are those whose edges are defined by measures of statistical similarity between the activity time series of node i and the activity time series of node j [36]. Across cellular and systems neuroscience, the use of a simple correlation as the measure of statistical similarity has proven useful in decoding uncertainty; probing the optimality of computations in the face of limited inputs; and predicting a subject’s identity, age, and response to interventions such as deep brain stimulation [211–215]. However, many other measures of statistical similarity exist, including those that assess non-linear relations, mutual information, and other types of conditional dependencies between time series [16, 216, 217]. Important open questions in building network models are whether insight into neural function is best obtained by considering multiple measures of statistical similarity, and how to quantify their relative capacity to capture neural information [218].

While far from a panacea, information theory - the mathematical study of the coding and transmission of information - provides useful tools for statistical inference that could prove increasingly important for network neuroscience [219, 220]. Although commonly used statistical metrics probe shared information between two processes, the theory also provides expectations such as maximum entropy and other metrics to probe time-asymmetric transfer of information between two or more processes, such as transfer entropy [119, 221, 222]. In measurements of calcium imaging at the cellular level, transfer entropy can be used to distinguish between causal influences between neurons and non-causal correlations due to light scattering artifacts [223]. Similar efforts for larger-scale network models have used transfer entropy to demonstrate that diverse states of information routing can be induced on the same structural network model, simply by minor modulations of background y activity [224]. Important open questions include how to quantify non-pairwise causal interactions, and how to think about causality in dynamic networks characterized by higherorder, non-pairwise interactions occurring over multiple spatiotemporal scales [56].

From elementary descriptions to coarse-grained approximations

The third and final dimension is from elementary descriptions to coarse-grained approximations. Over the past decade, it has been argued constructively that the foundations of network science rely on accurately identifying well-defined, discrete, non-overlapping units that become nodes in the network, and the organic, irreducible relations that become edges in the network [128]. For some scientific questions, these units and their relations take on natural elementary forms. For other questions, the units and relations are coarse-grained. Consider the canonical physicist’s cow: an elementary description might begin with quarks, whereas the coarsegrained description might begin with a spherical mass. The former model is useful for questions related to quantum mechanics, and the latter is more useful for questions related to classical mechanics. In the context of network neuroscience, this distinction is important because models based on elementary descriptions seek to understand how relationships between structure and function emerge directly from those descriptions, whereas models based on coarse-grained approximations focus on emergent network properties that may be best understood without explicitly considering the system’s elementary building blocks.

Many common network models are based on the elemental units of the Neuron Doctrine: individual nerve cells and their synaptic connections [73]. Such models can be either data representations or first-principles theories and can either include extensive biophysical realism or explain functional phenomenology [80, 108, 118, 129, 130]. Network models at this scale can be used to ask questions about cellular mechanisms of growth and development or transitions from neural progenitor cells to neurons [131, 132]. Recent work has extended these approaches to even smaller scales, for example to investigate specific sections of a cell such as neurite outgrowth [133]. Ongoing efforts are also beginning to extend to the molecular scale to study the network architecture of chromatin folding within the cell nucleus, which changes as cells transition from pluripotent stem cells to neural progenitor cells and is altered in neurodevelopmental disorders [134].

In contrast, coarse-grained models are based on simplified descriptions of ensembles of smaller units and finer-scale processes. One example for such a simplification scheme, which is common in physics, is a continuum or mean-field theory that models the dynamics of a collection of different units as equivalent to the dynamics of an average unit [135]. This kind of coarse-graining is frequently used in simulations of molecular dynamics, cellular biology, and ecology [136–139]. In the context of the brain, it has been used to bridge spiking neurons to collective neural dynamics, to better understand synaptic plasticity, and to predict the effects of exogenous input [140–143]. Another example is neural mass models, which are explicit, coarse-grained approximations of neural ensemble dynamics [46]. Implicit coarse-graining also occurs in practically all studies of large-scale brain network models, in which each node’s properties are a coarse approximation of the properties of smaller units that are typically not directly accessible to measurement methodologies. A commonly encountered example is neuroimaging data, for which network-specific coarse-graining approaches are being developed to better understand and control how data are aggregated when forming network models [13, 144, 145].

Network models at the extremes of this dimension have both advantages and disadvantages. For example, elementary models are often most useful for understanding neural codes and network function at the cellular level. In contrast, coarse-grained approximations are often most useful for understanding population and ensemble codes and network function at the ensemble level and beyond. A current focus of interest is the development of network models that cross these scales, using data and theory to better understand how the structure and function at one scale can be used to make inferences about structure and function at another scale [6, 146, 147].

Density of study in this three-dimensional space

We consider the dimensions described above to be relatively independent, such that, for example, a data-driven model can be structurally or functionally realistic, or fine- or coarse-grained. These dimensions thus describe a three-dimensional space in which many different kinds of network models can be placed. It is interesting to consider whether there are particular parts of this volume that have been more or less well-studied. The answer is intertwined with the history of how the field of network neuroscience emerged, as well as with changes in the landscape of technology that have quickened the pace of data acquisition and broadened the extent of computational modeling. Network neuroscience largely began with observations of structural connectivity at the large- scale represented as graphs or networks devoid of any explicit dynamics [51, 65, 148]. This early focus has continued, with more extensive efforts in data representations than first-principles theories, more biophysical realism than functional phenomenology, and more coarse-grained approximations than elementary descriptions. Therefore, the least well-studied extreme in this cube represents first-principles theories of functional phenomenology at the elementary level of description.

Looking ahead, we emphasize two features of this space that are likely to promote new advances. The first is the increasing accessibility of the region of convergence at the center of our three-dimensional scheme. The growth of technology and data science has increased efforts that constrain or parameterize first-principles theories with real data representations [149], filling out the middle of the first dimension [97]. Efforts linking biophysical realism with functional phenomenology seek to understand structure-function relations in the brain facilitated by both its physical and informational nature, filling out the middle of the second dimension [49]. Computational methods and novel data-acquisition methods have also increased efforts to bridge elementary descriptions with coarse-grained approximations in explicit, multiscale models, filling out the middle of the third dimension. These integrative efforts, along with those that work across these dimensions, will help bridge levels of understanding of brain structure and function.

The second important feature of this space is the usefulness of its full volume, which comprises network models that seek to explain different parts, processes, or principles of the nervous system. In general, it is not necessary for any one model to provide the same insights as any other model. For example, a biophysical model of synaptic transmission in the dentate gyrus is not likely to provide direct insight into the functional phenomenology of the default-mode network. Similarly, a map of the whole structural connectome of the human at a resolution of 1-mm voxels is not likely to provide insight into the transmission of spontaneous or task-induced action potentials in auditory cortex. Therefore, in addition to integration at the center of this space we hope for continued exploration at its underdeveloped frontiers.

HOW CAN WE ASSESS THE VALIDITY AND EFFECTIVENESS OF MODELS IN NETWORK NEUROSCIENCE?

Assessing the validity of a particular network model typically involves standard statistical model-selection methods. These methods balance goodness-of-fit to the data with penalties for complexity to avoid overfitting and provide parsimonious and generalizable conclusions. However, it can be challenging to achieve this balance for network models because of their diversity of goals and uses. For example, a close fit to known anatomical connectivity patterns is likely to be a more valid approach for understanding principles that govern interactions between elementary, biophysically realistic components of the nervous system than for network models of abstract computations. Here we propose a classification system for validating network models based on different goals and domains of inquiry. This system is based on principles developed in the context of both statistical model selection and the evaluation of the efficacy of animal models for psychiatric disorders [150–153]. The categories, which are not necessarily mutually exclusive in terms of their relevance to assessing a particular network model, are: descriptive, explanatory, and predictive (see Fig. 3). Below we consider each in detail.

FIG. 3. Illustrations of different categories of model assessment.

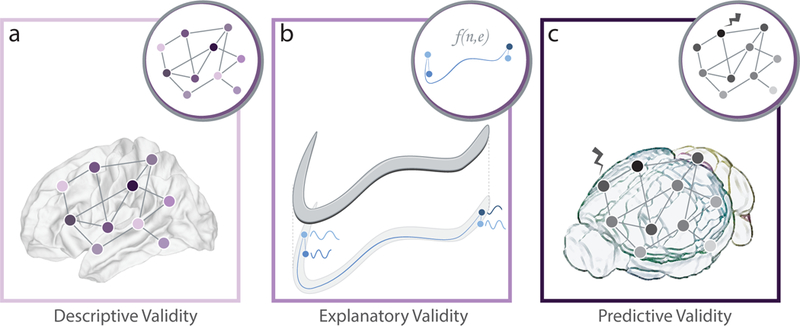
(a) Descriptive validity addresses the question of whether the model resembles in some key way(s) the system it is constructed to model. For network models, descriptive validity naturally aligns with questions about how well the specific patterns of nodes and edges (circular inset) matches the anatomical and/or functional data that it represents (main panel). (b) Explanatory validity focuses on a theoretical construct that is ultimately used to develop statistical tests and support conclusions drawn from the use of the model. A network model can be considered to have explanatory validity if its architecture can be justified in terms of brain data and if it can then be used to test for causal relationships to dynamics or behavior based on that architecture. Here we show a formal model of network node dynamics (circular inset) that can be used to test for causal relationships with dynamics in the true system (main panel). (c) Predictive validity occurs when there is an organism-model correlation in response to a perturbation, such as a drug, electrical or chemical stimulation, neurofeedback, or training. Here we show the model’s response to perturbation (circular inset) matching the organism’s response to perturbation (main panel).

Descriptive validity

The first category is descriptive and is related to the concept of “face validity” that is commonly discussed in the context of animal models. It addresses the question of whether the model resembles in some key way(s) the system it is constructed to model. In considering animal models, face validity is often assessed by comparing symptoms of, for example, an animal model of depression to those listed in the Diagnostic and Statistical Manual of Mental Disorders [154]. For network models in neuroscience, descriptive validity naturally aligns with questions about how well the structure of the model (i.e., the specific patterns of nodes and edges) matches the anatomical and/or functional data that it represents. This match can be assessed using standard model- selection procedures with an emphasis on the goodness- of-fit to the measured data, but it also can reflect choices about how to construct the model in light of potentially relevant neurobiological features. For example, network models in which nodes represent brain areas that obey cytoarchitectonic or functional boundaries have more descriptive validity than those in which nodes represent randomly chosen volumes of tissue [22]. Similarly, network models in which edges are assigned continuous weights representing the strengths of anatomical connections or functional relations have more descriptive validity than those in which edges are assigned binary weights [51, 155].

Establishing the descriptive validity of network models faces two major challenges. One is that the neural architecture and functional dynamics being modeled are highly complex, with nontrivial structure and function present across multiple spatial and temporal scales [13, 156]. Thus, identifying the appropriate level of complexity that should be modeled can be difficult, both in principle and in practice [157]. In principle, problems arise because there is almost always uncertainty about which spatial and temporal scales in the brain are relevant for a particular anatomical architecture, neuro-physiological process, cognitive task, or behavior [77]. In practice, problems arise because the available imaging, physiological, anatomical, and other data used to build the model typically provide particular spatial and temporal resolutions that are constrained primarily by the measurement methodology and not by any consideration of the scales that are most appropriate for the model [158]. One way to address this challenge is to improve the descriptive validity of node definitions, for example by detecting node boundaries using structural or functional connectivity or using clustering methods to agglomerate smaller regions into larger regions [159–161]. Another useful approach is to integrate information from different sets of measurements, including anatomical and functional data, micro- and macro-scale network mapping, and integration of neurotransmitter function and chemoarchitecture to functional magnetic resonance imaging (fMRI) [6, 122, 124, 146, 162–167].

The second major challenge for establishing the descriptive validity of network models is extensive individual variability. Individual variability exacerbates problems of underfitting and overfitting, because of uncertainty associated with whether idiosyncratic network features are relevant to a particular model or are just noise and should be ignored. In general, little is known about the principles that govern individual differences in neural connectivity patterns in organisms with central nervous systems. However, network architecture and function show differences across people that are associated with cognitive functions and symptom severity for certain diseases, and these differences may be modulated or constrained by the environment, socio-economic status, and genetics [75, 168–175]. Network dynamics also can show appreciable individual differences that are reproducible across iterative measurements and can be separated into state and trait components [176, 177]. Efforts to overcome the challenges posed by these kinds of individual differences should include schemes to test for both general principles that are robust to individual variability and specific markers of behaviorally meaningful between- subject differences that are robust to measurement noise. Ideally, future first-principles models could use these tests to construct a general form for population-level features, as well as variable parameters to account for individual variability.

Explanatory validity

The second category in our proposed classification system for validating network models is explanatory. This category is related to the concept of “construct validity” that is commonly discussed in the context of animal models. It focuses on a theoretical construct that is ultimately used to develop statistical tests and support conclusions drawn from the use of the model. Thus, for example, an animal model of depression is considered to have construct validity based on arguments about not just how it relates to what is known about depression in humans, but also how the model is used to probe causal questions about mechanisms, symptoms, and/or treatments that cannot be easily tested in humans. Likewise, a network model of the brain can be considered to have construct or explanatory validity if its architecture can be justified in terms of brain data and if it can then be used to test for causal relationships based on that architecture [77].

Explanatory validity thus requires an assessment of both a model’s architecture (i.e., a form of descriptive validity) and its ability to test for causal relationships. This dual assessment can be accomplished using statistical model-selection approaches, with goodness-of-fit metrics applied to both structural and functional data balanced by penalties for the complexity of particular instantiations of the model [178–181]. Model-selection approaches have played an important role in both graphical modeling and neuroimaging [182–184]. They also have been applied to model selection at several scales, ranging from the small scale of a network subgraph (e.g., dynamic causal modeling) to the large scale of a statistic or statistical distribution estimated from the entire network (e.g., the degree distribution or Rentian scaling [99, 185, 186]). Formal frameworks for building and evaluating such models include exponential random graph models, which create a class of graphs with fixed values for topological statistics, and generative network models, which create a class of graphs from a wiring rule [93, 149, 187, 188].

Model-selection procedures to maximize explanatory validity involve two particular challenges. One is that model complexity, often quantified in terms of the number of free parameters, may involve other degrees of freedom in network models that are harder to quantify and account for, particularly when considering both structure and function. That is, the effective dimensionality of a particular network model may be difficult to define. For example, many network features can have non-trivial dependencies, making the number of parameters in a model ill-defined [189]. These dependencies can occur from known mathematical relations and therefore remain true across all types of networks and be relatively easy to account for, or they can occur from unknown constraints on - or drivers of - network topology and therefore require different approaches across different network ensembles or classes [190–192]. The second challenge is that the complexity of a neural network model may be defined or constrained by the desire to maintain biological realism in the model’s architecture (descriptive validity) beyond that which is necessary for the model’s function. Under these conditions, it can be challenging to identify the statistically simplest explanation under those constraints. Efforts to meet this challenge include model-selection procedures that aim to identify a reduced structural subsystem or slow functional manifold that captures the system’s effective architecture and dynamics in the simplest way possible [193].

Predictive validity

The third category in our proposed classification system for validating network models is predictive. By comparison, an animal model has predictive validity if there is a human-animal correlation of therapeutic outcomes. That is, a treatment, such as a particular drug, should affect a condition in an animal in a manner that corresponds to - and thus is predictive of - how that treatment affects that condition in a human [152]. Likewise, a statistical model is predictive if there is an organism-model correlation in response to perturbation. That is, a perturbation to the network, such as the addition, removal, strengthening, or weakening of a node or edge, or the alteration of the function of that node or edge via drug, stimulation, neurofeedback, or training, should affect the network in a model or simulation in a manner that corresponds to, and thus is predictive of, how that perturbation affects the network in the organism. These models, like explanatory models, often combine both structural and functional features. Accordingly, procedures for assessing and selecting models with predictive validity face many of the same challenges as for explanatory validity, concerning both model complexity and constraints imposed by a desire also to provide descriptive validity.

Opportunities for predictive validity often occur later in a field’s lifetime than opportunities for descriptive validity, as each discipline moves from developing a language for the subject matter, developing tools and techniques relevant to the subject matter, and finally using the language, tools, and techniques to answer novel questions and test novel predictions [194]. Thus, building models with predictive validity is a relatively new endeavor in network neuroscience, although several prominent examples exist. For models of large-scale network control, exogenous activation of strong modal controllers, which move the system to distant states on the intrinsic energy landscape, was predicted to induce task switching. This theoretical prediction was supported by observations of strong modal controllers in human brain areas that activate during task switching [90]. For models of smaller-scale network control, a theoretical prediction about the control function of a node inside the network model was confirmed by ablation studies in C. elegans [92]. For models of complex, nonlinear, high-frequency dynamics, a theoretical prediction of synchronization patterns produced by seizure dynamics at the onset zone which propagated along human white matter network architecture matched observed seizure dynamics in patients with medically refractory epilepsy [195]. For models of network dynamics, an observation that network flexibility was an intermediate phenotype for schizophrenia motivated the hypothesis that it was causally driven by the brain’s state of excitatory/inhibitory balance, thought to underlie the disease. This hypothesis was tested and validated in a separate set of healthy subjects undergoing a pharmacological challenge with an NMDA-receptor inhibitor (Dextromethorphan) [166]. These kinds of predictive models will need to play a more prominent role in network neuroscience for the field to grow beyond its current boundaries and affect other basic and translational studies of the brain.

A complementary but distinct line of work capitalizes on emerging methods from machine learning with the goal of developing network models that can inform other learning algorithms. For example, in translational research it is often of considerable interest to distinguish between patients and controls, to foreshadow conversion from one clinical phenotype to another, to distinguish between one pathology and another pathology leading to the same abnormal behavioral phenotype, or to predict the outcome of electroconvulsive therapy in major depression or of resection surgery in temporal lobe epilepsy [169, 196–200]. In these cases, summary statistics of network models have been used as features in machine- learning algorithms that make predictions [201]. A key challenge hampering the field is that it is not always known a priori which network statistics should be used. One useful benchmark could be to assess directly the predictive validity of the network model itself. An important area for future growth will be to use such approaches to infer fundamental and generalizable models that accurately predict the response of the brain to a perturbation or pathology.

FUTURE OUTLOOK

In the face of the multiplicity of model and validity types, it is imperative that investigators clearly specify their study’s goal(s). Insights that can be drawn reasonably from one type of model can be quite different than insights that can be drawn reasonably from another type of model. What is truth for one may be speculation for another. Furthermore, it is well established, although not always acknowledged in practice, that the different goals that motivate model construction can affect model fitting and selection in dramatic ways. For example, a model that provides the best explanation for how certain factors causally influence measured network dynamics might not, because of overfitting, be the best model for generating predictions of how the network will respond in the future to those factors. Conversely, a particular model that does not provide as effective explanations as another might be better suited to prediction problems. It is also possible to construct models that span types and dimensions, thereby bridging inferences and overcoming the limitations of one model with the advantages of another (see Fig. 4 and Box 3).

FIG. 4. Bridging model types in network neuroscience.

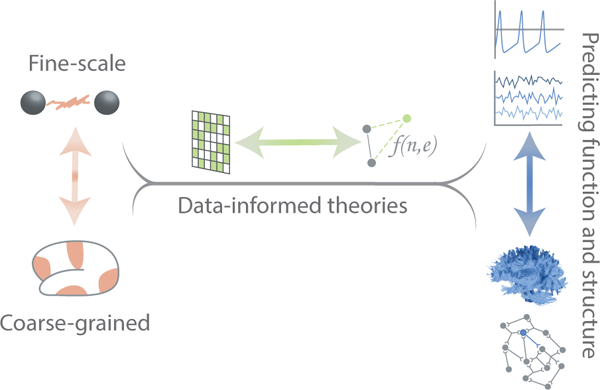
There are many ways to bridge model types. One natural path begins with fine-scale and coarse-grained information drawn from real systems (left) to create network models as data representations, which in turn are used to inform first-principles theories (middle). These theories then predict observed patterns of functional or structural connectivity (right).

BOX 3: BRIDGING MODEL TYPES.

The three model dimensions we considered (Fig. 2) are relatively independent of each other, but each encompasses principles that have been of great value to the field. It therefore is useful to consider ways to bridge two or more model types within and across these dimensions. The concept of bridging models raises the possibility of overcoming the limitations of one model type with the strengths of another. This benefit is particularly relevant when bridging models across two ends of a single dimension. For example, by informing first-principles theories with data, it is possible to overcome a common limitation of the former (impoverished empiricism) with a common strength of the latter (enriched empiricism) [96]. These bridges can also go in either direction: just as data can inform theories, so too can theories inform data-driven approaches [225]. A salient example of this latter approach is Latent Factor Analysis via Dynamical Systems (LFADS), a model of latent neural dynamics informed by an explicit dynamical-systems hypothesis regarding the generation of the observed neural spiking data [226].

The potential to link model types with one another, by either directed or undirected links, opens the possibility of building multiscale network models, where one type of model informs another type of model in a scale either above or below it. Conceptually, such multiscale models become meta-network models in which nodes represent models, and edges represent inter-model relations such as how one model predicts, informs, or is combined with another model (Fig. 4). For example, a network representation of fine-grained data (node) can inform (edge) a first-principles theory (node), as can a network representation of coarse-grained data (node). In turn, the first-principles theory (node) can predict (edge) patterns of functional connectivity (node) or patterns of structural connectivity (node). When one considers building such a meta-network model, the same challenges arise as with building a simple network: how to accurately identify well-defined, discrete, non-overlapping model units that become nodes in the network, and the organic, irreducible relations between models that become edges in the network [128]. Care must also be taken to consider the relative advantages and disadvantages of model complexity, biological realism, and interpretational simplicity.

A primary strength of network neuroscience is its natural descriptive validity. A key goal should be to use models that build on this strength and press forward towards better explanations and predictions [77]. However, care must be taken to assess the validity of these efforts using appropriate statistical approaches, which can differ for explanation versus prediction [150]. Models designed to explain are assessed according to goodness-of-fit, with various kinds of penalties assigned to model complexity. In general, these procedures minimize bias to obtain accurate representations, which tends to emphasize more complex models that can overfit the data. In contrast, models designed to predict are often assessed according to their ability to generalize, which can be tested by holding out subsets of data during fitting to then compare to predictions from the best-fitting model. These procedures typically minimize both bias and variance (overfitting to noise), which tends to emphasize simpler models. Finding the appropriate balance in these procedures is particularly challenging for network models because the models themselves, and the data to which they are applied, are often highly complex. Moreover, there is often a lot of uncertainty about how to match the complexity of the model to the complexity of the data in some reasonable and appropriate way. Thus, new tools must be developed to measure and compare the complexity of network models and to make principled decisions that balance the need for biological realism, which may demand complex physical network models, with the desire for computational simplicity.

CONCLUSION

Because of the recent explosion of work in the emerging field of network neuroscience, the current usage of the term “network model” is broad and multifaceted, encompassing multiple dimensions of scientific inquiry. Many practitioners are unaware of complementary work being done by others in distinct regions of the three-dimensional space that we define. The accompanying potential for myopia increases domain-specific usage and interpretation of terms. Because of this multiplicity of meanings, we suggest that practitioners provide explicit definitions corresponding to their particular usage when appropriate, so as to avoid confusion and facilitate interdisciplinary collaboration. While such care is critical in all areas of science, it is particularly worth raising in the collective awareness when a field is young and expanding. We suggest that concerted efforts to extend current frontiers in evaluating and assessing model types, as well as bridging model types, will be necessary in order to gain a fuller understanding of how networked brain structure and function give rise to our mental capacities.