Preliminary Results Comparing Thin Plate Splines with Finite Element Methods for Modeling Brain Deformation during Neurosurgery using Intraoperative Ultrasound

Abstract

Brain shift compensation attempts to model the deformation of the brain which occurs during the surgical removal of brain tumors to enable mapping of presurgical image data into patient coordinates during surgery and thus improve the accuracy and utility of neuro-navigation. We present preliminary results from clinical tumor resections that compare two methods for modeling brain deformation, a simple thin plate spline method that interpolates displacements and a more complex finite element method (FEM) that models physical and geometric constraints of the brain and its material properties. Both methods are driven by the same set of displacements at locations surrounding the tumor. These displacements were derived from sets of corresponding matched features that were automatically detected using the SIFT-Rank algorithm. The deformation accuracy was tested using a set of manually identified landmarks. The FEM method requires significantly more preprocessing than the spline method but both methods can be used to model deformations in the operating room in reasonable time frames. Our preliminary results indicate that the FEM deformation model significantly out-performs the spline-based approach for predicting the deformation of manual landmarks. While both methods compensate for brain shift, this work suggests that models that incorporate biophysics and geometric constraints may be more accurate.

PURPOSE

Neuro-navigation can be combined with image-guide therapy to provide surgeons with tools to plan and execute optimal surgical trajectories for brain tumor resection and other intracranial procedures (e.g., [2–5]). Magnetic resonance imaging (MRI), functional MRI (fMRI), diffusion tensor imaging (DTI) and other imaging modalities provide detailed non-invasive information about the location, extent and quantitative features of the tumor as well as the anatomy, functional cortex and white matter tracts surrounding tumors [6, 7]. Pre-surgical planning software (e.g., [8]) helps surgeons to plan and visualize the surgical approach; and navigation systems help register preoperative images to intraoperative patient coordinates so surgeons can view the locations of their surgical instruments relative to their surgical plan. Unfortunately, the utility of neuro-navigation is diminished after surgery begins due to brain shift which is caused by brain deformation (e.g., from changes in intracranial pressure, osmolarity, CSF levels, air pockets, head position, etc.), tissue retraction and tumor resection. Brain shift occurs as soon as the dura is opened, increases as surgery progresses and has been measured to be as large as 2–3cm at the brain cortex [9]. As illustrated in Figure 1, brain shift invalidates the assumption of most neuro-navigation systems that preoperative imaging can be mapped to patient coordinates using rigid registration, thus reducing their accuracy and ability to guide neurosurgeons to achieve maximal resections with minimal damage.

Figure 1.

A. Preoperative MRI showing a low grade glioma (dark region). B. iMRI after near-complete resection with significant brain shift. Brain shift significantly reduces the validity of neuronavigation from preoperative data. Brain shift can occur far from the surgical site (in blue). More clinically relevent, it can cause significant deformation and displacement near margins of the resection cavity (in red), precisely where surgeons could most benefit from accuracte image guidance.

Brain shift has been measured and modeled for more than 20 years (as reviewed in [10–12]). To mitigate brain shift, some centers augment preoperative image data with intraoperative imaging. Intraoperative MRI (iMRI), available in advanced neurosurgical centers, has been shown to help maximize the extent of resections [13, 14]. However, iMRI is expensive, requires specialized equipment and personnel and is disruptive to surgical workflow. Intraoperative ultrasound (iUS) has been used successfully for navigation (e.g. [15]). However, iUS can be hard for neurosurgeons to interpret, has a limited field of view, suffers from artifacts at acoustic boundaries and cannot distinguish some tumors from healthy brain tissue. In addition, iUS cannot provide the high-quality anatomical, structural (DTI) and functional (fMRI) imaging that can be acquired preoperatively.

An alternative approach is to use intraoperative data, such as iMRI [16–19], iUS [20–28] or measurements of the cortical surface derived from stereo imaging [29] or laser range scanning [30] to derive a model of brain shift and to use the model to map (or ‘deform’ or ‘non-rigidly register’) presurgical images to the brain-shifted brain. In previous work, we have shown that cortical surface data can be combined with the finite element method (FEM) to model brain shift and have validated the accuracy of this approach with clinical data [31]. We recently presented a method that automatically generates sets of matched feature points for pairs of 3D iUS images [32] and showed that the matched feature points could be used to model brain shift using thin plate spline deformation.

In this paper, we present preliminary results comparing the accuracy of these two approaches. More specifically, we automatically generate matched feature points from 3D iUS images taken at different times during surgery, use the matched feature points to model brain shift using both thin plate splines and FEM, and compare the accuracy of the resultant deformations using manually identified landmarks. The purpose of this work is to investigate the difference between two commonly used deformation methods: thin plate splines, which are relatively simplistic but are readily available, fast, and require no preprocessing; and FEM, which can incorporate physical and geometric constraints and heterogeneous material properties but are less readily available, slower and require significant pre-processing.

METHODS

Data collection

Prior to brain tumor resection, preoperative imaging was acquired as clinically indicated for diagnosis, surgical planning and neuro-navigation. Typical preoperative imaging includes T1 and T2-weighted MRI, fMRI and DTI. For this study preoperative T1-weighted MRI was also used to construct an initial brain model for FEM modeling. Intraoperative imaging, including iMRI and 3D iUS, was recorded under IRB protocol in Brigham and Women’s Hospital’s Advanced Multimodality Image Guided Operating (AMIGO) suite. The iMRI was acquired after significant tumor resection to characterize any residual tumor. iUS was acquired through the craniotomy using a 2D BK5000 cranial probe [33]. To generate 3D US images, a sequence of registered US images is acquired as the probe is swept over the cortical surface. 3D iUS is reconstructed from this sequence using the ultrasound module of Brainlab’s Cranial Navigation system [2]. Typically, iUS was recorded at three time points during surgery: after the craniotomy but before the dura was opened; immediately after the dura was opened; and after significant tumor resection (typically immediately before iMRI was acquired).

Matched feature extraction

For each pair of 3D iUS images, a set of matched features was automatically generated, where a matched feature consists of a pair of corresponding points in the two images (i.e., the point locations of a feature common to both images). The SIFT-Rank method [1] was used to detect and match feature points. Features detected by this method are typically dark or light regions with a roughly spherical geometry. Figure 2 shows some typical features that were automatically generated in 3D iUS image of a Grade III Astrocytoma. A detailed description of this approach and a validation of the quality and accuracy of the matched features in iUS are presented in [32].

Figure 2.

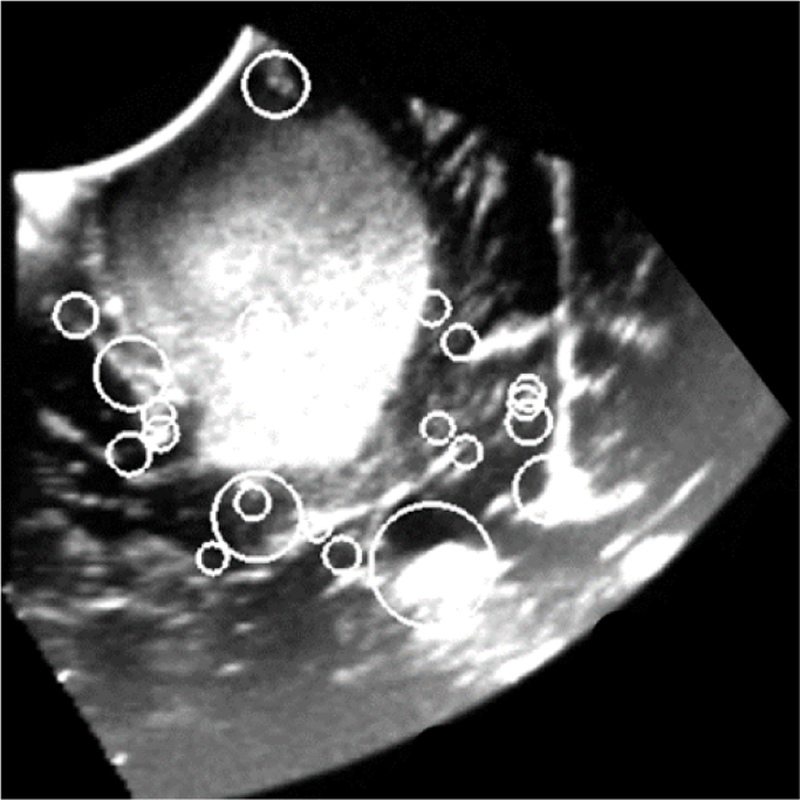
2D slice of a reconstructed 3D iUS image of a Grade III Astrocytoma acquired before opening the dura. Circles indicate the position and scale of image features that were automatically detected using 3D SIFT-Rank [1]. Each feature is characterized by a geo-metry and an appearance which are used to match features in paired images.

Thin plate spline deformation

A thin plate spline deformation algorithm available in the open source 3D Slicer medical imaging processing platform [34] was used to model brain shift for each pair of 3D iUS images. Specifically, the matched feature points were used as manual landmarks in the ThinPlate deformation method of 3D Slicer’s Landmark Registration Module. This module uses VTK’s vtkThinPlateSpline transform [35], which generates a mapping between sets of source and destination landmarks and a smooth interpolation function for points between landmarks to model the global deformation.

Finite element method (FEM)

Methods for constructing the FEM model, generating an atlas of FEM deformations and performing the optimization for modeling brain shift are detailed in [31]. The patient’s brain, tumor and dural septa (falx, tentorium) were segmented via a combination of manual and automatic methods and used to generate surface models of these neuroanatomical structures. A custom mesh generator was used to generate a patient-specific tetrahedral model of the brain. The Galerkin finite element method (FEM) with C^o local Lagrange polynomial basis/weight functions was used to resolve the partial differential equations associated with a biphasic soft-tissue biomechanical model the brain continuum [36, 37]. A systematic deployment of boundary conditions was applied to this brain model to generate an atlas of volumetric deformation estimates. To model brain shift from a set of measured displacements, deformation estimates from this atlas are combined to generate a deformation estimate that optimally reduces the measured displacements in a least-squared error sense. In this study, displacements between the matched feature points for each pair of iUS images were used to drive the optimization. While the modeling and analysis in this study was performed retrospectively, in practice the atlas of deformations can be generated prior to surgery so that only the final combinatorial optimization need be performed during surgery, facilitating brain shift compensation using high resolution FEM models in less than one minute.

Both the spline-based and FEM methods used displacements measured from iUS images in patient coordinates, but the FEM model was initialized from preoperative MRI. Thus, to ensure that both deformation methods were compared in the same coordinate space and to account for possible registration errors in the neuro-navigation system and/or brain shift that occurred before opening the dura, an initial rigid registration was performed to map the preoperative MRI image to the iUS image acquired before opening the dura. This rigid registration was determined using 3D Slicer’s Fiducial Registration module with manually identified landmarks from the preoperative MRI and the initial 3D iUS image.

Analysis

Two methods were used to measure the effectiveness of the two deformation methods. First, we note that a perfect deformation from iUS image A to iUS image B would map each point in A onto its corresponding point in B. In other words, P_A and P_B were the positions of a corresponding point in the two images and the deformation mapped P_A onto P_A’, then for a perfect deformation, P_A’ = P_B, for all corresponding points in A and B. To measure the quality of a deformation, we compare the average distance between corresponding points before and after deformation. Distances between corresponding points before deformation provide a measure of brain shift, while distances between corresponding points after deformation provide a measure of ‘residual error’. For a given amount of brain shift, smaller residual errors indicate a better deformation model (although, as described below, choice of the corresponding points can confound results).

To compare the thin plate spline method to the FEM method, we used two sets of corresponding points, the automatic features (which were also used to drive both deformation methods) and a set of manually identified landmarks. The manual landmarks are points distinguishable in 3D that were manually located by an expert in computer vision (SF) and validated by a clinical expert (AB). Typical manual landmarks were bifurcations of blood vessels or sulcal folds near the cortex or falx cerebri. Both localization and validation were performed in 3D cross-sectional views in 3D Slicer. Because the thin plate spline is an interpolating spline (rather than an approximating spline), the residual error for automatic features is very close to zero by design. Thus, it does not make sense to compare the residual error for automatic features in the two methods.

RESULTS

In this preliminary study, we analyzed two patient cases, both with small to moderate amounts of brain shift (up to an average of 3.25 ± 0.98 mm). In both cases, deformation models were created for two time intervals during surgery: deformation that occurred between performing the craniotomy and opening the dura (dural opening) and deformation that occurred between the craniotomy and at time point after significant resection. Table 1 summarizes the measure brain shift and residual error for each interval and each deformation method. In all cases, the residual error for manual landmarks was smaller with the FEM method than the thin plate spline method. As expected, residual errors of matched feature points were close to zero for the thin plate spline method and reasonable close to the residual errors of manual landmarks for the FEM method.

Table 1.

Average displacements between automatically matched feature points and manual landmarks without brain shift compensation and with either spline-based or FEM-based brain shift compensation. Results are reported for two time intervals during surgery: 1) for deformation that occurred between iUS images acquired immediately prior to and immediately after opening the dura (Dural opening) and 2) for deformation that occurred between iUS images acquired immediately prior to opening the dura and after significant tumor resection (Subtotal resection). In all cases, the FEM method provided better results for manual landmarks than the spline-based method. We note that because very small residuals for feature points are expected after applying the thin plate spline (since they were used to train the spline), feature point residuals for the spline-based and FEM method cannot be compared to each other in a meaningful way. They are included here for completeness.

	Without compensation		After thin-plane spline		After FEM
	Manual landmarks	Automatic features	Manual landmarks	Automatic features	Manual landmarks	Automatic features
Case 1
Dural opening	1.96 ± 1.22	1.34 ± 0.66	1.72 ± 0.75	3.5e−3 ± 2.8e−2	1.64 ± 0.86	0.99 ± 0.60
Subtotal resection	3.25 ± 0.99	2.60 ± 1.39	2.10 ± 1.20	6.4e−7 ± 2.3e−7	1.27 ± 0.62	1.33 ± 1.04
Case 2
Dural opening	0.77 ± 0.40	0.81 ± 0.63	0.84 ± 0.50	6.6e−7 ± 2.5e−7	0.82 ± 0.50	0.80 ± 0.64
Subtotal resection	2.33 ± 1.11	2.01 ± 0.16	1.54 ± 1.37	9.7e−7 ± 2.6e−7	1.46 ± 1.06	0.77 ± 0.25

The average initial brain shifts measured for the cases in this study were significantly smaller than brain shifts reported in the literature. There are a number of explanations for this discrepancy. First, most reported brain shift measurements are for cortical shifts; the results here are for sub-cortical shifts which are known to be significantly smaller [38]. Second, the initial rigid registration from preoperative MRI to the first iUS image performed for this study may have masked significant initial shift. Finally, modern surgical and anesthesiology practice has resulted in reduced craniotomy sizes and changes in the management of brain swelling and relaxation that may reduce brain shift. Future work will analyze a larger set of cases to further investigate these observations.

Both deformations were applied to the preoperative MRI to simulate brain shift compensation. Some of these results are shown in Figure 3 to illustrate an additional difference between using FEM and spline-based methods. Because the FEM approach models the entire brain and its boundary constraints, it provides a reasonable deformation of the entire brain. In contrast, spline-base methods are most accurate near points used to train them and their accuracy is not guaranteed for regions far from these points. For this application, when trained with iUS images, the spline-based approach is not accurate for parts of the brain not observed by the iUS. As seen in Figure 3, this can result in unrealistic deformations in the opposite hemisphere and on surfaces of the brain and skull. While these results are not unexpected and it can be argued that accuracy is only required near the tumor where the iUS is centered, care must be taken when presenting brain shift compensation to surgeons; The appearance of a badly deformed head could reduce surgeons’ confidence in the whole model even when brain shift compensation is accurate near the tumor.

Figure 3.

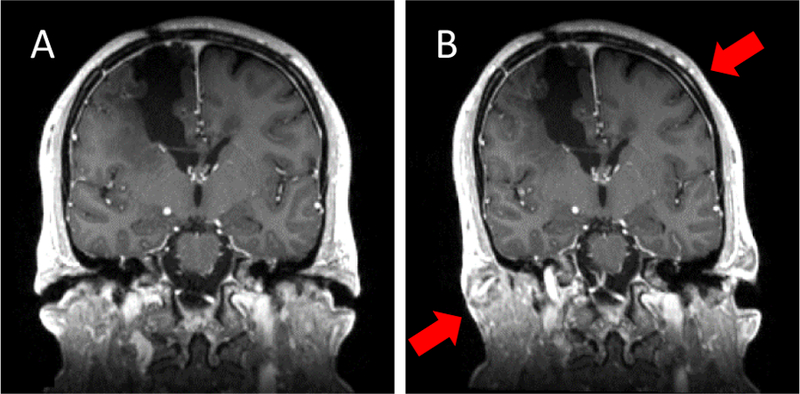
Coronal view before (A) and after (B) applying the thin plate spline for subtotal resection to the full head of case 2. Although Table 1 indicates that the thin plate spline deformation is accurate for manually identified landmarks near the tumor, this figure shows unrealistic deformation when it is applied to the full head (e.g., stretching and shearing of the skull as indicated by the red arrows in B). In contrast, boundary constraints applied in the FEM approach ensure realistic deformation throughout the brain.

New and breakthrough work presented

This work presents preliminary data that uses sparse features automatically derived from iUS to drive FEM-based brain shift compensation. To our knowledge, this is the first time this approach has been reported. We provide the first results that compare the accuracy of a simple spline-based deformation model and a more sophisticated FEM deformation model when both methods were driven by the same set of displacements. A more in-depth comparison of these methods will allow us to bracket the accuracy that is possible when modeling brain shift and provide insight into the relative importance of focusing on improving modeling accuracy vs. reducing processing time and complexity when the objective is to bring brain shift compensation into clinical practice.

CONCLUSIONS

Brain shift continues to be a limiting factor in neuro-navigation for tumor resection. Although there has been more than 20 years of research in measuring modeling and compensating for brain shift, very little of this work has advanced to clinical use and there are currently no commercial systems available that provide non-rigid brain shift compensation. This paper provides preliminary results that focus on one aspect of brain shift compensation, the difference between using a simple spline method and a more complex FEM method to model brain deformation. Both methods were driven by the same set of displacements derived from automatically detected matched feature points in 3D iUS images. Our preliminary results show that while FEM requires significantly more preprocessing and computation, its deformation model is more accurate than a thin plate spline method at manually identified landmarks. In addition, FEM produces more realistic deformation at points far away from the matched feature points. Our next steps are to look at a larger sampling of cases, including cases with larger sub-cortical brain shift, to compare model behavior as a function of the number, accuracy and location of the driving matched feature points, and to consider additional deformation methods.