Optimizing Energy Expenditure Detection in Human Metabolic Chambers

Abstract

Whole-room indirect calorimeters are capable of measuring human metabolic rate in conditions representative of quasi-free-living state through measurement of oxygen consumption (VO₂) and carbon dioxide production (VCO₂). However, the relatively large room size required for patient comfort creates low signal-to-noise ratio for the VO₂ and VCO₂ signals. We proposed a wavelet-based approach to efficiently remove noise while retaining important dynamic changes in the VO₂ and VCO₂. We used correlated noise modeled from gas-infusion experiments superimposed on theoretical VO₂ sequences to test the accuracy of a wavelet based processing method. The wavelet filtering is demonstrated to improve the accuracy and sensitivity of minute-to-minute changes in VO₂, while maintaining stability during steady-state periods. The wavelet method is shown to have a lower mean absolute error and reduced total error when compared to standard methods of processing calorimeter signals.

I. Introduction

INDIRECT calorimetry is the current gold standard for assessing minute-to-minute changes in human metabolic rate. This process relies on the measurement of a subject’s oxygen consumption (VO₂) and carbon dioxide production (VCO₂) to compute his/her energy expenditure (EE) from the standard equation [1;12]: EE (kcal/min) = 3.941VO₂ + 1.106VCO₂. Whole-room indirect calorimeters (metabolic chambers) measure human EE by continually measuring the changing composition of the air contained in a respiratory chamber with limited, tightly controlled air inflow and outflow. These devices are useful for measuring a wide range of metabolic states and the large room size increases patient comfort, permitting longer studies (up to several days).

However, the accurate measurement of “near free-living” human metabolism using the metabolic chamber is not without its challenges. For instance, the size of a typical metabolic chamber (15,000-30,000 L) is large when compared to the amount of O₂ consumed by an average individual at rest (0.2-0.4 L/min). Electromagnetic noise from other devices also corrupts the electronic output of the gas analyzers used to measure room O₂ and CO₂ composition. For these reasons, the response time and accuracy of the whole-room system is reduced, making it difficult to study rapid changes in EE caused by activity, pharmacology, or diet [11]. Consequently, it is necessary to implement some form of software-based algorithm to suppress noise associated with EE measurement using whole-room calorimeters.

Precise calculation of the rate of O₂ depletion and CO₂ accumulation in the room air composition has the most substantial influence on the accuracy of EE measurement in whole-room calorimetery [11]. This requires estimating the derivative of the measured room air concentrations of O₂ and CO₂ over time. What in theory appears to be a simple calculation, in practice has two major obstacles: (1) The rate of gas accumulation/depletion changes each time the subject changes metabolic state (e.g. from sitting to standing and then walking) and (2) The derivative calculation is made much more difficult when measurement of the O₂ and CO₂ concentration is corrupted by noise.

To overcome these challenges, we propose a wavelet-based approach to efficiently remove noise while retaining important dynamic changes in VO₂ and VCO₂. We have used correlated (colored) noise modeled from real gas-infusion experiments in an indirect calorimeter superimposed on theoretical VO₂ sequences with both dynamic and steady-state periods to test the accuracy of a wavelet based processing method. The wavelet filtering is demonstrated to improve the accuracy and sensitivity of minute-to-minute changes in VO₂, while maintaining stability during steady-state periods. The wavelet method is shown to have a lower mean absolute error and reduced total error when compared to standard methods of processing calorimeter VO₂ signals.

II. Experimental Procedure

A. Calorimeter Design

The experimental portion of this project was carried out in the three newly-constructed metabolic chambers housed in the National Institutes of Health (NIH) Metabolic Clinical Research Unit in Bethesda, MD. Each chamber consists of an 11.5’ × 11’ × 8’ air-tight room enclosed with aluminum faced doors surround by an isolated U-shaped corridor (buffer region) that serves as fresh air plenum. Air is actively pulled out of the chamber from equidistant points around the room at a constant flow rate (~60 LPM) maintained by a voltage-controlled blower (Ametek, Windjammer). The air drawn from the chamber is then passively replaced by fresh air from the positive pressure buffer region which enters through a small 2 inch opening, thus creating an open-circuit system. The chamber is otherwise sealed and isolated from the outer environment. The precise outflow rate is measured by a mass flowmeter (Teledyne-Hastings, Inc) and digitally recorded for further calculations. A small quantity of air (1 LPM) is drawn separately from both the effluent chamber air stream and the buffer region air supply. Both samples are continuously passed through a condenser (ABB SCC-C and F series cooler and feed unit) which cools the air to 1°C and eliminates water vapor moisture before pumping them at a constant pressure to the differential CO₂ (ABB AO2000 near-infrared CO₂ analyzer, range 0-1 %) and O₂ (Siemens Oxymat 6E Paramagnetic O₂ analyzer, range 20-21%) analyzers, which measure the respective gas concentrations to within 0.001%. Each chamber is equipped with a separate air-handling unit to ensure a stable internal temperature (±0.2°C), relative humidity (30-50%), and thorough mixing of the air. A GE Optica unit was responsible for measuring the temperature (0.1°C), humidity (0.1%), and barometric pressure (0.1mmHg) inside the chamber once each minute.

B. Calculation of VO₂

Oxygen consumption (VO₂) and carbon dioxide production (VCO₂) in a metabolic chamber can be modeled using first order differential equations, the derivations of which are shown in detail elsewhere [7]. Since the measurement of O₂ has a higher noise level than CO₂ [11] most likely due to differences in the measurement mode of the two analyzers (paramagnetic versus near-infrared), we have elected to present data related to VO₂ only, but the process of computing the VCO₂ is identical. The VO₂ was computed using the following equation:

$$V{O}_2=-\left[F\left(f_{O_2}^o-f_{O_2}^i{H}^{-1}\right)+V_c\frac{d}{dt}(f_{O_2}^o)\right]$$ (1)

$$H=\frac{1-f_{O_2}^i-f_{C{O}_2}^i}{1-f_{O_2}^o-f_{C{O}_2}^o}$$ (2)

where F is the outflow rate and V_c is the air volume of the chamber, both corrected for standard temperature, pressure, and dry (STPD) conditions. H is commonly referred to as the “Haldane correction”. The concentrations of O₂ and CO₂ in the inlet air ($f_{O_2}^i$ and $f_{C{O}_2}^i$) are assumed to be constant at 20.930% and 0.03%. The concentration of O₂ and CO₂ in the outlet air ($f_{O_2}^o$ and $f_{C{O}_2}^o$) are measured by the respective analyzer.

C. Simulated Signals

Gas infusion tests were performed to identify the steady-state noise characteristics of the metabolic chamber. Dried, compressed gas from one bottle of N₂ (UHP Grade, 99.99% pure, Roberts Oxygen Inc) and one bottle of CO₂ (SFC Grade, 99.9% pure, Matheson Tri-Gas Inc) was simultaneously infused into the three metabolic chambers at a constant, controlled rate for three hours. The rate of infusion of each gas into each chamber was controlled using separate thermal mass flow controllers (MKS Instruments, 1179a) connected to a mass flow programmer (MKS Instruments, 647C). During the infusion, the voltage output of the O₂ and CO₂ analyzers was digitized (National Instruments, NI9215) and recorded at 120 samples/sec using a Labview program, yielding $f_{O_2}^o$ and $f_{C{O}_2}^o$ signals. The $f_{O_2}^o$ and $f_{C{O}_2}^o$ were resampled posthoc at 1 sample/sec. This process was repeated in the three chambers on five consecutive days, with constant flow rates ranging from 0.149 - 0.265 LPM for CO₂ and 0.74 - 1.32 LPM for N₂.

Once all gas infusion data was collected, the $f_{O_2}^o$ and $f_{C{O}_2}^o$ collected from each chamber during each day (N = 15 total) were detrended by subtracting off the best-fit quadratic polynomial. This resulted in an error sequence. Since the length of the error sequence was generally too short for an appropriate simulation (3 hours), an autoregressive (AR) model was created using the Burg method [10]. The order of the model was determined using the Akaike’s Final Prediction Error [10]. The model coefficients were then used to filter randomly generated white noise to yield a sequence of colored noise (n) used during the simulation. The variance of the simulated colored noise sequence was set to the variance of the error sequence to provide a realistic signal-to-noise ratio.

To generate an appropriate set of test data, separate theoretical sequences for oxygen consumption and CO₂ production ($V{O}_2^T$ and $VC{O}_2^T$) were created for each of the 15 sequences. Each $V{O}_2^T$ and $VC{O}_2^T$ sequence was approximately 24 hours long and incorporated rates that corresponded to various metabolic states, including rest, exercise, and post-meal response. The sequences also contained 1 and 2 minute impulse increases in VO₂ and VCO₂, to test the sensitivity of each method. The theoretical O₂ concentration sequence, $f_{O_2}^T$, was then back computed from the ideal $V{O}_2^T$ and $VC{O}_2^T$ sequences by inverting Eq. (1) and letting $d\left(f_{O_2}^T\right)∕dt=f_{O_2}^T\left[k\right]-f_{O_2}^T\left[k-1\right]$.

$$\begin{gathered} f_{O_2}^T[k]=\frac{1}{(V_C+F\Delta t)}\left[f_{O_2}^i\Delta t(F+V{O}_2-VC{O}_2)- \\ V{O}_2\Delta t+V_C{f}_{O_2}^T[k-1]\right] \end{gathered}$$ (3)

In Eq. (3), Δt is the time between steps k-1 and k, in minutes. The noise sequences are then added to the theoretical $f_{O_2}^T$ sequences and the resultant noisy simulated signals, $f_{O_2}^n$, are used to test the following processing algorithms.

$$f_{O_2}^n=f_{O_2}^T+n$$ (4)

D. Standard Processing Methods

Several methods have been implemented to compute the rate of change in the O₂ concentration, $d\left(f_{O_2}^o\right)∕dt$, during noisy measurement conditions. The two most widely used are the Henning algorithm [3; 8] and the central difference method [7; 11].

The Henning algorithm finds the piecewise fit of two exponential functions in each 30 minute sliding window of $f_{O_2}^n$ data which minimize the squared error. The fits take on the form:

$$\begin{gathered} {\widehat{f}}_{O_2}^o={\phantom{\mid }\left[A_1+B_1\text{exp}\left(-t\frac{F}{V_c}\right)\right]\mid }_{t=0\to bpt}+ \\ {\phantom{\mid }\left[A_2+B_2\text{exp}\left(-t\frac{F}{V_c}\right)\right]\mid }_{bpt+1\to 29} \end{gathered}$$ (5)

where bpt is the breakpoint between the first and second exponential fit. The derivative of the fits can then be used to compute the VO₂.

The central difference method (CDM) is a discrete time derivative that follows the form presented by Sun, et. al. [11].

$$\frac{d\left(f_{O_2}^n\right)}{dt}[i]=\frac{1}{L}\left[\sum _{k=l}^L{f}_{O_2}^n\left[i+k\right]-\sum _{k=l}^L{f}_{O_2}^n\left[i-k\right]\right].$$ (6)

In this case, a 3 minute central difference was used; meaning the $f_{O_2}^n$ value of minute 1 was subtracted from the $f_{O_2}^n$ of minute 3, yielding $d\left(f_{O_2}^n\right)∕dt$ of minute 2.

E. Wavelet Correction of Central Difference Method

The main obstacle in calculating VO₂ during indirect calorimetry is the low signal-to-noise ratios in the gas concentrations, particularly for O₂, which can be exacerbated during calculation of their derivative over time (see central difference method in Fig. 1). To algorithmically reduce the amount of system (colored) noise corrupting $d\left(f_{O_2}^n\right)∕dt$ we chose to use a mathematical technique known as wavelet de-noising [2;4;5]. In wavelet de-noising, the noisy derivative sequence is mathematically decomposed into several frequency sub-bands using a series of filters whose structures are dependent on the choice of an initial “Mother Wavelet”. A unique, pre-determined mathematical threshold is applied to each frequency sub-band in order to suppress the noise (underneath the threshold) and retain important details (above the threshold) specific to each frequency range. It is important to note that the thresholds for each frequency range are not fixed, but rather they are flexible and based on the statistical characterization of the system noise. The derivative sequence can then be reconstructed with the thresholded sub-band information. The advantage of the wavelet de-noising technique is that unwanted noise is suppressed while important information is retained with limited smoothing of detail [6]. This quality is essential to detect dynamic changes in VO₂ while reducing system noise.

Fig. 1.

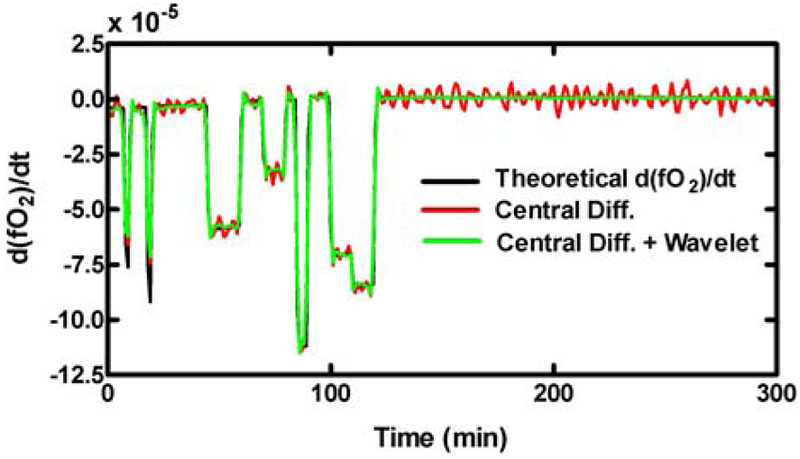
The derivative of a simulated room O₂ concentration, d(fO₂)/dt, corrupted by colored noise. The Central Difference method of calculating the d(fO₂)/dt (red line) captures sharp changes, but contains significant noise during the steady-state period (>150 min). Applying the wavelet transform to the central difference (green line) reduces the noise while retaining sharp features.

For the problem presented here, we applied the wavelet de-noising technique to the derivative calculated using the central difference method (Fig. 1). A stationary wavelet transform [9] with a Haar Wavelet [5] was used to decompose the $d\left(f_{O_2}^n\right)∕dt$ into the three frequency subbands. The universal threshold rule for colored noise [4] was used (Eq. 7).

$$T_j={\sigma }_j\sqrt{2{\log }_e(N)}$$ (7)

Here N is the number of discrete samples in the signal being decomposed. The term σ_j is a robust estimate of the noise-level in each wavelet frequency sub-band (j), which is computed as the median absolute deviation from the mean divided by 0.6745 [4].

F. Analysis of Performance

All three methods were used to compute the VO₂ in 15 of the noisy different $f_{O_2}^n$ signals. The resultant VO₂ from each method was compared to the respective theoretical $V{O}_2^T$ sequence. The mean absolute error (MAE) was used to quantify minute-to-minute errors in the VO₂ calculations and total daily error was used to assess the long term performance of each method. Total daily error was defined as the sum of all the minute-to-minute differences between the theoretical $V{O}_2^T$ sequence and the calculated VO₂ sequence.

III. Results

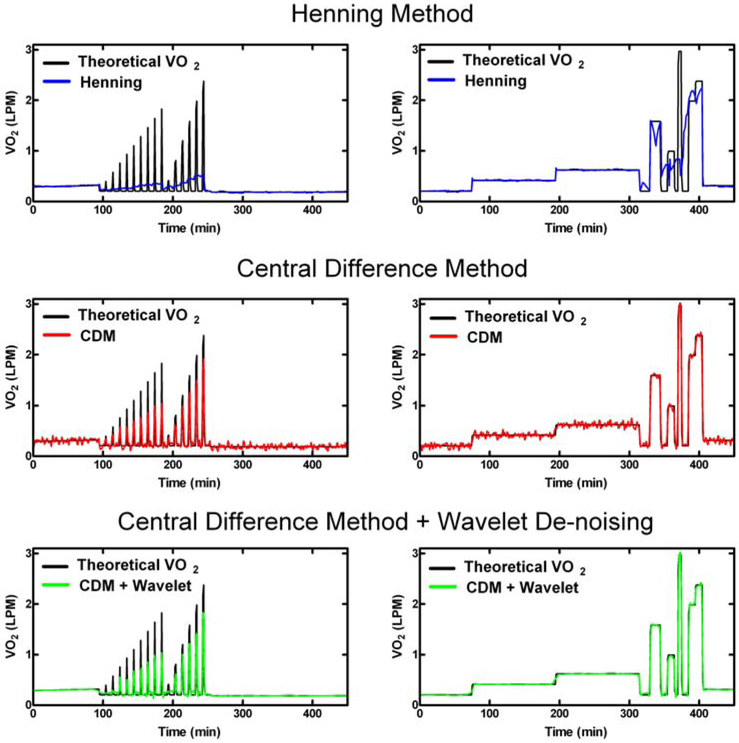
Representative results from the three VO₂ processing methods are demonstrated in Fig. 2. The Henning method (Fig. 2, top row) appears to follow the theoretical VO₂ during steady-state periods >30 minutes. However, during short impulses of 1 to 2 minutes (left column), and longer pulses of 10 – 30 minutes (right column) the Henning method oversmoothes the data, and thus yields inaccurate results on a minute-to-minute basis. In contrast, the VO₂ computed using the Central Difference Method (CDM, Fig. 2, middle row) captures short term changes in the theoretical VO₂, but is noisy during the steady-state periods >30 minutes. When the wavelet transform is applied to the central difference (Fig. 2, bottom row), the detailed shortterm changes are retained, but the steady-state noise is smoothed, yielding a computed VO₂ which is closer to the theoretical VO₂.

Fig. 2.

Methods of calculating VO₂ from noisy fO₂ data. The Henning Method (blue line, top row), Central Difference Method (CDM, red line, middle row), and Central Difference Method with Wavelet De-noising (green line, bottom row) were tested with various theoretical VO₂ sequences, such as short (1 and 2 minute) pulses (left column) and longer (10-30 minute) pulses (right column).

The quantitative results from the 24-hour simulation experiments (N=15) is displayed in Table 1. The mean absolute error for the wavelet method of computing VO₂ (0.021 ± 0.006 LPM) was significantly lower (p<0.001) than both the Henning VO₂ (0.066 ± 0.005 LPM) and the CDM VO₂ (0.058 ± 0.015 LPM). This suggests that the wavelet denoising improved the minute-to-minute calculation of VO₂. The total daily error was highest for the Henning Method (3.605 ± 1.850 L/day, p<0.001 compared to the other two methods). The Wavelet method increased the total daily error from the CDM, but the increase was not significant (0.061 ± 0.244 vs. 0.075 ± 0.144 L/day, p=0.85).

TABLE I.

24-Hour Simulation Results (N=15)

Method	MAE in VO2 (LPM)	Total Error in VO2 (L/day)
Henning	0.066 ± 0.005	3.605 ± 1.8502
	(0.057, 0.075)	(−0.415, 6.112)
CDM	0.058 ± 0.015	0.061 ± 0.244
	(0.037, 0.082)	(−0.314, 0.588)
CDM +	0.021 ± 0.0061	0.075 ± 0.144
Wavelet	(0.010, 0.029)	(−0.187, 0.379)

Values reported in Mean ± SD (Min, Max)

¹Significantly lower than both Central Difference and Henning

²Significantly larger than both Wavelet and Central Difference Methods

IV. Conclusions

We investigated the performance of three processing methods on simulated 24-hour VO₂ signals with a wide range of dynamic and steady-state metabolic activities corrupted by additive, correlated noise modeled from gas infusion experiments. The Henning Method, which determines the two best fit exponential equations to each 30 minute sliding window of $f_{O_2}^n$ data, appeared to work well on steady-state (>30 min) VO₂ periods (Fig. 2), which were incorporated to simulate changes to basal energy expenditure, exercise bouts longer than 30 minutes, and post-meal responses. However, the minute-to-minute performance of the Henning Method during durations of 10 – 30 min. (Fig. 2, top row, right col.), meant to simulate physical activity of daily living, and short impulses (1 – 2 min., Fig. 2, top row, left col.) was poor. Overall, this method had the largest MAE and under-predicted the daily VO₂ by an average of 3.6 L/day. On the other hand, the Central Difference Method (CDM) was able to identify very sharp changes in VO₂ over time, but did not demonstrate stability during steady-state periods (Fig. 2, middle row). When Wavelet De-noising was applied to the Central Difference Method, the wavelet processing appeared to balance features of the other two methods, by demonstrating similar steady-state stability and retaining the detail during both the long and short pulse sequences (Fig 2, bottom row). The combination of CDM and wavelet-de-noising demonstrated an MAE which was nearly 1/3 of both the other two methods without a significant increase in the total daily error.

In conclusion, wavelet-based noise removal appears to improve the accuracy of calculated VO₂ values during simulation. Further testing is required to optimize the process for real-time calculations.